-
Experimental results on the composition and interaction of matter at high density remain inconclusive. Therefore, understanding of the properties of dense matter is largely dependent on various theoretical models. Theoretically, hadronic matter may undergo phase transition to quark matter at high density or at high temperature. This hadron-quark transition density largely depends on the various theoretical models and the interactions considered. In the very low temperature and high baryon density domain of a quantum chromodynamics (QCD) phase diagram, the first-principle predictions via lattice QCD (LQCD) calculations are missing due to the infamous sign problem [1]. However, the high temperature and low/vanishing baryon density domain of the QCD phase diagram has been well studied for more than three decades [2, 3]. Reference [4] for the latest status: They concluded a cross-over type phase transition, which was alternatively realized from estimations of thermodynamic quantities at low and high temperature ranges considering the hadron resonance gas (HRG) model [5] and finite temperature perturbative QCD (pQCD) calculations [6, 7], respectively. Similar kind of mapping in the low/vanishing temperature and high baryon density domain may be possible [8] by fusing ultra-high density (approximately 10 times larger than the hadronic saturation density) pQCD calculations [9−11] and low density hadronic model calculations. In this context, the present work attempts to compare the estimations of transport coefficients, obtained from the standard massless outcome for the quark phase [12] and the hadronic phase using two relativistic mean field (RMF) models, i.e., the effective chiral model [13−21] and the RMF model [22−25]. At high density, the formation of heavier and strange baryons like the hyperons is theoretically possible. However, for simplicity as well as due to the uncertainty in the hyperon couplings, we considered only the nucleons in the hadronic phase. Both the hadronic models adopted in this work have been explored thoroughly to construct the equation of state (EoS) of dense matter and successfully determine the structural properties of neutron stars (NSs) or hybrid stars (HSs) regarding recent constraints from various astrophysical observations [13−17, 24, 25]. For the quark phase, we considered the massless two flavor quark matter with u and d quarks. Similar to the hadronic phase, we did not consider the strange degree of freedom (the s quark) in the quark phase. The present work aimed to compare the estimations of the transport coefficients of both hadronic and quark matter in the high baryon density and low/vanishing temperature domain of the QCD phase diagram. The motivation for this investigation comes from the equivalent pattern of LQCD thermodynamics [3, 4] and normalized transport coefficients [26] in the high temperature and low/vanishing baryon density domain of the QCD phase diagram. From analyzing the temperature (T) profiles of thermodynamical quantities including pressure P, energy density
$ \epsilon $ , entropy density s, and transport coefficients such as the shear viscosity η and electrical conductivity σ for massless quark matter, the following proportional relations can be determined:$P=\dfrac{1}{3}\epsilon=\dfrac{1}{4}TS\propto T^4$ and$ \eta\propto \tau T^4 $ ,$ \sigma\propto\tau T^2 $ , where τ is relaxation time of massless quark matter. Accordingly, their normalized values$ P/T^4 $ ,$ \epsilon/T^4 $ ,$ s/T^3 $ ,$ \eta/(\tau T^4) $ , and$ \sigma/(\tau T^2) $ will appear as horizontal lines against the T-axis and they can be marked as their upper or massless or the Stefan-Boltzmann (SB) limits. At very high T, these limiting values can be realized. Then, from high to low T, the values of thermodynamical quantities and transport coefficients will decrease and their maximum decrement will occur around the quark-hadron transition temperature [26]. Thus, we were interested to determine similar kind of graphs along the baryon density axis.Literature presents a long list of works [27−46] that have concentrated on the microscopic calculation of transport coefficients of the dense hadronic matter system. Refs. [27−30] demonstrate the long history of research regarding microscopic calculations of transport coefficients of dense hadronic matter, which continues today as reflected in [39−46]. For calculation of the transport coefficients of neutron star matter at high density, the electromagnetic interaction is included, whose timescale is far away from the QCD timescale. Many of the corresponding works [27−46] focused on beta stable neutron star matter and thus considered the contribution of electrons and muons apart from nucleons [36, 47]. However, in the present work, we focused only on hadronic matter contribution and calculated the transport properties of dense hadronic matter. Moreover, the transport coefficients were estimated within the QCD timescale (fm), as only the strong interaction related to dense hadronic and massless quark matter were considered separately. The QCD timescale was considered for comparing the hadronic and quark phase patterns in terms of momentum and charge transportation due to QCD interactions. Regarding only the hadronic matter contribution in works [39−46], then the main factors for calculating the transport coefficients of hadronic matter are the effective masses of the nucleons and the quasiparticle relaxation time. Both quantities can have medium modification, which can vary in different models of many-body approach [39]. Owing to this model-dependent estimation scope, we attempted to estimate transport coefficients including the shear viscosity and electrical conductivity of dense hadronic matter using two different hadronic models. Although an alternative model estimation is provided only, we followed a unique presentation of the transport coefficients along the density axis, which is generally adopted in the scenario of heavy-ion collisions [26], where the normalized transport coefficients were studied with respect to temperature to understand the nearly perfect fluid nature of hadronic matter.
This article is organized as follows. Next in section II, we summarize the two different models for the hadronic phase and the MIT Bag model for the massless quark phase. Then, in section III, the relaxation time approximation for calculating the transport coefficients is briefly addressed. After obtaining the final expressions for the transport coefficients and the effective kinematic information for the hadronic and the quark phases in the formation part, we present their variations relative to density in section IV along with a detailed discussion. Finally, in section V, we summarize our findings.
-
In this section, we briefly address the two hadronic calculation models and the standard massless or zero-mass quark matter (z-MQM) calculations. We adopted two different hadronic models, as detailed in the next two subsections. Subsequently, we discuss the z-MQM calculation for the quark phase.
-
Considering only the nucleons as the baryonic degrees of freedom, the Lagrangian density for the effective chiral model [19−21] is given by:
$ \begin{aligned}[b] {\cal{L}} =& \overline{\psi} \Biggl[ \left({\rm i} \gamma_{\mu} \partial^{\mu} - g_{\omega}\; \gamma_{\mu} \omega^{\mu} -\frac{1}{2} g_{\rho}\; \overrightarrow{\rho_{\mu}} \cdot \overrightarrow{\tau} \gamma^{\mu} \right)\\&-g_{\sigma} \left(\sigma + {\rm i} \gamma_5 \overrightarrow{\tau} \cdot \overrightarrow{\pi} \right) \Biggr] \psi + \frac{1}{2} \left(\partial_{\mu} \overrightarrow{\pi} \cdot \partial^{\mu} \overrightarrow{\pi} + \partial_{\mu} \sigma \; \partial^{\mu} \sigma \right)\\& -{\frac{\lambda}{4}} \left(\chi^2-\chi_0^2\right)^2 - \frac{\lambda B}{6} (\chi^2-\chi_0^2)^3 - \frac{\lambda C}{8}(\chi^2-\chi_0^2)^4 \\& - \frac{1}{4}F_{\mu\nu}F^{\mu\nu} +\frac{1}{2} {g_{\omega}}^2\; \chi^2\; \omega_\mu \omega^\mu - \frac{1}{4}\; \overrightarrow{R_{\mu\nu}} \cdot \overrightarrow{R^{\mu\nu}}+\frac{1}{2}\; m_\rho^2 \; \overrightarrow{\rho_\mu} \cdot \overrightarrow{\rho^\mu}\; , \end{aligned} $

(1) where ψ is the nucleon isospin doublet. The nucleons interact with each other via the scalar σ meson, the vector ω meson (783 MeV), and the isovector ρ meson (770 MeV) with corresponding coupling strengths
$ g_{\sigma} $ ,$ g_{\omega} $ , and$ g_{\rho} $ , respectively. As mean field treatment was considered, the pions do not contribute. The model is based on chiral symmetry with the σ and the pseudo-scalar π mesons as chiral partners and$ \chi^2 = (\pi^2 + \sigma^2 ) $ . The σ field attains a vacuum expectation value (VEV)$ \sigma_0=x_0 $ with the spontaneous breaking of the chiral symmetry at ground state [48]. The masses of the nucleons (m) and the scalar and vector mesons can be expressed in terms of$ \chi_0 $ as:$ m = g_{\sigma} \chi_0,\; \; m_{\sigma} = \sqrt{2\lambda}\; \chi_0,\; \; m_{\omega} = g_{\omega} \chi_0\; , $

(2) where
$ \lambda=({m_\sigma}^2 -{m_\pi}^2)/(2{f_\pi}^2) $ is derived from chiral dynamics;$ f_\pi $ is the pion decay constant, relative to the VEV of σ field as$ <\sigma>=\sigma_0\; =f_\pi $ [19, 21]. Because in mean field approximation,$ <\pi> = 0 $ and the pion mass becomes$ m_{\pi} = 0 $ , the explicit contributions of the pions do not play any role in the interactions and in the expression of λ. Term$ \frac{1}{2} {g_{\omega}}^2 \chi^2 \omega_\mu \omega^\mu $ in Eq. (1) implies an explicit dependence of the nucleon effective mass on both the scalar and the vector fields, and this is one of the salient features of the present model. The isospin triplet ρ mesons are incorporated to account for the asymmetric hadronic matter. An explicit mass term for the isovector ρ meson$\dfrac{1}{2}\; m_\rho^2 \; \overrightarrow{\rho_\mu} \cdot \overrightarrow{\rho^\mu}$ was chosen following [19−21, 49]. The coupling strength of the ρ mesons with the nucleons was obtained with fixed symmetry energy coefficient$ J = 32 $ MeV at hadronic saturation density$ \rho_0 $ . In terms of the baryon density ρ and the Fermi momentum$k_{\rm F}=(6\pi^2 \rho/{\gamma})^{1/3}$ ($ \gamma=2 $ is degeneracy factor of nucleon), the isovector coupling strength is related to J as:$ J = \frac{C_{\rho}\; k_{\rm F}^3}{12\pi^2} + \frac{k_{\rm F}^2}{6\sqrt{(k_{\rm F}^2 + m^{* 2})}} , $

(3) where
$ C_{\rho} = g^2_{\rho}/m^2_{\rho} $ and$ m^* $ is the nucleon effective mass. The scalar density is obtained as:$ \begin{aligned}[b] \rho_S=&<\overline{\psi}\psi>=\frac{1}{ \pi^2} \Bigg[\int^{k_{Fn}}_0 {\rm d}k_n \; k_n^2 \frac{m^*}{\sqrt{k_n^2 + {m^{*}}^2}}\\&+\int^{k_{Fp}}_0 {\rm d} k_p \; k_p^2 \frac{m^*}{\sqrt{k_p^2 + {m^{*}}^2}}\Bigg], \end{aligned} $

(4) while the baryon density for asymmetric hadronic matter is given by:
$ \rho=<\psi^\dagger\psi>=\rho_n + \rho_p=\frac{1}{\pi^2} \Bigg[\int^{k_{Fn}}_0 {\rm d} k_n \; k_n^2 + \int^{k_{Fp}}_0 {\rm d} k_p \; k_p^2\Bigg]. $

(5) Symmetric nuclear matter (SNM) is defined as hadronic matter with equal number of neutrons and protons (N = Z), while at high density, matter becomes asymmetric (
$N \gg Z$ ). The effective nucleon chemical potential is expressed as:$ \mu_B=\sqrt{k_{\rm F}^2 + {m^*}^2} + g_{\omega}\omega_0 + g_{\rho}I_{3B}\rho_{03}\; , $

(6) where,
$ I_{3B} $ (with$ B=n,p $ ) is the third component of isospin of the individual nucleons, and$ \omega_0 $ and$ \rho_{03} $ are the mean field values of the vector and isovector mesons, respectively. In Eq. (6) the chemical potential of the individual nucleons in the absence of the meson field terms is given by the first term$\mu_0=\sqrt{k_{\rm F}^2 + {m^*}^2}$ , which is modified into the effective chemical$ \mu_B $ due to the interaction between the nucleons via exchange of the mesons, as seen from the last two terms in Eq. (6). Thus, effective chemical potential$ \mu_B $ (where$ B=n,p $ ) of the individual nucleons differs by the third component of isospin of the individual nucleons$ I_{3B} $ , as described in Eq. (6).The scalar EoM of the scalar field is:
$ \begin{aligned}[b]& (1-Y^2)-\frac{B}{C_{\omega}}(1-Y^2)^2+\frac{C}{C_{\omega}^2}(1-Y^2)^3 \\&\quad+ \frac{2\; C_{\sigma}\; C_{\omega}\; \rho^2}{m^2 \; Y^4} - \frac{2\; C_{\sigma}\; \rho_{S}}{m\; Y}=0. \end{aligned} $

(7) Here,
$ C_i={g_i}^2/{m_i}^2 $ are the scaled couplings ($ i=\sigma\; \&\; \omega $ and$ m_i $ is the mass of the mesons);$ Y=m^*/m $ ; and B and C are the coefficients of higher order scalar field terms. The EoM of the vector field is given by:$ \omega_0=\frac{\rho}{g_{\omega} \chi^2} , $

(8) while that of the isovector field is:
$ \rho_{03}=\sum\limits_{B}\frac{g_{\rho}}{m_\rho^2}I_{3_B}\rho_B . $

(9) The five model parameters, i.e.,
$ C_{\sigma}, C_{\omega}, C_{\rho} $ , and coefficients$ B\; \&\; C $ , of higher order scalar field terms were determined by reproducing the properties of SNM at saturation density$ \rho_0 $ . The corresponding procedure is detailed in [21]. For the present work, the parameter set was chosen from [21] and is presented in Table 1 along with the SNM properties yielded by this parameter set.$ C_{\sigma} $ /

$ \rm{fm^2} $ 

$ C_{\omega} $ /

$ \rm{fm^2} $ 

$ C_{\rho} $ /

$ \rm{fm^2} $ 

$(B/m^2)$ /

$ \rm{fm^2} $ 

$(C/m^4)$ /

$ \rm{fm^2} $ 

6.772 1.995 5.285 −4.274 0.292 $ m^{*}/m $ 

K/MeV $(B/A)$ /MeV

J/MeV $ L_0 $ /MeV

$ \rho_0 $ /fm−3

0.85 303 −16.3 32 87 0.153 Table 1. Model parameters chosen for the present work (adopted from [21]).
As nucleon effective mass
$ m^{*} $ for this model depends on both the scalar and vector fields, it is quite high compared with well-known RMF models. Further, at high density, unlike RMF models, the value of$ m^{*} $ increases after a certain high value of density [13, 16, 20, 21]. This is due to the dominance of the vector potential at such density. Moreover, at high density, the higher order terms of the scalar field with coefficients B and C as well as the mass term of the vector field of the present model become highly nonlinear and dominant [13, 16, 20, 21]. Although the hadronic imcompressibility K obtained with the chosen parameter set is consistent with the results of [50], it is larger than those estimated in [51, 52]. The other SNM properties such as the binding energy per nucleon$ B/A $ , symmetry energy J, and the saturation density$ \rho_0 $ match well with the estimates provided in Refs. [53, 54]. The slope parameter$ L_0 $ is also quite consistent with the ranges specified by [53, 55, 56]. The same model parameter set was also adopted successfully in [13−18, 57] to investigate different properties of NSs as well as HSs regarding various constraints specified on their structural properties. -
In the conventional RMF theory [22−25, 58−64] nucleons are treated as elementary particles and interactions between the nucleons are mediated by the exchange of σ, ω, and ρ mesons. The σ mesons generate the strong attractive force, while the ω mesons cause the strong repulsive force between the nucleons. In addition, several self and cross interaction terms between the mesons are considered to yield the saturation properties correctly. The Lagrangian density for the extended RMF model can be written as:
$ {{\cal{L}}}= {{\cal{L}}_{\cal{NM}}}+{{\cal{L}}_{\sigma}} + {{\cal{L}}_{\omega}} + {{\cal{L}}_{{\bf{\rho}}}} +{{\cal{L}}_{\sigma\omega{\bf{\rho}}}}\; , $

(10) where Lagrangian
${{\cal{L}}_{\cal{NM}}}$ describing the interactions of the nucleons with mass m through the mesons is:$ {{\cal{L}}_{\cal{NM}}} = \sum\limits_{B=n,p} \overline{\psi}_{i}[{\rm i}\gamma^{\mu}\partial_{\mu}- (m-g_{\sigma} \sigma) -(g_{\omega }\gamma^{\mu} \omega_{\mu}+\frac{1}{2}g_{{\bf{\rho}}}\gamma^{\mu}\tau .{\bf{\rho}}_{\mu})]\psi_{i}.\; \; \; \; \; \; $

(11) Here, the sum is taken over the neutrons and protons, and τ represents the isospin matrices. The Lagrangians for the σ, ω, and ρ mesons including their self interaction terms can be written as:
$\begin{aligned}[b]{{\cal{L}}_{\sigma}} =& \frac{1}{2}(\partial_{\mu}\sigma\partial^{\mu}\sigma-m_{\sigma}^2\sigma^2) -\frac{{\kappa_3}}{6m} g_{\sigma}m_{\sigma}^2\sigma^3\\&-\frac{{\kappa_4}}{24m^2}g_{\sigma}^2 m_{\sigma}^2\sigma^4,\\ {{\cal{L}}_{\omega}} =& -\frac{1}{4}\omega_{\mu\nu}\omega^{\mu\nu}+\frac{1}{2}m_{\omega}^2\omega_{\mu}\omega^{\mu} +\frac{1}{24}\zeta_0 g_{\omega}^{2}(\omega_{\mu}\omega^{\mu})^{2},\\ {{\cal{L}}_{{\bf{\rho}}}}=& -\frac{1}{4}{\bf{\rho}}_{\mu\nu}{\bf{\rho}}^{\mu\nu}+\frac{1}{2}m_{\rho}^2{\bf{\rho}}_{\mu}{\bf{\rho}}^{\mu} \end{aligned}$

(12) where
$ \omega^{\mu\nu} $ and$ {\bf{\rho}}^{\mu\nu} $ are field tensors corresponding to the ω and ρ mesons, defined as$ \omega^{\mu\nu}=\partial^{\mu}\omega^{\nu}-\partial^{\nu}\omega^{\mu} $ and$ {\bf{\rho}}^{\mu\nu}=\partial^{\mu}{\bf{\rho}}^{\nu}- \partial^{\nu}{\bf{\rho}}^{\mu} $ . Here,$ m_{\sigma} $ ,$ m_{\omega} $ , and$ m_{\rho} $ are the masses of$ \sigma, \omega $ , and$ {\bf{\rho}} $ mesons, respectively. The cross interactions of$ \sigma, \omega $ , and$ {\bf{\rho}} $ mesons are described by$ {{\cal{L}}_{\sigma\omega\rho}} $ as:$ \begin{aligned}[b] {{\cal{L}}_{\sigma\omega\rho}} =& \frac{\eta_1}{2m}g_{\sigma}m_{\omega}^2\sigma\omega_{\mu}\omega^{\mu}+ \frac{\eta_2}{4m^2}g_{\sigma}^2 m_{\omega}^2\sigma^2\omega_{\mu}\omega^{\mu} \\&+\frac{\eta_{\rho}}{2m}g_{\sigma}m_{\rho }^{2}\sigma\rho_{\mu}\rho^{\mu} +\frac{\eta_{1\rho}}{4m^2}g_{\sigma}^2m_{\rho }^{2}\sigma^2\rho_{\mu}\rho^{\mu} \\&+\frac{\eta_{2\rho}}{4m^2}g_{\omega}^2m_{\rho }^{2}\omega_{\mu}\omega^{\mu}\rho_{\mu}\rho^{\mu}\; .\end{aligned} $

(13) The field equations derived from the above Lagrangian can be solved self-consistently via a mean-field approximation, i.e., the meson-field operators are replaced by their expectation values. The effective mass of the nucleon is:
$ m^*=m-g_{\sigma} \sigma $

(14) and the equilibrium densities are defined as
$ \rho = \rho_p + \rho_n $ and$ \rho_3 = \rho_p -\rho_n $ .The values of the coupling constants are usually determined in such a way that they yield appropriate values for finite nuclei properties (e.g., binding energy, charge radii) and various quantities associated with the hadronic matter at the saturation density. The expression for the effective chemical potential of the individual nucleons in this model is also same as that in HM1 Eq. (6), given as:
$ \mu_B= \sqrt{k_{\rm F}^2 + {m^*}^2} + g_{\omega}\omega_0 + g_{\rho}I_{3B}\rho_{03} $

(15) where
$ I_{3B} $ is the isospin 3-component of nucleon. The fields involved in the expressions for the effective mass (Eq. (14)) and chemical potential (Eq. (15)) of nucleons can be obtained by solving the following field-equations self-consistently:$ \begin{aligned}[b] \sigma_0 =& -\frac{g_{\sigma}}{m_{\sigma}^2} {\sum\limits_{i=n,p} \frac{1}{\pi^2} \int_0^{k_{F_i}} {\rm d} k\,k^2\, \frac{m_i^{*}}{\sqrt{k^2+{m_i^*}^2}}} \\&-\frac{1}{m_{\sigma}^2}\Biggl[ \frac{{\kappa_3}}{2m}g_{\sigma}m_{\sigma}^2\sigma_0^2 +\frac{{\kappa_4}}{6m^2}g_{\sigma}^2 m_{\sigma}^2\sigma_0^3 \\ &-\frac{\eta_1}{2m}g_{\sigma}m_{\omega}^2\omega_0^2 -\frac{\eta_2}{2m^2}g_{\sigma}^2 m_{\omega}^2\sigma_0\omega_0^2 \\ &-\frac{\eta_{\rho}}{2m}g_{\sigma}m_{\rho }^{2}\rho_{03}^2 -\frac{\eta_{1\rho}}{2m^2}g_{\sigma}^2m_{\rho }^{2}\sigma_0\rho_{03}^2 \Biggr]\; , \end{aligned} $

(16) $ \begin{aligned}[b] \omega_0 = & \frac{g_{\omega}}{m_{\omega}^2} \rho -\frac{1}{m_{\omega}^2}\Biggl[ \frac{1}{6}\zeta_0 g_{\omega}^{2}\omega_0^3 - \frac{\eta_1}{m}g_{\sigma}m_{\omega}^2\sigma_0\omega_0 \\ &-\frac{\eta_2}{2m^2}g_{\sigma}^2 m_{\omega}^2\sigma_0^2\omega_0 -\frac{\eta_{2\rho}}{2m^2}g_{\omega}^2m_{\rho }^{2}\rho_{03}^2\omega_0\Biggr] , \end{aligned} $

(17) $ \begin{aligned}[b] \rho_{03} = & \frac{g_{\rho}}{m_{\rho}^2} \rho_3 +\frac{1}{m_{\rho}^2}\Biggl[ \frac{\eta_{\rho}}{m}g_{\sigma}m_{\rho }^{2}\sigma_0\rho_{03} \\&+\frac{\eta_{1\rho}}{2m^2}g_{\sigma}^2m_{\rho }^{2}\sigma_0^2\rho_{03} +\frac{\eta_{2\rho}}{2m^2}g_{\omega}^2m_{\rho }^{2}\omega_0^2\rho_{03} \Biggr]. \end{aligned} $

(18) We use the BSP parametrization [22] for our calculation, which describe the properties of finite nuclei very well. This parameterization includes the quartic order cross-coupling between ω and σ mesons to model the high density behavior of the EoS. The parametrization along with the obtained values of the properties of the hadronic matter at the saturation density using this parameter are tabulated in Table 2 and Table 3, respectively.
$ g_\sigma/4\pi $ 

$ g_\omega/4\pi $ 

$ g_\rho/4\pi $ 

$ \kappa_3 $ 

$ \kappa_4 $ 

$ \eta_1 $ 

$ \eta_2 $ 

$ \eta_{\rho} $ 

$ \eta_{1\rho} $ 

$ \eta_{2\rho} $ 

$ \zeta_0 $ 

$ m_\sigma/m $ 

$ m_\omega/m $ 

$ m_\rho/m $ 

0.8764 1.1481 1.0508 1.0681 14.9857 0.0872 3.1265 0.0 0.0 53.7642 0.0 0.5383 0.8333 0.8200 Table 2. BSP parameter sets for the extended RMF model with the nucleon mass
$ m = $ 939.2 MeV.$ m^*/m $ 

$(B/A)/$ 

$\rho_0 /$ 

K/ J/ $L_0 /$ 

MeV /fm−3 MeV MeV MeV 0.60 −15.9 0.149 230 28.83 50 Table 3. Properties of the hadronic matter at the saturation density.
In the present work we consider asymmetric matter motivated by the asymmetry of dense neutron star matter. In typical dense neutron star matter the proton content is
$ \sim $ 10%–15% of the total matter. Therefore in the present work we consider the proton fraction to be 15% in case of both the hadronic models HM1 and HM2. However, as discussed in the Introduction section I, we do not consider the leptonic contribution in the hadronic sector of the present work to calculate the transport coefficients. -
We consider the MIT bag model [12, 65] with u and d quarks to describe the pure massless quark phase. The chemical potential of the quarks is expressed as:
$ \mu_f=\sqrt{{k_{F}}_f^2 + m_f^2} , $

(19) where
$ k_f $ is the Fermi momenta of individual flavors$ f= $ u and d, and$ m_f $ is the mass of individual quarks. We consider$ m_u= $ 2.2 MeV and$ m_u= $ 4.7 MeV, which are low enough to assume the quark matter as massless in the absence of the massive s quark. The total baryonic density is given by:$ \rho=\frac{\rho_u+\rho_d}{3}=\frac{1}{3}(2\times 3) \frac{1}{6\pi^2} \left[{k_{Fu}^3} + {k_{Fd}^3}\right], $

(20) where the spin and color degeneracy factors of quark matter are considered as 2 and 3, respectively, and
$ k_{Fu} $ and$ k_{Fd} $ are the Fermi-momentum of the u and d quarks, respectively. The factor 1/3 conserves the net baryon number as the MIT Bag model is based on deconfinement of hadrons (nucleons) and the fact that there are three quarks per nucleon, each having baryon number 1/3. -
Here, we address the standard kinetic theory framework for obtaining the transport coefficients like shear viscosity η and electrical conductivity σ, which are the basic part of the dissipation component of any many-body system or medium or fluid. First, the expression for shear viscosity was dervied. Considering the matter as a dissipative fluid, the energy-momentum tensor can be expressed in macroscopic form as:
$ T^{\mu \nu}={T_0}^{\mu\nu} + {T_D}^{\mu\nu}\; , $

(21) where ideal (
$ {T_0}^{\mu\nu} $ ) and dissipation ($ {T_D}^{\mu\nu} $ ) parts in terms of fluid quantities like fluid four velocity$ u^\mu $ , energy density$ \epsilon $ , pressure P, and metric tensor$ g^{\mu\nu} $ can be expressed as:$ {T_0}^{\mu \nu}=-g^{\mu\nu} + (\epsilon +P) u^{\mu}u^{\nu} $

(22) and
$ T_D^{\mu\nu}=\pi^{\mu\nu} +...=\eta^{\mu\nu\alpha\beta}\; {{\cal{U}}}_{\alpha \beta}^{\eta} +.. $

(23) respectively. In the expression of the dissipative part of the energy-momentum tensor, the viscous stress tensor is
$ \pi^{\mu\nu} $ , velocity gradient tensor is${{\cal{U}}}^{\mu \nu}_{\eta}= D^{\mu}u^{\nu} + D^{\nu}u^{\mu}- \dfrac{2}{3} \Delta^{\mu \nu} \partial_{\rho} u^{\rho}$ , with$ D^\mu= \partial^\mu - u^{\mu}u^{\sigma} \partial_{\sigma} $ ,$ \Delta^{\mu\nu}=g^{\mu\nu}-u^\mu u^\nu $ , and$ \eta^{\mu\nu\alpha\beta} $ is the shear viscosity tensor. Moreover, the dissipative part can include components of shear, bulk, and thermal dissipation, but only the shear part is regarded here. The notation of$ (+... ) $ indicates the other dissipation components. The picture of relativistic shear viscosity η as a proportional constant between viscous stress tensor$ \pi^{\mu\nu} $ and tangential fluid velocity gradient$ {{\cal{U}}}^{\mu \nu}_{\eta} $ can be compared with Newton-Stoke law, applicable in the non-relativistic domain, where the shear viscosity is defined as the proportionality constant between shear stress and velocity gradient.Considering the hadronic matter to include nucleons, the microscopic expression of its energy-momentum tensor can be written in kinetic theory framework as:
$ T^{\mu \nu}= \gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{\mu}k^{\nu}}{E} (f_N + f_{\bar{N}}), $

(24) where
$ f_N $ and$ f_{\bar{N}} $ are assumed as nonequilibrium distribution functions for nucleons N and anti-nucleons$ {\bar{N}} $ . Now splitting$ f_{N,{\bar{N}}} $ as the sum of equilibrium distribution$ f_{N,{\bar{N}}}^0 $ and a small deviation$ \delta f_{N,{\bar{N}}} $ i.e,$ f_{N,{\bar{N}}}= f_{N,{\bar{N}}}^0 + \delta f_{N,{\bar{N}}} $ , the microscopic expressions of$ {T_0}^{\mu\nu} $ and$ {T_D}^{\mu\nu} $ parts can be separately identified in terms of the quantities like particle's four momenta$ k^\mu $ or degeneracy factor γ, among others, as:$ {T_0}^{\mu \nu}=\gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{\mu}k^{\nu}}{E} (f^0_N + f^0_{\bar{N}}) $

(25) and
$ T_D^{\mu\nu}=\pi^{\mu\nu} +...=\gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{\mu}k^{\nu}}{E} (\delta f_N + \delta f_{\bar{N}}) +... $

(26) Then, using the standard relaxation time approximation (RTA) methods of Boltzmann transport equation [26]:
$ \delta f_{N,{\bar{N}}}=\frac{k^\alpha k^\beta}{E}\tau_{N,{\bar{N}}}\beta f^0_{N,{\bar{N}}}(1-f^0_{N,{\bar{N}}}){{\cal{U}}}_{\alpha \beta}^{\eta}\; , $

(27) where
$ \tau_{N,{\bar{N}}} $ represents relaxation time and E indicates the energy of a nucleon and anti-nucleon. Accordingly, combining Eq. (27) into (26) and comparing with Eq. (23), the shear viscosity tensor was obtained as:$ \eta^{\mu\nu\alpha\beta}=\gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{\mu}k^{\nu}k^\alpha k^\beta}{E^2} \tau_{N,{\bar{N}}} [f^0_{N}(1-f^0_{N}) + f^0_{\bar{N}}(1-f^0_{\bar{N}})]/T . $

(28) Using tensor identity [26, 66, 67], the isotropic expression could be determined as:
$ \eta=\frac{\gamma}{15} \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^4}{E^2} \tau_{N,{\bar{N}}} [f^0_{N}(1-f^0_{N}) + f^0_{\bar{N}}(1-f^0_{\bar{N}})]/T . $

(29) If we analyze Eq. (29), then we can find two components: relaxation time
$ \tau_{N,{\bar{N}}} $ , whose order of magnitude will fix the strength of viscosity for the system, and the remaining part of the expression of η, which can be called the phase-space part of η and decides the temperature and density dependence of η. The expression for any transport coefficient will have these two component structures.Now, regarding T = 0 in the calculation instead of finite T, the equilibrium Fermi-Dirac distribution takes the form of a step function as:
$ \begin{aligned}[b] f_{N}^0 =& 1,~~ {\rm{if}}~~ E<\mu, \\ f_{N}^0 =& 0,~~ {\rm{if}}~~ E>\mu, \\ f_{\bar{N}}^0 =& 1,~~ {\rm{if}}~~ E<-\mu, \\ f_{\bar{N}}^0 =& 0,~~ {\rm{if}}~~ E>-\mu \; . \end{aligned} $

(30) The above conditions imply that the anti-nucleons do not contribute anymore to the positive energy for the
$ T=0 $ case. Thus, the following replacement was used:$ \frac{\partial f^0_N}{\partial E} = - f^0_N(1-f^0_N)/T \rightarrow \frac{\partial}{\partial E}\theta(\mu-E)=-\delta(E-\mu)\; . $

(31) Incorporating these replacements into Eq. (29), we get:
$ \begin{aligned}[b] \eta = \frac{\gamma}{15} \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^4}{E^2} \tau_{N}\delta(E-\mu) =\frac{\gamma}{30\pi^2}\tau_N\frac{(\mu^2-m^{*2})^{5/2}}{\mu} . \end{aligned} $

(32) Here, μ is the weighted average of the effective chemical potentials of neutron and proton, obtained from Eqs. (6) and (15) for HM1 and HM2, respectively.
Another transport coefficient is the electrical conductivity, which presents a proportionality constant between electric current density and the field. This macroscopic definition comes from Ohm's law, which can be expressed in three dimensional notation as:
$ J^{i}= \sigma^{ij} E_{j}\; , $

(33) where the electrical conductivity tensor
$ \sigma^{ij} $ connects the electric field$ E_j $ and the electric current density$ J^i $ . Realizing current due to electric field as a dissipation phenomenon, we can microscopically express this as:$ J^i= q\gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{i}}{E} \delta f_N\; , $

(34) where q is the electric charge of nucleon, i.e.,
$ q=0, e $ for neutron and proton. Here, the RTA methods of Boltzmann transport equation were again considered to realize the following form of$ \delta f_N $ [26]:$ \delta f_{N}=\frac{k^j}{E}\tau_{N}\beta f^0_{N}(1-f^0_{N})qE_j\; . $

(35) Combining Eqs. (35) and Eq. (34), and comparing with Eq. (33), the conductivity tensor was obtained as:
$ \sigma^{ij}= q^2\gamma \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^{i}k^j}{E^2} \tau_{N}\beta f^0_{N}(1-f^0_{N})\; , $

(36) whose isotropic expression at
$ T=0 $ will be:$ \begin{aligned}[b] \sigma = &\frac{q^2\gamma}{3} \int \frac{{\rm d}^3 \vec{k}}{(2\pi)^3} \frac{k^2}{E^2} \tau_{N}\delta(E-\mu) \\ =&\frac{q^2\gamma}{6\pi^2}\tau_N\frac{(\mu^2-m^{*2})^{3/2}}{\mu}. \end{aligned} $

(37) The final expressions of shear viscosity and electrical conductivity for hadronic matter are given by Eqs. (32) and (37), respectively. The neutrons will not contribute to the electrical conductivity given in Eq. (37). Hence, only protons contribute to the electrical conductivity, and thus, in Eq. (37),
$ \mu=\mu_p $ is the effective proton chemical potential, calculated from Eqs. (6) and (15) for HM1 and HM2, respectively. Moreover, in Eq. (37) only protons will contribute to the relaxation time, i.e.,$ \tau_N=\tau_p $ .When we apply these two expressions for quark phase, then nucleon effective mass
$ m^* $ will be replaced by quark mass and the degeneracy factor γ will be replaced by the corresponding quark degeneracy factor g (for example). Considering two flavor quark matter with u and d quarks,$g=3\times 2\times 2=12$ for Eq. (32) and$gq^2=3\times 2 \bigg(\dfrac{4e^2}{9}+\dfrac{e^2}{9} \bigg)=\dfrac{10e^2}{3}$ for Eq. (37). The values of η and σ for quark matter will be very close to their massless limits:$\begin{aligned}[b]\eta =&\frac{g}{30\pi^2}\tau_Q \mu^4 \\ \sigma =&\frac{g q^2}{6\pi^2}\tau_Q \mu^2,\end{aligned}$

(38) whose normalized values become constant. These massless limits may act as reference line at
$ T=0 $ and finite μ case.The relaxation time can also be calculated microscopically. For the degenerate scenario, the medium constituents will occupy all the energy levels from
$ {m^*} $ to μ, and ideally have zero probability to move outside μ. However, in reality, due to very low T instead of exactly$ T=0 $ , we established a small deviation from step function-type distribution function. Therefore, medium constituents, having energy near Fermi energy μ and velocity near Fermi velocity$v_{\rm F}=\sqrt{\mu^2 - {m^*}^2}/\mu$ , will participate in the momentum transfer scattering process. Accordingly, the relaxation time can be defined as:$ \begin{aligned}[b] \tau_c =& 1/[\sigma_s v_{\rm F} \rho] \\ =& \mu/[\sigma_s \sqrt{\mu^2-{m^*}^2} \; \rho]\; ,\end{aligned} $

(39) where ρ is the density of the medium and
$ \sigma_s=4\pi a^2 $ is the cross-section with scattering length a. Depending upon the system, the inputs for the medium constituents are used to calculate their relaxation time. We first normalized the quantities η and σ as$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ to obtain dimensionless forms. For electrical conductivity, we considered$ \tau_c=\tau_{cp} $ and$ \mu=\mu_p $ for the scaling. -
We obtained the transport coefficients of the hadronic and quark phases based on the formalism previously discussed, and investigated the variation of these coefficients with respect to density. The phenomenon of phase transition at vanishing temperature and the transition density remain inconclusive in literature. Therefore, rather than achieving phase transition, in the present work, we compared the order of magnitudes of the transport coefficients for the hadronic and quark phases.
We calculated the shear viscosity of hadronic and quark matter using Eq. (32). The electrical conductivity for hadronic matter was calculated using Eq. (37), while that of quark matter is calculated using Eq. (38). We then normalized these quantities as
$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ to obtain dimensionless forms, where$ \tau_c $ is the relaxation time of quark or hadronic matter in general, i.e.,$ \tau_c=\tau_N $ for hadronic matter and$ \tau_c=\tau_Q $ for quark matter. These quantities$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ are plotted against the normalized density in the left and right panels of Fig. 2, respectively. Note an approximate difference of 10-20 times between hadronic model-1 (HM1) and hadronic model-2 (HM2) considering the estimations of$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ . This is because of the difference in chemical potential (μ) as well as the nucleon effective mass ($ m^* $ ) between the two hadronic models. Both chemical potential and the effective mass are quite different for HM1 and HM2, as seen from Fig. 1. Rechecking Eqs. (32) and (37), the numerical and physical impact of Fig. 1 on Fig. 2 can be understood. The difference in the order of magnitudes between the two hadronic models reflects a numerical band of transport coefficients for hadronic matter along the density axis. For both$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ , there is a sharp increase in the estimated values of the hadronic models and the quark model (z-MQM). For shear viscosity, this is from 0.001 (HM1) or 0.02 (HM2) to 0.05 (z-MQM), while for electrical conductivity this rise is from 0.0003 (HM1) or 0.003 (HM2) to 0.005 (z-MQM). Notice the saturation trend of the normalized transport coefficients, depicting its thermodynamical phase-space part (or more specifically, the thermodynamical probability of shear and electrical charge transportation). The saturation profile of HM1 (red solid line) and HM2 (green dash line) exhibit mildly increasing trends with μ due to their dependence$ \eta \propto \tau_c\mu^4 (1-m^{*2}/\mu^2)^{5/2} $ and$ \sigma\propto\tau_c\mu^2(1-m^{*2}/\mu^2)^{5/2} $ . They saturate at different values due to the difference in$ m^* $ between the two hadronic models.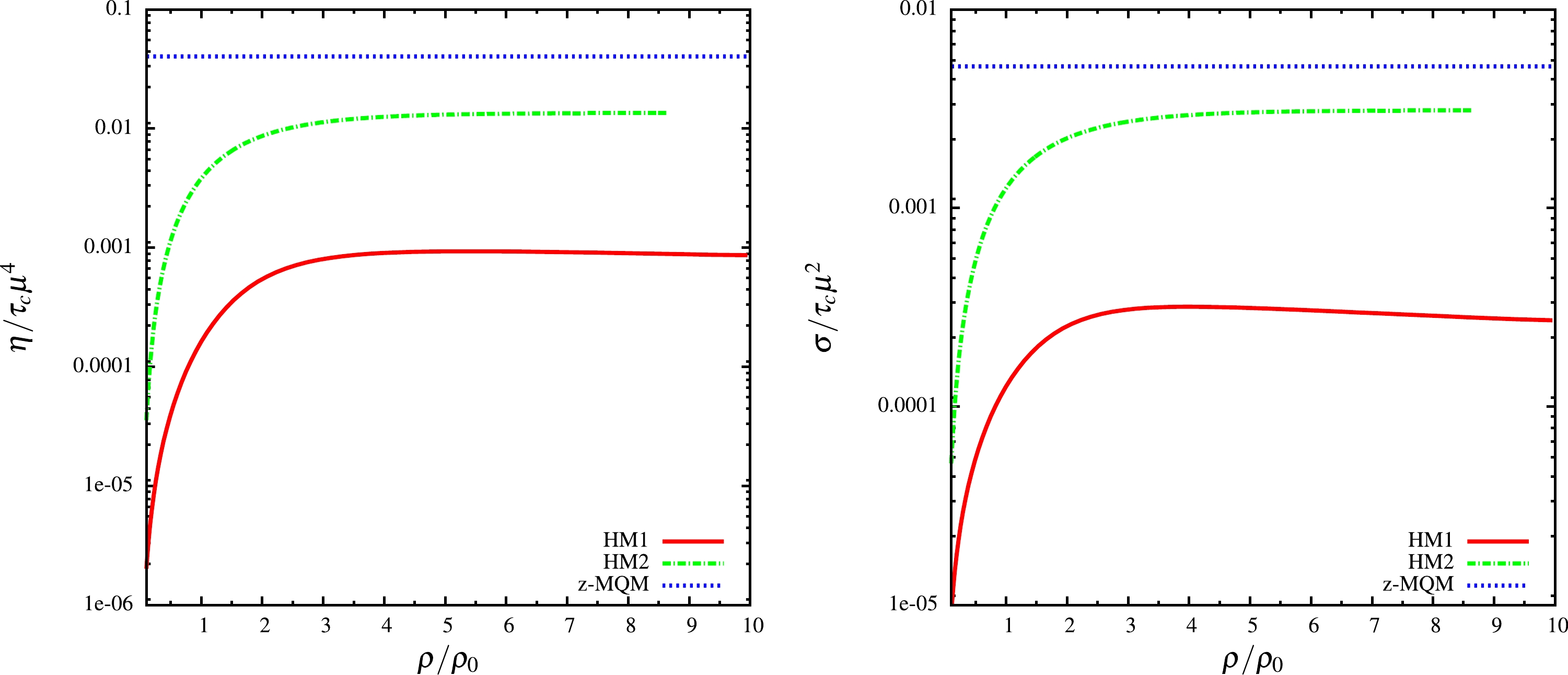
Figure 2. (color online) Normalized shear viscosity (left) and electrical conductivity (right) with respect to scaled baryon density of hadronic matter and zero-mass quark matter (z-MQM).

Figure 1. (color online) Weighted average of the effective chemical potential of hadronic matter with two different hadronic models HM1 and HM2 and zero-mass quark matter (z-MQM (left) and the effective nucleon mass of hadronic matter with HM1 and HM2 (right) vs normalized baryon density.
Meanwhile, the quark matter estimation follows the massless transport relation along the entire density axis
$ \eta \propto \tau_c\mu^4 $ and$ \sigma\propto\tau_c\mu^2 $ as we considered exact massless limit for the quark phase. In the actual case, one should sketch the estimations of HM1 or HM2 at low density domain and the z-MQM estimation at high density domain, and at some intermediate density quark-hadron phase transition will take place, connecting the estimations of the low and high density domains. However, due to lack of proper knowledge regarding phase transition density (which is highly model dependent), we restricted our focus only on the order of magnitude of the transport coefficients for two phases.These estimations of the transport coefficients, i.e., the shear viscosity and the electrical conductivity at
$ T=0 $ and$ \mu\neq 0 $ , can be compared with the estimations of the transport coefficients at$ T\neq 0 $ and$ \mu= 0 $ given in Ref. [26] and the references therein. The quark-hadron transition at$ T\neq0 $ and$ \mu=0 $ is understood by estimating the thermodynamics of massless quark gluon plasma (QGP) and hot pion gas for high and low temperature zones, respectively. However, deeper LQCD calculations [2–4] were performed and the crossover-type nature of the quark-hadron transition at$ T\neq 0 $ and$ \mu= 0 $ was revealed. The values of normalized thermodynamical quantities including$ P/T^4 $ and$ \epsilon/T^4 $ , among others, for massless QGP will act as reference line or upper limits of QCD matter for the$ \mu=0 $ case. The values of thermodynamical quantities, obtained from LQCD, remain quite lower than the massless QGP limit in low (or hadronic matter) temperature domain, which can be realized as non-perturbative aspects of QCD. Near transition temperature, their values increase to toward the massless limits, but in a smooth crossover way instead of increasing similar to a first-order phase transition. Beyond the transition temperature, LQCD thermodynamical values remained little suppressed with respect to their massless limits. This small suppression was also realized from the direction of finite temperature perturbative QCD (pQCD) theory, whose latest status can be found in [6]. Similar investigation of thermodynamical variations with respect to density or chemical potential at$ T=0 $ have been attempted over a very long time to understand the properties of dense matter [68]. Due to problems in LQCD calculations at finite μ, present knowledge regarding the quark-hadron phase transition along the μ-axis is not quite converging like the understanding of phase transition along the T-axis. In this context, in the present work, we considered the effective hadronic models and the Bag model to establish the order of magnitudes for different transport coefficients of the hadronic and quark phases along the ρ- or μ-axis. The normalized transport coefficients$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ against the ρ- or μ-axis will exhibit thermodynamical phase-space of transportation, which follow similar suppression in hadronic μ-domain (at$ T=0 $ ), as noticed for hadronic T-domain (at$ \mu=0 $ ) in [26]. In [26], the normalized coefficients were chosen as$ \eta/(\tau_c T^4) $ and$ \sigma/(\tau_c T^2) $ , while in the present work, they were$ \eta/(\tau_c\mu^4) $ and$ \sigma/(\tau_c\mu^2) $ . In both cases, around$ 10^{1-2} $ suppression was observed in hadronic T or μ domain with respect to their massless limits. The suppressed values in both the cases can be realized as the non-pQCD effect in the phase-space of transportation. This equivalence between normalized phase-space of transport coefficients along the T-axis and ρ-axis may be considered as an unique finding of the present investigation.Thus far, transport coefficients have been normalized considering relaxation time. Thus, we realized the phase space part of transport coefficients. However, the actual estimation of relaxation time will be important for determining the absolute values of the transport coefficients. The relaxation times for the hadronic and massless quark matter were calculated using Eq. (39). The effective nucleon mass and two possible orders of cross-section were considered as
$ \sigma_s=4\pi a^2\approx 5340\; \rm{fm^2} $ and$ 12.56\; \rm{fm^2} $ for hadronic matter case with scattering lengths$ a\approx 20 $ fm and$ 1 $ fm. The former value of$ \sigma_s\approx 5340\; \rm{fm^2} $ or$ a\approx 20 $ fm is the isospin averaged cross section/scattering length of NN interactions, taken from [69, 70]. This value was used for the calculation of relaxation time of nucleons at finite temperature in [71]. Here, we considered a finite density system, as well as another small value of scattering length$ a=1 $ fm.In Fig. 3, the variation of
$ \tau_c $ for HM1 and HM2 and z-MQM are plotted. For hadronic matter, two scattering lengths were considered: one was determined guided by the vacuum scattering interaction strength while the other was estimated assuming that scattering length may decrease with density. As a rough order of magnitude,$ \tau_c\approx 10-0.1 $ fm and$ \tau_c\approx 0.01-0.0002 $ fm were obtained for scattering lengths$ a\approx 1 $ fm and$ a=20 $ fm, respectively. In this context, the ranking of$ \tau_c $ is HM1$ > $ HM2$ > $ z-MQM. This is because of the inverse relation of relaxation time with a thermodynamic quantity e.g., density ρ, as seen from Eq. (39).
Figure 3. (color online) Relaxation time with respect to scaled baryon density of hadronic matter and zero-mass quark matter (z-MQM) for different values of cross-section.
When the relaxation time was determined for each phase, we calculated the shear viscosity and the electrical conductivity using the density dependent relaxation time values. The normalized estimations of
$ \eta/\rho $ and$ \sigma/\mu $ are presented in the left and right panels of Fig. 4, respectively. Though$ \eta/\mu^3 $ is also a possible dimensionless quantity,$ \eta/\rho $ was chosen for fluid property [72] measurement of quark and hadronic matter in the dense sector. This ratio$ \eta/\rho=\eta\mu/(\epsilon+P) $ at$ T= 0 $ ,$ \mu\neq 0 $ can have equivalent role like viscosity to entropy density ratio$ \eta/s $ for early universe or RHIC/LHC environment with$ T\neq 0 $ ,$ \mu=0 $ . From the Euler's thermodynamical relation, we get a general relation$ Ts=\epsilon+P -\mu\rho $ , which transforms into$ Ts=\epsilon+P $ for$ T\neq 0 $ ,$ \mu=0 $ and$ \mu \rho=\epsilon+P $ for$ T= 0 $ ,$ \mu\neq 0 $ respectively. Thus, for measuring the fluid property, we may choose dimensionless ratio either$ \eta T/(\epsilon +P) $ or$ \eta \mu/(\epsilon +P) $ for intermediate T, μ. Then, from the intermediate T-μ domain to the limit of$ T\neq 0 $ ,$ \mu=0 $ ,$ \eta T/(\epsilon +P) $ will be better quantity [72] and in limiting case, we can write$ \eta T/(\epsilon +P)=\eta/s $ . Similarly, from the intermediate T-μ domain to the limit of$ T=0 $ ,$ \mu\neq 0 $ ,$ \eta \mu/(\epsilon+P) $ will be the better quantity to study and in limiting case, we can write$ \eta \mu/(\epsilon+P)=\eta/\rho $ . A good discussion on this fluidity quantity is provided in [72, 86].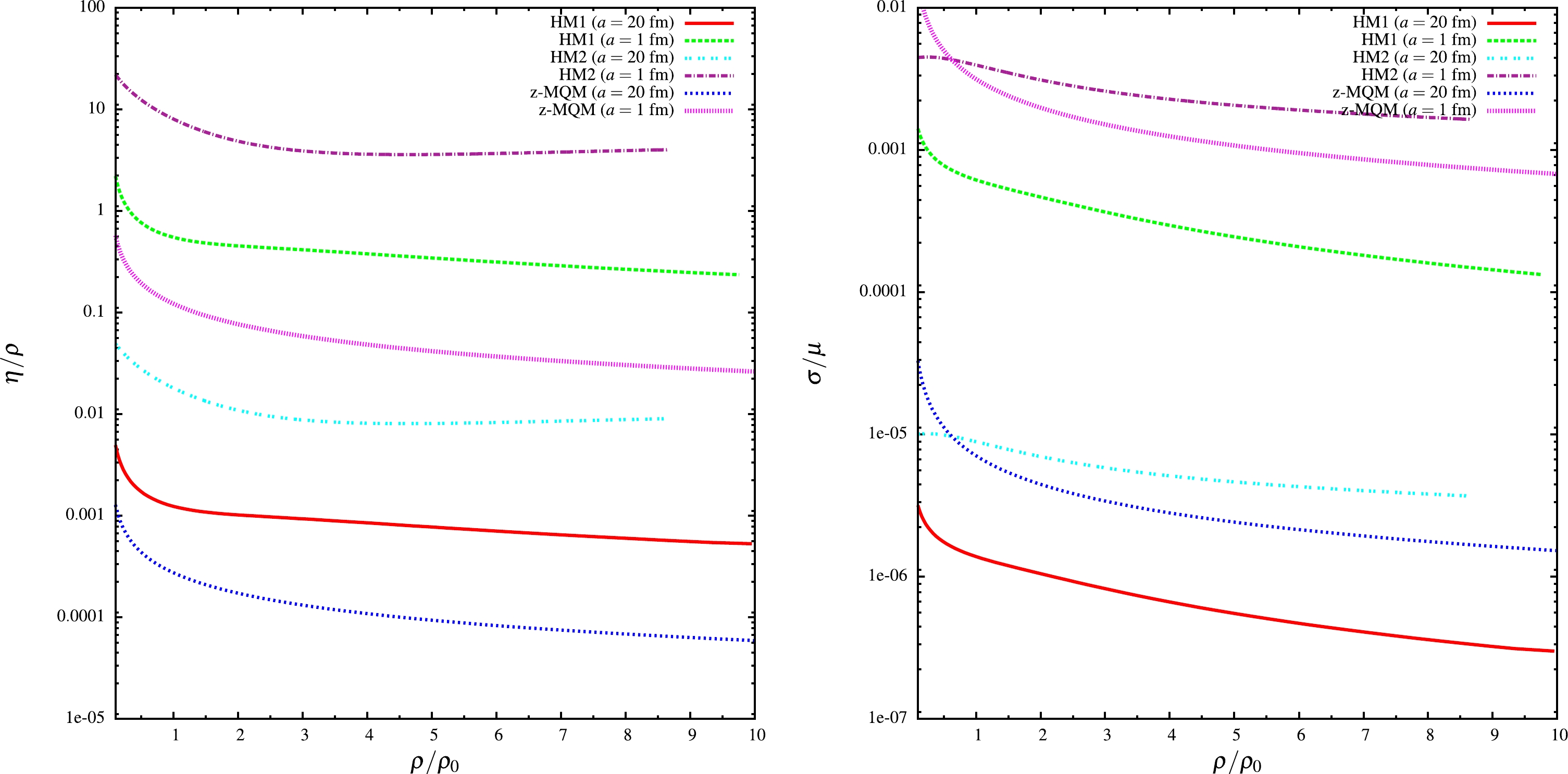
Figure 4. (color online) Shear viscosity to density ratio (left) and electrical conductivity upon chemical potential (right) with respect to scaled baryon density of hadronic matter and zero-mass quark matter (z-MQM) for different values of cross-section.
We know that the data of RHIC and LHC experiments [73−77] indicate very small values of
$ \eta/s $ , ever observed in nature [78]. On the other hand, a string theory-based calculation [79] tells$ \dfrac{\eta}{s}\geq \dfrac{1}{4\pi} $ , which may be considered as lower bound conjecture of$ \eta/s $ . This lower bound is popularly known as the Kovtun-Son-Starinet (KSS) bound [79]. The existence of a non-zero (but may not be equal to$ {1}/{4\pi} $ ) lower bound of$ \eta/s $ can also be realized from quantum aspects, which can prevent the classical possibility$ \eta/s\rightarrow 0 $ . Being roughly proportional to the ratio of mean free path to de-Broglie wavelength of medium constituent, the ratio$ \eta/s $ of any fluid can never vanish because the mean free path of any constituent can never be lower than its de-Broglie wavelength. It indicates that quantum fluctuations prevent the existence of perfect fluid in nature and$ \eta/s $ of any fluid should have some lower bound. Along with the support from quantum aspect, this lower bound of$ \eta/s $ is also validated through supersymmetric Yang–Mills (SYM) theory [82], which provide$\dfrac{\eta}{s}=\dfrac{1}{4\pi}$ in the infinite limit of the 't Hooft coupling. From experimental direction also, we noticed that$ \eta/s $ of all fluids, including super-fluid helium and even trapped Li atom at strong coupling [83], remain well above the bound for the range of measured temperatures and pressures. All these directions, ultimately support the lower bound conjecture of$ \eta/s $ , which was used as a gross reference point in the present work. The term "gross" is used because we have to accept the possibility of violation of the KSS bound [84, 85].Interestingly, the values of
$ \eta/s $ for RHIC and LHC matter are very close to this quantum lower bound$ 1/(4\pi) $ . Hence, a natural question arises - whether this nearly perfect fluid nature is also expected along the μ-axis at$ T=0 $ like that along the T-axis at$ \mu=0 $ of the QCD phase diagram? The present investigation aims in this direction for the first time but to get more conclusive outcome, probably further (alternative) research is required in future. The question becomes more important as recently [80] have experimentally found the value$ \eta/s\approx 1/(4\pi) $ for hadronic matter in the low energy hadronic physics experiment. We have plotted$ \eta/\rho $ of hadronic and quark matter with two values of scattering length in the left panel of Fig. 4. We notice that the results for$ a\approx 20 $ fm cross the KSS values ($ \approx 0.08 $ ), which may not be considered as a physically acceptable order of magnitude. Probably the magnitude of the cross section/scattering length in vacuum may be largely modified in the finite density picture, which is missing in the present calculation. In this regard, our guess value scattering$ a=1 $ fm provides an acceptable range of$ \eta/\rho $ in the hadronic density range, which still crosses the KSS boundary in the quark density range. Therefore, a safe zone may be considered as scattering lengths$ a<1 $ fm for getting$ \eta/\rho>1/(4\pi) $ . For mathematical guidance we can get a lower limit curve of the relaxation time τ as a function of density or chemical potential for massless quark matter by imposing the KSS limit. For finite temperature we get$ \tau=5/(4\pi T) $ [81] by imposing KSS limit$ \eta/s=1/(4\pi) $ . Similarly, for finite density, one can easily find the corresponding expression$ \tau=5/(4\pi \mu) $ by using η from Eq. (38), ρ from Eq. (20) and then by imposing KSS limit$ \eta/\rho=1/(4\pi) $ . In terms of density ρ, the KSS limit of relaxation time for massless quark matter with$ N_f=2 $ flavor will be$ \tau=\frac{5}{4\pi}\Big(\frac{2}{\pi^2}\Big)^{1/3}\frac{1}{\rho^{1/3}}. $

(40) Another interesting outcome here is that we still see the jump in
$ \eta/\rho $ is possible in case of a possible scenario of hadron-quark phase transition as in terms of$ \eta/\rho $ the ranking is noticed as HM2 > HM1 > z-MQM. So phase transition from hadronic to quark phase may imply a reduction in$ \eta/\rho $ . However, for normalized electrical conductivity$ \sigma/\mu $ , we observed that the ranking is HM2 > z-MQM > HM1. So the ranking of magnitude of$ \sigma/\mu $ for the two different phases may be model dependent. We cannot get any conclusive picture in this regard. The present work reveals this uncertainty. We also do not go into any comparative discussion of two hadronic models, rather we intend to show that a possible numerical uncertainty pertains to the estimations of$ \sigma/\mu $ by using two different hadronic models. Hence, future research with other existing hadronic models is probably necessary for getting any conclusive or broader picture. Only an order of magnitude difference in transport coefficients for two phases can be considered as conclusive message in present study. -
To summarize, we attempted to visualize the variation of shear viscosity and electrical conductivity of hadronic and quark matter along the density axis. Inspiration of such calculation comes from the calculations of transport coefficients of RHIC or LHC matter, where we obtained a cross-over type of quark-hadron phase transition along temperature axis. The temperature dependence of shear viscosity and electrical conductivity of RHIC or LHC matter mainly contain two parts: thermodynamical phase-space part and the relaxation time part. If we exclude the relaxation time part by normalizing it, then we obtain their nice pattern along temperature axis as one notices for other thermodynamical quantities like pressure, energy density etc. from lattice QCD calculations. The pattern of normalized thermodynamical quantities and transport coefficients is as follows. At high temperature, they reach close to their massless limits and they are gradually suppressed as temperature goes down. Similar kind of pattern is observed in the present work when we go from high density quark phase to low density hadronic phase. The finite density calculations of hadronic phase is obtained with two RMF models and massless quark model for the quark phase. The equivalence of thermodynamic phase-space profile of transportation along temperature axis and density axis is a very interesting finding of the present work.
Instead of normalizing relaxation time, if we use its microscopic estimated values, which is generally of the order of fm due to strong interaction, then we can get the final profile of the transport coefficients. A long list of references can be found for RHIC or LHC matter, where most of them found that shear viscosity to entropy density ratio will decrease first then increase with temperature. In this regard, we find shear viscosity to density ratio decreases with density in the hadronic phase and may suddenly drop in a possible scenario of hadron-quark phase transition at
$ T=0 $ . In the pure quark phase, a mild decreasing trend with density is observed. This is the qualitative trend of the fluidity measurement of quark and hadronic matter along the density axis, observed in the present investigation. During the computation of the quantitative values, we use the quantum lower bound of fluidity or shear viscosity to density ratio as a physical reference point and we found an interesting finding which is as follows. The experimental data for standard nucleon-nucleon scattering length in vacuum is of the order of 20 fm and using this as a hard-sphere scattering cross section, we find that the fluidity values cross the lower bound. We also found that scattering length less than 1 fm can only provide physical fluidity, beyond its lower bound. It indicates that a good amount of in-medium modification will play an important role in the dense sector, for which vacuum scattering length 20 fm will be reduced to lower values, less than 1 fm. By using scattering length as an input parameter, the present work just unfolds this issue but not well equipped for the microscopic calculation of density dependent scattering length, which may be explored in future. We believe that other hadronic models, whose mass and chemical potential undergo almost similar kind of modification in terms of order of magnitude, will face same problem of fluidity calculation in the dense sector, which should be checked with other hadronic models. -
The authors thank Dr. Sandeep Chatterjee, Department of Physical Sciences, IISER Berhampur for useful discussions.
Estimation of transport coefficients of dense hadronic and quark matter
- Received Date: 2022-09-19
- Available Online: 2023-04-15
Abstract: In this study, we calculated transport coefficients including the shear viscosity and electrical conductivity relative to the density of dense hadronic and quark matter. By considering the simple massless limit for the quark matter and two different effective models for the hadronic matter, we estimated the transport coefficients of the two phases separately. Accordingly, density profiles of the transport coefficients were depicted in two parts: the phase-space part and the relaxation time part. From calculating the shear viscosity to density ratio, we also explored the nearly perfect fluid domain of the quark and hadronic matter.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: