-
Since the discovery of nuclear fission in the late 1930s [1], finding a method of accurately describing the nuclear fission process has become one of the biggest challenges in theoretical research. The fission process not only involves the collective motion of a large number of nucleons but is also affected by various structural effects. Moreover, the complexity and richness of fission have been revealed theoretically and experimentally over more than 80 years [2–4]. Nuclear fission data have many practical applications, including nuclear safety measures, accelerator technology, homeland security, medicine, nuclear energy, nuclear reactor waste transmutation [5–7], and the r-process of neutron star mergers [8]. A precise description of the pre-neutron fragment mass yield, which is one of the most important quantities for neutron-induced fission, is of great importance in understanding the fission mechanism and practical applications [9].
Several important theories and models have been developed to understand the fission mechanism or quantitatively calculate fragment mass yields [10, 11]. Calculating fission observables based on the time-dependent generating coordinate method and Hartree-Fock-Bogoliubov (HFB) microscopic model is difficult and time-consuming when considering the effective interaction of the finite force range [12]. Although the macro-dynamic model has been used to calculate the mass distribution of fission fragments, no accurate calculation methods could be obtained for several parameters that are sensitive to the viscosity coefficient and mass tensor of the fission process [13].
The GEF model, a semi-empirical phenomenological model, combines physical concepts from quantum mechanics and statistical mechanics with specific experimental information to adjust a set of suitable parameters for different fission systems. It can avoid the limitation of microscopic calculation, simplify the calculation process, and give reliable predictions for a variety of fission observables for a large number of fissile nuclei [14].
The pre-neutron fragment mass yields of actinide nuclei induced by neutrons in a region of several MeVs have been theoretically studied based on the empirical fission potential (EFP) model proposed in our previous study [15]. Immediately, the EFP model was extended up to 60 MeV for the
$ ^{232} $ Th(n, f) and$ ^{238} $ U(n, f) reactions to quantitatively describe the pre-neutron fragment mass yields [9, 16]. However, there are still no publications describing pre-neutron fragment mass yields in the vicinity of thermal neutron energy. It is worth mentioning that several quantities after scission are highly important for applications because of the larger cross sections in the low incident energy region. Thus, the feasibility of this EFP model at the incident energies from thermal up to 20 MeV should be verified. In particular, the neutron-induced$ ^{235} $ U and$ ^{239} $ Pu (as important fuel nuclides) reactions have no threshold. Unfortunately, there is little experimental data on pre-neutron fragment mass yields at incident energies from thermal up to 20 MeV for these two reactions. Therefore, pre-neutron fragment mass yields should be theoretically recommended at incident energies from thermal up to the 20 MeV region.This paper is organized as follows: In Sec. II, the EFP model is briefly introduced. The calculated results of the pre-neutron fragment mass yields for the
$ ^{232} $ Th(n, f) and$ ^{238} $ U(n, f) reactions are shown and compared with the results of the GEF model in Sec. III. Finally, a brief summary is given in Sec. IV. -
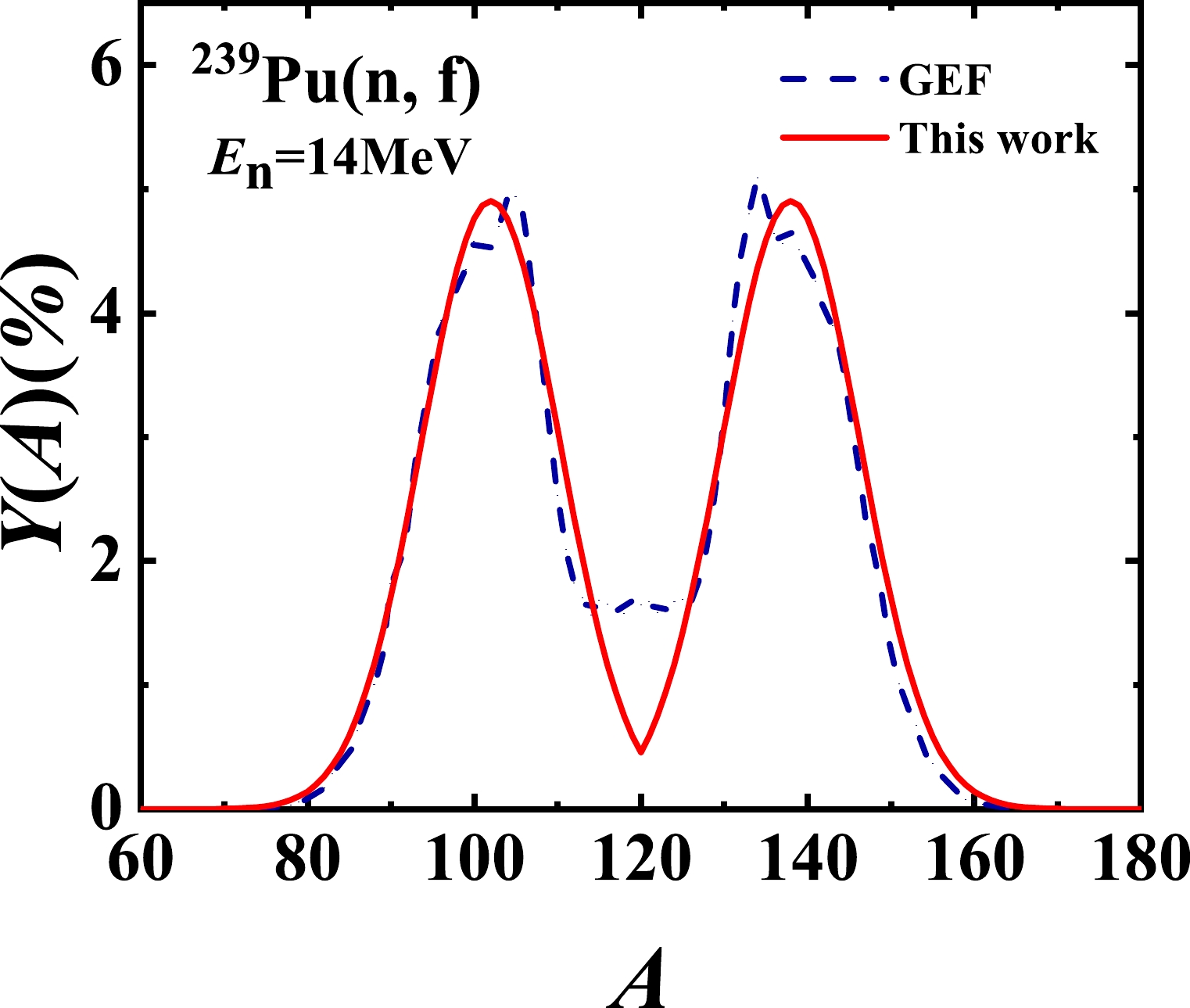
Figure 8. (color online) Predicted pre-neutron fragment mass yields for the
$ ^{239} $ Pu(n, f) reaction at an incident energy of 14 MeV.Based on the bimodal characteristic of actinide nuclear fission, the EFP model is proposed to describe the pre-neutron fragment mass yield [9, 15, 16]. In terms of the EFP model, the pre-neutron fragment mass yield can be expressed as
$ \begin{array}{*{20}{l}} Y(A)=C {\rm e}^{-U(A)}, \end{array} $

(1) where C is the normalization constant, and the variable A denotes the mass number of the primary fragment.
The empirical fission potential U(A) is expressed as
$ \begin{array}{*{20}{l}} U(A)=\left\{\begin{array}{ll} u_{1}\left(A-A_{1}\right)^{2}, & A \leq a \\ -u_{0}\left(A-A_{0}\right)^{2}+R, & a \leq A \leq b ,\\ u_{2}\left(A-A_{2}\right)^{2}, & A \geq b \end{array}\right. \end{array} $

(2) where the parameters a and
$ b=\dfrac{\left(A_{0}-a\right)\left(A_{0}-A_{1}\right)}{A_{2}-A_{0}}+A_{0} $ are the smooth connection points,$ A_{1} $ and$ A_{2} $ are the positions of the light and heavy fragment peaks of the pre-neutron fragment mass yields, respectively, and$ A_{0} $ denotes the corresponding position at the symmetric fission point. The potential parameters$ u_{0} $ ,$ u_{1} $ , and$ u_{2} $ are expressed as$ \begin{aligned}[b] u_{0}=&\dfrac{R}{\left(A_{0}-a\right)\left(A_{0}-A_{1}\right)},\\ u_{1}=&\dfrac{R}{\left(A_{0}-A_{1}\right)\left(a-A_{1}\right)},\\ u_{2}=&\dfrac{R}{\left(A_{2}-A_{0}\right)\left(A_{2}-b\right)}. \end{aligned} $

(3) The pre-neutron fragment mass yield of binary fission should be normalized to 200
$ \% $ . Therefore, the normalization constant C can be analytically expressed as$ \begin{array}{*{20}{l}} \begin{aligned} C=\dfrac{200 {\text%}}{\displaystyle\int_{0}^{\infty} \exp [-U(A)] {\rm d} A}=\dfrac{200 {\text%}}{I_{0}+I_{1}+I_{2}}, \end{aligned} \end{array} $

(4) with
$ \begin{aligned}[b] I_{0}=&\dfrac{\sqrt{\pi} {\rm e}^{-R}}{2 \sqrt{u_{0}}}\left\{\operatorname{erfi}\left[\left(A_{0}-a\right) \sqrt{u_{0}}\right]+\operatorname{erfi}\left[\left(b-A_{0}\right) \sqrt{u_{0}}\right]\right\}, \\ I_{1}=&\dfrac{\sqrt{\pi}}{2 \sqrt{u_{1}}}\left\{\operatorname{erf}\left[\left(a-A_{1}\right) \sqrt{u_{1}}\right]+\operatorname{erf}\left(A_{1} \sqrt{u_{1}}\right)\right\}, \\ I_{2}=&\dfrac{\sqrt{\pi}}{2 \sqrt{u_{2}}}\left\{1+\operatorname{erf}\left[\left(A_{2}-b\right) \sqrt{u_{2}}\right]\right\}. \end{aligned} $

(5) With increasing incident neutron energy, the valley values of the pre-neutron fragment mass yields obviously increase, in contrast with the peak values. That is, the peak-to-valley ratios decrease with increasing incident neutron energy. The parameter R in Eq. (2) can easily be obtained as
$ \begin{array}{*{20}{l}} \begin{aligned} R=\ln \dfrac{Y\left(A_{1}\right)}{Y\left(A_{0}\right)}, \end{aligned} \end{array} $

(6) where
$ Y(A_1) $ and$ Y(A_0) $ represent the peak and valley values of the pre-neutron fragment mass yields, respectively. Thus, all of the model parameters are functions of$a, A_0, A_1, A_2$ , and R. In particular, the parameter a can be obtained by solving Eq. (1) and only defining$ A = A_2 $ . Therefore, there are no artificially adjustable parameters.With the increase in incident neutron energy, the excitation energy of the compound nucleus increases, and a few neutrons (known as pre-neutrons, that is, evaporation neutrons) are evaporated before scission. The number of pre-neutrons can be obtained from the corresponding multi-chance fission cross sections. The relationship between the positions of the peak and valley and the mass number
$ A_{FN} $ of the fissile nucleus is expressed as$ \begin{array}{*{20}{l}} \left\{\begin{array}{l} A_{1}=A_{FN}-A_{2},\\ A_{0}=(A_{1}+A_{2})/2,\\ A_2=A_2^{gs}-\widetilde{n}\left(E_{n}\right), \end{array}\right. \end{array} $

(7) where
$ A_2^{gs} \approx $ 140 denotes the peak position of the heavy fragment mass yields for neutron-induced actinide fission at low incident energies [15],$ \widetilde{n}(E_{n}) $ is the number of pre-neutrons corresponding to the different multi-chance fission channels, and$ E_{n} $ denotes the incident energy of the neutron [15]. When the number of pre-neutrons is zero (that is,$ \widetilde{n}(E_{n}) $ =0), the mass number of the compound nucleus$ A_{CN} $ is that of the fissile nucleus, that is,$ A_{FN}=A_{CN} $ . -
With increasing incident neutron energy, the excitation energy of the compound nucleus increases; hence, a few pre-neutrons evaporate before scission. The number of pre-neutrons can be obtained from the corresponding multi-chance fission cross sections. Therefore, the fission cross sections of the
$ ^{235} $ U(n, f) reaction are investigated. Figure 1 shows the experimental and evaluated fission cross sections of the$ ^{235} $ U(n, f) reaction. The experimental data are obtained from Refs. [17–19]. The evaluated values of ENDF/B-VIII, indicated by the pink dotted line, are recommended as standard cross sections for this reaction [20]. There is an obvious step phenomenon, and every step corresponds to the number of pre-neutrons. From Fig. 1, it can be established that the number$ \widetilde{n}\left(E_{n}\right) $ of pre-neutrons can be roughly expressed as follows: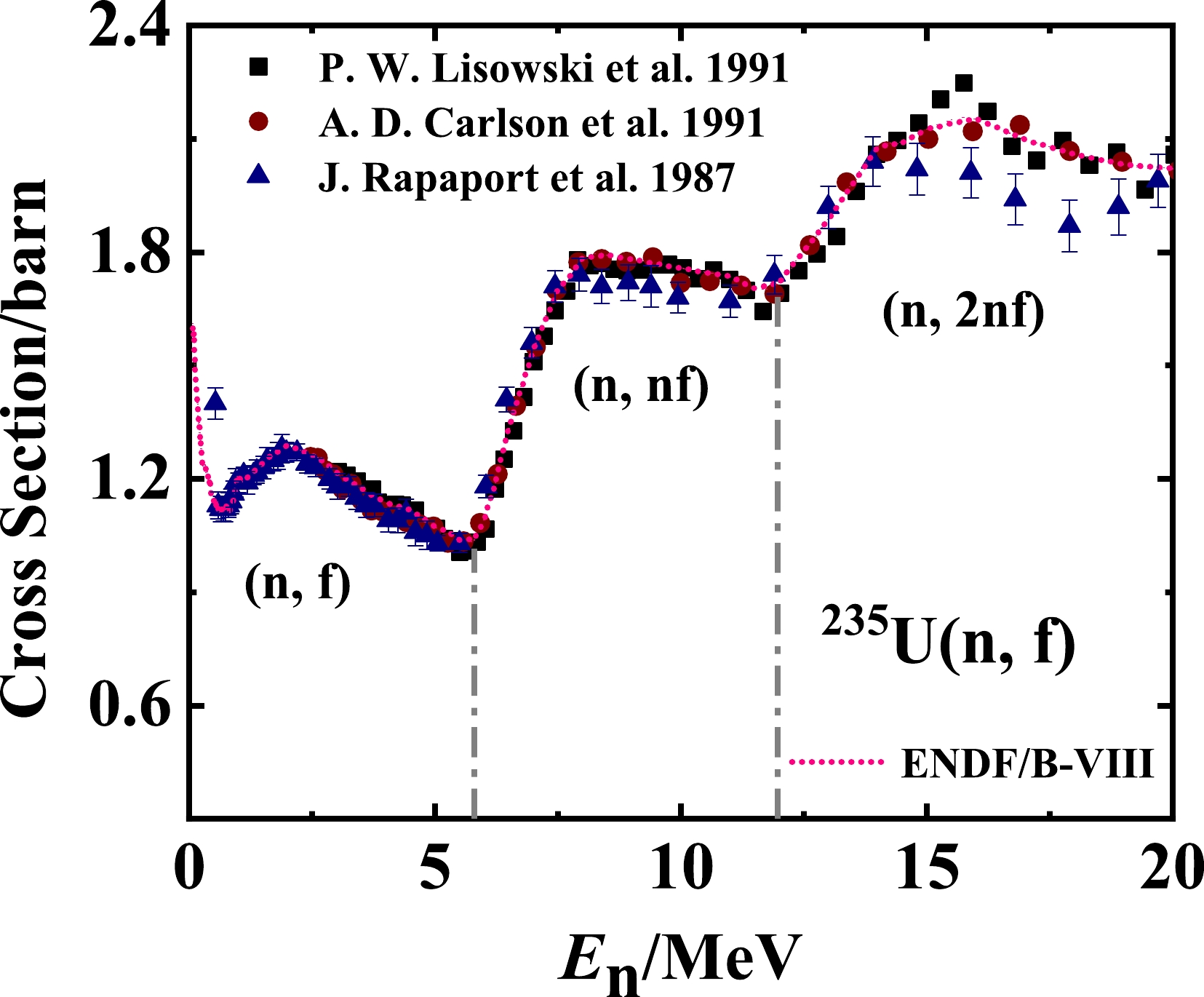
Figure 1. (color online) Fission cross section of the
$ ^{235} $ U(n, f) reaction for incident neutron energies up to 20 MeV. The experimental data are obtained from Refs. [17] (circles), [18] (triangles), and [19] (squares). The pink dotted line represents the evaluated values of ENDF/B-VIII [20]. The perpendicular dashed lines label the incident energy regions corresponding to different multi-chance fission channels, such as (n, f), (n, nf), and (n, 2nf).$ \begin{array}{*{20}{l}} \widetilde{n}\left(E_{n}\right)=\left\{\begin{array}{ll} 0, \quad \quad & E_{n} < 5.5 \ \mathrm{MeV}, \\ 1, \quad \quad & 5.5 \leq E_{n} < 11.5 \ \mathrm{MeV}, \\ 2, \quad \quad & 11.5 \leq E_{n} < 20 \ \mathrm{MeV}. \end{array}\right. \end{array} $

(8) The experimental values of
$ Y(A_0) $ and$ Y(A_1) $ [21–24], which denote the valleys and peaks of the pre-neutron fragment mass yields for the$ ^{235} $ U(n, f) reaction, are fitted to the functions of the incident neutron energies,$ \begin{aligned}[b] Y\left(A_{0}\right)=&\alpha_{0}+\beta_{0} \operatorname{Exp}\left(-E_{n} / \lambda_{0}\right),\\ Y\left(A_{1}\right)=&\alpha_{1}+\beta_{1} \operatorname{Exp}\left(-E_{n} / \lambda_{1}\right), \end{aligned} $

(9) where the parameters
$ \alpha_{0} $ ,$ \beta_{0} $ ,$ \lambda_{0} $ ,$ \alpha_{1} $ ,$ \beta_{1} $ , and$ \lambda_{1} $ are finally determined by the experimental data of$ Y(A_{1}) $ and$ Y(A_{0}) $ and listed in Table 1. The exponential energy dependences of the peaks$ Y(A_{1}) $ and valleys$ Y(A_{0}) $ of the pre-neutron fragment mass yields for the$ ^{235} $ U(n, f) reaction are shown in Fig. 2 as red solid lines. The experimental data are obtained from Refs. [21] (rhombus), [22] (squares), [23] (circles), and [24] (triangles). Furthermore, Eq. (9) approximately equals the linear results in the incident energy region 0.5$ < E_{n} < $ 5.5 MeV, as shown in Ref. [15].$ \alpha_{i} $ 

$ \beta_{i} $ 

$ \lambda_{i} $ 

$ ^{235} $ U(n, f)

$ i=0 $ 

−0.215 0.218 −10.754 $ i=1 $ 

2.052 4.620 43.161 $ ^{239} $ Pu(n, f)

$ i=2 $ 

0.039 0.024 0 $ i=3 $ 

6.060 −0.135 0 Table 1. Parameters of the exponential dependences in Eq. (9) and Eq. (11) for this study.

Figure 2. (color online) Peak
$ Y(A_{1}) $ and valley$ Y(A_{0}) $ of the pre-neutron fragment mass yields for the$ ^{235} $ U(n, f) reaction as a function of incident neutron energy. The experimental data are obtained from Refs. [21] (rhombus), [22] (squares), [23] (circles), and [24] (triangles). The red solid lines represent the results of this study.Using Eqs. (1)–(9) and Table 1, the calculated pre-neutron fragment mass yields for the
$ ^{235} $ U(n, f) reaction are shown by the red solid lines in Fig. 3 and Fig. 4 at different incident energies. We can see that the theoretical results of this study agree well with the experimental data, which are obtained from Refs. [21–26]. In particular, Fig. 4 shows the results at the thermal neutron energy, which have not been previously published. The results of the GEF model [14] are also simultaneously compared in Fig. 3 and Fig. 4 as blue dash lines. The root mean square deviations at different incident energies of this study and the GEF model are listed in Table 2. As an example, the potential parameters at different incident energies ($E_{n}=$ 0.0253 eV, 6 MeV, and 14 MeV) are listed in Table 3. This indicates that the EFP model can reasonably describe existing data on pre-neutron fragment mass yields for the$ ^{235} $ U(n, f) reaction at incident energies from thermal up to 20 MeV.
Figure 3. (color online) Pre-neutron fragment mass yields for the
$ ^{235} $ U(n, f) reaction at incident energies of 5.5 MeV (a), 6 MeV (b), 7.04 MeV (c), and 15.5 MeV (d). The scattered symbols denote the experimental data, which are taken from Refs. [21] (rhombus), [22] (squares), [23] (circles), and [24] (triangles). The blue dashed and red solid curves denote the calculated results of the GEF model[14] and this study, respectively.$E_{n}/\mathrm{MeV}$ 

$ ^{235} $ U(n, f)

$ ^{239} $ Pu(n, f)

Model 2.53 $ \times 10^{-8} $ 

0.542 0.554 GEF 0.536 0.376 This study 0.72 $ \setminus $ 

0.585 GEF $ \setminus $ 

0.299 This study 1.72 $ \setminus $ 

0.503 GEF $ \setminus $ 

0.324 This study 2.72 $ \setminus $ 

0.457 GEF $ \setminus $ 

0.310 This study 4.48 $ \setminus $ 

0.540 GEF $ \setminus $ 

0.267 This study 5.05 0.546 $ \setminus $ 

GEF 0.355 $ \setminus $ 

This study 6 0.397 $ \setminus $ 

GEF 0.239 $ \setminus $ 

This study 7.04 0.499 $ \setminus $ 

GEF 0.330 $ \setminus $ 

This study 15.5 0.338 $ \setminus $ 

GEF 0.179 $ \setminus $ 

This study Table 2. Root mean square deviation at different incident energies compared with existing experimental data and the theoretical results.
${\rm Reaction}$ 

$ E_\mathrm{n}/\mathrm{MeV} $ 

a b $ I_0 $ 

$ I_1 $ 

$ I_2 $ 

R $ ^{235} $ U(n, f)

2.53 $ \times 10^{-8} $ 

117.99 118.01 0.000 14.207 14.207 7.529 6 111.64 124.36 0.531 16.181 16.181 3.596 14 109.71 126.29 2.552 17.246 17.246 2.216 $ ^{239} $ Pu(n, f)

2.53 $ \times 10^{-8} $ 

119.99 120.01 0.000 15.789 15.789 5.031 6 119.99 120.01 0.000 18.371 18.371 3.325 14 119.99 120.01 0.002 21.531 21.531 2.373 Table 3. Potential parameters adopted in this study.
-
Besides the
$ ^{235} $ U(n, f) reaction, the EFP model was also applied to the$ ^{239} $ Pu(n, f) reaction. First, the fission cross sections of the$ ^{239} $ Pu(n, f) reaction are investigated, as shown in Fig. 5. The experimental data are obtained from Refs. [27–29], and the pink dotted line represents the evaluation results of ENDF/B-VIII [20], which are recommended as standard cross sections. There is also an obvious step phenomenon, and every step corresponds to the number of pre-neutrons. From Fig. 5, it can be established that the number$ \widetilde{n}\left(E_{n}\right) $ of pre-neutrons can be roughly expressed as follows:$ \begin{array}{*{20}{l}} \widetilde{n}(E_{n})=\left\{\begin{array}{ll} 0, \quad & E_{n} < 5.6 \ \mathrm{MeV}, \\ 1, \quad & 5.6 \leq E_{n} < 12 \ \mathrm{MeV}, \\ 2, \quad & 12 \leq E_{n} < 20 \ \mathrm{MeV}. \end{array}\right. \end{array} $

(10) Based on monoenergetic experimental data from Ref. [30], the values of the valleys
$ Y(A_{0}) $ and peaks$ Y(A_{1}) $ of the pre-neutron fragment mass yields for the$ ^{239} $ Pu(n, f) reaction are fitted as linear functions of the incident neutron energies [15],$ \begin{aligned}[b] Y\left(A_{0}\right)=&\alpha_{2}+\beta_{2} E_{n},\\ Y\left(A_{1}\right)=&\alpha_{3}+\beta_{3} E_{n}, \end{aligned} $

(11) where the parameters
$ \alpha_{2} $ ,$ \beta_{2} $ ,$ \alpha_{3} $ , and$ \beta_{3} $ are finally determined by the experimental data of$ Y(A_{1}) $ and$ Y(A_{0}) $ and listed in Table 1. Because of scarce measured data, the linear energy dependences of the peaks$ Y(A_{1}) $ and valleys$ Y(A_{0}) $ of the pre-neutron fragment mass yields for the$ ^{239} $ Pu(n, f) reaction are shown in Fig. 6 as red solid lines. The experimental data are obtained from Refs. [30]. Eq. (11) and its parameters can reproduce the results of Ref. [15]. It is expected that there are some measurements at higher incident energies to verify these linear dependences in the future.According to Eqs. (1)–(7), (10), (11), and Table 1, the calculated pre-neutron fragment mass yields for the
$ ^{239} $ Pu(n, f) reaction can reproduce our previous results [15] at different incident energies ($E_{n}=$ 0.72, 1.72, 2.72, and 4.48 MeV). Furthermore, Fig. 7 shows the calculated results at the thermal neutron energy, which have not previously been published. We can see that the theoretical results of this study agree well with the experimental data, which are obtained from Refs. [30] (triangles), [31] (circles), and [32] (squares). Simultaneously, the results of the GEF model [14] are also compared in Fig. 7 as blue dash lines. The root mean square deviations at different incident energies in this study and the GEF model are listed in Table 2. As an example, the potential parameters at different incident energies ($ E_{n} = $ 0.0253 eV, 6 MeV, and 14 MeV) are listed in Table 3. This indicates that the EFP model can also reasonably describe the pre-neutron fragment mass yields for the$ ^{239} $ Pu(n, f) reaction at incident energies from thermal up to 20 MeV, as well as those of the$ ^{235} $ U(n, f) reaction. Figure 8 also gives the predicted results of both this study and the GEF model at an incident energy of 14 MeV.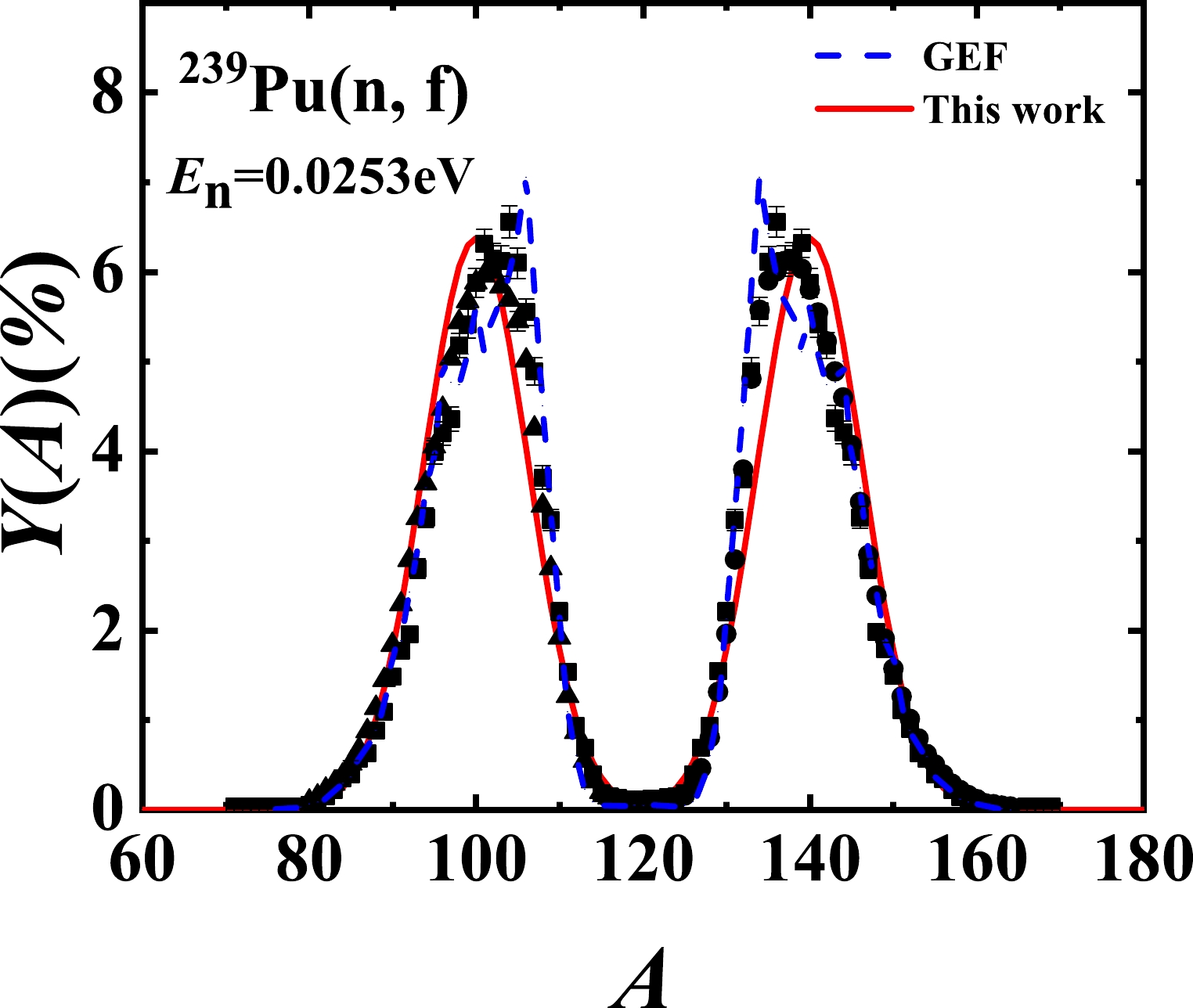
Figure 7. (color online) Pre-neutron fragment mass yields at thermal neutron energies for the
$ ^{239} $ Pu(n, f) reaction. The scattered symbols denote the experimental data, which are taken from Refs. [30] (triangles), [31] (circles), and [32] (squares). The blue dashed and red solid curves denote the calculated results of the GEF model and this study, respectively. -
In this paper, the pre-neutron fragment mass yields for the
$ ^{235} $ U(n, f) and$ ^{239} $ Pu(n, f) reactions at incident energies from thermal up to 20 MeV are calculated on the basis of the EFP model, the potential parameters of which are uniquely obtained from the existing experimental values of the peaks and valleys. The energy dependences of the peaks and valleys are reasonably described by explicit exponential and linear functions for the$ ^{235} $ U(n, f) and$ ^{239} $ Pu(n, f) reactions, respectively. The energy dependences of the number of evaporation neutrons are also derived from multi-chance fission cross sections, which play a crucial role in the reasonable description of pre-neutron fragment mass yields. The calculated results of this study can not only reproduce our previous results but also agree well with existing data at incident energies from thermal up to 20 MeV. This extended energy region is exactly what nuclear data libraries need.Furthermore, the calculated results of the GEF model are also compared. The root mean square deviations of this study and the GEF model at different incident energies are listed in Table 2. As shown, the EFP model in this study can feasibly describe pre-neutron fragment yields quantitatively. The results show that the feasibility of this EFP model is verified in this extended energy region. Therefore, the EFP model is expected to be a tool used to set up the nuclear database files of pre-neutron fragment mass yields for the
$ ^{235} $ U(n, f) and$ ^{239} $ Pu(n, f) reactions at incident energies from thermal up to 20 MeV. -
We thank Profs. Ning Wang, Li Ou, Min Liu, Dr. Yuting Rong, and anonymous referees for valuable suggestions.
Pre-neutron fragment mass yields for 235U(n, f ) and 239Pu(n, f ) reactions at incident energies from thermal up to 20 MeV
- Received Date: 2022-02-19
- Available Online: 2023-04-15
Abstract: Pre-neutron fragment mass yields in the vicinity of the thermal neutron energy are highly important for applications because of the larger fission cross sections of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: