-
The large rate of Z boson production at the LHC may facilitate the experimental analysis of rare Z-boson decay channels. In 2019, a search for rare Z-boson decays into a pair of heavy vector quarkonia,
$ Z \to V V $ ($ V=J/\Psi, \Upsilon $ ), was performed for the first time by the CMS Collaboration [1], and the upper limits on the branching fractions were obtained. Very recently, these upper limits were updated in Ref. [2] as$ {\cal B}(Z\to J/\Psi J/\Psi) < 11\times 10^{-7} $

(1) and
$ {\cal B}(Z\to \Upsilon(1S) \Upsilon(1S)) < 1.8\times 10^{-6} $

(2) at the 95% confidence level.
In the standard model (SM), rare decays of
$ Z\to VV $ have already been calculated in Refs. [3, 4]. It is generally believed that the lowest QCD diagrams, as displayed in Fig. 1, would give rise to the dominant contributions to these transitions in the SM. In this study, we reexamined the analysis of these decays in the SM. It was shown that, besides the diagrams in Fig. 1, some other diagrams, as displayed in Fig, 2, may also bring about important contributions due to the virtual photon exchange. Therefore, it is necessary to perform a systematical calculation of the branching ratios of$ Z\to VV $ decays by including all of the relevant diagrams. In future studies, this will help to compare the SM predictions with experimental measurements.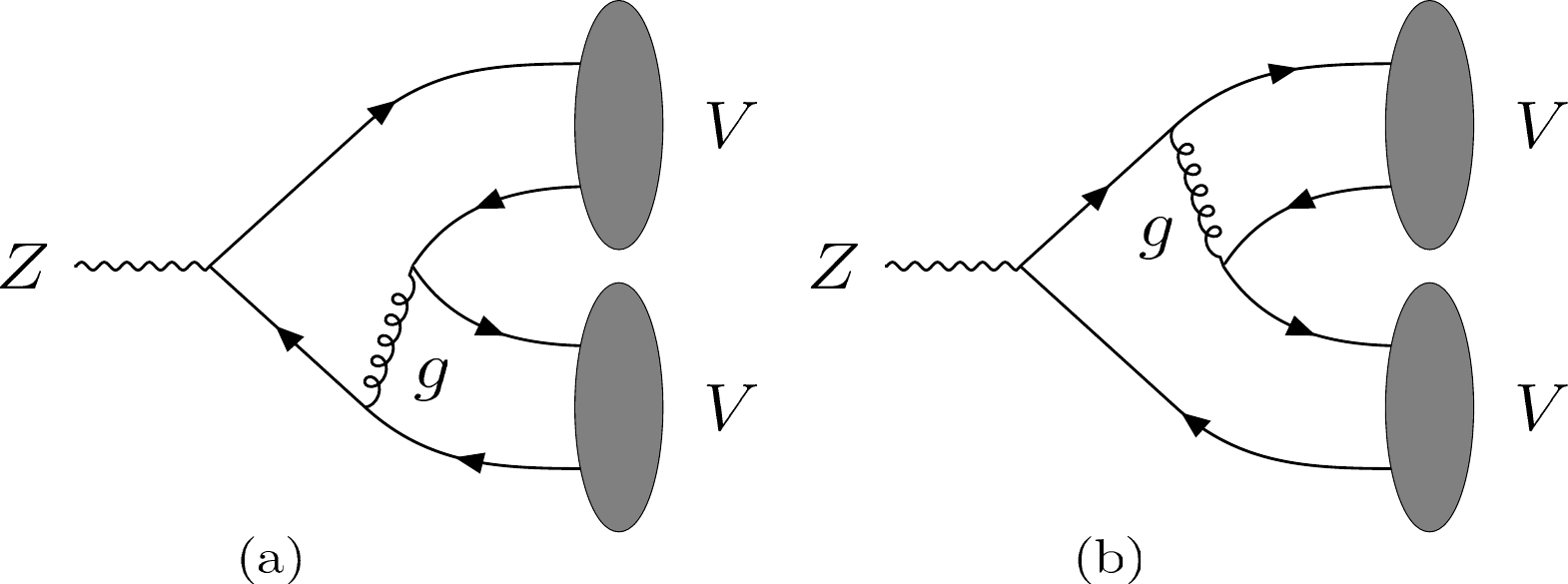
Figure 1. Lowest-order QCD diagrams contributing to
$ Z\to VV $ decays. The solid line with arrows denotes the heavy quarks Q or$ \bar{Q} $ . Owing to the exchange of final identical particles, there are four diagrams in total.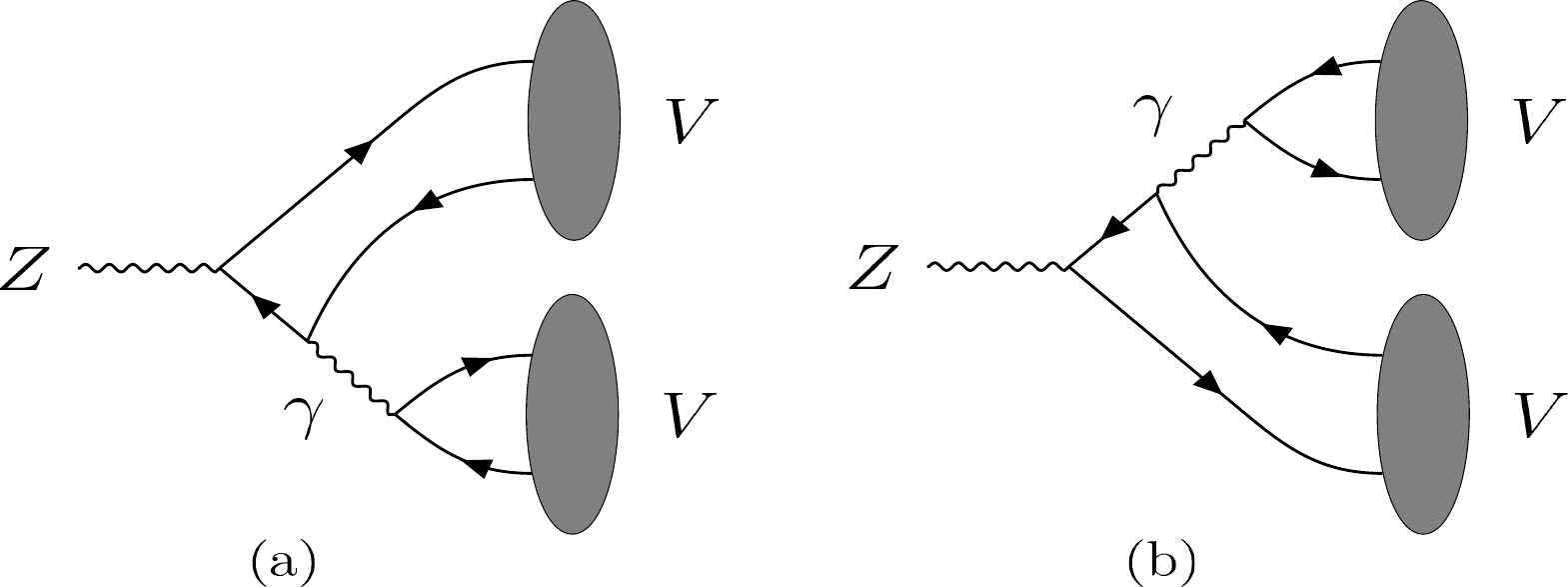
Figure 2. Diagrams contributing to
$ Z\to VV $ decays in the standard model (SM) through the virtual photon exchange. The solid line with arrows denotes the heavy quarks Q or$ \bar{Q} $ . Owing to the exchange of final identical particles, there are four diagrams in total.This paper is organized as follows. In Sec. II, we update the leading-order QCD analysis of
$ Z\to VV $ . The virtual photon contributions to Z-boson decays into the same fianl states will be studied in Sec. III. In Sec. IV, a rare$ Z\to V P $ mode, with P denoting pseudoscalar heavy quarkonia, is similarly analyzed. Finally, we summarize our results in Sec. V. -
Let us first deal with Fig. 1, which gives the leading-order QCD contributions to
$ Z\to VV $ transitions. To evaluate the decay amplitudes explicitly, one should project$ Q\bar{Q} $ into the corresponding hadron states. As a reasonable approximation for the leading order calculation, in the present work, we adopt the nonrelativistic color-singlet model [5–13], in which the quark momentum and mass are taken to be one half of the corresponding quarkonium momentum p and mass$ m_V $ , i.e.,$ p_Q=p_{\bar{Q}}= p/2 $ and$ m_{V}=2m_Q $ . Thus, for the$ Q\bar{Q} $ pair to form the heavy quarkonium V, one can replace the combination of the Dirac spinors for Q and$ \bar{Q} $ by the following projection operator [14, 15]:$ {v(p_{\bar{Q}})} {\bar{u}(p_Q)} \longrightarrow \frac{\psi_{V}(0)I_c}{2\sqrt{3m_V}} {\not \epsilon}^*(\not p+m_V), $

(3) where
$ I_c $ is the$ 3\times 3 $ unit matrix in color space, and$ \epsilon^{*\mu} $ is the polarization vector of the heavy quarkonium V.$ \psi_{V}(0) $ is the wave function at the origin for V, which is a nonperturbative parameter.Using the standard Z-boson and gluon couplings to quark pair, one can perform the direct calculation from Fig. 1, which gives
$ {\cal M}_1=\frac{256\pi g^Q_a g \alpha_s m_V^2}{3\cos\theta_W m_Z^4}\left(\frac{\psi_V(0)}{\sqrt{m_V}}\right)^2\varepsilon^{\alpha\beta\mu\nu}\epsilon^*_\alpha(q) \epsilon^*_\beta(p)\epsilon^Z_\mu(k) (p-q)_\nu. $

(4) Here, we take the two quarkonia in the final state and Z-boson momenta to be p, q, and
$ k=p+q $ , respectively. g is the weak SU(2)$ _L $ coupling constant,$ \theta_W $ is the Weinberg angle,$ g_a^Q $ is the axial-vector coupling of the Z to the quark Q, and$ g_a^Q=T_3^Q $ , with$ T_3^Q $ denoting the third component of the weak isospin of the heavy quark.$ \alpha_s= g_s^2/4\pi $ , and$ g_s $ is the strong coupling constant.One can find that only
$ g_a^Q $ appears in the amplitude$ {\cal M}_1 $ , and the vector-component of the$ ZQ\bar{Q} $ coupling cannot contribute to$ Z\to VV $ decays due to the charge conjugate invariance①. This has also been shown explicitly in Ref. [3]. After squaring the amplitude and summing/averaging over the polarizations of the final or initial particles, one can obtain the decay rate as$ \Gamma(Z\to VV)=\frac{512\pi g^2\alpha_s^2}{27 \cos^2\theta_W m_Z^5}|\psi_V(0)|^4 \left(1-\frac{4m_V^2}{m_Z^2}\right)^{5/2}. $

(5) Note that
$ \Gamma(Z\to VV) $ will not vanish when we set$ m_V=0 $ . This seems to be in contrast with the Landau-Yang theorem [16, 17], which states that a massive vector such as the Z-boson cannot decay into two one-shell photons. Here, the difference is that the final vector particle V is also massive, and it has the longitudinal polarization. In the limit of$ m_V\to 0 $ , the longitudinal component will be proportional to$ 1/m_V $ . One can easily find that, from Eq. (4), when one of the final vector bosons is longitudinally polarized, the$ m_V $ dependence of the amplitude disappears. Thus, numerically, by taking$ \begin{aligned}[b]& \psi^2_{J/\psi}(0)=0.073^{+0.011}_{-0.009}~ {\rm GeV}^3,\\\\ &\psi^2_\Upsilon(0)=0.512^{+0.035}_{-0.032}~ {\rm GeV}^3 \end{aligned} $

(6) from Refs. [18–20] and
$ \alpha_s(m_Z)=0.118 $ , we have$ {\cal B}(Z\to J/\Psi J/\Psi) = 1.5\times 10^{-13} $

(7) and
$ {\cal B}(Z\to \Upsilon(1S) \Upsilon(1S)) = 6.8 \times 10^{-12}, $

(8) which predict small branching fractions for these processes.
Note that our analytic expression for
$ \Gamma(Z\to VV) $ in Eq. (5) will be identical to the one shown in Eq. (3) of Ref. [3] if we take$ \psi_V(0)\to \sqrt{\frac{1}{4\pi}}R_S(0),\;\;\;\; g^2\to \frac{4\pi \alpha_{\rm em}}{\sin^2\theta_W} $

with
$ \alpha_{\rm em}=e^2/4\pi $ . However, our numerical results are not in good agreement with the predictions obtained in Ref. [3]:$ {\cal B}(Z\to J/\Psi J/\Psi) = 7.2 \times 10^{-13} $ and$ {\cal B}(Z\to \Upsilon(1S) \Upsilon(1S)) = 6.6 \times 10^{-11} $ . Even if the numerical values for$ R_S(0) $ 's of Ref. [3] are used in our calculation, one still cannot reproduce their results②.Moreover, our prediction for the charmonium mode is larger than the one by the authors of Ref. [4], in which they obtained
$ {\cal B}(Z\to J/\Psi J/\Psi)=2.3\times 10^{-14} $ by taking the nonperturbative matrix element$ \langle O_1\rangle_{J/\Psi}=0.22 $ GeV$ ^3 $ and the strong coupling$ \alpha_s(m_Z^2)=0.13 $ . Furthermore, using the relation$ \langle O_1\rangle_{J/\Psi}=2 N_C |\psi_{J/\Psi}(0)|^2 $ [18], one may find that Eq. (5) will give$ {\cal B}(Z\to J/\Psi J/\Psi)=4.7\times 10^{-14} $ , which is still larger by a factor of approximately 2. -
We have updated the analysis of the leading-order QCD contributions to
$ Z\to VV $ decays. One may argue that the next-to-leading order QCD corrections could be important. This is of course interesting but not the main purpose of the present study. As pointed out in Introduction, the diagrams in Fig. 2 could also lead to significant contributions to these transitions. Thus, the Z-boson decays into double vector heavy quarkonia could also occur via$ Z\to V \gamma^* $ , with the virtual photon transforming into V. A similar mechanism has been studied in rare Higgs and other Z-boson decays, such as in$ h\to \gamma V $ [20],$ h\to Z V $ [21],$ h\to VV $ [22], and$ Z\to J/\Psi \ell^+\ell^- $ [23–26] processes.Now, from Fig. 2, it is straightforward to derive the corresponding decay amplitude for
$ Z\to VV $ , which reads$ {\cal M}_2=\frac{96\pi g^Q_a g \alpha_{\rm em} e_Q^2}{\cos\theta_W m_Z^2}\left(\frac{\psi_V(0)}{\sqrt{m_V}}\right)^2\varepsilon^{\alpha\beta\mu\nu}\epsilon^*_\alpha(q) \epsilon^*_\beta(p)\epsilon^Z_\mu(k) (q-p)_\nu. $

(9) Here,
$ e_Q $ is the electric charge of the heavy quark,$ e_c=2/3 $ , and$ e_b=-1/3 $ . As mentioned above, due to the charge conjugation symmetry, only the axial-vector component of the$ ZQ\bar{Q} $ coupling contributes to the amplitude. One can find that$ {\cal M}_1 $ and$ {\cal M}_2 $ have the same structure but different signs. It is generally assumed that$ {\cal M}_2 $ will be suppressed because of the electromagnetic coupling. However, by computing$ {\cal R}_V=\frac{{\cal M}_2}{{\cal M}_1}=-\frac{9 e_Q^2 \alpha_{\rm em}}{8\alpha_s}\frac{m_Z^2}{m_V^2}, $

(10) it is evident that the smallness of the vector quarkonia masses will give rise to a large factor
$ m_Z^2/m_V^2 $ , which thus counteracts the suppression of$ \alpha_{\rm em} $ . Explicitly, we have$ {\cal R}_{J/\Psi}=-27.7 $

(11) for the charmonium case, and
$ {\cal R}_{\Upsilon(1S)}=-0.75 $

(12) for the bottomonium case. In the above numerical calculation, we used
$ \alpha_{\rm em}(m_{J/\Psi})= $ 1/132.64 and$ \alpha_{\rm em}(m_{\Upsilon(1S)})= 1/131.87 $ . Combining$ {\cal M}_1 $ and$ {\cal M}_2 $ , we thus obtain the leading order SM predictions for the decay rates of$ Z\to VV $ processes as follows:$ {\cal B}(Z\to J/\Psi J/\Psi) = (1.1\pm 0.3) \times 10^{-10}, $

(13) and
$ {\cal B}(Z\to \Upsilon(1S) \Upsilon(1S)) = (4.4\pm 0.6) \times 10^{-13}. $

(14) Here, the errors of these results are only due to the uncertainties of the
$ \psi^2_V(0) $ 's in Eq. (6). Obviously, comparing with the leading-order QCD contributions [Eqs. (7) and (8)], the large amplitude$ {\cal M}_2 $ for the charmonioum final states leads to a significant enhancement of$ {\cal B}(Z\to J/\Psi J/\Psi) $ , which could reach up to$ 10^{-10} $ , while the comparable$ {\cal M}_1 $ and$ {\cal M}_2 $ with different signs in the bottomonium case result in accidental cancellation in the amplitude, which substantially decreases the decay rate of$Z\to \Upsilon(1S) \Upsilon(1S)$ . In the Note added in proof of their paper, the authors of Ref. [3] pointed out that these decays could be via$ Z\to V\gamma^*\to VV $ , and the decay rate could be approximated by$ \Gamma(Z\to V\gamma){\cal B}(\gamma^*\leftrightarrow V)/2 $ . Using the results for$ {\Gamma}(Z\to V\gamma) $ in Ref. [27], they further obtained${\cal B}(Z\to J/\Psi J/\Psi)=2.7\times 10^{-11}$ and${\cal B}(Z\to \Upsilon \Upsilon)= 2.1\times 10^{-12}$ . In the present study, we included both types of contributions to predict$ {\cal B}(Z\to VV) $ .Only uncertainties of the
$ \psi^2_V(0) $ 's are included to evaluate the errors on our results because our present study is performed in the framework of a nonrelativistic color-singlet model. Further, one can use the nonrelativistic QCD (NRQCD) factorization method [28, 29] to calculate corrections in powers of$ \alpha_s $ and v (v is the heavy-quark velocity in the quarkonium rest frame). Our results are equal to the ones from the NRQCD approach at the leading order. To estimate the theoretical errors, one may simply assume that the uncalculated QCD corrections in$ \alpha_s $ are of relative size$ \alpha_s(m_V) $ and that the uncalculated corrections in v are of relative size$ v^2 $ . This leads to${\cal B}(Z\to J/\Psi J/\Psi) = (1.1\pm 0.4) \times 10^{-10}$ and${\cal B}(Z\to \Upsilon(1S) \Upsilon(1S)) = (4.4\pm 0.9) \times 10^{-13}$ by taking$ \alpha_s(m_V)\approx 0.25 $ and$ v^2 \approx 0.3 $ for charmonium and$ \alpha_s(m_V)\approx 0.18 $ and$ v^2\approx 0.1 $ for bottomonium, respectively. These errors are comparable to the ones in Eqs. (13) and (14).A systematical analysis of corrections to our leading-order predictions from higher order
$ \alpha_s $ and v in the framework of NRQCD will be an interesting theoretical investigation. Very recently, next-to-leading-order QCD corrections to Z-boson decays into double charmonium were studied, and$ {\cal B}(Z\to J/\Psi J/\Psi) $ was predicted to be$ (1.0\sim 1.3)\times 10^{-10} $ [30], which is consistent with our result. -
Similarly, rare decays of
$ Z\to V P $ can also be analyzed. The leading-order QCD contributions to these processes come from diagrams such as that in Fig. 1, in which one of the V's is replaced by P, as calculated in Refs. [3, 4]. The corresponding decay amplitude can be written as$ {\cal M}_1^{VP}={\rm i}\frac{512\pi g_v^Q g \alpha_s\psi_V(0)\psi_P(0)}{3\cos\theta_W m_Z^4}\varepsilon^{\alpha\beta\mu\nu}\epsilon^*_\alpha(p)\epsilon^Z_\beta(k)p_\mu q_\nu, $

(15) where
$ g_v^Q=T_3^Q-2 e_Q \sin^2\theta_W $ is the vector coupling of the$ ZQ\bar{Q} $ vertex, and the following projector$ {v(p_{\bar{Q}})} {\bar{u}(p_Q)} \longrightarrow \frac{\psi_{P}(0) I_c}{2\sqrt{3 m_{P}}} {\rm i}\gamma_5(\not p + m_{P}) $

(16) for the pseudoscalar quarkonium P has been used in the derivation. As a good approximation, we set
$ m_V=m_P $ . Meanwhile, similar to the$ VV $ final states, as shown in Fig. 2, these channels can also happen through$ Z\to P\gamma^* $ with$ \gamma^*\to V $ , which gives$ {\cal M}_2^{VP}=-{\rm i}\frac{96\pi g_v^Q g \alpha_{\rm em} e_Q^2\psi_V(0)\psi_P(0)}{\cos\theta_W m_Z^2m_V^2}\varepsilon^{\alpha\beta\mu\nu}\epsilon^*_\alpha(p)\epsilon^Z_\beta(k)p_\mu q_\nu. $

(17) One can directly find that the ratio of the two amplitudes
$ {\cal M}_2^{VP} $ and$ {\cal M}_1^{VP} $ is now only half of the value for the$ Z\to VV $ decays. If we only consider the leading-order QCD contributions, i.e., the amplitude$ {\cal M}_1^{VP} $ , we have$ {\cal B}(Z\to J/\Psi \eta_c) = 9.1\times 10^{-14} $

(18) and
$ {\cal B}(Z\to \Upsilon(1S) \eta_b(1S)) = 4.9 \times 10^{-11}, $

(19) where we have assumed that
$ \psi_V(0)=\psi_P(0) $ in the numerical calculation. When both of the amplitudes are included, we obtain$ {\cal B}(Z\to J/\Psi \eta_c) = (1.5\pm 0.4)\times 10^{-11} $

(20) and
$ {\cal B}(Z\to \Upsilon(1S) \eta_b(1S)) = (1.9\pm 0.2) \times 10^{-11}, $

(21) where the errors are also only due to the uncertainties of the
$ \psi_V(0) $ 's. -
We have presented a theoretical analysis of rare Z-boson decays into double heavy quarkonia in the SM. Our study explicitly shows that, besides the leading-order QCD diagrams, other transitions via
$ Z\to V\gamma^* $ and$ Z\to P\gamma^* $ , followed by$ \gamma^*\to V $ , can also bring about significant contributions to these processes. To provide up-to-date theoretical predictions for these rare Z-boson decay for use in the LHC or other future high-precision experimental facilities, we calculate both of them in the present study. The branching fractions for these decays are predicted as shown in Eqs. (13), (14), (20), and (21), respectively, which are far below the current experimental limits reported by the CMS Collaboration [2]. In general, it will be challenging to search for such rare processes. However, some interesting room for new physics may be expected in these decays. One could directly utilize some non-standard$ ZQ\bar{Q} $ interactions, which, for instance, have been analyzed in Refs. [31–33]. The novel couplings might give rise to possible deviations from the SM predictions. Nevertheless, a careful investigation is definitely needed to construct some realistic and significant models. This topic is meaningful for the future study.The enormous events of Z bosons will be produced in the high-luminosity LHC [34, 35] or other future experiments such as the FCC-ee [36] and CEPC [37], both of which will be planned to run at the Z mass region for a period time. Particularly, at the CEPC, running as both a Higgs factory and a Z factory, a huge number of Z bosons, approximately
$ {\cal O} (10^{12}) $ , would be accumulated. We look forward to other interesting searches for rare Z-boson decays being performed at these machines.
Note on rare Z-boson decays to double heavy quarkonia
- Received Date: 2023-01-11
- Available Online: 2023-04-15
Abstract: Within the standard model, we have investigated rare Z-boson decays into double heavy quarkonia,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: