-
One of the most fundamental questions in hadron physics is related to the mechanism of color confinement in Quantum Chromodynamics (QCD). Color-singlet hadronic configurations of quarks and gluons can form bound states or resonances. Besides the well-known combinations of
$ q\bar{q} $ for mesons and$ qqq $ for baryons, other combinations, such as$ gq\bar{q} $ for hybrid states [1], multi-gluons for glueball states [2],$ q\bar{q}q\bar{q} $ for tetraquark states [3],$ qqqq\bar{q} $ for pentaquark states [4] and hexaquark states$ (qqqqqq) $ [5], are also allowed by QCD. Di-baryon [6] and hexaquark states have been searched for in a range of nucleon-nucleon scattering reactions. Recently, an isoscalar resonant structure was observed in the isoscalar two-pionic fusion process$ pn \to d\pi^0\pi^0 $ [7] by the WASA Collaboration and was later confirmed in the other two-pionic fusion processes$ pn\to d\pi^+\pi^- $ [8] and$ pp\to d\pi^+\pi^0 $ [9], and the two-pionic non-fusion process$ pn\to pp\pi^0\pi^- $ [10] and$ pn\to pn\pi^0\pi^0 $ [11]. This state was denoted by$ d^*(2380) $ following the convention used for nucleon excitations. These observations indicate the possibility of the existence of hexaquark and di-baryon configurations. In 2021, the BESIII Collaboration reported the search for hexaquark and di-baryon states in examining the invariant mass spectra of two baryons in the process$e^+e^- \to 2(p\bar{p})$ [12], and no significant signal was observed.Analyzing data sets corresponding to a total integrated luminosity of approximately
$18.8 ~\rm fb^{-1}$ taken at center-of-mass energies$ \sqrt s $ between$ 4.16 $ and$ 4.70 $ GeV with the BESIII detector, we present in this paper the first measurement of the cross section of the process$e^+e^- \to pp\bar{p}\bar{n}\pi^{-} + c.c.$ . We search for the$ d^*(2380) $ and other possible hexaquark or di-baryon states with the data samples with energies above$ 4.60 $ GeV, where the$ \bar{p}\bar{n} $ system with a mass around$ 2.4 $ GeV for$ d^*(2380) $ is kinematically accessible. The mass range of the$ \bar{p}\bar{n} $ system around 2.4 GeV/$ c^2 $ , in which the$ d^*(2380) $ might contribute, is covered by the data samples with energies above$ 4.60 $ GeV. Throughout this paper, charge conjugation is always implied unless explicitly stated, and in discussing systematic uncertainties. -
The BESIII detector [13] records symmetric
$ e^+e^- $ collisions provided by the BEPCII storage ring [14], which operates in the center-of-mass energy range from$ 2.0 $ to$ 4.95 $ GeV. BESIII has collected large data samples in this energy region [15]. The cylindrical core of the BESIII detector covers$ 93\% $ of the full solid angle and consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a$ 1.0 $ T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identification modules interleaved with steel. The charged-particle momentum resolution at$ 1\; {\rm GeV}/c $ is$ 0.5 $ %, and the specific energy loss (dE/dx) resolution is$ 6\% $ for electrons from Bhabha scattering. The EMC measures photon energies with a resolution of$ 2.5\% $ ($ 5\% $ ) at$ 1 $ GeV in the barrel (end cap) region. The time resolution in the TOF barrel region is$ 68 $ ps, while that in the end cap region is$ 110 $ ps. The end cap TOF system was upgraded in$ 2015 $ using multi-gap resistive plate chamber technology, providing a time resolution of$ 60 $ ps [16, 17].The data sets were collected at
$ 29 $ center-of-mass energies between$ 4.16 $ and$ 4.70 $ GeV. The nominal energies of the data sets from$ 4.16 $ to$ 4.60 $ GeV are measured by the di-muon process$ e^+e^- \to (\gamma_{\rm ISR/FSR})\mu^{+}\mu^{-} $ [18, 19], where the subscript ISR/FSR stands for the initial-state or final-state radiation process, respectively. Those for the data sets from$ 4.61 $ to$ 4.70 $ GeV are calibrated by the process$ e^+e^- \to \Lambda_{\rm c}^{+}\bar{\Lambda}_{\rm c}^{-} $ [20]. The integrated luminosity$ \mathcal{L}_{\rm int} $ is determined using large-angle Bhabha scattering events [20, 21]. The total integrated luminosity of all data sets is approximately$18.8 ~\rm fb^{-1}$ .The response of the BESIII detector is modeled with Monte Carlo (MC) simulations using the software framework BOOST [22] based on geant4 [23], which includes the geometry and material description of the BESIII detector, the detector response and digitization models, as well as a database that keeps track of the running conditions and the detector performance. Large MC simulated event samples are used to optimize the selection criteria, evaluate the signal efficiency, and estimate background contributions.
Inclusive MC simulation samples are generated at different center-of-mass energies to study potential background reactions. These samples consist of open charm processes, the ISR production of vector charmonium and charmonium-like states, and the known hadronic continuum processes incorporated in KKMC [24, 25]. The known decay modes are modeled with EVTGEN [26, 27] using branching fractions taken from the Particle Data Group (PDG) [28], and the remaining unknown decays of the charmonium states are simulated with LUNDCHARM [29, 30]. Final-state radiation from charged final-state particles is incorporated with PHOTOS [31]. The signal MC simulation sample of
$ e^+e^- \to p p \bar{p} \bar{n} \pi^{-} $ at each energy point is generated with the events being uniformly distributed in phase space. -
Events with two positive and two negative charged tracks are selected. For each charged track, the polar angle in the MDC with respect to the z direction must satisfy
$ | \cos\theta|<0.93 $ . All charged tracks are required to originate from the interaction region, defined as$ R_{xy}<1 $ cm and$ |V_{z}|<10 $ cm, where$ R_{xy} $ and$ |V_{z}| $ are the distances from the point of closest approach of the tracks to the interaction point in the$ x-y $ plane and in the z direction, respectively. The combined dE/dx and TOF information are used to calculate particle identification (PID) confidence levels for the pion, kaon, and proton hypotheses. Each track is assigned as the particle hypothesis with the highest confidence level. The final state in the$e^+e^- \to p p \bar{p} \bar{n} \pi^{-}$ process is reconstructed with two protons, one antiproton and one$ \pi^{-} $ . In this paper, charge conjugated process is implied.Since the neutron can not be well reconstructed with the BESIII detector, the signal process is determined via the recoiling mass of the reconstructed charged particles, defined as
$ \begin{equation} M_{\rm rec}c^2= \sqrt{(E_{e^+e^-} - E_{pp\bar{p}\pi^-})^{2} - (\vec{P}_{e^+e^-} - \vec{P}_{pp\bar{p}\pi^-})^{2} \cdot c^2}, \end{equation} $

(1) where
$ E_{e^{+}e^{-}} $ and$ \vec{P}_{e^{+}e^{-}} $ are the center-of-mass energy and the momentum of the$ e^{+}e^{-} $ system, respectively;$ E_{pp\bar{p}\pi^{-}} $ and$ \vec{P}_{pp\bar{p}\pi^{-}} $ are the total reconstructed energy and total momentum of the$ pp\bar{p}\pi^{-} $ system, respectively. Events with$ M_{\rm rec} $ greater than$ 0.8 $ GeV/$ c^2 $ are kept for further analysis.Studies based on the inclusive MC simulation samples [32] show that no peaking background events survive the selection criteria. To further suppress background events, two additional selection criteria are imposed on the accepted candidate events. First, the invariant mass
$ M_{p\pi^-} $ of the reconstructed$ p\pi^- $ system is required to be outside the Λ signal region, i.e.$ |M_{p\pi^-}- 1.115|>0.010 $ GeV/$ c^2 $ , to remove the possible background associated with Λ decays. Here, 1.115 GeV/$ c^2 $ is the known Λ mass [33], and 0.010 GeV/$ c^2 $ corresponds to about three times the mass resolution. Second, the invariant mass of$ pp\bar{p} $ ($ M_{pp\bar{p}} $ ) must be less than$ 3.6 $ GeV/$ c^2 $ due to the remaining neutron and pion in the event.The
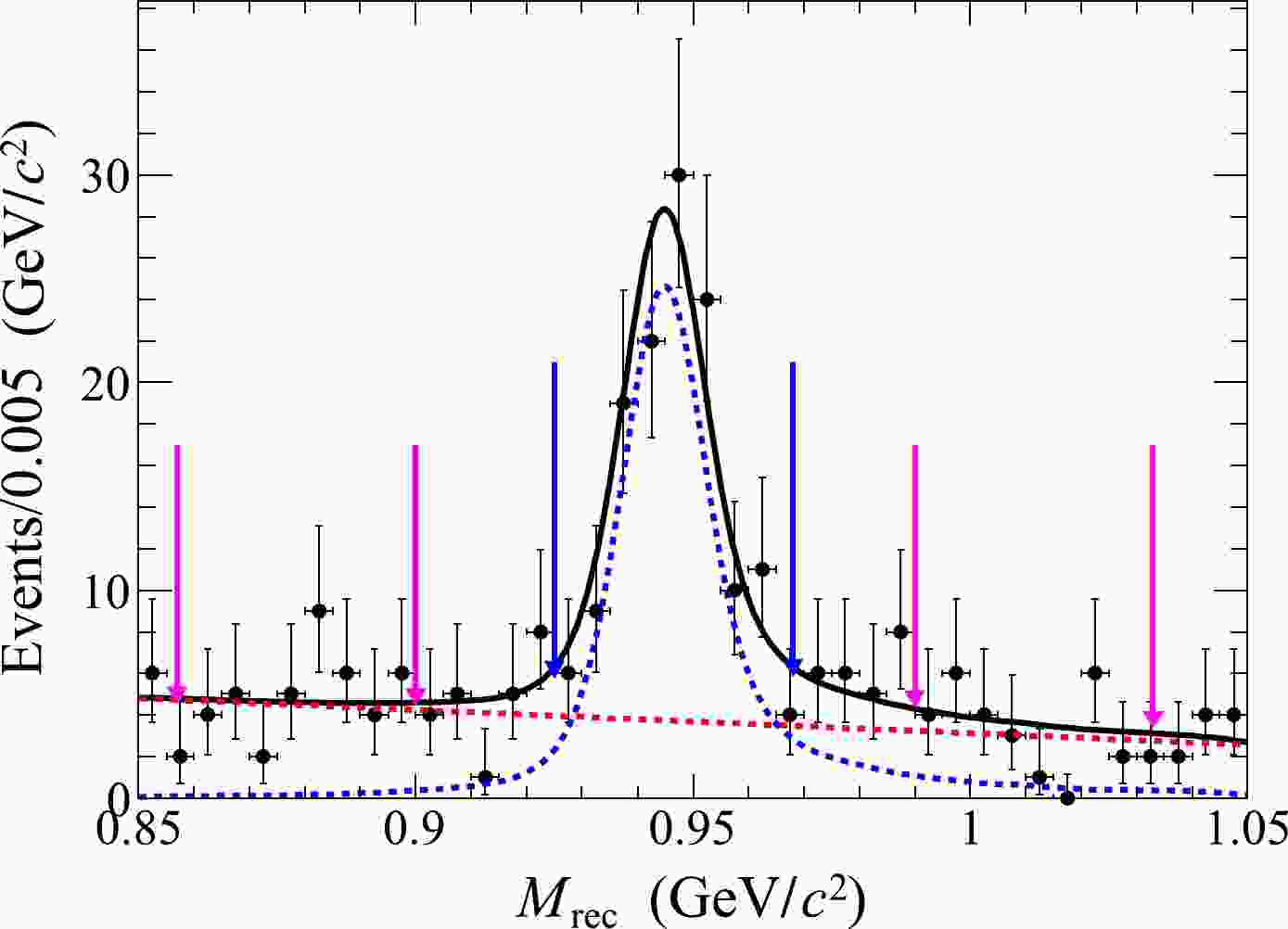
$ M_{\rm rec} $ distribution of the accepted candidates after the above selection criteria from the combined data sets is displayed in Fig. 1, where a significant neutron signal is observed. The signal yield is determined by a maximum likelihood fit to this distribution. In the fit, the signal is represented by the luminosity weighted MC-simulated shape convolved with a Gaussian function and the remaining background is described by a linear function. From the fit, the signal yield is determined to be$ 123\pm14 $ . The statistical significance of the signal is determined to be$ 11.5\sigma $ , which is evaluated as$ \sqrt{-2\ln(\mathcal{L}_0/\mathcal{L}_{\rm max})} $ , where$ \mathcal{L}_{\rm max} $ is the maximum likelihood of the nominal fit and$ \mathcal{L}_0 $ is the likelihood of the fit without involving the signal component. The change of the degree of freedom is$ 1 $ . The neutron signal region is defined as$ M_{\rm rec}\in(0.925, 0.968) $ GeV/$ c^2 $ and the corresponding sideband regions are defined as$ M_{\rm rec}\in $ (0.857, 0.900)$ \cup $ (0.990, 1.033) GeV/$ c^2 $ .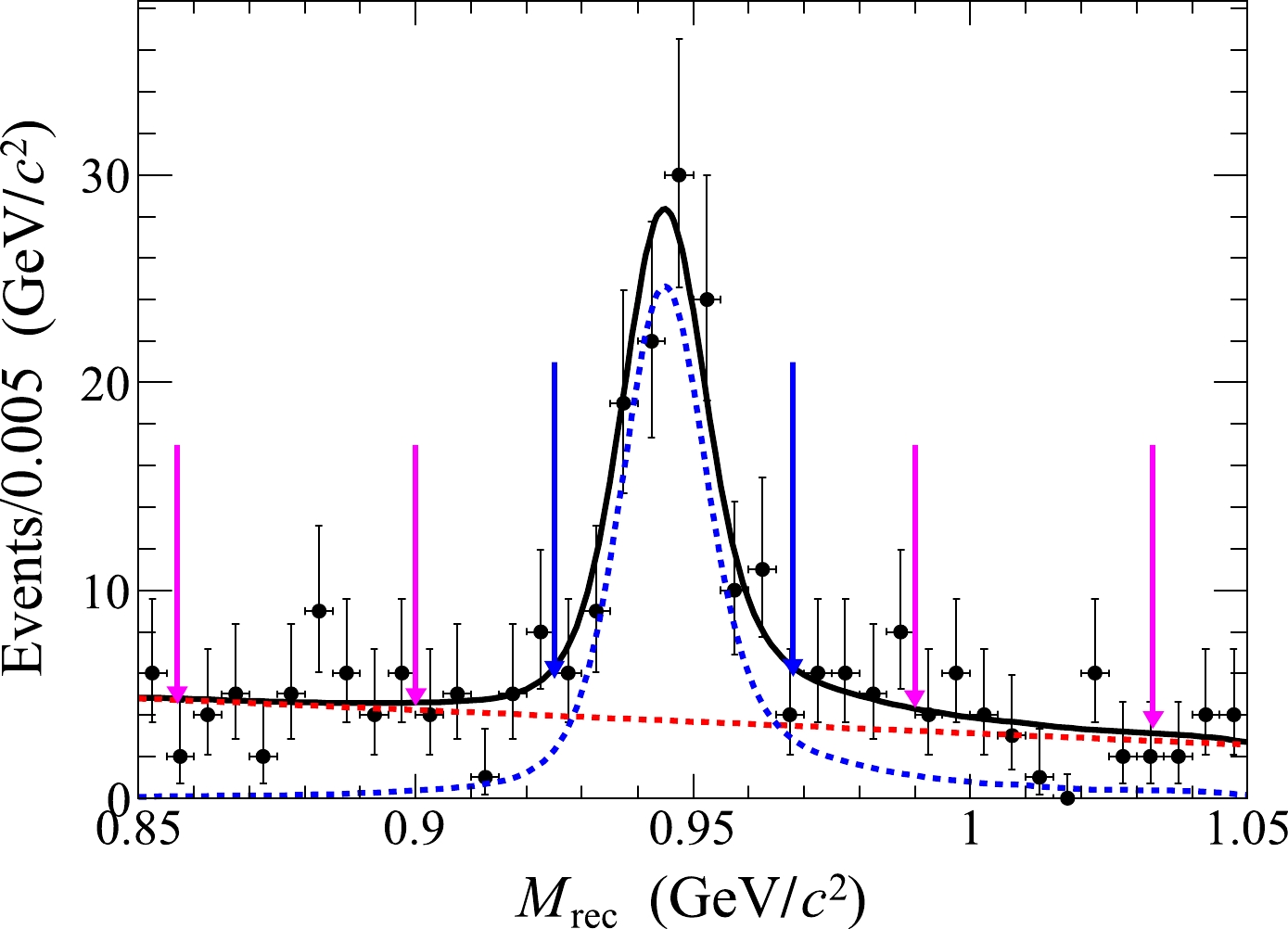
Figure 1. (color online) Distribution of the recoiling mass
$ M_{\rm rec} $ of the candidate events for the reaction$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-} $ with the fit results overlaid. The dots with error bars are from the combined data sets, the black curve shows the total fit result, and the dashed blue (red) curve represents the signal (background) shape. The pair of blue arrows marks the neutron signal region, whereas the neutron sideband regions are visualized by the two pairs of pink arrows.Figure 2 shows the comparisons of the momentum and polar angle distributions of the neutron of the accepted candidate events between data and signal MC simulation samples, where the data distribution is from the combined data sets and the MC simulation distribution has been weighted by the signal yields in data. The invariant mass of any two or three particles, the momentum and
$ \cos\theta $ distributions of the other final state particles have also been examined. The agreement between data and MC simulation allows to determine the detection efficiency with the signal MC simulation events generated uniformly distributed in the five-body phase space.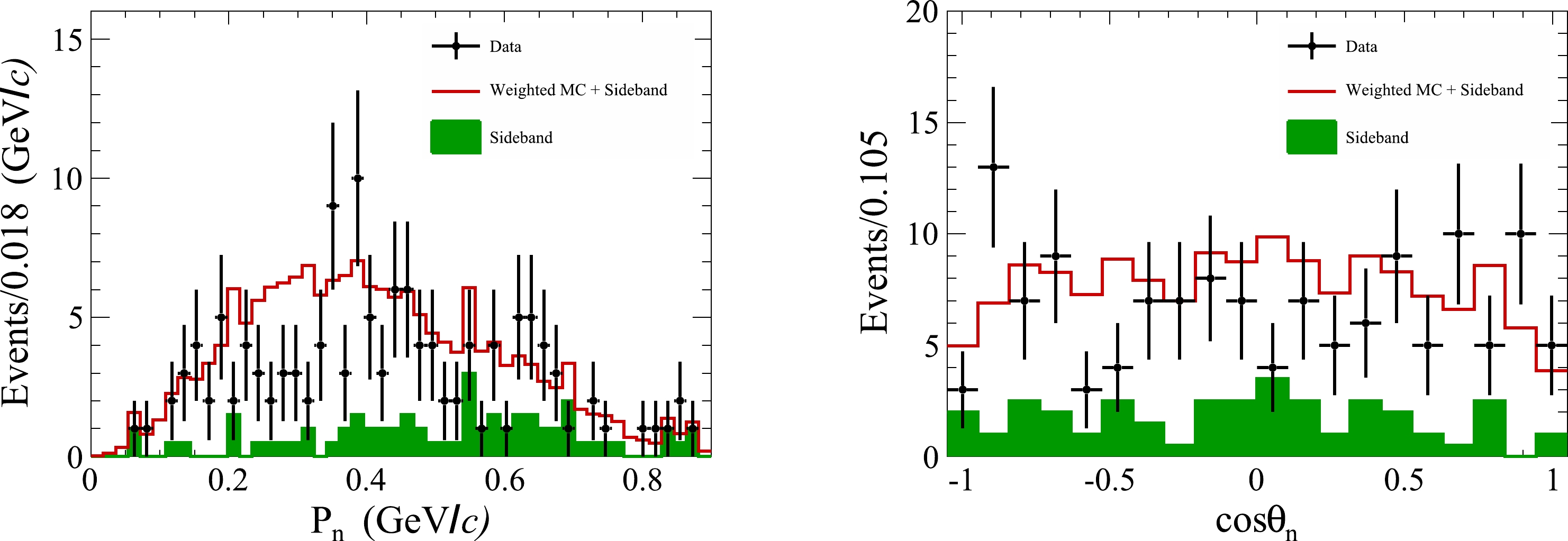
Figure 2. (color online) Momentum (left) and polar angular distributions (right) of the neutrons of the candidate events for the reaction
$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-} $ . The dots with error bars represent the combined data sets. The green histograms represent the sideband events. The red histograms represent the weighted signal MC simulation events plus the normalized neutron sideband regions in data.To search for hexaquark and di-baryon states, the
$ \bar{p}\bar{n} $ invariant mass spectrum is examined. Figure 3 shows the$ pp\pi^{-} $ and$ \bar{p}\bar{n} $ invariant mass spectra of the candidate events for the reaction$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-} $ . In the fit to$ M_{\bar{p}\bar{n}} $ , the signal is represented by the luminosity weighted phase space MC simulation shape and the remaining combinatorial background is described by a linear function. The goodness-of-fit is$ \chi^2/ndf= 38.21/37 $ . Here,$ ndf $ is the number of degrees of freedom. Compared to the phase space hypothesis, no obvious structure is observed.
Figure 3. (color online) The
$ pp\pi^{-} $ (left) and$ \bar{p}\bar{n} $ (right) invariant mass spectra of the candidate events for$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-} $ . The dots with error bars represent the combined data sets. The green histograms are the normalized neutron sideband events in data. The red histogram represents the weighted signal MC simulation events plus the normalized neutron sideband events in data. The black solid curve shows the total fit result, the blue dashed curve is the signal shape derived from the signal MC simulation sample, and the red dashed line is the linear background shape. -
In a data set for each energy point, only a few events have been observed in the neutron signal region, with a statistical significance of less than
$ 3\sigma $ . To obtain significant neutron signals the data sets are combined into three sub-samples in the energy ranges of (4.160, 4.380), (4.400, 4.600) and (4.610, 4.700) GeV for further analysis.The average observed cross section for
$ e^+e^- \to p p \bar{p} \bar{n} \pi^{-} $ is calculated by$ \begin{equation} \overline{\sigma}_j^{\rm obs} = \frac{N_j^{\rm sig}}{ {\Sigma_i {\epsilon_{ ji}}} \cdot {\mathcal{L}_{ ji}} } , \end{equation} $

(2) where
$ N_j^{\rm sig} $ is the number of signal events from the j-th combined data set,$ \mathcal{L}_{i} $ and$ \epsilon_{i} $ are the integrated luminosity and efficiency of data set i, respectively, i represents the i-th energy point in j-th combined data set. The detection efficiency is corrected by correction factors for the PID and tracking efficiencies,$ {f_{\rm PID}} $ and$ {f_{\rm trk}} $ , which are determined to be$ 0.92 $ and$ 0.98 $ by weighting the differences between efficiency experimentally determined and that in the MC simulation in different momentum ranges, respectively. Inserting the numbers which are listed in Table 1 into Eq. (2) yields the average observed cross sections$ (19.4\pm5.1\pm1.0) $ fb,$ (42.8\pm9.8\pm2.3) $ fb and$(54.2\pm 8.6\pm 2.9)$ fb for the three combined data sets, respectively, where the first uncertainties are statistical and the second are systematic.$ \sqrt{s} $ /GeV

$ \mathcal{L} $ /pb

$ ^{-1} $ 

$ \epsilon $ (%)

$ (1+\delta^{\gamma}) $ 

$ N_{\rm sig} $ 

$ \overline{\sigma}^{\rm obs} $ /fb

$ \overline{\sigma}^{\rm Born} $ /fb

4.1574 408.70 4.2 0.8408 4.1780 3189.0 6.0 0.8388 4.1889 526.70 7.1 0.8430 4.1990 526.00 8.1 0.8456 4.2092 517.10 8.8 0.8485 4.2188 514.60 9.6 0.8509 4.2263 1056.40 10.1 0.8489 4.2358 530.30 11.4 0.8530 4.2439 538.10 12.0 0.8552 $ 22.7\pm6.0 $ 

$ 19.4\pm5.1 $ 

$ 21.5\pm5.7 $ 

4.2580 828.40 13.5 0.8559 4.2668 531.10 14.0 0.8587 4.2777 175.70 14.8 0.8593 4.2878 502.40 14.2 0.8612 4.3121 501.20 16.2 0.8628 4.3374 505.00 18.6 0.8646 4.3583 543.90 21.8 0.8693 4.3774 522.70 21.0 0.8668 4.3965 507.80 22.6 0.8674 $ 30.9\pm7.1 $ 

$ 42.8\pm9.8 $ 

$ 46.3\pm10.6 $ 

4.4156 1043.90 24.8 0.8764 4.4362 569.90 25.0 0.8683 4.4671 111.09 27.4 0.8794 4.5271 112.12 30.7 0.8838 4.5995 586.90 34.0 0.8876 4.6152 103.83 33.5 0.8712 $ 69.4\pm11.0 $ 

$ 54.2\pm8.6 $ 

$ 59.0\pm9.4 $ 

4.6304 521.52 34.1 0.8710 4.6431 552.41 34.5 0.8708 4.6639 529.63 35.7 0.8712 4.6842 1669.31 36.3 0.8711 4.7008 536.45 36.6 0.8710 Table 1. The average observed cross sections for the reaction
$ e^+e^- \to p p \bar{p} \bar{n} \pi^{-} + c.c. $ . Summary of the number of signal events ($ N_{\rm sig} $ ), integrated luminosity ($ \mathcal{L} $ ), detection efficiency ($ \epsilon $ ), radiative correction factors$ (1+\delta^{\gamma}) $ , the average observed cross section ($ \overline{\sigma}^{\rm obs} $ ) and average Born cross section ($ \overline{\sigma}^{\rm Born} $ ) at different c.m. energies ($ \sqrt{s} $ ). The uncertainties are statistical only.To measure the average Born cross section of
$e^+e^- \to p p \bar{p} \bar{n} \pi^{-}$ , a similar lineshape as that of$e^+e^- \to 2(p\bar{p})$ [12] is assumed to determine the ISR and vacuum polarization correction factors,$ (1+\delta^{\gamma}) $ and$ \frac{1}{\vert 1-\Pi\vert^2} $ , as they are similar reactions where one of the$ \bar{p} $ has been exchanged by$ \bar{n}\pi^- $ . The lineshape is constructed as$ \begin{equation} \sigma^{\rm Born}(s) = \frac{1}{s} \times {\rm e}^{p_{\rm0}(\sqrt{s}-M_\text{th})} \times p_{\rm 1}, \end{equation} $

(3) where
$ p_{0} $ and$ p_{1} $ are free parameters,$M_\text{th} = (3m_{p}+ m_{n}+ m_{\pi^-})$ ,$ m_p $ ,$ m_n $ , and$ m_{\pi^-} $ are the known masses of p, n, and$ \pi^- $ taken from the PDG [33]. The average Born cross section is calculated by$ \begin{equation} \overline{\sigma}_j^{\rm Born} = \frac{\overline{\sigma}_j^{\rm obs}}{(1+\delta^{\gamma})_j \cdot \left(\dfrac{1}{\vert 1-\Pi\vert^2}\right)_j} . \end{equation} $

(4) The obtained Born cross sections are then used as input in the generator and the cross section measurements are iterated with the updated detection efficiencies. This process is repeated until the
$ (1+\delta^{\gamma}) \cdot \epsilon $ values become stable at all energies,$ i.e. $ the difference of$ (1+\delta^{\gamma}) \cdot \epsilon $ between the last two iterations is less than$ 4\% $ . Figure 4 shows the obtained average Born cross sections in the defined sub-samples. The average Born observed cross sections are calculated with Eq. (4), and the results are$ (21.5\pm5.7\pm 1.2) $ fb,$ (46.3\pm10.6\pm2.5) $ fb and$(59.0\pm9.4\pm 3.2)$ fb for the three combined data sets, respectively, where the first uncertainties are statistical and the second are systematic. Two different functions are used to compare the trend of the average Born cross section to a reaction where a similar behaviour is expected. The first one is a simple five-body energy-dependent phase space lineshape [12, 34] and the second one is an exponential function [12, 35], which are shown in Fig. 4. However, it should be noted that the two functions in Fig. 4 are not fit results, but drawn with arbitrary scale factors for comparison since a qualitative fit is not possible due to the limited statistics.
Figure 4. (color online) Average Born cross sections for the process
$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-} + c.c. $ . The dots with error bars are the measured values, the blue line shows the exponential function curve and the red-dashed line shows the five-body energy-dependent phase spase (PHSP) lineshape curve.The systematic uncertainties in the cross section measurements will be discussed in the next section.
-
In the cross section measurements, the systematic uncertainties mainly comes from the integrated luminosity, tracking efficiency, PID efficiency, ISR correction,
$ M_{\rm rec} $ fit, and veto of background events associated with Λ decays.The integrated luminosity of the data set is measured by large-angle Bhabha scattering events, and the uncertainty in the measurement is
$ 1.0 $ % [21], which is dominated by the precision of the MC generator used for efficiency correction. The tracking and PID efficiencies have been studied with high purity control samples of$ J/\psi\to p\bar{p}\pi^+\pi^- $ and$ \psi(3686)\to \pi^+\pi^-J/\psi\to \pi^+\pi^-p\bar{p} $ decays [36, 37]. The differences of the tracking and PID efficiencies between data and MC simulation in different transverse momentum and total momentum ranges are obtained separately. The averaged differences for the tracking (PID) efficiencies are corrected by the factors$ f_{\rm trk} $ ($ f_{\rm PID} $ ) as mentioned in Sec. IV. The uncertainties of the tracking and PID efficiencies are reweighted by the p/$ \bar{p} $ and$ \pi^{+} $ /$ \pi^{-} $ momenta of the signal MC simulation events. The reweighted uncertainties for tracking (PID) efficiencies,$ 0.1 $ % ($ 0.3 $ %) per p,$ 0.1 $ % ($ 0.4 $ %) per$ \bar{p} $ ,$ 1.0 $ % ($ 0.5 $ %) per$ \pi^{+} $ and$ 0.8 $ % ($ 0.4 $ %) per$ \pi^{-} $ , are assigned as the systematic uncertainties. Adding them linearly gives the total systematic uncertainties due to the tracking and PID efficiencies to be$ 1.1 $ % and$ 1.6 $ % for the process$e^+e^-\to p p \bar{p} \bar{n} \pi^{-}$ , and$ 1.3 $ % and$ 1.9 $ % for the process$e^+e^-\to p \bar{p} \bar{p} n \pi^{+}$ , respectively.The input Born cross sections in the generator are iterated until the
$ (1+\delta^{\gamma}) \cdot \epsilon $ values converge. The largest difference of$ (1+\delta^{\gamma}) \cdot \epsilon $ between the last two iterations at all energy points,$ 3.2 $ %, is taken as the corresponding systematic uncertainty.Three different tests were performed to estimate the uncertainty associated with the
$ M_{\rm rec} $ fit. The fit range is increased or decreased by$ 5 $ MeV/$ c^2 $ . The background shape is replaced with a second-order Chebychev polynomial function, and the signal shape is replaced with an MC simulation-derived shape. The quadrature sum of these changes,$ 3.6 $ %, is taken as the relevant uncertainty.The systematic uncertainty due to the veto of Λ background events is estimated by changing the Λ veto mass window from
$ \pm3\sigma $ to$ \pm5\sigma $ , where σ is the invariant mass resolution and the value is 3 MeV/$ c^2 $ . The change of the measured cross section,$ 0.03 $ %, is assigned as the uncertainty.Adding the above systematic uncertainties summarized in Table 2 in quadrature yields the total systematic uncertainties of
$ 5.3 $ % and$ 5.4 $ %, for the processes$e^+e^-\to p p \bar{p} \bar{n} \pi^{-}$ and$ e^+e^-\to p \bar{p} \bar{p} n \pi^{+} $ , respectively. The average systematic uncertainty,$ 5.35 $ %, is taken as the total systematic uncertainty in the cross section measurement for the process$ e^+e^-\to p p \bar{p} \bar{n} \pi^{-}+c.c. $ .Mode $ \mathcal{L} $ 

Trk PID ISR Fit Λ veto $ \rm Total $ 

$ p p \bar{p} \bar{n} \pi^{-} $ 

$ 1.0 $ 

$ 1.1 $ 

$ 1.6 $ 

$ 3.2 $ 

$ 3.6 $ 

$ 0.03 $ 

$ 5.3 $ 

$ p \bar{p} \bar{p} n \pi^{+} $ 

$ 1.0 $ 

$ 1.3 $ 

$ 1.9 $ 

$ 3.2 $ 

$ 3.6 $ 

$ 0.03 $ 

$ 5.4 $ 

Table 2. The relative systematic uncertainties (in %) from the integrated luminosity of data set (
$ \mathcal{L} $ ), the tracking efficiency ($ \rm Trk $ ), the PID efficiency (PID), the ISR correction (ISR), the$ M_{\rm rec} $ fit (Fit), and the Λ veto in the cross section measurements. -
By using the data sets taken at the center-of-mass energies between
$ 4.16 $ and$ 4.70 $ GeV, the process$e^+e^- \to p p \bar{p} \bar{n} \pi^{-} + c.c.$ has been observed for the first time with a statistical significance of$ 11.5\sigma $ . The average Born cross sections in the three energy ranges of (4.160, 4.380), (4.400, 4.600) and (4.610, 4.700) GeV are measured to be$ (21.5\pm5.7\pm1.2) $ fb,$ (46.3\pm10.6\pm2.5) $ fb and$(59.0\pm 9.4\pm 3.2)$ fb, respectively, where the first uncertainties are statistical and the second systematic. The shape of the invariant-mass spectra of$ \bar{p}\bar{n} $ and$ pp\pi^- $ are in good agreement with the phase-space distributions, thereby indicating no hexaquark or di-baryon state observed with the current data sample size. -
The BESIII collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support.
Observation of ${ {\boldsymbol e^+\boldsymbol e^- \to\boldsymbol p\boldsymbol p \bar{\boldsymbol p} \bar{\boldsymbol n} \boldsymbol\pi^{-} + \boldsymbol c.\boldsymbol c. }}$
- Received Date: 2022-11-25
- Available Online: 2023-04-15
Abstract: Using data taken at 29 center-of-mass energies between 4.16 and 4.70 GeV with the BESIII detector at the Beijing Electron Positron Collider corresponding to a total integrated luminosity of approximately 18.8







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: