-
Millisecond pulsars (MSPs) are remarkable objects born via type II supernova (SN) explosions and characterized by short spin periods (P
$_{\rm spin} \leq$ 20 ms), weak magnetic fields, (B$ \leq 10^{9} $ G) and extremely old age ($ \sim 10^{9} $ yr) based on the recycling process. The ATNF census comprises 445 Galactic MSPs in both the Galactic plane and in globular clusters, see, e.g., [1–3]. They are frequently found in binaries (about 65%) with white dwarfs (WDs) in circular orbits with companions with masses ranging from$\sim 0.15 M_{\odot} - 0.45M_{\odot}$ , see e.g., [4–8].It has been suggested that MSPs are formed in low-mass X-ray binary systems (LMXBs). This argument called for a recycling process in which a slowly rotating, old Neutron Star (NS) may be spun-up into an MSP via accretion from a binary companion, see, e.g., [4, 5, 9–11]. This link has been more recently reinforced by the discovery of many pulsars like PSR J1023+0038 [12], whose radio emission is likely to have switched on only recently after the LMXB phase.
An alternative formation scenario is the accretion induced collapse (AIC) of a ONeMg white dwarf (WD), see, e.g., [2, 7, 13–18]. In this scenario, the mass transfer can increase the mass of a WD toward the Chandrasekhar mass. When the star reaches this mass limit, degeneracy pressure can no longer support it because the supporting electron pressure is robbed by inverse β decays [19], consequently losing enough energy in neutrinos. This causes it to collapse and violently release a substantial amount of gravitational energy, which might be observable by gravitational wave observatories such as the LIGO-Virgo Collaboration and GEO [20–26].
The NS equation of state, along with the mass-radius relation, plays a role in modeling the baryonic and gravitational masses as well as binding energy [27]. The majority of efforts have been made to calculate the effect of the binding energy by estimating the amount of evolution driven by mass accretion in order to understand the evolutionary tracks of binary models [28–34].
Reference [32] constrained the baryonic mass and binding energy associated with the equation of state of two double pulsars (J0737-3039B and J1756-2251), finding that they are thought to have formed from an ultra-stripped progenitor. It was also found that these systems are consistent with forming from the AIC.
This work aims to consider the pre-AIC and post-AIC binding energies of the binary system. Then, taking into account the non-zero velocity of ejected matter, I derive several elementary analytic formulae for evaluating the variation of orbital energy and the possibility of binary survival.
-
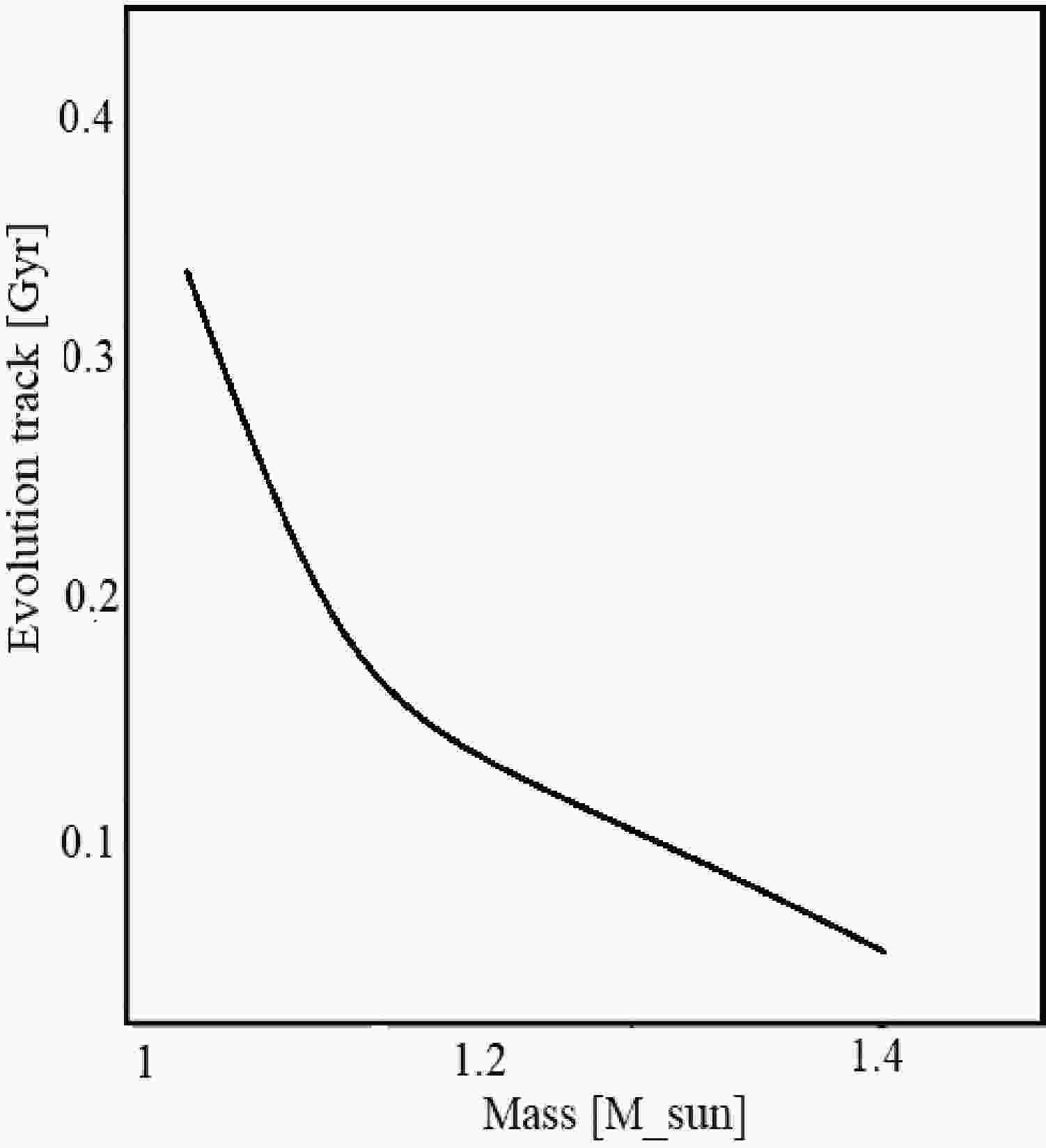
The impact of kick velocity on the companion depends on the binding energy of the system and the kinetic energy of the kick exerted on the orbit. It is noteworthy to mention here that, after AIC, the mass transfer starts once more due to the evolution of the companion star. Figure 1 shows the evolutionary track of the AIC process as it decreases in mass. However, given a particular initial mass of the WD
$ 1.1M_{\odot} $ [35], it takes a time interval shorter than 0.4 Gyr, see, e.g., [36] to trigger the AIC. The mass transfer model used in this work is based on the Roche model and ignores the secondary spin angular momentum. The angular momentum loss due to the gravitational radiation is calculated. This is valid for the WD primary [37]. This further changes the orbital period and the eccentricity [38]. This section covers the binding energy of a dynamical system based on the change in orbital energy. This could occur during the pre-SN orbit and immediately before the explosion, as described by the equation$ E_{{\rm orb},i} = \frac{- GM_{\rm WD} M_{c,i}}{2a_{i}} , $

(1) $ \quad\quad = - \frac{GM_{\rm WD} M_{c,i}}{a_{i}} + \frac{M_{\rm WD}M_{c,i}}{M_{\rm NS}+M_{c,i}} v^{2}_{i} , $

(2) where the
$ v_{i} $ is WD's initial velocity relative to its companion (mass = Chandrasekhar mass$M_{\rm ch}$ ). M$_{\rm NS}$ is the NS mass. G is Newton’s gravitational constant. At the evolution of a binary under instantaneous mass loss, the initial mass of the companion$M_c,\;i$ is assumed to be at least$4M_{\odot}\leq M_{\rm com} \leq6M_{\odot}$ , which may be reasonable for AIC binaries where the companion is on the main sequence of helium.$ a_{i} $ is the system's initial semi-major axis, which is approximately (1.5 R$ _{\odot} $ ). For more information, see, e.g., [39] and references therein.The orbital energy after the SNe
$ E_{{\rm orb},f} = \frac{- GM_{\rm NS} M_{c,f}}{2a_{f}}, $

(3) $ \;\;\quad\quad = - \frac{GM_{\rm NS} M_{c,f}}{a_{f}} + \frac{M_{\rm NS}M_{c,f}}{M_{\rm NS}+M_{c,f}} v^{2}_{f} , $

(4) where the companion
$ M_{c,f} $ 's final mass is estimated to be at least 1.4M$ _{\odot} $ , see, e.g., [9]. The final velocity of WD relative to its companion is given by$ v_{f} $ . a$ _{f} $ is the system's final semi-major axis after the AIC process, which is approximately (3R$ _{\odot} $ ), see i.e, [40, 41]. The geometry of an asymmetric SN in the binary system is illustrated in Fig. 2. This depends on the mass loss and angular momentum variations. The low binding energy of the ejecta and the low explosive energy are, of course, related. The slow rotation is caused by the accretion of gas with small angular momentum during this process.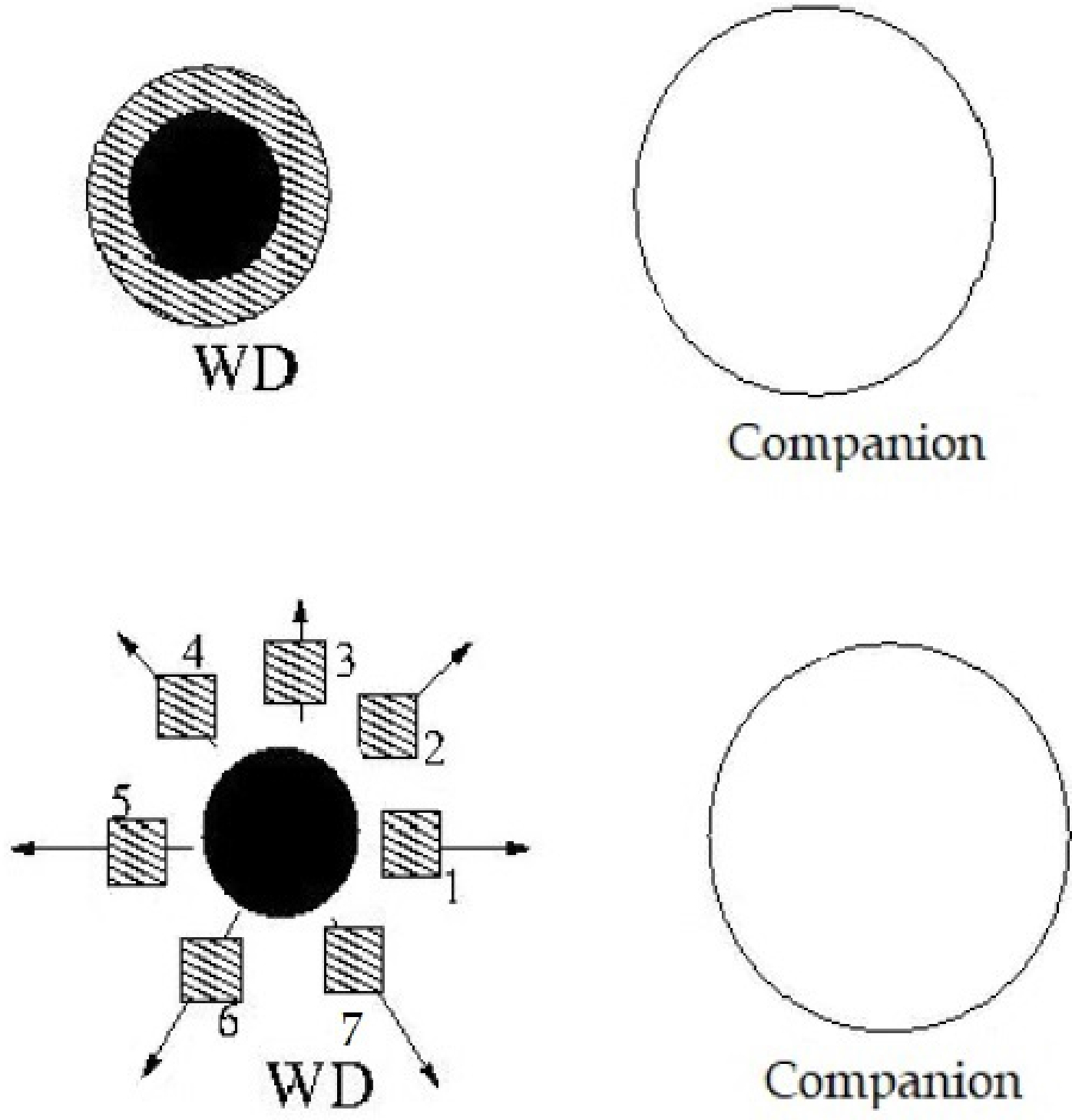
Figure 2. Simple diagram illustrating how the companion star,
$ M_c $ , receives some of the mass ejected by the exploding WD during the AIC. The top panel corresponds to an instant right before the explosion. The bottom panel corresponds to an instant immediately after it happens. The ejected material has been schematically divided into blobs 1, 2, 3, 4, 5, 6, 7. The sum of the masses of all blobs is asymmetric mass ejection. The motion of each blob is shown with an arrow. Blobs 1, 2 and 7 reach the surface of$ M_c $ . Therefore, the masses of blobs 1, 2 and 7 are received and set to be ($\Delta M \sim 0.18M_{\odot}$ ).It is worth noting that different amounts of deposition energy into the common envelope should make a noticeable difference in the two different phases (pre- and post-AIC). This is due to the dissipating mechanism acting on the dynamical orbital evolution. In addition, I also consider the angular momentum that could affect the separation distance for the system based on the amount of accreted mass, see, i.e, [40].
$ J= \frac{M_{\rm NS} M_{c,f}}{M_{\rm NS}+ M_{c,f}} a_{f} \frac{2\pi}{P} . $

(5) However, this effect could be observed from the gravitational radiation emitted by the binary motion in a circular orbit [34]. In addition, the role of the compactness C = GM/(c
$ ^{2} $ R), where c is the speed of light and G is the gravitational constant, during accretion is adopted from [32], and points out the need to constrain the equation of state. As a result, a more accreted baryonic mass is transformed into binding energy instead of gravitational mass [33].Here, I consider the pre-AIC and post-AIC binding energies of the binary system by assuming the difference in final and initial orbital energies
$E_{{\rm orb},f}$ and$E_{{\rm orb},i}$ , respectively (see Fig. 3). This could cause the system's orbit to continually circularize and contract due to losing orbital energy.
Figure 3. Dynamical evolution of the post-AIC and pre-AIC systems as can be seen from the initial and final binding energies. Note that the typical mass loss taken for this is
$ 0.18M_{\odot} $ .$ \begin{array}{*{20}{l}} \Delta E_{\rm orb}= E_{{\rm orb},f} - E_{{\rm orb},i} .\end{array} $

(6) Following Ref. [42], I employ the efficiency parameter (ζ) during a common envelope evolution [43] to obtain the binding energy, which is dependent on the detailed structure (i.e., radius of the companion at an evolutionary stage) of the dynamical process in binaries [44]. Thus, I have
$ \zeta = \frac{\Delta E_{\rm orb}}{\Delta E_{\rm binding}}. $

(7) From this, I calculate the
$ a_{f} $ of the new binary after the AIC process (see Fig. 4). If the value of$ a_{f} $ is too small, the core overfills its new Roche lobe [45], and the cores then merge. As a result, gravitational waves may be produced during the pre-SN phase [16].
Figure 4. Final separation distance as a function of time. An indicator of the presence of a dynamical AIC process in a given system is the strong sensitivity to initial conditions. i.e.. masses and semi-major axes (see system details in the text).
I also deal with a system that orbits around a common center of mass, see e.g., [36, 46]. Then,
$ a_{f} $ grows, but the system remains bounded by$a = \dfrac{r(1+e\; {\rm cos\theta})}{1-{\rm e}^{2}}$ . As a result, I can obtain both$\Delta E_{{\rm orb},i}$ and$E_{{\rm orb},f}$ .The initial binding energy of the system can be given by
$ E_{{\rm binding},i} \simeq {G\; M_{b}} \left(\frac{1}{2a_{f}} - \frac{1}{2a_{i}} \right), $

(8) where
$M_{b} = (M_{\rm WD}+M_{c,i}) = (M_{\rm NS}+M_{c,f}$ ).Hence, the final binding energy can be given as
$ E_{{\rm binding},f}= E_{{\rm binding},i} + \frac{\Delta E_{\rm orb}}{\zeta}. $

(9) In the picture presented here, I find that the initial binding energy has a significant effect on the final fate of both evolution of the components (see Fig. 5) and the orbital parameters that change during the conservative mass transfer. The majority of the mass is lost in an AIC binary system coming from the WD converting baryonic mass into binding energy during the collapse of the newborn NS, with a mass change of the order of
$ 0.18M_{\odot} $ [36]. This can happen due to their larger compactness [32]. If enough orbital energy continues to be lost, this causes a merger of the binary components (like in some CO WDs merging). At this stage of evolution, this phenomenon creates a common envelope phase by reducing the orbital energy by envelope binding energy [45, 47] (see Fig. 6).
Figure 5. (color online) Final orbital energy as a function of the final fate of the mass companion. The correlation is roughly linear, as predicted by the H-R diagram.
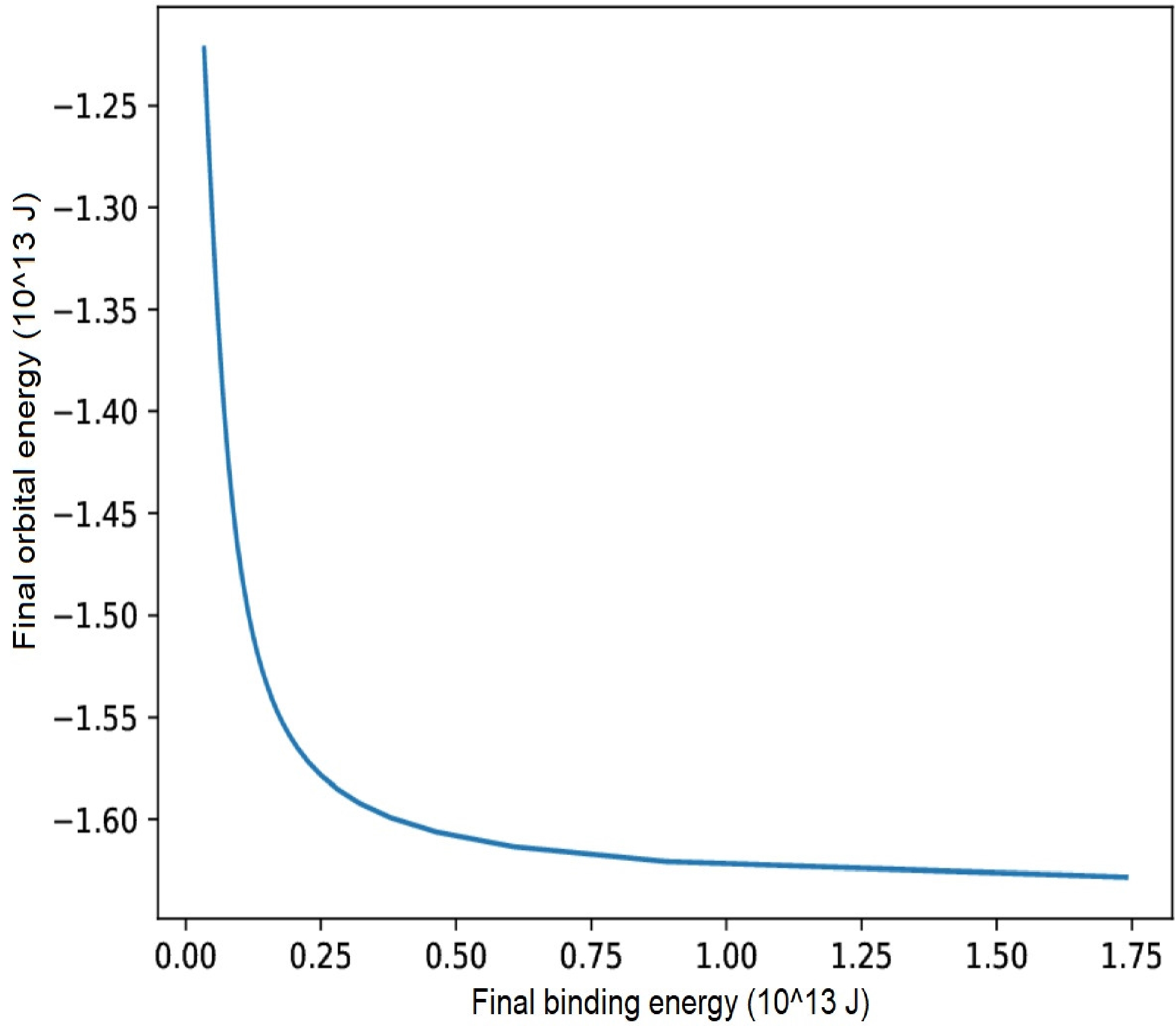
Figure 6. (color online) Final orbital energy as a function of the final binding energy through the AIC process.
A note should be made concerning the given equation of state, because it will govern the specific binding energy for determining the binary's evolution. In [48] a strong correlation was found between several equations of state and tidal deformability associated with NS binding energies. Furthermore, they discovered that the lower limit of NS mass has a binding energy of 1.52
$ \times10^{53} $ ergs. Based on these interesting results. [49] estimated the amount of the gravitational mass of the NS, which is$\sim 1.2 M_{\odot}$ . This result is consistent with the NS observations made by [50, 51].The result from the mass estimation benefits from the mildly recycled pulsar J0453+1559 [52, 53]. This system consists of a double NS with masses of
$ 1.56M_{\odot} $ and$ 1.17M_{\odot} $ , an orbital period of 4.07-day, a spin period of 45 ms, and an orbital eccentricity of (e = 0.11). The amount of gravitational binding energy is expected to be around ($\Delta M \sim 0.18M_{\odot}$ ) as shown in Fig. 6. This can be used to add some additional constraints when given a gravitational mass measurement for double NSs. -
An interesting point should be made about the outcome of the final binding energy within the framework of the AIC process, taking into consideration the non-zero velocity of the ejected matter. However, the equation of state influences how much binding energy a NS has. As a result, the larger the binding energy, the more compact the NS. The binding energy thus dominates the gravitational waves at a given amount of accreted mass associated with the angular momentum loss. This provides more insight into AIC observations in the future. I have also investigated the effect of accretion on the orbital period on an NS's binding energy. With the use of the orbital period along with a donor star mass evolution, I have shown that it is possible to add some constraints on the expected values of both mass and binding energy for NS energy parameters that depend on the accretion rate. However, this depends on the initial binding energy associated with the two systems' initial orbital energies, whether an envelope is present or not, since the final binding energy depends on the initial binding energy. This can help us figure out the accretion-driven evolution modes for binaries. The corresponding increase in orbital energy propels the binary into a longer-period orbit. This causes it to collapse and violently release its gravitational energy, which might be observable by gravitational wave observatories such as the LIGO-Virgo Collaboration.
-
Part of the content of this manuscript has been presented at the IAU Symposium 366, [doi:10.5281/zenodo.5759007]. Special thanks to Nour AlMusleh for helping the calculations. The author would like to thank the anonymous referees for the careful reading of the manuscript and for all suggestions and comments which allowed us to improve both the quality and the clarity of the paper.
Binding energy produced within the framework of the accretion of millisecond pulsars
- Received Date: 2022-11-10
- Available Online: 2023-04-15
Abstract: The role and implication of binding energy through the accretion-induced collapse (AIC) of accreting white dwarfs (WDs) for the production of millisecond pulsars (MSPs) are investigated. The binding energy model is examined due to the dynamic process in closed binary systems, and the possible mass of the companion sufficient to induce their orbital parameters is investigated. The deterministic nature of this interaction has a strong sensitivity to the equation of state of the binary systems (where the compactness of a neutron star is proportional to the amount of binding energy) associated with their initial conditions. This behavior mimics the commonly assumed mass and amount of accreted matter under the instantaneous mass loss (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: