-
Local Lorentz invariance (LI) is the most fundamental spacetime symmetry of the special/general relativity (SR/GR) and the standard model (SM) of particle physics [1]. LI means that the equations of motion for particles and fields are invariant under all Lorentz transformations (global for SR, local for GR) and diffeomorphism transformation for a particle. However, LI may fail to be an exact principle at very high energy scales [2]. GR and the SM are the best theories up to now describing the four fundamental forces. Nonetheless, they are fundamentally different in that the SM is a quantum theory disregarding the gravitational effects of all particles, while GR is a classical geometrical theory ignoring all the quantum features of particles. For particles with energies on the order of
$ 10^{30} $ eV (above the Planck scale), the gravitational interactions estimated by GR are very powerful, and so one should not ignore them [3]. Thus, on the very high energy scales, one has to reconsider combining the SM with GR in a unified theory, i.e., "quantum gravity." An effective field theory combining GR and the SM on low energy scales is called standard model extension (SME), which couples the SM to GR, and involves extra items embracing information about the violations of LI (Lorentz violation, LV) happening on the Planck scale [4].Studying the LV is a useful approach toward investigating the foundations of modern physics. Besides the SME, string theory [5], noncommutative field theories [6–8], spacetime-varying fields [9–11], loop quantum gravity theory [12, 13], brane world scenarios [14–16], massive gravity [17], and Einstein-aether theory [18, 19], there are other proposals of LV. The SME is experimentally accessible for studying possible observable signals of violation of the particle Lorentz symmetry. In this model, the local LV is provided by a spontaneous symmetry breaking potential due to self-interacting tensor fields, whose vacuum expectation value (VEV) yields to background tensor fields. A specific theory is the bumblebee field
$ B^\mu $ , a self-interacting tensor field that has a nonzero VEV$ b^\mu $ , which defines a privileged direction in spacetime and spontaneously breaks the local Lorentz symmetry.There are many forms of the bumblebee potential. One is the smooth functional bumblebee potential
$ V(X)=kX^2/2 $ , which has a minimum when the bumblebee field equals its VEV, i.e.,$ V=0 $ and$ V'(X)=kX=0 $ if$ X=0 $ , where k is a constant [20] and$ X=B^\mu B_\mu\pm b^2 $ . With this potential, the four dimensional static black hole solutions were found by Bertolami et al. [21] and Casana et al. [22], the higher D-dimensional static black hole was found by Ding et al. [23], and the rotating black hole solutions were built by Ding et al. [24] and Jha et al. [25]. Another form of bumblebee potential is a linear multiplier function$ V(X)=\lambda X/2 $ , where λ is a Lagrange-multiplier. With this potential, the Schwarzschild-anti-de Sitter-like and Schwarzschild-de Sitter-like black hole solutions in the$ D=4 $ dimensional spacetime were found by Maluf et al. [26], wherein the radial and tangential pressures are different, like those of an anisotropic fluid.The quantum field theory in a spacetime with a horizon exhibits thermal behavior, which must be thought of as an emergent phenomena [27]. A black hole event horizon has the conceptions of temperature and entropy [28], and the first law of thermodynamics
${\rm d}U=T{\rm d}S-P{\rm d}V$ can be built, where P is the radial pressure of the matter, U is the internal energy, and V is the volume of the black hole. There is also transfer of heat energy and the conception of phase transition [29]. Then, the gravity system can be mapped to a thermodynamic system, and studying on black hole thermodynamics can help to construct a quantum theory of gravity.In this work, we obtain solutions of the higher dimensional
$ D > 4 $ black hole and study its thermodynamics and phase transition with a negative cosmological constant in the theory of Einstein-bumblebee gravity. The rest of this paper is organized as follows. In Sec. II we present the background for the Einstein-bumblebee theory and derive the black hole solution by solving the gravitational field equations. In Sec. III, we study its thermodynamical properties. In Sec. IV, we study the phase transitions and find some effects of the Lorentz breaking constant$ \ell $ . Sec. V presents a summary. -
In the bumblebee gravity model, one introduces the bumblebee vector field
$ B_{\mu} $ , which has a nonzero vacuum expectation value, leading to a spontaneous Lorentz symmetry breaking in the gravitational sector via a given potential. In the higher$ D \geqslant 4 $ dimensional spacetime, the action of Einstein-bumblebee gravity is [30]$ \begin{aligned}[b] \mathcal{S}= &\int {\rm d}^Dx\sqrt{-g}\Big[\dfrac{R-2\Lambda}{2\kappa}+\dfrac{\varrho}{2\kappa} B^{\mu}B^{\nu}R_{\mu\nu}\\ &-\dfrac{1}{4}B^{\mu\nu}B_{\mu\nu} -V(B_\mu B^{\mu}\mp b^2)+\mathcal{L}_M\Big], \end{aligned} $

(1) where R is Ricci scalar, and Λ is a negative cosmological constant.
$ \kappa=8 \pi G_D/c^4 $ , where$ G_D $ is the D-dimensional gravitational constant and has the relation to Newton's constant G as$ G_D=G\Omega_{D-2}/4\pi $ [31];$ \Omega_{D-2}=2\sqrt{\pi}^{D-1}/ \Gamma[(D-1)/2] $ is the area of a unit$ (D-2) $ -sphere. Here and hereafter, we take$ G_D=1 $ and$ c=1 $ for convenience.The coupling constant
$ \varrho $ dominates the non-minimal gravity interaction to bumblebee field$ B_\mu $ . The term$ \mathcal{L}_M $ represents possible interactions with matter or external currents. The potential$ V(B_\mu B^{\mu}\mp b^2) $ triggers Lorentz and/or$ CPT $ (charge, parity, and time) violation, where the field$ B_{\mu} $ acquires a nonzero VEV,$ \langle B^{\mu}\rangle= b^{\mu} $ , satisfying the condition$ B^{\mu}B_{\mu}\pm b^2=0 $ . The constant b is a real positive constant. The vector$ b^{\mu} $ is a function of the spacetime coordinates and has a constant value$ b_{\mu}b^{\mu}= \mp b^2 $ , where the$ \pm $ signs mean that$ b^{\mu} $ is timelike or spacelike, respectively. It gives a nonzero VEV for bumblebee field$ B_{\mu} $ , indicating that the vacuum of this model obtains a prior direction in the spacetime. The bumblebee field strength is$ \begin{array}{*{20}{l}} B_{\mu\nu}=\partial_{\mu}B_{\nu}-\partial_{\nu}B_{\mu}. \end{array} $

(2) This antisymmetry of
$ B_{\mu\nu} $ implies the constraint [20]$ \begin{array}{*{20}{l}} \nabla ^\mu\nabla^\nu B_{\mu\nu}=0. \end{array} $

(3) Varying the action (1) with respect to the metric yields the gravitational field equations
$ \begin{array}{*{20}{l}} G_{\mu\nu}+\Lambda g_{\mu\nu}=\kappa T_{\mu\nu}^B+\kappa T_{\mu\nu}^M, \end{array} $

(4) where
$ G_{\mu\nu}=R_{\mu\nu}-g_{\mu\nu}R/2 $ , and the bumblebee energy momentum tensor$ T_{\mu\nu}^B $ is$ \begin{aligned}[b] T_{\mu\nu}^B= & B_{\mu\alpha}B^{\alpha}_{\;\nu}-\dfrac{1}{4}g_{\mu\nu} B^{\alpha\beta}B_{\alpha\beta}- g_{\mu\nu}V+ 2B_{\mu}B_{\nu}V'\\ &+\dfrac{\varrho}{\kappa}\Big[\dfrac{1}{2}g_{\mu\nu}B^{\alpha}B^{\beta}R_{\alpha\beta} -B_{\mu}B^{\alpha}R_{\alpha\nu}-B_{\nu}B^{\alpha}R_{\alpha\mu}\\ &+\dfrac{1}{2}\nabla_{\alpha}\nabla_{\mu}(B^{\alpha}B_{\nu}) +\dfrac{1}{2}\nabla_{\alpha}\nabla_{\nu}(B^{\alpha}B_{\mu}) \\ &-\dfrac{1}{2}\nabla^2(B_{\mu}B_{\nu})-\dfrac{1}{2} g_{\mu\nu}\nabla_{\alpha}\nabla_{\beta}(B^{\alpha}B^{\beta})\Big]. \end{aligned} $

(5) The prime denotes differentiation with respect to the argument,
$ \begin{array}{*{20}{l}} V'=\dfrac{\partial V(x)}{\partial x}\Big|_{x=B^{\mu}B_{\mu}\pm b^2}. \end{array} $

(6) Varying instead with respect to the bumblebee field generates the bumblebee equations of motion (supposing that there is no coupling between the bumblebee field and
$ \mathcal{L}_M $ ),$ \begin{array}{*{20}{l}} \nabla ^{\mu}B_{\mu\nu}=2V'B_\nu-\dfrac{\varrho}{\kappa}B^{\mu}R_{\mu\nu}. \end{array} $

(7) The contracted Bianchi identities (
$ \nabla ^\mu G_{\mu\nu}=0 $ ) lead to conservation of the total energy-momentum tensor$ \begin{array}{*{20}{l}} \nabla ^\mu T_{\mu\nu}=\nabla ^\mu\big( T^B_{\mu\nu}+T^M_{\mu\nu}-\Lambda g_{\mu\nu}\big)=0. \end{array} $

(8) We suppose that there is no matter field and the bumblebee field is frozen at its VEV as in Refs. [21, 22], i.e., it is
$ \begin{array}{*{20}{l}} B_\mu=b_\mu. \end{array} $

(9) For the forms of potential V, there are both classes: the smooth functionals of x, i.e.,
$ \kappa x^2/2 $ , minimized by the condition$ x=0 $ , and the Lagrange-multiplier form$ \lambda x/2 $ , where λ is a non-zero constant and serves as a Lagrange-multiplier field [20]. The smooth potential does not admit a new black hole solution with the nonzero cosmological constant Λ [26]. The proof is in Appendix A, with further details.To generate a black hole solution in the case of the non-zero cosmological constant Λ, we should apply a linear function form of the Lagrange-multiplier potential
$ \begin{array}{*{20}{l}} V=\dfrac{\lambda}{2}(B_\mu B^\mu-b^2). \end{array} $

(10) This potential is
$ V=0 $ under condition (9) and its derivative is$ V'=\lambda/2 $ , which can modify the Einstein equations. However, this additional degree of freedom of the λ field is auxiliary. Then, the first two terms in Eq. (5) are like those of the electromagnetic field, and the only differences are the coupling items to the Ricci tensor and this λ term. Under this condition, Eq. (4) leads to the gravitational field equations [30]$ \begin{aligned}[b] G_{\mu\nu}+\Lambda g_{\mu\nu}=&\kappa (\lambda b_\mu b_\nu+b_{\mu\alpha}b^{\alpha}_{\;\nu}-\dfrac{1}{4}g_{\mu\nu} b^{\alpha\beta}b_{\alpha\beta})\\ &+\varrho\Big(\dfrac{1}{2} g_{\mu\nu}b^{\alpha}b^{\beta}R_{\alpha\beta}- b_{\mu}b^{\alpha}R_{\alpha\nu} -b_{\nu}b^{\alpha}R_{\alpha\mu}\Big) +\bar B_{\mu\nu}, \end{aligned} $

(11) with
$ \begin{aligned}[b] \bar B_{\mu\nu}=&\dfrac{\varrho}{2}\Big[ \nabla_{\alpha}\nabla_{\mu}(b^{\alpha}b_{\nu}) +\nabla_{\alpha}\nabla_{\nu}(b^{\alpha}b_{\mu}) \\ &-\nabla^2(b_{\mu}b_{\nu})-g_{\mu\nu}\nabla_\alpha\nabla_\beta(b^\alpha b^\beta)\Big]. \end{aligned} $

(12) The static spherically symmetric black hole metric in the D dimensional spacetime has the form
$ \begin{array}{*{20}{l}} {\rm d}s^2=-{\rm e}^{2\phi(r)}{\rm d}t^2+{\rm e}^{2\psi(r)}{\rm d}r^2+r^2{\rm d}\tilde{\Omega}_{D-2}^2, \end{array} $

(13) where
$ \tilde{\Omega}_{D-2} $ is a standard$ (D-2) $ sphere$ \begin{array}{*{20}{l}} {\rm d}\tilde{\Omega}^2={\rm d}\theta_1^2+\displaystyle\sum\limits_{j=2}^{D-2}\displaystyle\prod\limits_{i=1}^{j-1}\sin^2\theta_i{\rm d}\theta^2_j. \end{array} $

(14) In this static spherically symmetric spacetime, the most general form for the bumblebee field would be
$ b_\mu= (b_t,b_r,0,0,\cdots,0) $ , where$ b_t $ and$ b_r $ are functions of r subject to the constraint$-b_t^2 {\rm e}^{ -2\phi}+ b_r^2 {\rm e}^{-2 \psi} = b^2$ ; here, b is a positive constant. In this general case, the bumblebee field has both radial and a time component for the vacuum expectation value. In the purely radial case$ b_t=0 $ , the authors in Refs. [21, 22] obtained new black hole solutions indeed. However, for the general case (temporal and radial), the authors in Ref. [21] obtained a slightly perturbed metric, where one cannot constrain the physical parameters from the observed limits on the parameterized post-Newtonian (PPN) parameters. Hence, here we consider only the purely radial case to obtain a black hole solution and let the general case for the future work.We pay attention to the fact that the bumblebee field has a radial vacuum energy expectation because the spacetime curvature has a strong radial variation. On the contrary, the temporal changes are very slow. The bumblebee field is supposed to be spacelike as
$ \begin{array}{*{20}{l}} b_\mu=\big(0,be^{\psi(r)},0,0,\cdots,0\big). \end{array} $

(15) Then, the bumblebee field strength is
$ \begin{array}{*{20}{l}} b_{\mu\nu}=\partial_{\mu}b_{\nu}-\partial_{\nu}b_{\mu}, \end{array} $

(16) whose components are all zero, and their divergences are all zero, i.e.,
$ \begin{array}{*{20}{l}} \nabla^{\mu}b_{\mu\nu}=0. \end{array} $

(17) From the bumblebee field motion, Eq. (7), we have the projection of the Ricci tensor along the bumblebee field as follows:
$ \begin{array}{*{20}{l}} b^{\mu}R_{\mu\nu}=\dfrac{\kappa\lambda}{\varrho}b_\nu . \end{array} $

(18) As to gravitational field, Eq. (11), one can obtain the following three component equations
$ \begin{aligned}[b] &(D-2)(1+\ell)\big[2r\psi'-(D-3)\big] \\+& {\rm e}^{2\psi}\big[(D-2)(D-3)-2\Lambda r^2\big]=0, \end{aligned} $

(19) $ \begin{aligned}[b] & 2\ell r^2(\phi''+\phi'^2-\phi'\psi')-2\ell(D-2)r(\psi'+\phi')\\ - & 2(D-2)r\phi'+{\rm e}^{2\psi}\big[(D-2)(D-3)+2\kappa \lambda b^2r^2\\ - &2\Lambda r^2\big]-(1+\ell)(D-2)(D-3)=0, \end{aligned} $

(20) $ \begin{aligned}[b] &(1+\ell)\Big[r^2(\phi''+\phi'^2-\phi'\psi')+\dfrac{(D-3)(D-4)}{2}\\ + & (D-3)r(\phi'-\psi')\Big]+ {\rm e}^{2\psi}\Big[\Lambda r^2-\dfrac{(D-3)(D-4)}{2}\Big]=0 , \end{aligned} $

(21) where we have redefined the Lorentz-violating parameter
$ \ell=\varrho b^2 $ , and the prime$ ' $ is the derivative with respect to the corresponding argument. From Eq. (19), one can obtain a metric function as$ \begin{array}{*{20}{l}} {\rm e}^{2\psi}=\dfrac{1+\ell}{f(r)}, \end{array} $

(22) where
$ \begin{array}{*{20}{l}} f(r)=1-\dfrac{16\pi M}{(D-2)\Omega_{D-2}r^{D-3}}-\dfrac{2\Lambda}{(D-1)(D-2)}r^2, \end{array} $

(23) and M is the mass of the black hole. To recover the 4-dimensional Schwarzschild-like solution [22] in the cases of
$ \Lambda=0 $ , we have another function,$ \begin{array}{*{20}{l}} {\rm e}^{2\phi}=f(r). \end{array} $

(24) It is easy to prove that the above results of
${\rm e}^{2\phi}=f(r), {\rm e}^{2\psi}=(1+\ell)/f(r)$ can meet the gravitational Eq. (21). Then, the bumblebee field is$ \begin{array}{*{20}{l}} b_\mu=\big(0,b\sqrt{(1+\ell)/f(r)},0,0,\cdots,0\big). \end{array} $

(25) With the bumblebee field motion Eq. (18) or the gravitational Eq. (20), a solution of this type will be possible if and only if
$ \begin{array}{*{20}{l}} \Lambda=\dfrac{(D-2)\kappa\lambda}{2\varrho}(1+\ell), \end{array} $

(26) which is the constraint on the additional field λ coming from the potential (10). It is easy to see that if the Lagrange-multiplier field
$ \lambda=0 $ , then$ \Lambda=0 $ and the metric (23) is the D-dimensional Schwarzschild-like black hole [23]. Thus, λ is not a new freedom, and we can define the effective cosmological constant$ \Lambda_e $ as follows to absorb it:$ \begin{array}{*{20}{l}} \Lambda_e=\dfrac{(D-2)\kappa\lambda}{2\varrho}. \end{array} $

(27) Then,
$ \Lambda=(1+\ell)\Lambda_e $ , and the present black hole metric is$ \begin{array}{*{20}{l}} {\rm d}s^2=-f(r){\rm d}t^2+\dfrac{1+\ell}{f(r)}{\rm d}r^2+r^2{\rm d}\tilde{\Omega}_{D-2}^2, \end{array} $

(28) with the metric function
$ f(r) $ as$ \begin{array}{*{20}{l}} f(r)=1-\dfrac{16\pi M}{(D-2)\Omega_{D-2}r^{D-3}}-\dfrac{2(1+\ell)\Lambda_e}{(D-1)(D-2)}r^2. \end{array} $

(29) When LV constant
$ \ell\rightarrow0 $ , the effective cosmological constant$ \Lambda_e\rightarrow \Lambda $ and it recovers the Schwarzschild-AdS black hole. When$ r\rightarrow \infty $ , the metric function$ \begin{array}{*{20}{l}} f(r)=1-\dfrac{2(1+\ell)\Lambda_e}{(D-1)(D-2)}r^2, \end{array} $

(30) and the metric (28) becomes a D-dimensional anti-de Sitter (AdS)-like spacetime. The black hole horizon locates at the largest real root of the following equation:
$ \begin{array}{*{20}{l}} 1-\dfrac{16\pi M}{(D-2)\Omega_{D-2}r_h^{D-3}}-\dfrac{2(1+\ell)\Lambda_e}{(D-1)(D-2)}r_h^2=0. \end{array} $

(31) It is easy to see that it can give the black hole mass M from the horizon radius,
$ \begin{array}{*{20}{l}} M=\dfrac{(D-2)\Omega_{D-2}}{16\pi }r_h^{D-3}-\dfrac{(1+\ell)\Lambda_e}{8\pi(D-1)}\Omega_{D-2}r_h^{(D-1)}. \end{array} $

(32) It shows that the bumblebee field affects the location of the event horizons, contrary to the Schwarzschild-like solution in which the horizon radius is the same as of the Schwarzschild black hole.
-
A black hole is not only a gravity system, but also a special thermodynamic system because its surface gravity κ and horizon area A have close similarity to the temperature T and entropy S,
$ T=\kappa/2\pi $ ,$ S=A/4 $ . Four laws of black hole thermodynamics were established in Ref. [32]. LV can modify the geometry of a black hole, and thus, in this type of black hole, can the thermodynamical laws still hold? In this section we study the Smarr formula and the first law of this LV black hole. -
Suppose that
$ \mathcal{M} $ is this D-dimensional spacetime satisfying the Einstein equations,$\xi^a=(1,~0,~0,~\cdots,~0)$ is a Killing vector on$ \mathcal{M} $ , timelike near infinity. In$ \mathcal{M} $ , there is a spacelike hypersurface S with a co-dimension 2-surface boundary$ \partial S $ , and$ \xi^a $ is normal to the S. The boundary$ \partial S $ has two components: an inner boundary at the event horizon$ \partial S_h $ and an outer boundary at infinity$ \partial S_\infty $ . To construct a Komar integral relation for non-zero cosmological constant, one should introduce the Killing potential$ \omega^{ab} $ [33], which can be obtained according to the relation$ \xi^b=\nabla_a\omega^{ab} $ . For the static Killing vector$ \xi^a $ , we have$ \begin{array}{*{20}{l}} \omega^{rt}=-\omega^{tr}=\dfrac{r}{D-1}. \end{array} $

(33) We can integrate the Killing equation
$ \nabla_b(\nabla^b\xi^a) = -R^a_b\xi^b $ over a hypersurface S,$ \begin{array}{*{20}{l}} \displaystyle\int_{\partial S}\nabla^b\xi^a{\rm d}\Sigma_{ab}=-\displaystyle\int_SR^a_b\xi^b{\rm d}\Sigma_a, \end{array} $

(34) where
${\rm d}\Sigma_{ab}$ and${\rm d}\Sigma_{a}$ are the surface elements of$ \partial S $ and S, respectively. With the metric (13) in mind, we have the relation$ \begin{array}{*{20}{l}} R^a_b\xi^b=\dfrac{2}{D-2}(\Lambda_e,0,0,\cdots,0)=\dfrac{2\Lambda_e}{D-2}\xi^a, \end{array} $

(35) and then, Eq. (34) can be rewritten as
$ \begin{array}{*{20}{l}} \dfrac{D-2}{8\pi}\displaystyle\int_{\partial S}\left(\nabla^b\xi^a+\dfrac{2}{D-2}\Lambda_e\omega^{ab}\right){\rm d}\Sigma_{ab}=0, \end{array} $

(36) which is multiplied by the normalization factor
$ (D-2)/8\pi $ and is called the Komar integral relation. The non-vanishing components of the tensor$ \nabla^b\xi^a $ are given by$ \begin{array}{*{20}{l}} \nabla^r\xi^t=-\nabla^t\xi^r=\dfrac{1}{(1+\ell)(D-2)}\left[\dfrac{(D-3)8\pi M}{\Omega_{D-2}r^{D-2}}-\dfrac{2(1+\ell)\Lambda_er}{(D-1)}\right]. \end{array} $

(37) The closed 2-surface
$ \partial S $ has two parts, horizon$ \partial S_h $ and infinite$ \partial S_\infty $ , so Eq. (36) can be rewritten as$ \begin{aligned}[b] & \dfrac{D-2}{8\pi}\displaystyle\int_{\partial S_\infty}\left(\nabla^b\xi^a+\dfrac{2}{D-2}\Lambda_e\omega^{ab}\right){\rm d}\Sigma_{ab}\\ =\;&\dfrac{D-2}{8\pi}\displaystyle\int_{\partial S_h}\left(\nabla^b\xi^a+\dfrac{2}{D-2}\Lambda_e\omega^{ab}\right){\rm d}\Sigma_{ab}. \end{aligned} $

(38) If we use the 2-surface element
${\rm d}\Sigma_{rt}= -\sqrt{1+\ell}r^{D-2} {\rm d}\Omega_{D-2}/2$ , which is slightly modified by the factor$ \sqrt{1+\ell} $ , the left hand side of this integral is$ \begin{array}{*{20}{l}} \dfrac{D-2}{8\pi}\displaystyle\int_{\partial S_\infty}\left(\nabla^b\xi^a+\dfrac{2}{D-2}\Lambda_e\omega^{ab}\right){\rm d}\Sigma_{ab} =-\dfrac{(D-3)M}{\sqrt{1+\ell}}; \end{array} $

(39) the second term of its right hand side is
$ \begin{array}{*{20}{l}} \dfrac{\Lambda_e}{8\pi}\displaystyle\int_{\partial S_h}2\omega^{ab}{\rm d}\Sigma_{ab} =\dfrac{2PV}{\sqrt{1+\ell}}, \end{array} $

(40) where the pressure P and the thermodynamic volume V are
$ \begin{array}{*{20}{l}} P=-\dfrac{\Lambda_e}{8\pi},\;\;V=(1+\ell)\dfrac{\Omega_{D-2}}{D-1}r_h^{D-1}; \end{array} $

(41) and the first term of its right hand side is
$ \begin{array}{*{20}{l}} \dfrac{D-2}{8\pi}\displaystyle\int_{\partial S_h}\nabla^b\xi^a{\rm d}\Sigma_{ab} =-\dfrac{(D-2)TS}{\sqrt{1+\ell}}, \end{array} $

(42) where the temperature T and entropy S are
$ \begin{aligned}[b] & T=\dfrac{4}{(D-2)\sqrt{1+\ell}r_h}\left[\dfrac{(D-3) M}{\Omega_{D-2}r_h^{D-3}}-\dfrac{(1+\ell)\Lambda_er_h^2}{4\pi(D-1)}\right],\\ & S=\dfrac{A}{4}=\dfrac{\sqrt{1+\ell}}{4}\Omega_{D-2}r_h^{D-2}. \end{aligned} $

(43) Lastly, integral (38) can give the Smarr formula
$ \begin{array}{*{20}{l}} (D-3)M=(D-2)TS-2PV. \end{array} $

(44) One can see that the Smarr formula can still be constructed in this LV black hole spacetime as long as its entropy and volume are redefined.
-
In conventional physics, the surface area of the event horizon can be obtained via the metric (28) on the horizon, i.e.,
${\rm d}s^2=r_h^2{\rm d}\tilde\Omega^2_{D-2}$ (cf. Eq. (8.92) in p. 377 of [27]), which gives the horizon area$ \tilde A $ ,$ \begin{array}{*{20}{l}} \tilde A=\displaystyle\int r_h^{D-2}{\rm d}\Omega_{D-2}=r_h^{D-2}\Omega_{D-2}. \end{array} $

(45) This result is correct for the conventional static black hole horizon without LV and precisely the proper area of the flat Euclidean space. The geometric volume
$ \tilde V $ associated with the horizon is defined by integrating the full D-dimensional volume element over a$t=\rm const.$ slice,$\tilde V=\int {\rm d}r\sqrt{-g_D}d\Omega_{D-2}$ , (cf. Eqs. (6) and (7) in [34]), where$ g_D $ is the determinant of the given metric. This volume stays constant in time for all choices of Killing time and invariant under stationary time slices, and thus, it can be considered to be the black hole volume. For the metric (28), it gives$ \begin{array}{*{20}{l}} \tilde V=\displaystyle\int {\rm d}r\sqrt{-g_D}{\rm d}\Omega_{D-2}=\sqrt{1+\ell}\dfrac{r_h^{D-1}}{D-1}\Omega_{D-2}. \end{array} $

(46) This result is also correct for the conventional static black hole without LV, i.e.,
$ \ell=0 $ .Are these definitions still valid in this LV spacetime? From Eqs. (41) and (43) in the above subsection, one can see that those are not valid. Therefore, one needs to redefine the horizon area A and volume V as follows:
$ \begin{array}{*{20}{l}} A=\sqrt{1+\ell}\displaystyle\int r_h^{D-2}{\rm d}\Omega_{D-2}=\sqrt{1+\ell}r_h^{D-2}\Omega_{D-2}, \end{array} $

(47) $ V =\sqrt{1+\ell}\displaystyle\int {\rm d}r\sqrt{-g_D}{\rm d}\Omega_{D-2} =(1+\ell)\dfrac{r_h^{D-1}}{D-1}\Omega_{D-2}, $

(48) whose results are consistent with Eqs. (41) and (43). These results are all greater than those in the conventional case if
$ \ell>0 $ . Why? It can be interpreted by its anisotropic pressure, because a volume is commonly connected with its pressure. Its radial pressure$ p_r $ and tangential pressure$ p_t $ are given by (cf. Eqs. (20) and (21) in Ref. [26]),$ \begin{array}{*{20}{l}} p_r=\kappa T^r_r=-\dfrac{(D-2)(D-3)\ell}{2(1+\ell)r^2}-\Lambda_e,\qquad p_t=\kappa T^\theta_\theta=-\Lambda_e. \end{array} $

(49) One can see that
$ p_t-p_r = (D-2)(D-3)\ell/2(1+\ell)r^2>0 $ , which has stretched the horizon surface.From the thermodynamic viewpoint, one can also see that the conceptions of the horizon area A and volume V should be renewed. These two quantities characterize a spacetime and show the black hole entropy, and thus they can be entirely derived from thermodynamic considerations. Then, one first determines its temperature. The temperature T should be given by the black hole's thermodynamic process – its Hawking radiation process [35]
$ \begin{aligned}[b] T & =\dfrac{\sqrt{f'(r_h)g'(r_h)}}{4\pi} \\ & =\dfrac{1}{4\pi\sqrt{1+\ell}\;r_h}\left[(D-3)-\dfrac{2}{D-2}(1+\ell)\Lambda_er_h^2\right], \end{aligned} $

(50) where
$ g(r)=f(r)/(1+\ell) $ .For the thermodynamic volume V, it is the quantity thermodynamically conjugate to the pressure P, then it should be (see the formula 3.1 in Ref. [36])
$ \begin{array}{*{20}{l}} V\equiv\Big(\dfrac{\partial M}{\partial P}\Big)_S=(1+\ell)\dfrac{\Omega_{D-2}}{D-1}r_h^{D-1}, \end{array} $

(51) with Eq. (32) for the mass M. For the thermodynamic area A, it is the quantity thermodynamically conjugate to the temperature T; then it should be
$ \begin{array}{*{20}{l}} A=4S\equiv4\displaystyle\int\dfrac{{\rm d}M}{T}=\sqrt{1+\ell}\Omega_{D-2} r_h^{D-2}. \end{array} $

(52) Therefore, one can see that the LV has affected the known spacetime geometry by redefinition of the geometrical area and volume.
-
Next, we derive the first law of black hole thermodynamics via the Hamiltonian perturbation method. Note that in Ref. [33], the authors used this method to lead to the first law and they found it was equivalent to the derivative of M method, which is presented in Appendix B, where M is determined by Eq. (32).
In the D-dimensional manifold
$ \mathcal{M} $ with metric$ g_{ab} $ of signature$ (-,+,\cdots,+) $ , let Σ be a family of$ (D-1) $ -dimensional spacelike submanifolds with unite timelike normal field$ n_a $ and induced metric$ s_{ab} $ , i.e.,$ \begin{array}{*{20}{l}} g_{ab}=-n_an_b+s_{ab},\qquad n_cn^c=-1,\qquad n_cs^{cb}=0. \end{array} $

(53) The Hamiltonian variables are
$ s_{ab} $ and their conjugate momentum$ \pi_{ab} $ . The energy density$ \rho=T_{ab}n^an^b $ and momentum density$ J_a=T_{bc}n^bs^c_{\;a} $ must satisfy the Hamiltonian and momentum constrain equations,$ \begin{array}{*{20}{l}} H=16\pi G\rho,\qquad H_a=-16\pi GJ_a, \end{array} $

(54) where
$ \begin{aligned}[b] &H=-2G_{ab}n^an^b=-\left[\dfrac{(D-2)(D-3)\ell}{(1+\ell)r^2}+2\Lambda_e\right],\\ & H_a=-2G_{bc}n^bs^c_{\;a}=0 \end{aligned} $

(55) for the given case. Let the Killing vector
$ \xi ^a=Fn^a+\beta^a $ with$ n_c\beta^c=0 $ . The Hamiltonian density$ \mathcal{H} $ for evolution along$ \xi ^a $ is given by$ \begin{array}{*{20}{l}} \mathcal{H}=\sqrt{s}\left\{F\left[H+2\Lambda_e+\dfrac{(D-2)(D-3)\ell}{(1+\ell)r^2}\right]+\beta_aH^a\right\}. \end{array} $

(56) We assume that the linear approximation metric
$ \tilde{g}_{ab} = g_{ab} + \delta g_{ab} $ is another nearby solution to the Einstein equations with a perturbed cosmological constant$ \Lambda_e +\delta\Lambda_e $ . The induced spatial metric and momentum for this perturbed metric are$ \tilde{s}_{ab}=s_{ab}+h_{ab} $ and$ \tilde{\pi}_{ab}=\pi_{ab}+p_{ab} $ , where$ h_{ab}=\delta s_{ab}, p_{ab}=\delta \pi_{ab} $ [37]. Here, the term$ h_{\theta_1\theta_1} $ is as follows:$ \begin{aligned}[b] h_{\theta_1\theta_1}& =\delta s_{\theta_1\theta_1}=\delta r^2=\delta\left(\dfrac{\sqrt{1+\ell}\Omega_{D-2}r^{D-2}}{\sqrt{1+\ell}\Omega_{D-2}r^{D-4}}\right) \\ & =\dfrac{\delta A}{\sqrt{1+\ell}\Omega_{D-2}r^{D-4}}+\dfrac{ A}{\sqrt{1+\ell}\Omega_{D-2}}\delta\dfrac{1}{r^{D-4}}\\ & \simeq\dfrac{\delta A}{\sqrt{1+\ell}\Omega_{D-2}r^{D-4}}, \end{aligned} $

(57) where the term
$ \delta(1/r^{D-4}) $ is very small at a large distance.From Hamilton's equations for the zeroth order, the linearized constrain operators
$ \delta H $ and$ \delta H_a $ combine to form a total derivative,$ \begin{array}{*{20}{l}} F\delta H +\beta^a \delta H_a =-D_cB^c, \end{array} $

(58) where
$ D_a $ is the covariant derivative operator on Σ compatible with$ s_{ab} $ , and①$ \begin{array}{*{20}{l}} B^a=F(D^ah-D_bh^{ab})-hD^aF+h^{ab}D_bF. \end{array} $

(59) The linear constraints (54) take the form of a Gauss law②
$ \begin{array}{*{20}{l}} D_cB^c=2F\delta \Lambda_e. \end{array} $

(60) Using Killing potential
$ \omega^{ab} $ , we have$ F=-n_a\xi^a= -D_c(n_a\omega^{ca}) $ , and rewrite Eq. (60) in the integral form,$ \begin{array}{*{20}{l}} I=\displaystyle\int_{\partial\Sigma}{\rm d}a_c(B^c+2\omega^{cd}n_d\delta \Lambda_e)=0, \end{array} $

(61) which is taken to extend from a boundary
$ \partial \Sigma_h $ at the bifurcation sphere of the horizon to a boundary$ \partial\Sigma_\infty $ at infinity, i.e.,$ I_\infty-I_h=0 $ ,$ \begin{array}{*{20}{l}} \displaystyle\int_{\partial\Sigma_\infty} {\rm d}a_c(B^c+2\omega^{cd}n_{\rm d}\delta \Lambda_e)-\displaystyle\int_{\partial\Sigma_h} {\rm d}a_c(B^c+2\omega^{cd}n_d\delta \Lambda_e)=0. \end{array} $

(62) We choose
$ F\simeq\sqrt{f} $ ,$n_a=-F\nabla_at $ ,${\rm d}a_r=\sqrt{1+\ell}\;r^{D-2} {\rm d}\Omega_{D-2}/\sqrt{f}$ , and$ \begin{aligned}[b] & h_{rr}\simeq\delta\left(\dfrac{1+\ell}{f}\right),\\ & \delta f=-\left[\dfrac{16\pi\delta M}{(D-2)\Omega_{D-2}r^{D-3}}+\dfrac{2(1+\ell)\delta \Lambda_er^2}{(D-1)(D-2)}\right], \end{aligned} $

(63) and then, integral (61) can be simplified by
$ \begin{aligned}[b] I= & \dfrac{1}{\sqrt{1+\ell}}\displaystyle\int_{\partial\Sigma} r^{D-2}{\rm d}\Omega_{D-2}\left[\dfrac{D-2}{r}\delta f \right.\\ & \left. +\dfrac{2f}{\sqrt{1+\ell}}\left(\dfrac{\delta A}{A}\right)'-\dfrac{f'\delta A}{\sqrt{1+\ell}A}+\dfrac{2(1+\ell)r\delta \Lambda_e}{(D-1)}\right], \end{aligned} $

(64) where the prime
$ ' $ denotes the derive with the argument, and A is the area of the boundary. Thus,$ I_\infty=-16\pi\delta M/ \sqrt{1+\ell} $ $ 1/A\rightarrow0 $ at infinite, and$ \begin{array}{*{20}{l}} I_h=\dfrac{16\pi}{\sqrt{1+\ell}}[-T\delta S-V\delta P], \end{array} $

(65) because
$ f(r_h)=0,\;f'(r_h)=4\pi\sqrt{1+\ell}T,\;\Lambda_e=-8\pi P,\;A=4S $ , and$ V=(1+\ell)\Omega_{D-2}r_h^{D-1}/(D-1) $ ③. Lastly, the first law is obtained,$ \begin{array}{*{20}{l}} \delta M=T\delta S+V\delta P, \end{array} $

(66) which still also holds in this LV black hole spacetime.
-
A phase transition is a discontinuous change in the properties of a substance, as its environment is changed only infinitesimally. An isolated Schwarzschild black hole is thermodynamically unstable owing to its negative heat capacity. However, for a Schwarzschild AdS black hole, besides the negative heat phase, a phase of positive heat capacity will occur. At a given temperature and pressure, the stable phase is always that with the lower Gibbs free energy. In an AdS space, the Gibbs energy of the thermal radiation phase is zero [38]. Thus, the negative free energy of the positive heat capacity black hole phase is a stable phase. In this section, we study this two phase transitions.
From Eq. (31), we can express the mass M as
$ \begin{array}{*{20}{l}} M=\dfrac{(D-2)\Omega_{D-2}}{16\pi}r_h^{D-3}+PV. \end{array} $

(67) M can be interpreted as an enthalpy [33]
$ H=U+PV $ , so the black hole internal energy U is$ \begin{array}{*{20}{l}} U=\dfrac{(D-2)\Omega_{D-2}}{16\pi}r_h^{D-3}. \end{array} $

(68) Then, the first law (90) can be rewritten as follows:
$ \begin{array}{*{20}{l}} {\rm d}U=T{\rm d}S-P{\rm d}V, \end{array} $

(69) which is the same as the fundamental thermodynamical equation of a simple gas system. The temperature (50) can be rewritten as
$ \begin{array}{*{20}{l}} T=\dfrac{1}{4\pi\sqrt{1+\ell}\;r_h} \left[(D-3)+\dfrac{16\pi P}{D-2}(1+\ell)r_h^2\right], \end{array} $

(70) which is shown in Fig. 1 when
$ D=4 $ . There exist a minimum temperature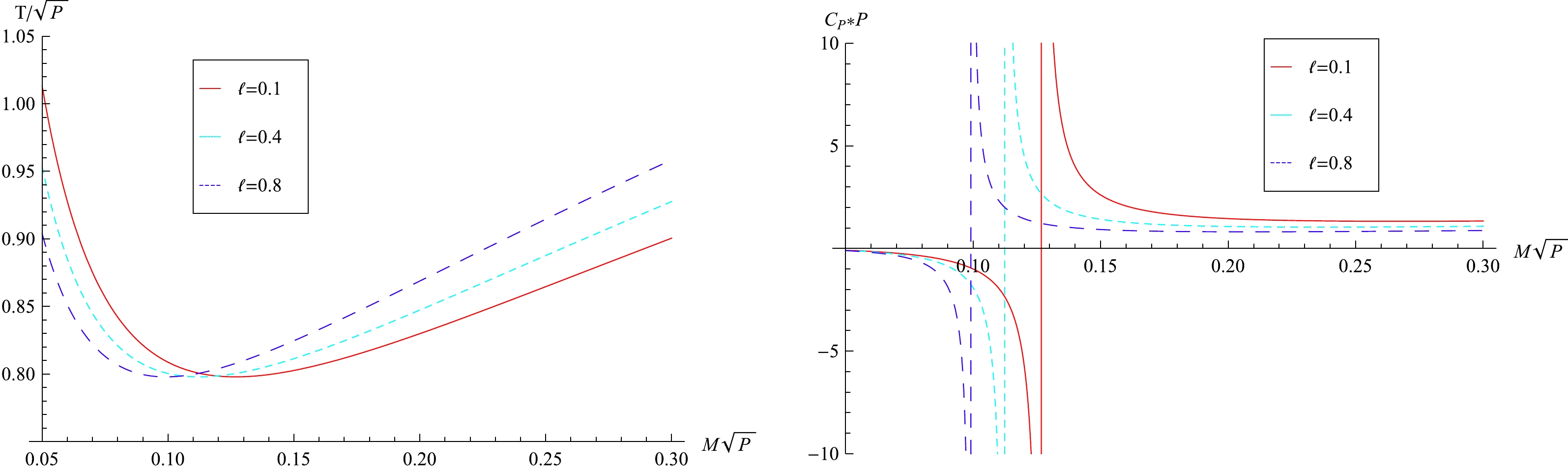
Figure 1. (color online) Black hole temperature and heat capacity
$ C_P $ at constant pressure P vs. black hole mass M with$ D=4 $ and different coupling constant$ \ell $ . The temperature has a minimum value and the heat capacity is divergent at the point of black hole mass$ M=M_d $ , where$ M_{d}=1/\sqrt{18(1+\ell)\pi P} $ .$ \begin{array}{*{20}{l}} T_{\rm min}=2\sqrt{\dfrac{(D-3)P}{(D-2)\pi}}, \end{array} $

(71) when
$ r_h=\sqrt{(D-2)(D-3)/[16(1+\ell)\pi P]} $ . Note that$T_{\rm min}$ is not dependent on$ \ell $ . From the left panel of Fig. 1, when$T > T_{\rm min}$ , there are two possible black hole masses [29], which can be in equilibrium with thermal radiation, i.e.,$ M>M_d $ or$ M<M_d $ , where$ M_d $ (defined by Eq. (73) is the black hole mass whose heat capacity is divergent. Fig. 1 shows that the temperature of the large black hole ($ M>M_d $ ) increases when the LV coupling constant$ \ell $ becomes bigger. At a fixed pressure P, the black hole heat capacity$ C_P $ is$ \begin{aligned}[b] C_P & =\Big(\dfrac{\partial H}{\partial T}\Big)_P\\ & =\dfrac{(D-2)\Omega_{D-2}}{4} r_h^{D-2}\dfrac{16\pi(1+\ell)Pr_h^2+(D-2)(D-3)}{16\pi(1+\ell)Pr^2_h-(D-2)(D-3)}, \end{aligned} $

(72) which is also shown in Fig. 1 when
$ D=4 $ . From the right panel of Fig. 1, one can see that the small black hole mass has negative specific heat, and hence it is unstable and will decay. Meanwhile, the large black hole mass has positive heat capacity and therefore it is thermally stable. It is easy to see that the heat capacity at constant pressure is divergent at the black hole mass$ M_d $ ,$ \begin{array}{*{20}{l}} M_d=\dfrac{(D-2)^2\Omega_{D-2}}{8\pi(D-1)} \left[\dfrac{(D-2)(D-3)}{16(1+\ell)\pi P}\right]^{(D-3)/2}. \end{array} $

(73) It can be observed that the LV constant
$ \ell $ decreases the mass$ M_d $ , showing that the phase transition from a small black hole to a large one will more easily occur. At this divergent point, the black hole entropy is$ \begin{array}{*{20}{l}} S_d=4^{(1-D)}\Omega_{D-2}\sqrt{1+\ell}^{(3-D)} \left[\dfrac{(D-2)(D-3)}{\pi P}\right]^{(D-2)/2}. \end{array} $

(74) Figure 2 shows the entropy with the temperature at unit pressure when
$ D=4 $ . The phase transition between these two phases is called small-large black hole phase transition.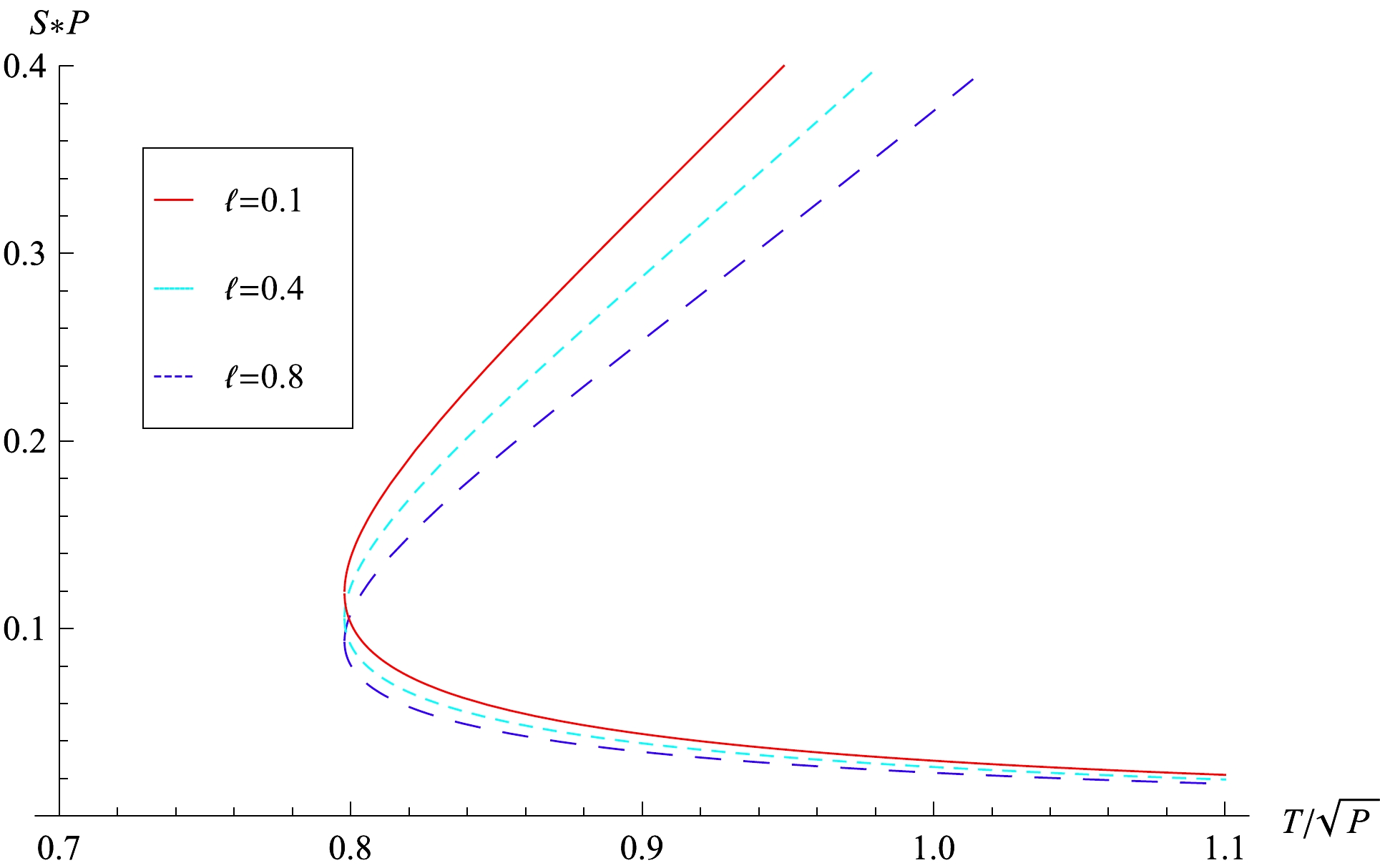
Figure 2. (color online) Black hole entropy S vs. black hole temperature T with
$ D=4 $ and different coupling constant$ \ell $ . They all have both branches, the one above corresponds to the large black hole$ M>M_d $ , the one below to the small black hole$ M<M_d $ . At the temperature$T=T_{\rm min}$ , the entropy is$ S_d=1/8\sqrt{1+\ell}P $ . At the HP temperature$T_{\rm HP}=\sqrt{8P/3\pi}$ ,$S_{\rm HP}=3/8\sqrt{1+\ell}P$ for the large black hole,$S_{\rm small}=1/24\sqrt{1+\ell}P$ for the unstable small black hole.There is another type of phase transition called Hawking-Page (HP) phase transition, which is between a metastable large black hole phase and a stable large black hole phase in an AdS spacetime. Witten [39] explained that this HP phase transition is a confinement/deconfinement phase transition in the AdS/CFT correspondence. It can also be understood as a solid/liquid phase transition in black hole chemistry [40]. HP phase transition occurs when the Gibbs free energy is zero. The black hole Gibbs free energy can be obtained as follows:
$ \begin{array}{*{20}{l}} G=H-TS=\dfrac{\Omega_{D-2}}{8\pi (D-1)}\left[(D-2)-2\pi\sqrt{1+\ell}Tr_h\right]r_h^{D-3}, \end{array} $

(75) which is shown in Fig. 3 when
$ D=4 $ . It can be observed that there are two branches; the parts above correspond to the small black hole phase whose free energy are positive for any temperature, whereas the ones below correspond to the metastable large black hole phase when$ G>0 $ and the stable large black hole phase when$ G<0 $ . When the temperature$T < T_{\rm min}$ , the spacetime has only one phase – thermal radiation, whose free energy is zero. At the temperature$T=T_{\rm min}$ , its free energy has a maximum value$G_{\rm max}$ ,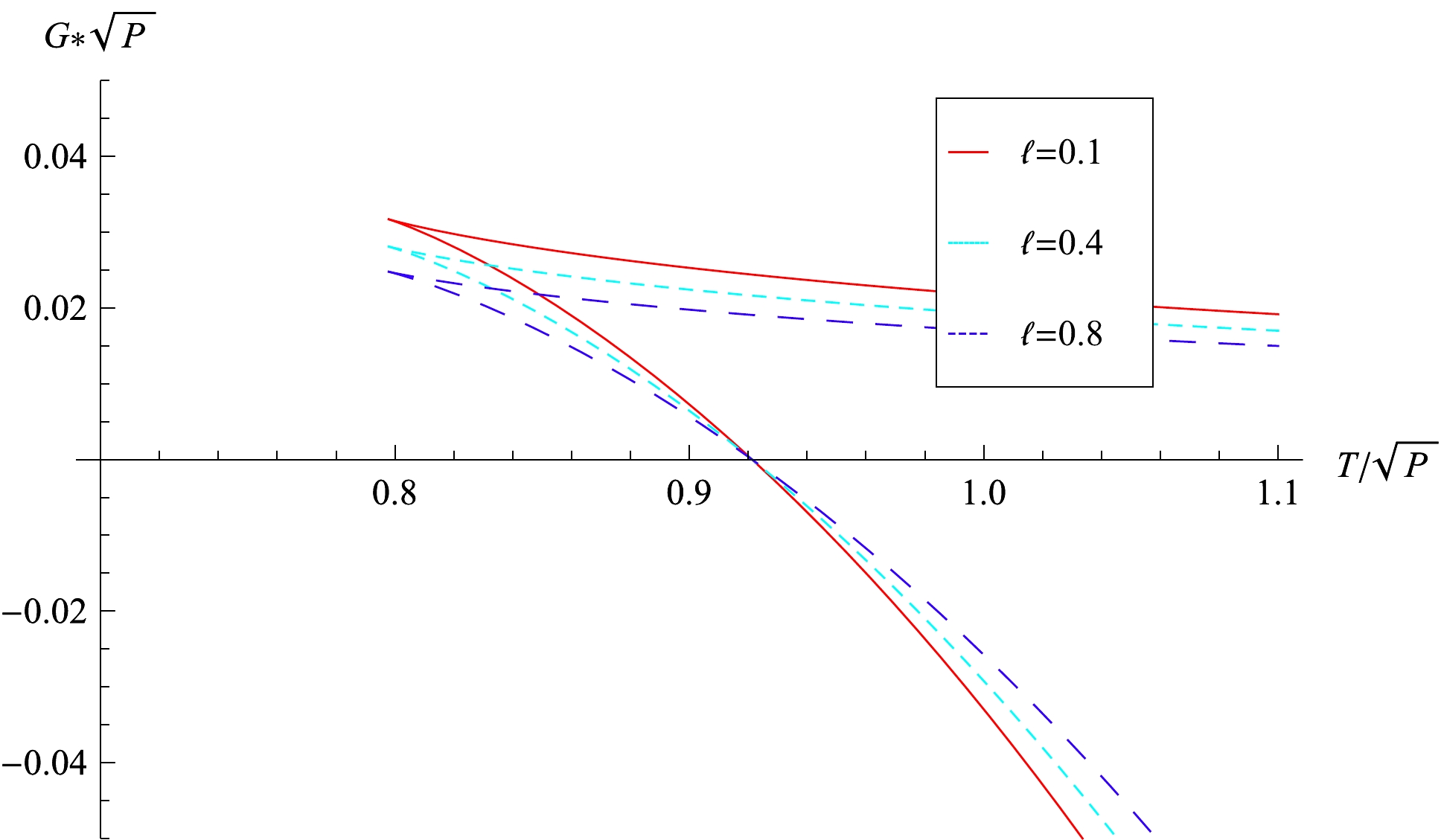
Figure 3. (color online) Black hole Gibbs free energy vs. temperature with
$ D=4 $ and different coupling constant$ \ell $ . They vanish at the point$T_{\rm HP}=\sqrt{8P/3\pi}$ . They all have both branches, the one above corresponds to the small black hole$ M<M_d $ , the one below to the large black hole$ M>M_d $ . At the temperature$T = T_{\rm min}$ , the free energy has a maximum$G_{\rm max} = 1/12\sqrt{2(1+\ell)\pi P}$ .$ \begin{array}{*{20}{l}} G_{\rm max}=\dfrac{\Omega_{D-2}}{(D-1)\pi}2^{(3-2D)} \left[\dfrac{(D-2)(D-3)}{(1+\ell)\pi P}\right]^{(D-3)/2}. \end{array} $

(76) The temperature at Hawking-Page phase transition point can be obtained when
$ G=0 $ ,$ \begin{array}{*{20}{l}} T_{HP}=2\sqrt{\dfrac{(D-2)P}{(D-1)\pi}}, \end{array} $

(77) which is also independent on
$ \ell $ like the minimum temperature$T_{\rm min}$ . At this point$ r_h=\sqrt{(D-1)(D-2)/[16(1+\ell)\pi P]} $ and the black hole mass is$ \begin{array}{*{20}{l}} M_{\rm HP}=\dfrac{(D-2)\Omega_{D-2}}{8\pi} \left[\dfrac{(D-1)(D-2)}{16(1+\ell)\pi P}\right]^{(D-3)/2}, \end{array} $

(78) and its entropy is
$ \begin{array}{*{20}{l}} S_{\rm HP}=4^{(1-D)}\Omega_{D-2}\sqrt{1+\ell}^{(3-D)} \left[\dfrac{(D-1)(D-2)}{\pi P}\right]^{(D-2)/2}. \end{array} $

(79) We summarize the three phases: unstable small black hole, metastable large black hole, and stable large black hole in Table 1. The stable large black hole, metastable large black hole, and thermal radiation are shown in Fig. 4.
Black hole mass Heat capacity Entropy Temperature Free energy Unstable small black hole $ 0<M<M_d $ 

$ C_p<0 $ 

$ S<S_d $ 

$ T>T_{\min} $ 

$ G>0 $ 

Metastable large black hole $ M_d<M<M_{\rm HP} $ 

$ C_p>0 $ 

$ S_d<S<S_{\rm HP} $ 

$ T_{\min}<T<T_{\rm HP} $ 

$ 0<G<G_d $ 

Stable large black hole $ M>M_{\rm HP} $ 

$ C_p>0 $ 

$ S>S_{\rm HP} $ 

$ T>T_{\rm HP} $ 

$ G<0 $ 

Table 1. Quantities of heat capacity, entropy, temperature, and Gibbs free energy for three phases of the AdS black hole in Einstein-bumblebee gravity.

Figure 4. (color online) Phase diagram (
$ T-P $ figure at unit mass M) for$ D=4 $ AdS-like black hole in Einstein-bumblebee gravity. The red solid and green dashed curves respectively correspond to the black hole minimum temperature and the HP phase transition temperature. Both curves extend to infinity.From Figs. 1 to 4 and Table 1, one can see the following picture for the formation of an AdS black hole: i) in an AdS space, the thermal radiation with zero Gibbs free energy has a very high temperature, and accidentally, a tiny mass black hole begins to form due to quantum fluctuation; ii) the tiny black hole begins to grow, its temperature decreases quickly, and its free energy increases slowly; iii) when the black hole mass grows to
$ M_d $ , its free energy approaches to a maximum, its temperature approaches to a minimum, and the small-large black hole phase transition occurs; iv) the black hole mass continues to grow, its positive free energy decreases, its temperature increases slowly, and it is a metastable black hole; v) when the mass grows to$M_{\rm HP}$ , the HP phase transition occurs; and vi) finally, the stable large black hole has formed.Figure 3 also shows that the LV constant
$ \ell $ decreases the Gibbs free energy of the meta-stable large black hole with the mass$ M_d < M < M_{\rm HP} $ , showing that the HP phase transition from a meta-stable large black hole to a large stable one will occur more easily.Now, we consider some relationships between both types of phase transition. Wei and Liu [38] found a novel exact dual relation between the minimum temperature of the
$ D+1 $ -dimensional black hole and the HP phase transition temperature in D dimensions, reminiscent of the holographic principle. Here, we will examine wether it still holds or not to this LV black hole. The first relationship is for the temperature and entropy,$ \begin{array}{*{20}{l}} \dfrac{T_{\rm HP}}{T_{\rm min}}=\dfrac{D-2}{\sqrt{(D-1)(D-3)}},\; \dfrac{S_{\rm HP}}{S_{d}}=\left(\dfrac{D-1}{D-3}\right)^{(D-2)/2}, \end{array} $

(80) which are only dependant on the dimension number D and are the same as those in Refs. [38, 41]. The second relationship is between the D dimensional Hawking-Page temperature
$T_{\rm HP}$ and the$ D+1 $ dimensional minimum temperature$T_{\rm min}$ ,$ \begin{array}{*{20}{l}} T_{\rm HP}(D)=T_{\rm min}(D+1), \end{array} $

(81) which is the novel dual relation found in Ref. [38]. This relation is independent of the pressure and the bumblebee coupling constant and is like the AdS/CFT correspondence.
$T_{\rm min}$ is a physical quantity in the bulk, and then$T_{\rm HP}$ can be treated as the dual physical quantity on the boundary. -
In this work, we have derived the high dimensional AdS-like black hole solution in Einstein-bumblebee gravity theory. It can exist only under the condition that the bumblebee potential has a linear functional form with a Lagrange-multiplier field λ. This additional field is strictly constrained by the bumblebee motion equation and can be absorbed by the definition of an effective cosmological constant
$ \Lambda_e $ . Like the Schwarzschild-like black hole [22], it cannot be asymptotically to the AdS spacetime, so it is a Schwarzschild-AdS-like black hole solution [26]. Contrary to the Schwarzschild-like black hole, the bumblebee field will affect the locations of the black hole horizon.By using black hole chemistry, we have studied the thermodynamics and phase transitions of this high dimensional Schwarzschild-AdS-like black hole. Via the Komar integral method, we found that the Smarr formula can still be constructed, but the conceptions of the horizon area/entropy
$ A/S $ and the volume V inside the horizon should be renewed, i.e., the LV has affected the known spacetime geometry by the anisotropy of pressure. Via the Hamiltonian perturbation method, there still exists the first law of black hole thermodynamics with the renewed conceptions of area and volume.Its temperature has a minimum value
$T_{\rm min}$ , corresponding to the black hole mass$ M_d $ . The small black hole with mass$ 0<M<M_d $ has a negative heat capacity$ C_p $ , while the large black hole with mass$ M>M_d $ has a positive one. At the point$ M_d $ , the$ C_p $ is divergent. The LV constant$ \ell $ decreases the mass$ M_d $ , showing that the phase transition from a small black hole to a large one will more easily occur.Its Gibbs energy has a maximum value
$G_{\rm max}$ at the point of mass$ M_d $ and has a zero point$ G=0 $ at the point of mass$ M_{\rm HP} $ . The small black hole with mass$ 0<M<M_d $ and the large black hole with mass$ M_d<M<M_{\rm HP} $ have a positive Gibbs free energy, while the large black hole with mass$ M>M_d $ has a negative one. The LV constant$ \ell $ decreases the Gibbs free energy of the meta-stable large black hole with the mass$ M_d<M<M_{\rm HP} $ , showing that the HP phase transition from a meta-stable large black hole to large stable one will occur more easily.The dualities found in Ref. [38] still hold when the Lorentz symmetry is spontaneously broken: the ratio of temperature between the small/large black hole phase transition and HP phase transition
$T_{\rm HP}/T_{\rm min}$ , and the equivalence of the temperature of D-dimensional HP phase transition to the temperature of$ D+1 $ dimensional small/large black hole phase transition$T_{\rm HP}(D)=T_{\rm min}(D+1)$ . -
If one uses the smooth potential
$ V=\kappa {x^2}/2 $ , then under condition (9), it becomes$ V=V'=0 $ , and the motion Eq. (18) becomes$ b^rR_{rr}=0 $ . In a four dimensional spacetime, the gravitational Eqs. (19)–(21) become$ \begin{array}{*{20}{l}} (1+\ell)(2r\psi'-1)+{\rm e}^{2\psi}(1-\Lambda r^2)=0 \end{array} \tag{A1}$

$ \ell r^2(\phi'' + \phi'^2 - \phi'\psi') - 2\ell r(\psi' + \phi') - 2r\phi' + {\rm e}^{2\psi}(1 - \Lambda r^2) = 0 \tag{A2}$

$ \begin{array}{*{20}{l}} (1+\ell)[r^2(\phi''+\phi'^2-\phi'\psi')+r(\phi'-\psi')]+{\rm e}^{2\psi}\Lambda r^2=0 , \end{array}\tag{A3} $

and
$ R_{rr}=0 $ becomes$ \begin{array}{*{20}{l}} R_{rr}=\dfrac{2}{r}\psi'-(\phi''+\phi'^2-\phi'\psi')=0. \end{array}\tag{A4} $

by using Eq. (A4), Eqs. (A2) and (A3) become
$ \begin{array}{*{20}{l}} -(1+\ell)(2r\phi'+1)+{\rm e}^{2\psi}(1-\Lambda r^2)=0, \end{array} \tag{A5}$

$ \begin{array}{*{20}{l}} (1+\ell)r(\phi'+\psi')+{\rm e}^{2\psi}\Lambda r^2=0 . \end{array} \tag{A6}$

Combining Eq. (A5) and (A1), one can obtain
$ \phi'+\psi'= 0 $ , which will lead Eq. (A6) to the result$ e^{2\psi}\Lambda r^2=0 $ , i.e.,$ \Lambda=0 $ . Therefore, it is proved that there is no black hole solution with nonzero Λ for the above gravitational Eqs. (A1) to (A3) under the smooth potential$ V=\kappa x^2/2 $ . -
By using the thermodynamical volume V (51) and the entropy S (52), one can rewrite the mass formula (32) as
$ \begin{array}{*{20}{l}} M=M(S,P)=\dfrac{(D-2)S(r_h)}{4\pi \sqrt{1+\ell}r_h}+PV(r_h). \end{array} \tag{B1}$

Then, its total differential is
$ \begin{array}{*{20}{l}} {\rm d}M=\Big(\dfrac{\partial M}{\partial S}\Big)_P{\rm d}S+\Big(\dfrac{\partial M}{\partial P}\Big)_S{\rm d}P. \end{array} \tag{B2}$

In it, the partial derivative
$ \left(\dfrac{\partial M}{\partial P}\right)_S=V $ , another partial derivative is$ \begin{array}{*{20}{l}} \Big(\dfrac{\partial M}{\partial S}\Big)_P=\Big(\dfrac{\partial M}{\partial S}\Big)_{P,V,r_h}+\Big(\dfrac{\partial M}{\partial r_h}\Big)_{P,S}\Big(\dfrac{{\rm d}r_h}{{\rm d}S}\Big), \end{array} \tag{B3}$

whose result is the same as that of Eq. (50). Finally, Eq. (B2) gives the first law of black hole thermodynamics,
$ \begin{array}{*{20}{l}} {\rm d}M=T{\rm d}S+V{\rm d}P. \end{array} \tag{B4}$

High dimensional AdS-like black hole and phase transition in Einstein-bumblebee gravity
- Received Date: 2022-11-10
- Available Online: 2023-04-15
Abstract: In this study, we obtained an exact high dimensional anti-de Sitter (AdS) black hole solution in Einstein-bumblebee gravity theory. This AdS-like black hole can only exist with a linear functional potential of the bumblebee field. We found that the Smarr formula and the first law of black hole thermodynamics can still be constructed in this Lorentz symmetry breaking black hole spacetime, but the conceptions of the black hole horizon area/entropy and the volume inside the horizon should be renewed due to its anisotropy. We also found that two types of phase transition exist: small-large black hole phase transition and Hawking-Page phase transition, like those of the Schwarzschild AdS black hole. After Lorentz symmetry breaking, the black hole mass at the divergent point of heat capacity becomes small, and the Gibbs free energy of the meta-stable large black hole is also smaller, showing that the large stable black hole can be more easily formed.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: