Strange cousin of Z_c(4020/4025) as a tetraquark state

I. INTRODUCTION

• I. INTRODUCTION
• II. QCD SUM RULES FOR THE $Z_{c}$, $Z_{cs}$, and $Z_{cs{\bar{s}}}$ TETRAQUARK STATES WITH $J^{PC}=1^{+-}$
• III. DECAY WIDTHS OF THE $Z_c$ AND $Z_{cs}$ STATES WITH QCD SUM RULES
• IV. CONCLUSION

In 2013, the BESIII Collaboration observed $Z^{\pm}_c(4025)$ in the $\pi^\mp$ recoil mass spectrum of the process $e^+e^- \to (D^{*} {\bar{D}}^{*})^{\pm} \pi^\mp$, where the measured Breit-Wigner mass and width were $M=(4026.3\pm2.6\pm3.7)\,{\rm{MeV}}$and $\Gamma=(24.8\pm 5.6\pm7.7)\,{\rm{MeV}}$, respectively [1]. Two years later, the BESIII Collaboration observed its neutral partner $Z^{0}_c(4025)$ in the $\pi^0$ recoil mass spectrum of the process $e^+e^- \to (D^{*} {\bar{D}}^{*})^{0} \pi^0$, where the measured Breit-Wigner mass and width were $M=(4025.5^{+2.0}_{-4.7}\pm3.1)\,{\rm{MeV}}$ and $\Gamma=(23.0\pm 6.0\pm 1.0) {\rm{MeV}}$, respectively [2]. The masses and widths of the charged structures $Z_c^{\pm}(4025)$ and neutral structure $Z_c^0(4025)$ were consistent with each other. Moreover, in 2013, the BESIII Collaboration observed $Z_c^\pm(4020)$ in the $\pi^\pm h_c$ mass spectrum of the process $e^+e^- \to \pi^+\pi^- h_c$, where the measured Breit-Wigner mass and width were $M=(4022.9\pm 0.8\pm 2.7)\,{\rm{MeV}}$ and $\Gamma=(7.9\pm 2.7\pm 2.6)\,{\rm{MeV}}$, respectively [3]. $Z_c(4020)$ and $Z_c(4025)$ were assigned to be the same particle by the Particle Data Group and listed in the Review of Particle Physics as $X(4020)$ [4], although the widths differed from each other considerably.

The spin and parity have not yet been measured. S-wave $D^{*} {\bar{D}}^{*}$ systems have the quantum numbers $J^{PC}=0^{++}$, $1^{+-}$, and $2^{++}$, S-wave $\pi^\pm h_c$ systems have the quantum numbers $J^{PC}=1^{--}$, P-wave $\pi^{\pm} h_c$ systems have the quantum numbers $J^{PC}=0^{++}$, $1^{+-}$, and $2^{++}$, and we can tentatively assign the quantum numbers $J^{PC}=1^{+-}$ for $Z_c(4020/4025)$. According to the nearby $D^*{\bar{D}}^*$ threshold, one may expect to assign $Z_c(4020/4025)$ as the tetraquark molecular state [5–12]. In the picture of tetraquark states, $Z_c(4020/4025)$ can be assigned as the $A{\bar{A}}$-type tetraquark state with $J^{PC}=1^{+-}$ [13–15], whereas $Z_c(3900)$ can be assigned as the $S{\bar{A}}-A{\bar{S}}$ type tetraquark state according to calculations via QCD sum rules [16], where S and A represent the scalar and axialvector diquark states, respectively.

In 2020, the BESIII Collaboration observed the $Z_{cs}^-(3985)$ structure in a $K^{+}$ recoil-mass spectrum with a significance of 5.3 σ in the processes $e^+e^-\to K^+ (D_s^- D^{*0} + D^{*-}_s D^0)$ [17]. The measured Breit-Wigner mass and width were $M=3985.2^{+2.1}_{-2.0}\pm1.7\,{\rm{MeV}}$ and $\Gamma=13.8^{+8.1}_{-5.2}\pm4.9\,{\rm{MeV}}$, respectively [17]. In 2021, the LHCb Collaboration observed two new exotic states, $Z_{cs}^+(4000)$ and $Z_{cs}^+(4220)$, in the $J/\psi K^+$ mass spectrum of the process $B^+ \to J/\psi \phi K^+$ [18]. The most significant state, $Z_{cs}^+(4000)$, had a Breit-Wigner mass and width of $M=4003 \pm 6 {}^{+4}_{-14}\,{\rm{MeV}}$ and $\Gamma=131 \pm 15 \pm 26\,{\rm{MeV}}$, respectively, and the spin-parity $J^P =1^+$ [18]. Although we can reproduce the mass of $Z_{cs}(3985/4000)$ using QCD sum rules in the pictures of both the tetraquark and molecular states [19–26], direct calculations of the decay widths based on QCD sum rules support assigning $Z_{cs}(3985)$ and $Z_{cs}(4000)$ as the hidden-charm tetraquark state and molecular state with $J^{PC}=1^{+-}$, respectively. Alternatively, at least, $Z_{cs}(3985)$ may have a large diquark-antidiquark type Fock component, while $Z_{cs}(4000)$ may have a large color-singlet-color-singlet type Fock component [27].

$Z_c(3900/3885)$ and $Z_{cs}(3985/4000)$ are cousins and have analogous decay modes.

and we expect that $Z_{c}(4020/4025)$ also has strange cousins $Z_{cs}$, which have analogous decay modes. The $Z_{cs}$ states may be observed in decays to final states, such as $D^*{\bar{D}}_s^*$, $D_s^*{\bar{D}}^*$, and $h_cK$. In this study, we tentatively assign $Z_c(4020/4025)$ as the $A{\bar{A}}$-type hidden-charm tetraquark state with $J^{PC}=1^{+-}$ and extend our previous study to investigate the mass and width of its strange cousin using QCD sum rules [20, 23, 27, 28]. The predictions can be confronted with experimental data in the future, which may contribute to disentangling the pictures of tetraquark and molecular states. As a byproduct, we obtain the mass of the hidden-strange/charm tetraquark state and the partial decay widths of $Z_c(4020/4025)$.

The article is arranged as follows. We derive QCD sum rules for the masses and pole residues of the $A{\bar{A}}$-type tetraquark states without strange, with strange, and with hidden-strange in Section II. In section III, we derive QCD sum rules for the hadronic coupling constants in the decays of the $Z_c$ and $Z_{cs}$ states. Section IV is reserved for our conclusion.

II. QCD SUM RULES FOR THE $Z_{c}$, $Z_{cs}$, and $Z_{cs{\bar{s}}}$ TETRAQUARK STATES WITH $J^{PC}=1^{+-}$

• I. INTRODUCTION
• II. QCD SUM RULES FOR THE $Z_{c}$, $Z_{cs}$, and $Z_{cs{\bar{s}}}$ TETRAQUARK STATES WITH $J^{PC}=1^{+-}$
• III. DECAY WIDTHS OF THE $Z_c$ AND $Z_{cs}$ STATES WITH QCD SUM RULES
• IV. CONCLUSION

First, we present the two-point correlation functions $\Pi_{\mu\nu\alpha\beta}(p)$ in the QCD sum rules,

where $J_{\mu\nu}(x)=J_{\mu\nu}^{u{\bar{d}}}(x)$, $J_{\mu\nu}^{u{\bar{s}}}(x)$, and $J_{\mu\nu}^{s{\bar{s}}}(x)$,

where i, j, k, m, and n are color indexes, and C is the charge conjugation matrix [15, 28]. We choose the currents $J_{\mu\nu}^{u{\bar{d}}}(x)$, $J_{\mu\nu}^{u{\bar{s}}}(x)$, and $J_{\mu\nu}^{s{\bar{s}}}(x)$ to explore the hidden-charm tetraquark states without strange, with strange, and with hidden-strange, respectively.

On the hadronic side, we explicitly isolate the ground state contributions of the hidden-charm tetraquark states with $J^{PC}=1^{+-}$ and $1^{--}$ and acquire the following results:

where Z and Y denote the tetraquark states with $J^{PC}=1^{+-}$ and $1^{--}$, respectively. The pole residues $\lambda_{Z}$ and $\lambda_{Y}$ are defined by

the $\zeta_\mu$ are the polarization vectors of the tetraquark states. We can rewrite the correlation functions $\Pi_{\mu\nu\alpha\beta}(p)$ in the form

according to Lorentz covariance.

We project the components $\Pi_Z(p^2)$ and $\Pi_Y(p^2)$ by the tensors $P_{A,p}^{\mu\nu\alpha\beta}$ and $P_{V,p}^{\mu\nu\alpha\beta}$to

where

We accomplish operator product expansion up to the vacuum condensates of dimension 10 and take account of the vacuum condensates $\langle {\bar{q}}q\rangle$, $\langle \dfrac{\alpha_s GG}{\pi}\rangle$, $\langle {\bar{q}}g_s\sigma Gq\rangle$, $\langle {\bar{q}}q\rangle^2$, $\langle {\bar{q}}q\rangle \langle \dfrac{\alpha_s GG}{\pi}\rangle$, $\langle{\bar{q}}q\rangle\langle {\bar{q}}g_s\sigma Gq\rangle$, $\langle {\bar{q}}g_s\sigma Gq\rangle^2$, and $\langle {\bar{q}}q\rangle^2 \langle \dfrac{\alpha_s GG}{\pi}\rangle$, where $q=u$, d, or s, as in previous studies [14–16, 20, 23]. We project the components

on the QCD side. In the present study, we are only interested in the component $\widetilde{\Pi}_Z(p^2)$ as we investigate the axialvector tetraquark states. We take the truncations $n\leq 10$ and $k\leq 1$ in a consistent manner, and the operators of the orders $\mathcal{O}(\alpha_s^{k})$ with $k> 1$ are discarded. The operators in the condensates $\langle g_s^3 GGG\rangle$, $\langle \dfrac{\alpha_s GG}{\pi}\rangle^2$, and $\langle \dfrac{\alpha_s GG}{\pi}\rangle\langle {\bar{q}} g_s \sigma Gq\rangle$ are of the orders $\mathcal{O}(\alpha_s^{3/2})$, $\mathcal{O}(\alpha^2_s)$, and $\mathcal{O}(\alpha_s^{3/2})$, respectively, and play minor roles; hence, they can be safely ignored [12, 29].

We obtain the QCD spectral densities $\rho_Z(s)$ through the dispersion relation,

supposing quark-hadron duality below the continuum threshold $s_0$, and accomplish a Borel transform in regard to the variable $P^2=-p^2$ to obtain the QCD sum rules

where $\tilde{\lambda}_Z=\lambda_{Z}M_{Z}$.

We differentiate Eq. (12) with respect to $\dfrac{1}{T^2}$, eliminate the re-defined pole residues $\tilde{\lambda}_{Z}$, and obtain QCD sum rules for the masses of the axialvector hidden-charm tetraquark states,

We take the standard values of the vacuum condensates, $\langle {\bar{q}}q \rangle=-(0.24\pm 0.01\, {\rm{GeV}})^3$, $\langle{\bar{s}}s\rangle=(0.8\pm0.1)\langle{\bar{q}}q\rangle$, $\langle{\bar{q}}g_s\sigma G q \rangle=m_0^2\langle {\bar{q}}q \rangle$, $\langle{\bar{s}}g_s\sigma G s \rangle=m_0^2\langle {\bar{s}}s \rangle$, and $m_0^2=(0.8 \pm 0.1)\, {\rm{GeV}}^2$ at the energy scale $\mu=1\, {\rm{GeV}}$ [30–32] and take the $\overline{MS}$ quark masses $m_{c}(m_c)=(1.275\pm0.025)\,{\rm{GeV}}$ and $m_s(\mu=2\,{\rm{GeV}})=(0.095\pm0.005)\,{\rm{GeV}}$ from the Particle Data Group [4]. We set $m_q=m_u=m_d=0$ and consider the energy-scale dependence of the input parameters,

from the renormalization group equation, where $t=\log \dfrac{\mu^2}{\Lambda_{\rm QCD}^2}$, $b_0=\dfrac{33-2n_f}{12\pi}$, $b_1=\dfrac{153-19n_f}{24\pi^2}$, $b_2=\dfrac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi^3}$, and $\Lambda_{\rm QCD}=210$ MeV, $292$ MeV, and $332$ MeV for the flavors $n_f=5$, $4$, and $3$, respectively [4, 33]. We choose the flavor number $n_f=4$ because there are u, d, s, and c quarks.

As in our previous studies, we acquire the acceptable energy scales of the QCD spectral densities for the hidden-charm tetraquark states according to the energy scale formula

with the effective c-quark mass ${\mathbb{M}}_c=1.82\,{\rm{GeV}}$ [11, 15, 34–35]. Furthermore, we consider the $S U(3)$ mass-breaking effects according to the modified energy scale formula

where ${\mathbb{M}}_s$ is the effective s-quark mass and fitted to be $0.2\,{\rm{GeV}}$ [23], and k is the number of valence s-quarks.

We search for suitable Borel parameters $T^2$ and continuum threshold parameters $s_0$ to satisfy the two criteria (pole or ground state dominance and convergence of operator product expansion) via trial and error. The Borel parameters, continuum threshold parameters, energy scales of the QCD spectral densities, pole contributions, and contributions from the vacuum condensates of dimension 10 are shown in Table 1. From the table, we can clearly see that the modified energy scale formula is well satisfied. Then, we consider the uncertainties on the input parameters and acquire the masses and pole residues of the hidden-charm tetraquark states without strange, with strange, and with hidden-strange having quantum numbers $J^{PC}=1^{+-}$, which are also shown in Table 1. In Fig. 1, we plot the masses of $Z_{cs}$ and $Z_{cs{\bar{s}}}$ with variations in the Borel parameters. As shown in the figure, platforms appear in the Borel windows, thus enabling reliable extraction of tetraquark masses.

Table 1

Table 1.  Borel parameters, continuum threshold parameters, energy scales, pole contributions, contributions from the vacuum condensates of dimension $10$, and masses and pole residues for the axialvector tetraquark states.

	$T^2 /{\rm{GeV} }^2$	$\sqrt{s_0}\,/\rm GeV$	$\mu /{\rm{GeV} }$	pole	$|D(10)|$	$M_Z/{\rm{GeV} }$	$\tilde{\lambda}_Z /(10^{-2}{\rm{GeV} }^5)$
$Z_c$	$3.3-3.7$	$4.6\pm0.1$	$1.7$	$(40-59)\ $%	$\ll 1\ $%	$4.02\pm0.09$	$3.00\pm0.45$
$Z_{cs}$	$3.4-3.8$	$4.7\pm0.1$	$1.7$	$(41-60)\ $%	$\ll 1\ $%	$4.11\pm0.08$	$3.49\pm0.51$
$Z_{cs{\bar{s}}}$	$3.5-3.9$	$4.8\pm0.1$	$1.7$	$(42-61)\ $%	$\ll 1\ $%	$4.20\pm0.09$	$4.00\pm0.58$

DownLoad: CSV

Show Table

Figure 1

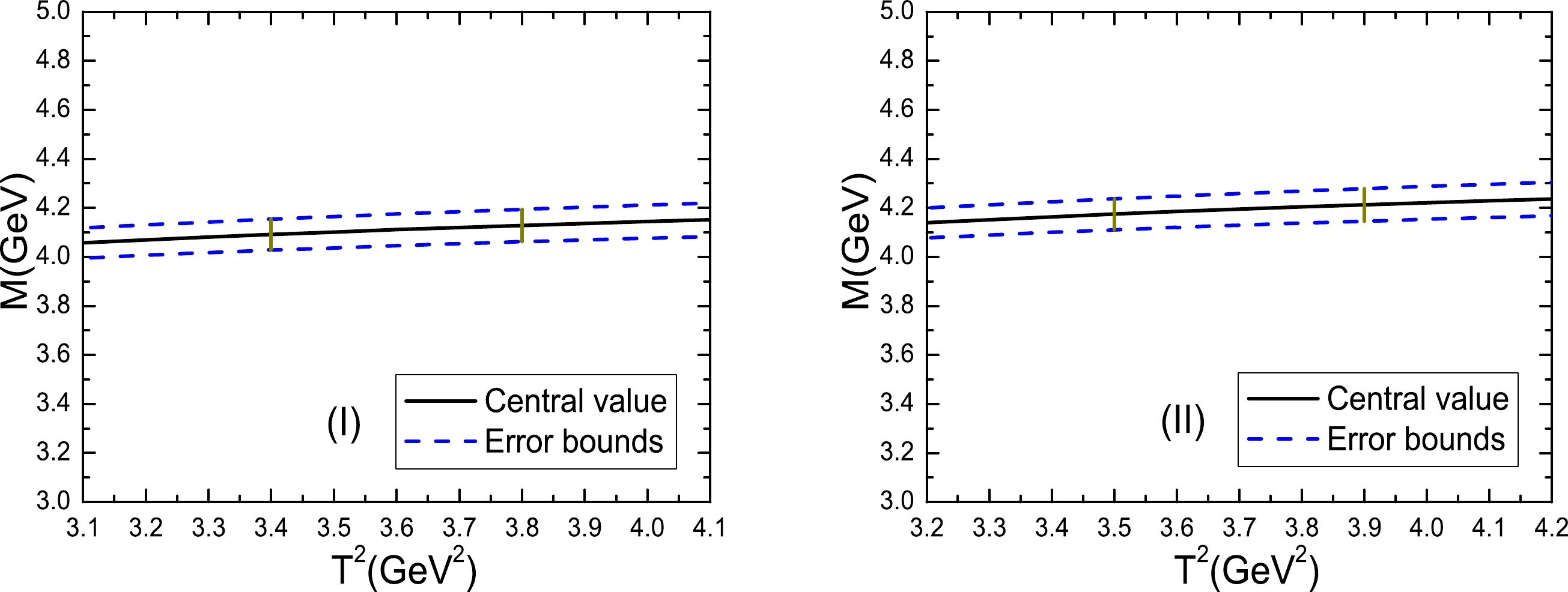
Figure 1.  (color online) Masses of the tetraquark states with variations in the Borel parameters $T^2$, where (I) and (II) correspond to $Z_{cs}$ and $Z_{cs{\bar{s}}}$, respectively, and the regions between the two vertical lines are the Borel windows.

DownLoad: Full-Size Img PowerPoint

The present prediction, $M_{Z_c}=\left(4.02\pm0.09\right) \, {\rm{GeV}}$ (also in Ref. [28]), is consistent with the experimental values $M_{Z_c^\pm}=(4026.3\pm2.6\pm3.7)$ MeV, $M_{Z_c^\pm}=(4022.9\pm 0.8\pm 2.7)$ MeV, and $M_{Z_c^0}=(4025.5^{+2.0}_{-4.7}\pm3.1)$ MeV from the BESIII Collaboration [1–3], which supports assigning $Z_c$(4020/ 4025) as the $J^{PC}=1^{+-} A{\bar{A}}$-type tetraquark state. We cannot assign a hadron unambiguously with the mass alone; we must calculate the partial decay widths and total width to perform a more robust assignment.

III. DECAY WIDTHS OF THE $Z_c$ AND $Z_{cs}$ STATES WITH QCD SUM RULES

• I. INTRODUCTION
• II. QCD SUM RULES FOR THE $Z_{c}$, $Z_{cs}$, and $Z_{cs{\bar{s}}}$ TETRAQUARK STATES WITH $J^{PC}=1^{+-}$
• III. DECAY WIDTHS OF THE $Z_c$ AND $Z_{cs}$ STATES WITH QCD SUM RULES
• IV. CONCLUSION

We investigate the two-body strong decays $Z_{cs}\to h_cK$, $J/\psi K$, and $\eta_cK^{*}$ with the three-point correlation functions $\Pi_{\alpha\beta\mu\nu}(p,q)$, $\Pi_{\alpha\mu\nu}^{1}(p,q)$, and $\Pi_{\alpha\mu\nu}^{2}(p,q)$, respectively,

where the currents

interpolate the mesons $h_c$, $J/\psi$, K, $\eta_c$, and $K^*$, respectively. With the simple substitution of $s\to d$, we obtain the corresponding ones for the $Z_c$ tetraquark state.

We insert a complete set of intermediate hadronic states having possible (non-vanishing) couplings with the current operators into the three-point correlation functions and explicitly isolate the ground state contributions.

where $\lambda_K=\dfrac{f_{K}M_{K}^2}{m_u+m_s}$, $\lambda_\eta=\dfrac{f_{\eta_c}M_{\eta_c}^2}{2m_c}$, $\lambda_{J/\psi}=f_{J/\psi}M_{J/\psi}$, $\lambda_{K^*}=f_{K^*}M_{K^*}$, $p^\prime=p+q$, and the decay constants of the mesons $h_c$, $J/\psi$, K, $\eta_c$, and $K^*$ are defined by

where ξ are polarization vectors of $h_c$, $J/\psi$, and $K^*$, and the hadronic coupling constants are defined by

The tensor structures in Eqs. (19)–(21) are sufficiently complex, and we must project the relevant components with suitable tensor operators,

where

which correspond to the two-body strong decays $Z_{cs}\to h_c K$, $J/\psi K$, and $\eta_c K^*$, respectively; the other components in Eqs. (19)–(21) have no contributions or contaminations. In Eq. (19), there are four channels, $Z_{cs}\to h_c K$, $Y_{cs}\to h_c K$, $Z_{cs}\to J/\psi K$, and $Y_{cs}\to J/\psi K$, which correspond to four different tensor structures and therefore four different components. We project the channel $Z_{cs}\to h_c K$ explicitly. In Eq. (20), there are two channels, $Z_{cs}\to J/\psi K$ and $Y_{cs}\to J/\psi K$, which correspond to two different tensor structures and therefore two different components. We project the channel $Z_{cs}\to J/\psi K$ explicitly. In Eq. (21), there are two channels, $Z_{cs}\to \eta_cK^*$ and $Y_{cs}\to \eta_cK^*$, which correspond to two different tensor structures and therefore two different components. We project the channel $Z_{cs}\to \eta_cK^*$ explicitly. The $\cdots$ in Eq. (25) represents the neglected contributions from the higher resonances and continuum states. According to the analysis in Refs. [27, 36–40], we can introduce the parameters $C_{h_cK}$, $C_{J/\psi K}$, and $C_{\eta_cK^*}$ to parametrize the higher resonance and continuum states involving the $Z_{cs}$ channel,

Moreover, we perform Fierz re-arrangement both in the color and Dirac-spinor spaces to obtain the result

where the component $\frac{\rm i}{2}\varepsilon^{\mu\nu\alpha\beta}{\bar{c}}\sigma_{\alpha\beta}c\,{\bar{s}}{\rm i}\gamma_5u$ leads to the correlation function

and we introduce a parameter κ to represent the possible factorizable contributions on the hadron side as we choose the local currents. The conventional mesons and tetraquark states have average spatial sizes of the same order, and $J_{u{\bar{s}}}^{\mu\nu}(0)$ potentially couples to the tetraquark state rather than the two-meson scattering states; therefore, $\kappa \ll 1$ [41]. However, such a term makes a contribution to the component $\Pi_{h_cK}(p^{\prime2},p^2,q^2)$,

where the coefficient $\widetilde{C}_{h_c K}$ can be absorbed into the coefficient $C_{h_cK}$. We can clearly see that the parameter $C_{h_cK}$ is necessary, and the parameters $C_{J/\psi K}$ and $C_{\eta_cK^*}$ are implied in the same way.

We accomplish operator product expansion up to the vacuum condensates of dimension 5 and neglect the minor gluon condensate contributions [27, 36–40]. We then obtain the QCD spectral densities $\rho_{\rm QCD}(p^{\prime2},s,u)$ through the double dispersion relation,

where $\Delta_s^2$ and $\Delta_u^2$ are the thresholds. On the hadron side, we obtain the hadronic spectral densities $\rho_H(s^\prime,s,u)$ through the triple dispersion relation,

according to Eq. (25), where $\Delta_{s}^{\prime2}$ are the thresholds. We match the hadron side with the QCD side below the continuum thresholds to acquire rigorous quark-hadron duality [36, 37],

where $s_0$ and $u_0$ are the continuum thresholds. We first take the integral over ${\rm d}s^\prime$ and introduce some unknown parameters, such as $C_{h_cK}$, $C_{J/\psi K}$, and $C_{\eta_cK^*}$, to parametrize contributions involving higher resonances and continuum states in the $s^\prime$ channel.

We set $p^{\prime2}=p^2$ in the correlation functions $\Pi(p^{\prime 2},p^2,q^2)$ and perform a double Borel transform in regard to the variables $P^2=-p^2$ and $Q^2=-q^2$. We then set the Borel parameters $T_1^2=T_2^2=T^2$ to obtain three QCD sum rules.

where $\langle {\bar{q}}Gq\rangle=\langle {\bar{q}}g_s \sigma Gq\rangle$, $\langle {\bar{s}}Gs\rangle=\langle {\bar{s}}g_s \sigma Gs\rangle$, $\lambda_{Zh K}= \lambda_{K}f_{h}\lambda_{Z}$, $\lambda_{ZJ/\psi K}=\lambda_{K}\lambda_{J/\psi}\lambda_{Z}$, and $\lambda_{Z\eta K^*}=\lambda_{K^*}\lambda_{\eta}\lambda_{Z}$. We neglect the dependencies of the parameters $C_{h_c K}$, $C_{J/\psi K}$, and $C_{\eta_c K^*}$ on the Lorentz invariants $p^{\prime2}$, $p^2$, and $q^2$. Instead, we take them as free parameters and search for the best values to delete the contamination from high resonances and continuum states and hence acquire stable QCD sum rules. The corresponding hadronic coupling constants for the $Z_c(4020/4025)$ state can be obtained with the simple substitution of $s \to d$ and are treated in the same manner.

On the QCD side, we choose the flavor number $n_f=4$ and set the energy scale to be $\mu=1.3\,{\rm{GeV}}$, as in a previous study on the decays of $Z_{cs}(3985/4000)$ [27]. On the hadron side, we take the parameters as $M_{K}=0.4937\,{\rm{GeV}}$, $M_{\pi}=$ 0.13957 GeV, $M_{K^*}=$ 0.8917 GeV, $M_{\rho}=$ 0.77526 GeV, $M_{J/\psi}=$ 3.0969 GeV, $M_{\eta_c}=$ 2.9834 GeV, $M_{h_c}=$ 3.525 GeV [4], $f_{K}=$ 0.156 GeV, $f_{\pi}=$ 0.130 GeV [4], $f_{K^*}=$ 0.220 GeV, $f_{\rho}=$ 0.215 GeV, $\sqrt{s^0_{K}}=$ 1.0 GeV, $\sqrt{s^0_{\pi}}=$ 0.85 GeV, $\sqrt{s^0_{K^*}}=$ 1.3 GeV, $\sqrt{s^0_{\rho}}=$ 1.2 GeV [42], $f_{h_c}=$ 0.235 GeV, $f_{J/\psi}=$ 0.418 GeV, $f_{\eta_c}=$ 0.387 GeV [43], $\sqrt{s^0_{h_c}}=$ 4.05 GeV, $\sqrt{s^0_{J/\psi}}=$ 3.6 GeV, $\sqrt{s^0_{\eta_c}}=$ 3.5 GeV [4], $\dfrac{f_{K}M^2_{K}}{m_u+m_s}= -\dfrac{\langle {\bar{q}}q\rangle+\langle {\bar{s}}s\rangle}{f_{K}(1-\delta_K)}$, and $\dfrac{f_{\pi}M^2_{\pi}}{m_u+m_d}=-\dfrac{2\langle {\bar{q}}q\rangle}{f_{\pi}}$ from the Gell-Mann-Oakes-Rennerrelation $\delta_K=0.50$ [44].

In calculations, we fit the unknown parameters to be $C_{h_c K}=0.000064+0.000014\times T^2{\rm{GeV}}^4$, $C_{h_c \pi}=0.00006+ 0.000010\times T^2{\rm{GeV}}^4$, $C_{J/\psi K}=0.00335+0.000096\times T^2{\rm{GeV}}^7$, $C_{J/\psi \pi}=0.00305+0.000096\times T^2 {\rm{GeV}}^7$, $C_{\eta_c K^*}=0.00368+ 0.00012\times T^2\,{\rm{GeV}}^7$, and $C_{\eta_c \rho}=0.00302+0.00012\times$ $T^2\,{\rm{GeV}}^7$ to acquire flat Borel platforms with the interval $T^2_{\max}-T^2_{\min}=1\,{\rm{GeV}}^2$, where max and min represent the maximum and minimum values, respectively. The Borel windows are $T^2_{h_c K}=(4.0-5.0)\,{\rm{GeV}}^2$, $T^2_{h_c \pi}=(4.0- 5.0) {\rm{GeV}}^2$, $T^2_{J/\psi K}= (4.3-5.3)\,{\rm{GeV}}^2$, $T^2_{J/\psi \pi}=(4.1-5.1)\,{\rm{GeV}}^2$, $T^2_{\eta_c K^*}=(3.9-4.9) {\rm{GeV}}^2$, and $T^2_{\eta_c \rho}=(3.9-4.9)\,{\rm{GeV}}^2$, where we add the subscripts $h_cK$, $h_c\pi \cdots$ to denote the corresponding decay channels. In the Borel windows, the uncertainties $\delta G$ originating from the Borel parameters $T^2$ must be less than or approximately $0.01\, (\rm GeV)$. Such a strict and powerful constraint plays a decisive role and works well, as in our previous studies [27, 36–40]. In Fig. 2, we plot the hadronic coupling constants $G_{Z_{cs} h_c K}$, $G_{Z_{cs}J/\psi K}$, $G_{Z_{cs}\eta_c K^*}$, $G_{Z_{c} h_c \pi}$, $G_{Z_{c}J/\psi \pi}$, and $G_{Z_{c}\eta_c \rho}$ with variations in the Borel parameters. We can explicitly observe flat platforms, which enable reliable extraction of the hadronic coupling constants.

Figure 2

Figure 2.  (color online) Hadronic coupling constants with variations in the Borel parameters $T^2$, where A, B, C, D, E, and F correspond to $G_{Z_{cs} h_c K}$, $G_{Z_{cs}J/\psi K}$, $G_{Z_{cs}\eta_c K^*}$, $G_{Z_{c} h_c \pi}$, $G_{Z_{c}J/\psi \pi}$, and $G_{Z_{c}\eta_c \rho}$, respectively.

DownLoad: Full-Size Img PowerPoint

If we take the symbol ξ to represent the input parameters on the QCD side, then, for example, the uncertainties ${\bar{\xi}} \to {\bar{\xi}} +\delta \xi$ result in the uncertainties ${\bar{f}}_{J/\psi}{\bar{f}}_{K}{\bar{\lambda}}_{Z}{\bar{G}}_{ZJ/\psi K} \to {\bar{f}}_{J/\psi}{\bar{f}}_{K}{\bar{\lambda}}_{Z}{\bar{G}}_{ZJ/\psi K}+\delta\,f_{J/\psi}f_{K}\lambda_{Z}G_{ZJ/\psi K}$and ${\bar{C}}_{J/\psi K} \to {\bar{C}}_{J/\psi K}+\delta C_{J/\psi K}$, where

in which we add the index $^-$ to all the variables to denote the central values. In the case where the uncertainty $\delta C_{J/\psi K}$ is small enough to be ignored, error analysis is easy to perform by approximately setting $\dfrac{\delta f_{J/\psi}}{{\bar{f}}_{J/\psi}} =\dfrac{\delta f_{K}}{{\bar{f}}_{K}}=\dfrac{\delta \lambda_{Z}}{{\bar{\lambda}}_{Z}}=\dfrac{\delta G_{ZJ/\psi K}}{{\bar{G}}_{ZJ/\psi K}}$. However, if the uncertainty $\delta C_{J/\psi K}$ is considerable, it must be considered for every uncertainty $\delta \xi$. We must adjust $\delta C_{J/\psi K}$ via fine tuning with the help of trial and error according to the variation $\delta \xi$ to acquire enough flat platforms in the same region, as in the case of the central values ${\bar{\xi}}$ and ${\bar{C}}_{J/\psi K}$. This error analysis is difficult to perform. We typically set $\dfrac{\delta f_{J/\psi}}{{\bar{f}}_{J/\psi}} =\dfrac{\delta f_{K}}{{\bar{f}}_{K}}=\dfrac{\delta \lambda_{Z}}{{\bar{\lambda}}_{Z}}=0$ to estimate the uncertainty $\delta G_{ZJ/\psi K}$; however, the validity of such an approximation is yet to be proved.

Now, let us methodically obtain the hadronic coupling constants according to above error analysis.

by setting

If we set

the uncertainty $\delta G_{ZJ/\psi K}$ will be four times as large as that given in Eq. (37). Other uncertainties can be understood in the same way. According to Eq. (37), the $S U(3)$ breaking effects in the hadronic coupling constants are small.

It is then easy to obtain the partial decay widths by taking the relevant masses from the Particle Data Group [4],

and the total widths,

where the values in the brackets are obtained from Eq. (39). The prediction $\Gamma_{Z_{c}} =29.57\pm2.30\, ({\rm or}\, \pm 9.20)\,\,{\rm{MeV}}$ is compatible with the upper bound of the experimental data $\Gamma=(24.8\pm5.6\pm7.7)\,{\rm{MeV}}$ [1], $(23.0\pm 6.0\pm 1.0)\,{\rm{MeV}}$ [2], and $(7.9\pm 2.7\pm 2.6)\,{\rm{MeV}}$ [3] from the BESIII Collaboration and also supports assigning $Z_c(4020/4025)$ to be the $A{\bar{A}}$-type hidden-charm tetraquark states with $J^{PC}=1^{+-}$. In the present study, we neglect the decays $Z_c(4020/4025)\to D^*{\bar{D}}^*$ and $Z_{cs}\to D^*{\bar{D}}_s^*$, $D_s^*{\bar{D}}^*$ because the $Z_c$ and $Z_{cs}$ states lie near the corresponding two-meson thresholds, and the available phase-spaces are small and even lead to the possible assignments of molecular states [5–12]. The most favorable channels are $Z_{cs}\to \eta_c K^*$ and $Z_{c}\to \eta_c \rho$ at present, even for $Z_c(4020/4025)$. The decay $Z_c(4020/4025) \to \eta_c\rho$ has not yet been observed, and observation of this channel may lead to a more robust assignment and shed light on the nature of $Z_c$ states. We can search for the $Z_{cs}$ state in the invariant mass spectra of $h_c K$, $J/\psi K$, $\eta_c K^*$, $D^*{\bar{D}}_s^*$, and $D_s^*{\bar{D}}^*$ in the future.

In the picture of diquark-antidiquark type tetraquark states, $Z_c(3900)$ and $Z_{cs}(3985)$ can be assigned tentatively as the $S{\bar{A}}-A{\bar{S}}$ type hidden-charm tetraquark states, and the hadronic coupling constants have the relations $|G_{ZD^*{\bar{D}}/ZD{\bar{D}}^*}|\ll |G_{ZJ/\psi\pi/Z\eta_c\rho}|$ and $|G_{ZD^*{\bar{D}}_s/ZD{\bar{D}}_s^*}|\ll |G_{ZJ/\psi K/Z\eta_c K^*}|$. Furthermore, the allowed phase-spaces in the decays to open-charm meson pairs are significantly smaller than those of decays to meson pairs involving charmonium. The contributions of decays to open-charm meson pairs to the total decay widths can be ignored [27, 36]. We expect that the conclusion holds in the present study for the $Z_c(4020/4025)$ and $Z_{cs}(4110)$ states and make a crude estimation of the partial decay widths, $\Gamma\left(Z_{c}\to D^* {\bar{D}}/D {\bar{D}}^*\right)< 1\,{\rm{MeV}}$ and $\Gamma\left(Z_{cs}\to D^* {\bar{D}}_s/D {\bar{D}}_s^*\right) <1$ MeV, based on the relations between the hadronic coupling constants obtained in Refs. [27, 36]; the contributions to the total widths from the decays to the final states $D^* {\bar{D}}/D {\bar{D}}^*$ and $D^* {\bar{D}}_s/D {\bar{D}}_s^*$ are also ignored.

IV. CONCLUSION

• I. INTRODUCTION
• II. QCD SUM RULES FOR THE $Z_{c}$, $Z_{cs}$, and $Z_{cs{\bar{s}}}$ TETRAQUARK STATES WITH $J^{PC}=1^{+-}$
• III. DECAY WIDTHS OF THE $Z_c$ AND $Z_{cs}$ STATES WITH QCD SUM RULES
• IV. CONCLUSION

In this article, we tentatively assign $Z_c(4020/4025)$ as the $A{\bar{A}}$-type hidden-charm tetraquark state with $J^{PC}=1^{+-}$ and construct $A{\bar{A}}$-type tensor currents to investigate the tetraquark states without strange, with strange, and with hidden-strange via QCD sum rules. We consider the contributions of the vacuum condensates up to dimension-10 in operator product expansion. Then, we resort to the modified energy scale formula $\mu=\sqrt{M^2_{X/Y/Z}-(2{\mathbb{M}}_c)^2}-k{\mathcal{M}}_s$ to account for the $S U(3)$ mass-breaking effects to choose suitable energy scales for the QCD spectral densities and obtain the tetraquark masses in a self-consistent manner. We introduce three-point correlation functions to investigate the hadronic coupling constants in the two-body strong decays of the tetraquark states without strange and with strange via QCD sum rules based on rigorous quark-hadron duality, which is a unique feature of our studies. The numerical results indicate that the $S U(3)$ breaking effects in the hadronic coupling constants are small. We then obtain the partial decay widths and total widths of the $Z_c$ and $Z_{cs}$ states and find that the total width $\Gamma_{Z_c}$ is compatible with that of $Z_c(4020/4025)$ and also supports assigning $Z_c(4020/4025)$ as the $J^{PC}=1^{+-} A{\bar{A}}$-type tetraquark state. Further experimental data are required to achieve a more robust assignment because $Z_c(4020/4025)$ has not yet been observed in the $J/\psi \pi$ and $\eta_c\rho$ channels. In future, we may search for the strange cousin $Z_{cs}$ in the $D^*{\bar{D}}_s^*$, $D_s^*{\bar{D}}^*$, $h_cK$, $J/\psi K$, and $\eta_c K^*$ invariant mass spectra, the observation of which would shed light on the nature of $Z_c$ states.

References