-
Historically, magic nuclei are famous, similar to inert gas elements. The emergence of a large shell gap leads to more stability for these nuclei in comparison with neighboring nuclei. By introducing a strong spin-orbital coupling term into the single-particle potential, the magic numbers could finally be reproduced, such as 28, 50, 82, and 126. The corresponding spin (s)-orbital (l) doublets involved in generating these numbers are f7/2-f5/2 (l = 3), g9/2-g7/2 (l = 4), h11/2-h9/2 (l = 5), and i13/2-i11/2 (l = 6), respectively. Here, l denotes the angular momentum number, and the subscript indicates the total spin number, j = l ± s. Notice that those are the highest l value orbitals for each harmonic oscillator (principal) number N. In addition, the numbers of 14 and 6, which are based on shell gaps due to splits of the d5/2-d3/2 (l = 2) and p3/2-p1/2 (l = 1) orbitals, should be regarded as magic numbers as well.
The nuclei 14C (Z = 6, N = 8), 34Si (Z = 14, N = 20), and 68Ni (Z = 28, N = 40) have a common shell character; proton magic-numbers occur due to spin-orbital splits, while neutron numbers occur due to harmonic oscillator shell gaps. From these, we examine the level structure of 34Si. To date, the excited states of 34Si have been identified for an energy of up to Ex = 6233 keV, but the spin-parity assignment has been made only for the first 2+, 3- and the second 0+, 2+ states [1−7]. Moreover, no overall study of the level structure of this nucleus has been made. Instead, most studies are concerned with identifying the second 0+ state to prove the deformed
$2\hbar \omega $ pf-shell nature [2−11] and the bubble matter distribution of the protons in the spherical ground state [12−14]. In this work, we first construct the level scheme from existing data, then compare it to those of the neighboring isotones with N = 20 and finally discuss the underlying shell and collective structures using large-scale shell-model approaches. -
Figure 1 shows the currently-known level scheme of 34Si. The 2+ and 3- states were firstly identified through the β-decay of 34Al [2−4]. The levels at 4379 and 4969 keV were tentatively assigned (3-, 4-, 5-) on the basis of logft values [4]. The 4519 keV level was also observed in β-decay measurements [4, 8]. Conversely, the levels at 4920 and 6233 keV were observed only in a fusion-evaporation reaction, 18O (18O, 2p) 34Si [5]. The second 0+ at 2719 keV, including the populated 607-keV transition, has been identified using positron-electron internal pair-creation spectroscopy on the β-decay of 34Al [6].
By looking closely at the γ-ray transitional properties of the 18O (18O, 2p) 34Si reaction [5], we are able to assign spin-parities with an argument concerning fusion-evaporation reactions. Generally, the fusion-evaporation reaction yields mainly yrast states, which are the lowest levels in energy for a given spin. According to the γ-ray intensities from a given level scheme in Ref. [5], the yrast states were found to be along the 6233 - 4969 - 4379 - 4255 (3-) - 3326 (2+) keV line. Thus, the 4379, 4969, and 6233 keV levels could be assigned the spins J = 4, 5, and 6, respectively. Among them, the 4379 and 4969 keV levels were suggestive of negative parity states, possibly (3-,4-,5-) from β-decay measurements [1, 4]. Accordingly, we propose the 4969 and 4379 keV levels to be 5- and 4-, respectively. We find that the 1594-keV transition from the 4920 keV to the 2+ level at 3326 keV is relatively strong in intensity. Further, the 4920-keV level has another branch with a weak intensity connected to the 3- state at 4255 keV. Consequently, the 4920-keV level is supposed to have spins of 4 rather than of 3. Considering the higher probability of E2 than M2 transitions, we assign the 4920- and 6233-keV levels to be 4+ and 6+, respectively. Finally, let us look at the 4519-keV level with a 1193-keV transition connected to the 2+ state at 3326 keV. The 1193-keV transition has been observed in both β-decay and in-beam fusion-evaporation γ-ray measurements. Further, this transition was also seen in the β-decay of the 1+ isomer of 34Al from the precursor 34Mg nucleus [8]. Thereby, a spin assignment of 3 should be excluded. Moreover, observation from the in-beam reaction [5] excludes the possibility of 0+ or 1+. Eventually, this level must be 2+. Our assignment is certainly consistent with the recent result by Han et al. [9].
We show the constructed level scheme of 34Si in Fig. 2, in which the level schemes of the isotones 36S and 38Ar are also included. At first glance, a similarity appears for the negative-parity states 3-, 4-, and 5-.
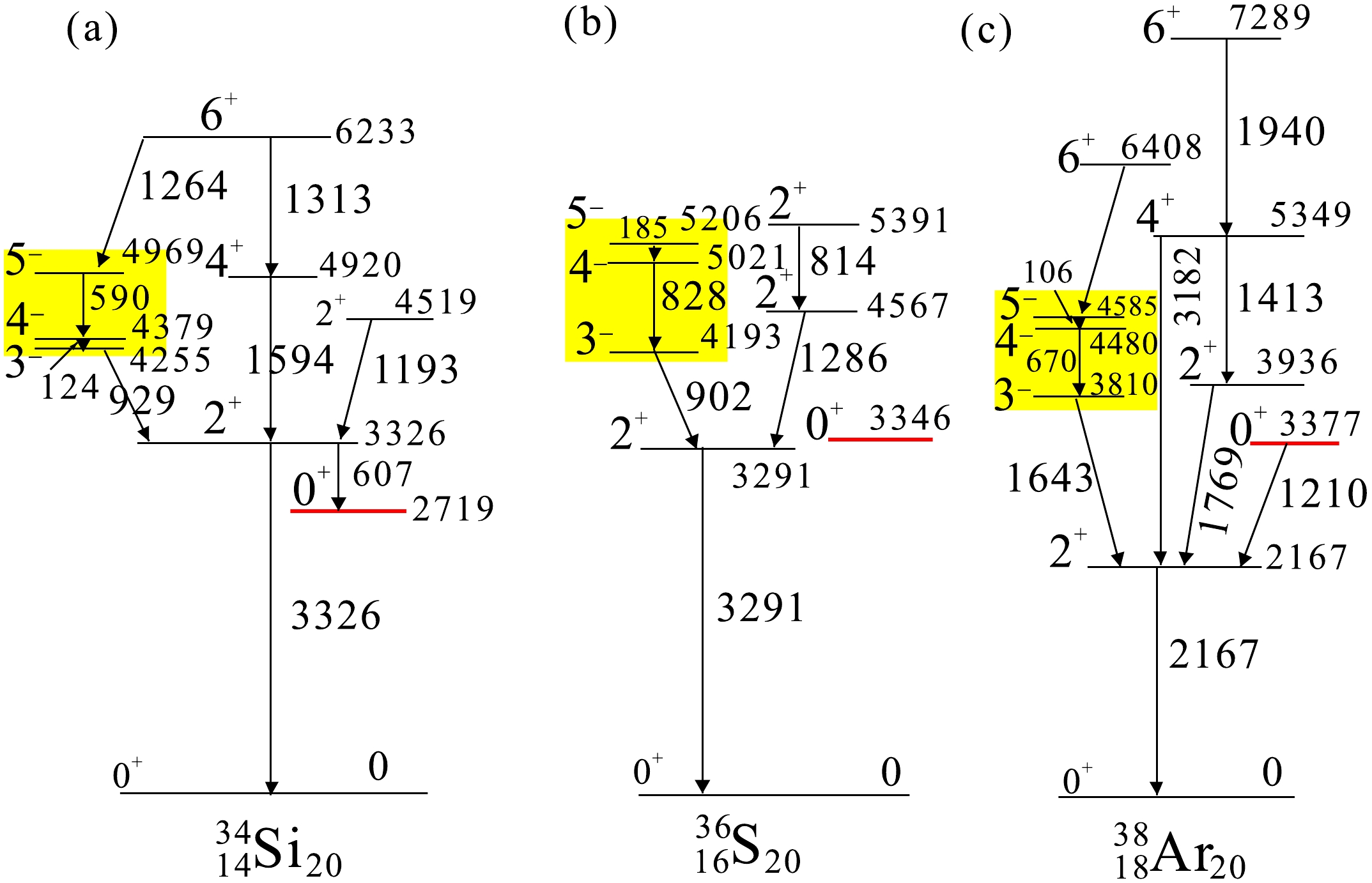
Figure 2. (color online) The level schemes of 34Si (a) as obtained from the present work, 36S (b), and 38Ar (c) [ 1]. For comparison, the negative states are denoted in yellow.
As will be discussed below, these negative-parity states are associated with neutron one particle-one hole excitations across the N = 20 shell gap. What we notice next is that the second 2+ states show a similar property, connecting the first 2+ states. Despite no observation of the 4+ state in 36S, the 4+ and 6+ states of 34Si show a similar pattern to those of 38Ar. Overall, we conclude that our spin assignments of the observed excited states in 34Si are reasonable. In addition, as we will see later, the large-scale shell-model calculations prove that the present result is correct.
-
To explain the underlying nuclear structure of the presented level scheme of 34Si, we performed theoretical calculations with a large-scale shell model. The space spans over d5/2, s1/2, d3/2, f7/2, and p3/2 for both protons and neutrons. The used effective shell-model interaction was sdpf-m [15]. The calculations were performed with the shell-model code, KSHELL [16, 17]. In this calculation, up to three particle-three hole (0 − 3
$\hbar\omega $ ) configurations were employed. It is found that the neutron cross-shell excitations are rather dominant over the protons, leading to the neutron (d5/2)6(d3/2s1/2)4(f7/2p3/2)2 configurations. This is more evident at the onset of deformation when they are between orbitals across N = 20 with spin-differences of two units Δj = 2. In this case, the spherical closed-shell configuration has a zero particle-zero hole character, whereas the deformed configuration has a two-particle-two-hole configuration from the occupied orbital, d3/2, to the empty valence orbital, f7/2. The level structure derived from our shell-model calculations is displayed in Fig. 3, in which the constructed level scheme is also included for comparison. For discussion, we denote the values of the predicted quadrupole transition strengths. Here, the effective charges used were ep = 1.5e for protons and en = 0.5e for neutrons. As is apparent in Fig. 3, the shell model predictions agree well with the experimental data.
Figure 3. (color online) (a) Level scheme of 34Si proposed by the present work. (b) The predicted level scheme of 34Si according to the large-scale shell-model calculations over the space of d5/2, s1/2, d3/2, f7/2, and p3/2 for both protons and neutrons. Numbers in parentheses are the expected electric quadrupole transition strengths, B(E2; J+2→J), in e2fm4. The experimental value in (a) is from [ 6].
In Table 1, we show the calculated probabilities of the main configurations for the states of interest. The ground state is found to exhibit the dominance of both proton (π) and neutron (ν) closed shells, indicating the π(d5/2)6 ν(d5/2)6(s1/2)2(d3/2)4 configuration with 73%. However, we find that two-neutron excitations from d3/2 to f7/2, (d3/2)2(f7/2)2 contribute as well, which amounts to about 8%. On the contrary, the proton excitations to the s1/2 orbital across Z = 14 are negligible. Hence, we see that a large depletion occurs at the center of the proton matter. This toroidal-like structure, sometimes called a bubble structure, in the ground state has been proven experimentally by one proton removal reaction [13]. In contrast to the ground state, the excited 22+, 31+, 23+, and 32+ states are produced dominantly by occupations of the proton s1/2 orbital. From the ground state to the first 6+ state through the first 2+ and 4+ states, the π(d5/2)6 ν(d5/2)6(s1/2)2(d3/2)2(f7/2)2 component increases rapidly. The calculated 21+, 41+, and 61+ energies are in good agreement with the experimental data. Here, the 61+ state can be understood in terms of full spin alignment of the neutron f7/2 orbital. This type of energetically favored state has been commonly observed as a spin trap caused by a non-collective oblate distribution.
The second 0+, 02+ state is certainly reproduced in energy by the neutron two particles-two holes (d3/2)2(f7/2)2 configuration, which amounts to about 40%, including a proton s1/2 excitation with 9%. Moreover, the expected value, 77 e2fm4, of the reduced quadrupole transitional strength, B(E2;21+ to 02+) is consistent with that of the experimental result, 61(40). According to the monopole strength in [6], this second 0+ state was found to have a deformation with β = 0.29(4). To confirm this result, we investigated a level crossing between the d3/2 and f7/2 orbitals using a deformed shell model with a stretched harmonic oscillator potential. It is found that the crossing between the d3/2[2, 2, 3/2, 3/2] orbital and the f7/2[3, 3, 7/2, 1/2] orbital occurs around ε2 = 0.22. Here, [2, 2, 3/2, 3/2] indicates the harmonic oscillator number (N), angular momentum (l), total spin (j), and total spin projection (jz), respectively, and the quadrupole deformation parameter ε2 corresponds to 0.95β2. This result proves the deformation derived from the monopole transition strength.
The negative-parity states 3−, 4−, and 5− located above the 2+ state are dominated by the neutron one particle-one hole excitation, viz., (d3/2)-1(f7/2)1 by promoting a neutron from the d3/2 orbital to the f7/2 orbital, which is the π(d5/2)6v(d5/2)6 (s1/2)2 (d3/2)3(f7/2)1 configuration in the last column of Table 1. This one hole-one particle configuration energetically favors the generation of angular momenta 3− to 5− as shown in Fig. 3(b). Even though the ordering of the 3- and 4- states is predicted to be reversed, this explains the small energy separation between them. In this configuration, two neutrons, on one hand, as a particle in the f7/2 orbital and, on the other hand, as a hole in the d3/2 orbital, yield the maximal spins J = 5 (7/2 + 3/2). Then, two neutrons favor organization in a doughnut distribution, as shown in Fig. 4. In contrast to neutrons, no (or little) occupancy of the proton s1/2 orbital in these negative-parity states implies that the spherical core has a proton center depletion similar to the ground state. Recently, new experimental results for 34Si were reported [18], and the suggested level structure and shell model descriptions strengthen our discussion of the present work.
π(d5/2)6
ν(d5/2)6 (s1/2)2
(d3/2)4π(d5/2)6
ν(d5/2)6 (s1/2)2
(d3/2)2(f7/2)2π(d5/2)5(s1/2)1
ν(d5/2)6 (s1/2)2
(d3/2)4π(d5/2)5(s1/2)1
ν(d5/2)6 (s1/2)2
(d3/2)2(f7/2)2π(d5/2)6
ν(d5/2)6 (s1/2)2
(d3/2)2(f7/2)1(p3/2)1π(d5/2)5(s1/2)1
ν(d5/2)6 (s1/2)2
(d3/2)3(f7/2)1π(d5/2)6
ν(d5/2)6 (s1/2)2
(d3/2)3(f7/2)10+
2+
4+
6+
02+
22+
31+
42+
23+
32+
24+
5+
62+
1+
3−
4−
5−73
68
26
31
42
29
10
17
8
32
22
26
34
24
30
36
13
9
6
9
7
9
10
9
6
14
10
7
9
10
5
8
22
5
5
61
62
65Table 1. Shell model calculations for contributions, %, of the orbital configurations of 34Si. The shell model is based on the sdfp-m interaction including
$2\hbar\omega $ pf shell two particle-two hole excitations.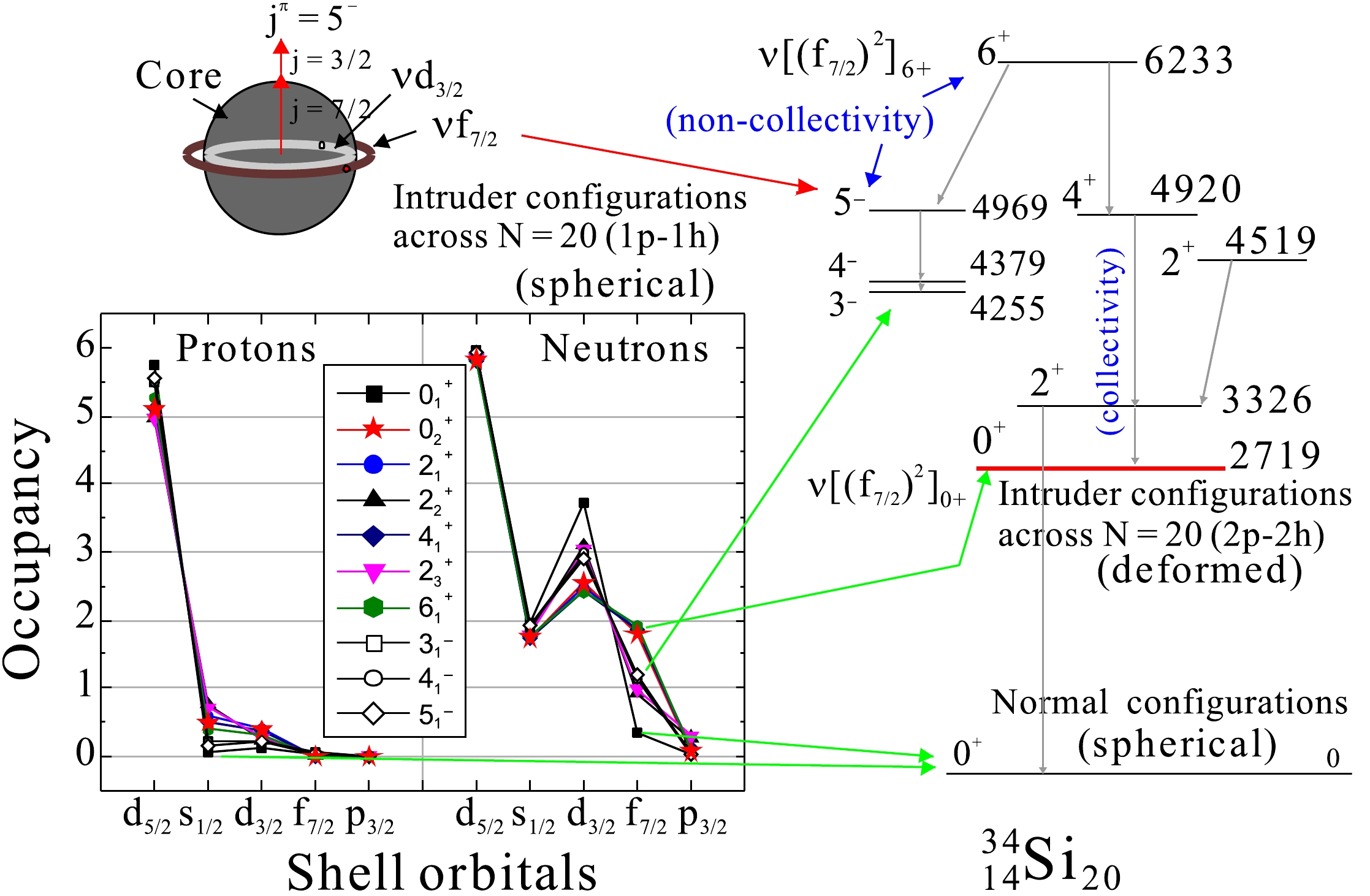
Figure 4. (color online) Occupancies of the orbitals involved in the states observed in 34Si. Following the shell model results, some distinctive structures are indicated in the level scheme.
A surprising outcome occurs at 62+. Comparing the configurational probabilities between 61+ and 62+, the dominance of the π(d5/2)6ν(d5/2)6(s1/2)2(d3/2)2(f7/2)2 configuration, 42%, at 61+ weakens at 62+, 22%. Instead, at the 62+ state, the π(d5/2)5(s1/2)1ν(d5/2)6(s1/2)2(d3/2)2(f7/2)2 and π(d5/2)6ν(d5/2)5(s1/2)1(d3/2)2(f7/2)2 configurations contribute largely, 14% and 12% (not shown in Table 1), respectively. Such broad contributions, namely the richness of configuration mixing, might induce a deformed collective structure at 62+. In fact, the quadrupole transition of 62+ to 41+ is stronger by two times than that of 61+ to 41+. We find that such strong quadrupole strengths are maintained along the 62+→41+→21+→02+ cascade with values near 60 − 80 e2fm4, which are 10 to 13 times the Weisskopf single-particle transition unit. Further, the cascading energies, 2290-1448-862 keV, definitely show a rotational pattern. We propose a deformed rotational band built on the second 0+, as shown in Fig. 3(b). To confirm our suggestion, the second 6+ state needs to be identified by an experiment. Interestingly, we find a γ-ray peak at and near 1940 keV in Fig. 2 in Ref. [5], where the coincidence γ-ray spectra gated on the 3326 and 929-keV transitions are displayed. We suggest that this peak might be the γ-ray transition of the 62+ state, which corresponds to the 6860-keV level, to the 4+ state at 4920 keV. It is also interesting to find a close resemblance between the collective bands, the 62+ - 41+ - 21+ - 02+ sequence in 34Si and the 62+- 41+ - 22+ - 02+ sequence in 38Ar.
A spherical ground band consists of the 22+ and 43+ states. The doubly magic nature of 34Si is indicated by the high energy positions of the 22+ state at 4.519 MeV and the 3-, 4-, and 5- states of the one-particle one-hole cross-shell states at around 4.5 MeV, and the calculated E(43+/22+) = 1.38. As a doubly magic nucleus, the 2+ state of the spherical ground band has the highest energy among all even-even nuclei with Z = 10 ~ 18 [1]. In this view, all excitation states stay relatively high with a small E(4+/2+) value compared with other nuclei. The structure of 34Si is similar to that of many spherical nuclides with a large shell gap (magic shells), such as 68Ni [ 1].
In another view, taking the 02+ state as a reference, E(41+/21+) = 2.68 is calculated, indicating certain deformation and a possible γ-soft nature, as shown with the O(6) limit of the interacting boson model (IBM) [19, 20]. Such observations show the co-existence structure of 34Si, with the spherical 01+ state and deformed 02+ state. Combining the observed data, the present shell-model calculation, IBM, and the discussion in Ref. [18], the 02+, 21+, 41+, and 62+ states belong to a deformed band of γ-soft nature, while the 23+, 31+, and 42+ states can be assigned to the corresponding γ-vibrational band.
As seen in Table 1, all 02+, 21+, 41+, and 62+ states have a similar configuration and structure, forming a rotational band with strong in-band transitions. A γ-soft state should have certain large transition strengths from states outside the band because of the mixing between different bands. As seen from the shell-model results, all 2+ states except for the 21+ state have extremely weak transition strengths to the 02+ state. For the 21+ and 41+ states, several states decay to them with transition strengths of 30 ~ 40 e2fm4. Table 2 compares the B(E2) transitions between the present shell-model calculation and the IBM O(6) limit. The transition rates generally agree with the O(6) limit for 41+ → 21+, 31+ → 41+, 42+ → 21+, and 42+ → 41+. However, for the transition rates related to the 23+ state, the deviations between the shell model and the O(6) limit become large. The energies and B(E2) values for the γ-soft states are rather consistent with the O(6) limit, though there seems to be a certain mixing between the K = 0 and K = 2 bands. More γ-ray transitional investigations, namely timing measurements, are essential for understanding 34Si, especially the possible γ-soft rotational band and the mixing between different bands.
Ji → Jf Shell-model B(E2)
in unit e2fm4Shell-model B(E2)
in unit B(E2; 21+ → 02+)IBM O(6) limit B(E2)
in unit B(E2; 21+ → 02+)21+ → 02+
41+ → 21+
62+ → 41+
42+ → 23+
31+ → 23+
31+ → 41+
23+ → 21+
42+ → 21+
42+ → 41+77.1
84.3
62.7
16.7
34.9
32.2
29.0
29.5
46.21
1.09
0.81
0.22
0.45
0.42
0.38
0.38
0.601
10/7 ≈ 1.43
5/3 ≈ 1.67
55/63 ≈ 0.87
25/21 ≈ 1.19
10/21 ≈ 0.48
10/7 ≈ 1.43
0
50/63 ≈ 0.79Table 2. Shell model calculations for E2 transitions and comparison with IBM O(6) limit.
-
In conclusion, we successfully develop the existing level scheme of 34Si by assigning spin-parities up to 6+ to the available experimental data. Figure 4 summarizes our results by showing distributions of the orbital occupancies for the states of interest together with the constructed level scheme. The observed states could be understood by finding certain differences in both the occupancies and contributions of the respective shell configurations as well as the resultant transition strengths. For example, the dominance of either protons or neutrons and the extent of mixing of their configurations are directly related to an understanding of the emerging features, i.e., nuclear shapes, singles or collective degrees of freedom, and specific matter distributions. As denoted by the collectivity and non-collectivity in Fig. 4, the distinctive level properties are noted; a proton center depletion due to the empty s1/2 orbital of the spherical ground state, a neutron two particle-two hole, (d3/2)-2(f7/2)2 configuration in the deformed second 0+ state, a neutron one hole-one particle, (d3/2)-1(f7/2)1 configuration for the negative parity states, and non-collective fully-aligned spin states, ν[(d3/2)-1(f7/2)1]5− and ν[(f7/2)2]6+. The proposed rotational band, as predicted by the second 6+ state, is built on the second 0+ state in 34Si and provides new insights into shape co-existence in isotones with N = 20; 32Mg, 36S, 38Ar, and 40Ca.
Level structure of the double-shell closure system with Z = 14 and N = 20: 34Si
- Received Date: 2022-07-04
- Available Online: 2022-12-15
Abstract: The level structure of the double-magic nucleus 34Si (Z = 14, N = 20) was investigated by evaluating the available data. On the basis of experimental results from the beta-decay and fusion-evaporation reactions, we established the level scheme by assigning spin-parities up to 61+ at 6233 keV. The high energy positions of the excited states are consistent with the magicity at 34Si, such as the 22+ state of the spherical ground band at 4.519 MeV and the 3-, 4-, and 5- states of the one-particle one-hole cross-shell states at approximately 4.5 MeV. This nucleus, for a long time, has attracted much attention because of, on one side, a proton bubble structure in the ground state and, on the other side, a deformation in the second 0+ state, 02+. By a comparison of the constructed level scheme with the shell model calculations, we describe the emerging structures in the ground and second 0+ states and the negative-parity 3- states within the framework of the shell model context. We propose a deformed rotational band with the cascading 62+ − 41+ − 21+ transitions built on the 02+ state.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: