Emission of high-energy alpha particles in nuclear reactions of ⁴⁸Ca and ⁵⁶Fe ions on ¹⁸¹Ta and ²³⁸U targets

The interaction of two heavy atomic nuclei may be accompanied by emission of alpha particles. The cross section of alpha particle production may be very large and even comparable to the total reaction cross section [1–3]. The study of energy spectra of alpha particles at different angles showed that there is a significant increase in the yield of high-energy alpha particles compared to that expected from calculations within the statistical model of compound nucleus decay [4]. It was shown that fast particles are emitted at the early stage of the reaction, before the statistical equilibrium is reached [5]. Thus, two components are observed in the energy spectra of alpha particles formed in reactions with heavy ions. The first component is associated with evaporation particles from excited reaction products; the properties of these particles are described by the statistical model (e.g., [6]). The second component is associated with pre-equilibrium particles [7, 8]; it contains a high-energy part and has a forward-peaked angular distribution [5, 9, 10]. Therefore, important information about the mechanisms of formation of fast charged particles can be obtained from measurements of their energy spectra at forward angles.

The analysis of experimental data showed that after emission of a fast particle in the beam direction at the stage of a direct process, there is a high probability of formation of a compound nucleus or a di-nuclear system which, after the exchange of mass, energy, and angular momentum, decays, forming products typical of deep inelastic collisions of heavy ions [4]. Thus, the process of emission of fast alpha particles in reactions with heavy ions is extremely interesting from the perspective of producing cold heavy and superheavy nuclei because emission of fast alpha particles may lead to a decrease in the excitation energy of the formed compound nucleus and therefore a greater probability of its survival [11].

The ${}^{48}$Ca nucleus has been widely used for the synthesis of superheavy nuclei (e.g., [12]). However, further advancement into the region of superheavy nuclei requires the use of heavier projectile nuclei because target nuclei heavier than Cf will not be experimentally available in the conceivable future. In this respect, the isotopes of Fe are considered as one of the alternatives (e.g., [13]). In addition, lower energies of separation of an alpha particle from colliding nuclei may favor alpha particle emission. The energies of separation of an alpha particle for some nuclei taken from [14] are given in Table 1.

Nucleus (spin and parity)	${E_{{\rm{sep}}}}$ /MeV
${}^{48}$Ca (0${}^{+}$)	13.98
${}^{56}$Fe (0${}^{+}$)	7.61
${}^{181}$Ta (7/2${}^{+}$)	–1.52
${}^{208}$Pb (0${}^{+}$)	–0.517
${}^{209}$Pb (9/2${}^{+}$)	–2.25
${}^{209}$Bi (9/2${}^{-}$)	–3.14
${}^{210}$Bi (0${}^{+}$)	–5.04
${}^{238}$U (0${}^{+}$)	–4.27

Table 1.  Energies of separation of an alpha particle ${E_{{\rm{sep}}}}$ for some nuclei taken from [14].

Many empirical and semimicroscopic models have been developed to describe the emission of light charged particles in heavy-ion collisions, e.g., the Fermi momentum distribution and Goldhaber model [15], surface model of Friedman [16], model of moving sources [17, 18], and model of direct processes [19, 20]. A good review of experimental results on the yield of light charged particles in nucleus-nucleus collisions at low and intermediate energies and the main theoretical models used for description of light particle formation is found in [4].

This study was conducted to obtain information about the mechanism of emission of fast alpha particles in reactions with ions of ${}^{48}$Ca and ${}^{56}$Fe. In this study, the analysis of the obtained experimental data was carried out using the kinematic limits for two- and three-body exit channels within the model of moving sources [17, 18]. Note that it was predicted that the kinematic limits for three-body exit channels may, in principle, be greater than those for two-body exit channels [4].

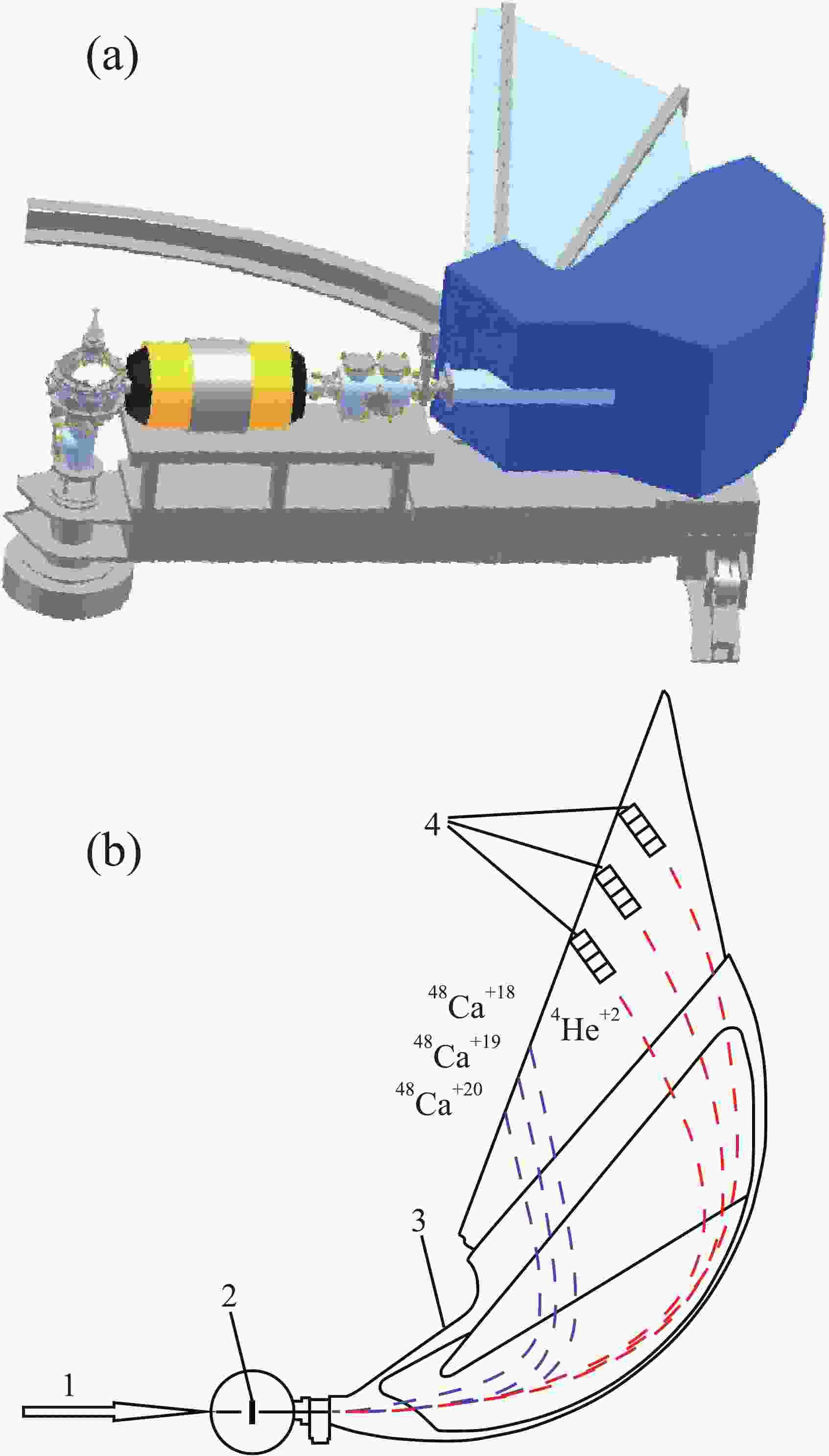
The experiment was carried out using the beams of ${}^{48}$Ca (280 MeV) and ${}^{56}$Fe (320 and 400 MeV) on the U400 cyclotron at the Flerov Laboratory of Nuclear Reactions (FLNR), Joint Institute for Nuclear Research (JINR). The beam profile was formed using the magnetic optics of the U400 cyclotron supplemented by a system of diaphragms; the beam profile was monitored by two profilometers. The size of the beam on the targets ${}^{181}$Ta (2 μm thick) and ${}^{238}$U (1 μm thick) was $5\times 5$ mm at an intensity of 50 nA. Taking into account the beam spread on the targets, the angular resolution of the registering detectors was $\pm$ 0.8$^{\circ}$.

The high-resolution magnetic analyzer MAVR [21–23] with a focal plane length of 150 cm was used in the vacuum mode to separate alpha particles and the beam nuclei at an angle of 0$^{\circ}$ by position. The energy range of the reaction products that could be registered by the analyzer was ${E_{\max }}$/${E_{\min }}$ = 5.2 with an energy resolution of $\Delta E/E$ = $5\times 10{}^{-4}$. The analyzer had a good linear dependence of dispersion and resolution over the entire length of the focal plane. The particle deflection angle in the analyzer was 110.7$^{\circ}$. The analyzing and detecting system made it possible to measure the energy spectra of alpha particles in the energy range of 30–120 MeV. The use of the MAVR analyzer for detecting alpha particles made it possible to carry out experiments with high-intensity beams (up to $5\times 10{}^{12}$ s${}^{-1}$) and to measure the energy spectra of alpha particles up to the energies at which their yield was 10${}^{-4}$–10${}^{-5}$ of the maximum value.

The products of nuclear reactions and the beam nuclei entered the magnet of the analyzer where they were separated and identified in its focal plane by their charge, mass number, energy loss, and total energy using a system of three semiconductor silicon telescopes $\Delta {E_1}$, $\Delta {E_2}$, and E with detector thicknesses of 50, 700, and 3200 μm, respectively (Fig. 1). The thicknesses of the detectors were selected in such a way that identification of alpha particles in the energy range of 30–120 MeV was ensured. Almost all light nuclei heavier than alpha particles were stopped in the $\Delta {E_2}$ detector. The size of the telescope determined the energy range of the registered alpha particles, ${\Delta {E_\alpha }} \sim$ 1.1–1.3 MeV. The position of the products in the focal plane and the corresponding ion charges were compared with the values obtained in the lise++ program [24, 25].

Figure 1.  (color online) (a) Three-dimensional model of the high-resolution magnetic analyzer MAVR. (b) Scheme of the experiment: (1) beam of projectile nuclei; (2) target; (3) MSP-144 magnet; (4) focal plane detectors. Trajectories of Ca and He ions are shown.

To protect the detectors from the scattered beam ions, a 80 μm thick aluminum foil was installed in front of each telescope. The foil thickness was selected in such a way that the beam nuclei completely stopped in it. The use of three telescopes made it possible to register alpha particles of three energies simultaneously. Only alpha particles with certain magnetic rigidities, determined by the position of the telescopes in the focal plane of the analyzer, entered each telescope. The intensity of the ion beams on the targets was determined by an elastic scattering detector installed at an angle of 28$^{\circ}$ in the reaction chamber.

The solid angle of the setup was ${\Delta \Omega } = 5\times 10{}^{-4}$ sr; it was determined using an alpha source of a known intensity installed at the target position. The small value of the solid angle was due to the purpose of detecting fast alpha particles that fly forward at zero angle with the highest energy. The energy range of the registered alpha particles was varied by changing the magnetic field of the analyzer.

The obtained identification matrices for light nuclei measured at an angle of 0$^{\circ}$ in the reactions ${}^{48}$Ca + ${}^{181}$Ta and ${}^{48}$Ca + ${}^{238}$U at a beam energy of 280 MeV are shown in Fig. 2 for alpha particle energies ${E_{\alpha}} = 66\pm 0.5\Delta {E_\alpha }$ [MeV] (a) and $79\pm 0.5\Delta {E_\alpha}$ [MeV] (b). It can be observed that alpha particles are clearly separated from other reaction products because most of them were stopped in the $\Delta {E_2}$ detector.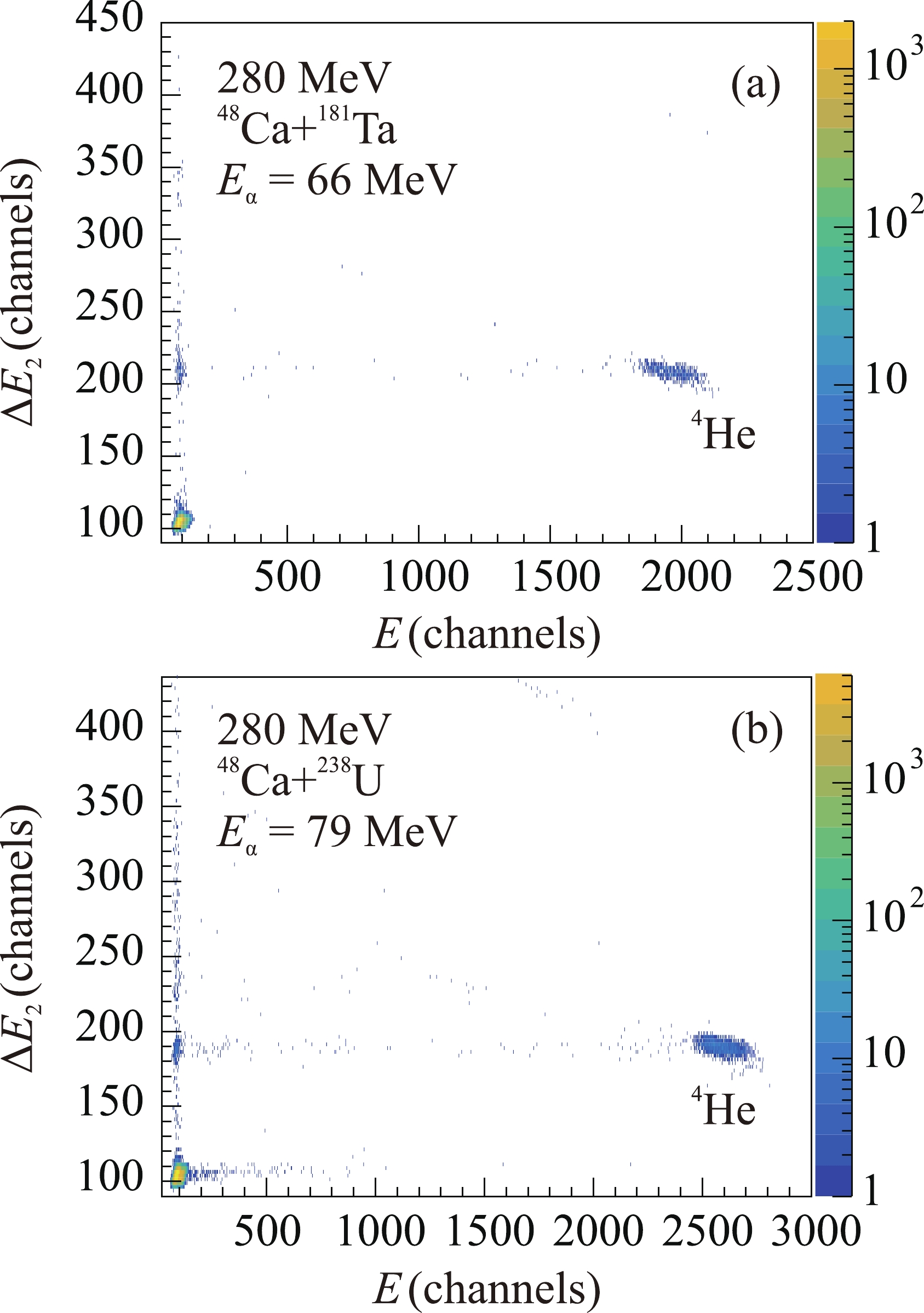

Figure 2.  (color online) Identification matrices for light nuclei measured at an angle of 0$^{\circ}$ in the reactions ${}^{48}$Ca + ${}^{181}$Ta (a) and ${}^{48}$Ca + ${}^{238}$U (b) at a beam energy of 280 MeV for alpha particle energies ${E_{\alpha}} = 66\pm 0.5\Delta {E_\alpha }$ [MeV] (a) and $79\pm 0.5\Delta {E_\alpha}$ [MeV] (b).

The double differential cross sections were determined as

where ${{N_{{\rm{alpha}}}}}$ is the number of alpha particles detected by a semiconductor telescope in the focal plane, ${{N_{{\rm{target}}}}}$ is the number of nuclei in the target per unit area, and ${{N_{{\rm{beam}}}}}$ is the number of nuclei of the beam that hit the target.

Using the beams of ${}^{48}$Ca (280 MeV) and ${}^{56}$Fe (320 and 400 MeV) on the${}^{181}$Ta and ${}^{238}$U targets, the double differential hyphen="true"/>cross sections for formation of alpha particles were measured at an angle of 0$^{\circ}$ in a wide energy range. The obtained inclusive energy spectra for are shown in Fig. 3.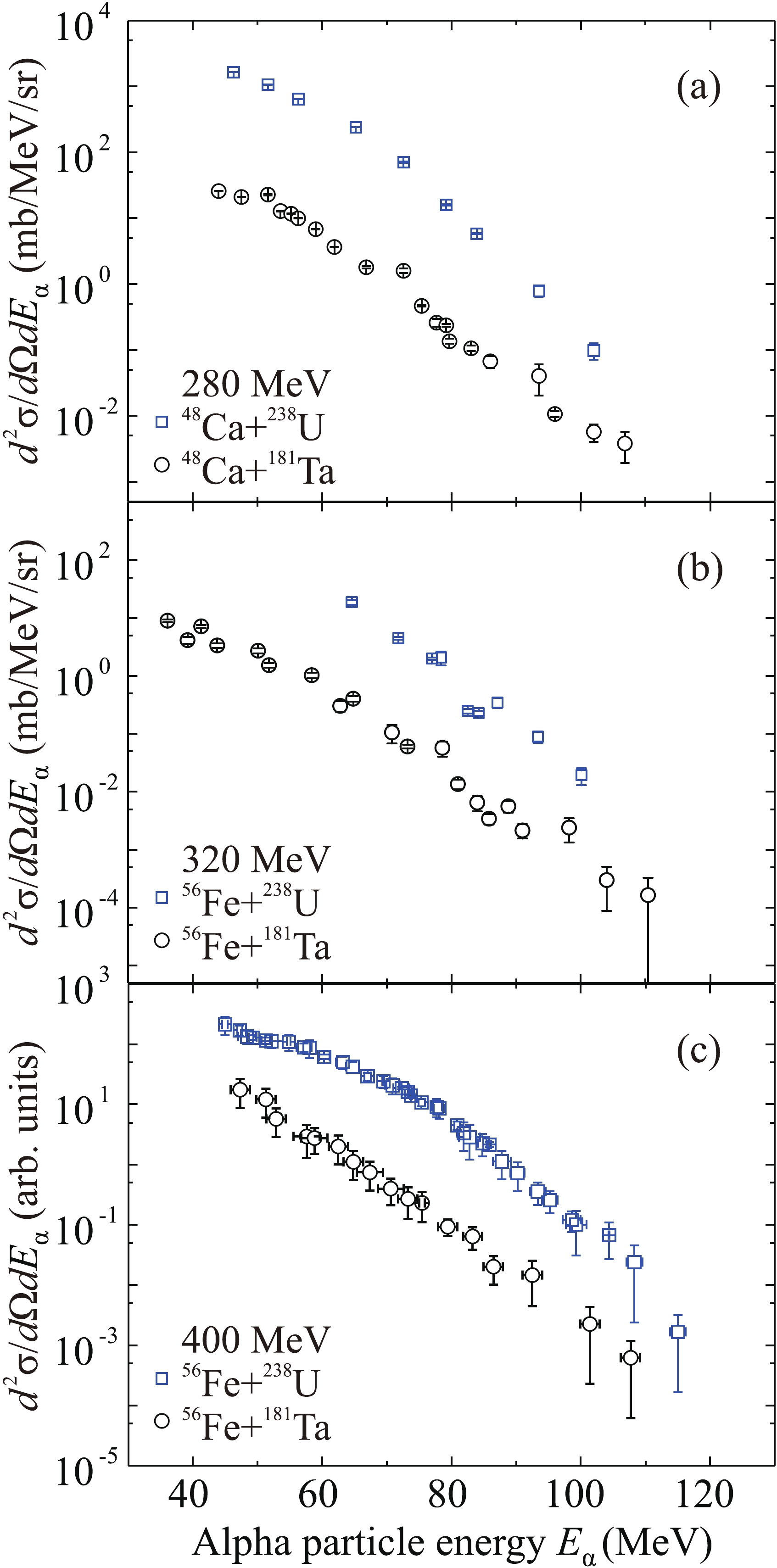

Figure 3.  (color online) Energy spectra of alpha particles measured at an angle of 0$^{\circ}$ in reactions on targets ${}^{181}$Ta (circles) and ${}^{238}$U (squares) for beams of (a) ${}^{48}$Ca (280 MeV), (b) ${}^{56}$Fe (320 MeV), and (c) ${}^{56}$Fe (400 MeV).

It should be mentioned that alpha particles with lower energies were not registered owing to the large thicknesses of the detectors, whereas alpha particles with higher energies were not registered owing to the limitations on magnetic rigidity of the MAVR analyzer. It can be observed that the cross sections for emission of alpha particles in the reactions on the ${}^{238}$U target are significantly (by one or two orders of magnitude) greater than those on the ${}^{181}$Ta target. A similar picture was observed in earlier experiments for the lighter projectile nucleus ${}^{22}$Ne [9]. A strong dependence of the yield of alpha particles on the atomic number of the target nucleus is observed in all the studied cases. The maximum yield of alpha particles is found in the low-energy part of the spectra; the yield falls by 4–5 orders of magnitude with the increase of alpha particle energy for all the studied reactions.

The strong dependence of the yield of alpha particles on the atomic number of the target nucleus leads to the conclusion that their emission is mainly a result of their knockout from the target nucleus. The energy of separation of an alpha particle for the ${}^{238}$U nucleus is significantly different from that for the ${}^{181}$Ta nucleus (Table 1). It can be observed that the separation energy of an alpha particle decreases after filling of the nucleon shells of the magic nucleus ${}^{208}$Pb, which can be due to filling of the higher-lying shells with lower nucleon separation energy: the neutron shell $2{g_{{9 \mathord{\left/ {\vphantom {9 2}} \right. } 2}}}$ and the proton shell $1{h_{{9 \mathord{\left/ {\vphantom {9 2}} \right. } 2}}}$. Additional nucleon shells of the target nucleus ${}^{238}$U can also lead to a significantly different driving potential and therefore a significantly different evolution of the resulting di-nuclear system compared to the case of the target nucleus ${}^{181}$Ta [26].

The fact that the maximum yield of alpha particles is observed in the low-energy part of the spectra, where alpha particles do not carry away large energy from the compound nucleus, means that here this process does not lead to a significant decrease in the excitation energy of the compound nucleus and greater probability of its survival. The yield decreases by several orders of magnitude in the high-energy part of the spectra where the energies of alpha particles are limited by the so-called kinematic limits due to the laws of conservation of energy and momentum.

The energy distribution of the model of moving sourceswas used to approximate the spectra of alpha particles and to describe their shape. The model of moving sources [4, 17, 18] is an empirical model based on several assumptions, which we modified to consider the physical processes in nucleus-nucleus collisions. We took into account the kinematic limits for emission of alpha particles and real physical sources of alpha particle emission.

(i) It is assumed that alpha particles are emitted isotropically from several (or one) sources with intensities ${N_i}$ moving in the direction of the beam of projectile nuclei with velocities ${v_i}$. We associate each source with a certain exit channel or a group of exit channels of a reaction. For the channels with emission of an alpha particle from a compound nucleus or a di-nuclear system, there are physical constraints on the source velocities: they must be equal to or close to the velocity of the center of mass in the laboratory system, ${v_i} \simeq {v_{{\rm{c}}{\rm{.m}}{\rm{.}}}}$. For the channels with breakup of the projectile nucleus and emission of an alpha particle from it in grazing collisions of the nuclei, the velocities of the sources must be equal to or close to the velocity of the projectile nucleus in the laboratory system, ${v_i} \simeq {v_{{\rm{lab}}}}$.

(ii) It is assumed that the kinetic energies of alpha particles for each source have a distribution that decreases smoothly with increasing energy. If an alpha cluster is formed in one of the nuclei during their fusion, the energy of the alpha cluster can sharply increase. The probability of this diminishes with increasing excitation energy, so that the energy distribution of alpha clusters is to some extent similar to the Boltzmann exponent with some effective temperature ${T_i}$. In general, such an approximation of the statistical weights of various excited states of alpha clusters is not related to the establishment of statistical equilibrium in the formed compound nucleus or di-nuclear system. Therefore, we consider ${T_i}$ as the formal parameter, which may not have the meaning of the Boltzmann temperature.

(iii) It is assumed that the kinetic energy of an alpha particle emitted from a stationary source is ${E_{\rm{C}}} + {{mv_\alpha ^2} \mathord{\left/ {\vphantom {{mv_\alpha ^2} 2}} \right. } 2}$; the potential energy ${E_{\rm{C}}}$ at the point of emission is called the Coulomb energy of the alpha particle. The value of ${E_{\rm{C}}}$ is close to the height of the Coulomb barrier for the pairs alpha particle + target nucleus and alpha particle + compound nucleus.

(iv) When approximating the shape of the energy spectrum of alpha particles in the model of moving sources, we take into account the kinematic limits by introducing step functions of the form

where i is the source number, and ${\rm{erf}}(x)$ is the error function with the parameters ${\delta _i}$ and ${E_{{\rm{0}}{\rm{,}}i}}$. Taking into account the experimental uncertainty, ${\delta _i} =$ 0.5 MeV; ${E_{{\rm{0}}{\rm{,}}i}}$ is approximately equal to kinematic limits of two- and three-body exit channels, ${E_{{\rm{0}}{\rm{,}}i}} \approx E_{{\rm{lim}}}^{(2,3)}$.

Under the above assumptions, the formula for the double differential cross section of alpha particles emitted at an angle of 0$^{\circ}$ has the following form [4, 17, 18]:

where ${E_i} = {{{m_\alpha }v_i^2} \mathord{\left/ {\vphantom {{{m_\alpha }v_i^2} 2}} \right. } 2}$. The spectrum of one source with distribution

is a convenient phenomenological curve with an exponential decrease with increasing energy and a maximum at the point

The laws of conservation of energy and momentum limit the maximum energy of alpha particles that can be emitted in a two-body exit channel with formation of a heavy nucleus or in a three-body exit channel with formation of two nuclei. In the first case, the value of the kinematic limit $E_{{\rm{lim}}}^{(2)}$ for the energy of the alpha particle in the laboratory system is uniquely determined by the following quantities: the reaction energy Q (see, for example, [14]), the energy of the projectile nucleus in the laboratory system ${E_{{\rm{lab}}}}$ (${E_{{\rm{c}}{\rm{.m}}{\rm{.}}}}$ in the center of mass system), the masses of the projectile and target nuclei ${m_1}$and${m_2}$, and the mass of the alpha particle ${m_\alpha }$:

The values of the kinematic limits for the two-body exit channels of the studied reactions are listed in Table 2 and shown by short arrows in the figures in Sec. VI.

Reaction	Exit channel	Q/MeV	${E_{ {\rm{lab} } } } /{\rm{MeV} }$	${E_{ {\rm{c.m.} } } } /{\rm{MeV} }$	$E_{ {\rm{lim} } }^{(2)} /{\rm{MeV} }$
${}^{56}$Fe + ${}^{181}$Ta	${}^{233}$Bk + ${}^{4}$He	–164.3	400	305.5	170.2
${}^{56}$Fe + ${}^{181}$Ta	${}^{233}$Bk + ${}^{4}$He	–164.3	320	244.4	100.0
${}^{48}$Ca + ${}^{181}$Ta	${}^{225}$Pa + ${}^{4}$He	–119.4	280	221.3	121.4
${}^{48}$Ca + ${}^{238}$U	${}^{282}$Ds + ${}^{4}$He	–149.7	280	224.7	97.5
${}^{56}$Fe + ${}^{238}$U	${}^{290}$Lv + ${}^{4}$He	–200.8	400	323.8	144.9
${}^{56}$Fe + ${}^{238}$U	${}^{290}$Lv + ${}^{4}$He	–200.8	320	259.1	72.1

Table 2.  Kinematic limits $E_{{\rm{lim}}}^{(2)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in two-body exit channels of the studied reactions.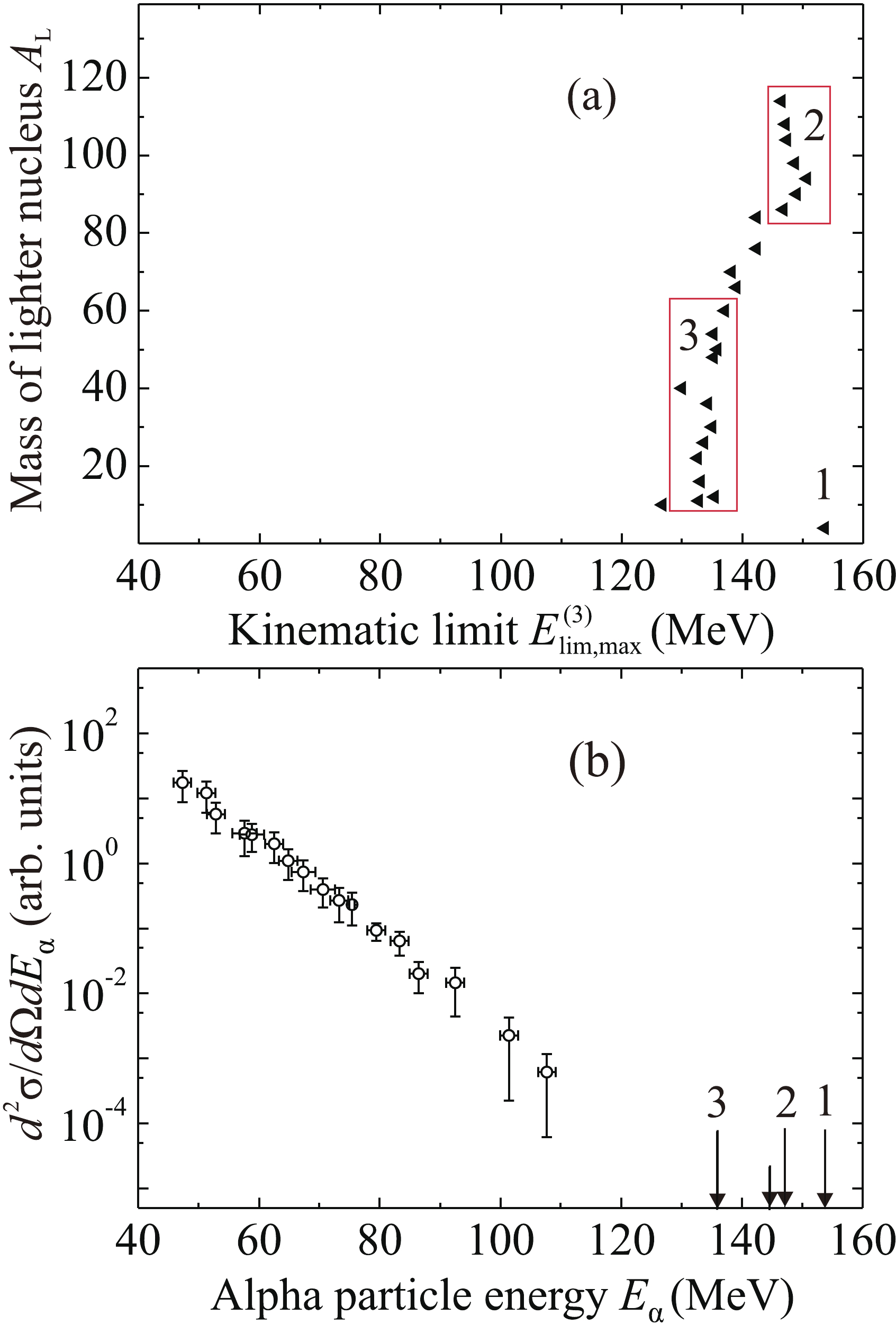

Figure 4.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the reaction ${}^{56}$Fe + ${}^{181}$Ta at an energy of 400 MeV as a function of the mass number ${A_{\rm{L}}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2 and 3).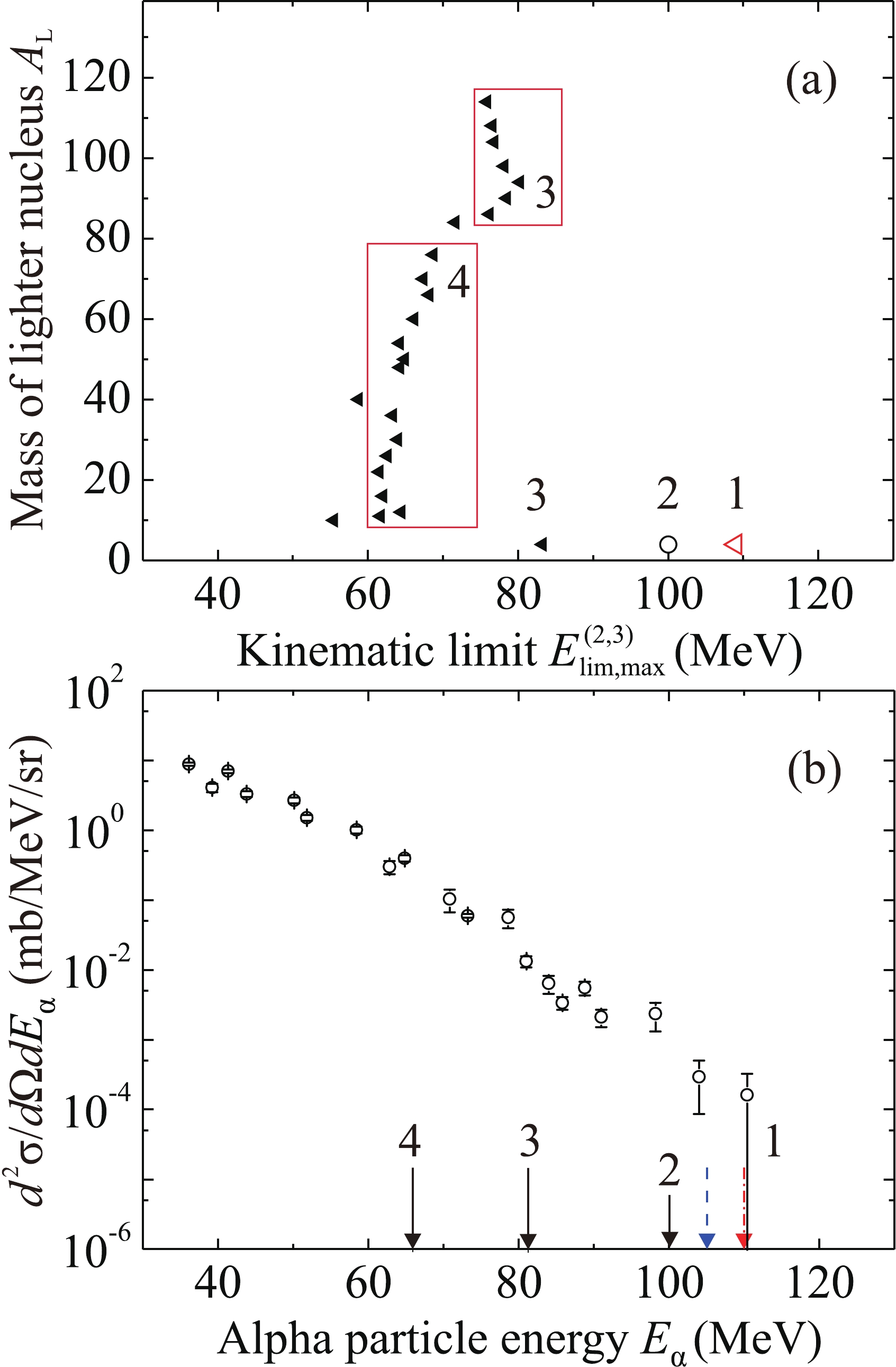

Figure 5.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(2,3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in two- and three-body exit channels of the reaction ${}^{56}$Fe + ${}^{181}$Ta at an energy of 320 MeV as a function of the mass number ${A_{\rm{L}}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2 and 3).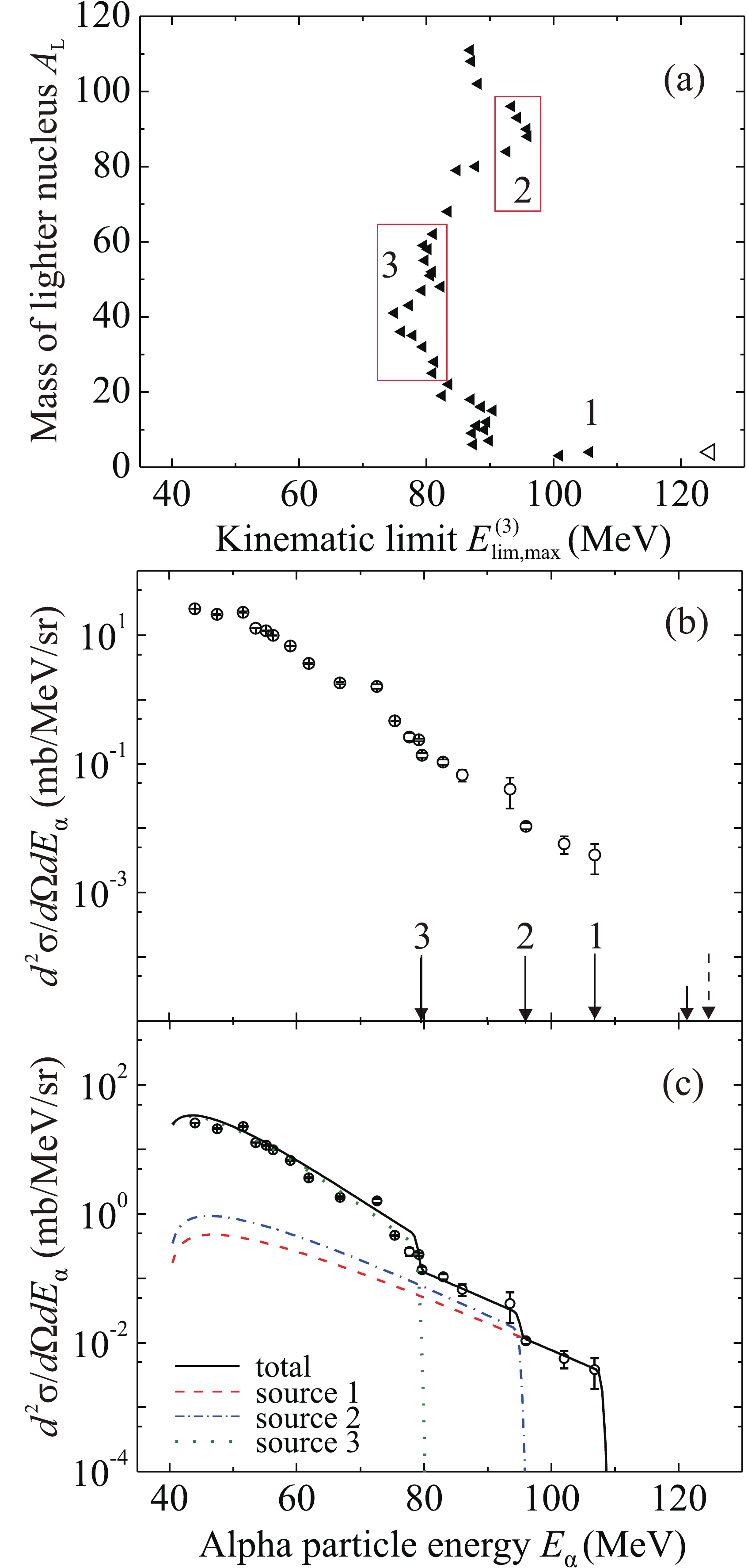

Figure 7.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the reaction ${}^{48}$Ca + ${}^{181}$Ta at an energy of 280 MeV as a function of the mass number ${A_{\rm{L}}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2 and 5). (c) Spectrum approximation within the model of moving sources with the parameters given in Table 4: source 1 (dashed curve), source 2 (dashed-dotted curve), source 3 (dotted curve), and the total spectrum from all sources (solid curve).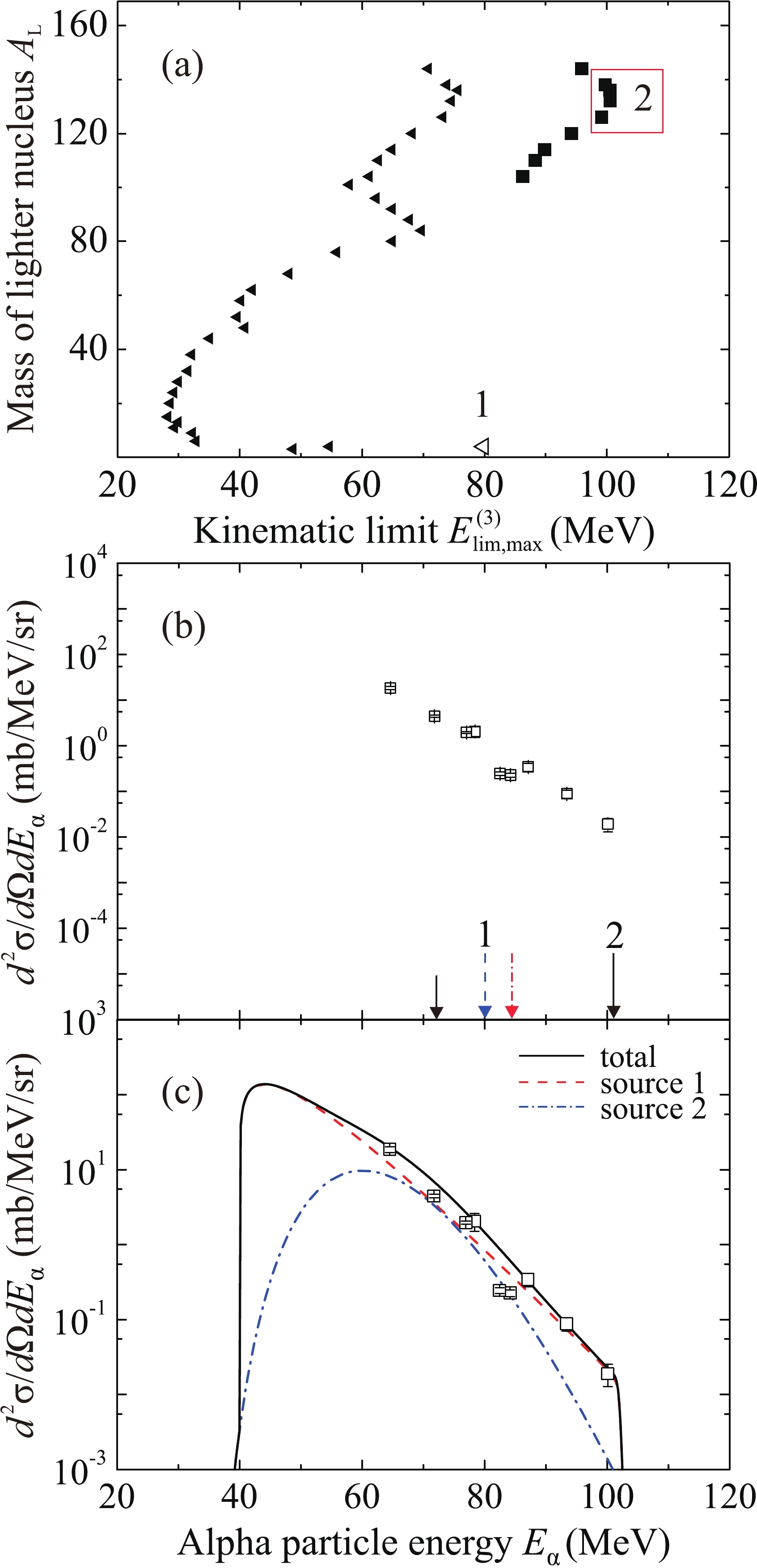

Figure 10.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(2)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the reaction ${}^{56}$Fe + ${}^{238}$U at an energy of 320 MeV as a function of the mass number ${A_{L}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2 and 7). (c) Spectrum approximation within the model of moving sources with the parameters given in Table 6: source 1 (dashed curve), source 2 (dashed-dotted curve), and the total spectrum from all sources (solid curve).

In the case of a three-body exit channel with various combinations of formed nuclei and the potential energy $U_{\rm{f}}$ of their interaction with each other at the moment of separation (when their relative velocity is zero), the kinematic limit $E_{{\rm{lim}}}^{(3)}$ for the energy of the alpha particle in the laboratory system also depends on $U_{\rm{f}}$:

The value of ${U_{\rm{f}}}$ is usually chosen as the height of the Coulomb barrier for formed nuclei with mass numbers $A_{\rm{L}}$ of the lighter nucleus and $A_{\rm{H}}$ of the heavier nucleus. For spherical formed nuclei, ${V_{\rm{B}}} = {V_{\rm{f}}}({R_{\rm{B}}})$ (see, for example, [14]), where ${V_{\rm{f}}}(r)$ is the potential energy of interaction of the spherical formed nuclei, and ${R_{\rm{B}}}$ is the position of the Coulomb barrier. Below, we use the Akyüz–Winther form [27, 28] as ${V_{\rm{f}}}(r)$. For a more accurate description of the experimental data, we may vary the value of ${U_{\rm{f}}}$ in some range to take into account the effect of tunneling through the Coulomb barrier (for an alpha particle) and through the fission barrier (for a compound nucleus), as well possible deformation of the formed nuclei [29].

For the lighter nucleus with mass number ${A_{\rm{L}}} \le {A_{\rm{H}}}$ in the three-body exit channel, the values of $E_{{\rm{lim}}}^{(3)}$ correspond to the points in the plane $\left({E_{{\rm{lim}}}^{(3)},{A_{\rm{L}}}} \right)$. Let us denote the right boundary of the region containing all such points as $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$; we will use its properties for analysis of energy spectra of alpha particles.

The derivation of the kinematic limits for alpha particle emission at an angle of 0$^{\circ}$ in the two- and three-body exit channels is described in Appendix A.

The values of the maximum kinematic limit $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels depending on the mass number of the lighter nucleus ${A_{\rm{L}}}$ for the reaction ${}^{56}$Fe + ${}^{181}$Ta at energies of 400 and 320 MeV are listed in Table 3 and shown in Figs. 4(a) and 5(a), respectively. The measured spectra of alpha particles are shown in Figs. 4(b) and 5(b), respectively. The short arrows indicate the kinematic limits of the two-body exit channel ${}^{233}$Bk + ${}^{4}$He, $E_{{\rm{lim}}}^{(2)} = 170.2$ MeV and $E_{{\rm{lim}}}^{(2)} = 100.0$ MeV, respectively. The numbered arrows in Figs. 4(b) and 5(b) correspond to the values of $E_{{\lim}{\rm{,max}}}^{(3)}$ in the numbered points or frames in Figs. 4(a) and 5(a). An interesting fact is that the maximum values of alpha particle energies are approximately 110 MeV in both cases, i.e., they do not change when the beam energy increases from 320 to 400 MeV.

Exit channel and	Q	${U_{\rm{f}}}$	$E_{{\lim}{\rm{,max}}}^{(3)}$
designations in Fig. 5(b)	/MeV	/MeV	/MeV
${}^{4}$He + ${}^{229}$Am + ${}^{4}$He $\downarrow$ 3	–156.1	23.3	83.2
${}^{4}$He + ${}^{229}$Am + ${}^{4}$He $\downarrow$	–156.1	{3.7}	105.0
${}^{4}$He + ${}^{229}$Am + ${}^{4}$He $\downarrow$ 1	–156.1	{0}	109.1
${}^{11}$B + ${}^{222}$U + ${}^{4}$He	–144.4	54.0	61.7
${}^{16}$O + ${}^{217}$Ac + ${}^{4}$He	–115.4	82.7	62.0
${}^{50}$Ti + ${}^{183}$Re + ${}^{4}$He $\downarrow$ 4	−14.2	181.4	64.9
${}^{70}$Zn + ${}^{163}$Ho + ${}^{4}$He $\downarrow$ 4	24.5	217.9	67.3
${}^{84}$Se + ${}^{149}$Eu + ${}^{4}$He	40.9	230.6	71.6
${}^{94}$Zr + ${}^{139}$La + ${}^{4}$He $\downarrow$ 3	63.0	245.1	80.2
${}^{114}$Cd + ${}^{119}$In + ${}^{4}$He $\downarrow$ 3	66.2	252.2	75.8

Table 3.  Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}\left( {{A_{\rm{L}}}} \right)$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the ${}^{56}$Fe + ${}^{181}$Ta reaction at an energy of 320 MeV. The modified values of $U_{\rm{f}}$ for the right edge of the experimental spectrum are given in braces; otherwise, $U_{\rm{f}} = V_{\rm{B}}$.

In the case of the ${}^{56}$Fe + ${}^{181}$Ta reaction at an energy of 400 MeV in Fig. 4(b), the whole spectrum lies to the left of the two-body kinematic limit $E_{{\rm{lim}}}^{(2)}$ for the energy of alpha particles (see Table 2) and to the left of the boundary $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ for three-body exit channels [see Fig. 4(a) and Table 3; we used $U_{\rm{f}} = V_{\rm{B}}$]. The spectrum decreases smoothly with increasing energy; its shape can be approximated by simple functions in a phenomenological approach. The result of approximation of the spectrum of alpha particles using formula (3) for two sources is shown in Fig. 6(a); the parameters of the sources are listed in Table 4. Because the two- and three-body kinematic limits are located far to the right of the spectrum, we used ${g_i}({E_\alpha }) = 1$. Both sources have velocities equal to the velocity of the center of mass in the laboratory system; they correspond to the formation of an alpha particle and two nuclei during decay of the compound nucleus (or di-nuclear system) or as a result of incomplete fusion of the colliding projectile and target nuclei.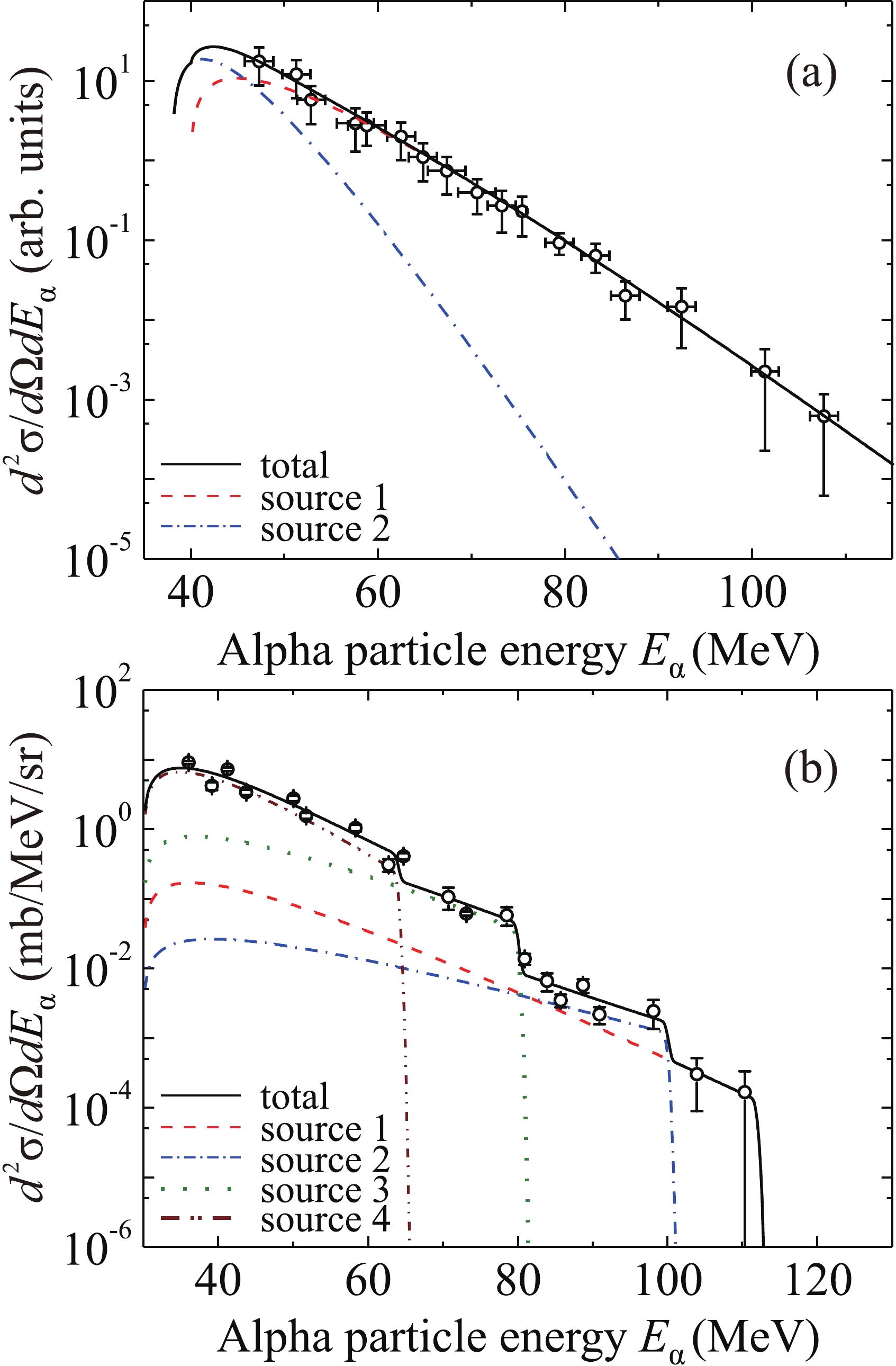

Figure 6.  (color online) Experimental energy spectrum of alpha particles emitted at an angle of 0$^{\circ}$ in the reaction ${}^{56}$Fe + ${}^{181}$Ta approximated within the model of moving sources with the parameters given in Table 4 at collision energies of 400 MeV [(a): source 1 (dashed curve), source 2 (dashed-dotted curve), the total spectrum from all sources (solid curve)] and 320 MeV [(b): source 1 (dashed curve), source 2 (dashed-dotted curve), source 3 (dotted curve), source 4 (dashed-dot-dotted curve), the total spectrum from all sources (solid curve)].

Source number	${E_i}$/MeV	${E_{Ci}}$/MeV	${T_i}$/MeV	${E_{{\rm{0}}{\rm{,}}i}}$/MeV	${N_i}$
${}^{56}$Fe (400 MeV) + ${}^{181}$Ta
1	1.6	40	4.3	–	0.28
2	1.6	38	2.0	–	0.6
${}^{56}$Fe (320 MeV) + ${}^{181}$Ta
1	1.12	30	7.3	112	0.09
2	1.12	30	12.0	100	0.012
3	1.12	30	8.3	80	0.4
4	1.12	30	5.0	64	3.9
${}^{48}$Ca (280 MeV) + ${}^{181}$Ta
1	1.025	39	8.2	108	0.28
2	1.025	39	7.5	95	0.6
3	1.025	39	4.7	79	18
${}^{48}$Ca (280 MeV) + ${}^{238}$U
1	0.66	43	4.1	104	1200
2	25.9	34	1.0	104	17
${}^{56}$Fe (400 MeV) + ${}^{238}$U
1	1.04	40	4.95	115	120
2	28	36	1.0	115	3
${}^{56}$Fe (320 MeV) + ${}^{238}$U
1	0.83	40	4.5	102	90
2	23.0	36	1.1	102	2

Table 4.  Parameters of moving sources used to approximate the energy spectrum of alpha particles emitted at an angle of 0$^{\circ}$. For ${}^{56}$Fe (400 MeV) + ${}^{181}$Ta, we used ${g_i}({E_\alpha })=1$.

In the case of the ${}^{56}$Fe + ${}^{181}$Ta reaction at an energy of 320 MeV in Fig. 5(b), the decrease of the spectrum with increasing energy is not smooth, in contrast to the spectrum in Fig. 4(b). This may be due to the disappearance of the contributions of many three-body exit channels when passing through the values of $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$. The dashed arrow and the dash-dotted arrow 1 in Fig. 5(b) indicate the maximum kinematic limits of the three-body exit channel ${}^{4}$He + ${}^{229}$Am + ${}^{4}$He for the modified values of ${U_{\rm{f}}} = 3.7$ MeV and 0, respectively; arrows 3 and 4 correspond to the values of $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ in frames 3 and 4 in Fig. 5(a). The frames in Fig. 3 and below include points with close maximum three-body kinematic limits; for them, the boundary of the region containing all such points is arranged vertically. In Fig. 5(a), solid triangles are for $U_{\rm{f}} = V_{\rm{B}}$; the empty triangle is for ${}^{4}$He + ${}^{229}$Am + ${}^{4}$He with the modified value of ${U_{\rm{f}}} =$0; the circle and the short arrow 2 in Fig. 5(b) show the kinematic limit $E_{{\rm{lim}}}^{(2)} = 100$ MeV for the two-body exit channel ${}^{233}$Bk + ${}^{4}$He. It can be observed that the boundary $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ passes through the central part of the spectrum. Fast alpha particles with energies of 80–110 MeV are emitted in the three-body channel with formation of two alpha particles and the heavy nucleus ${}^{229}$Am with a relatively low excitation energy.

The kinematic limit $E_{{\rm{lim}}}^{(2)} = 100$ MeV for the two-body exit channel ${}^{233}$Bk + ${}^{4}$He lies within the measured range of alpha particle energies; therefore, the presence of alpha particles with energies from 100 to 110 MeV in the measured spectrum cannot be explained as the consequence of the two-body exit channel. A possible reason may be the three-body channel ${}^{4}$He + ${}^{229}$Am + ${}^{4}$He with formation of a fast alpha particle and a slow alpha particle at the energy value of ${U_{\rm{f}}}$ , which is much lower than the height of the Coulomb barrier for the pair {heavy nucleus + alpha particle}. In the case of alpha decay of heavy atomic nuclei in the tunneling mode, the energy of alpha particles (from 4 to 9 MeV) is much lower than the height of the Coulomb barrier (from 20 to 30 MeV; see, for example, [14]). Alpha decay (or cluster decay) during fusion of nuclei may be called stimulated; it can occur in a time τ shorter than alpha decay half-life. Due to the uncertainty principle, the energy spread of alpha particles in such a process can be of the order of $\Delta {E_\alpha } \sim {\hbar \mathord{\left/ {\vphantom {\hbar \tau }} \right. } \tau }$. Taking into account the value of the energy of alpha decay ${E_{{\rm{dec}}}}$ for the compound nucleus in the ground state, we can estimate ${U_{\rm{f}}}$ as $0 \leq {U_{\rm{f}}} \leq {E_{{\rm{dec}}}}$. When ${U_{\rm{f}}} = {E_{{\rm{dec}}}}$, the equality $E_{{\rm{lim, max}}}^{(3)} = E_{{\rm{lim}}}^{(2)}$ is true. When ${U_{\rm{f}}} < {E_{{\rm{dec}}}}$, the maximum kinematic limit of three-body channels is higher than the kinematic limit of the two-body channel, $E_{{\rm{lim, max}}}^{(3)} > E_{{\rm{lim}}}^{(2)}$. As a result, if ${U_{\rm{f}}} = 0$ MeV, the maximum possible energy of an alpha particle emitted at an angle of 0$^{\circ}$ for the spectrum in Fig. 5(a) indeed turns out to be close to the maximum measured alpha particle energy, 110 MeV. The experimental yield of alpha particles near the kinematic limit $E_{{\rm{lim}}}^{(2)} = 100$ MeV for the two-body exit channel ${}^{233}$Bk + ${}^{4}$He is approximately an order of magnitude higher than the yield near the kinematic limit for the same channel with emission of one of the alpha particles in the tunneling mode. Therefore, near the high-energy edge of the alpha particle spectrum, the probability of emission of a second alpha particle from the ${}^{233}$Bk compound nucleus in the tunneling mode can be estimated as a value of the order of 0.1.

The result of application of the model of moving sources to the approximation of the spectrum of alpha particles in the ${}^{56}$Fe + ${}^{181}$Ta reaction at an energy of 320 MeV is shown in Fig. 6(b); the parameters of the sources are listed in Table 4. All sources have velocities equal to the velocity of the center of mass in the laboratory system; they correspond to the formation of an alpha particle and two nuclei during breakup of a compound nucleus or di-nuclear system in the course of incomplete fusion of the colliding projectile and target nuclei. Source 1 corresponds to emission of two alpha particles, one of which is very slow. Source 2 corresponds to the two-body exit channel ${}^{233}$Bk + ${}^{4}$He with possible emission of one more slow alpha particle via alpha decay of the ${}^{233}$Bk nucleus. The weights of these sources are very small. Sources 3 and 4 can be associated with the groups of three-body exit channels with the close values of the kinematic limits. For source 3, these are three-body exit channels with formation of two heavy nuclei of comparable masses, ${A_{\rm{L}}} > 90$; for source 4, the mass of a lighter nucleus is ${A_{\rm{L}}} < 60$. Different effective temperatures of the sources correspond to different energy distributions of pre-equilibrium fast alpha particles in the compound nucleus or di-nuclear system before their emission.

The values of the maximum kinematic limit $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels depending on the mass number of the lighter nucleus ${A_{\rm{L}}}$ for the ${}^{48}$Ca + ${}^{181}$Ta reaction at an energy of 280 MeV are listed in in Table 5 and shown in Fig. 7(a). The solid triangles represent the quantity ${U_{\rm{f}}}$ equal to the height of the Coulomb barrier for the spherical formed nuclei, $U_{\rm{f}} = V_{\rm{B}}$; the empty triangle denotes the channel ${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He with the modified value of ${U_{\rm{f}}} = 4.5$ MeV.

Exit channel and	Q	${U_{\rm{f}}}$	$E_{{\lim}{\rm{,max}}}^{(3)}$
designations in Fig. 7(b)	/MeV	/MeV	/MeV
${}^{3}$H + ${}^{222}$Th + ${}^{4}$He	–127.2	11.0	100.9
${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He $\downarrow$ 1	–112.0	21.9	105.6
${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He $\downarrow$	–112.0	{4.5}	124.5
${}^{6}$Li + ${}^{219}$Ra + ${}^{4}$He	–118.6	32.0	87.4
${}^{7}$Li + ${}^{218}$Ra + ${}^{4}$He	–116.7	31.6	89.9
${}^{32}$Si + ${}^{193}$Ir + ${}^{4}$He $\downarrow$ 3	–36.5	121.3	79.5
${}^{36}$S + ${}^{189}$Re + ${}^{4}$He $\downarrow$ 3	–26.5	134.4	76.1
${}^{62}$Fe + ${}^{163}$Tb + ${}^{4}$He $\downarrow$ 3	28.4	184.7	81.1
${}^{88}$Kr + ${}^{137}$Cs + ${}^{4}$He $\downarrow$ 2	71.2	213.9	96.0
${}^{96}$Zr + ${}^{129}$Sb + ${}^{4}$He $\downarrow$ 2	75.0	220.1	93.4

Table 5.  Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}\left( {{A_{\rm{L}}}} \right)$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the ${}^{48}$Ca + ${}^{181}$Ta reaction at an energy of 280 MeV. The modified value of ${U_{\rm{f}}}$ for the right edge of the experimental spectrum is given in braces; otherwise, $U_{\rm{f}} = V_{\rm{B}}$.

The energy spectrum of alpha particles measured at an angle of 0$^{\circ}$ in the ${}^{48}$Ca + ${}^{181}$Ta reaction at an energy of 280 MeV is shown in Fig. 7)(b). The whole spectrum lies to the left of the two-body kinematic limit $E_{{\rm{lim }}}^{(2)} = 121.4$ MeV (the short arrow) for the energy of alpha particles. It can be observed that the boundary $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ passes through the high-energy part of the spectrum in the interval 40–107 MeV, which is approximately the same as in Fig. 5(b). The dashed arrow indicates the kinematic limit for the exit channel ${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He with the modified value of ${U_{\rm{f}}} = 4.5$ MeV; arrows 1–3 correspond to the values of $E_{{\lim}{\rm{,max}}}^{(3)}$ in point 1 and frames 2 and 3 in Fig. 7(a). The decrease of the spectrum with increasing energy is not smooth, which may be due to the disappearance of the contributions of many three-body channels when passing through the values of $E_{{\lim}{\rm{,max}}}^{(3)}$. It can be observed that fast alpha particles with energies from 95 to 107 MeV are emitted in the three-body channel with the formation of two alpha particles and the heavy nucleus ${}^{221}$Ac of a relatively low excitation energy. The energy spectrum measured in the experiment falls by four orders of magnitude with respect to the maximum value and disappears near the maximum kinematic limits for the three-body exit channels ${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He and ${}^{3}$H + ${}^{222}$Th + ${}^{4}$He with $U_{\rm{f}} = V_{\rm{B}}$. In the energy range from 105 MeV to the kinematic limit $E_{{\rm{lim }}}^{(2)} = 121.4$ MeV for the two-body exit channel, alpha particles were not registered. The reason for this may be the low probability of the two- and three-body exit channels with emission of one of the alpha particles in the tunneling mode.

The result of application of the model of moving sources to the approximation of the spectrum of alpha particles in the ${}^{48}$Ca + ${}^{181}$Ta reaction at an energy of 280 MeV is shown in Fig. 7(c). Due to the fact that the boundary $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ for three-body channels and the kinematic limit $E_{{\rm{lim}}}^{(2)}$ are located more to the right than in Fig. 5(a), only three sources were used to approximate the shape of the spectrum; their parameters are listed in Table 4. The velocities of all sources are equal to the velocity of the compound nucleus or di-nuclear system. Source 1 corresponds to the three-body channel ${}^{4}$He + ${}^{221}$Ac + ${}^{4}$He with formation of the heaviest nucleus; the value of ${U_{\rm{f}}}$ is equal to the height of the Coulomb barrier for the formed nuclei ${}^{221}$Ac + ${}^{4}$He, $U_{\rm{f}} = V_{\rm{B}}$. Sources 2 and 3 in Fig. 7(c) correspond to three-body reaction channels with close values of $E_{{\lim}{\rm{,max}}}^{(3)}$. For source 2, these are three-body channels with formation of two heavy nuclei of comparable masses, $90 < {A_{3}} < 100$; for source 3, the mass of the lighter nucleus is $50 < {A_{3}} < 70$.

The values of the maximum kinematic limit $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels depending on the mass number of the lighter nucleus ${A_{\rm{L}}}$ for the reaction ${}^{48}$Ca + ${}^{238}$U at an energy of 280 MeV are listed in Table 6 and shown in Fig. 8(a). The solid triangles represent the quantity ${U_{\rm{f}}}$ equal to the height of the Coulomb barrier for the spherical formed nuclei, $U_{\rm{f}} = V_{\rm{B}}$; the squares denote the modified value of ${U_{\rm{f}}} = {V_{\rm{f}}}({R_{\rm{B}}} + d)$ with $d = 1.3$ fm, for ${A_{\rm{L}}} \geq 130$; the empty triangle represents the channel ${}^{4}$He + ${}^{278}$Hs + ${}^{4}$He with the modified value of ${U_{\rm{f}}} = 3.9$ MeV. The shape of the boundary $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ in Fig. 8(a) significantly differs from the shape of the boundary for the ${}^{48}$Ca + ${}^{181}$Ta reaction in Fig. 7(a). It is this difference that can lead to a significant excess of the yield of alpha particles in reactions on the ${}^{238}$U target compared to that on the ${}^{181}$Ta target [Fig. 3(a)] and a smooth decrease of the alpha particle spectrum with increasing energy, which is noticeably different from the nonsmooth decrease for the ${}^{48}$Ca + ${}^{181}$Ta reaction.

Exit channel and	Q	${U_{\rm{f}}}$	$E_{{\lim}{\rm{,max}}}^{(3)}$
designations in Fig. 8(b)	/MeV	/MeV	/MeV
${}^{4}$He + ${}^{278}$Hs + ${}^{4}$He	–141.6	25.4	78.9
${}^{4}$He + ${}^{278}$Hs + ${}^{4}$He $\downarrow$ 1	–141.6	{3.9}	102.1
${}^{8}$Li + ${}^{274}$Bh + ${}^{4}$He $\downarrow$ 6	–154.0	36.5	53.1
${}^{40}$S + ${}^{242}$Pu + ${}^{4}$He $\downarrow$ 6	–31.2	160.1	52.2
${}^{62}$Cr + ${}^{220}$Rn + ${}^{4}$He $\downarrow$ 5	30.9	215.3	59.8
${}^{76}$Zn + ${}^{206}$Hg + ${}^{4}$He $\downarrow$ 3	83.9	248.6	81.4
${}^{100}$Zr + ${}^{182}$Yb + ${}^{4}$He $\downarrow$ 4	116.9	287.5	75.0
${}^{130}$Sn + ${}^{152}$Nd + ${}^{4}$He	150.9	306.4	91.4
${}^{130}$Sn + ${}^{152}$Nd + ${}^{4}$He $\downarrow$ 2	150.9	{295.8}	102.7
${}^{134}$Te + ${}^{148}$Ce + ${}^{4}$He	153.6	308.0	92.5
${}^{134}$Te + ${}^{148}$Ce + ${}^{4}$He $\downarrow$ 2	153.6	{296.7}	104.6
${}^{141}$Cs + ${}^{141}$Cs + ${}^{4}$He	149.6	308.8	87.2
${}^{141}$Cs + ${}^{141}$Cs + ${}^{4}$He	149.6	{297.1}	99.8

Table 6.  Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}\left( {{A_{\rm{L}}}} \right)$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the ${}^{48}$Ca + ${}^{238}$U reaction at an energy of 280 MeV. The modified values of ${U_{\rm{f}}}$ for the right edge of the experimental spectrum are given in braces; otherwise, ${U_{\rm{f}}} = {V_{{\rm{B}}}}$.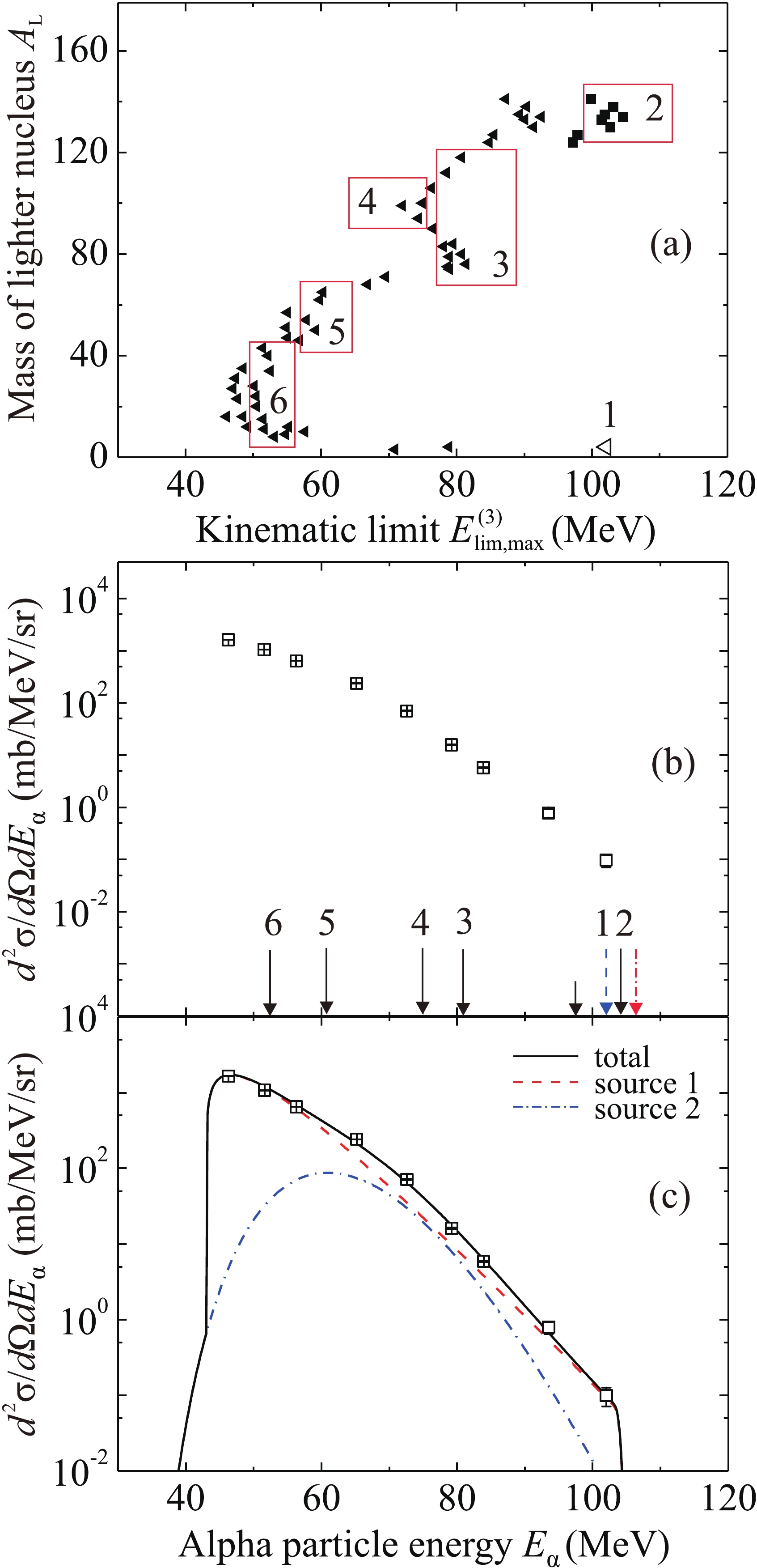

Figure 8.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the reaction ${}^{48}$Ca + ${}^{238}$U at an energy of 280 MeV as a function of the mass number ${A_{L}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2 and 6). (c) Spectrum approximation within the model of moving sources with the parameters given in Table 4: source 1 (dashed curve), source 2 (dashed-dotted curve), and the total spectrum from all sources (solid curve).

The energy spectrum of alpha particles measured at an angle of 0$^{\circ}$ in the ${}^{48}$Ca + ${}^{238}$U reaction at an energy of 280 MeV is shown in Fig. 8(b). The short arrow indicates the kinematic limit $E_{{\rm{lim }}}^{(2)} = 97.5$ MeV for the two-body exit channel ${}^{282}$Ds + ${}^{4}$He; arrows 1–6 correspond to the values of $E_{{\lim}{\rm{,max}}}^{(3)}$ in point 1 and frames 2–6 in Fig. 8(a); the maximum kinematic limits of the three-body channel with a slow tunneling alpha particle are shown with dashed arrow 1 for the modified value of ${U_{\rm{f}}} = 3.9$ MeV and a dash-dotted arrow for ${U_{\rm{f}}} = 0$. The maximum alpha particle energy 102 MeV exceeds the kinematic limit $E_{{\rm{lim}}}^{(2)} = 97.5$ MeV for the two-body exit channel ${}^{282}$Ds + ${}^{4}$He. This can be explained by the contribution of three-body channels of two different types. The first type is the channels with emission of a slow alpha particle in the tunneling mode when the quantity ${U_{\rm{f}}}$ can be noticeably lower than the height of the Coulomb barrier. The second type is the channels with formation of two nuclei of similar masses in addition to a fast alpha particle. In this case, the value of ${U_{\rm{f}}}$ is approximately 10 MeV lower than the height of the Coulomb barrier for spherical nuclei (see Table 6). This can be a barrier for deformed nuclei or for nuclei formed in α-accompanied ternary fission (see, e.g., [29–32]). A significant contribution of several channels of the second type may explain the significant increase, approximately by an order of magnitude, in the yield of fast alpha particles compared to that from the reaction on the ${}^{181}$Ta target [Fig. 3(a)]. Thus, the part of the spectrum of alpha particles with energies from 84 to 102 MeV may be explained as a result of their emission in three-body channels with formation of two nuclei of similar masses. The yield for the three-body channels of the first type (two alpha particles and a heavy nucleus) apparently remains approximately the same as in the case of the ${}^{181}$Ta target due to an insignificant increase in the atomic number of the target nucleus and compound nucleus.

The result of application of the model of moving sources to approximation of the spectrum of alpha particles in the ${}^{48}$Ca + ${}^{238}$U reaction at an energy of 280 MeV is shown in Fig. 8(c). To describe the shape of the spectrum, two sources were used; their parameters are given in Table 4. The velocity of the first source is equal to the velocity of the compound nucleus (stable or undergoing fission); this source corresponds to emission of alpha particles during fusion of the colliding nuclei or during fission of the compound nucleus. The second source is approximately two orders of magnitude weaker and has a formal nature, since it corresponds to alpha particles resulting from a large number of three-body channels with kinematic limits in a wide energy range.

The values of the maximum kinematic limit $E_{{\lim}{\rm{,max}}}^{(3)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels depending on the mass number of the lighter nucleus ${A_{\rm{L}}}$ for the reaction ${}^{56}$Fe + ${}^{238}$U at energies 400 MeV and 320 MeV are listed in Table 7 and shown in Figs. 9(a) and 10(a), respectively. The measured spectra of alpha particles are shown in Figs. 9(b) and 10(b), respectively. The short arrows indicate the kinematic limits of the two-body exit channel ${}^{290}$Lv + ${}^{4}$He, $E_{{\rm{lim}}}^{(2)} = 144.9$ MeV and $E_{{\rm{lim}}}^{(2)} = 72.1$ MeV, respectively. It can be observed that there are no correlations between the shape, the right edge of the spectrum, and the values of these kinematic limits, which may indicate an insignificant contribution of this channel to the yield of alpha particles. The numbered arrows in Figs. 9(b) and 10(b) correspond to the values of $E_{{\lim}{\rm{,max}}}^{(3)}$ in the numbered points or frames in Figs. 9(a) and 10(a).

Exit channel and	Q	${U_{\rm{f}}}$	$E_{{\lim}{\rm{,max}}}^{(3)}$
designations in Figs. 9(b), 10(b)	/MeV	/MeV	/MeV
${}^{56}$Fe (400 MeV) + ${}^{238}$U
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He $\downarrow$ 1	–189.8	26.7	127.9
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He	–189.8	{4}	152.4
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He	–189.8	{0}	156.7
${}^{6}$Li + ${}^{284}$Nh + ${}^{4}$He $\downarrow$ 3	–196.3	39.2	107.2
${}^{38}$S + ${}^{252}$Fm + ${}^{4}$He $\downarrow$ 3	–65.7	170.4	106.5
${}^{58}$Cr + ${}^{232}$U + ${}^{4}$He $\downarrow$ 2	1.5	230.7	114.0
${}^{76}$Zn + ${}^{214}$Rn + ${}^{4}$He $\downarrow$ 1	50.9	266.3	129.1
${}^{96}$Zr + ${}^{194}$Os + ${}^{4}$He	102.2	311.8	135.3
${}^{126}$Sn + ${}^{164}$Dy + ${}^{4}$He	136.3	336.1	145.9
${}^{56}$Fe (320 MeV) + ${}^{238}$U
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He	–189.8	26.7	54.6
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He $\downarrow$ 1	–189.8	{4}	79.8
${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He	–189.8	{0}	84.2
${}^{6}$Li + ${}^{284}$Nh + ${}^{4}$He	–196.3	39.19	32.9
${}^{38}$S + ${}^{252}$Fm + ${}^{4}$He	–65.7	170.4	32.1
${}^{58}$Cr + ${}^{232}$U + ${}^{4}$He	1.5	230.7	40.1
${}^{76}$Zn + ${}^{214}$Rn + ${}^{4}$He	50.9	266.3	55.9
${}^{96}$Zr + ${}^{194}$Os + ${}^{4}$He	102.2	311.8	62.3
${}^{126}$Sn + ${}^{164}$Dy + ${}^{4}$He	136.3	336.1	73.2
${}^{126}$Sn + ${}^{164}$Dy + ${}^{4}$He $\downarrow$ 2	136.3	{312.3}	99.2
${}^{132}$Te + ${}^{158}$Gd + ${}^{4}$He	140.2	338.7	74.6
${}^{132}$Te + ${}^{158}$Gd + ${}^{4}$He $\downarrow$ 2	140.2	{314.9}	100.6
${}^{144}$Ce + ${}^{146}$Ce + ${}^{4}$He	140.3	342.3	70.8
${}^{144}$Ce + ${}^{146}$Ce + ${}^{4}$He	140.3	{319.4}	95.9

Table 7.  Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(3)}\left( {{A_{\rm{L}}}} \right)$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the ${}^{56}$Fe + ${}^{238}$U reaction. The modified values of ${U_{\rm{f}}}$ for the right edge of the experimental spectrum are given in braces; otherwise, $U_{\rm{f}} = V_{\rm{B}}$.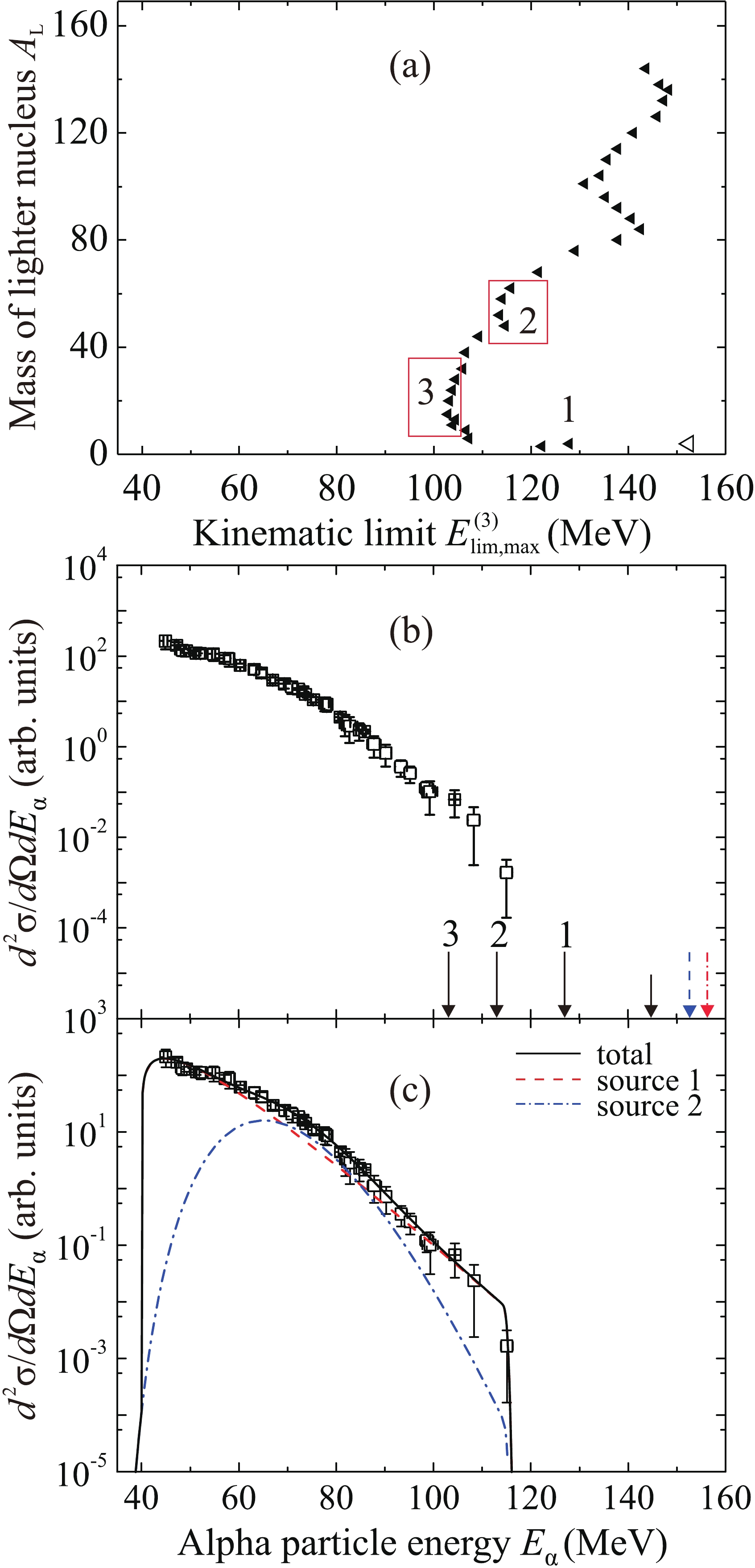

Figure 9.  (color online) (a) Maximum kinematic limits $E_{{\lim}{\rm{,max}}}^{(2)}$ for the energy of an alpha particle emitted at an angle of 0$^{\circ}$ in three-body exit channels of the reaction ${}^{56}$Fe + ${}^{238}$U at an energy of 400 MeV as a function of the mass number ${A_{L}}$ of the lighter nucleus. (b) Experimental energy spectrum of alpha particles. Arrows show some kinematic limits (see text and Tables 2, 7). (c) Spectrum approximation within the model of moving sources with the parameters given in Table 4: source 1 (dashed curve), source 2 (dashed-dotted curve), and the total spectrum from all sources (solid curve).

In the case of the ${}^{56}$Fe + ${}^{238}$U reaction at an energy of 400 MeV in Fig. 9(b), the maximum kinematic limits of three-body channels with a slow tunneling alpha particle are shown by a dashed arrow for the modified value of $U_{\rm{f}} = 4$ MeV and a dash-dotted arrow for $U_{\rm{f}} = 0$. In Fig. 9(a), the values for $U_{\rm{f}} = V_{\rm{B}}$ are shown by solid triangles; the empty triangle is $E_{{\rm{lim,max}}}^{(3)}$ for the channel ${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He with the modified value of ${U_{\rm{f}}} = 4$ MeV. The maximum energy of alpha particles in this reaction, 115 MeV, is significantly lower than the kinematic limit $E_{{\rm{lim}}}^{(2)} = 144.9$ MeV of the two-body exit channel ${}^{290}$Lv + ${}^{4}$He and the maximum kinematic limit $E_{{\lim}{\rm{,max}}}^{(3)} = 156.7$ MeV of the three-body channel with emission of a slow alpha particle in the tunneling mode with the modified value of $U_{\rm{f}}$ = 0. The slightly nonsmooth behavior of the spectrum near the energies of 103 and 113 MeV, the maximum kinematic limits for the channels with formation of light nuclei of mass numbers in the ranges of 10–40 and 50–70, respectively, together with a fast alpha particle and a heavy nucleus, can be explained by the significant probability of such channels.

In the case of the ${}^{56}$Fe + ${}^{238}$U reaction at an energy of 320 MeV in Fig. 10(b), the maximum kinematic limits of three-body channels with a slow tunneling alpha particle are shown by dashed arrow 1 for the modified value of ${U_{\rm{f}}} = 4$ MeV and the dash-dotted arrow for ${U_{\rm{f}}} = 0$. In Fig. 10(a), the values for $U_{\rm{f}} = V_{\rm{B}}$ are shown by solid triangles, and the modified values of ${U_{\rm{f}}} = {V_{\rm{f}}}({R_{\rm{B}}} + {d})$ with ${d} = 2$ fm are represented by squares, for ${A_{\rm{L}}} \geq 100$; the empty triangle is $E_{{\rm{lim,max}}}^{(3)}$ for the channel ${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He with the modified value of ${U_{\rm{f}}} = 4$ MeV. It can be observed that the values of $E_{{\lim}{\rm{,max}}}^{(3)}\left({{A_{\rm{L}}}} \right)$ are almost evenly distributed in the range from 30 to 100 MeV [Fig. 10(a)], as in the case of the ${}^{48}$Ca + ${}^{238}$U reaction. The maximum energy of alpha particles, 100 MeV, significantly exceeds the kinematic limit $E_{{\rm{lim}}}^{(2)} = 72.1$ MeV of the two-body exit channel ${}^{290}$Lv + ${}^{4}$He and the maximum kinematic limit $E_{{\rm{lim,max}}}^{(3)} = 84.2$ MeV of the three-body channel with emission of a slow alpha particle in the tunneling mode in addition to a fast one with the modified value of ${U_{\rm{f}}} = 0$.

The part of the spectrum of alpha particles with energies from 84 to 100 MeV can be explained as the result of three-body channels with formation of two nuclei of similar masses. In this case, the quantity ${U_{\rm{f}}}$ can be approximately 20 MeV lower than the height of the Coulomb barrier for spherical nuclei (see Table 7). As in the case of the ${}^{48}$Ca + ${}^{238}$U reaction, this can be the height of the barrier for deformed nuclei or for nuclei formed in α-accompanied ternary fission. Some kink in the spectrum near the energy of 80 MeV, the maximum kinematic limit for formation of a heavy nucleus in the exit channel ${}^{4}$He + ${}^{286}$Fl + ${}^{4}$He with emission of a slow alpha particle at an energy of 4 MeV in addition to a fast one, may indicate a small contribution of this channel compared to the channels with formation of nuclei of similar masses.

The approximation of the spectrum of alpha particles in the reaction ${}^{56}$Fe + ${}^{238}$U as the sum of distributions from moving sources would be of a formal nature (as in the case of the reaction ${}^{48}$Ca + ${}^{238}$U) because the yield of alpha particles may result from a large number of three-body channels with kinematic limits in a wide energy range. The results of the approximation are shown in Figs. 9(c) and 10(c), respectively.

The results of the analysis of alpha particle spectra may be summarized as follows.

(i) The energy spectrum of alpha particles falls by 4–5 orders of magnitude with the increase in their energy for all the studied reactions, which cover a wide collision energy range (280, 320, and 400 MeV). This may indicate that the mechanism of emission of alpha particles with energies close to the maximum energy may be associated with an object whose velocity changes insignificantly when the bombarding energy changes from 280 to 400 MeV. It can be a compound nucleus or di-nuclear system moving at the velocity of the center of mass.

(ii) The maximum energy of fast alpha particles can to some extent (by 5–10 MeV) exceed the kinematic limit of the two-body exit channel. This may be explained by the emission of a fast alpha particle during the process of fusion of nuclei along with the emission of a slow alpha particle in the tunneling mode (with lower energy than in the alpha decay of the heavy nucleus in the two-body exit channel).

(iii) In reactions with the target nucleus ${}^{181}$Ta, which is lighter than the magic nucleus ${}^{208}$Pb, three-body channels with emission of two alpha particles (a fast one and a slow one) and the two-body channel contribute to the high-energy part of the alpha particle spectrum. In this case, a cold heavy nucleus is formed. In reactions with the target nucleus ${}^{238}$U, which is heavier than ${}^{208}$Pb, the main contribution to the high-energy part of the alpha-particle spectrum is from three-body channels with emission of an alpha particle and formation of two nuclei of similar masses. This explains the increase in the total yield of alpha particles by one or two orders of magnitude in comparison with the reactions on the ${}^{181}$Ta target. We may expect that alpha particle spectra for other target nuclei heavier than ${}^{208}$Pb will be similar to that for ${}^{238}$U.

(iv) The presence of regions with nonsmooth decrease in the energy spectra of alpha particles indicates the presence of three-body exit channels of reactions. The yield of alpha particles is described well by the modified phenomenological model of moving sources, which includes kinematic limits for two- and three-body reaction channels.

The above analysis of the spectra of the fast alpha particles showed that they may be emitted during fusion of the colliding nuclei with formation of the compound nucleus and simultaneous emission of another alpha particle of significantly lower energy.

Let us consider qualitatively the mechanism of this process within the model [22, 33], which assumes formation of alpha particles in the surface region of nuclei, i.e., it is assumed that the potential energy $V (r)$ of interaction of an alpha particle cluster with a core of mass ${A_{{\rm{core}}}}$ has a minimum in the vicinity of a nuclear surface. The potential $V (r)$ can be selected in the form of the sum of the Coulomb field of a uniformly charged sphere of radius ${R_{\rm{C}}} = 1.3A_{{\rm{core}}}^{1/3}$ fm and two functions of the Woods–Saxon type:

The parameters ${V_0}$, ${R_V}$, and ${a_V}$ of the attractive part of potential (8) are

The repulsive part of potential (8) prevents penetration of alpha particle clusters into the nucleus interior, densely filled with nucleons. For this part, we used the values of the parameters ${U_0} = 30$ MeV and ${a_U} = 0.5$ fm. The radius ${R_U}$ was a variable parameter determined by assigning the sign-reversed ground state energy of the alpha particle cluster to the experimental energy of separation of an alpha particle from the nucleus taken from [14]. Calculations for a wide set of nuclei with mass numbers ranging from 20 to 240 showed that

is a reasonable representation of the radius ${R_U}$ [22].

The experimental charge density of the ${}^{181}$Ta nucleus [34], potential energy (8) of the alpha particle cluster in ${}^{181}$Ta, and radial part of its wave function $\phi (r)$ for the ground state 1s are shown in Fig. 11(a), (b), and (c), respectively. Once it has been formed, the alpha particle cluster is localized predominantly in the surface layer of the nucleus. The radial parts of the wave functions of the outer neutron state $1{i_{13/2}}$ and the outer proton state $1{h_{11/2}}$ are also shown in Fig. 11(c). They are similar to the radial part of the wave function of the alpha particle cluster, and this ensures satisfaction of the Pauli exclusion principle, according to which the cluster nucleons must correspond to shell model orbitals outside of the core (e.g., [35, 36]).

Figure 11.  (color online) (a) The experimental charge density of the ${}^{181}$Ta nucleus [34]. (b) Potential energy (8) of the alpha particle cluster in ${}^{181}$Ta and its ground state 1s (horizontal segment). (c) The radial parts of the wave functions for the alpha particle cluster ground state 1s (solid curve), outer proton state $1{h_{11/2}}$ (dash-dotted curve), and outer neutron state $1{i_{13/2}}$ (dashed curve).

Evolution of the wave function $\Psi (\vec{r},t)$ of the alpha particle (alpha cluster) during the collision of nuclei was determined by numerical solution of the time-dependent Schrödinger equation [22, 37]

where ${V_1}(r), {V_2}(r)$ are the potentials of interaction of the alpha particle with nuclei (or cores) 1 and 2; ${\vec{r}_1}(t)$ is the trajectory of the center of mass of nucleus 1; ${\vec{r}_2}(t)$ is the trajectory of the center of mass of the system {core $+$ alpha particle}; and ${m_\alpha }$ is the alpha particle mass.

At low collision impact parameters and energies above the Coulomb barrier, the surfaces of nuclei may touch and their volumes overlap, which leads to redistribution of nucleons. To describe this process, the simplest model was used, in which part of nucleons of the lighter projectile nucleus was transferred to the heavier target nucleus; this part corresponded to the fraction of the volume of the projectile nucleus that entered inside the volume of the target nucleus. The equations of motion of the centers of mass of the nuclei included this redistribution of the masses of the nuclei.

Equation (15) was numerically solved by the difference method [38] in the Cartesian coordinate system with grid steps $\Delta x = \Delta y = \Delta z = 0.2$ fm and time step $\Delta t = 0.05{t_0}$, where ${t_0} = {{{m_\alpha }x_0^2} \mathord{\left/ {\vphantom {{{m_\alpha }x_0^2} \hbar }} \right. } \hbar } = 6.28 \times {10^{ - 23}}$ s, ${x_0} = 1$ fm. The results of calculations of the probability density ${\left| {\Psi (\vec{r},t)} \right|^2}$ for the alpha particle formed in the target nucleus showing its forward emission in the process of complete fusion of ${}^{56}$Fe (320 MeV) + ${}^{181}$Ta are presented in Fig. 12. The comparison of the figures showing the probability densities with the time interval $120\Delta t = 6{t_0} \approx 4 \times {10^{ - 22}}$ s made it possible to determine the characteristic time $\tau \sim{\ }{{10}^{-22}}$ s for emission of alpha particles during complete fusion of the nuclei. According to the uncertainty principle, the uncertainty of energies of alpha particles in the shown process is of the order of several MeV. The state of the alpha particle formed in the target nucleus is perturbed during fusion of the nuclei and is a superposition of states with different energies, both above and below the stationary Coulomb barrier for the isolated nucleus at rest. Fast alpha particles are emitted from the states with energies above the barrier. Slow alpha particles are emitted from the states with energies below the barrier due to tunneling. The alpha particle can be emitted forward in a certain range of angles and backward, with lower probability. The results of calculations of the alpha particle emission probability w in the process of complete fusion of ${}^{48}$Ca (280 MeV) + ${}^{181}$Ta and ${}^{56}$Fe (320 and 400 MeV) + ${}^{181}$Ta depending on the collision impact parameter b are shown in Fig. 13(a) and (b), respectively. It can be concluded that forward emission at zero angle occurs for the impact parameters in a certain range close to that leading to complete fusion of the nuclei; the emission probability w is approximately constant throughout this range. The cross section of alpha particle emission ${\sigma _\alpha }$ is proportional to the fusion cross section ${\sigma _{{\rm{fus}}}}$: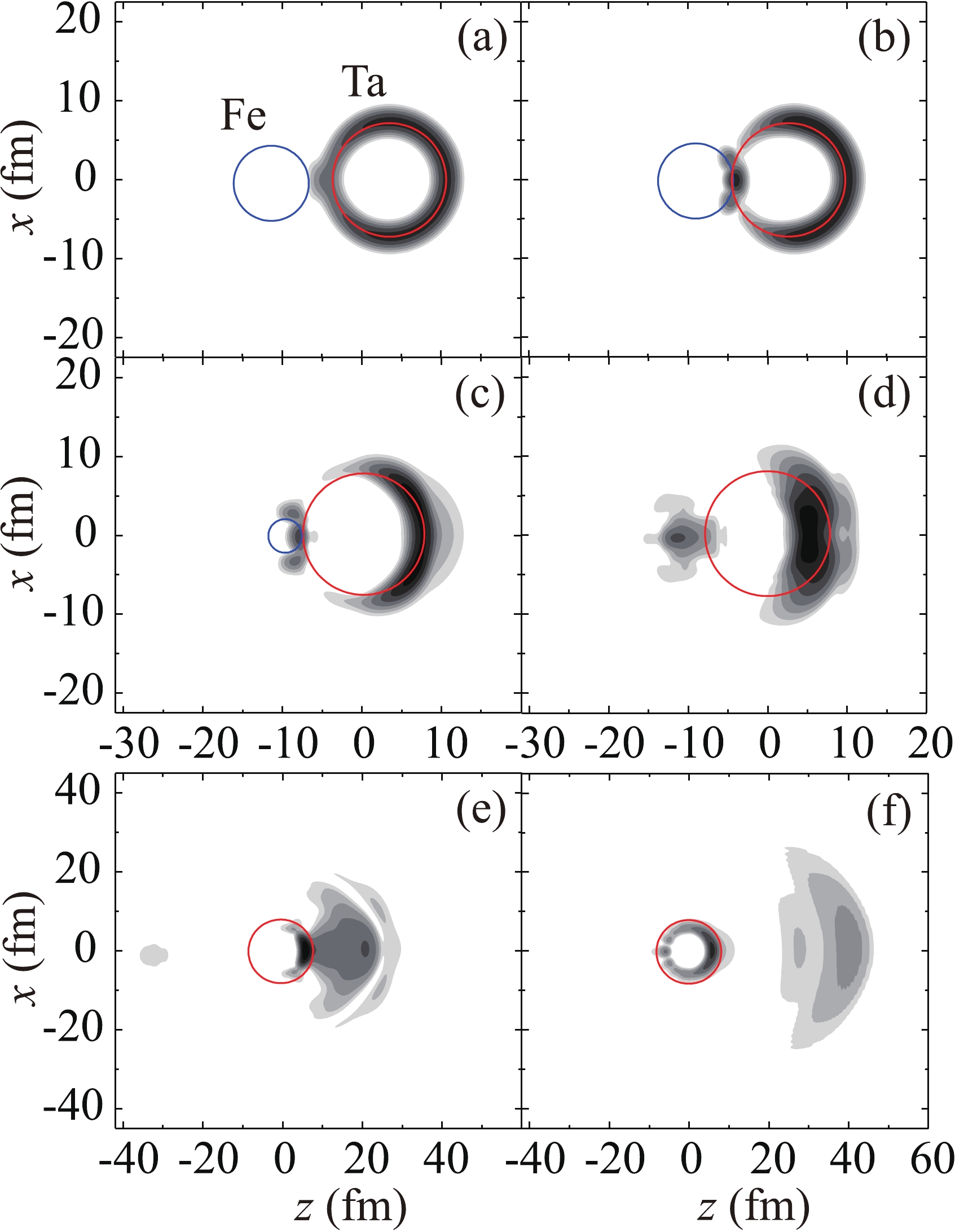

Figure 12.  (color online) Evolution of the probability density of the alpha particle formed in the target nucleus in the process of complete fusion of ${}^{56}$Fe (320 MeV) + ${}^{181}$Ta for collision impact parameter $b = 0.2$ fm (logarithmic scale); the course of time corresponds to the panel locations (a)–(f); the radii of the circles are equal to the radii of spherical nuclei.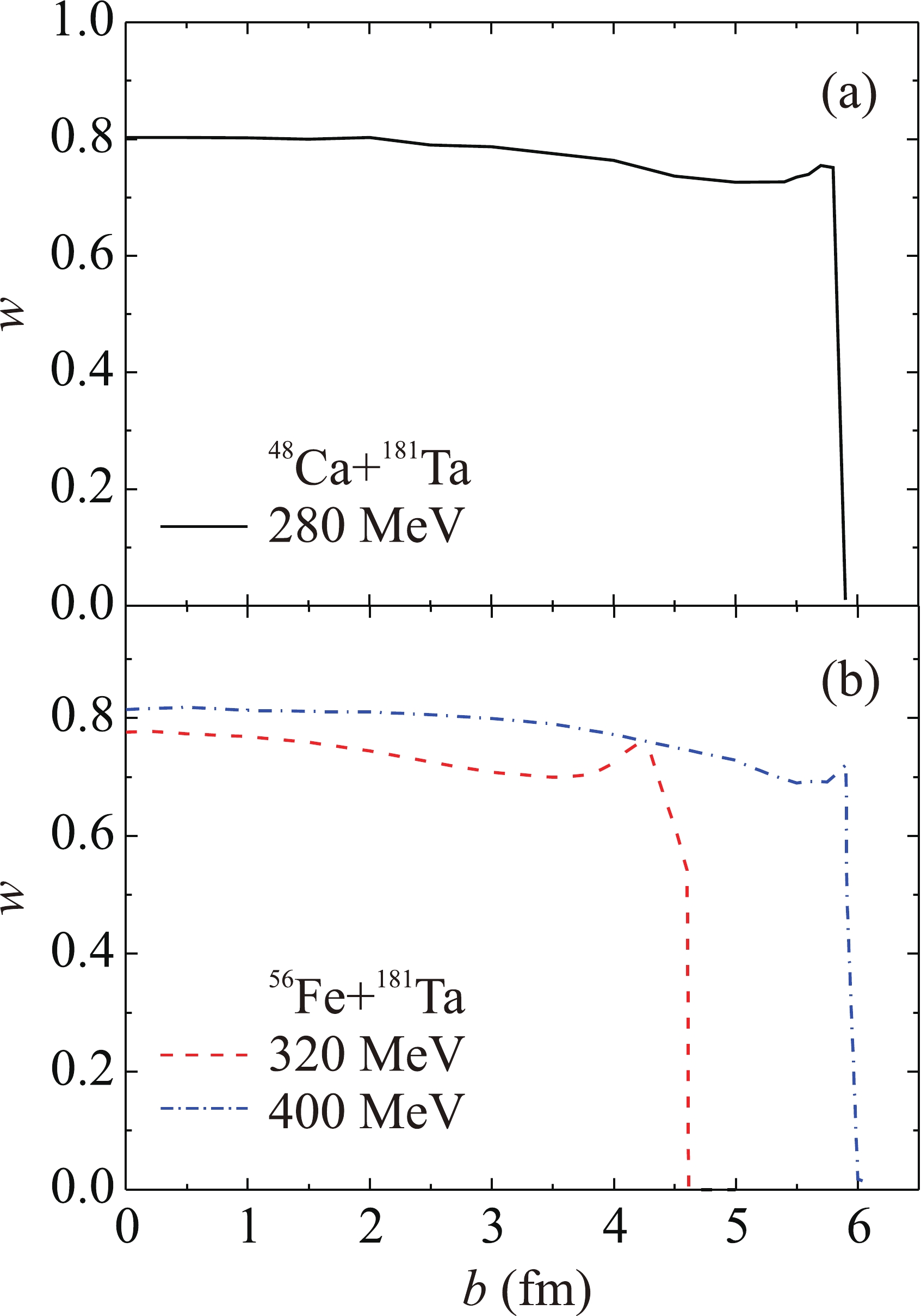

Figure 13.  (color online) The results of calculations of the alpha particle emission probability w in the process of complete fusion depending on the collision impact parameter b: (a) ${}^{48}$Ca (280 MeV) + ${}^{181}$Ta; (b) ${}^{56}$Fe (320 and 400 MeV) + ${}^{181}$Ta (dashed and dash-dotted curves, respectively).

where ${P_{{\rm{form}}}}$ is the probability of alpha cluster formation, and ${P_{{\rm{br}}}}$ is the probability of alpha cluster breakup depending on the shell structure of the target nucleus.

The energy spectra of fast alpha particles emitted at an angle of 0$^{\circ}$ were measured in the reactions of the projectile nuclei ${}^{48}$Ca and ${}^{56}$Fe with the target nuclei ${}^{181}$Ta and ${}^{238}$U at energies of 280, 320, and 400 MeV. A strong dependence of the double differential cross sections for production of alpha particles on the atomic number of the target nucleus indicates that fast alpha particles are mainly emitted from the target nucleus; this conclusion was also confirmed by calculations within the time-dependent Schrödinger equation approach.

Analysis of the spectra was performed within the model of moving sources, which was modified to take into account the kinematic limits for two- and three-body exit channels. The nonsmooth behavior of alpha particle spectra was explained as a consequence of different groups of three-body exit channels with similar kinematic limits. Analysis of the spectra made it possible to estimate the relative contributions of these groups of exit channels in the formation of the high-energy part of alpha particle spectra.

It was experimentally established that the maximum energy of fast alpha particles can to some extent exceed the kinematic limits of two-body exit channels. This fact was explained by their formation in three-body exit channels with emission of another slow alpha particle in the tunneling mode. Thus, the kinematic limits for three-body exit channels may indeed be greater than those for two-body exit channels.

The process of emission of fast alpha particles from colliding nuclei is extremely interesting from the perspective of producing cold heavy and superheavy nuclei. The use of reactions of the projectile nuclei ${}^{48}$Ca and ${}^{56}$Fe with ${}^{181}$Ta and heavier target nuclei is promising for conducting experiments on registering the formation of a heavy compound nucleus with emission of fast and slow alpha particles, which leads to a decrease in the excitation energy of compound nuclei and a greater probability of their survival. However, despite the larger yield of alpha particles in reactions with heavier target nuclei (e.g., ${}^{238}$U), the probability of formation of high-energy alpha particles (leading to formation of cold heavy and superheavy nuclei) remains approximately the same as in the case of the target nucleus ${}^{181}$Ta. Therefore, large amount of experimental time and high experimental sensitivity will still be required for production of cold heavy and superheavy nuclei in the channels with emission of fast alpha particles.

For this purpose, the magnetic analyzer MAVR is planned to be upgraded. This will allow us to perform experiments at a new methodological level, including the possibilities of measuring energy spectra of light charged particles with energies up to 70 MeV/nucleon and measuring their angular distribution in a wide range of angles. The new setup will allow simultaneous measurement of fast charged particles along with heavy and superheavy product nuclei.

The authors express their gratitude to the staff of the U400 cyclotron for producing high-quality, intense beams of accelerated heavy ions. We are also grateful to S. I. Sidorchuk for the helpful discussions of the results of this work and to D. Aznabayev, I. V. Butusov, T. Issatayev, K. Mendibaev, A. V. Shakhov, and S. S. Stukalov for their assistance in conducting the experiment on the MAVR analyzer.

Let us consider a collision of nuclei with masses ${m_1}$ and ${m_2}$ in the center of mass system with initial energy ${E_{{\rm{c}}{\rm{.m}}{\rm{.}}}}$ and energy ${E_{{\rm{c}}{\rm{.m}}{\rm{.}}}} + Q$ in a two-body exit channel with formation of an alpha particle and a nucleus with mass $M = {m_1} + {m_2} - {m_\alpha }$ moving along the direction of the initial motion of the projectile nucleus (along the Oz axis) with velocities ${u_\alpha }$ and ${u_M}$, respectively. From the laws of conservation of energy and the projection of momentum,

It follows that the velocity of the alpha particle in the center of mass system is equal to

The velocity of the center of mass in the laboratory system is

where ${v_1}$ is the velocity of the projectile nucleus in the laboratory system. When the alpha particle is emitted forward, its velocity in the laboratory system is ${v_\alpha } = {u_\alpha } + V$, and its kinetic energy is

where

Quantity (21) is the kinematic limit of the two-body exit channel.

Let us consider a three-body exit channel with formation of an alpha particle and two nuclei moving at the moment of separation of the alpha particle with the same velocities ${u_M}$ in the center of mass system and with the potential energy of their interaction with each other ${U_{\rm{f}}}$. After the nuclei fly apart in their center of mass system, the kinetic energy of their relative motion is equal to ${U_{\rm{f}}}$. Similar to formulas (17)–(22), the maximum energy of the alpha particle is equal to

where

Quantity (A7) is the kinematic limit of the three-body exit channel. Results (A7) and (A8) can also be obtained by applying the laws of conservation of energy and momentum in the center of mass system to the motion of nuclei at certain angles with respect to the direction of alpha particle emission (Oz axis).