-
Semi-magic Sn isotopes (Z = 50) play an important role in low-energy nuclear structure research. Their low-lying states are textbook examples of shell-model approaches. It is well known that Sn isotopes exhibit the coexistence of both spherical and prolate shapes. Spherical states are expected to be dominated by neutron quasiparticle excitations. Deformed structures are understood as proton particle-hole excitations through the Z = 50 shell having a 2p-2h proton configuration
$ \pi g_{7/2}^{2}g_{9/2}^{-2} $ in even mass nuclei and a configuration such that the valence neutron is coupled to the 2p-2h intruder states in odd mass Sn nuclei. So far, the coexistence of both spherical states and a deformed collective band has been systematically observed in even-even 106-118Sn [1–7] and odd-A 109-117Sn [3, 6, 8–11] isotopes. Whether the phenomenon of shape coexistence still exists in heavier Sn isotopes is an open question that deserves further investigation.Because of the lack of appropriate stable beam-target combinations, experimental information about excited states of 119Sn is very limited. Prior to this study, deep inelastic and fusion-fission reactions were used to study excited states of 119Sn [12–14]. However, a band structure has not been observed yet in 119Sn. Recently, the 7Li-induced incomplete-fusion reaction has proved to be effective for studying high-spin states of nuclei near the line of stability [15, 16]. In this paper, we report investigation on excited states in 119Sn using the 7Li + 116Cd reaction via the (7Li,
$ 1p3n $ ), (7Li,$ 1d2n $ ) and (7Li,$ 1t1n $ ) channels. We also demonstrate that possible collective behavior appears in the 119Sn nucleus. To some extent, the 7Li-induced incomplete-fusion reaction is equivalent to fusion-evaporation reactions using a radioactive beams of 4,5,6He from the breakup of 7Li [16]. This work is also part of a series of systematic studies of ours [7, 11, 17–21] about the level structures of nuclei near the magic number Z = 50. -
Excited states in 119Sn were populated in the 7Li + 116Cd reaction via the (7Li,
$ 1p3n $ ), (7Li,$ 1d2n $ ), and (7Li,$ 1t1n $ ) channels. A 7Li beam of 42 MeV was provided by the HI-13 Tandem Accelerator at the China Institute of Atomic Energy in Beijing (CIAE). The target was self-supporting 116Cd with a thickness of 2.5 mg/cm2. The γ rays of the product nuclei were detected with an array consisting of nine Compton-suppressed HPGe detectors and two low-energy photon spectrometer (LEPS) detectors. The detectors were calibrated for both energy and efficiency using 152Eu and 133Ba sources placed at the target position. A total of approximately 1.2×108 γ-γ coincidence events were accumulated during the experiment. After proper gain matching, these coincidence events were sorted into a symmetric matrix and two ADO (angular distribution from oriented nuclei) matrices for off-line analysis. In the present geometry, the ADO values were found to be approximately 1.1 for known stretched quadrupole transitions and 0.7 for stretched pure dipole transitions according to the examination of strong transitions of known multipolarities in 118Sn [7]. -
The level scheme of 119Sn deduced from the present study is shown in Fig. 1. All γ rays observed in this work were fed eventually toward a
$ I^{\pi} $ =11/2- isomeric state with the$ E_{\rm x} $ =89.5 keV and$ T_{1/2} $ =293.1 d [22]. For convenience, this 11/2- isomer is taken as a reference state in Fig. 1. A total of eight new transitions, i.e., 1417.1, 846.6, 947.5, 1066.0, 1092.3, 1212.6, 789.8, and 720.5 keV, have been identified and marked in red in the level scheme. The ordering of the transitions in the present level scheme was determined based on γ ray relative intensities, γ-γ coincidence relationships, and γ ray energy sums. The γ-γ coincidence spectra showing the presence of new transitions are displayed in Fig. 2. The spectrum (a) gated on the 1219.7+1417.1 keV transitions shows most newly identified transitions. To ensure that the 789.8 and 720.5 keV transitions emerge from 119Sn rather than contaminations, Fig. 2(b) presents the coincidence relationship between the 1289.3 and 720.5 keV transitions. In this way, the energy sum of the 1219.7 and 789.8 keV transitions is equal to that of the 1289.3 and 720.5 keV transitions within experimental accuracy, thereby dismissing the possibility of contaminations. The spin-parity assignments are mainly based on a previous study [14] and the measured ADO ratios of the γ rays. Transition energies, relative intensities, spin and parity assignments, and ADO ratios of the transitions identified in 119Sn are listed in Table 1.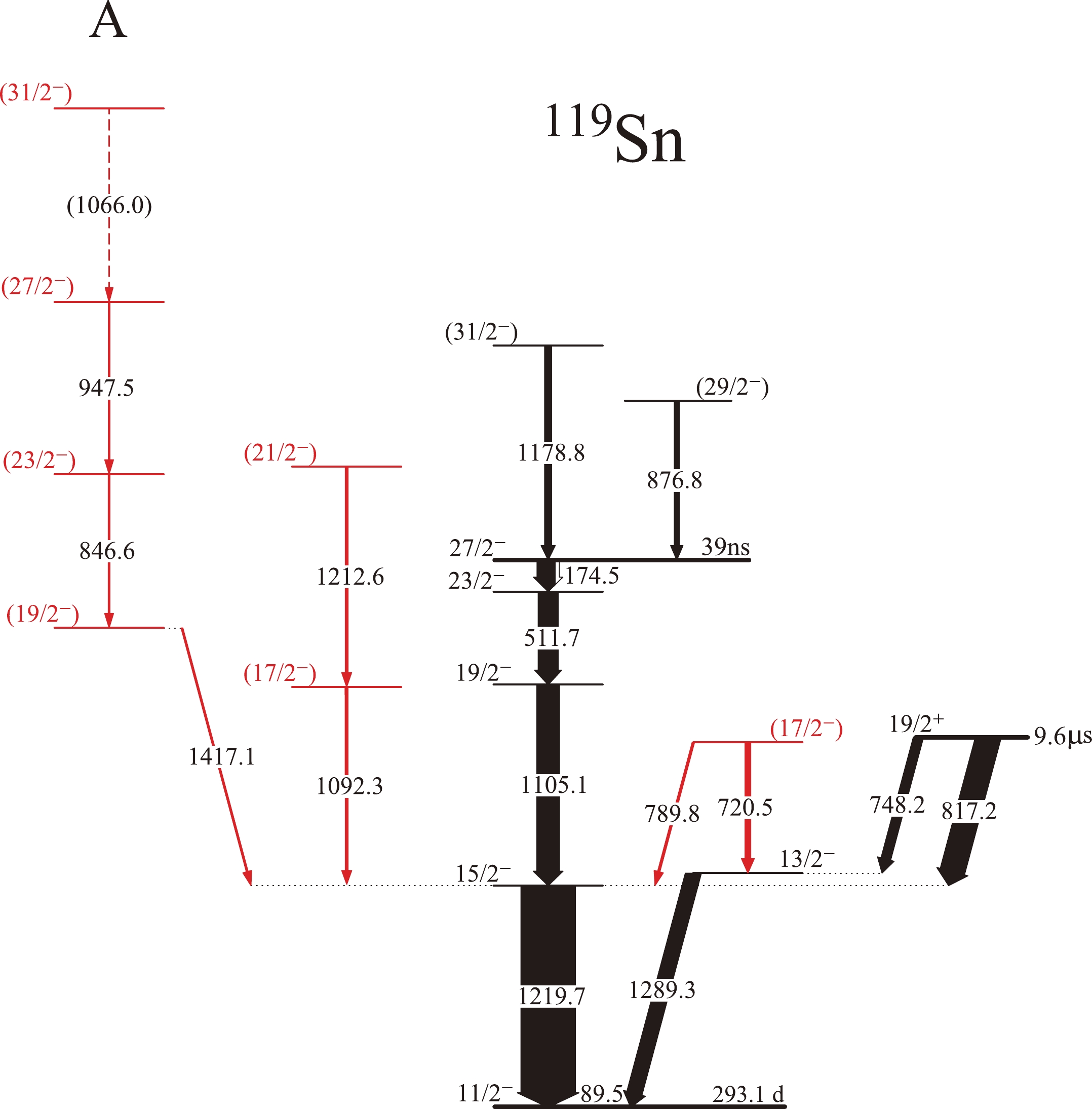
Figure 1. (color online) Level scheme of 119Sn deduced from the present study. All energies are expressed in keV. New levels and transitions are marked in red. The widths of the arrows represent the relative intensities of the transitions.
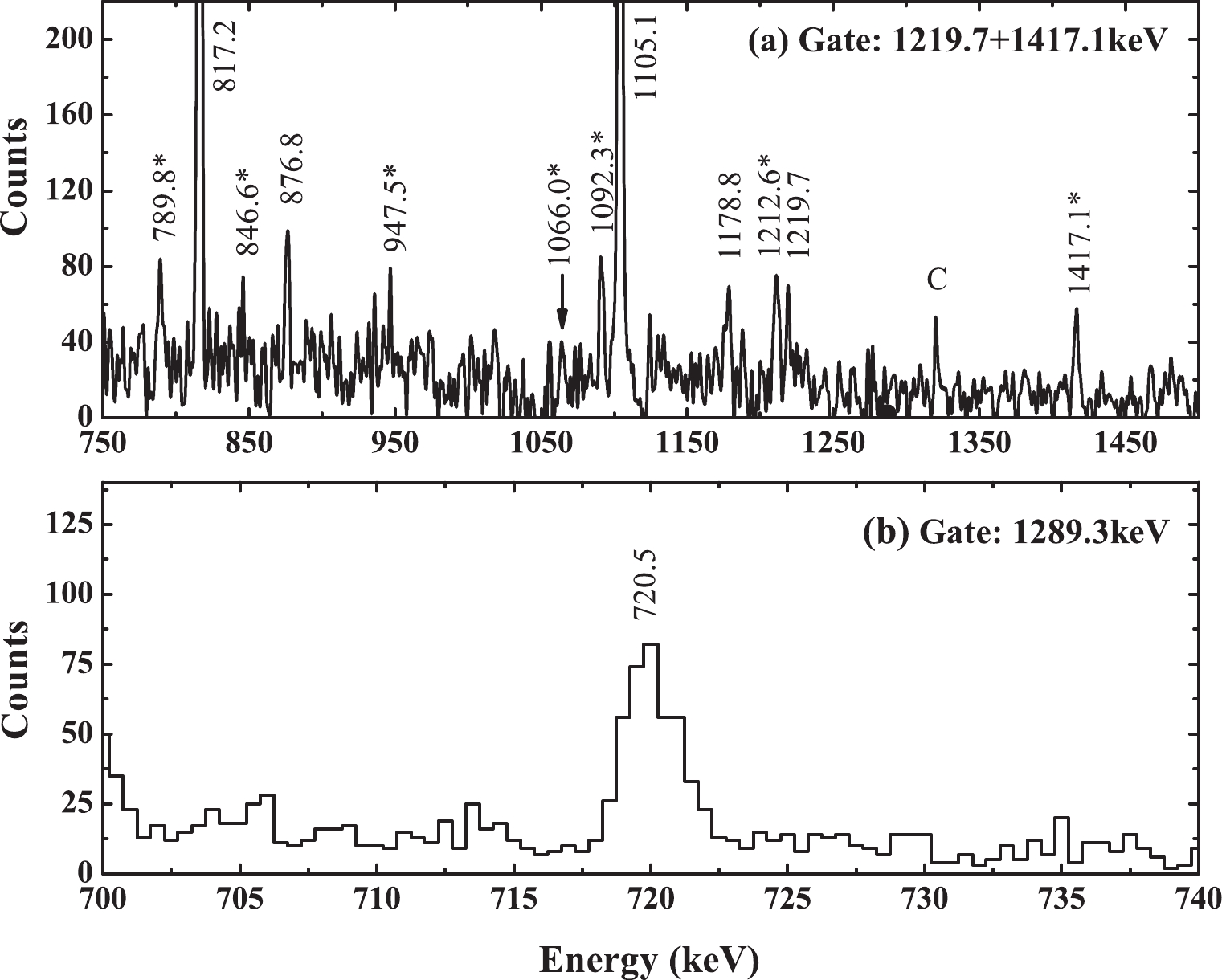
Figure 2.
$ \gamma-\gamma $ coincidence spectra gated on the 1219.7+1417.1 and 1289.3 keV transitions. New transitions and contaminants are labeled with the asterisk and C, respectively.$ E_{\gamma} $ /keV

$ I_{\gamma} $ 

$ I_{i}^{\pi}\rightarrow I_{f}^{\pi} $ 

ADO ratio 174.5 33.3(3.4) ${27}/{2}^{-}\rightarrow {23}/{2}^{-} $ 

1.06(0.16) 511.7 36.4(3.6) $ {23/}{2}^{-}\rightarrow {19}/{2}^{-} $ 

1.53(0.23) 720.5 10.3(1.2) $ ({17}/{2}^{-})\rightarrow {13}/{2}^{-} $ 

1.07(0.23) 748.2 18.1(1.8) $ {19}/{2}^{+}\rightarrow {13}/{2}^{-} $ 

1.04(0.19) 789.8 4.2(0.6) $ ({17}/{2}^{-})\rightarrow {15}/{2}^{-} $ 

0.84(0.21) 817.2 45.7(2.9) $ {19}/{2}^{+}\rightarrow {15}/{2}^{-} $ 

1.15(0.18) 846.6 2.9(0.9) $ ({23}/{2}^{-})\rightarrow ({19}/{2}^{-}) $ 

1.19(0.29) 876.8 9.5(1.5) $ ({29}/{2}^{-})\rightarrow {27}/{2}^{-} $ 

947.5 2.8(1.3) $ ({27}/{2}^{-})\rightarrow ({23}/{2}^{-}) $ 

1066.0 <2.8 $ ({31}/{2}^{-})\rightarrow ({27}/{2}^{-}) $ 

1092.3 5.1(0.7) $ ({17}/{2}^{-})\rightarrow {15}/{2}^{-} $ 

0.83(0.19) 1105.1 41.7(2.8) $ {19}/{2}^{-}\rightarrow {15}/{2}^{-} $ 

1.28(0.20) 1178.8 12.7(1.6) $ ({31}/{2}^{-})\rightarrow {27}/{2}^{-} $ 

1212.6 5.0(2.0) $ ({21}/{2}^{-})\rightarrow {17}/{2}^{-} $ 

1.29(0.30) 1219.7 100(5.1) $ {15}/{2}^{-}\rightarrow {11}/{2}^{-} $ 

1.40(0.22) 1289.3 28.5(2.6) $ \{13}/{2}^{-}\rightarrow {11}/{2}^{-} $ 

0.98(0.18) 1417.1 3.3(0.5) $ ({19}/{2}^{-})\rightarrow {15}/{2}^{-} $ 

1.48(0.40) Table 1. Energies, relative intensities, spin and parity assignments, and ADO ratios for transitions of 119Sn.
-
In previous studies [12–14], it is indicated that the observed states in 119Sn mainly originate from single-particle excitations and can be described in terms of weak coupling of the odd neutron to an excited 118Sn core. The known 19/2+ and 27/2- isomers have been assigned the pure
$ \nu (h_{11/2})^{2}s_{1/2} $ and$ \nu (h_{11/2})^{3} $ configurations, respectively [12].An interesting aspect of the present study is the observation of a new level sequence (labeled as A in Fig. 1) that consists of a bandlike structure and follows the rotational
$ I(I+1) $ rule. The existence of transitions in level sequence A is demonstrated by the gated spectrum depicted in Fig. 2. Level sequence A feeds the 15/2- state via the 1417.1 keV transition. The measured ADO ratio indicates that the 1417.1 keV transition might be an E2 transition. Therefore, we assigned$ I^{\pi} $ = 19/2- for the lowest observed state in level sequence A. Owing to the weak statistics of band A, the ADO ratios of the only 846.6 keV transition can be obtained. The measured ADO ratio indicates that the 846.5 keV transition has a stretched quadrupole transition character. Given that the 947.5 and 1066.0 keV transitions continue to follow the rotational sequence, we tentatively assign the stretched E2 character to them.As already mentioned in the introduction, the deformed bands built on 2p-2h proton excitations had been systematically observed in odd-A 109-117Sn isotopes [3, 6, 8–11]. The present observed level sequence A in 119Sn is likely to be the expected collective band built on 2p-2h proton excitations. The energy systematics of the
$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ band in odd-A 111,113,115,117,119Sn isotopes are displayed in Fig. 3 based on the proposal that the level sequence A in 119Sn results from the proton-pair excitations across the Z = 50 shell gap with$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ configuration. The first$ 11/2^{-} $ ,$ 15/2^{-} $ , and$ 19/2^{-} $ states from the coupling of$ \nu h_{11/2} $ to the$ 0^{+} $ ,$ 2^{+} $ , and$ 4^{+} $ states in the even-A Sn core are also shown in Fig. 3 for completeness. As shown in Fig. 3, the level spacings and the decay pattern in 119Sn are similar to those of 111,113,115,117Sn isotopes. It supports the interpretation of level sequence A as the collective structure with$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ configuration. In addition, this configuration assignment can be also supported by the following theoretical calculations.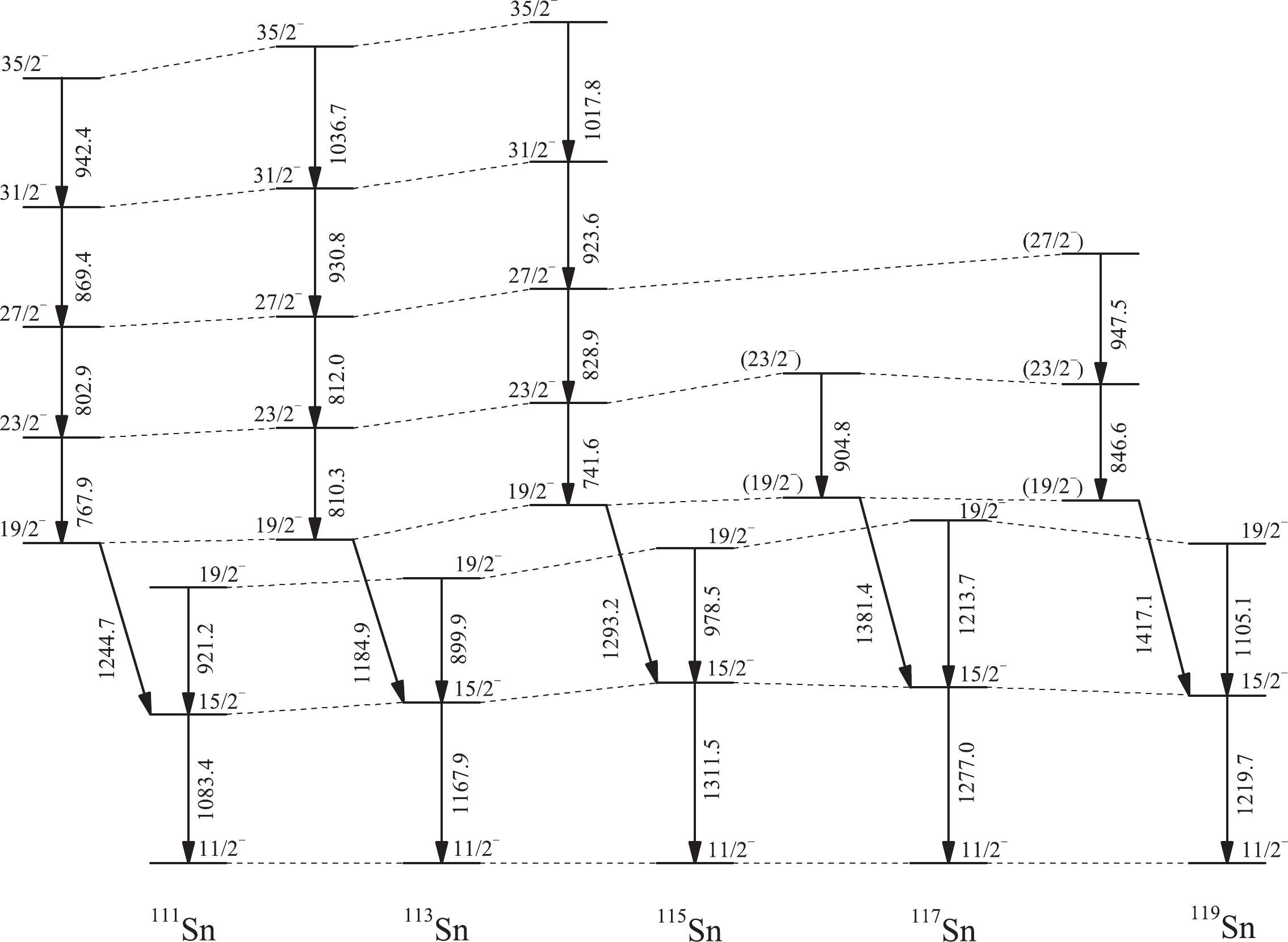
Figure 3. Energy systematics of the
$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ band in odd-A 111,113,115,117,119Sn together with the first$ 11/2^{-} $ ,$ 15/2^{-} $ , and$ 19/2^{-} $ states from the coupling of$ \nu h_{11/2} $ to the$ 0^{+} $ ,$ 2^{+} $ , and$ 4^{+} $ states in the even-A Sn core. Information about 111,113,115,117Sn is taken from Refs. [6, 11, 23, 24]. -
To understand the level structures of 119Sn, adiabatic and configuration-fixed constrained triaxial relativistic mean-field (RMF) calculations [25] were performed to obtain the potential energy surfaces (PESs) for each configuration. In the present calculations, the point-coupling density functional PC-PK1 [26] with a basis of 12 major oscillator shells was employed. The configurations, total energies (Etot), triaxial deformation parameters (β and γ), and energy information corresponding to minima of states are listed in Table 2, and compared with the experimental excitation energies. The four states, A, B, C, and D, in Table 2 correspond to four different configurations. State A with the unpaired nucleon configuration
$ \nu s_{1/2} $ represents the ground state, which is consistent with the spin and parity$ 1/2^{+} $ of the reported ground state in 119Sn [22]. The calculated deformation parameters indicate that the ground state of 119Sn has spherical shape. States B, C, and D have the valence nucleon configurations$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ ,$ \nu (h_{11/2})^{2}s_{1/2} $ , and$ \nu (h_{11/2})^{3} $ corresponding to the level sequence A,$ I^{\pi} $ = 19/2+ isomer, and$ I^{\pi} $ = 27/2- isomer, respectively. As shown in Table 2, the calculated excitation energies for the B, C, and D states are in good agreement with the experimental observations, further supporting the given configuration assignments. The$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ band has a prolate deformation with$ \beta_{2} $ = 0.27 and γ = 0.0°, which is similar to those of the lighter odd-A Sn isotopes. For the 19/2+ and 27/2- isomers, the calculations show that both states have oblate shapes. Such noncollective oblate states usually lead to some irregularities in the yrast line, thereby forming isomeric states [27]. Based on the above discussion, the present calculations show that three shapes, namely spherical, prolate, and oblate, coexist in 119Sn.State Configuration $E_{\rm tot}$ /MeV

$E_{\rm x}$ (cal.)/MeV

$E_{\rm x}$ (exp.)/MeV

β γ A $ \nu s_{1/2} $ 

−1008.45 0 0 0.01 $ 0.0^{\circ} $ 

B $ \pi g_{7/2}^{2}g_{9/2}^{-2}\otimes\nu h_{11/2} $ 

−1005.75 2.70 2.73 0.27 $ 0.0^{\circ} $ 

C $ \nu h_{11/2}^{2} s_{1/2} $ 

−1006.28 2.17 2.13 0.15 $ 55.0^{\circ} $ 

D $ \nu h_{11/2}^{3} $ 

−1004.81 3.64 3.10 0.17 $ 60.0^{\circ} $ 

Table 2. Configurations, total energies
$E_{\rm tot}$ , calculated and experimental excitation energies$ E_{\rm x} $ (cal.),$ E_{\rm x} $ (exp.) and triaxial deformation parameters β and γ relevant to minima of states A–D in triaxial RMF calculations. -
In summary, we conducted an investigation on the level structures of 119Sn using the heavy-ion fusion-evaporation reaction 116Cd (7Li,
$ 1p3n $ ). According to the level systematics, the new level sequence A is suggested to be based on the$ \pi (g_{7/2}^{2}g_{9/2}^{-2})\otimes \nu h_{11/2} $ configuration, which is supported by the configuration-fixed constrained triaxial RMF calculations. This observation extends the boundaries of the 2p-2h deformed collective band to A = 119 in the Sn isotopes. In addition, the present calculations show that spherical, prolate, and oblate shapes coexist in 119Sn. -
The numerical calculations in this study were performed on the supercomputing system in the Supercomputing Center and an HP Proliant DL785G6 server hosted by the Institute of Space Science in Shandong University.
Possible collective band in neutron-rich 119Sn
- Received Date: 2022-01-26
- Available Online: 2022-09-15
Abstract: Excited states of 119Sn have been studied using an in-beam γ-ray spectroscopic technique following the incomplete fusion of 7Li on a 116Cd target at a beam energy of 42 MeV. A new bandlike structure is proposed to result from deformed two-particle-two-hole (2p-2h) proton excitations across the Z = 50 closed shell based on the systematics of odd-A Sn isotopes and configuration-fixed constrained triaxial relativistic mean-field calculations. This observation extends the boundaries of the deformed 2p-2h collective band to A = 119 in Sn isotopes.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: