-
The discovery of new isotopes is the first step in studying the properties of the most exotic nuclei. The synthesis of new light and medium-mass neutron-rich isotopes, proton-rich isotopes, and new neutron-rich or proton-rich heavy and superheavy isotopes through low-energy heavy ion collisions near the Coulomb barrier is an important frontier of nuclear physics research [1–3]. The use of the fusion-evaporation reaction, spallation reaction, fragmentation reaction, etc. have achieved remarkable progress in the production of nuclei far from β stability lines over the last three decades. Many experiments have been also performed to study the mechanism of multinucleon transfer (MNT) reactions and have produced some neutron-rich isotopes [4–19], which indicates that the MNT reaction is an important tool for generating new neutron-rich nuclei [3, 13, 20].
Many approaches have been developed to explain and predict the experimental data of MNT reactions. The current theoretical models can be roughly divided into macroscopic-microscopic [21–35] and purely microscopic models [36, 40–47]. Among them, the improved dinuclear system (DNS) model can be used to describe the process of massive nucleon transfer between two colliding nuclei from the perspective of diffusion on the multi-dimensional potential energy surface (PES) by solving the four-variables master equations [27, 28]. The improved DNS model has been used to study the MNT processes in
$ ^{40} $ Ca+$ ^{208} $ Pb,$ ^{58} $ Ni+$ ^{208} $ Pb,$ ^{40} $ Ar+$ ^{208} $ Pb,$ ^{64} $ Ni+$ ^{208} $ Pb,$ ^{136} $ Xe+$ ^{208} $ Pb,$ ^{136} $ Xe+$ ^{198} $ Pt,$ ^{48} $ Ca+$ ^{238} $ U, and$ ^{48} $ Ca+$ ^{248} $ Cm,$ ^{238} $ U+$ ^{238} $ U,$ ^{238} $ U+$ ^{248} $ Cm,$ ^{136} $ Xe+$ ^{248} $ Cm, and$ ^{136} $ Xe+$ ^{249} $ Cf reactions [34, 35] at energies near the Coulomb barrier. Studies have shown that the improved DNS model is effective in describing the observed production cross-sections around the average values.MNT reactions are promising for the synthesis of proton-rich isotopes [16]. In addition, the proton radioactivity, α decay, and cluster radioactivity of proton-rich nuclei in the
$ 40 \leq Z \leq 60 $ region can provide us with reliable nuclear structure information for studying atomic nuclei, which strongly suggests that the synthesis of proton-rich new nuclei for medium-mass proton-rich isotopes is also worth studying.To reveal the mechanism of MNT reactions and search for the optimal projectile-target combination to produce new neutron-rich and proton-rich isotopes, systematic studies on the existing experimental production cross sections may facilitate an assessment of possible deficiencies and methods to improve various parts of the model. The philosophy we adopt is to implement as simple a model as possible with one set of parameters and with the same assumptions, with sufficient degrees of freedom, a well-tested model for the nuclear binding energy as a function of shape, and simple models for the nucleus-nucleus interaction potential. A comparison of predictions using the improved DNS model with the measured properties of transfer cross sections and mass distributions is useful in determining the target-projectile combinations, which is beneficial to the synthesis of neutron-rich and proton-rich isotopes, and to reveal the limitations of the improved DNS model to further improve it.
In this paper, we adopt the improved DNS model+GEMINI++ to describe MNT reactions with the target nuclei selected near the magic nucleus of Z=50 and predict the corresponding production cross sections. Current approaches consider the MNT reaction as a two-step processes. The improved DNS model can be used to calculate the primary cross sections. To systematically describe evaporation spectra for light and heavy compound nuclei over a large range of excitation energies, we can use GEMINI++ to address the continuous statistical evaporation of excited fragments. The improved DNS model+GEMINI++ is effective in describing the observed production cross-sections for a wide range of transfer nucleons and projectile-target combinations around the average values. To test our calculated abilities on the production cross sections using the DNS model +GEMINI++ [48, 49], our investigations are performed with one set of parameters and with the same assumptions as our previous study [34]. The first objective of this paper is to test the effectiveness of the improved DNS model+GEMINI++ in describing the cross section of final products of the reaction systems
$ ^{40,48} $ Ca+$ ^{124} $ Sn and$ ^{64} $ Ni+$ ^{130} $ Te. The second aim of this paper is the feasibility of using MNT reactions to produce new proton-rich nuclei of$ 40 \leq Z \leq 60 $ . Therefore, the$ ^{64} $ Ni+$ ^{106,110,116,120} $ Sn and$ ^{64} $ Ni+$ ^{110,120} $ Te,$ ^{48} $ Ca+$ ^{110,120} $ Te reactions are selected for the prediction of transfer cross sections for proton-rich nuclei with$ 40 \leq Z \leq 60 $ . In addition, this paper also aims to verify the possibility that MNT reactions, in contrast to fusion evaporation and fragmentation reactions, produce extremely proton-rich or even rare isotopes in the$ 40 \leq Z \leq 60 $ region by selecting a radioactive nuclear beam as a projectile to collide with a target nuclei. Therefore, we select the radioactive nuclear beam$ ^{36} $ Ca as the projectile for the transfer reaction, study its product cross section, and compare it with other reactions. -
Theoretically, the nucleon rearrangement process between a projectile and target nuclei can be divided into two stages. The production cross section of primary products in the MNT reaction based on the improved DNS model [34, 35] is expressed as a sum over all partial waves J:
$ \begin{aligned}[b] \sigma_{Z_{1},N_{1}}^{pri}(E_{\rm c.m.})=&\frac{\pi\hbar^{2}}{2\mu E_{\rm c.m.}}\sum\limits_{J}(2J+1)T(E_{\rm c.m.},J) \\ & \sum\limits_{\beta_{1}}\sum\limits_{\beta_{2}}P(Z_{1},N_{1},\beta_{1},\beta_{2},J,\tau_{\rm int}), \end{aligned} $

(1) where
$E_{\rm c.m.}$ is the incident energy in the center-of-mass frame. The range of angular momentum J is from 0 to the grazing angular momentum. The grazing angular momentum$ J_{gr} $ can be expressed as$ \begin{array}{*{20}{l}} J_{gr}=0.22R_{\rm cont}[A_{\rm red}(E_{\rm c.m.}-V(R_{\rm cont}))]^{1/2}, \end{array} $

(2) where
$V(R_{\rm cont})$ denotes the Coulomb barrier at the interaction radius$R_{\rm cont}$ , and$A_{\rm red}$ is the reduced mass. The penetration coefficient$T(E_{\rm c.m.},J)$ in Eq. (1) is estimated to be 1 when the incident energy is higher than the Coulomb barrier.To consider the influence of the strong Coulomb and nuclear interactions on multinucleon rearrangement processes between the projectile and target, four-variable master equations (MEs) have been developed such that the deformations and nucleon transfer are considered to be consistently governed by MEs in the potential energy surface of the system. The MNT processes can be described as a diffusion process by numerically solving a set of four-variable MEs. The evolution of the probability distribution function
$ P(Z_{1},N_{1},\beta_{1},\beta_{2},t) $ in Eq. (1) can be expressed as [34, 35]$ \begin{aligned}[b] \frac{{\rm d}P(Z_{1},N_{1},\beta_{1},\beta_{2},t)}{{\rm d}t} =&\sum\limits_{Z'_{1}}W_{Z_{1},N_{1},\beta_{1},\beta_{2};Z'_{1},N_{1},\beta_{1},\beta_{2}}(t)\\&\times [d_{Z_{1},N_{1},\beta_{1},\beta_{2}}P(Z'_{1},N_{1},\beta_{1},\beta_{2},t)\\&-d_{Z'_{1},N_{1},\beta_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{1},\beta_{2},t)] \\& +\sum\limits_{N'_{1}}W_{Z_{1},N_{1},\beta_{1},\beta_{2};Z_{1},N'_{1},\beta_{1},\beta_{2}}(t)\\&\times [d_{Z_{1},N_{1},\beta_{1},\beta_{2}}P(Z_{1},N'_{1},\beta_{1},\beta_{2},t)\\&-d_{Z_{1},N'_{1},\beta_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{1},\beta_{2},t)] \\& +\sum\limits_{\beta'_{1}}W_{N_{1},Z_{1},\beta_{1},\beta_{2};N_{1},Z_{1},\beta'_{1},\beta_{2}}(t)\\&\times [d_{Z_{1},N_{1},\beta_{1},\beta_{2}}P(Z_{1},N_{1},\beta'_{1},\beta_{2},t) \\&-d_{Z_{1},N_{1},\beta'_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{1},\beta_{2},t)] \\& +\sum\limits_{\beta'_{2}}W_{N_{1},Z_{1},\beta_{1},\beta_{2};N_{1},Z_{1},\beta_{1},\beta'_{2}}(t)\\&\times [d_{Z_{1},N_{1},\beta_{1},\beta_{2}}P(Z_{1},N_{1},\beta_{1},\beta'_{2},t)\\&-d_{Z_{1},N_{1},\beta_{1},\beta'_{2}}P(Z_{1},N_{1},\beta_{1},\beta_{2},t)] \end{aligned} $

(3) where
$ \beta_{1} $ and$ \beta_{2} $ denote quadrupole deformations of the projectile-like fragments (PLFs) and target-like fragments (TLFs), respectively. They are considered as two discrete variables [27, 28].$ W_{Z_{1},N_{1},\beta_{1},\beta_{2};Z'_{1},N_{1},\beta_{1},\beta_{2}} $ is the mean transition probability from channel ($ Z'_{1},N_{1},\beta_{1},\beta_{2} $ ) to ($ Z_{1},N_{1},\beta_{1},\beta_{2} $ ).$ d_{N_{1},Z_{1},\beta_{1},\beta_{2}} $ denotes microscopic dimensions corresponding to the macroscopic state ($ N_{1},Z_{1},\beta_{1},\beta_{2} $ ). See Refs. [27–29] for more details.The mean transition probabilities
$ W_{Z_{1},N_{1},\beta_{1},\beta_{2};Z'_{1},N_{1},\beta_{1},\beta_{2}} $ and microscopic dimensions$ d_{N_{1},Z_{1},\beta_{1},\beta_{2}} $ in Eq. (3) are related to the local excitation energy,$ \varepsilon^{*} $ , which is defined as [34]$ \begin{aligned}[b] \varepsilon^{*}(J)=&E_{x}(J,t)-[U(N_{1},Z_{1},N_{2},Z_{2},R_{\rm cont},\beta_{1},\beta_{2},J)\\&- U(N_{P},Z_{P},N_{T},Z_{T},R_{\rm cont},\beta_{10},\beta_{20},J)], \end{aligned} $

(4) where the first term indicates that the dissipation energy
$ E_{x}(J,t) $ is converted from the relative kinetic energy loss. The second term in Eq. (4) is the driving potential energy of the system for the nucleon transfer of the DNS, which is$ \begin{aligned}[b]& U(N_{1},Z_{1},N_{2},Z_{2},R_{\rm cont},\beta_{1},\beta_{2},J) \\ =& B(N_{1},Z_{1},\beta_{1})+B(N_{2},Z_{2},\beta_{2}) \\ &+V_{CN}(N_{1},Z_{1},N_{2},Z_{2},R_{\rm cont},\beta_{1},\beta_{2}) \\ & +V_{\rm rot}(N_{1},Z_{1},N_{2},Z_{2},R_{\rm cont},\beta_{1},\beta_{2},J), \end{aligned} $

(5) where
$ N=N_{1}+N_{2} $ ,$ Z=Z_{1}+Z_{2} $ , and$ \beta_{1} $ and$ \beta_{2} $ represent quadrupole deformations of the two fragments, respectively. The nucleon transfer process can be assumed to be$R_{\rm cont}=R_{1}(1+\beta_{1}Y_{20}(\theta_{1}))+R_{2}(1+ \beta_{2}Y_{20}(\theta_{2}))$ +0.5 fm, where$ R_{i} = 1.16A^{1/3}_{i} $ . The deformation dependent binding energies$ B(N_{1},Z_{1},\beta_{1}) $ and$ B(N_{2},Z_{2}, \beta_{2}) $ are calculated using the macroscopic-microscopic model [50]. The nucleus-nucleus interaction potential energy$V_{CN}(N_{1},Z_{1},N_{2},Z_{2}, R_{\rm cont},\beta_{1},\beta_{2})$ between two interacting nuclei of the DNS configuration is the sum of the nuclear interaction potential$ V_{N} $ obtained from the folding integral of a zero-range nucleon-nucleon interaction [51, 52] and Coulomb interaction potential$ V_{C} $ calculated using Wong's formula [53]. The rotational energy$V_{\rm rot} = \hbar^{2}J(J + 1)/I_{\rm tot}$ , where the moment of inertia$I_{\rm tot}$ is approximated by its rigid-body value.The deformation of the PLFs and TLFs at the exit channel is no longer the ground state when the primary products are separated, and the total excitation energy is considered:
$ \begin{array}{*{20}{l}} E_{\rm tot}=E_{\rm c.m.}-TKE+Q_{gg}, \end{array} $

(6) where
$ Q_{gg} $ denotes the reaction$ Q_{gg} $ value that represents the energy released during the process of the nuclear reaction. We assume that the sharing of the total excitation energy between the PLFs and TLFs are proportional to their masses :$ E^{*}_{Z_{1},N_{1}}=E_{\rm tot}\times \frac{A_{1}}{(A_{1}+A_{2})}, $

(7) where
$ E^{*}_{Z_{1},N_{1}} $ is excitation energy, and$ A_{1} $ and$ A_{2} $ are the corresponding mass numbers.The code GEMINI++ is used to study the sequential statistical evaporation of excited fragments. Owing to the statistical nature of GEMINI++, the deexcitation process should be simulated many times [34]. The details of GEMINI++ are given in Refs. [48, 49], the resulting cross sections of the final fragment can be described as follows:
$ \begin{aligned}[b] \sigma_{\rm fin}(Z_{1},N_{1})=&{\sum\limits_{Z_{1}^{'},N_{1}^{'}J^{'}}}\sigma_{\rm pri}(Z_{1}^{'},N_{1}^{'},J^{'})\\&\times P(Z_{1},N_{1};Z_{1}^{'},N_{1}^{'},J^{'}), \end{aligned} $

(8) where
$ P(Z_{1},N_{1};Z_{1}^{'},N_{1}^{'},J^{'} $ ) represents the decay probability. -
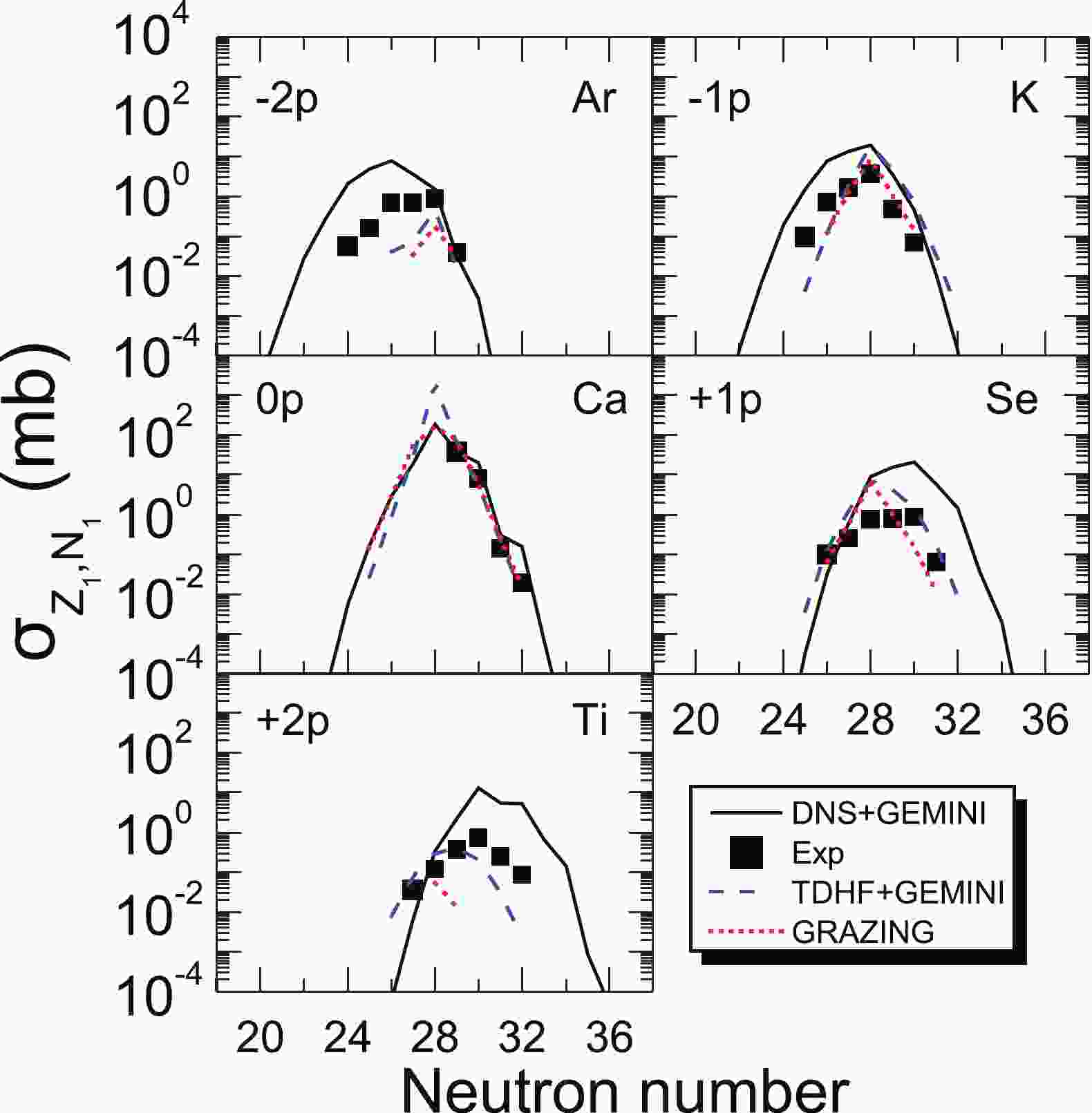
To test the effectiveness of the improved DNS model+GEMINI++ in describing the production cross sections for magic nuclei of Z=50, Fig. 1 shows production cross sections of the
$ ^{48} $ Ca+$ ^{124} $ Sn reaction at$E_{\rm c.m.}$ =125.44 MeV (1.16$V_{\rm Coul.}$ ); the measured production cross sections are obtained from Ref. [37] and are represented by solid squares. We observe that the production cross sections obtained using the improved DNS model+GEMINI++ match well with the experimental data for the$ 0p $ and$ \pm1p $ transfer channels. For$ \pm2p $ transfer channels, the distribution width, peak position, and transfer trend based on the DNS model overestimate the experimental results.
Figure 1. (color online) PLF distributions in the transfer reaction
$^{48}$ Ca+$^{124}$ Sn at$E_{\rm c.m.}$ =125.44 MeV. The measured cross sections are obtained from Ref. [37] and represented by solid squares. The blue dotted lines and the red short dotted lines represent the final transfer cross sections using the TDHF model+GEMINI++ [54] and GRAZING [37] model, respectively.The final production cross sections using the time-dependent Hartree-Fock (TDHF) model+GEMINI++ [54] and GRAZING [37] model are shown in Fig. 1. We can observe that the measured cross sections are reproduced reasonably for the
$ 0p $ and$ \pm1p $ transfer channels using the TDHF model+GEMINI++ [54]. The TDHF model+GEMINI++ adequately describes the experimental data of$ 0p $ ,$ \pm1p $ ,$ +2p $ channels in the distribution width, but underestimates the experimental data in the$ -2p $ channel. The GRAZING model underestimates both the distribution width and cross-sectional transmission trends in$ \pm2p $ channels. The TDHF approach has been combined with a statistical model to evaluate effects of secondary processes of excited reaction products. The current TDHF model combined with statistical models respectively offers quantitative predictions for few-nucleon transfers; it underestimates production cross sections for MNT channels, which prevents systematic investigations for various projectile-target combinations to MNT channels for production neutron-rich isotopes. This is related to the well known limitations of the TDHF approach in that it cannot describe the fluctuations of the collective dynamics.The calculated production cross sections of the
$ ^{40} $ Ca+$ ^{124} $ Sn reaction at$E_{\rm c.m.}$ =128.53 MeV (1.15$V_{\rm Coul.}$ ) as functions of the neutron number of the TLFs are shown in Fig. 2. Each plot is the isotope distribution for a particular proton stripping channel. The solid squares denote measured cross sections, and the black solid lines denote results of the DNS calculations. Comparing the experimental data with the production cross sections calculated using the improved DNS model+GEMINI++, the results show that the measured cross sections of isotopes$ ^{41-43} $ Ca,$ ^{39-41} $ K, and$ ^{35-39} $ Ar shown in the$ 0p $ ,$ -1p $ and$ -2p $ proton transfer channels are systematically underestimated. As the number of transferred protons increases, the production cross sections obtained using the improved DNS model in the –3p to –4p transfer channels reasonably describe the experimental results in terms of distribution width and overall transfer trend. For the$ -5p $ and$ -6p $ transfer channels, the distribution width, peak position, and transfer trend based on the improved DNS model+GEMINI++ overestimate the experimental results.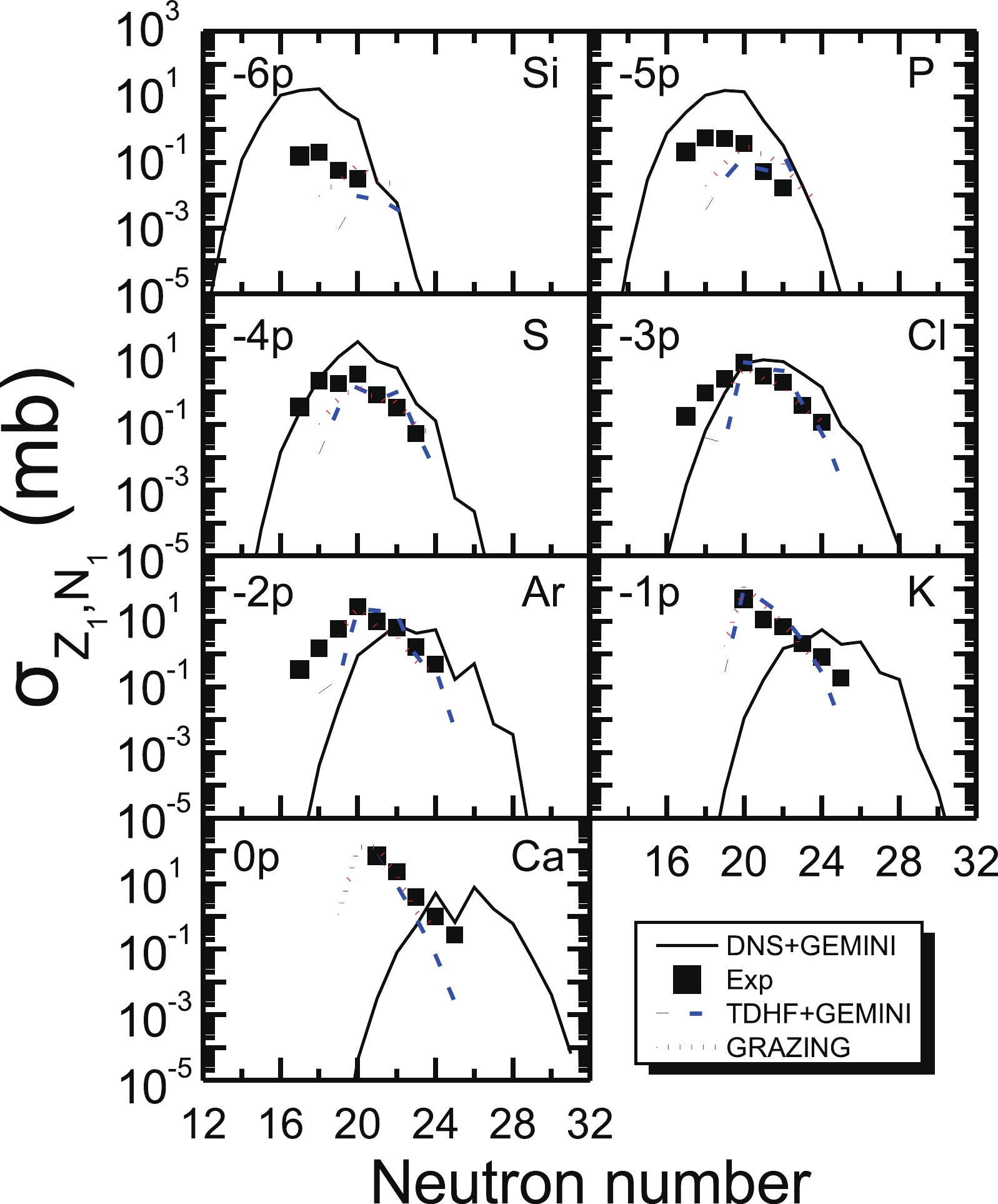
Figure 2. (color online) PLF distributions in the transfer reaction
$^{40}$ Ca+$^{124}$ Sn at$E_{\rm c.m.}$ =128.53 MeV. The measured cross sections are obtained from Ref. [37] and are represented by solid squares. The blue dotted lines and the red short dotted lines represent the final transfer cross sections using the TDHF model+GEMINI++ [54] and GRAZING [37] models, respectively.We can observe that the results obtained using the TDHF model agree well with the experimental results for
$ 0p $ ,$ -1p $ ,$ -2p $ ,$ -3p $ , and$ -4p $ proton transfer channels. The distribution width, peak position, and transfer trend based on the TDHF model+GEMINI++ [54] underestimate the experimental data.As shown in Fig. 1 and Fig. 2, the TDHF and GRAZING models are better than the DNS model at the distribution width, peak position, and transfer trend when the number of proton transfers is small. However, for larger p transfer channels, both models become progressively less effective in predicting the experimental cross sections and appear to underestimate the experimental data [36–38].
To investigate the production cross sections of the target nuclei in the vicinity of Z=50 based on the DNS model+GEMINI++, we depict the calculated production cross sections in the
$ ^{64} $ Ni+$ ^{130} $ Te reaction at the incident energy$E_{\rm c.m.}$ =184.27 MeV (1.15$V_{\rm Coul.}$ ) as functions of the neutron number of the TLFs in Fig. 3. The calculated and measured [55] data are represented by black solid lines and solid squares, respectively. By comparing the calculated cross sections based on the improved DNS model+GEMINI++ with measured cross sections, we observe that the calculated TLF distributions of proton pickup and stripping channels correctly describe the magnitude and maxima of the observed production cross sections for a wide range of transfers (from$ \Delta Z =-12 $ to$ \Delta Z =+5 $ ).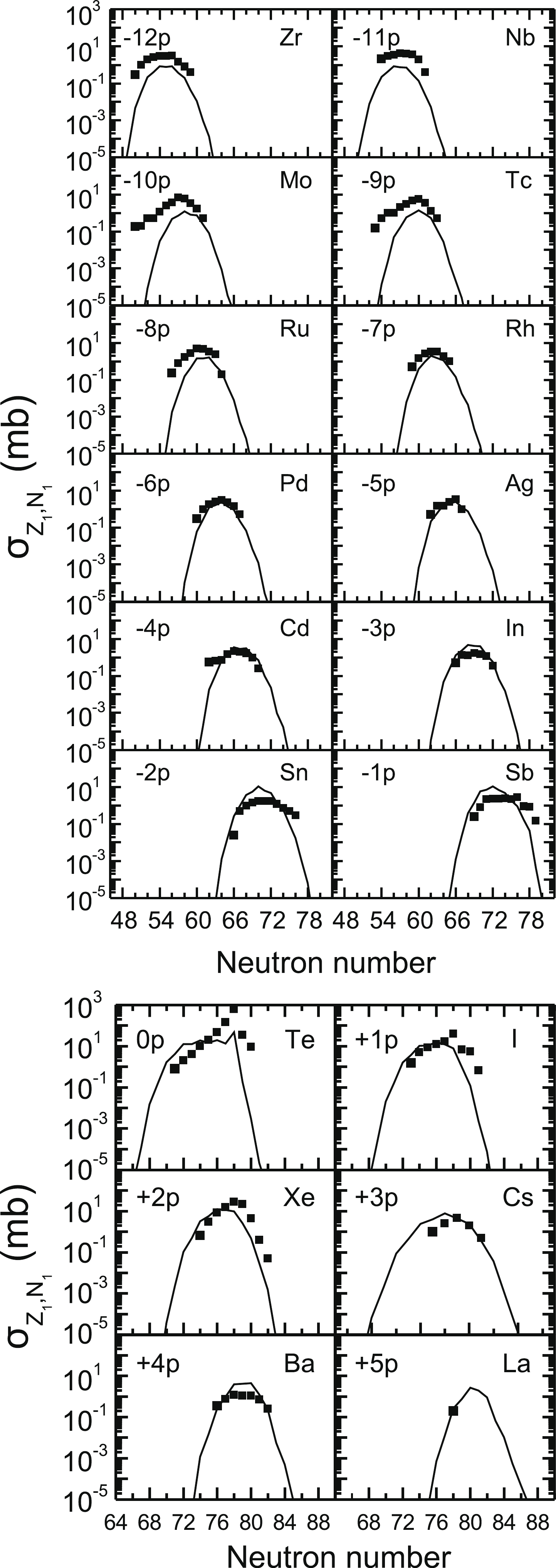
Figure 3. TLF distributions in the transfer reaction
$^{64}$ Ni+$^{130}$ Te at$E_{\rm c.m.}$ =184.27 MeV. The measured cross sections are obtained from Ref. [55] and represented by solid squares.The production yield as a function mass number is calculated based on the sum of different Z and N values with fixed mass number. The distribution of fragments mass yields is used to test the reliability of the theoretical models for MNT reactions. The mass distribution of the
$ ^{64} $ Ni+$ ^{130} $ Te reaction is shown in Fig. 4 and compared with available experimental data. As the figure shows, the mass distribution of this reaction is characterized by a bimodal structure. At the bimodal position, the calculated final yield is in good agreement with the experimental results. In the mass symmetric region, the calculated results underestimate the experimental results. This is primarily because, in addition to deep inelastic scattering and quasi-fission, fusion evaporation has an important role in the system$ ^{64} $ Ni+$ ^{130} $ Te (compound nucleus$ ^{194} $ Hg), whereas our theoretical model (DNS model) primarily considers the role of deep inelastic scattering and quasi-fission processes. However, for the$ ^{58,64} $ Ni+$ ^{208} $ Pb [39],$ ^{136} $ Xe+$ ^{208} $ Pb [29], and$ ^{136} $ Xe+$ ^{198} $ Pt [34] reactions, the calculated mass distributions of the final yields are reasonably consistent with experimental results; it is primarily a function of deep inelastic scattering and quasi-fission processes, with few or no fission components from the compound nucleus. Based on the cross section distribution of the above reactions, we can conclude that the improved DNS model is suitable for analyzing MNT reactions. Thus, we perform theoretical predictions about the selection of projectile-target combinations for the synthesis of proton-rich nuclei in the following text.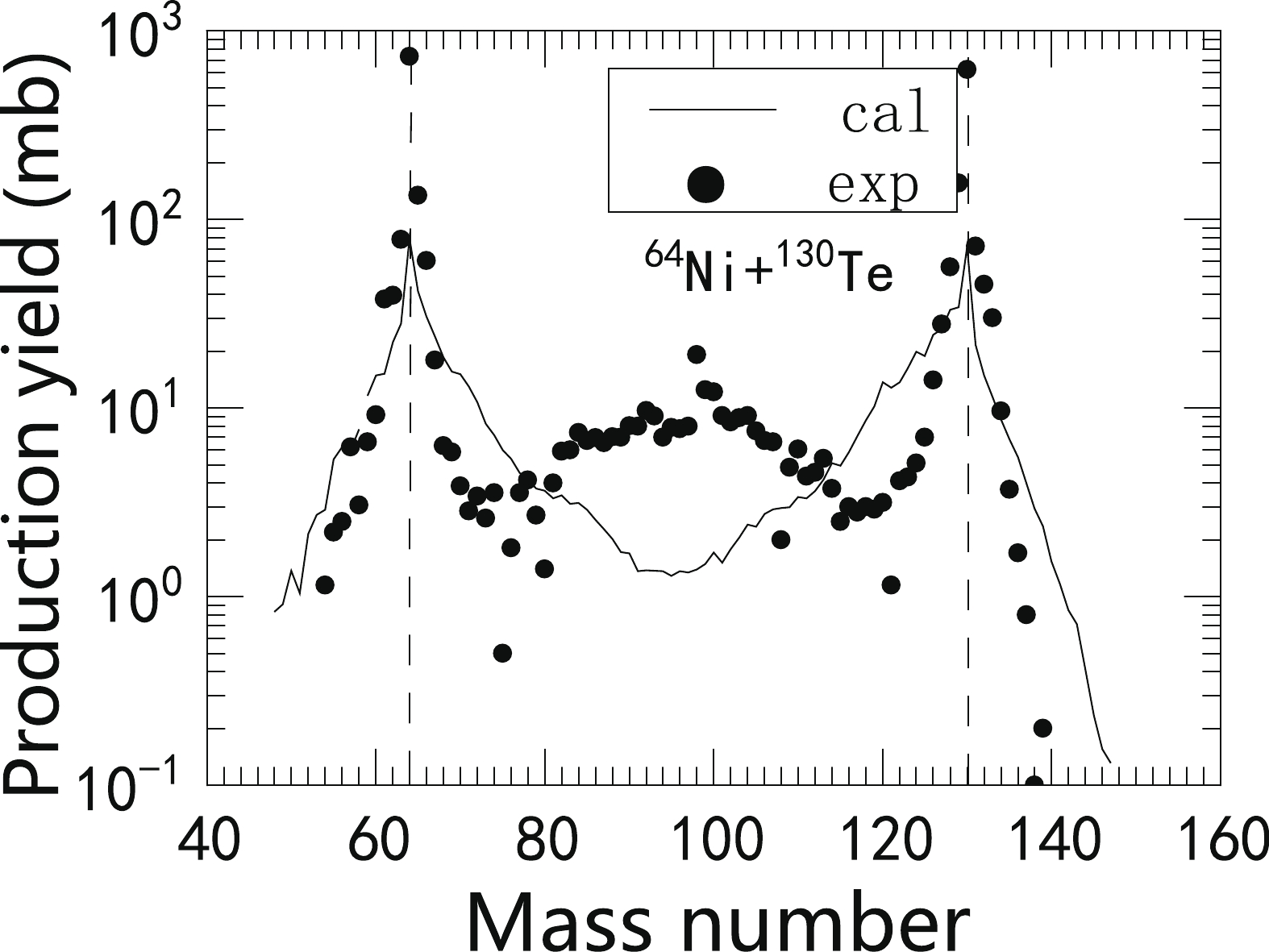
Figure 4. Mass distributions of final products in the
$^{64}$ Ni+$^{130}$ Te reaction with bombarding energy$E_{\rm c.m.}$ =184.27 MeV. The solid line represents the calculated results, and the dots represent the measured results obtained from Ref. [55].To predict the most suitable projectile-target combination among the probable candidates, we systematically analyze production cross sections of proton-rich isotopes with
$ 40 \leq Z \leq 60 $ with different$ ^{106,110,116,120} $ Sn targets. The aim of this choice is to analyze the influence of the target neutron number on production cross sections. The TLF distributions of the$ ^{64} $ Ni+$ ^{106} $ Sn reaction at$E_{\rm c.m.} = $ 168.31 MeV,$ ^{64} $ Ni+$ ^{110} $ Sn reaction at$E_{\rm c.m.}=$ 166.89 MeV,$ ^{64} $ Ni+$ ^{116} $ Sn reaction at$E_{\rm c.m.}=$ 164.86 MeV, and$ ^{64} $ Ni+$ ^{120} $ Sn reaction at$E_{\rm c.m.}=$ 163.55 MeV as functions of the neutron number are given in Figs. 5–6. The figures show that the$ ^{64} $ Ni+$ ^{106} $ Sn reaction is always more inclined to the proton-rich side than the$ ^{64} $ Ni+$ ^{110,116,120} $ Sn reactions, which indicates that the$ ^{64} $ Ni+$ ^{106} $ Sn reaction is more suitable for the synthesis of proton-rich nuclei. This is because the strongest driving force for proton and neutron transfer should begin from the injection point in the potential energy surface in the direction that minimizes the potential energy of the system. The probability distribution begins at the injection point; first, it is preferable to reach the valley, then along the valley, it flows both to the symmetrical direction and direction of the compound nuclear formation. We observe that the calculated results indicate large cross sections ($ \sigma_{1n}\geq $ 1 pb) for many transfer channels, but unknown isotopes of proton-rich nuclei with$ 40 \leq Z \leq 60 $ cannot be produced compared with the fusion-evaporation reactions and spallation or fragmentation reactions. We observe that the fusion-evaporation reactions and spallation or fragmentation reactions are still favorable to producing the new proton-rich isotopes with$ 40 \leq Z \leq 60 $ . This also provides the idea of selecting reaction mechanism for the experiment.
Figure 5. (color online) TLF distributions of the
$^{64}$ Ni+$^{106}$ Sn reaction at$E_{\rm c.m.}$ =168.31 MeV,$^{64}$ Ni+$^{110}$ Sn reaction at$E_{\rm c.m.}$ =166.89 MeV,$^{64}$ Ni+$^{116}$ Sn reaction at$E_{\rm c.m.}$ =164.86 MeV, and$^{64}$ Ni+$^{120}$ Sn reaction at$E_{\rm c.m.}$ =163.55 MeV in proton pickup channels.
Figure 6. (color online) Same as Fig. 5 but in proton stripping channels.
It is also of interest to analyze the production cross sections from different projectiles bombarding the same target through the MNT reaction. We also compare two reactions with the same target nuclei but different projectiles. Figs. 7–8 show the production cross sections of the protons number of TLFs in the
$ ^{48} $ Ca+$ ^{110} $ Te reaction at$E_{\rm c.m.}$ =121.61 MeV and$ ^{48} $ Ca+$ ^{120} $ Te reaction at$E_{\rm c.m.}$ =118.99 MeV,$ ^{64} $ Ni+$ ^{110} $ Te reaction at$E_{\rm c.m.}$ =175.08 MeV, and$ ^{64} $ Ni+$ ^{120} $ Te reaction at$E_{\rm c.m.}$ =171.62 MeV as a function of the neutrons number of TLFs. In Figs. 7–8, we observe that the distribution from the$ ^{48} $ Ca ($ N/Z=1.40 $ ) induced reaction appears to extend out to larger neutron numbers than the$ ^{64} $ Ni ($ N/Z=1.28 $ ) induced reaction. The more neutron-rich$ ^{48} $ Ca projectile provides a TLF distribution that peaks at a larger neutron number compared with the less neutron-rich$ ^{64} $ Ni projectile. We observe that the mass distribution width increases with increasing projectile mass.
Figure 7. (color online) TLF distributions of the
$^{48}$ Ca+$^{110}$ Te reaction at$E_{\rm c.m.}$ =121.61 MeV,$^{48}$ Ca+$^{120}$ Te reaction at$E_{\rm c.m.}$ =118.99 MeV,$^{64}$ Ni+$^{110}$ Te reaction at$E_{\rm c.m.}$ =175.08 MeV, and$^{64}$ Ni+$^{120}$ Te reaction at$E_{\rm c.m.}$ =171.62 MeV.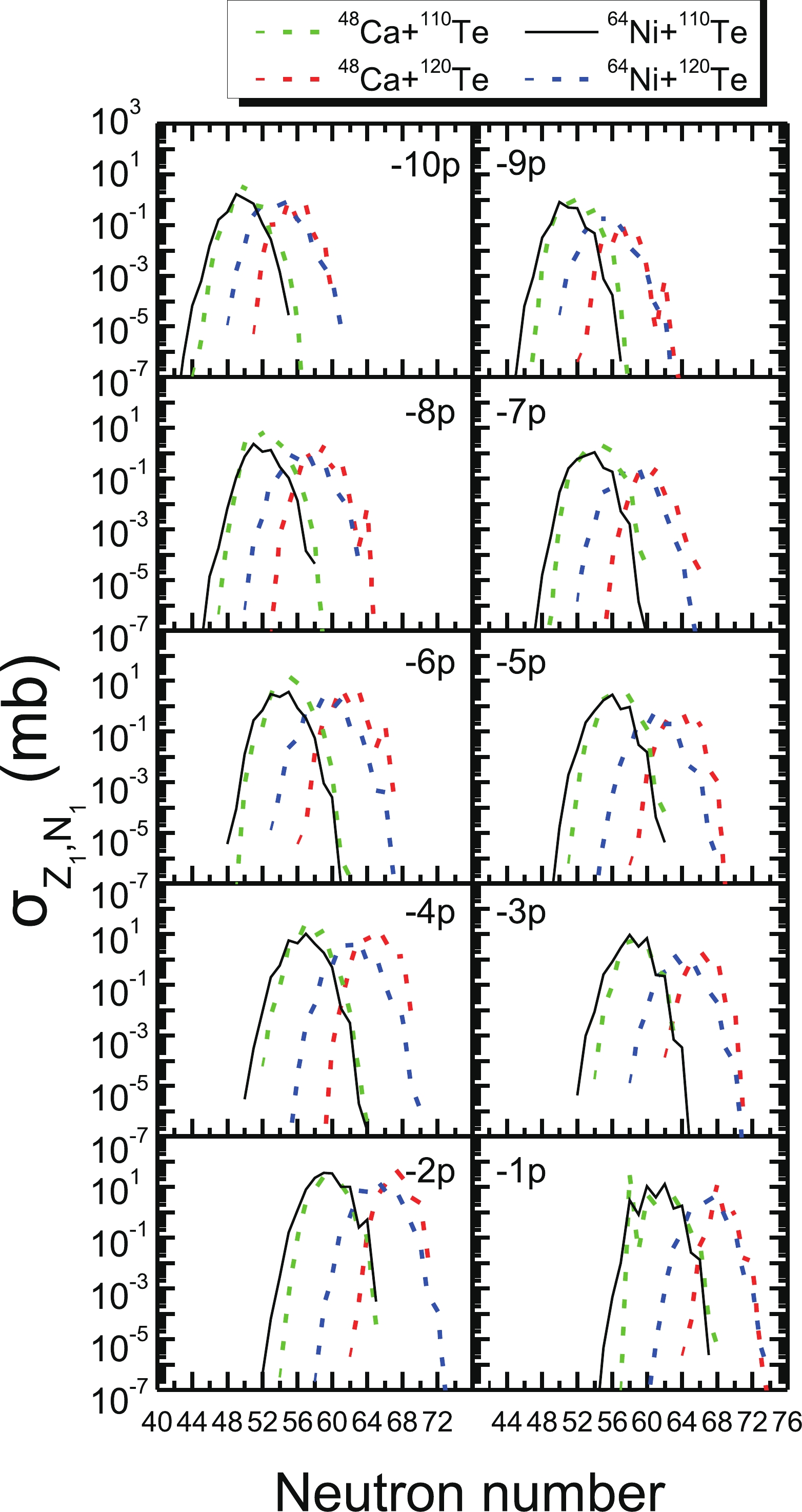
Figure 8. (color online) Same as Fig. 7 but in proton stripping channels.
In addition to the above reactions to analyze the influence of the neutron number of the target on the production cross sections, we also select the radioactive beam projectile
$ ^{36} $ Ca and the relatively neutron-deficient stable beam projectile$ ^{58} $ Ni to bombard the neutron-deficient targets$ ^{110} $ Te and$ ^{110} $ Sn to analyze the influence of the neutron number of the projectile on the production cross section. The TLF distributions of the$ ^{36} $ Ca+$ ^{110} $ Te reaction at$E_{\rm c.m.}$ =138.74 MeV,$ ^{36} $ Ca+$ ^{110} $ Sn reaction at$E_{\rm c.m.}$ =133.2 MeV,$ ^{58} $ Ni+$ ^{110} $ Sn reaction at$E_{\rm c.m.}$ =178.45 MeV, and$ ^{58} $ Ni+$ ^{110} $ Te reaction at$E_{\rm c.m.}$ =185.87 MeV are shown in Fig. 9. As the figure shows, the$ ^{36} $ Ca+$ ^{110} $ Te reaction tends to be on the proton-rich side. The isospin effect mentioned above also has an impact on these reactions. In addition, it is worth noting that although$ ^{36} $ Ca is a radioactive nuclear beam, its beam intensity can reach$ 10^{9} $ orders of magnitude, which is not a low beam intensity and does not cause the production cross sections of this reaction to be exceedingly low. Therefore, the result of this reaction is effective and we believe that the$ ^{36} $ Ca+$ ^{110} $ Te reaction is more suitable for the synthesis of proton-rich nuclei.
Figure 9. (color online) TLF distributions of the
$^{36}$ Ca+$^{110}$ Te reaction at$E_{\rm c.m.}$ =138.74 MeV,$^{36}$ Ca+$^{110}$ Sn reaction at$E_{\rm c.m.}$ =133.2 MeV,$^{58}$ Ni+$^{110}$ Sn reaction at$E_{\rm c.m.}$ =178.45 MeV, and$^{58}$ Ni+$^{110}$ Te reaction at$E_{\rm c.m.}$ =185.87 MeV.In previous studies, we observed that the generation of proton-rich isotopes in the region near Z=50 was primarily achieved by spallation or fragmentation and fusion-evaporation, and rarely by MNT reaction. Therefore, we compare the results of these reactions. Fig. 10 shows the fusion-evaporation cross sections [56–65], spallation or fragmentation cross sections [66–68], and the experimental data [55] and measured MNT cross sections for some nuclear isotopes with
$ 40 \leq Z \leq 60 $ . The theoretical data of MNT reaction are obtained from the$ ^{36} $ Ca+$ ^{110} $ Te reaction in Fig. 9. We plot the maximum evaporation residual section in each fusion-evaporation reaction in Fig. 10. As the figure shows, the evaporation residual cross sections produced by the fusion-evaporation reaction are 1–3 orders of magnitude higher than those of the other two reactions. Clearly, fusion-evaporation is suitable for the synthesis of proton-rich nuclei. By comparing the experimental production cross sections of the fragmentation reaction with that of the MNT reaction, we observe that although the order of magnitude of cross sections is not significantly different, the former is also more inclined to the proton-rich side. Fusion-evaporation reactions and spallation or fragmentation reactions are dominant in the field of producing relatively protone-rich nuclei in the$ 40 \leq Z \leq 60 $ region. However, the theoretical MNT reaction data we calculated in the figure, which uses a radioactive nuclear beam$ ^{36} $ Ca as a projectile, is significantly more skewed towards the extreme proton-rich side of the cross section than the other reaction data. The results shown that in the$ 40 \leq Z \leq 60 $ region, fusion-evaporation and fragmentation reactions have good results in the relatively proton-rich region, but in the extreme proton-deficient region, the MNT reaction is still promising for synthesizing proton-rich nuclei.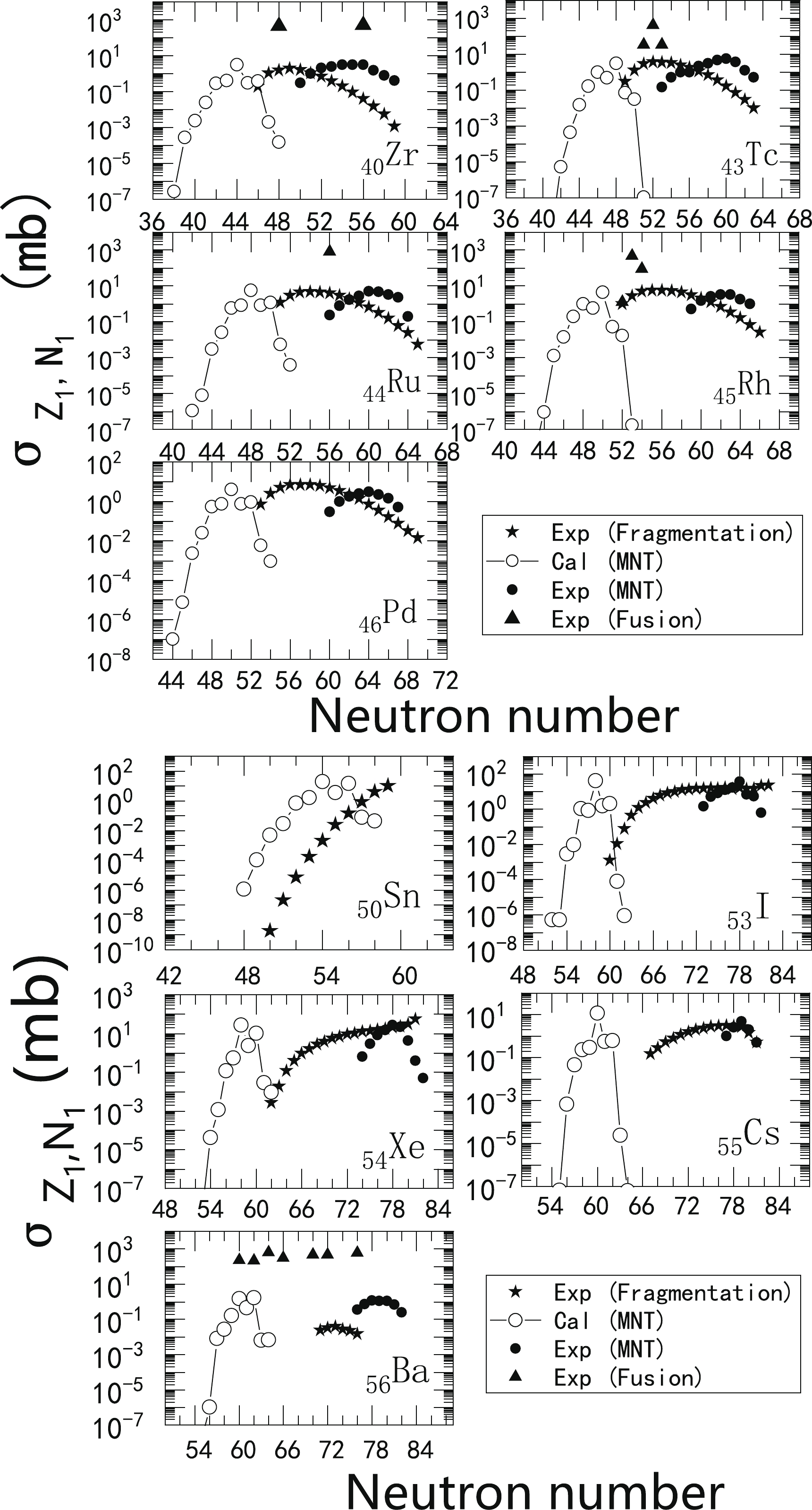
Figure 10. Cross sections of fusion-evaporation reactions (solid triangles), spallation or fragmentation reactions (solid pentacles), and MNT reactions of products in the Z=50–60 region (experimental and measured data).The measured data (open circles) of MNT reactions are connected by lines and experimental data are presented by solid circles.
-
In summary, the evolution of a DNS system is considered a diffusion process by solving a set of microscopically derived master equations in the potential energy surface coupled to the dissipation of relative kinetic energy and angular momentum. The reactions of
$ ^{40,48} $ Ca+$ ^{124} $ Sn and$ ^{64} $ Ni+$ ^{130} $ Te for the magic nuclei of Z = 50 and nuclei near the magic number as the target have been studied and compared with experimental data. We conclude that the DNS model is suitable for the analysis of MNT reactions.The cross sections of
$ ^{40,48} $ Ca+$ ^{124} $ Sn reactions obtained using the DNS , TDHF, and GRAZING models are compared with experimental cross sections, and we observe that all three models have some applicability. The advantage of the prediction using the DNS model is reflected when the number of transferred nuclei is large, while the other two models are more accurate for transferring small amounts of nucleons.In this paper, the selection of materials for the synthesis of proton-rich nuclei is predicted theoretically from the aspects of projectiles and target nuclei. The results show that fusion-evaporation and fragmentation reactions have good results in the relatively proton-rich region, but in the extreme proton-deficient region, the MNT reaction is still promising for synthesizing proton-rich nuclei in the
$ 40 \leq Z \leq 60 $ region.
Possibilities of synthesizing new proton-rich nuclei with 40 ≤ Z ≤ 60 using multinucleon transfer reactions
- Received Date: 2022-03-09
- Available Online: 2022-09-15
Abstract: Multinucleon transfer reactions near the Coulomb barrier are investigated based on the improved dinuclear system (DNS) model, and the deexcitation process of primary fragments are described using the statistical model GEMINI++. The production cross sections of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: