-
Over the last several decades, abundant astronomical evidence for black holes (BH) has accumulated from various sources. The observations of gravitational waves emitted from BH mergers by the Laser-Interferometer Gravitational Wave-Observatory (LIGO) are the first evidence of the existence of BHs from astronomical observations [1]. The Event Horizon Telescope (EHT) reported an image of the supermassive BH in M87
$ ^{*} $ , offering direct evidence of BH existence in our universe [2–7]. The main feature of this image is that the BH event horizon is surrounded by a dark area known as a BH shadow with a bright ring-shaped lump of radiation surrounding the BH shadow. Based on the strong gravitational lensing, the formation mechanism of the BH shadow is as follows: the specific photons around a BH collapse inward to produce the shadow, indicating the shadow can reflect the information of the jets and matter dynamics around the compact objects [8]. The shadow can limit the mass, spin, charge, and other physical parameters of the BH, providing abundant sources of data information for new gravity theories [9–12].The most striking feature of a BH - namely, the event horizon - is only indirectly inferred. The BH shadow is an observable quantity that may replace the event horizon when displaying some physical properties of BHs. The BH as a thermodynamic system is similar to classical thermodynamic systems. For BHs in AdS spacetime, charged AdS BHs are almost equivalent to the van der Waals (vdW) liquid-gas system [13–18]. A BH is not only regarded as a thermodynamic system but also a strong gravitational one. Hence, it is necessary to establish the connection between its thermodynamics and dynamics. Wei
$ et\; al. $ found that the unstable circular orbital motion can connect the BH phase transitions by establishing the relationship between the null geodesics and thermodynamic phase transition for the charged AdS BH [19]. In Refs. [20, 21], the authors deemed that the radius of a test particle's time-like or light-like circular orbital motion can be used as a characterized quantity of BH phase transition information.Based on the above research, a fundamental connection between the BH thermodynamics and shadow is proposed. Zhang
$ et\; al. $ found that the shadow radius can reflect the BH phase structure [22]. By investigating the relations between the shadow and critical behavior of a charged AdS BH, Belhaj$ et\; al. $ obtained a critical exponent that perfectly matched the vdW system [23]. Cai$ et\; al. $ studied the relationship between the shadow radius and microstructure of a charged AdS BH and found that the shadow can provide the dynamic characteristics of BHs [24]. By constructing a connection between the shadow and Ruppeiner geometry, Wang$ et\; al. $ believed that the BH shadow can provide information on the small/large phase transition of a charged AdS BH and found that the normalized curvature scalar at the critical point has a constant value of$ -3/2 $ [25].Nevertheless, the above connections between the BH shadow and thermodynamics are only for singular spacetime. Penrose and Hawking's famous work showed that the existence of singularity is inevitable [26]. To avoid singularity, Bardeen obtained the first regular BH solution in 1968 [27]. Ayón-Beato and García noted the physical source of a regular BH to be nonlinear electrodynamics [28]. We discussed the thermodynamic properties of a regular AdS BH and found their different features from singular AdS BHs [29, 30]. Meanwhile, the observation feature of the shadows and rings of regular BHs are being investigated [31, 32]. Based on these results, it is natural to ask whether the dependence of the BH shadow and thermodynamics may be structured in regular spacetime and how the singularity affects this relation. This paper focuses on this issue.
Taking the Bardeen-AdS BH as an example, we attempt to establish the relationship between the BH shadow and thermodynamic phase structure. The remainder of this paper is organized as follows: In Sec. II, we calculate the shadow radius of the Bardeen-AdS BH and discuss the relationship between the shadow radius and event horizon radius. In Sec. III, we apply this relation to analyze the phase transition on the
$ T-r_{\rm{s}} $ plane. In Sec. IV, we present the thermal profile of the Bardeen-AdS BH under the shadow context. We present our conclusions and discussions in Sec. V. In this paper, we use the units$G_{\rm{N}}=\hbar= \kappa_{\rm{b}}= c=1$ . -
The static spherically symmetric metric of the BH is given by [28]
$ \begin{equation} {\rm{d}}s^{2}=-f(r){\rm{d}}t^{2}+\frac{1}{u(r)}{\rm{d}}r^{2}+r^{2}{\rm{d}}\theta^{2}+r^{2}\sin^{2}\theta {\rm{d}}\phi^{2}, \end{equation} $

(1) where
$ f(r) $ and$ u(r) $ are the function of the radius parameter r. The photon motion around a BH satisfies the Euler-Lagrangian equation$ \begin{equation} \frac{{\rm{d}}}{{\rm{d}}\lambda}\Bigg(\frac{\partial \mathcal{L}}{\partial \dot{x}^{\rm{\mu}}}\Bigg)=\frac{\partial \mathcal{L}}{\partial x^{\rm{\mu}}}, \end{equation} $

(2) in which λ is the affine parameter, and
$ \dot{x}^{\rm{\mu}} $ is the photon four-velocity.$ \mathcal{L} $ is the Lagrangian density, which is expressed as$ \begin{equation} \mathcal{L}=-\frac{1}{2}g_{\mu \nu}\frac{{\rm{d}} x^{\mu}}{{\rm{d}} \lambda}\frac{{\rm{d}} x^{\nu}}{{\rm{d}} \lambda}=\frac{1}{2}\Big(f(r)\dot{t}^{2}-\frac{\dot{r}^{2}}{u(r)}-r^{2}(\dot{\theta}^{2}+\sin^{2}\theta \dot{\phi}^{2})\Big). \end{equation} $

(3) In this paper, we consider the photons to move on the equatorial plane (
$ \theta=\pi/2 $ ); therefore, the metric does not explicitly depend on the time t and azimuthal angle ϕ. The corresponding conserved constants are written as$ \begin{equation} E=-g_{\rm{t \rm t}}\frac{{\rm{d}} t}{{\rm{d}} \lambda}=f(r)\frac{{\rm{d}} t}{{\rm{d}} \lambda},\; \; \; \;\; L=g_{\rm{\phi \rm \phi}}\frac{{\rm{d}} \phi}{{\rm{d}} \lambda}=r^{2} \frac{{\rm{d}} \phi}{{\rm{d}} \lambda}, \end{equation} $

(4) where E and L represent the energy and angular momentum of the photons. Based on the null geodesic
$ g_{\rm{\mu \nu}}\dot{x}^{\rm{\mu}}\dot{x}^{\rm{\nu}}=0 $ , the motion equation of photons is obtained.$ \begin{eqnarray} &&\frac{{\rm{d}} t}{{\rm{d}} \lambda}= \frac{E}{f(r)}, \end{eqnarray} $

(5) $ \begin{eqnarray} &&\frac{{\rm{d}}\phi}{{\rm{d}} \lambda}= \frac{L}{r^{2}}, \end{eqnarray} $

(6) $ \begin{eqnarray} &&\frac{{\rm{d}} r}{{\rm{d}} \lambda}= \pm \frac{\sqrt{u(r)E^{2}r^{4}-u(r)L^{2}r^{2}f(r)}}{r^{2}\sqrt{f(r)}}, \end{eqnarray} $

(7) where the symbol "
$ \pm $ " indicates the counterclockwise ($ - $ ) and clockwise ($ + $ ) directions of photon motion. These three equations offer a complete description of photon dynamics around the BH, at which the effective potential can be written as$ \begin{equation} \Bigg(\frac{{\rm{d}} r}{{\rm{d}} \lambda}\Bigg)^{2} + \mathcal{V}_{\rm{eff}}(r) = 0, \end{equation} $

(8) where
$ \begin{equation} \mathcal{V}_{\rm{eff}}(r) = u(r)\Bigg(\frac{L^2}{r^2}-\frac{E^{2}}{f(r)}\Bigg). \end{equation} $

(9) The critical photon ring orbit satisfies the effective potential critical conditions
$ \begin{equation} \mathcal{V}_{\rm{eff}}(r)=0,\; \; \; \; \mathcal{V}'_{\rm{eff}}(r)=0,\; \; \; \; \mathcal{V}''_{\rm{eff}}(r)>0. \end{equation} $

(10) Substituting Eq. (9) into Eq. (10), we can obtain
${L}/{E}= {r_{pp}}/{\sqrt{f(r_{pp})}} $ , where$ r_{pp} $ is the radius of the photon ring. Based on Eqs. (6) and (7), we have$ \begin{equation} \frac{{\rm{d}} r}{{\rm{d}} \phi} = \Bigg(\frac{{\rm{d}} r}{{\rm{d}} \lambda}\Bigg) {\Bigg /} \Bigg(\frac{{\rm{d}}\phi}{{\rm{d}} \lambda}\Bigg) = \pm r \sqrt{\frac{r^{2}E^{2}u(r)}{L^{2}f(r)}-u(r)}. \end{equation} $

(11) Considering the turning point of the photon orbits satisfies
$ \dfrac{{\rm{d}} r}{{\rm{d}} \phi}{\big |}_{r=\chi}=0 $ , Eq. (11) can be rewritten as$ \begin{equation} \frac{{\rm{d}} r}{{\rm{d}} \phi} = \pm r \sqrt{\frac{r^{2}f(\chi)^{2}u(r)}{\chi^{2}f(r)}-u(r)}. \end{equation} $

(12) Following Refs. [22–25], a light ray sent from a static observer at position
$ r_{\rm{O}} $ transmits into the past with an angle β relative to the radial direction, that is,$ \begin{equation} \cot \beta = \frac{\sqrt{g_{\rm{rr}}}}{\sqrt{g_{\rm{\phi \phi}}}}{\Bigg |}_{r=r_{\rm{O}}} = \pm \sqrt{\frac{r_{\rm{O}}^{2}f(\chi)}{\chi^{2}f(r_{\rm{O}})}-1}. \end{equation} $

(13) Using elementary trigonometry, we can obtain
$ \begin{equation} \sin^{2} \beta = \frac{\chi^{2}f(r_{\rm{O}})}{r_{\rm{O}}^{2}f(\chi)}, \end{equation} $

(14) and the shadow radius of the BH observed by a static observer at
$ r_{\rm{O}} $ can be written as$ \begin{equation} r_{\rm{ss}}= r_{\rm{O}} \sin \beta = \chi\sqrt{\frac{f(r_{\rm{O}})}{f(\chi)}}{\Bigg |}_{\chi \rightarrow r_{pp}}. \end{equation} $

(15) For a regular Bardeen-AdS BH, the metric potential can be expressed by [33]
$ \begin{equation} f(r)= 1 + \frac{8\pi P r^{2}}{3}-\frac{2 M r^{2}}{(r^{2}+g^{2})^{3/2}}, \end{equation} $

(16) where M is the BH mass, and g is the BH magnetic charge. The radius of the event horizon
$ r_{\rm{h}} $ is the largest root of$ f(r_{\rm{h}})=0 $ . The BH mass reads as$ \begin{equation} M=\frac{(3+8 P \pi r_{\rm{h}}^{2})(r_{\rm{h}}^{2}+g^{2})^{{3}/{2}}}{6 r_{\rm{h}}^{2}}. \end{equation} $

(17) Based on the first law of BH thermodynamics, the Bardeen-AdS BH temperature is
$ \begin{equation} T = \frac{r_{\rm{h}}^{2}+8 \pi P r_{\rm{h}}^{4}-2g^{2}}{4 \pi r_{\rm{h}} (r_{\rm{h}}^{2}+g^{2})}. \end{equation} $

(18) The state equation can be expressed as
$ \begin{equation} P = \frac{T}{2 r_{\rm{\rm h}}}-\frac{1}{8 \pi {r_{\rm{h}}}^{3}}+\frac{g^2 T}{2r_{\rm{h}}^{3}}+\frac{g^{2}}{4 \pi {r_{\rm{h}}}^{4}}. \end{equation} $

(19) According to Eq. (10), the photon circular orbit radius of the Bardeen-AdS BH is
$ \begin{equation} r_{p} = \frac{1}{2}\sqrt{3 M + \sqrt{9 M^{2} - 10 g^{2}}}. \end{equation} $

(20) Utilizing Eq. (15), the radius of the Bardeen-AdS BH shadow can be written as
$ \begin{equation} r_{\rm{s}} = r_{\rm{p}} \sqrt{\frac{f(r_{\rm{O}})}{f(r_{p})}}, \end{equation} $

(21) Considering Eqs. (16), (20), and (21), we have a specific expression for the Bardeen-AdS BH shadow radius related to the horizon radius, that is, Eq. (22).
$ \begin{equation} r_{\rm{s}}=\frac{1}{2}\sqrt{\frac{3 f(r_{\rm{O}}) A^{2}B}{15(r_{\rm{h}}^{2}+g^{2})^{{3}/{2}}(3+8 P \pi r_{\rm{h}}^{2})+3B+2 \pi P A^{2}B}}, \end{equation} $

(22) where
$\begin{aligned}[b]A \equiv & \frac{(r_{\rm{h}}^{2}+g^{2})^{{3}/{2}}(3+8 P \pi r_{\rm{h}}^{2})}{2r_{\rm{h}}^{2}}\\&+ \Bigg(\frac{(r_{\rm{h}}^{2}+g^{2})^{3} (3+8 \pi P r_{\rm{h}}^{2})^{2} }{4r_{\rm{h}}^{4}}-10g^{2}\Bigg)^{-1/2},\\ B \equiv & 6(r_{\rm{h}}^{2}+g^{2})^{3/2}(3+8 \pi P r_{\rm{h}}^{2})\\&+3r_{\rm{h}}^{2}\Bigg(\frac{(r_{\rm{h}}^{2}+g^{2})^{3} (3+8 \pi P r_{\rm{h}}^{2})^{2} }{4r_{\rm{h}}^{4}}-10g^{2}\Bigg)^{-1/2}.\end{aligned} $

Based on the constraint, a static observer at spatial infinity has
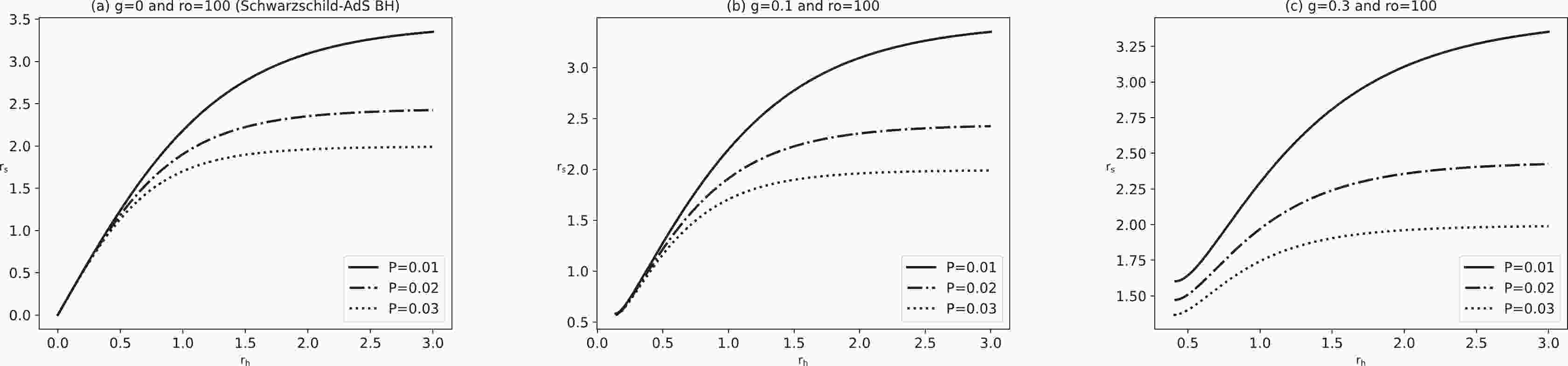
$ f(r_{\rm{O}})=1 $ for$ r_{\rm{O}}=100 $ [22], and when the magnetic charge$ g \rightarrow 0 $ , the Bardeen-AdS BH will degenerate into the Schwarzschild-AdS BH. Figure 1 shows the radius of the Bardeen-AdS BH shadow radius$ r_{\rm{s}} $ as a function of the event horizon radius$ r_{\rm{h}} $ under several representative values of magnetic charge.$ r_{\rm{s}} $ and$ r_{\rm{h}} $ display a positive correlation, indicating that the BH temperature can be rewritten as a function of shadow radius in regular spacetime. Furthermore, the trend of$ r_{\rm{s}} $ with an increase in$ r_{\rm{h}} $ gradually flattens. As the magnetic charge increases, the radius of the event horizon increases, and the corresponding shadow radius increases. For a magnetic charge equal to zero, the regular Bardeen-AdS BH is replaced by a singular Schwarzschild-AdS BH; hence, Eq. (22) can be used to describe the relationship between the shadow radius and event horizon radius of the Schwarzschild-AdS BH ($ g=0 $ ). The left panels of Fig. 1 report the shadow radius of the Schwarzschild-AdS BH as a function of the event horizon radius. It is observed that these two radii still exhibit positive correlation characteristics, whereas the slopes of the function curves are greater than those of the regular AdS BH. As a result, we believe that the relationship between the shadow and BH temperature can be constructed in regular spacetime.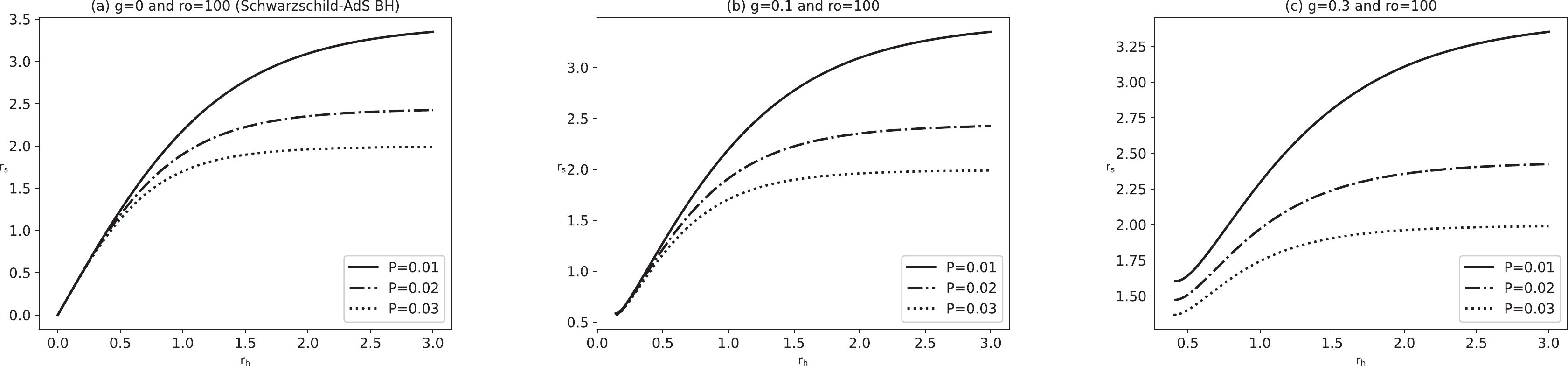
Figure 1. Variation in shadow radius
$ r_{\rm{s}} $ in terms of the event horizon radius$ r_{\rm{h}} $ for the Bardeen-AdS BH. Panel (a) magnetic charge$ g=0 $ and$ r_{\rm{O}}=100 $ (Schwarzschild-AdS BH). Panel (b) magnetic charge$ g=0.1 $ and$ r_{\rm{O}}=100 $ . Panel (c) magnetic charge$ g=0.3 $ and$ r_{\rm{O}}=100 $ . The solid, segment point, and dotted lines correspond to$ P=0.001,\; 0.002,\;0.003 $ , respectively. -
In this section, we investigate the phase transition of the Bardeen-AdS BH from the shadow perspective. Based on the state Eq. (19) and critical condition
$ ({\partial P}/{\partial r_{\rm{h}}})= 0=({{\partial}^{2}P}/{\partial r_{\rm{h}}^{2}}) $ , the critical thermodynamic quantities of the Bardeen-AdS BH are obtained.$ \begin{eqnarray} &&P_{\rm{c}}=\frac{219-13\sqrt{273}}{1152 \pi g^{2}} \simeq {0.00116}{g^{-2}}, \end{eqnarray} $

(23) $ \begin{eqnarray} &&r_{\rm{c}}=\frac{\sqrt{15g^{2}+\sqrt{273}g^{2}}}{\sqrt{2}} \simeq 3.97006g, \end{eqnarray} $

(24) $ \begin{eqnarray} &&T_{\rm{c}}=\frac{\sqrt{2(15+\sqrt{273})}}{(51 \pi + 3\sqrt{273}\pi)g} \simeq {0.02513}{g^{-1}}. \end{eqnarray} $

(25) Based on Eqs. (22)–(24), the critical shadow radius of the Bardeen-AdS BH is
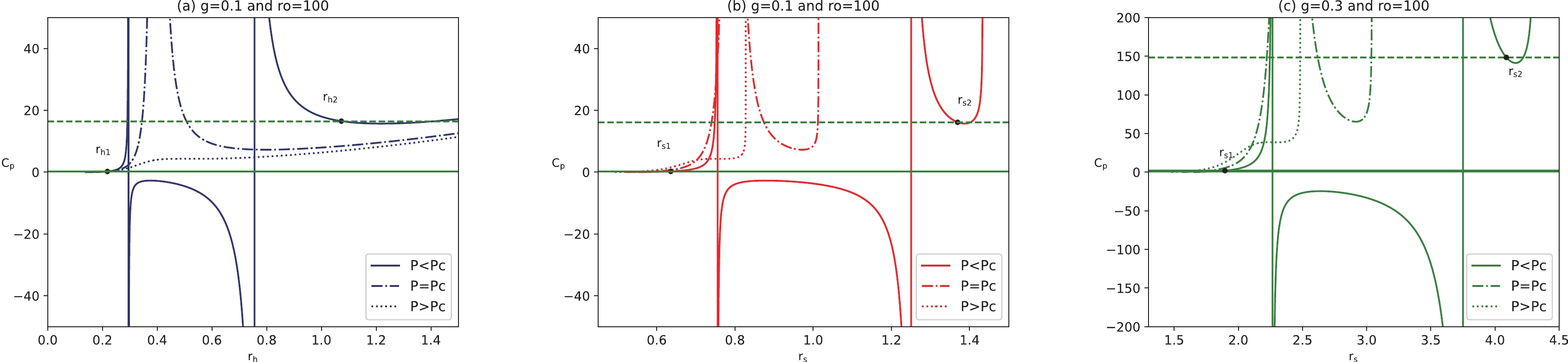
$ r_{\rm{sc}} \simeq 7.91886g $ . It is shown that the critical shadow radius is approximately twice as large as the standard critical radius. Considering the temperature expression in Eq. (18), the BH temperature as a function of$ r_{\rm{h}} $ for a fixed value of magnetic charge is shown in the left panels of Fig. 2. We can see that the function curves exhibit different characteristics for different pressures. Above the critical isobar ($ P>P_{\rm{c}} $ ), the curve does not have an inflection point. The temperature is a monotonically increasing function of radius, indicating that the BH is in the supercritical phase. At the critical isobar ($ P=P_{\rm{c}} $ ), the curve has an inflection point, where the BH is thermodynamically unstable, corresponding to the critical temperature. Two-phase transition branches exist below the critical pressure ($ P<P_{\rm{c}} $ ), one is in the small radius region, corresponding to the fluid phase in the vdW system, and the other is in the large radius region, corresponding to the gas phase.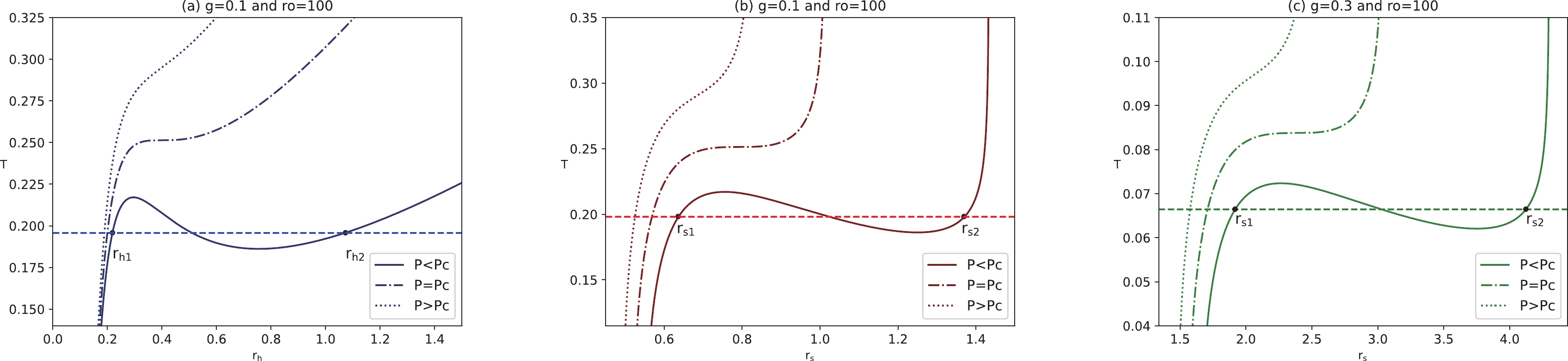
Figure 2. (color online) Panel (a) temperature as a function of
$ r_{\rm{h}} $ with$ g=0.1 $ . Panel (b) temperature as a function of$ r_{\rm{s}} $ with$ g=0.1 $ . Panel (c) temperature as a function of$ r_{\rm{s}} $ with$ g=0.3 $ . A static observer at$ r_{\rm{O}}=100 $ .The middle and right panels of Fig. 2 present the BH temperature as a function of the shadow radius
$ r_{\rm{s}} $ with different pressures under several representative values of magnetic charge. We find that the shadow radius can replace the event horizon radius to present the Bardeen-AdS BH phase transition process. An$ r_{\rm{s}} $ less than$ r_{\rm{s1}} $ corresponds to a stable small BH, and an$ r_{\rm{s}} $ great than$ r_{\rm{s2}} $ corresponds to a stable large BH. The unstable intermediate branch appears in$ (r_{\rm{s1}} $ ,$ r_{\rm{s2}}) $ . A larger magnetic charge leads to a weaker phase transition temperature, and the corresponding shadow radius increases. Meanwhile, Maxwell's equal area is constructed on the$ T-r_{\rm{h}} $ plane and$ T-r_{\rm{s}} $ plane, that is,$ \begin{eqnarray} T_{\rm{h0}}(r_{\rm{h2}}-r_{\rm{h1}}) = {\int_{r_{\rm{h2}}}^{r_{\rm{h1}}} T {\rm{d}}r_{\rm{h}}}, \end{eqnarray} $

(26) $ \begin{eqnarray} T_{\rm{s0}}(r_{\rm{s2}}-r_{\rm{s1}}) = {\int_{r_{\rm{s2}}}^{r_{\rm{s1}}} T {\rm{d}}r_{\rm{s}}}. \end{eqnarray} $

(27) We find that the equal area law can also be established using the shadow radius in regular spacetime, which implies that the shadow radius may serve as a probe for phase structure in regular spacetime. Note that
$ T_{\rm{h0}} $ and$ T_{\rm{s0}} $ are not entirely equivalent because the position of the static observer is relatively remote. In transferring the phase transition results to the characterization of the shadow radius, the temperature increases slightly with the Hawking radiation.Furthermore, the phase transition grade can be determined by heat capacity. The heat capacity mutation and specific heat diverge represent the second-order phase transition at the critical point. The heat capacity of the Bardeen-AdS BH at constant pressure can be written as
$ \begin{equation} C_{P}=T\Bigg(\frac{{\rm d}S}{{\rm d}T}\Bigg)_{P,g}=\frac{2\pi r_{\rm{h}}^2 (g^{2}+r_{\rm{h}}^2)(8\pi P r_{\rm{h}}^4 -2g^{2}+r_{\rm{h}}^2)}{8\pi P r_{\rm{h}}^6+8g^{4}+4g^{2}r_{\rm{h}}^2-r_{\rm{h}}^4}. \end{equation} $

(28) Figure 3 shows the heat capacity as a function of the event horizon radius and shadow radius of the Bardeen-AdS BH. It is found that the specific heat exhibits infinite divergence at the critical point, which is a strong signal for the beginning of the higher-order phase transition. By exploring the relationship between
$ C_{P} $ and$ r_{\rm{s}} $ , the shadow radius can also reveal the BH phase transition grade. -
We establish a thermal profile in this section to more intuitively report the relationship between the BH phase structure and shadow in regular spacetime. According to Ref. [34], the shadow boundary curve at the celestial coordinate reads as
$ \begin{eqnarray} && x = \lim\limits_{r \rightarrow \infty}\left(-r^{2}\sin\theta_{0}\frac{{\rm{d}}\phi}{{\rm{d}}r}\right)_{\rm{\theta_{\rm 0}} \rightarrow \frac{\pi}{2}}, \end{eqnarray} $

(29) $ \begin{eqnarray} && y = \lim\limits_{r \rightarrow \infty}\left(r^{2}\frac{{\rm{d}}\theta}{{\rm{d}}r}\right)_{\rm{\theta_{\rm 0}} \rightarrow \frac{\pi}{2}}. \end{eqnarray} $

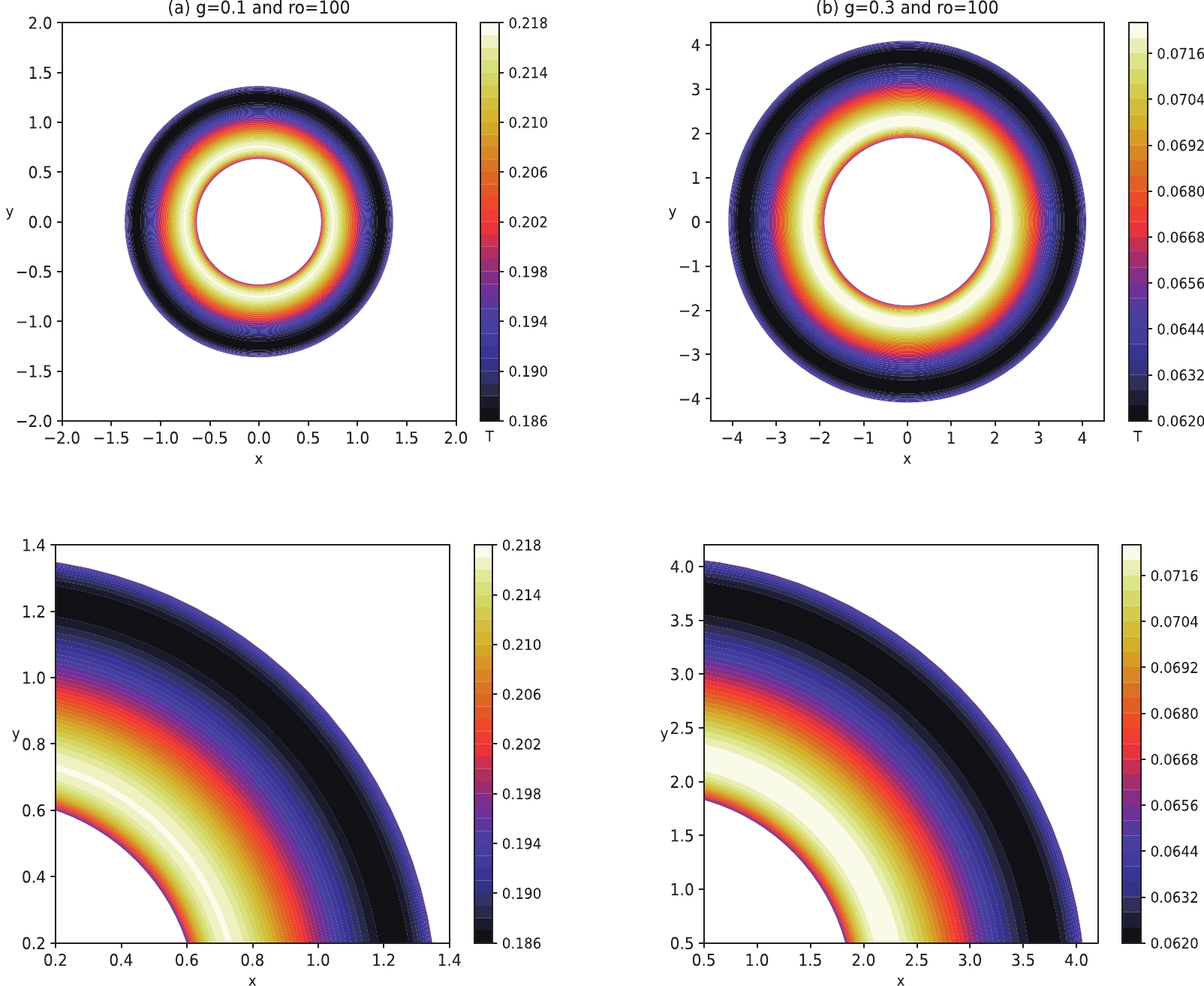
(30) Figure 4 illustrates the shadow contour for a static observer. It is found that the size of the BH shadow depends on the pressure. The point line represents
$ P>P_{\rm{c}} $ , the shadow corresponding to the BH at the supercritical phase. The segment point line corresponds to$ P=P_{\rm{c}} $ , and we find that the shadow radius is more significant than in the$ P>P_{\rm{c}} $ situation. The dotted line only supports$ P<P_{\rm{c}} $ in which the shadow radius is in the large radius region. Additionally, we also observe that the radius of the BH shadow expands the BH outward by increasing the magnetic charge.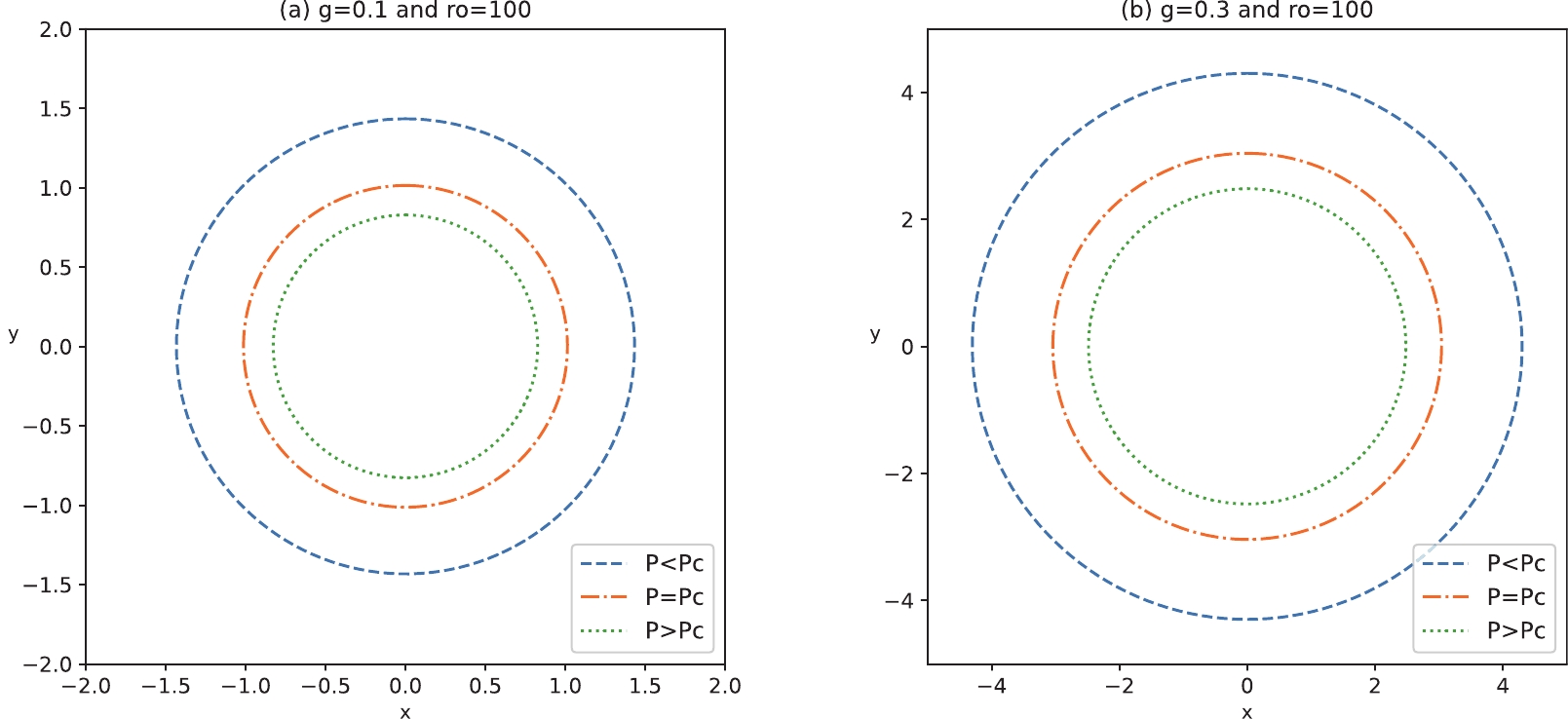
Figure 4. (color online) Shadow cast of the Bardeen-AdS BH. Panel (a) magnetic charge
$ g=0.1 $ . Panel (b) magnetic charge$ g=0.3 $ . Here, the BH mass is$ M=60 $ , and$ r_{\rm{O}}=100 $ .By overlaying Figs. 2 and 4, the BH thermal profile is built utilizing the temperature-shadow radius function. Under several representative values of magnetic charge, Fig. 5 presents three different scenarios:
$ P>P_{\rm{c}} $ ,$ P=P_{\rm{c}} $ , and$ P<P_{\rm{c}} $ . It is found that the change in temperature with$ r_{\rm{s}} $ in the celestial coordinate is consistent with the previous analysis results. As the pressure decreases, the radius of the thermal profile increases, and the corresponding BH temperature decreases. The left panels of Fig. 5 represent$ P>P_{\rm{c}} $ , showing that the temperature increases gradually from the center of the shadow to the boundary in this case. This corresponds to the dotted lines in Fig. 2. The middle panels of Fig. 5 correspond to the$ P=P_{\rm{c}} $ situation, where the BH is thermodynamically unstable, and the temperature remains constant in the critical region, corresponding to the segment point lines in Fig. 2. The right panels of Fig. 5 support the$ P<P_{\rm{c}} $ case. In this sense, the temperature exhibits an N-type change trend. We further refine the region from$ r_{\rm{s1}} $ to$ r_{\rm{s2}} $ . Fig. 6 show that the temperature variation law is: increasing$ \rightarrow $ decreasing$ \rightarrow $ increasing (N-type), which corresponds to the description of the solid lines in Fig. 2. Note that the increase in the BH magnetic charge g leads to a decrease in the phase transition temperature, and there is a large unstable phase transition region. Our results suggest that the phase transition process of the Bardeen-AdS BH can be presented entirely in the thermal profile.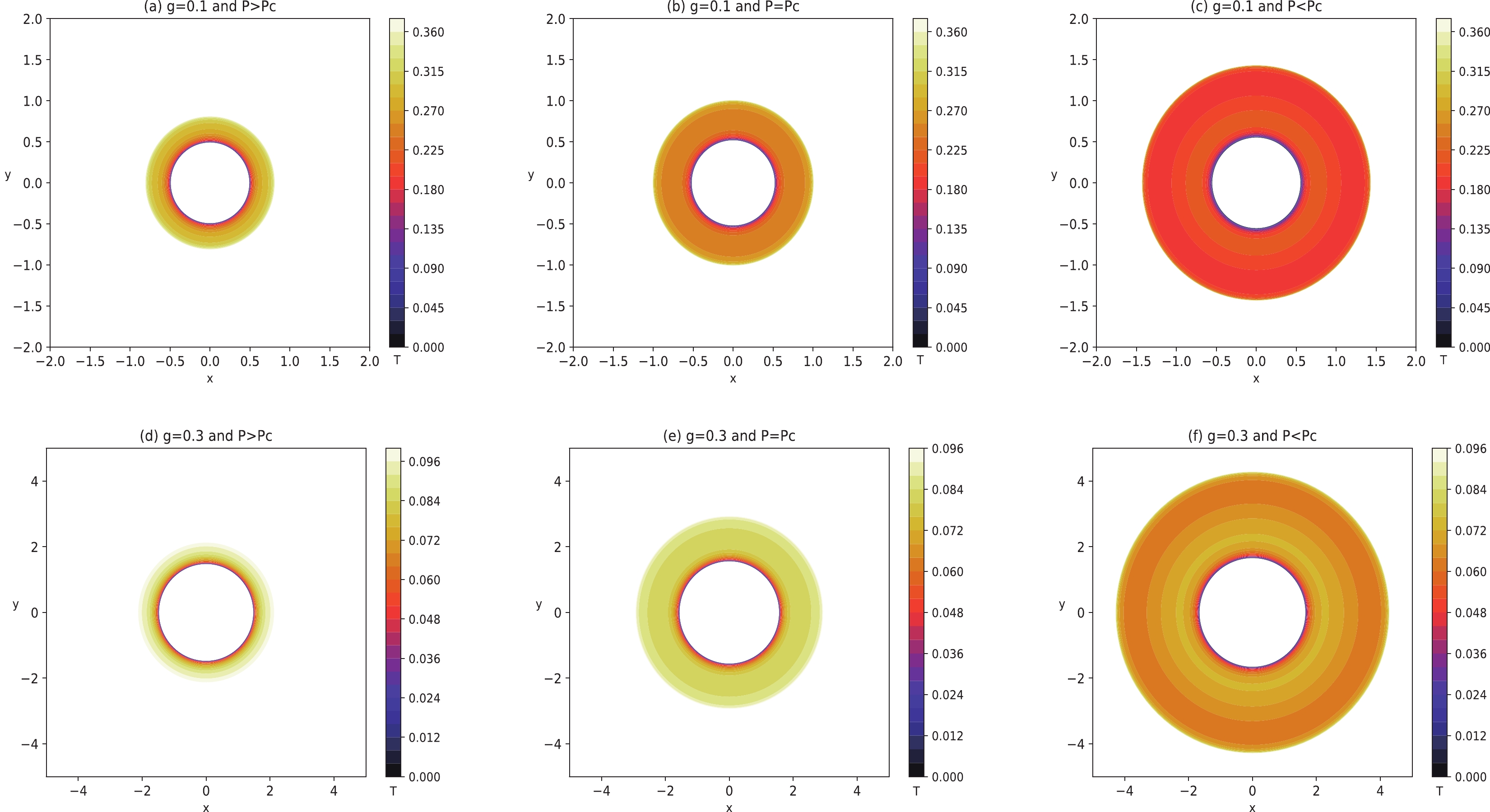
Figure 5. (color online) Thermal profile of the Bardeen-AdS BH for different thermodynamical cases. Panel (a)
$ P>P_{\rm{c}} $ with$ g=0.1 $ . Panel (b)$ P=P_{\rm{c}} $ with$ g=0.1 $ . Panel (c)$ P<P_{\rm{c}} $ with$ g=0.1 $ . Panel (d)$ P>P_{\rm{c}} $ with$ g=0.3 $ . Panel (e)$ P=P_{\rm{c}} $ with$ g=0.3 $ . Panel (f)$ P<P_{\rm{c}} $ with$ g=0.3 $ . The BH mass is taken as$ M=60 $ . -
The dependence of the BH shadow and thermodynamics in regular spacetime has been revealed in this analysis. We find that the shadow radius and event horizon radius display a positive correlation, implying that the BH temperature can be rewritten as a function of the shadow radius in regular spacetime. For a Schwarzschild-AdS BH, Eq. (22) remains valid (
$ g=0 $ ). This can be used to describe the relationship between the shadow radius and event horizon radius of the Schwarzschild-AdS BH. These two radii still exhibit positive correlation characteristics, whereas the slopes of the function curves are greater than those of a regular AdS BH. As the magnetic charge increases, the radius of the event horizon increases, and the corresponding$ r_{\rm{s}} $ increases. As a result, we believe that the shadow radius can be used to analyze the phase transition structure of a regular AdS BH.We investigate the phase transition curves in the shadow context. It is found that the shadow radius can replace the event horizon radius to present the Bardeen-AdS BH phase transition process. On the
$ T-r_{\rm{s}} $ plane, the BH is in the supercritical phase above the critical isobar, and the BH is thermodynamically unstable at the critical pressure. Two-phase transition branches exist below the critical pressure: an$ r_{\rm{s}} $ less than$ r_{\rm{s1}} $ corresponds to a stable small BH, and the$ r_{\rm{s}} $ great than$ r_{\rm{s2}} $ corresponds to a stable large BH. The unstable intermediate branch appears in$ (r_{\rm{s1}},r_{\rm{s2}}) $ . By exploring the relationship between the heat capacity and shadow radius, we find that the shadow radius can reveal the BH phase transition grade. Furthermore, the equal area law can be constructed using the shadow radius, indicating that the shadow radius may serve as a probe for phase structure in regular spacetime.Utilizing the temperature-shadow radius function, the thermal profile of the Bardeen-AdS BH is established under several representative values of magnetic charge. We find that the size of the BH shadow depends on the pressure. As the pressure decreases, the radius of the thermal profile increases, and the corresponding BH temperature decreases. For
$ P>P_{\rm{c}} $ , the temperature increases gradually from the center of the shadow to the boundary. The BH is thermodynamically unstable, and the temperature remains constant in the critical region in the$ P=P_{\rm{c}} $ situation. The temperature shows an N-type change trend with$ P<P_{\rm{c}} $ , and its variation law is: increasing$ \rightarrow $ decreasing$ \rightarrow $ increasing. These results suggest that the regular AdS BH phase transition process can be presented entirely in the thermal profile, and the relationship between the BH shadow and thermodynamics can be established in regular spacetime.
Shadow thermodynamics of an AdS black hole in regular spacetime
- Received Date: 2022-04-07
- Available Online: 2022-09-15
Abstract: The dependence of the black hole (BH) shadow and thermodynamics may be structured in regular spacetime. Taking a regular Bardeen-AdS BH as an example, the relationship between the shadow radius and event horizon radius is derived. It is found that these two radii display a positive correlation, implying that the BH temperature can be rewritten as a function of shadow radius in regular spacetime. By analyzing the phase transition curves under the shadow context, we find that the shadow radius can replace the event horizon radius to present the BH phase transition process, and the phase transition grade can also be revealed by the shadow radius, indicating that the shadow radius may serve as a probe for phase structure in regular spacetime. Utilizing the temperature-shadow radius function, the thermal profile of the Bardeen-AdS BH is established. Moreover, the temperature exhibits an N-type change trend in the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: