-
In high energy hadronic collisions, quantum chromodynamics (QCD) predicts rapid gluon emissions with increasing collision energy (or decreasing Bjorken-x), which leads to an overabundance of gluons squeezed into a confined hadron and the formation of a new state of matter. This is known as the gluon saturation state, also called the Color Glass Condensate (CGC) [1]. In the CGC, a projectile (target) does not behave as a simple incoherent superposition of its constituent partons. The non-linear and multiple scattering effects are important and dominate not only the rapidity evolution of the scattering amplitude but also the dynamics of hadron production in the scattering process, which makes the theory restore the unitarity limit as that due to the growth of the gluon density tamed by the gluon recombination process①. These properties of the CGC make it a good candidate theory for describing single inclusive hadron production in high energy hadronic collisions in which the physical processes are governed by a large gluon density and non-linear coherence phenomena.
Pioneering studies in the phenomenological applications of the CGC effective theory for particle production in high energy proton-proton (p-p), proton (deuteron)-nucleus (p-A), and nucleus-nucleus (A-A) collisions have been performed using the Kharzeev, Levin, Nara (KLN) model [2–4] inspired by the CGC evolution equation (B-JIMWLK equations [5–12]). Subsequently, several sophisticated CGC hadron production models were proposed in literature [13–16], all of which provided good qualitative descriptions of the experimental data at a time when the CGC theory was insufficiently developed and gluon saturation physics was far from being widely accepted. The shared feature of these models is that their unintegrated gluon distributions (UGDs) are inspired by the B-JIMWLK evolution equations. The B-JIMWLK equations are a set of non-linear hierarchy renormalization group equations that cannot be directly used in phenomenological studies. In the large
$ N_c $ limit, the B-JIMWLK equations can be reduced to a closed equation known as the Balitsky-Kovchegov (BK) equation [5, 17]. Although the simplified BK equation can be easily used to study the observables of interest, it only qualitatively accounts for the energy and centrality dependence of integrated multiplicities and the transverse momentum ($ p_{\rm T} $ ) distribution of single inclusive hadron production and vector meson production in p-p, p-A and A-A collisions at the RHIC and LHC [18–21] owing to its insufficient accuracy. The B-JIMWLK and BK equations were derived with leading logarithmic accuracy with fixed QCD coupling. Therefore, they are leading order (LO) evolution equations, which are disfavored by experimental data, e.g., the small-x behavior of structure functions measured in electron-proton scattering at HERA [22–25].A key piece of progress that promoted the CGC effective theory to a practical phenomenological tool was achieved by calculations of the next-to-leading order (NLO) corrections of the B-JIMWLK and BK equations. In particular, a running coupling Balitsky-Kovchegov (rcBK) equation was derived by considering quark loop corrections on top of leading logarithmic
$ (\alpha_s\ln1/x)^n $ resummation [26, 27]. The running coupling improved CGC theory can provide a successful description of single inclusive hadron production data at the RHIC and LHC, which significantly narrows the gap between theory and data [19, 28–35]. However, the quark loop corrections are not the only source of NLO contributions to the LO BK or B-JIMWLK equations. Gluon loop corrections are also important NLO contributions to LO CGC theory. A full NLO BK (fnloBK) was derived by considering all these NLO contributions in Ref. [36]. Unfortunately, the fnloBK cannot be directly applied to phenomenology owing to the instability issues caused by a large double transverse logarithmic term in the evolution kernel [37]. Two methods, the kinematical constraint on successive gluon emissions [38] and the resummation of the leading double logarithms [39], have been used to solve the unstable issues of the fnloBK equation [40–42]②. A kinematical constraint Balitsky-Kovchegov (kcBK) equation non-local in rapidity and a collinearly-improved Balitsky-Kovchegov (ciBK) equation local in rapidity have been derived. It was found that these two stabilized equations are equivalent, although they are formulated in different ways. More importantly, numerical and analytic studies on the ciBK equation have shown that the collinear-improved effect plays an important role in both stabilizing the BK equation and slowing down the rapidity or energy evolution of the UGD (dipole scattering amplitude) [43]. In fact, the latter feature was essential for the success of the description of hadron production data at the RHIC and LHC based on the rcBK equation. Consequently, the ciBK equation provided good fits to the inclusive HERA data [25, 44].Inspired by successful applications of the ciBK equation to inclusive structure functions in electron-proton (e-p) deep inelastic scattering at HERA, we provide, for the first time, phenomenological applications of the ciBK equation to physics at LHC energies in this paper by using it to describe single inclusive hadron production in p-p collisions. To observe the significance of the correction of the collinearly-improved effect, we first solve the ciBK equation numerically with techniques developed in our previous studies [42, 45, 46] and compare the solutions with those resulting from the rcBK equation. We find that the collinearly-improved effect does suppress the rapidity evolution of the dipole amplitude (see Fig. 1) and therefore suppresses the small-x evolution of the UGD. More importantly, it shows that the ciBK evolved UGD has a sharper
$ p_{\rm T} $ distribution than that of the rcBK evolved UGD (see Fig. 3), which leads to a relatively steeper slope of the hadron$ p_{\rm T} $ distribution than that of the rcBK and significantly improves the predictive power of the ciBK equation. Second, we use the$ k_{\rm T} $ -factorization formalism [47], where the UGDs of both the projectile and target protons are evolved using the ciBK equation, to calculate the transverse momentum and integrated multiplicity distributions of charged hadron and neutral pion productions in the framework of the CGC. We find that the collinearly-improved UGDs provide successful descriptions of the data measured at the LHC. Finally, the scale dependence of the fragmentation function (FF) is investigated based on the ciBK evolved UGDs. This reveals that the scale dependence of the FF is significantly reduced in the collinearly-improved$ k_{\rm T} $ -factorization formalism and can be fully absorbed into the K factor that appears in Eq. (1).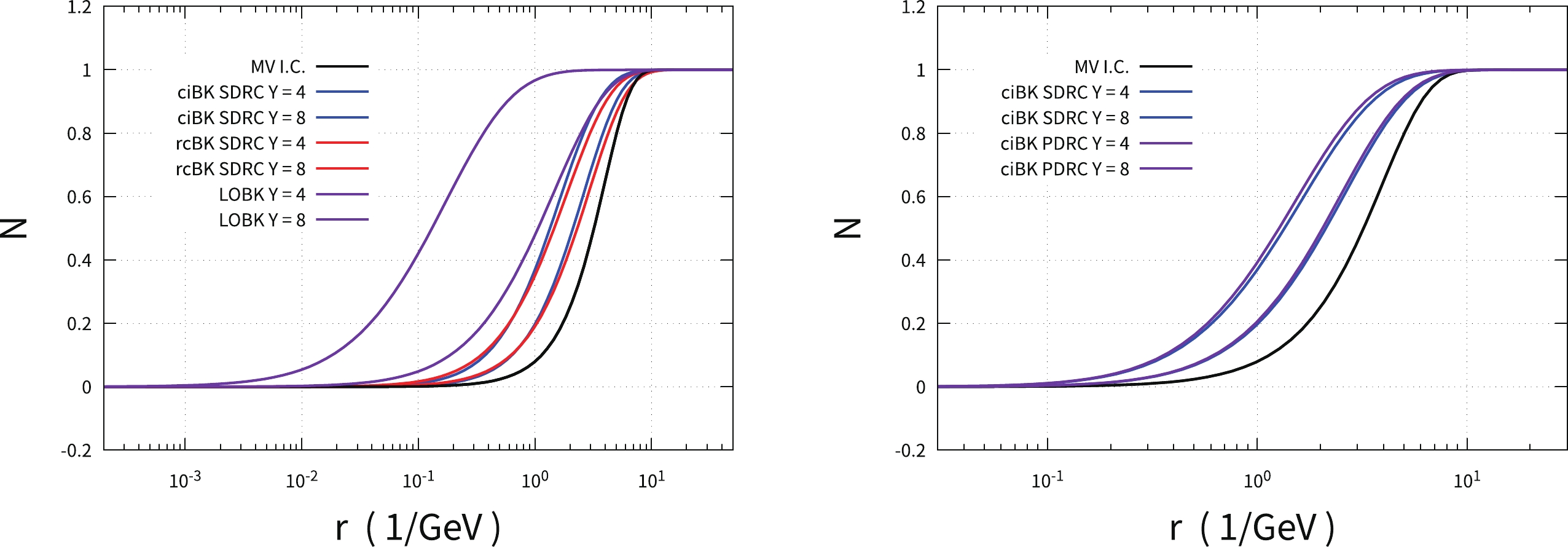
Figure 1. (color online) (left) Comparison of the dipole scattering amplitudes
$ {\cal{N}}(r, Y) $ resulting from the solutions of the LO BK, rcBK, and ciBK equations with the SDRC prescription at rapidity Y = 0, 4, and 8. (right) The dipole scattering amplitudes$ {\cal{N}}(r, Y) $ originating from the solutions of the ciBK equation with the PDRC and SDRC prescriptions at rapidity Y = 0, 4, and 8.This paper is organized as follows. Sec. II gives a brief review of single inclusive hadron production in the
$ k_{\rm T} $ -factorization formalism in the framework of the CGC. Sec. III provides the derivation of the UGD, which is a key component of the$ k_{\rm T} $ -factorization formalism. We briefly recall the ciBK equation and numerically solve it to obtain UGDs for use in later sections. Sec. IV presents the main results of this paper: the transverse momentum and integrated multiplicity distributions, the impact of running coupling prescriptions, and the scale dependence of the FF along with their physical discussions. Finally, a summary is given in Sec. V. -
In this section, we discuss single inclusive hadron production in high energy p-p collisions in terms of the
$ k_{\rm T} $ -factorization formalism within the framework of the CGC. First, we provide the number of gluons produced per unit rapidity [47]:$\begin{aligned}[b] \frac{{\rm d} N^{p+p \rightarrow gX}}{{\rm d} y {\rm d}^{2} p_{\rm T}}=&K\frac{2}{\sigma_sC_{\rm F}} \frac{1}{p_{\rm T}^{2}} \int \frac{{\rm d}^{2} k_{\rm T}}{4} \int {\rm d}^{2} b \alpha_{s}(Q) \phi_{\rm P}\\&\times\left(\frac{\left|p_{\rm T}+k_{\rm T}\right|}{2}, x_{1} ; b\right) \phi_{\rm T}\left(\frac{\left|p_{\rm T}-k_{\rm T}\right|}{2}, x_{2} ; B_{\rm T}-b\right), \end{aligned} $

(1) where
$ C_{\rm F} = (N_c^2 - 1)/2N_c $ ,$ x_{1,2} = (p_{\rm T}/\sqrt{s_{NN}})\exp(\pm y) $ ,$ B_{\rm T} $ is the impact parameter of the collision,$ \sigma_{s} $ is the effective interaction area, and$ p_{\rm T} $ and y are the transverse momentum and rapidity of the produced inclusive gluon, respectively. Note that the b integral in Eq. (1) gives rise to a transverse area factor, which is canceled with$ \sigma_s $ . In addition, one can easily observe a feature in Eq. (1) that it is symmetric under the exchange between the projectile and target.The key component of Eq. (1) is the UGDs,
$ \phi_{\rm P} $ and$ \phi_{\rm T} $ , which encode all information on hadronic collisions, where the subscripts P and T represent abbreviations of the projectile and target, respectively. To include the collinearly-improved effect in hadron production, the ciBK evolved UGDs are used to replace the rcBK evolved ones in this study. The ciBK evolved UGDs are obtained by numerical solving the ciBK equation. Details on the ciBK equation and its numerical solutions are present in Sec. III.Generally, the QCD coupling
$ \alpha_{s} $ in Eq. (1) is fixed. However, we allow it to run with the momentum to agree with the running coupling treatment of the ciBK evolved UGDs. Therefore, we choose$ Q = \max\{|p_{\rm T} + k_{\rm T}|/2, |p_{\rm T} - k_{\rm T}|/2\} $ as the argument for QCD coupling. Moreover, we study the dependence of the running coupling prescription through the parent dipole running coupling (PDRC) and smallest dipole running coupling (SDRC) prescriptions. The detailed formalism of these two running coupling prescriptions are introduced in Sec. III.Note that a normalization factor K is introduced in Eq. (1), which is used to complement the higher order corrections and other possible dynamical effects not included in the CGC effective theory. The value of K is fixed via matching to the experimental data. The precise value of K also depends on the FFs and UGDs.
Now, with the inclusive gluon distribution on hand, charged hadron multiplicity can be calculated by an integral over
$ p_{\rm T} $ ,$ \frac{{\rm d} N_{{\rm{ch}}}}{{\rm d} y}=\frac{2}{3} \kappa_g \int {\rm d}^{2} p_{\rm T} \frac{{\rm d} {\cal{N}}^{p+p \rightarrow g}}{{\rm d} y {\rm d}^{2} p_{\rm T}}, $

(2) and the transverse momentum distribution can be computed via convolution with a FF,
$ \frac{d N^{p+p \rightarrow h}}{{\rm d} y {\rm d}^{2} p_{\rm T}}=\int \frac{{\rm d} z}{z^{2}} D_{g}^{h}\left(z=\frac{p_{\rm T}}{k_{\rm T}}, Q\right) \frac{{\rm d} {\cal{N}}^{p+p \rightarrow g}}{{\rm d} y {\rm d}^{2} k_{\rm T}}. $

(3) In Eq. (2), we assume that the gluon multiplicity distribution is proportional to the final hadron multiplicity distribution via a multiplication factor
$ \kappa_g $ , and the factor 2/3 accounts for the occupation of charged hadrons among the total hadrons. In Eq. (3),$ D_{g}^{h} $ is the FF that gives the probability of a parton splitting into a hadron. To investigate the scale dependence of the FF, four FFs (two LO and another two NLO accuracy) are used in our study. We provide more detailed discussions on FFs in Sec. IV. To avoid violating the momentum sum rule, we place a lower limit of the hadron momentum fraction$ z\geq0.05 $ on the integral in Eq. (3) [31].Note that the
$ k_{\rm T} $ -factorization in Eq. (1) has been shown to be valid only in the central rapidity region, and it is not applicable at highly forward rapidities or large$ p_{\rm T} $ owing to large x contributions in which a hybrid formalism proposed in Refs. [13, 14] should be applied. In the central rapidity region, the rapidity is significantly different from the pseudo-rapidity, which is actually used in the measurement. Hence, for comparison with the experimental data, we must translate the rapidity distribution into the pseudo-rapidity distribution via the$ y\rightarrow \eta $ Jacobian$ \frac{{\rm d} N_{{\rm{ch}}}}{{\rm d} \eta}=\frac{\cosh \eta}{\sqrt{\cosh ^{2} \eta+\dfrac{m^2+p_{\rm T}^2}{p_{\rm T}^2}}} \frac{{\rm d} N_{{\rm{ch}}}}{{\rm d} y}, $

(4) with
$ y=\frac{1}{2}\ln\left[\frac{\sqrt{\cosh ^{2} \eta+\dfrac{m^2+p_{\rm T}^2}{p_{\rm T}^2}}+\sinh \eta}{\sqrt{\cosh ^{2} \eta+\dfrac{m^2+p_{\rm T}^2}{p_{\rm T}^2}}-\sinh \eta}\right], $

(5) where m is the typical mass of the produced hadron.
-
Because we know that the key component of
$ k_{\rm T} $ -factorization hadron production (Eq. (1)) is the UGD, which includes the most important information about the hadronic collisions between two protons, calculations of the UGD and its transverse momentum distribution are introduced. -
It is known that the UGD represents the probability of finding a gluon in the hadron/nuclei and corresponds to the number of gluons per unit transverse area and per transverse momentum space cell. In the framework of the CGC, the UGD can be obtained by two-dimensional Fourier transforms of the quark and gluon dipole scattering amplitudes:
$ \phi_{A}(k, x, b)=\frac{C_{\rm F}}{\alpha_{s}(k)(2 \pi)^{3}} \int {\rm d}^{2} {\boldsymbol{r}} {\rm e}^{-{\rm i} {\boldsymbol{k}} \cdot {\boldsymbol{r}}} \nabla_{\boldsymbol{r}}^{2} {\cal{N}}_{A}\left(r, Y, b\right), $

(6) where we take the transverse momentum as the argument for running coupling to match the running coupling treatment of the collinearly-improved dipole amplitude. The evolution rapidity Y takes the form
$ Y=\ln \left(x_{0} / x\right) $ , with$ x_0=0.01 $ as the evolution starting point. The subscript A represents the fact that the gluon scattering amplitude belongs to the adjoint representation of the$ {S U}(3) $ group. In the large$ N_c $ limit, one can obtain the gluon dipole scattering amplitude$ {\cal{N}}_{A} $ from the quark dipole scattering amplitude$ {\cal{N}}(r, Y) $ as follows:$ {\cal{N}}_{A}(r, Y)=2 {\cal{N}}(r, Y)-{\cal{N}}^{2}(r, Y), $

(7) where the quark dipole scattering amplitude
$ {\cal{N}}(r, Y) $ is calculated by solving the ciBK equation, which is discussed in detail later. -
From Eq. (6), we know that the UGD results from the Fourier transform of the dipole scattering amplitude, which is a solution of the Balitsky-Kovchegov evolution equation in the CGC effective theory. In this subsection, the LO BK equation and its higher order corrections are discussed to pave the way for calculations of single inclusive hadron production in Sec. IV.
First, we consider a high energy dipole consisting of a quark leg and anti-quark leg, with transverse coordinates x and y, scattering on a hadronic dense target (proton or nuclei). The rapidity (or small-x) evolution of the dipole scattering amplitude can be described by a suit of renormalization group equations, the B-JIMWLK equations, which are infinite hierarchy equations. In the large-
$ N_c $ limit, the B-JIMWLK hierarchy can be reduced to the BK equation, which is a closed equation and easy for phenomenological use [5, 17]. The BK equation can be written as$\begin{aligned}[b] \frac{\partial {\cal{N}}(r, x)}{\partial Y}=&\int {\rm d}^{2} r_{1} K\left(r, r_1, r_2\right)\big[{\cal{N}}\left(r_{1}, x\right)+{\cal{N}}\left(r_{2}, x\right)\\&-{\cal{N}}(r, x)-{\cal{N}}\left(r_{1}, x\right) {\cal{N}}\left(r_{2}, x\right)\big], \end{aligned}$

(8) with
$ r_1 $ and$ r_2 $ as the transverse sizes of the two daughter dipoles produced by gluon emission. r is the size of the parent dipole,$ r = |{\boldsymbol{x}} - {\boldsymbol{y}}| $ .$ K(r, r_1, r_2) $ in Eq. (8) is the evolution kernel. In the LO case, this reads as$ K^{\rm{LO}}(r, r_1, r_2)=\frac{N_{c} \alpha_{s}}{2 \pi^{2}} \frac{r^2}{r_1^2r_2^2}, $

(9) where
$ N_c $ is the number of colors. Note that the LO BK equation only considers the leading logarithmic contribution with fixed$ \alpha_s $ . It does not include higher order corrections; therefore, it is insufficient to provide a good description of experimental data [22–25].To improve the accuracy of the LO BK equation, we can consider the NLO corrections from quark bubble contributions, which lead to the rcBK equation. It has been shown that the rcBK equation has the same structure as the LO BK equation but with a modified evolution kernel
$\begin{aligned}[b] K^{{\rm{rc}}}\left(r, r_1, r_2\right)=&\frac{N_{c} \alpha_{s}\left(r^{2}\right)}{2 \pi^{2}}\left[\frac{r^{2}}{r_{1}^{2} r_{2}^{2}}+\frac{1}{r_{1}^{2}}\left(\frac{\alpha_{s}\left(r_{1}^{2}\right)}{\alpha_{s}\left(r_{2}^{2}\right)}-1\right)\right.\\&\left.+\frac{1}{r_{2}^{2}}\left(\frac{\alpha_{s}\left(r_{2}^{2}\right)}{\alpha_{s}\left(r_{1}^{2}\right)}-1\right)\right]. \end{aligned} $

(10) The fixed coupling
$ \alpha_s $ in Eq. (9) is replaced by a running one,$ \alpha_s(r) $ , in Eq. (10). The argument for$ \alpha_s $ is a function of dipole size. There are two popular running coupling prescriptions in literature [24, 44, 46, 48], the parent dipole running coupling (PDRC) and smallest dipole running coupling (SDRC) prescriptions, where the arguments for$ \alpha_s $ are parent dipole size,$ \alpha_s(r_{{\rm{pd}}}) $ , and the smallest dipole size among the parent and two daughter dipoles,$ \alpha_s(r_{\min}) $ with$ r_{\min}= \min\{r,r_1,r_2\} $ , respectively. We investigate the impact of the running coupling prescriptions on single inclusive hadron production in Sec. IV. To match the running coupling treatment of the dipole amplitude, the running coupling at one-loop accuracy is used.$ \alpha_{s}(r^2) = \frac{1}{b_{N_f}\ln\Bigg(\dfrac{4C^2}{r^2\Lambda^2}\Bigg)}, $

(11) with
$ b_{N_f}=(11N_c-2N_f)/12\pi $ , and$ \Lambda = 0.241 $ GeV. The constant C explains the uncertainty that is inherent to the Fourier transform from momentum space. Note that running coupling is fixed as$ \alpha_{fr}=0.711 $ when$ r>r_{fr} $ to regularize the infrared behavior.It is known that the quark loop is not the only source of NLO corrections to the LO BK equation. A fnolBK equation includes contributions from the quark and gluon loops as well as the tree gluon diagrams with quadratic and cubic nonlinearities. It has been found that the fnloBK equation is unstable due to a large contribution from a transverse double logarithmic term in its evolution kernel [37].
To solve this instability issue, the authors devised a novel method in Ref. [39] to resum the double transverse logarithms to all orders and obtained a resummed BK equation. The single transverse logarithms are also found to have large corrections to the BK equation. The ciBK equation was obtained by including corrections from the resummations of both single and double transverse logarithms in the fnloBK equation. The evolution kernel of the ciBK equation reads as
$ K^{\rm{ci}}\left(r, r_1, r_2\right)=\frac{N_{c} \alpha_{s}\left(r^{2}\right)}{2 \pi^{2}}\frac{r^2}{r_1^2r_2^2}K^{\rm{STL}}K^{\rm{DLA}}, $

(12) which includes the single transverse logarithms (STL)
$ K^{{\rm{STL}}} = \exp\bigg\{- \bar{\alpha}_s A_1\bigg|\ln\frac{r^2}{{\rm{min}}\{r_1^2, r_2^2\}}\bigg|\bigg\}, $

(13) and the double logarithmic approximation (DLA)
$ K^{{\rm{DLA}}} = \frac{J_1\bigg(2\sqrt{ \bar{\alpha}_s \rho^2}\bigg)}{\sqrt{ \bar{\alpha}_s\rho^2}} = 1 - \frac{ \bar{\alpha}_s \rho^2}2 + \frac{( \bar{\alpha}_s \rho^2)^2}{12} + \cdots , $

(14) corrections. In Eq. (13),
$ A_1=11/12 $ is the DGLAP anomalous dimension. In Eq. (14),$ J_1 $ is the Bessel function of the first kind with$ \rho = \sqrt{\ln\left(\dfrac{r_1^2}{r^2}\right)\ln\left(\dfrac{r_2^2}{r^2}\right)}, $

(15) and when
$ \ln({r_1^2}/{r^2})\ln({r_2^2}/{r^2})<0 $ , an absolute value is used in the calculation of ρ and the modified Bessel function of the first kind is used in the$ K^{\rm{DLA}} $ [44].To obtain the UGD, one must solve the BK equation numerically. In this study, we use the McLerran-Venugopalan (MV) model [49] to generate the initial condition (I.C.) of the BK equation:
$ {\cal{N}}(r, Y=0) = 1-\exp\left[-\left(\frac{r^2\bar{Q}_{s0}^2}{4}\right)^{\gamma}\ln\left(\frac{1}{r^2\Lambda^2}+e\right)\right], $

(16) where γ is a dimensionless parameter, and
$ \bar{Q}_{s0} $ is the initial saturation scale at$ x_0 = 0.01 $ , at which point the evolution begins. Note that the parameters$ \bar{Q}_{s0}^2 $ , γ, and$ C^2 $ are fixed by reproducing the experimental data in p-p collisions at 0.9 TeV.The dipole scattering amplitudes at a rapidity
$ Y=0 $ (I.C.),$ 4 $ (dashed curves), and$ 8 $ (solid curves) obtained by solving the rcBK and ciBK equations are shown in Fig. 1. To observe the difference between the LO BK and NLO BK (rcBK and ciBK) equations, the left hand panel of Fig. 1 gives the solutions of the LO BK, rcBK, and ciBK equations with the same running coupling prescription, SDRC. The purple curves denote the solutions of the LO BK equation, the red curves represent the solutions originating from the rcBK equation, and the blue curves denote the solutions resulting from the ciBK equation. We can see that the evolution speed of the rcBK and ciBK dipole scattering amplitudes are significantly suppressed compared to that of the LO BK, which makes the rcBK and ciBK equations yield a significantly better description of single inclusive hadron production in p+p collisions than the LO BK equation (see Sec. IV). To show the prescription dependence of QCD coupling, the right hand panel of Fig. 1 presents the solution of the ciBK equation with PDRC and SDRC prescriptions. The dashed curves denote the dipole amplitudes at$ Y=4 $ , whereas the solid curves denote the dipole amplitudes at$ Y=8 $ . By comparing the dipole scattering amplitudes at the same rapidity, we can see that the two prescriptions only render a slight difference. The relative differences are δ < 4.2% at$ Y =4 $ and δ < 6.5% at$ Y=8 $ . To reveal the rapidity dependence of the saturation momentum, we extract the values of$ Q_s $ via the definition$ N(r=2/Q_s,Y)= 1/2 $ . In Fig. 2, we demonstrate the rapidity dependence of the saturation momentum; the red curve denotes the outcomes resulting from the rcBK equation, whereas the blue curve represents the results calculated using the ciBK equation. This shows that the saturation momenta of the ciBK equation are relatively larger than those of the rcBK equation, which is consistent with the findings obtained from Ref. [45].We use Eq. (6) to numerically calculate the UGD. Fig. 3 shows the UGD as a function of transverse momentum. The blue curve denotes the ciBK evolved UGD, and the red curve represents the rcBK evolved UGD at
$ x=8\times10^{-4} $ . We can see that although the rcBK and ciBK evolved UGDs have similar distributions, the ciBK evolved UGD is significantly sharper than the rcBK evolved UGD at the transverse momentum region of interest. This feature leads to the ciBK evolved UGD being more favored by the$ p_{\rm T} $ and integrated multiplicity distributions of single inclusive hadron in p-p collisions at the LHC. Specifically, the ciBK evolved UGD provides a better description of the data than the rcBK one at large$ p_{\rm T} $ (see Sec. IV for details). -
In this section, we compute single inclusive hadron production in p-p collisions at LHC energies using the
$ k_{\rm T} $ -factorization formalism with the ciBK and rcBK evolved UGDs mentioned in the above section. The transverse momentum and integrated multiplicity distributions of charged hadrons and neutral pions with different running coupling prescriptions and FFs are presented. -
In Fig. 4, we show a comparison of the transverse momentum distributions of charged hadrons between the experimental measurements in p-p collisions at
$ \sqrt{s} = 0.9 \rm TeV $ at the LHC and our theoretical calculations using the ciBK and rcBK evolved UGDs under the PDRC and SDRC prescriptions. The black solid squares and circles are data points measured at central rapidities in CMS and ATLAS experiments, respectively [50, 51]. The blue and red curves are numerical results resulting from the ciBK and rcBK evolved UGDs, respectively (unless otherwise specified, the same applies hereinafter). We can clearly see that the results originating from both UGDs are in good agreement with the measurements; however, the slopes of the ciBK curves are more favored by the data than the rcBK ones owing to their steeper distribution in the$ p_{\rm T} $ region of interest (see Fig. 3), which implies that the ciBK equation gives a better description of the data than the rcBK equation. Therefore, we find that the shape of the spectra does provide a direct test of the capacity of the ciBK and rcBK equations. In Fig. 4, the solid curves denote the outcomes calculated by the PDRC prescription, and the dashed curves denote the results computed by the SDRC prescription (the same applies hereinafter). It shows that the PDRC and SDRC prescriptions give similar quality depictions of the data, which indicates that the prescription of the QCD coupling only has a negligible impact on hadron production in the central rapidities because the$ k_{\rm T} $ -formalism is valid in the central rapidity region, where the saturation scale$ Q_s $ is relatively small, giving rise to large$ r_{\rm sat}\sim1/Q_s $ . The sizes of the dipoles are larger than$ r_{\rm sat} $ in the saturation region, leading to an indistinguishable logarithmic increase$ \alpha_s(r) $ (see Eq. (11)). Here, note that the theoretical calculations are tuned to agree with the data points around$ p_{\rm T}\sim3 $ , which is also the method used to fix the K factor in Eq. (1). Moreover, we only use the KKP-LO FF in the calculation of the$ p_{\rm T} $ distributions in Fig. 4 to avoid ambiguities.The transverse momentum distributions of charged hadrons and neutral pions calculated by the ciBK and rcBK evolved UGDs with the PDRC and SDRC prescriptions in p-p collisions at
$ \sqrt s = 2.76\;\rm TeV $ (left panel) and 7 TeV (right panel) are shown in Fig. 5. The black solid squares and solid circles denote data for charged hadron production, whereas the pink solid triangles represent the data points for neutral pion production [51–55]. We can see that both calculations resulting from the ciBK and rcBK evolved UGDs are consistent with the charged hadron production data under certain uncertainties, whereas the ciBK evolved UGDs give a better description of the data both at the head and tail than those of rcBK. In particular, the neutral pion production data clearly indicate that the ciBK equation has a significantly higher priority over the rcBK equation in the description of the data. Note that the improvement in the predictive power of the ciBK equation can be attributed to the sharper distribution feature of the ciBK evolved UGD (see Fig. 3). The dependence of the running coupling prescriptions are also studied at these higher energies, which shows that the SDRC and PDRC prescriptions give indistinguishable depictions of the data. The outcomes indicate that the prescription dependence of QCD running coupling is not important at one-loop accuracy for central rapidity data.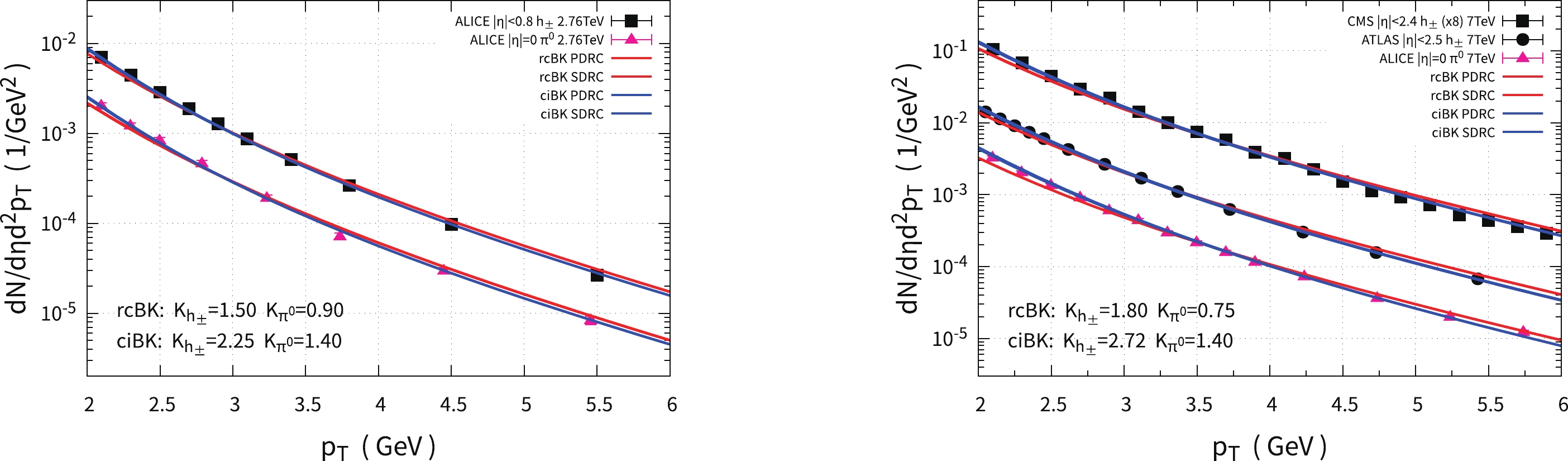
Figure 5. (color online) Transverse momentum distributions of charged hadrons and neutral pions with the ciBK and rcBK evolved UGDs under the PDRC and SDRC prescriptions in p-p collisions at
$ \sqrt s = 2.76 $ and 7 TeV, respectively. The experimental data are taken from the ALICE, ATLAS, and CMS collaborations at the LHC [51–55].From Figs. 4 and 5, we can see that the K factor has a strong dependence on the kinematical region where Eq. (1) is applied. It is shown that although the data points are measured at the same collision energy and different rapidity regions (
$ |\eta|<2.5 $ and$ |\eta|<0 $ ), the K factors are significantly different, see the right panel of Fig. 5.In the following, we study the accuracy sensitivity of the FFs and the scale dependence of the FFs based on the
$ k_{\rm T} $ -factorization formalism with the ciBK evolved UGDs under the SDRC prescription at different LHC collision energies. To compare the accuracy sensitivity of the FFs, we use the LO FFs (KKP-LO and DSS-LO) and NLO FFs (KKP-NLO and DSS-NLO) to calculate the transverse momentum distributions of charged hadron production in p-p collisions at the LHC. The scale dependence of the FFs is investigated by changing the argument for the FFs from$ Q=p_{\rm T}/2 $ to$ Q=p_{\rm T} $ to$ Q=2p_{\rm T} $ .The transverse momentum distributions of charged hadrons with different FF scales (
$ Q=p_{\rm T}/2 $ ,$ Q=p_{\rm T} $ , and$ Q=2p_{\rm T} $ ) are shown in Figs. 6, 7, and 8, respectively. The black solid squares, circles, triangles, and diamonds denote data points measured in p-p collisions at$ \sqrt s = 2.36 $ ,$ 5.02 $ ,$ 8 $ , and$ 13\;\rm TeV $ at the LHC [54–57]. The green solid (dashed) curves represent the theoretical results calculated with the LO (NLO) DSS FFs, whereas the blue solid (dashed) curves represent the theoretical outcomes computed with the LO (NLO) KKP FFs. From these figures, we can see that both the LO and NLO FFs provide good descriptions of the transverse momentum distributions of the charged hadron measurements, despite different K factor values being applied in the LO and NLO cases. In addition, relatively harder spectra are observed with the DSS FFs versus KKP FFs. In terms of the scale dependence of the FFs, it is revealed that this is significantly reduced in the collinearly-improved$ k_{\rm T} $ -factorization formalism [32] and can also be fully absorbed into the K factor that appears in Eq. (1). We find that the K factor increases as the scale of the FF increases, e.g., for the DSS-LO FF at 13 TeV in Figs. 6, 7, and 8,$ K\simeq1.2 $ ,$ K\simeq2.1 $ , and$ K\simeq3.0 $ for$ Q=p_{\rm T}/2 $ ,$ Q=p_{\rm T} $ , and$ Q=2p_{\rm T}$ , respectively.
Figure 6. (color online) Transverse momentum distributions of charged hadrons with the ciBK evolved UGD under the SDRC prescription in p-p collisions at
$ \sqrt s = 2.36$ , 5.02, 8, and 13 TeV. The scale of the FF is taken to be$ Q=p_{\rm T} $ . The experimental data are taken from the ALICE, CMS, and ATLAS collaborations at the LHC [54–57].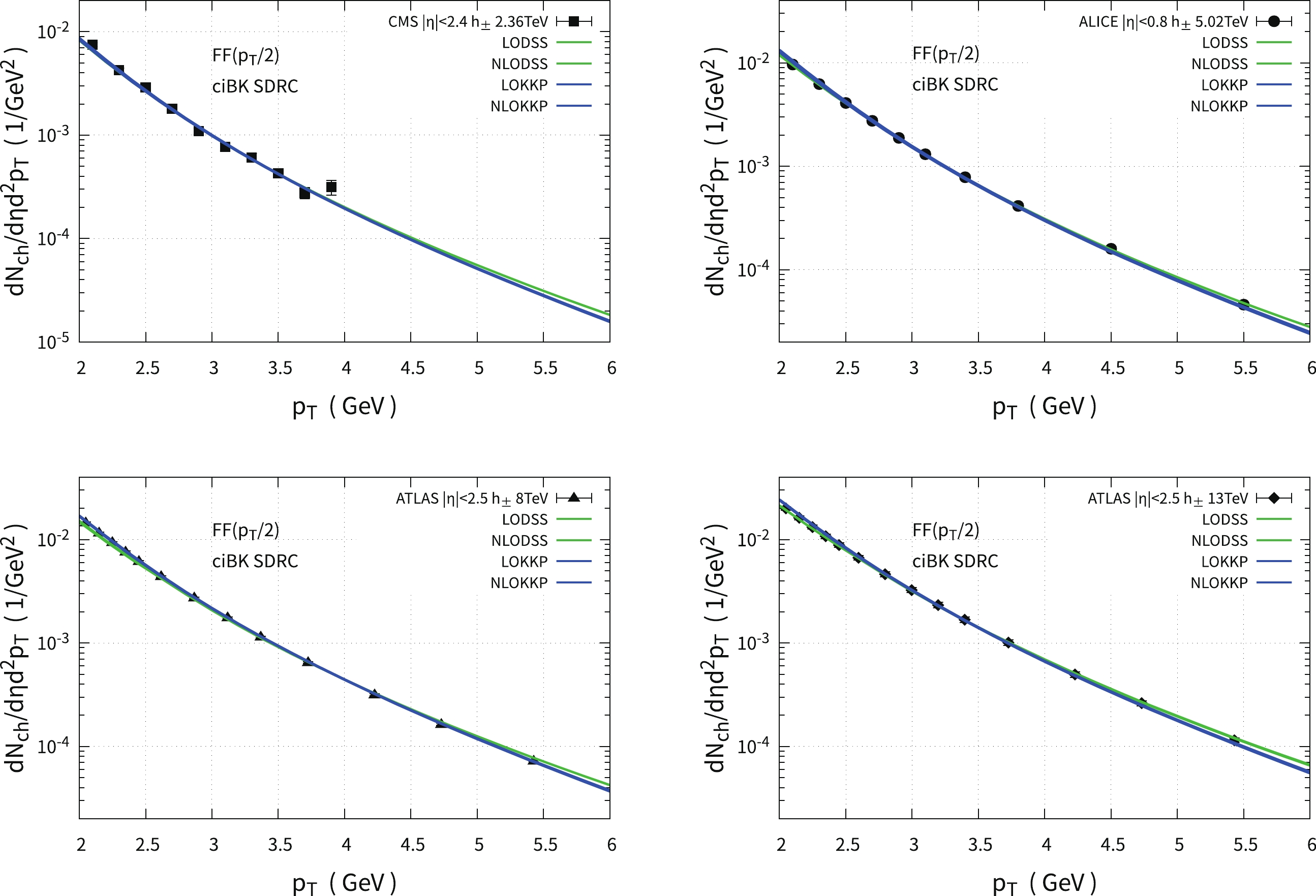
Figure 7. (color online) Same as Fig. 6, except the scale of the FF is taken to be
$ Q=p_{\rm T}/2 $ .
Figure 8. (color online) Same as Fig. 6, except the scale of the FF is taken to be
$Q=2p_{\rm T}$ . -
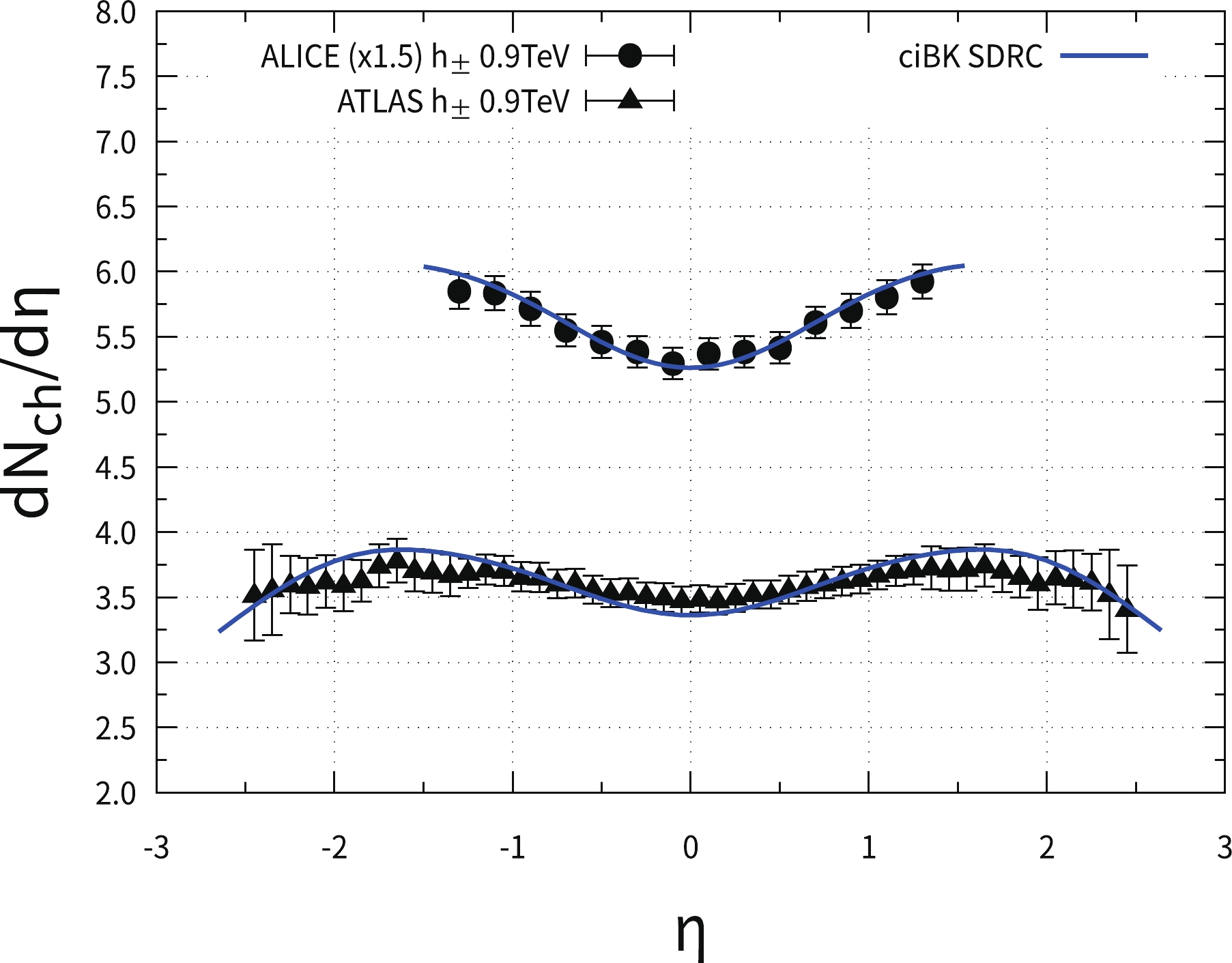
In Fig. 9, we show the pseudo-rapidity distributions of charged hadrons calculated using Eq. (2) with the ciBK evolved UGDs under the SDRC prescription in p-p collisions at
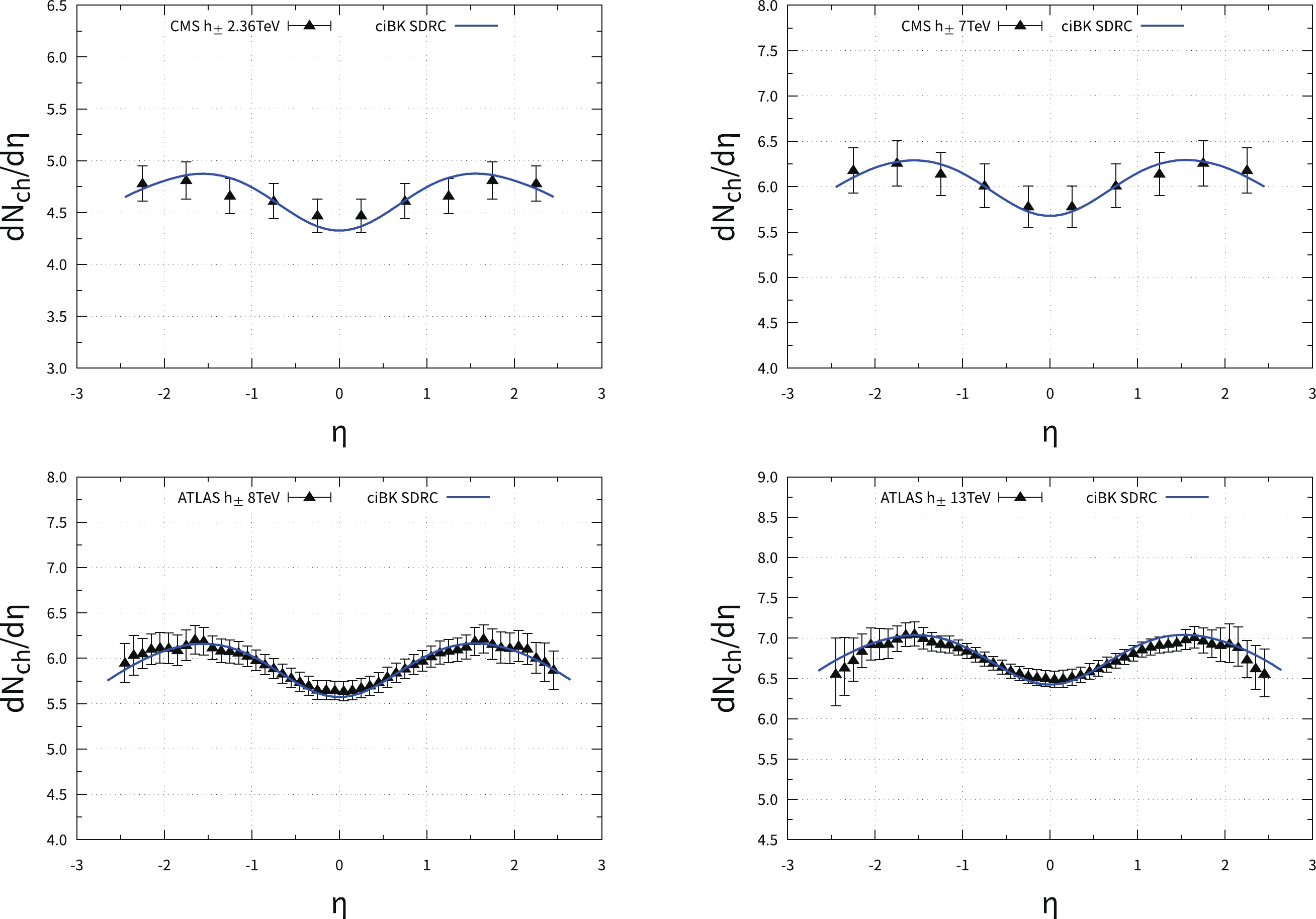
$ \sqrt s = 0.9\;\rm TeV $ compared to the ALICE (solid circles) and ATLAS (solid triangles) data from Refs. [51, 58]. To avoid overlaps between the two groups of data points, we multiply the ALICE data by 1.5. For simplicity, we use the LO KKP FF in the calculations because the difference of the FFs can always be absorbed into the K factor, as explained in the previous subsection, which does not affect the quality of the description of the data. The gluon multiplication factor is found to be$ \kappa_{g}\sim 5 $ to reproduce the hadron multiplicities in p-p collisions at the LHC. We can see that the theoretical calculations are consistent with both the ALICE and ATLAS data points, which indicates that the ciBK equation grasps the key factor of the evolution system produced in p-p collisions at the LHC.The pseudo-rapidity distributions of charged hadrons computed using the ciBK evolved UGDs under the SDRC prescription in p-p collisions at
$ \sqrt s = 2.36$ , 7, 8, and 13 TeV are shown in Fig. 10. Here, we use the same group of parameters fixed by the above transverse momentum distribution and integrated multiplicity data. We can also see that the ciBK equation gives successful descriptions of these integrated multiplicity data. -
In this paper, we use the ciBK equation, for the first time, to study single inclusive hadron production in p-p collisions at LHC energies in the framework of the Color Glass Condensate. The
$ k_{\rm T} $ -factorization formalism is employed to calculate the transverse momentum and integrated multiplicity distributions of the hadrons. We numerically solve the ciBK equation and use the Fourier transform to convert the solutions to momentum space in order to obtain the UGD, which is the key component of the$ k_{\rm T} $ -formalism. It shows that both the ciBK and rcBK evolved UGDs have similar transverse momentum distributions; however, the ciBK evolved UGD has a sharper slope than the rcBK one in the transverse momentum region of interest (see Fig. 3). We find that this feature makes the ciBK evolved UGD more favored by the measurements and leads to an even better description of the hadron production data than the rcBK evolved UGD in p-p collisions at LHC energies.The prescription dependence of QCD coupling is studied using the two most popular prescriptions in literature, the PDRC and SDRC, when the UGDs are calculated. The transverse momentum distributions of the single inclusive hadrons are computed under the PDRC and SDRC prescriptions. We find that both the PDRC and SDRC prescriptions give good descriptions of the experimental data (see Figs. 4 and 5), which indicates that the prescription dependence of QCD coupling can be negligible in
$ k_{\rm T} $ -formalism hadron production because the$ k_{\rm T} $ -formalism is valid in the central rapidity region where the saturation scale$ Q_s $ is relatively small, giving rise to large$ r_{\rm sat}\sim1/Q_s $ . The sizes of the dipoles are larger than$ r_{\rm sat} $ in the saturation region, leading to an indistinguishable logarithmic increase$ \alpha_s(r) $ (see Eq. (11)).The scale dependence of the FF is also investigated by changing the argument from
$ Q=p_{\rm T}/2 $ to$ Q=p_{\rm T} $ to$Q=2p_{\rm T}$ . Meanwhile, the accuracy sensitivity of the FFs is studied through comparisons of the$ p_{\rm T} $ distributions of the hadrons calculated by the LO and NLO FFs. We find that the difference resulting from the scale dependence and accuracy sensitivity of the FFs can be fully absorbed into the K factor, which lumps higher order corrections (see Eq. (1)). Moreover, this reveals that the scale dependence of the FF is reduced in the collinearly-improved$ k_{\rm T} $ -formalism.
Hadron production with collinearly-improved unintegrated gluon distributions in high energy proton-proton collisions
- Received Date: 2022-01-25
- Available Online: 2022-09-15
Abstract: The collinearly-improved Balitsky-Kovchegov (ciBK) equation evolved unintegrated gluon distribution (UGD) is used for the first time to study hadron production in high energy proton-proton collisions in order to improve the predictive power of the Color Glass Condensate effective theory. We show that the ciBK equation evolved UGD provides a relatively better description of LHC data on the transverse momentum and integrated multiplicity distributions of charged hadron and neutral pion production for several collision energies compared with the running coupling Balitsky-Kovchegov (rcBK) equation evolved UGD. This is because the ciBK evolved UGD has a sharper transverse momentum distribution than the rcBK UGD. The impact of running coupling prescriptions on hadron production is studied, and it is found that the parent dipole and smallest dipole running coupling prescriptions provide similar depictions of the data. Moreover, the scale dependence of the fragmentation function is investigated by taking three typical values of scale. We find that the differences resulting from the scale dependence of the fragmentation function can be fully absorbed into the normalization factor, which lumps higher order corrections.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: