-
The existence of dark matter (DM) has been established through extensive cosmological and astronomical observations. However, the microscopic properties of DM beyond the Standard Model (SM) are largely unknown. Recently, the XENON collaboration reported an excess of electronic recoil events with an energy of approximately 2–3 keV [1], and the event distribution has a broad spectrum for the excess. They collected low-energy electron recoil data from the XENON1T experiment with an exposure of 0.65 tonne-years and analyzed various backgrounds for the excess events. Although a small tritium background fits the excess data well [1], bosonic DM can also provide a plausible source for the peak-like excess.
The excess of electron recoil events may be induced by new long-lived particle scattering with electrons in a detector. The lifetime of the new particle must be sufficiently long to reach a detector on Earth after its production and it has an appreciable interaction with electrons. The mass of the new long-lived particle should be
$ \gtrsim $ MeV and the velocity should at the level of$ {\cal{O}}(0.1) $ c [2]. Meanwhile, it should be compatible with the structure formation of the universe and the constraints from Big Bang nucleosynthesis (BBN) as well as the cosmic microwave background (CMB). Thus, an exotic mechanism is required to produce many long-lived particles with a high speed. A plausible scenario for the electron excess events is boosted DM produced in the present universe via dark sector annihilation or decay [2–9]. Meanwhile, a fraction of the un-boosted DM with a regular velocity distribution (with a velocity of$ \sim 10^{-3}\; c $ in the galaxy) can also be present today and is detectable via the scattering off electron. Thus, the direct detection experiments would set stringent bounds on the un-boosted DM-electron scattering for the recoil energy of a few eV [10–14]. These bounds must be evaded when interpreting the XENON1T keV excess.In the interpretation of the XENON1T excess via the scattering between electron and boosted DM, the nature of the intermediating particle and interaction becomes a key aspect. For a long-lived light mediator with keV
$ \sim $ MeV mass, BBN and CMB would place stringent constraints [15, 16]. If the new mediator has a short lifetime, because of the constraint from BBN, its mass should be$ \gtrsim $ 10 MeV, and its lifetime is much shorter than a second [17–20]. In addition, the constraints from low-energy experiments, such as NA48/2 [21] and NA64 [22], should be considered. However, the new mediator and interaction may leave some traces in anomalous processes; for example, a new vector boson of about 17 MeV [23, 24], predominantly decaying into$ e^+ e^- $ , was suggested by two anomalous transitions of 8Be [25] and 4He [26]. Here, we consider a light vector boson X in general, which primarily decays into$ e^+ e^- $ and intermediates the scattering between electron and the boosted DM. Considering the constraints from low-energy experiments [21, 22], when$ 14\; {\rm{MeV}}\lesssim m_X\lesssim 30 $ MeV, as shown in Fig. 5 of Ref. [22], a part of the parameter$ \epsilon_e $ (the$ X$ -electron coupling is parameterized as$ \epsilon_e e $ ) in the range of$ 10^{-4} \lesssim \epsilon_e \lesssim 10^{-3} $ is still permitted by the experiments. Note that the rapid fluctuations in the NA48/2 limit [21] cause some uncertainty of the NA48/2 limit. Here we take the NA48/2 limit in a smooth way as shown in Fig. 5 of Ref. [22] instead of the rapid fluctuations. For instance, the range of$ 5\times 10^{-4} \lesssim \epsilon_e \lesssim 10^{-3} $ is permitted for$ m_X \sim 20 $ MeV of our interest.In this paper, we introduce two complex scalar DM particles,
$ S_A $ and$ S_B $ , to interpret the XENON1T excess with a light vector mediator X. The DM particles$ S_A $ and$ S_B $ are under possible dark symmetry in the hidden sector with$ m_{S_A}\simeq m_{S_B} $ , and some dark sector numbers are carried by both$ S_A $ and$ S_B $ to maintain the stability of DM.$ S_B $ is dark charged and$ S_A $ is neutral with a small mass splitting$ m_{S_A}-m_{S_B}>0 $ , which can be introduced from radiative corrections or substructures. The pair$ S_B S_B^\dagger $ can be produced via the dark annihilation process of$ S_A S_A^\dagger \to S_B S_B^\dagger $ mediated by a new scalar ϕ. Thus, the present dark annihilation can provide a source of boosted$ S_B $ . The scattering between electron and boosted$ S_B $ mediated by the X boson may explain the keV electron excess observed by XENON1T. In addition to the boosted$ S_B $ accounting for the XENON1T keV excess, there would be a fraction of un-boosted$ S_B $ around the Earth. The relic abundance of$ S_B $ can be significantly reduced by the transition of$ S_B S_B^\dagger \to X X $ . Thus, it will be compatible with the stringent bound on un-boosted$ S_B- $ electron scattering in DM direct detections. This tangible approach is explored in this paper. -
In this paper, we consider a scalar DM model to interpret the XENON1T excess. In this model,
$ S_A $ is dark neutral, and$ S_B $ is charged under possible dark symmetry in the hidden sector.$ S_B $ is intermediated by a new vector boson X to interact with an electron. X is assumed to couple to SM charged leptons, and the effective couplings are expressed as$ {\cal{L}}_{X} \supset e X_\mu \displaystyle\sum\limits_\ell \epsilon_\ell \bar{\ell} \gamma^\mu \ell\; . $

(1) X is considered to be a light vector boson in general; here, we do not specify a scenario such as a kinetic mixing portal or a new gauged U
$ (1) $ . The dark charged$ S_B $ couples to the X boson via$ {\cal{L}}_{X} \supset - e_D X_\mu J^\mu_{\mathrm{DM}} + e_D^2 X^\mu X_\mu S_B^\dagger S_B \; , $

(2) where
$ J^\mu_{\mathrm{DM}} $ is the charged current of scalar DM$ S_B $ and is given by$ \begin{array}{*{20}{l}} J^\mu_{\mathrm{DM}} = {\rm i} [S_B^\dagger (\partial^\mu S_B)- (\partial^\mu S_B^\dagger) S_B] \;. \end{array} $

Here, we assume that the X particle has a mass
$ \gtrsim $ 14 MeV [22] and predominantly decays into$ e^+ e^- $ .We also assume a real dark field ϕ coupled to both
$ S_A $ and$ S_B $ , and it mediates the transition between$ S_A $ and$ S_B $ . In addition to the kinetic energy terms, the scalar Lagrangian is given by$ \begin{aligned}[b] -{\cal{L}}_{\rm scalar} \supset& \frac{1}{2}m_\phi^2\phi^2+\lambda_4\phi^4 + \mu_{S_A} S_A S_A^\dagger \phi + \lambda_{S_A} S_A S_A^\dagger \phi^2 \\ +& \mu_{S_B} S_B S_B^\dagger \phi + \lambda_{S_B} S_B S_B^\dagger \phi^2 \; , \end{aligned} $

(3) The parameters
$ \mu_{S}\equiv \mu_{S_A} = \mu_{S_B} $ and$ \lambda_{S}\equiv \lambda_{S_A} = \lambda_{S_B} $ are adopted. Here, we assume$ m_{\phi} > m_{S_A} \simeq m_{S_B} > m_X $ for simplicity, and a small mass splitting Δ between$ S_A $ and$ S_B $ is introduced, i.e.,$ \Delta = m_{S_A} - m_{S_B} > 0 $ . To avoid the overabundance of ϕ in the early universe, we adopt$ m_{\phi} > 2 m_X $ ; thus, the decay mode$ \phi \to X X $ is generated at loop level from the$ \phi S_B S_B^\dagger $ coupling and the charged current of$ S_B $ . For$ m_{S_B} > m_X $ , the relic fraction of$ S_B $ can be significantly depleted when the on-shell annihilation mode$ S_B S_B^\dagger \to X X $ is opened. In addition, possible$ \phi- $ SM Higgs mixing is neglected here for simplicity (for the mixing case, the mixing with a rough upper limit of$ \sin^2\theta \ll 10^{-3} $ can be permitted by experiments [27]). Please note that there may be more particles in the new sector, and here we only consider the particles with key roles in transitions between the SM and dark sector.To induce the keV electron scattering events via boosted
$ S_B $ , the dark annihilation process of$S_A S_A^\dagger \to \phi \to S_B S_B^\dagger$ is considered to be dominant in$ S_A S_A^\dagger $ annihilation. The annihilation cross section is given by$ \sigma_0 v_r \simeq \frac{\mu_S^4}{32 \pi m_{S_A}^2} \frac{ \beta_f }{(s - m_\phi^2)^2 + m_\phi^2 \Gamma_{\phi}^2} \; , $

(4) where
$ v_r $ is the relative velocity, and s is the squared total invariant mass. In the non-relativistic limit, the phase space factor$ \beta_f $ is$ \beta_f = \sqrt{1- \frac{4m_{S_B}^2}{s} } \approx \sqrt{\frac{v_r^2}{4} + \frac{2 \Delta}{m_{S_A}} } \; . $

(5) The decay width of ϕ is
$ \Gamma_\phi = { \mu_X^2\over 8\pi m_\phi}\sqrt{1-{4m_X^2 \over m_\phi^2}} \Bigg({m_\phi^4 \over 4m_X^4}-{m_\phi^2 \over m_X^2}+3\Bigg) \; . $

(6) The annihilation of dark charged DM
$ S_B $ is primarily governed by$ S_B S_B^\dagger \to X X $ via the$ S_B-X $ coupling in Eq. (2). The annihilation cross section is$ \sigma_1 v_r \simeq {e_D^4 \sqrt{1- {4 m_X^2 / s} } \over 16\pi m_{S_B}^2} \frac{8 m_{S_B}^4 - 8 m_{S_B}^2 m_X^2 +3 m_X^4}{( 2m_{S_B}^2 -m_X^2)^2} \; . $

(7) The
$ p $ -wave process$ S_B S_B^\dagger \to X \to e^+ e^- $ is suppressed by$ \epsilon_e^2 $ and is negligible compared with the above annihilation process (see Ref. [19] for this$ p $ -wave dominant case). -
Assuming that the main component of DM is
$ S_A $ , which has a Navarro-Frenk-White (NFW) profile, the boosted DM particles$ S_B $ can be produced by the present dark annihilation process of$ S_A S_A^\dagger \to S_B S_B^\dagger $ . To obtain the benchmark velocity$ v_b \sim $ 0.06 in Ref. [3] for boosted$ S_B $ , the value of$ \Delta / m_{S_A} $ is required to be$ \sim 0.0018 $ as$\Delta \simeq \dfrac{1}{2} m_{S_B} v_b^2 \approx \dfrac{1}{2} m_{S_A} v_b^2$ . The flux of the boosted DM$ S_B $ over the full sky can be expressed as [28]$ \Phi_{\mathrm{BDM}}^{4 \pi} = 1.6 \times 10^{-4} \mathrm{cm}^{-2}\mathrm{s}^{-1} \Bigg(\frac{1 \; \mathrm{GeV}}{ m_{S_A}}\Bigg)^2 \times \frac{\langle \sigma_0 v_r \rangle_{0}}{5 \times 10^{-26} \mathrm{cm}^{3}\mathrm{s}^{-1} } \; , $

(8) where
$ \langle \sigma_0 v_r \rangle_{0} $ is today's thermally averaged annihilation cross section of$ S_A S_A^\dagger $ and is suppressed by the phase space factor$ \beta_f $ . Together with the flux of boosted DM$ S_B $ hitting the earth detectors, the number of signal events$ N_{\mathrm{sig}} $ via boosted DM$ S_B $ -electron scattering is$ \begin{array}{*{20}{l}} N_{\mathrm{sig}} \propto \sigma_\mathrm{elec} \times \Phi_{\mathrm{BDM}}^{4 \pi} \; , \end{array} $

(9) where
$ \sigma_\mathrm{elec} $ is the boosted$ S_B $ -electron scattering cross section mediated by the X boson:$ \sigma_\mathrm{elec} \simeq \frac{4 \alpha e_D^2 \epsilon_e^2 \mu_{e S_B }^2 }{m_X^4} \; , $

(10) with
$ \mu_{e S_B } $ being the reduced mass of$ m_e $ and$ m_{S_B } $ .The signal events
$ N_{\mathrm{sig}} $ observed by XENON1T is about 40$ - $ 70 events. In this case, the required scattering cross section$ \sigma_\mathrm{elec} $ is [3]$ \sigma_\mathrm{elec} = 2.1 \times 10^{-31} \mathrm{cm}^2 \Bigg( \frac{10^{-4} \mathrm{cm}^{-2}\mathrm{s}^{-1}}{\Phi_{\mathrm{BDM}}^{4 \pi}} \Bigg) \Bigg( \frac{N_{\mathrm{sig}}}{70} \Bigg) \; . $

(11) To obtain a large cross section in Eq. (10), the mass
$ m_X $ (parameter$ \epsilon_e $ ) should be as small (large) as possible. Substituting the mediator's mass$ m_X = 17 $ MeV,$ e_D = 1 $ , and$ \epsilon_e \lesssim 10^{-3} $ into Eq. (10), we observe that the scattering cross section$ \sigma_\mathrm{elec}\lesssim 10^{-35} \ \mathrm{cm}^2 $ for$ m_{S_B}\gg m_e $ , and this value is smaller than the scattering cross section required by Eq. (11) even when DM mass as light as$ \gtrsim $ 20 MeV. Thus, there is insufficient boosted$ S_B $ flux to produce the XENON1T excess for ordinary annihilations of$ S_A $ . However, if today's dark annihilation of$ S_A $ is enhanced, the result is different. We consider the annihilation of$ S_A $ is close to the ϕ resonance with the mass$ 2 m_{S_A} $ slightly above$ m_\phi $ . Thus, today's dark annihilation$ \langle \sigma_0 v_r \rangle_{0} $ will be significantly enhanced and can produce a large flux of boosted$ S_B S_B^\dagger $ . Moreover, for DM mass$ \lesssim $ 10 MeV, the scattering cross section required by Eq. (11) can be significantly lowered, while such light DM particles will be in tension with constraints from BBN and CMB.Now, we introduce a parameter
$ \xi \equiv m_\phi / 2 m_{S_A} $ in which ξ is slightly smaller than 1. The cross section$ \langle \sigma_0 v_r \rangle_{0} $ is sensitive to the value of$ 1 - \xi $ . The decay width is negligible in DM annihilations when$ 1 - \xi \gg \Gamma_{\phi} / 4 m_\phi $ is satisfied. In the early universe, DM chemically decouples from the thermal bath when the reaction rate$ \Gamma(n \langle \sigma v_r \rangle) $ of DM particles decreases below the Hubble expansion rate H. For$ \langle \sigma_1 v_r \rangle \gg \langle \sigma_0 v_r \rangle $ considered here, the DM$ S_B $ freeze-out occurs slightly later compared with the DM$ S_A $ . As the mass difference between$ S_A $ and$ S_B $ is very small, the number density is$ n_\mathrm{S_B} \simeq n_\mathrm{S_A}^\mathrm{eq} $ during the freeze-out period of$ S_A $ . Considering contributions from the$ S_B S_B^\dagger \to S_A S_A^\dagger $ transition, the effective annihilation cross section of DM$ S_A $ is equivalent to$ 2 \times \sigma_0 v_r $ during the freeze-out period (see Appendix A for details). The relic density of DM is determined by the annihilation cross section, and it can be evaluated using the general method without s-wave approximation [29–31]. The coupling parameter$ \mu_S $ as a function of$ 1 - \xi $ is derived with the relic density of$ S_A S_A^\dagger $ nearly equal to the total DM relic density$ \Omega_D h^2 =0.120 \pm 0.001 $ [32], as shown in Fig. 1. Today's$ S_A S_A^\dagger $ annihilation$ \langle \sigma_0 v_r \rangle_{0} $ as a function of$ 1 - \xi $ is shown in Fig. 2, with the value of$ 1 - \xi $ varying in a range of$ 10^{-3} - 10^{-1} $ . Note that the relative velocity$ v_r $ in the galaxy is$ \sim 10^{-3} $ , and$ \langle \sigma_0 v_r \rangle_{0} $ is insensitive to$ v_r $ in$ s - m_\phi^2 $ or the phase space factor$ \beta_f $ in$ \sigma_0 v_r $ in Eq. (4) for the range of$ 1 - \xi $ of concern. In Fig. 2, the solid curve is the corresponding$ \langle \sigma_0 v_r \rangle_{0} $ for a given$ 1 - \xi $ , and we observe that the annihilation is enhanced when ξ is very close to 1. The dot-dashed and dashed curves are the annihilation cross sections required by the XENON1T excess for two benchmark values of [$ m_X $ = 17 MeV,$ \epsilon_e = 1\times10^{-3} $ ] and [$ m_X $ = 19 MeV,$ \epsilon_e = 0.85 \times10^{-3} $ ] adopted here, respectively. We can observe that the resonance enhanced dark annihilation of today can produce large boosted$ S_B $ flux to account for the XENON1T excess.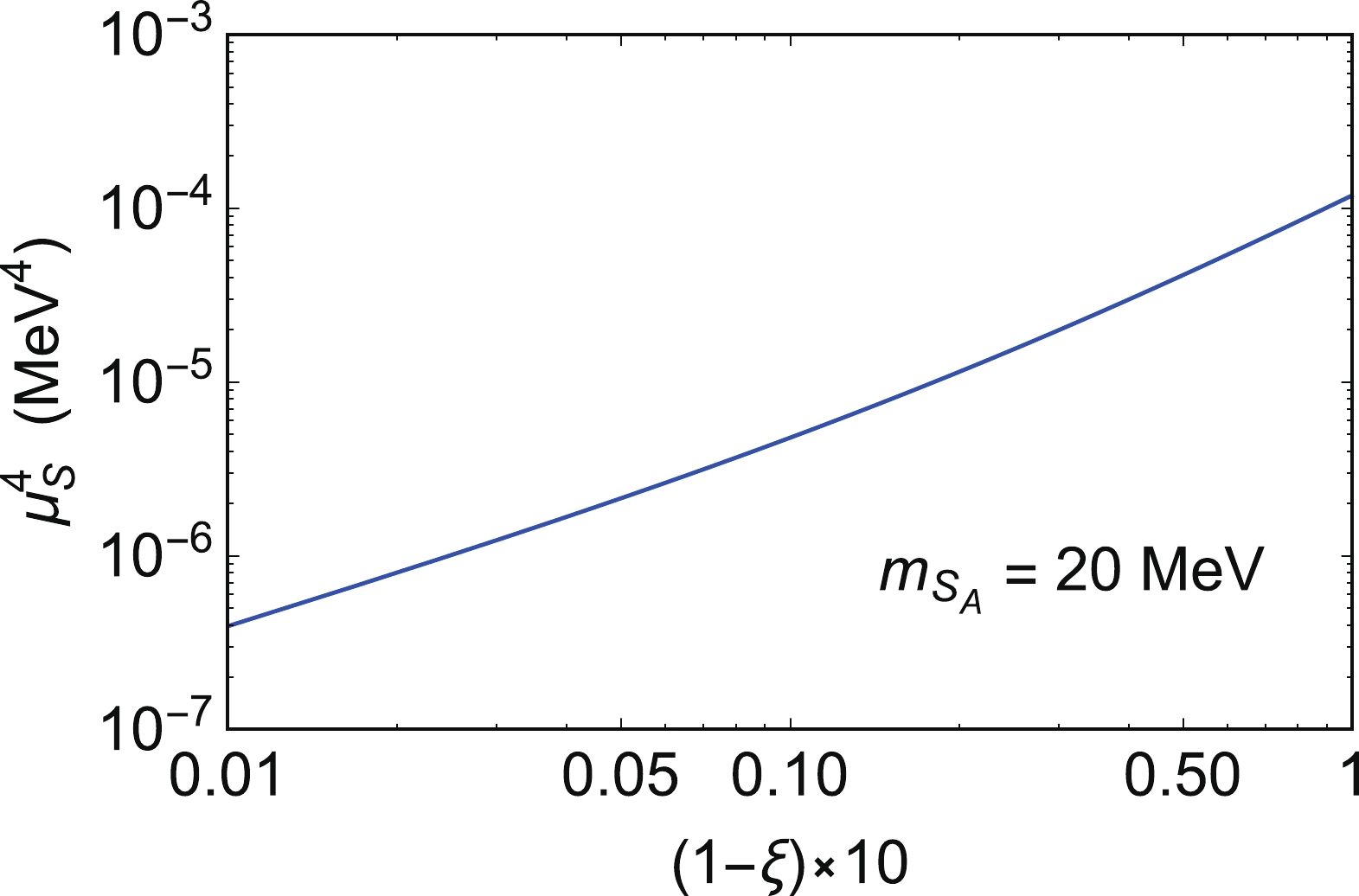
Figure 1. (color online) Coupling parameter
$ \mu_S^4 $ as a function of$ 1 - \xi $ for$ m_{S_A} = $ 20 MeV. Here, the relic density of$ S_A S_A^\dagger $ equal to 0.120 is adopted.
Figure 2. (color online) Relation between
$ \langle \sigma_0 v_r \rangle_{0} $ (solid curve) and$ 1 - \xi $ for$ m_{S_A} = $ 20 MeV. The dot-dashed and dashed curves are for$ m_X $ = 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections required by the XENON1T excess for$ e_D=1\; (0.5) $ .Next, we briefly discuss the annihilation of
$ S_B $ .$ S_B $ contributes only to a very small fraction$ f_{S_B} $ of the total DM relic density, and the relic fraction$ f_{S_B} $ (both$ S_B $ and$ S_B^\dagger $ included) can be obtained using the relation$ f_{S_B} \simeq 4.4 \times 10^{-26} $ cm$ ^3 s^{-1} $ /$ \langle \sigma_1 v_r \rangle $ [33, 34]. The annihilation of$ S_B S_B^\dagger $ is suppressed by the factor$ f_{S_B}^2 $ in observations, and revised annihilation cross section$ f_{S_B}^2 \langle \sigma_1 v_r \rangle /2 $ is shown in Fig. 3 for$ e_D = 1 $ and 0.5. For two benchmark values of$ m_X $ = 17 and 19 MeV, the dark matter masses$ m_{S_B} $ ($ m_{S_A} $ ) in a range of$ m_{S_B} $ ($ m_{S_A} $ )$ > m_X $ are permitted by the constraint from CMB [35] and the typical upper limit set by the anomalous 21-cm absorption [36], as depicted in Fig. 3. Given$ m_{S_A} = $ 20 MeV and$ e_D $ = 1,$ f_{S_B} $ is of order$ \sim 10^{-10} $ for$ m_X \approx $ 17$ - $ 19 MeV.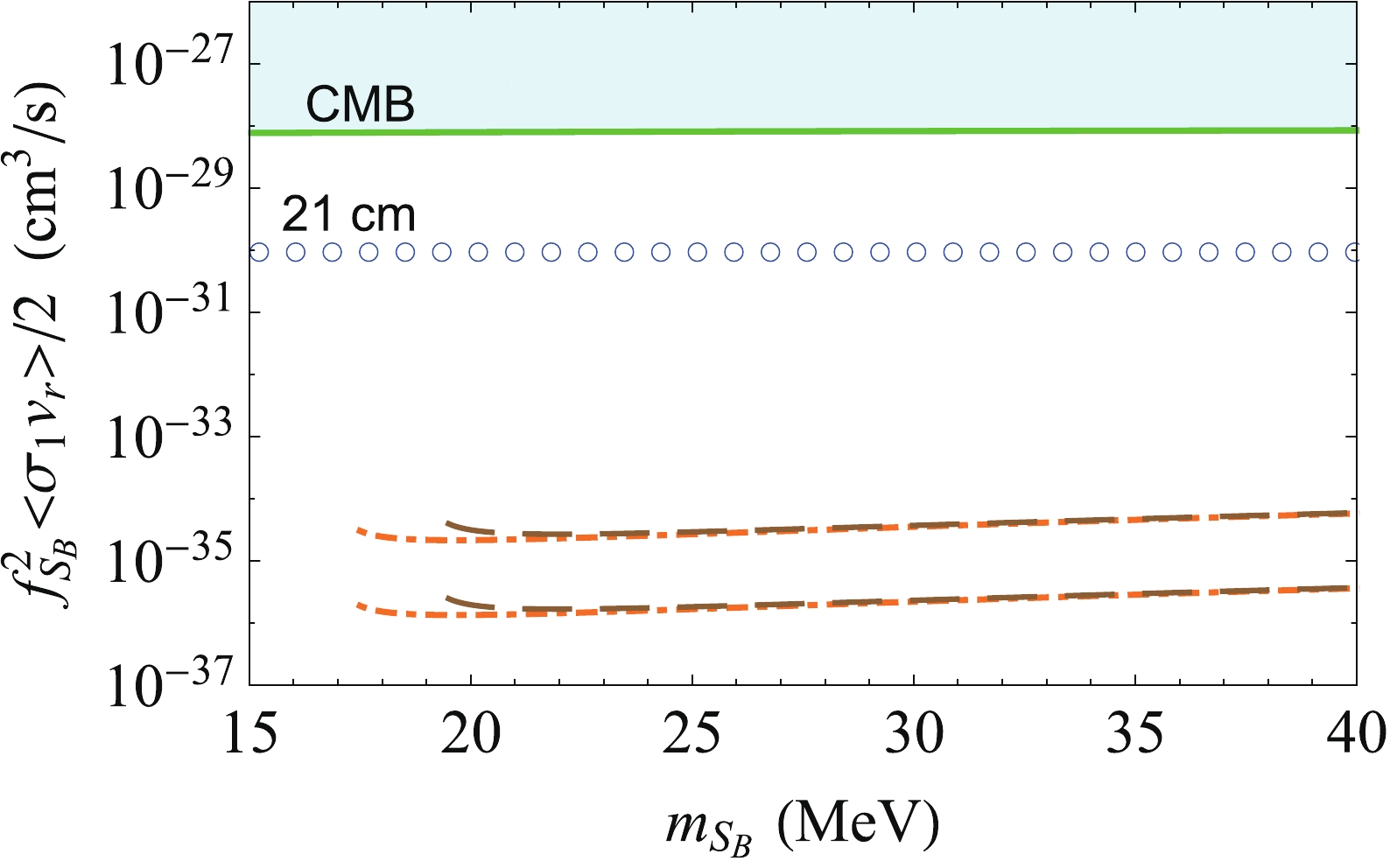
Figure 3. (color online) Revised annihilation cross section
$ f_{S_B}^2 \langle \sigma_1 v_r \rangle /2 $ as a function of$ m_{S_B} $ . The dot-dashed and dashed curves are the revised annihilation cross sections for$ m_X $ = 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections for$ e_D=1\; (0.5) $ . The solid curve is the constraint from CMB [35], and the empty dotted curve is the typical upper limit set by the anomalous 21-cm absorption with$ T_m < $ 4 K at z = 17.2 [36]. -
In addition to the boosted
$ S_B $ accounting for the XENON1T keV excess, a large amount of$ S_A $ and$ S_B $ with a regular velocity distribution are present around the earth. Now, we discuss the un-boosted DM-electron scattering. First, we consider the un-boosted$ S_A $ .$ S_A $ -electron scattering occurs at two-loop level from the$ \phi- X X $ transition and$ X $ -electron coupling. The scattering cross section is significantly below the neutrino floor [37, 38] in DM direct detections.For the un-boosted
$ S_B $ , the$ S_B $ -electron scattering is primarily contributed by the tree level process mediated by the X boson. The corresponding scattering cross section is$ \bar{\sigma}_{{e S_B}} \simeq \frac{4 \alpha e_D^2 \epsilon_e^2 \mu_{e S_B }^2 }{m_X^4} \; , $

(12) with the form factor
$ F_\mathrm{DM}(q) = 1 $ [39]. For$ m_X= $ 17 MeV,$ e_D=1 $ , and$ \epsilon_e = 10^{-3} $ , the scattering cross section is$ \simeq 10^{-35} \mathrm{cm}^2 $ , which is above the bound set by XENON10/100 [10, 11]. This is why the ordinary interpretation of the XENON1T keV excess via DM-electron scattering appears to be in tension with DM direct detections, although DM mass is as low as$ {\cal{O}}(10) $ MeV. In this paper, the DM particles$ S_B S_B^\dagger $ constitutes only a very small fraction$ f_{S_B} $ of the total DM; thus, the tension can be relaxed owing to the effective scattering cross section being$f_{S_B} \bar{\sigma}_{{e S_B}}$ in DM direct detections. The result of the effective scattering cross section$f_{S_B} \bar{\sigma}_{{e S_B}}$ is shown in Fig. 4. We can observe that the benchmarks we consider above can evade the constraints from CMB, 21 cm absorption, and DM direct detections.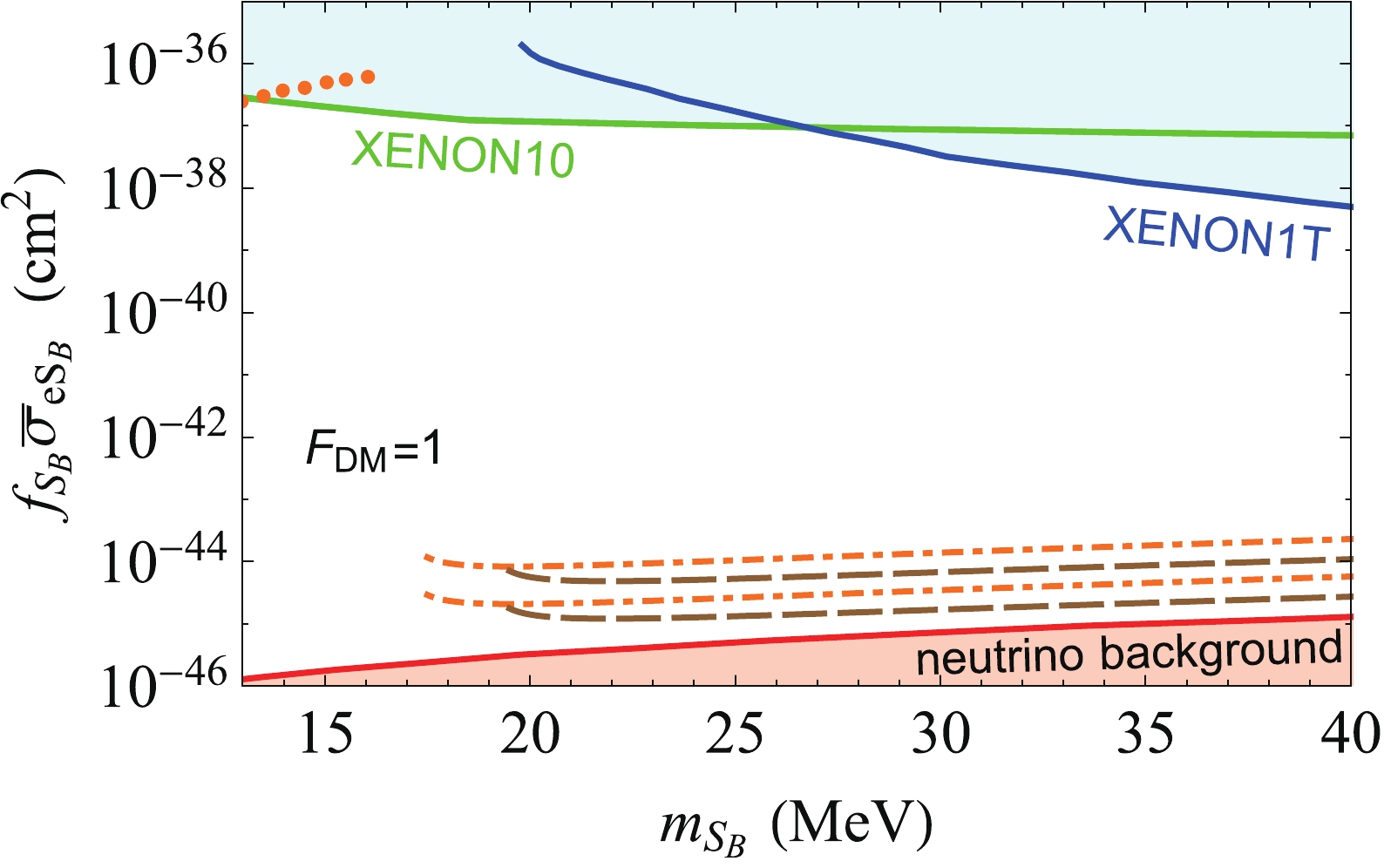
Figure 4. (color online) Effective scattering cross section
$f_{S_B} \bar{\sigma}_{{e S_B}}$ as a function of$ m_{S_B} $ for un-boosted$ S_B S_B^\dagger $ in DM direct detections. The dot-dashed and dashed curves are the effective scattering cross section for the benchmark values as labeled in Figs. 2 and 3. The lower (upper) limit of the dot-dashed and dashed curves correspond to the cross sections for$ e_D=1\; (0.5) $ . The upper two solid curves are the upper limits from XENON10 [11] and XENON1T [13]. For comparison, the dotted curve on the top left is for$m_{S_B} < $ $ m_X=16.7$ MeV [19]. The lower solid curve is the neutrino background [37].Moreover, for
$ m_{S_B} < m_X $ , sufficiently boosted$ S_B $ can also be produced, and it induces the XENON1T keV excess. The mass$ m_{S_B} $ should be$ \lesssim $ 13 MeV given the constraints from DM direct detections, as shown by the dotted curve in Fig. 4. Meanwhile, for$ S_A $ and$ S_B $ , the mass$ m_{S_B} $ ($ m_{S_A} $ ) should be$ \gtrsim $ 13 MeV with the bound from BBN [17]. Thus, a very small parameter space remains for the case of$ m_{S_B} < m_X $ when interpreting the XENON1T keV excess, and this case is beyond the scope of this paper. -
The boosted DM with a high speed of about 0.05-0.1 c and with a large DM-electron scattering cross section (as large as
$ 10^{-29} $ cm2 [3]) can interpret the XENON1T electron-event anomaly, as discussed in Refs. [2, 3]. However, can the boosted DM with such a large DM-electron scattering cross section be compatible with the present stringent bounds, such as the BBN, low energy experiments, and DM direct detections? This key question should be answered when proposing a model to explain the XENON1T anomaly. In this paper, we attempt to answer this question. The proposed GeV DM has a large scattering cross section ($ 10^{-29} $ cm2) between DM and an electron [3]. The required mediator mass is as light as 0.1 MeV. Such a light mediator is excluded by the BBN, which sets a lower mass bound on new thermal equilibrium particles, that is, the mass of a new particle should be above 10 MeV. Considering the constraints from BBN and low energy experiments, we observe that the scattering cross section between DM and an electron is smaller in reality, approximately smaller than$ 10^{-35} $ cm2. We observe that light DM in the MeV scale with an enhanced annihilation source and a scattering cross section of$ 10^{-35} $ cm2 can produce sufficient keV electron excess events observed by XENON1T and be permitted by present DM direct detections.We have investigated an interpretation of the XENON1T excess using two scalar DM particles,
$ S_A $ and$ S_B $ .$ S_A $ is neutral and$ S_B $ is dark charged in the hidden sector. The boosted$ S_B $ can be produced by the annihilation$ S_A S_A^\dagger\to \phi \to S_B S_B^\dagger $ mediated by a scalar ϕ.$ S_B $ -electron scattering is intermediated by a vector boson X. We focus on the range$ m_{\phi} > m_{S_A} \simeq m_{S_B} > m_X $ . Although the constraints from BBN, CMB, and low-energy experiments require the boosted$ S_B $ -electron scattering cross section mediated by X to be$ \lesssim 10^{-35}\; \mathrm{cm}^2 $ , MeV-scale DM with a resonance enhanced dark annihilation today can still produce sufficient boosted DM and induce the XENON1T keV electron excess. The relic density of$ S_B $ can be significantly reduced by the$ s $ -wave process of$ S_B S_B^\dagger \to X X $ ; thus, this$ s $ -wave annihilation is permitted by the constraints from CMB and 21-cm absorption. A very small relic fraction of$ S_B $ is compatible with the stringent bound on un-boosted$ S_B $ -electron scattering in DM direct detections. The$ S_A $ -electron scattering occurs at loop level, and the scattering cross section is below the neutrino floor in direct detections. We look forward to the further investigation of MeV DM and the corresponding new interactions in the future. -
For
$ \langle \sigma_1 v_r \rangle \gg \langle \sigma_0 v_r \rangle $ , the freeze-out of DM$ S_A $ occurs first, and the DM$ S_B $ decouples from the thermal bath later. For the DM particle$ S_A $ , the evolution of the number density$ n_\mathrm{S_A} $ is given by$ \begin{aligned}[b] \frac{{\rm d} n_{S_A}}{{\rm d}t} +3 n_{S_A} H =& - \langle \sigma_0 v_r \rangle_{S_A S_A^\dagger \to S_B S_B^\dagger} (n_{S_A}^2 - (n_{S_A}^{\rm eq})^2) \\&+ \langle \sigma_0 v_r \rangle_{S_B S_B^\dagger \to S_A S_A^\dagger} \left(n_{S_B}^2 - \frac{(n_{S_B}^{\rm eq})^2}{(n_{S_A}^{\rm eq})^2}n_{S_A}^2\right) , \end{aligned} \tag{A1}$

where
$n_{S_A}^\mathrm{eq}$ and$n_{S_B}^\mathrm{eq}$ are the equilibrium number densities, and H is the Hubble parameter. The DM particle$ S_B $ is still in the thermal equilibrium with the thermal bath during the freeze-out period of$ S_A $ , and in this case, we obtain the number density$n_{S_B} = n_{S_B}^\mathrm{eq} \simeq n_{S_A}^\mathrm{eq}$ with ignorable mass difference between$ S_A $ and$ S_B $ . Thus, Eq. (A1) can be rewritten as$ \frac{{\rm d} n_{S_A}}{{\rm d}t} +3 n_\mathrm{S_A} H \simeq - 2 \langle \sigma_0 v_r \rangle_{S_A S_A^\dagger \to S_B S_B^\dagger} (n_{S_A}^2 - (n_{S_A}^{\rm eq})^2) . \tag{A2}$

For DM
$ S_A $ , the effective annihilation cross section is equivalent to$ 2 \times \sigma_0 v_r $ during the freeze-out period for the$ S_B S_B^\dagger \to S_A S_A^\dagger $ transition considered.
Interpretation of XENON1T excess with MeV boosted dark matter
- Received Date: 2021-10-19
- Available Online: 2022-08-15
Abstract: The XENON1T excess of keV electron recoil events may be induced by the scattering of electrons and long-lived particles with an MeV mass and high speed. We consider a tangible model composed of two scalar MeV dark matter (DM) particles,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: