-
The standard model (SM) of particle physics [1–3] can explain high-energy experimental results successfully. Particle masses arise from the spontaneous breaking of electroweak symmetry, which is achieved through the Brout-Englert-Higgs (BEH) mechanism [4–9]. In the BEH mechanism, only one scalar field remains with its corresponding quantum, the Higgs boson, which was finally discovered at the LHC with a mass of approximately 125 GeV [10–13]. The latest measurements [14–18] of this Higgs boson at the LHC exhibited no bias from the SM predicted Higgs boson. However, numerous important questions about the nature and origin of the Higgs boson discovered at the LHC remain unanswered. The SM cannot explain many observations, such as dark matter and neutrino masses, and puzzles, including the hierarchy and strong-CP problems [19]. Physics beyond the SM (BSM) can provide a Higgs boson that is compatible with the observed 125 GeV Higgs boson and can address some of the questions that remain unanswered by the SM. The extended Higgs sector of the BSM models, for example, the next-to-minimal supersymmetric standard model (NMSSM) [20, 21] and generalized two Higgs doublet model (2HDM) [22, 23], can also provide additional Higgs bosons with masses below 125 GeV, which can give rise to a rich and interesting phenomenology [24–27].
Another phenomenologically interesting model is the Georgi-Machacek (GM) model [28, 29], which provides a prototype for extensions of the SM Higgs sector by adding scalars in isospin-triplet to preserve custodial SU(2) symmetry. The GM model can be generalized to include scalars in isospin representations larger than triplets under the custodial symmetry [30]. The physical fields of the generalized GM model can be transformed to a fiveplet, triplet, and two singlets. The couplings of the SM-like Higgs boson in the GM model to
$ WW $ and$ ZZ $ can be larger than those in the SM. The singly- and doubly-charged scalars couple at tree level to vector boson pairs. These futures make this model interesting to the experimental communities performing direct searches, for example, at the LHC [31–34]. LHC experiments have sensitivity to the production of the fermiophobic custodial-fiveplet states$ H_{5}^{0} $ ,$ H_{5}^{\pm} $ , and$ H_{5}^{\pm\pm} $ . Numerous studies with their masses ($ m_{5} $ ) greater than 200 GeV have been performed, guided with the so-called H5-plane benchmark by the LHC Higgs Cross Section Working Group [35]. Detailed phenomenological studies can be found in [36]. Both ATLAS and CMS have performed searches for diphoton resonances in mass regions lower than 125 GeV; it is interesting to verify the phenomenology of the neutral custodial fiveplet scalar$ H_{5}^{0} $ in the lower mass range. Recently, a new benchmark plane known as the low-$ m_{5} $ benchmark was introduced and studied [37]. To study the updated constraints on the GM model from LHC Run2 (see [38] for details), the ATLAS results of the diphoton resonance search using LHC Run1 8 TeV data [39] were compared with GM$ H_{5}^{0}\rightarrow \gamma\gamma $ decays from a general scan with 10000 points. The CMS Collaboration published the results of the search for low-mass Higgs bosons in the mass range from 70 to 110$ {\rm GeV} $ in the diphoton channel, with the full 2016 dataset at$ \sqrt{s} $ = 13 TeV [40], which exhibited greater sensitivity in the same mass range than that of the ATLAS result with 80$ \; {\rm fb}^{-1} $ data at$ \sqrt{s} $ = 13 TeV [41], as illustrated in Fig. 1 of Ref. [42]. Therefore, the CMS searching results have more stringent constraints on the GM model.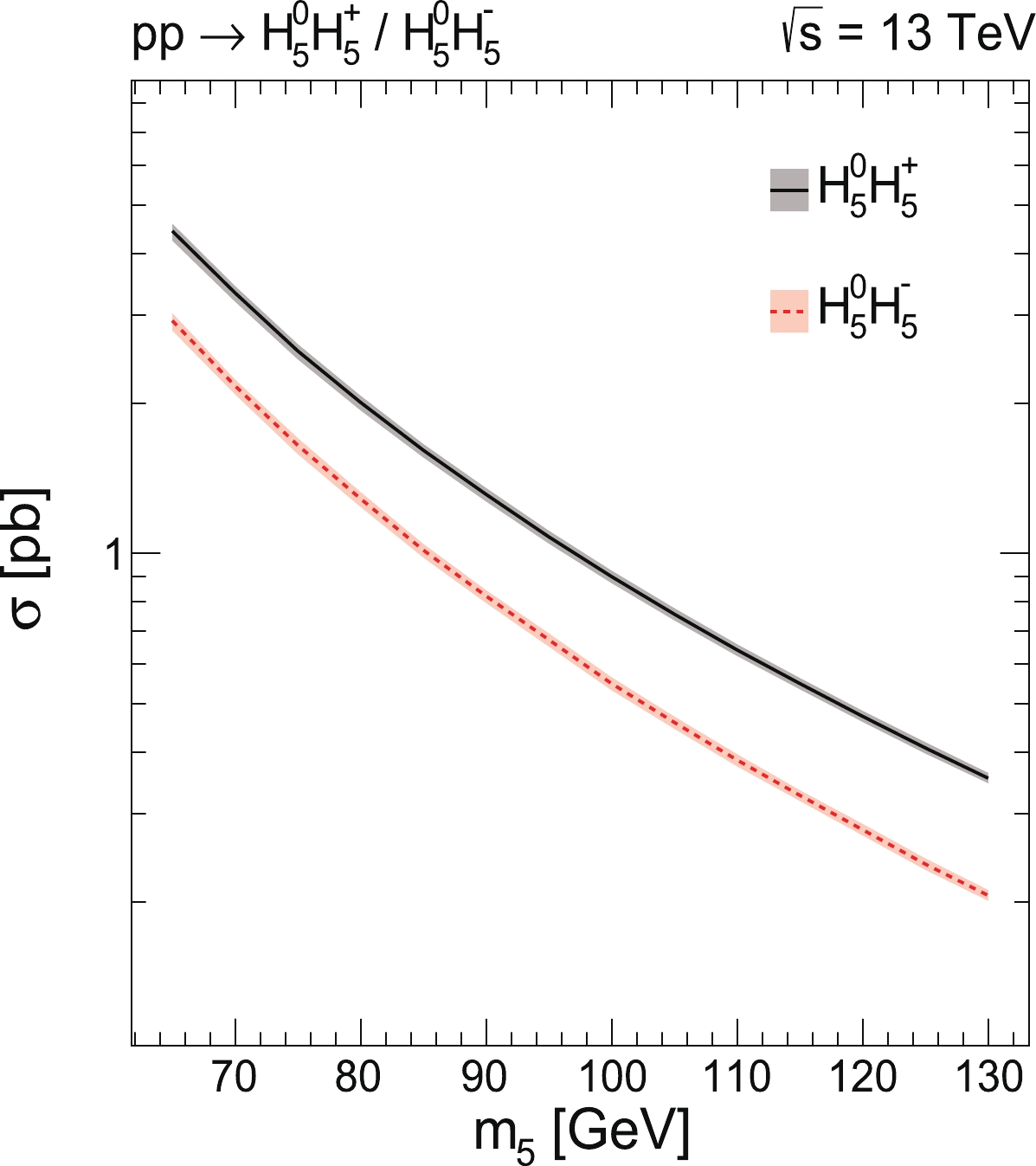
Figure 1. (color online) Cross sections of
$H_{5}^{0}H_{5}^{+}$ and$H_{5}^{0}H_{5}^{-}$ at the LHC with$\sqrt{s}$ = 13 TeV as a function of$H_{5}^{0}$ mass ($m_{5}$ ) in picobarns (pb), computed using$MadGraph5\_aMC@NLO$ at NLO in QCD, with the total uncertainties from the PDF,$\alpha_{s}$ , and QCD scales shown as the filled area around the central lines.In this paper, the phase space of the free parameters of the GM model, which is favored for the low-mass neutral custodial fiveplet scalar
$ H_{5}^{0} $ , is carefully studied. We explore the possibility of constraining the low-mass$ H_{5}^{0} $ in the GM model by comparing the production rates of the$ H_{5}^{0}\rightarrow \gamma\gamma $ decays with the latest CMS results [40] after applying theoretical constraints and constraints from experimental measurements. The phenomenology of the surviving GM parameter space from this comparison is summarized. In addition, the discovery potential of the other interesting decay channels of this low-mass neutral custodial fiveplet scalar is studied and discussed. This paper is organized as follows: In Section II, we briefly introduce the GM model and our chosen parameter ranges for the scan. The numerical analyses and results are described in Section III. Finally, the conclusions are presented in Section IV. -
The scalar sector of the GM model [28, 29] consists of the usual complex doublet (
$ \phi^+ $ ,$ \phi^0 $ ), a real triplet ($ \xi^+ $ ,$ \xi^0 $ ,$ \xi^- $ ), and a complex triplet ($ \chi^+ $ ,$ \chi^+ $ ,$ \chi^0 $ ). To make the global SU(2)$ _{\rm L} \times $ SU(2)$ _{\rm R} $ symmetry explicit, the doublet is expressed in the form of a bi-doublet Φ, whereas the triplets are combined to form a bi-triplet X.$ \Phi = \left( {\begin{array}{*{20}{c}} {{\phi ^{0*}}}&{{\phi ^ + }}\\ { - {\phi ^{ + *}}}&{{\phi ^0}} \end{array}} \right),\quad \;\;\;{\kern 1pt} X = \left( {\begin{array}{*{20}{c}} {{\chi ^{0*}}}&{{\xi ^ + }}&{{\chi ^{ + + }}}\\ { - {\chi ^{ + *}}}&{{\xi ^0}}&{{\chi ^ + }}\\ {{\chi ^{ + + *}}}&{ - {\xi ^{ + *}}}&{{\chi ^0}} \end{array}} \right).$

(1) The vevs (vacuum expectation values) are defined by
$ \langle \Phi \rangle = ({ v_{\phi}}/{\sqrt{2}}) I_{2\times2} $ and$ \langle X \rangle = v_{\chi} I_{3 \times 3} $ , where$ I_{2\times2} $ and$ I_{3\times3} $ are the unit matrices. The W and Z boson masses constrain$ v_{\phi}^2 + 8 v_{\chi}^2 \equiv v^2 = \frac{1}{\sqrt{2} G_{\rm F}} \approx (246\; {\rm GeV})^2 $

(2) with
$ G_{\rm F} $ as the Fermi constant.The most general gauge-invariant scalar potential involving these fields that conserves the custodial SU(2) is given by
$ \begin{aligned}[b] V(\Phi,X) =& \frac{\mu_2^2}{2} {\rm{Tr}}(\Phi^\dagger \Phi) + \frac{\mu_3^2}{2} {\rm{Tr}}(X^\dagger X) \\ & + \lambda_1 [{\rm{Tr}}(\Phi^\dagger \Phi)]^2 + \lambda_2 {\rm{Tr}}(\Phi^\dagger \Phi) {\rm{Tr}}(X^\dagger X) \\& + \lambda_3 {\rm{Tr}}(X^\dagger X X^\dagger X) + \lambda_4 [{\rm{Tr}}(X^\dagger X)]^2\\& - \lambda_5 {\rm{Tr}}( \Phi^\dagger \tau^a \Phi \tau^b) {\rm{Tr}}( X^\dagger T^a_1 X T^b_1) \end{aligned} $

$ \begin{aligned}[b]\quad\quad & - M_1 {\rm{Tr}}(\Phi^\dagger \tau^a \Phi \tau^b)(U X U^\dagger)_{ab} \\& - M_2 {\rm{Tr}}(X^\dagger T^a X T^b)(U X U^\dagger)_{ab}. \end{aligned} $

(3) Here, the SU(2) generators for the doublet representation are
$ \tau^a = \sigma^a/2 $ , where$ \sigma^a $ is the Pauli matrices, and the generators for the triplet representation$ T^a_1 $ are$\begin{aligned}[b]& {T^1} = \left( {\begin{array}{*{20}{c}} 0&{\dfrac{1}{{\sqrt 2 }}}&0\\ {\dfrac{1}{{\sqrt 2 }}}&0&{\dfrac{1}{{\sqrt 2 }}}\\ 0&{\dfrac{1}{{\sqrt 2 }}}&0 \end{array}} \right),\\& {T^2} = \left( {\begin{array}{*{20}{c}} 0&{ - \dfrac{\rm i}{{\sqrt 2 }}}&0\\ {\dfrac{\rm i}{{\sqrt 2 }}}&0&{ - \dfrac{\rm i}{{\sqrt 2 }}}\\ 0&{\dfrac{\rm i}{{\sqrt 2 }}}&0 \end{array}} \right),\\& {T^3} = \left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&0&0\\ 0&0&{ - 1} \end{array}} \right). \end{aligned} $

(4) The matrix U is given by [43]
$ U = \left( {\begin{array}{*{20}{c}} {- \dfrac{1}{\sqrt{2}}} & {0} & {\dfrac{1}{\sqrt{2}} }\\ {- \dfrac{\rm i}{\sqrt{2}}} & {0 } & { - \dfrac{\rm i}{\sqrt{2}} }\\ {0 } & { 1 } & { 0} \end{array}} \right). $

(5) The physical fields can be organized by their transformation properties under custodial SU(2) symmetry into two singlets, a triplet, and a fiveplet. The triplet and fiveplet states are given by
$ \begin{aligned}[b] H_3^+ = &- s_H \phi^+ + c_H \frac{\left(\chi^++\xi^+\right)}{\sqrt{2}}, \\ H_3^0 =& - s_H \phi^{0,i} + c_H \chi^{0,i}, \\ H_5^{++} =& \chi^{++}, \\ H_5^+ =& \frac{\left(\chi^+ - \xi^+\right)}{\sqrt{2}}, \\ H_5^0 =& -\sqrt{\frac{2}{3}} \xi^0 + \sqrt{\frac{1}{3}} \chi^{0,r}, \end{aligned} $

(6) where the vevs are parameterized by
$ c_H \equiv \cos\theta_H = \frac{v_{\phi}}{v}, \qquad s_H \equiv \sin\theta_H = \frac{2\sqrt{2}\,v_\chi}{v}, $

(7) and the neutral fields can be decomposed into real and imaginary parts according to
$ \begin{aligned}[b]& \phi^0 \to \frac{v_{\phi}}{\sqrt{2}} + \frac{\phi^{0,r} + {\rm i} \phi^{0,i}}{\sqrt{2}}, \qquad \chi^0 \to v_{\chi} + \frac{\chi^{0,r} + {\rm i} \chi^{0,i}}{\sqrt{2}}, \\& \xi^0 \to v_{\chi} + \xi^0. \end{aligned} $

(8) The masses within each custodial multiplet are degenerate at tree level, and after eliminating
$ \mu_2^2 $ and$ \mu_3^2 $ in favor of the vevs, the masses can be written as①$ \begin{aligned}[b]m_5^2 =& \frac{M_1}{4 v_{\chi}} v_\phi^2 + 12 M_2 v_{\chi} + \frac{3}{2} \lambda_5 v_{\phi}^2 + 8 \lambda_3 v_{\chi}^2, \\ m_3^2 =& \frac{M_1}{4 v_{\chi}} (v_\phi^2 + 8 v_{\chi}^2) + \frac{\lambda_5}{2} (v_{\phi}^2 + 8 v_{\chi}^2). \end{aligned} $

(9) The two singlet mass eigenstates are given by
$ \begin{aligned}[b]h =& \cos \alpha \, \phi^{0,r} - \sin \alpha \, H_1^{0\prime}, \\ H =& \sin \alpha \, \phi^{0,r} + \cos \alpha \, H_1^{0\prime}, \end{aligned} $

(10) where
$ H_1^{0 \prime} = \sqrt{\frac{1}{3}} \xi^0 + \sqrt{\frac{2}{3}} \chi^{0,r}. $

(11) The mixing angle and masses are given by
$ \begin{aligned}[b]\sin 2 \alpha =& \frac{2 {\cal{M}}^2_{12}}{m_H^2 - m_h^2}, \qquad \cos 2 \alpha = \frac{ {\cal{M}}^2_{22} - {\cal{M}}^2_{11} }{m_H^2 - m_h^2}, \\ m^2_{h,H} =& \frac{1}{2} \left[ {\cal{M}}_{11}^2 + {\cal{M}}_{22}^2 \mp \sqrt{\left( {\cal{M}}_{11}^2 - {\cal{M}}_{22}^2 \right)^2 + 4 \left( {\cal{M}}_{12}^2 \right)^2} \right]. \end{aligned} $

(12) The elements of their mass matrix are given by
$ \begin{aligned}[b]{\cal{M}}_{11}^2 =& 8 \lambda_1 v_{\phi}^2, \\ {\cal{M}}_{12}^2 =& \frac{\sqrt{3}}{2} v_{\phi} \left[ - M_1 + 4 \left(2 \lambda_2 - \lambda_5 \right) v_{\chi} \right], \\ {\cal{M}}_{22}^2 =& \frac{M_1 v_{\phi}^2}{4 v_{\chi}} - 6 M_2 v_{\chi} + 8 \left( \lambda_3 + 3 \lambda_4 \right) v_{\chi}^2. \end{aligned} $

(13) We define H to be heavier than h (
$ m_h < m_H $ ), and either h or H can be the observed 125 GeV Higgs boson at the LHC. -
The program package
$ GMCALC $ (version 1.5.0) [44] with Fortran code is employed in this study to calculate the mass spectrum of the Higgs bosons in the GM model, their decaying branching ratios (BR) and total widths, their relevant mixing angles, and the tree-level couplings of the Higgs bosons to other particles. It also includes a routine to generate the datacard "$ param\_card. dat $ " to be used by$ MadGraph5\_aMC@NLO $ [45] with implementation of the corresponding FeynRules [46] model for the cross sections of the GM Higgs bosons. The FeynRules implementation for the GM model includes the automatic calculation of the next-to-leading order QCD corrections. The Universal FeynRules Output (UFO) file of the FeynRules implementation for the GM model, which can be downloaded from [47], is used by$ MadGraph5\_ aMC@NLO $ (version 2.7.2) in this study. The theoretical constraints in this paper include the conditions for tree-level unitarity, the bounded-from-below requirement on the scalar potential, and the absence of deeper custodial symmetry-breaking minima, as detailed in [44]. Indirect constraints from the S parameter and flavor physics$ b \rightarrow s\gamma $ and$ B_{s}^{0} \rightarrow \mu^{+}\mu^{-} $ are also considered. Constraints from the public tools$ HiggsBounds $ -$ 5 $ [48] (version 5.8.0) and$ HiggsSignals $ -$ 2 $ [49] (version 2.5.1) are applied to further compare the predictions of the custodial-singlet mass eigenstate h or H with the LHC Higgs search results of various channels from Run2 at a center-of-mass energy of 13 TeV. These include the cross section limits, signal rate and mass measurements, and results in the form of simplified template cross section measurements.A new low-
$ m_{5} $ benchmark for the GM model, defined for the neutral custodial fiveplet scalar with a mass$ m_{5} $ $ \in $ (50,550) GeV, was proposed in [37] to study the phenomenological behavior of the$ H_{5} $ states and SM-like Higgs, h. In [37],$ \lambda_{3} $ (= −1.5),$ \lambda_{4} $ (= 1.5 =$ -\lambda_{3} $ ), and$ M_{2} $ (= 20 GeV) were fixed as constants, with the lightest custodial-singlet mass eigenstate h as the LHC observed 125 GeV Higgs boson. In addition, the parameters$ \lambda_{2} $ and$ \lambda_{5} $ were fixed as functions of the mass$ m_{5} $ :$ \lambda_{2} $ = 0.08 ($ m_{5} $ /100 GeV), and$ \lambda_{5} $ = −0.32 ($ m_{5} $ /100 GeV)= −4$ \lambda_{2} $ . Only$ m_{5} $ and$ s_{H} $ were permitted to vary in the studied ranges,$ m_{5} $ $ \in $ (65, 550) GeV and$ s_{H} $ $ \in $ (0, 1). After several iterations of the tests, to generate the points efficiently, we employ the following ranges for the six specific parameters:$ \begin{aligned}[b] &0.0 < M_{2} < 50, \quad 0.0 < s_{H} < 0.66, \quad -1.6 < \lambda_{3} < 0.0, \\ &0.0 < \lambda_{4} < 1.6, \quad 0.0 < \lambda_{2} < 0.08 (m_{5}/50\;{\rm{ GeV}}), \\& -0.32 (m_{5}/50\;{\rm{ GeV}}) < \lambda_{5} < 0.0. \end{aligned} $

(14) We find that wider parameters ranges have practically no impact on our conclusions. Similar to [37], the Fermi constant
$ G_{\rm F} $ is set as$ 1.1663787 \times 10^{-5} $ $ {\rm GeV}^{-2} $ . To study more stringent constraint on the GM model using the results of the search for low-mass Higgs bosons in the mass range from 70 to 110$ {\rm GeV} $ in the diphoton channel at the CMS [40] and to study the discovery potential of other interesting decay channels, the initial scan range of the$ H_{5}^{0} $ mass are specified in the range$ m_{5} $ $ \in $ (65,130) GeV. In addition, any of the custodial-singlet mass eigenstates h or H can be the LHC observed Higgs boson; therefore, we should consider the constraints on$ HiggsBounds $ -$ 5 $ and$ HiggsSignals $ -$ 2 $ , as mentioned in the above paragraph. -
In this study, we focus on the phenomenological behaviors of the neutral custodial fiveplet scalar state
$ H_{5}^{0} $ decaying into two photons and several other interesting final states. After implementation of the constraints, as mentioned in the previous subsection II.B, production of$ H_{5}^{0} $ from the scan is compared to the results of the search for low-mass Higgs bosons in the mass range from 70 to 110$ {\rm GeV} $ in the diphoton channel with the full 2016 dataset at$ \sqrt{s} $ = 13 TeV with the CMS experiment at the LHC [40]. The favored GM parameter phase space from this comparison is summarized. The discovery potential of the other interesting decay channels of this low-mass neutral custodial fiveplet scalar is also studied and discussed. -
The cross sections of the seperate Drell-Yan production of
$ H_{5}^{0}H_{5}^{+} $ and$ H_{5}^{0}H_{5}^{-} $ at next-to-leading order (NLO) in QCD from 13 TeV pp collisions are first generated using$ MadGraph5\_aMC@NLO $ (version 2.7.2) with the UFO file downloaded from [47] for the GM model and the datacard "$ param\_card.dat $ " generated with$ GMCALC $ (version 1.5.0). The PDF4LHC15 NLO parton distribution functions (PDFs) [50],$ PDF4LHC15\_nlo\_ 30\_pdfas $ , are employed. In these PDFs, 30 sets of symmetric eigenvectors provide the PDF systematic uncertainties, and two additional sets with$ \alpha_{s}(M_{Z}) $ = 0.1165 and$ \alpha_{s}(M_{Z}) $ = 0.1195 separately, which differ from the central value ($ \alpha_{s}(M_{Z}) $ = 0.118), are used to estimate the systematic uncertainties from$ \alpha_{s} $ . Typically, the combined PDF +$ \alpha_{s} $ uncertainty on the cross sections for both$ H_{5}^{0}H_{5}^{+} $ and$ H_{5}^{0}H_{5}^{-} $ is approximately 2.0%. The uncertainties from the QCD scales of the renormalization ($ \mu_{\rm R} $ ) and factorization scales ($ \mu_{\rm F} $ ) are practically obtained from the cross section results of nine scale configurations by combining$ \mu_{\rm R} $ /$ \mu_{0} $ = (0.5, 1, 2) and$ \mu_{\rm F} $ /$ \mu_{0} $ = (0.5, 1, 2) independently, with the central value of the scale factor$ \mu_{0} $ as the sum of the transverse masses divided by two of the final state particles and partons. Subsequently, the maximum and minimum values among these results are used to evaluate the scale uncertainties. Typically, the scale uncertainty varies from approximately 1.5% at$ m_{5} $ = 130 GeV to approximately 4.0% at$ m_{5} $ = 65 GeV. Figure 1 shows the total cross sections of these two processes as a function of the$ H_{5}^{0} $ mass in picobarns (pb), with the total uncertainties from the PDF,$ \alpha_{s} $ , and QCD scales included as the filled area around the central values. The Drell-Yan production cross sections of$ H_{5}^{0}H_{5}^{+} $ and$ H_{5}^{0}H_{5}^{-} $ are independent of the six specific parameters in formula 14 but dependent on the mass$ m_{5} $ . -
In this subsection, we explore the possibility that the signal may originate from the neutral custodial fiveplet scalar state
$ H_{5}^{0} $ in the GM model. First, we perform the comparison of the production cross sections of$ H_{5}^{0}\rightarrow \gamma\gamma $ from the GM scans with constrained parameters, as introduced in subsection II.B, and the CMS observed upper limit of the production cross sections with the full 2016 dataset at$ \sqrt{s} $ = 13 TeV [40]. Subsequently, the six specific parameters are studied in detail by applying the CMS searching results. A general scan of approximately six million points that satisfy all theoretical constraints and indirect constraints from the S parameter and flavor physics, as described in subsection II.B, are randomly generated in the parameter phase space, as specified in formula 14, and the mass region$ m_{5} $ $ \in $ (65, 130) GeV. With$ HiggsBounds $ -$ 5 $ , the predictions of either h or H from the scan should be consistent with the search results of the LHC observed Higgs boson in various channels from Run2 at a center-of-mass energy of 13 TeV. With$ HiggsSignals $ -2, the compatibility of h or H from the scans with the LHC measured results of the signal strengths and mass of the Higgs boson in Run2 is also verified by evaluating a$ \chi^{2} $ calculation and its associated p-value. For scan points compatible with the experimental constraints, the p-value given by$ HiggsSignals $ -2 should be greater than 0.05. By applying the constraints from these two programs, approximately 5.5 million points remain for further analysis in the subsequent paragraph and subsections.The production rates, in pb, of
$ H_{5}^{0} $ decaying into$ \gamma\gamma $ , (σ$ \times $ BR)$ _{H_{5}^{0}\rightarrow \gamma\gamma} $ , where σ is the cross section of$ H_{5}^{0} $ production, and$ BR $ is the branching ratio of$ H_{5}^{0} $ decaying into$ \gamma\gamma $ , versus$ H_{5}^{0} $ mass are shown in Fig. 2. The observed exclusions or upper limits of the CMS Collaboration with the 2016 dataset at$ \sqrt{s} $ = 13 TeV [40] are superimposed in the plot, as shown by the red line. It can be seen that many of the points above the CMS observed exclusions can be excluded in the mass region$ m_{5} $ ∈ (70, 110) GeV at the 95% confidence level (CL). However, there are still numerous points with lower production rates, which cannot be excluded by the CMS observed upper limits.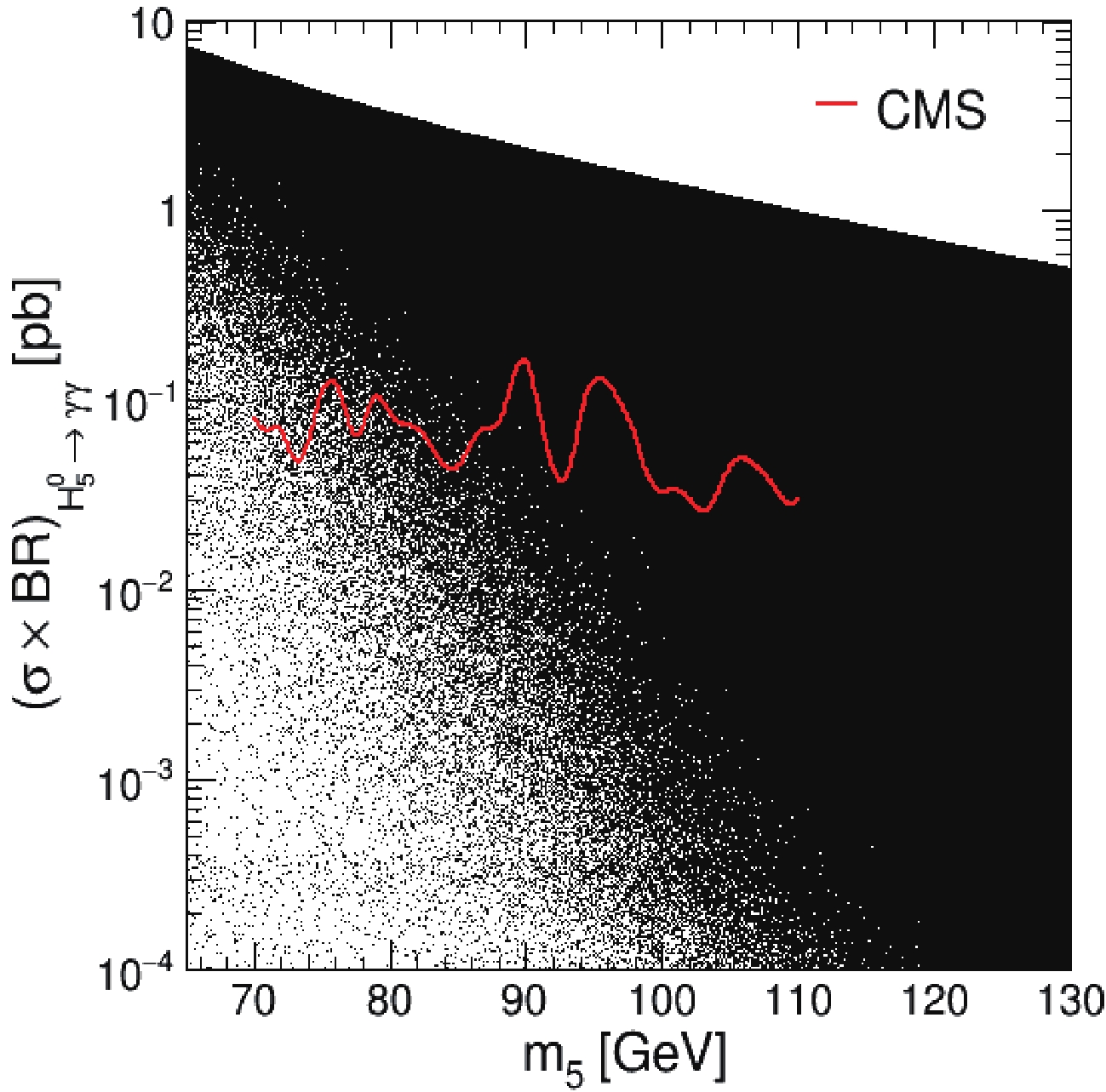
Figure 2. (color online) Cross sections multiplied by the branching ratio of
$H_{5}^{0}\rightarrow \gamma\gamma$ from the scan (black points) with the latest CMS observed exclusions [40] (red line) superimposed for comparison.Owing to this CMS analysis [40], we can attempt to constrain GM parameter spaces by checking the parameter distributions of the points below the CMS observed upper limits. Figure 3 shows comparisons between the distribution of all selected points (black histogram) and that of the points not excluded by the CMS observed upper limits (red filled histogram) on top of the constraints, as described in subsection II.B, for each parameter of
$ \lambda_2 $ ,$ \lambda_3 $ ,$ \lambda_4 $ ,$ \lambda_5 $ ,$ M_2 $ , and$ {\rm sin}{\theta_H} $ . Both distributions are normalized to unity. The CMS observation may exclude certain regions for some parameters, such as$ \lambda_3 $ and$ \lambda_4 $ . For these points, which are not excluded by the CMS observed upper limits,$ \lambda_3 $ exhibits a tendency toward higher values with points peaking at approximately -0.1, whereas$ \lambda_4 $ favors lower values with a peak at approximately 0.6, indicating an opposite behavior to$ \lambda_3 $ . One can also observe that$ M_2 $ prefers lower mass values, whereas$ {\rm sin}{\theta_H} $ tends to accumulate at the middle of the scanned range with a peak at approximately 0.45. For the other two parameters,$ \lambda_2 $ and$ \lambda_5 $ , clear tendencies are not observed in the scanned ranges.
Figure 3. (color online) Comparisons between the distribution of all selected points (black histogram) after the constraints and the distribution of the points not excluded by the CMS observed upper limits (red filled histogram) on top of the constraints for each parameter of
$\lambda_2$ ,$\lambda_3$ ,$\lambda_4$ ,$\lambda_5$ ,$M_2$ , and${\rm sin}{\theta_H}$ . Both distributions are normalized to unity. -
We also explore correlations between the scanned parameters of the scan points passing all the constraints, as described in subsection II.B, and surviving from the CMS exclusions at the 95% CL in the mass range from 70 to 110 GeV by checking the two-dimensional (2D) distributions of any two of the scanned parameters. As revealed by several of the 2D distributions shown in Fig. 4, correlations between certain scanned parameters are observed.
$ \lambda_2 $ tends to have smaller values when the mass of$ H_{5}^{0} $ decreases, whereas$ \lambda_5 $ tends to have larger values when$ m_{5} $ decreases.$ \lambda_3 $ and$ \lambda_4 $ have tight correlations. A polynomial fit is performed on each edge of the 2D distributions. We observe that all the events fall into the triangular region between the red line, with$ \lambda_3 $ = −1.45$ \lambda_4 $ + 0.87, and black line, with$ \lambda_3 $ = −$ \lambda_4 $ , with$ \lambda_4 $ $ \in $ (0.0, 1.55) and$ \lambda_3 $ $ < $ 0. The strong correlation between$ \lambda_3 $ and$ \lambda_4 $ is due to the constraints from the perturbative unitarity of scalar field scattering amplitudes and the bounded-from-below requirement on the scalar potential, as explained in [51]. Such a correlation supports the choosing of$ \lambda_3 $ =−$ \lambda_4 $ (= −1.5) for the studies in [37].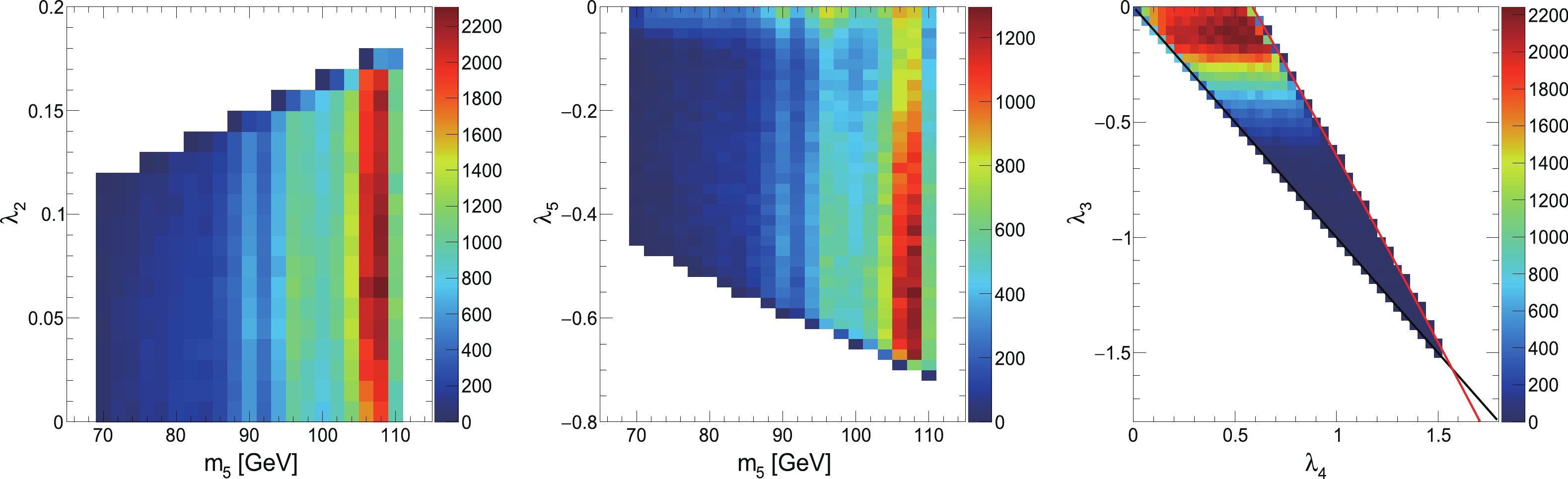
Figure 4. (color online) Two-dimensional distributions of the GM model parameters,
$\lambda_2$ versus${m_5}$ (left),$\lambda_3$ versus${m_5}$ (middle), and$\lambda_3$ versus$\lambda_4$ (right), for points that are not excluded by the CMS observed upper limits in the mass range of [70, 110] GeV. -
The production rates of the
$ W^+W^- $ ,$ ZZ $ , and$ Z\gamma $ decay channels of this low-mass neutral custodial fiveplet scalar in the GM model for 13 TeV pp collisions are also verified for the investigation of the discovery potential of$ H_{5}^{0} $ in these channels. Based on the randomly scanned points after all constraints, as described in subsection II.B, the scattering points in Fig. 5 show the production rates, in pb, for the$ W^+W^- $ decay channel in the left plot, the$ ZZ $ decay channel in the middle plot, and the$ Z\gamma $ decay channel in the right plot, as functions of$ {m_5} $ . The production rates in each decay channel are compared to the predictions (red lines in the plots) of the SM-like BSM Higgs boson reported by the LHC Higgs Cross Section Working Group [35]. One can expect that there are more chances of finding low-mass Higgs bosons in these decay channels. As shown in the left plot, for the$ WW $ decay channel, the largest production rate from the GM model prediction at 65 GeV is approximately 90 times greater than the prediction from the SM-like BSM Higgs boson. However, for the$ ZZ $ decay channel, as shown in the middle plot, the largest production rate from the GM model prediction at 65 GeV can reach up to 370 times that from the SM-like BSM Higgs boson. Because the cross sections of these two decay channels could become larger, by several pb, even after considering the branching ratios of the cascade decays of the W and Z bosons, it is worth performing a search for this low-mass neutral custodial fiveplet scalar at the LHC using current Run2 data and the upcoming Run3 data. In the$ Z\gamma $ channel, as shown in the right plot, the GM prediction can provide larger production rates than the SM-like BSM Higgs boson in the mass range [92, 107] GeV. Owing to the lower signal rates of$ Z\gamma $ decay and further consideration of the branching fractions of Z decaying into, for example, leptons, it is impossible to search for$ H_{5}^{0} $ in the$ Z\gamma $ channel using LHC Run2 data, and it could possible to attempt this with LHC Run3 data and the future High Luminosity LHC (HL-LHC) data.
Figure 5. (color online) Production rates (
$\sigma \times BR$ ) of the$W^+W^-$ (left),$ZZ$ (middle),$Z\gamma$ (right) decay channels of$H_{5}^{0}$ in the GM Model (black points) for 13 TeV pp collisions, with the production rates (red line) at$\sqrt{s}$ = 13 TeV of the SM-like BSM Higgs boson reported by the LHC Higgs Cross Section Working Group [35] superimposed for comparison. -
The search for additional Higgs bosons is one of the most important avenues for probing new physics beyond the standard model. In this paper, we explore the possibility of constraining a lighter custodial fiveplet scalar
$ H_{5}^{0} $ in the Georgi-Machacek model by restricting the custodial-singlet mass eigenstate h or H to the LHC observed Higgs boson after the application of phenomenological constraints and constraints from experimental measurements. To study the phenomenological behavior of the lighter scalar$ H_{5}^{0} $ , a new set of constraints on the six specific parameters of the GM model, as summarized in formula 14, is proposed to generate events efficiently. After comparison with the latest results of the search for a lighter Higgs boson using the diphoton decay channel at 13 TeV by the CMS Collaboration, we conclude that such a lighter scaler$ H_{5}^{0} $ has not yet been completely excluded by LHC experiments.The CMS observed exclusions at the 95% CL are also used to constrain the possible phase space of the six specific parameters of the GM model. The tendencies of the GM input parameters are summarized. For example,
$ \lambda_3 $ exhibits an tendency toward higher values populated at approximately −0.1 for points not excluded by the CMS observed exclusions. Conversely,$ \lambda_4 $ favors lower values with a peak at approximately 0.6, demonstrating an opposite behavior to$ \lambda_3 $ . The correlations of the GM input parameters are also verified.$ \lambda_2 $ and$ \lambda_5 $ are dependent on the$ H_{5}^{0} $ mass, and$ \lambda_3 $ and$ \lambda_4 $ have tight correlations.Finally, the discovery potential of the other interesting decay channels of this low-mass neutral custodial fiveplet scalar is studied. For the lighter custodial fiveplet scalar
$ H_{5}^{0} $ , it is worth performing a search at the LHC in the$ W^+W^- $ and$ ZZ $ decay channels using current Run2 data and the upcoming Run3 data. For the$ Z\gamma $ decay channel with lower signal rates, it could be possible to attempt this with LHC Run3 data and the upcoming HL-LHC data. -
The authors would like to thank Yongcheng Wu for helpful discussions and Shulan Zhang for useful suggestions.
Search for a lighter neutral custodial fiveplet scalar in the Georgi-Machacek model
- Received Date: 2022-03-11
- Available Online: 2022-08-15
Abstract: Many researches from both theoretical and experimental perspectives have been performed to search for a new Higgs Boson that is lighter than the 125






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: