-
Strong interaction physics in the presence of large magnetic fields has gained significant interest recently. The strength of the magnetic fields in non-central heavy-ion collision experiments was estimated to be
$ eB \sim 2{m_{\pi}}^2 \sim 6\times 10^{18} $ Gauss at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory (BNL) and eB$ \sim 15{m_{\pi}}^2 \sim 10^{19} $ Gauss at the Large Hadron Collider (LHC) at CERN [1−4]. In these studies, the electromagnetic fields were calculated using the Lienard-Wiechert potential using numerical simulations or analytical methods. The magnitude of the magnetic field produced is comparable to the quantum chromodynamics (QCD) scale. Such a strong magnetic field can modify the properties of hadrons at high baryon densities and/or temperatures, resulting from these ultra-relativistic nuclear collisions. These medium modifications of heavy flavor mesons can affect experimental observables, such as the production and propagation of these mesons in magnetized matter. As these experiments involve nuclei with more neutrons than protons, the effects of isospin asymmetry are also important to investigate. The study of magnetized hadronic matter is also important for compact astrophysical objects such as magnetars. The strength of magnetic fields may reach$ 10^{15}-10^{16} $ Gauss at the surface of magnetars and approximately$ 10^{18} $ Gauss in their interiors [5−8]. The discovery of novel quantum effects such as the chiral magnetic effect [1, 2, 9], chiral separation effect [9−12], magnetic catalysis, inverse magnetic catalysis [9], and chiral magnetic waves [13−15] has also motivated the study of strongly interacting matter in the presence of a magnetic field.The properties of open heavy flavor mesons and heavy quarkonia have been investigated using the QCD sum rule (QSR) approach in the absence of magnetic fields [16–31] and in the presence of magnetic fields [32–39]. The QSR approach connects the spectral density of a given current correlation function through a dispersion relation with the QCD operator product expansion (OPE). In Ref. [32], operators up to dimension-5 were considered in the OPE for the vacuum part to investigate open charm mesons. The magnetically induced mixing of the pseudoscalar and vector open charm mesons and that of charmonium states [32, 34-36, 40, 41] was observed to cause significant mass modifications. The effects of Landau quantization for charged D mesons were also included in the study. Refs. [34-36] investigated the mixing between the pseudoscalar
$ \eta_c $ and longitudinal component of the vector$ J/\psi $ meson using the QCD sum rule approach, and the spin mixing effects were studied for the charmonium and open charm mesons using a field theoretic model of composite hadrons in Refs. [40, 41]. The spin-mixing resulted in a level-repulsion in the mass spectra of the pseudoscalar meson and the longitudinal component of the vector meson.The properties of these mesons have been investigated using the quark meson coupling (QMC) model [42–44] and the coupled channel approach [45–51]. The properties of heavy quarkonia have also been investigated using potential models without considering magnetic fields [52–59] and in the presence of magnetic fields [60–63]. In potential models, the masses of heavy quarkonia are obtained by solving the Schrödinger equation using an effective potential. The standard form of the potential used in these models is the Cornell potential. The spin-mixing of heavy quarkonia is incorporated through a Hamiltonian, which contains the coupling of spin to the magnetic field through the magnetic moments of charm quarks [60–63]. Ref. [61] considered the anisotropies in the static
$ Q\bar{Q} $ potential in the presence of a magnetic field, which resulted in an increase in the masses of heavy quarkonia.The in-medium masses of open heavy flavor mesons and heavy quarkonia have been studied using the chiral effective model [64–70]. This model is based on a non-linear realization of chiral symmetry and the broken scale invariance of QCD. In this model, the underlying symmetries and symmetry breaking of low-energy QCD are realized in terms of an effective hadronic Lagrangian. The model has been used to study nuclear matter, finite nuclei [71], hyperonic matter [72], vector mesons [73], kaons and antikaons [74–77], as well as charge-neutral matter such as the bulk matter comprising (proto)neutron stars [78]. Chiral symmetry is spontaneously broken in QCD, resulting in non-vanishing chiral condensates. If the quarks are assumed to be massless, the scale invariance of QCD is broken by quantum effects in which the non-vanishing contributions from the gluon condensate result in the trace anomaly. The expectation values of quark and gluon condensates in the hadronic medium are calculated from the scalar meson and dilaton fields. In the chiral effective model, the scalar fields (σ, ζ, δ) simulate the chiral condensates, and the dilaton field χ simulate the gluon condensates of QCD.
The masses of open charm mesons are modified due to their interactions with baryons and scalar mesons (σ, ζ, δ) in a medium. The interaction of the quarkonium state with the gluonic field can be expanded in a multipole series if the distance between heavy quarks Q and
$ \bar Q $ is small compared with the characteristic scale of the non-perturbative gluonic fluctuations. In this expansion, the leading contribution to the mass of the quarkonium state is a dipole term that is proportional to gluon condensates [79−81]. Hence, the mass modifications of charmonia result from the modifications of gluon condensates. The modification of gluon condensates is calculated from the medium change in the dilaton field χ, introduced through a scale-breaking term within the chiral model [66]. The mass modifications of charmonium states in nuclear medium have been studied under linear density approximation using the leading order QCD formula [82, 83]. The in-medium partial decay widths of charmonia to$ D\bar{D} $ and bottomonia to$ B\bar{B} $ mesons have been studied using a field theoretical model for composite hadrons [84, 85]. The partial decay widths of heavy quarkonia have also been investigated within a light quark-antiquark pair creation model, namely the$ 3P_0 $ model [86−90]. The properties of open heavy flavor mesons and heavy quarkonia in the magnetized cold nuclear matter have been investigated within the chiral effective model [41, 91–97].In this paper, we investigate the masses of open charm mesons (
$ D(D^0,D^+) $ ,$ \bar{D}(\bar{D^0},D^-) $ ,$ D_s ({D_S}^+,{D_S}^-) $ ) and charmonium states ($ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ ,$ \chi_{c0} $ ,$ \chi_{c2} $ ) in strongly magnetized asymmetric strange hadronic matter within the chiral effective model. The remainder of this paper is outlined as follows: In Section II, we describe the chiral$ \ S U(3)_{\rm L} \times S U(3)_{\rm R} $ effective model and its extension to chiral SU(4) to study the aforementioned mesons in a magnetized medium. Here, we include the effects of anomalous magnetic moments (AMMs) of baryons and the strangeness fraction of the medium. In this investigation, we do not consider the effects of temperature and contributions from the mixing of the pseudoscalar and vector meson states in the presence of strong magnetic fields. In Section III, we present the interaction Lagrangian of open charm mesons with the magnetized strange hadronic matter. We also describe the dispersion relations of open charm mesons, which are to be solved to obtain their masses. In Section IV, we describe the medium mass shifts of charmonium states calculated using the modification of gluon condensates in the chiral model. We also include the contribution of light quark masses in the mass shift of charmonia. In Section V, we discuss and analyze the results obtained, and we summarize our findings in Section VI. -
In the presence of a magnetic field, the effective hadronic chiral Lagrangian density [91] is given by
$ \begin{aligned}[b]{ \cal L}_{{ \rm{eff}}} =& {\cal L}_{ {\rm{kin}}} + \sum\limits_{{\cal W}={\cal X,Y,A,V,}u}{\cal{L_ {\rm{BW}}}} + \cal{L_ \rm{vec}}+ \cal{L_ {\rm{0}}} \\ &+ \cal{L_ {\rm{scale \;break}}} + \cal{L_ {\rm{SB}}} + \cal{L_ {\rm{mag}}}. \end{aligned} $

(1) In this equation,
$ \cal{L_ \rm{kin}} $ refers to the kinetic energy terms of mesons and baryons.$ \cal{L_ \rm{BW}} $ is the baryon-meson interaction term, where the index$ \cal{ W} $ covers both spin-0 and spin-1 mesons. Here, the baryon masses are generated dynamically through baryon-scalar meson interactions.$ \cal{L_ \rm{vec}} $ involves the dynamical mass generation of vector mesons through couplings with scalar mesons, in addition to bearing the quartic self-interaction terms of these mesons.$ \cal{L_ \rm{0}} $ contains the meson-meson interaction terms that introduce the spontaneous breaking of the chiral symmetry.$ \cal{L_ \rm{scale break}} $ incorporates the scale invariance breaking of QCD through a logarithmic potential given in terms of scalar dilaton field χ.$ \cal{L_ \rm{SB}} $ is the explicit chiral symmetry breaking term, and$ \cal{L_ \rm{mag}} $ is the contribution by the magnetic field. We use the mean-field approximation to simplify the hadronic Lagrangian density under which all the meson fields are considered as classical fields. In this approximation, only the vector fields ($ \omega,\;\rho,\;\phi $ ) and scalar fields (nonstrange scalar field σ, strange scalar field ζ and scalar-isovector field δ) contribute as the expectation value of the other mesons vanishes. The baryon-meson interaction term simplifies to$ {{\cal L}_ {\rm{BW}}}=-\sum\bar\psi_{i}[ m_i^*+ g_{\omega i}\gamma_{0} \omega+ g_{\rho i}\gamma_{0} \rho+ g_{\phi i}\gamma_{0} \phi]\psi_{i}. $

(2) Here, the index i covers the eight lightest baryons n, p, Λ,
$ \Sigma^{-} $ ,$ \Sigma^{0} $ ,$ \Sigma^{+} $ ,$ \Xi^{-} $ ,$ \Xi^{0} $ , and$ g_{\omega i},\; g_{\rho i}, \;g_{\phi i} $ represent the coupling strengths of baryons with the vector mesons ω, ρ, and ϕ, respectively. The effective mass of the baryons denoted as$ m_i^* $ is given by$ \begin{equation} m_i^* = - (g_{\sigma i}\sigma+ g_{\zeta i}\zeta + g_{\delta i}\delta), \end{equation} $

(3) where
$ g_{\sigma i}, \;g_{\zeta i},\; g_{\delta i} $ represent the coupling strengths of baryons with the scalar mesons σ, ζ, and δ respectively. The other terms in the Lagrangian reduce to the following expressions:$ {{\cal L}_ {\rm{vec}}} = \frac{1}{2}( m_\omega^2\omega^2 + m_\rho^2\rho^2+ m_\phi^2\phi^2)\left(\frac{\chi^2}{{\chi_0}^2}\right) + g_4(\omega^4 + 6\rho^2\omega^2 + \rho^4 + 2\phi^4), $

(4) $ \begin{aligned}[b] {{\cal L}_ {\rm{0}}}+{{\cal L}_ {\rm{scale\; break}}}=&-\frac{1}{2}k_0\chi^2(\sigma^2+\zeta^2+\delta^2)+k_1(\sigma^2+\zeta^2+\delta^2)^2+k_2\left(\frac{\sigma^4}{2}+\frac{\delta^4}{2}+3\sigma^2\delta^2+\zeta^4\right)+k_3\chi(\sigma^2-\delta^2)\zeta\\&-k_4\chi^4 -\frac{1}{4}\chi^4\ln{\left(\frac{\chi^4}{\chi_0^4}\right)}+\frac{d}{3}\chi^4\ln\left(\left(\frac{(\sigma^2-\delta^2)\zeta}{{\sigma_0^2}\zeta_0}\right)\left(\frac{\chi}{\chi_0}\right)^3\right), \end{aligned} $ 
(5) $ {{\cal L}_ {\rm{SB}}}=-\left(\frac{\chi}{\chi_0}\right)^2 \Big[{m_\pi}^2f_\pi \sigma +(\sqrt{2}{m_K}^2f_K-\frac{1}{\sqrt{2}}{m_\pi}^2f_\pi)\zeta\Big]. $

(6) In Eq. (4),
$ g_4 $ is the renormalized coupling for the ω field [71, 72]. In the above equations,$ \sigma_0 $ ,$ \zeta_0 $ , and$ \chi_0 $ denote the vacuum values of the scalar fields σ, ζ, and the dilaton field χ, respectively. In Eq. (5), the parameters$ k_0 $ ,$ k_1 $ ,$ k_2 $ ,$ k_3 $ , and$ k_4 $ are phenomenological constants, and their fitting is described in detail in Section V. In Eq. (6),$ f_K $ is the kaon decay constant,$ f_\pi $ is the pion decay constant, and$ m_K $ ,$ m_\pi $ are their respective vacuum masses. Finally, the contribution of the magnetic field incorporated in the Lagrangian term given by$ \begin{array}{*{20}{l}} {{\cal L}_ {\rm{mag}}} =-\bar{\psi_{i}}q_{i}\gamma_{\mu}A^{\mu}\psi_{i}-\dfrac{1}{4}\kappa_{i}\mu_{N}\bar{\psi_{i}}\sigma^{\mu\nu}F_{\mu\nu}\psi_{i}-\dfrac{1}{4}F^{\mu\nu}F_{\mu\nu}. \end{array} $

(7) The second term in Eq. (7), which is a tensorial interaction term, is related to the anomalous magnetic moment (AMM) of the baryons. In this term,
$ \mu_{N} $ is the nuclear Bohr magneton, expressed as$ \mu_{N} $ =$ e/(2m_N) $ , where$ m_N $ is the vacuum mass of the nucleon. Here,$ \kappa_{i} $ is the gyromagnetic ratio corresponding to the anomalous magnetic moment of the baryons. The values of$ \kappa_{i} $ used in our calculations were obtained from Refs. [98–100]. We consider the magnetic field to be uniform and along the z-axis. We set the vector potential as$ A^{\mu} $ = (0, 0, Bx, 0). From the mean-field Lagrangian density, we obtain the coupled equations of motion for the scalar fields σ, ζ, δ, χ, and vector meson fields$ \omega,\; \rho,\; \phi $ . The equations of motion for the scalar fields σ, ζ, and δ are expressed in terms of the scalar densities of baryons [72, 73]. The equations of motion for vector meson fields$ \omega, \rho, \phi $ are expressed in terms of the number densities of baryons [72, 73]. The magnetic field introduces summation over Landau levels in the expressions of the number and scalar densities of charged baryons (i= p,$ \Sigma^{-} $ ,$ \Sigma^{+} $ ,$ \Xi^{-} $ ), which are given by [100–102]$ \;\;\; \rho_i = \frac{eB}{2\pi^2}\Bigg[{\sum\limits_{\nu}^{{\nu^{(S=1)}_{\rm max}}} k_{f, \nu, 1}^i} + {\sum\limits_{\nu}^{{\nu^{(S=-1)}_{\rm max}}} k_{f, \nu, -1}^i}\Bigg], $

(8) $ \begin{aligned}[b] \rho_s^i =& \frac{eBm_i^*}{2\pi^2}\Bigg[{\sum\limits_{\nu}^{\nu^{(S=1)}_{\rm max}} \frac{\sqrt[]{m_i^{*2} + 2eB\nu} + \Delta_i}{\sqrt[]{m_i^{*2} + 2eB\nu}} {\rm ln}\Bigg|\frac{k_{f,\nu,1}^i + E_f^i}{\sqrt[]{m_i^{*2} + 2eB\nu} + \Delta_i}\Bigg|} \\ &+ {\sum\limits_{\nu}^{\nu^{(S=-1)}_{\rm max}} \frac{\sqrt[]{m_i^{*2} + 2eB\nu} - \Delta_i}{\sqrt[]{m_i^{*2} + 2eB\nu}} \ln\Bigg|\frac{k_{f,\nu,-1}^i + E_f^i}{\sqrt[]{m_i^{*2} + 2eB\nu} - \Delta_i}\Bigg|}\Bigg]. \end{aligned} $

(9) Here,
$ k_{f, \nu, s}^i $ is the Fermi momentum of charged baryons,$ E_f^i $ is the Fermi energy, ν is the Landau level, and spin index S = +1($ -1 $ ) corresponds to spin up (spin down) projections for the baryons. The parameter$ \Delta_{i} $ refers to the anomalous magnetic moments of the baryons, expressed as$ \Delta_{i}=-({1}/{2})\kappa_i\mu_N B $ . The Landau levels of charged baryons is enumerated using the expression$ \nu = n+ \dfrac{1}{2}-\dfrac{q_B}{|q_B|}\dfrac{S}{2}, $ where$ q_B $ is the charge of the baryon ($ q_B=e $ for p,$ \Sigma^{+} $ and$ q_B=-e $ for$ \Sigma^{-} $ ,$ \Xi^{-} $ ). The lowest Landau level for a particular spin projection of the charged baryon is obtained by setting n=0 in this expression. The maximum allowed value of Landau level for a charged baryon is determined using the expression$\nu_{\rm max} = \Bigg\lfloor\dfrac{(E_f^i - S \Delta_i)^2 - m_i^{*2}}{2eB}\Bigg\rfloor. $ Here, the floor operator acting on a quantity x, i.e.,$ \lfloor x\rfloor $ is defined as the largest integer less than or equal to x. The Fermi momenta of charged baryons are related to their Fermi energies$ E_f^i $ as$ \begin{array}{*{20}{l}} k_{f, \nu, S}^i = \sqrt[]{(E_f^i)^2 - \Big(\sqrt[]{m_i^{*2} + 2eB\nu} + S\Delta_i\Big)^2}. \end{array} $

(10) For neutral baryons (i= n, Λ,
$ \Sigma^{0} $ ,$ \Xi^{0} $ ), there is no contribution of Landau quantization in the presence of an external magnetic field. The number and scalar densities are given by$ \begin{aligned}[b] \rho_i =& \frac{1}{4\pi^2}\sum\limits_{S=\pm1} \Bigg(\frac{2}{3}(k_{f,S}^i)^3 + S\Delta_i\Bigg[(m_i^* + S\Delta_i)k_{f, S}^i \\&+ (E_f^i)^2\Bigg\{{\rm arcsin}\Bigg(\frac{m_i^* + S\Delta_i}{E_f^i}\Bigg) - \frac{\pi}{2}\Bigg\}\Bigg]\Bigg), \end{aligned} $

(11) $ \rho_s^i = \frac{m_i^*}{4\pi^2}\sum\limits_{S=\pm1}\Bigg[k_{f,S}^iE_f^i - (m_i^* + S\Delta_i)^2\ln\Bigg|\frac{k_{f,S}^i + E_f^i}{m_i^* + S\Delta_i}\Bigg|\Bigg]. $

(12) The Fermi momenta of neutral baryons
$ k_{f,S}^i $ are related to their Fermi energies$ E_f^i $ as$ \begin{array}{*{20}{l}} k_{f, S}^i = \sqrt[]{(E_f^i)^2 - (m_i^* + S\Delta_i)^2}. \end{array} $

(13) We consider the hyperonic matter in equilibrium, resulting in five chemical equilibrium equations of baryons. They are given by
$ \begin{array}{*{20}{l}} \Lambda + \Lambda\rightleftharpoons p+{\Xi^-}, \end{array} $

(14) $ \begin{array}{*{20}{l}} \Lambda + \Lambda\rightleftharpoons n+\Xi^0, \end{array} $

(15) $ \begin{array}{*{20}{l}} \Sigma^-+p \rightleftharpoons \Lambda + n, \end{array} $

(16) $ \begin{array}{*{20}{l}} \Sigma^++n \rightleftharpoons \Lambda+p, \end{array} $

(17) $ \begin{array}{*{20}{l}} \Sigma^0+\Sigma^-\rightleftharpoons \Xi^-+n.\end{array} $

(18) The above equations constrain the chemical potentials
$ \mu_i $ of all the baryons in the medium. Because the particles on the left- and right-hand sides are in chemical equilibrium, their chemical potentials can be equated and expressed as$ \begin{array}{*{20}{l}} 2\mu_\Lambda=\mu_p+\mu_{\Xi^-}, \quad \end{array} $

(19) $ \begin{array}{*{20}{l}} 2\mu_\Lambda=\mu_n+\mu_{\Xi^0}, \quad \end{array} $

(20) $ \begin{array}{*{20}{l}} \mu_{\Sigma^-}+\mu_p=\mu_n+\mu_{\Lambda}, \end{array} $

(21) $ \begin{array}{*{20}{l}} \mu_{\Sigma^+}+\mu_n=\mu_p+\mu_{\Lambda}, \end{array} $

(22) $ \begin{array}{*{20}{l}} \mu_{\Sigma^-}+\mu_{\Sigma^0}=\mu_n+\mu_{\Xi^-}. \end{array} $

(23) These equations can be further rewritten in terms of the effective chemical potential of baryons
$ \mu_i^* $ through the relation$ \mu_i^* =\mu_i-(g_{\rho i}\rho+g_{\omega i}\omega+g_{\phi i}\phi) $ . The effective chemical potential$ \mu_i^* $ is numerically equal to the Fermi energy of baryons at temperature T=0. These chemical equilibrium equations provide the necessary equations of constraint in studying the strange hadronic matter under external magnetic fields. The equations of motion of scalar fields are then solved self-consistently at different magnetic fields for given values of the total baryon density$ \rho_B= \sum_i\rho_i $ , isospin asymmetry parameter$ \eta= ({-\sum_i{I_{3i}\rho_i}})/ {\rho_B} $ , and strangeness fraction$f_s= ({\sum_i|{S_{ i}|\,\rho_i})/}{\rho_B}$ . Here,$ I_{3i} $ is the third component of the isospin, and$ S_ i $ is the strangeness quantum number for the$ i^{\,\rm th} $ baryon. The strangeness fraction is a measure of the relative population of hyperons (with appropriate weight factors owing to the number of strange quarks in the hyperons) among all the baryons present in the medium.In the following section, we describe the interaction of open charm mesons with strongly magnetized strange hadronic matter and their medium mass modifications.
-
We examine the medium modifications of the masses of open charm mesons in asymmetric magnetized strange hadronic matter. These mesons interact with light quark condensates, which are modified significantly in the hadronic medium. Here, the chiral SU(3) has been generalized to the chiral SU(4) to include the charmed mesons and their interactions with the light hadronic sector [64–66, 74]. The interaction Lagrangian density of D and
$ \bar{D} $ mesons with the strange hadronic medium in the chiral effective model is given by [76]$ \begin{aligned}[b] {\cal L}_{\rm int} = & -\frac {\rm i}{8 f_D^2} \Big [3\Big (\bar p \gamma^\mu p +\bar n \gamma ^\mu n \Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) - (\partial_\mu {{D^0}}) {\bar D}^0 \Big ) +\Big(D^+ (\partial_\mu D^-) - (\partial_\mu {D^+}) D^- \Big )\Big ) + \Big (\bar p \gamma^\mu p -\bar n \gamma ^\mu n \Big) \Big( \Big({D^0} (\partial_\mu \bar D^0) - (\partial_\mu {{D^0}}) {\bar D}^0 \Big ) \\ &- \Big( D^+ (\partial_\mu D^-) - (\partial_\mu {D^+}) D^- \Big )\Big ) + 2\Big((\bar{\Lambda}^{0}\gamma^{\mu}\Lambda^{0}) \Big( \Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) + \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big) \Big)\\ &+ 2 \Big(\Big(\bar{\Sigma}^+\gamma^{\mu}\Sigma^+ + \bar{\Sigma}^-\gamma^{\mu}\Sigma^-\Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) + \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big)\Big)\\ &+ \Big(\bar{\Sigma}^+\gamma^{\mu}\Sigma^+ - \bar{\Sigma}^-\gamma^{\mu}\Sigma^-\Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) - \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big)\Big)\Big)\\ &+2\Big(\bar{\Sigma}^{0}\gamma^{\mu}\Sigma^{0}\Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) + \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big) \Big)\\ &+ \Big(\bar{\Xi}^{0}\gamma^{\mu}\Xi^{0} + \bar{\Xi}^-\gamma^{\mu}\Xi^-\Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) + \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big)\Big)\\ &+\Big(\bar{\Xi}^{0}\gamma^{\mu}\Xi^{0} - \bar{\Xi}^-\gamma^{\mu}\Xi^-\Big) \Big(\Big({D^0} (\partial_\mu \bar D^0) -(\partial_\mu {{D^0}}) {\bar D}^0 \Big) - \Big(D^+ (\partial_\mu D^-) - (\partial_\mu D^+) D^- \Big)\Big)\Big ]\\ &+ \frac{m_D^2}{2f_D} \Big [ (\sigma +\sqrt 2 \zeta_c)\big (\bar D^0 { D^0}+(D^- D^+) \big ) +\delta \big (\bar D^0 { D^0})-(D^- D^+) \big ) \Big ] - \frac {1}{f_D}\Big [ (\sigma +\sqrt 2 \zeta_c ) \Big ((\partial _\mu {{\bar D}^0})(\partial ^\mu {D^0}) +(\partial _\mu {D^-})(\partial ^\mu {D^+}) \Big )\\ &+ \delta \Big ((\partial _\mu {{\bar D}^0})(\partial ^\mu {D^0}) -(\partial _\mu {D^-})(\partial ^\mu {D^+}) \Big ) \Big ] + \frac {d_1}{2 f_D^2}(\bar p p +\bar n n +\bar{\Lambda}^{0}\Lambda^{0}+\bar{\Sigma}^+\Sigma^++\bar{\Sigma}^{0}\Sigma^{0} +\bar{\Sigma}^-\Sigma^-+\bar{\Xi}^{0}\Xi^{0}+\bar{\Xi}^-\Xi^-) \big ( (\partial _\mu {D^-})(\partial ^\mu {D^+}) \\ &+(\partial _\mu {{\bar D}^0})(\partial ^\mu {D^0}) \big ) + \frac {d_2}{2 f_D^2} \Big [ \Big(\bar p p+\frac{1}{6}\bar{\Lambda}^{0}\Lambda^{0} +\bar{\Sigma}^+\Sigma^++\frac{1}{2}\bar{\Sigma}^{0}\Sigma^{0}\Big) (\partial_\mu {\bar D}^0)(\partial^\mu {D^0}) \\ &+\Big(\bar n n+\frac{1}{6}\bar{\Lambda}^{0}\Lambda^{0} +\bar{\Sigma}^-\Sigma^-+\frac{1}{2}\bar{\Sigma}^{0}\Sigma^{0}\Big) (\partial_\mu D^-)(\partial^\mu D^+)\Big ]. \\[-8pt] \end{aligned} $ 
(24) In Eq. (24), the first term (with coefficient
$ -{\rm i}/8{f_D}^2 $ ) is the vectorial Weinberg-Tomozawa interaction term, which is obtained from the kinetic energy term$ \cal{L_ \rm{kin}} $ in Eq. (1) [64–66]. The general structure of the Weinberg-Tomozawa term for the SU(4) case is given in Ref. [65]. The second term (with coefficient$ m^2_D/2f_D $ ) is the scalar meson exchange term that is obtained from the explicit symmetry-breaking term$ \cal{L_ \rm{SB}} $ in Eq. (1) [64–66]. The next three terms in the above Lagrangian density ($ \sim(\partial_\mu {\bar D} $ )($ \partial^\mu {D} $ )) are known as the range terms. The first range term (with the coefficient ($ - 1/ f_D $ )) is obtained from the kinetic energy term of the pseudoscalar mesons [65]. Here,$ f_D $ is the decay constant of D mesons. The terms with coefficients ($ d_1/2f_D^2 $ ) and ($ d_2/2f_D^2 $ ) are the$ d_1 $ and$ d_2 $ range terms, respectively [65]. The parameters$ d_1 $ and$ d_2 $ are determined by a fitting of the empirical values of the Kaon-Nucleon scattering lengths [103–105] for I = 0 and I = 1 channels [76, 77].The interaction Lagrangian density of
$ D_s $ mesons in the strange hadronic medium is given by [70]$ \begin{aligned}[b] {\cal L}_{\rm int}=&-\frac{\rm i}{4 f_{D_{S}}^{2}}\big[(2(\bar{\Xi}^{0} \gamma^{\mu} \Xi^{0}+\bar{\Xi}^- \gamma^{\mu} \Xi^-)+\bar{\Lambda}^{0} \gamma^{\mu} \Lambda^{0}+\bar{\Sigma}^+ \gamma^{\mu} \Sigma^+ +\bar{\Sigma}^{0} \gamma^{\mu} \Sigma^{0}+\bar{\Sigma}^- \gamma^{\mu} \Sigma^-)(D_{S}^+(\partial_{\mu} D_{S}^-)-(\partial_{\mu} D_{S}^+) D_{S}^-)\big] \\&+\frac{m_{D_{S}}^{2}}{\sqrt{2} f_{D_{S}}}\big[(\zeta^{\prime}+\zeta_{c}^{\prime})(D_{S}^+ D_{S}^-)\big] -\frac{\sqrt{2}}{f_{D_{S}}}\big[(\zeta^{\prime}+\zeta_{c}^{\prime})((\partial_{\mu} D_{S}^+)(\partial^{\mu} D_{S}^-))\big] +\frac{d_{1}}{2 f_{D_{S}}^{2}}\big[(\bar{p} p+\bar{n} n+\bar{\Lambda}^{0} \Lambda^{0}+\bar{\Sigma}^+ \Sigma^++\bar{\Sigma}^{0} \Sigma^{0}\\&+\bar{\Sigma}^- \Sigma^-+\bar{\Xi}^{0} \Xi^{0} +\bar{\Xi}^- \Xi^-)((\partial_{\mu} D_{S}^+)(\partial^{\mu} D_{S}^-))\big] +\frac{d_{2}}{2 f_{D_{S}}^{2}}\big[(2(\bar{\Xi}^{0} \Xi^{0}+\bar{\Xi}^- \Xi^-)+\bar{\Lambda}^{0} \Lambda^{0}+\bar{\Sigma}^+ \Sigma^++\bar{\Sigma}^{0} \Sigma^{0}+\bar{\Sigma}^- \Sigma^-)((\partial_{\mu} D_{S}^+)(\partial^{\mu} D_{S}^-))\big]. \end{aligned} $ 
(25) In Eq. (25), the first term (with coefficient
$ -{\rm i}/4{f_{D_s}}^2 $ ) is the Weinberg-Tomozawa interaction term [70]. The second term (with coefficient$ m^2_{D_S}/\sqrt{2}f_{D_s} $ ) in Eq. (25) is the scalar meson exchange term. The third term (with the coefficient ($ -\sqrt{2}/ f_{D_s} $ )) is the first range term. The fourth and fifth terms with coefficients ($ d_1/2f_{D_s}^2 $ ) and ($ d_2/2f_{D_s}^2 $ ) are the$ d_1 $ and$ d_2 $ range terms, respectively. The interaction Lagrangian density given in Eqs. (24) and (25) lead to equations of motion for D,$ \bar{D} $ , and$ D_s $ mesons, respectively, and their Fourier transforms lead to the dispersion relations given by$ \begin{array}{*{20}{l}} -\omega^2 + \overrightarrow{k}^2 + m_{j}^2 - \Pi_{j}(\omega,|\overrightarrow{k}|) = 0. \end{array} $

(26) Here, the index j denotes the various open charm mesons D,
$ \bar{D} $ ,$ D_s $ , and$ m_{j} $ is the vacuum mass of the corresponding open charm meson. Here,$ \Pi_{j}(\omega,|\vec{k}|) $ denotes the self-energy of the open charm mesons in the medium. For D mesons, the self-energy is given by$ \begin{aligned}[b] \Pi_{{D}} (\omega, |\vec k|) = & \frac {1}{4 f_D^2}\Big [3 (\rho_p +\rho_n) \pm (\rho_p -\rho_n) +2\big(\left( \rho_{\Sigma^+}+ \rho_{\Sigma^-}\right) \pm \left(\rho_{\Sigma^+}- \rho_{\Sigma^-}\right) \big)+2(\rho_{\Lambda^{0}}+\rho_{\Sigma^{0}}) +( \left( \rho_{\Xi^{0}}+ \rho_{\Xi^-}\right) \pm \left(\rho_{\Xi^{0}}- \rho_{\Xi^-}\right)) \Big ] \omega \\ &+\frac {m_D^2}{2 f_D} (\sigma ' +\sqrt 2 {\zeta_c} ' \pm \delta ') + \Big [- \frac {1}{f_D} (\sigma ' +\sqrt 2 {\zeta_c} ' \pm \delta ') +\frac {d_1}{2 f_D ^2} (\rho_p ^s +\rho_n ^s\\ &+\rho_{\Lambda^{0}}^s+\rho_{\Sigma^+}^s+\rho_{\Sigma^{0}}^s +\rho_{\Sigma^-}^s +\rho_{\Xi^{0}}^s+\rho_{\Xi^-}^s) +\frac {d_2}{4 f_D ^2} \Big ((\rho _p^s +\rho_n^s) \pm ({\rho} _p^s -{\rho}_n^s)+\frac{1}{3}{\rho} _{\Lambda^0}^s\\ &+({\rho}_{\Sigma^+}^s +{\rho} _{\Sigma^-}^s) \pm ({\rho} _{\Sigma^+}^s -{\rho}_{\Sigma^-}^s) +{\rho} _{\Sigma^{0}}^s \Big ) \Big ] (\omega ^2 - {\vec k}^2), \end{aligned} $ 
(27) where
$ \pm $ refers to$ D^0 $ and$ D^+ $ , respectively. For$ \bar{D} $ mesons, the self-energy is given by$ \begin{aligned}[b] \Pi_{\bar{D}}(\omega, |\vec k|) = & -\frac {1}{4 f_D^2}\Big [3 (\rho_p +\rho_n) \pm (\rho_p -\rho_n) +2\big(\left( \rho_{\Sigma^+}+ \rho_{\Sigma^-}\right)\pm \left(\rho_{\Sigma^+}- \rho_{\Sigma^-}\right) \big)+2(\rho_{\Lambda^{0}}+\rho_{\Sigma^{0}}) +( \left( \rho_{\Xi^{0}}+ \rho_{\Xi^-}\right) \pm \left(\rho_{\Xi^{0}}- \rho_{\Xi^-}\right))\Big ] \omega \\ &+\frac {m_D^2}{2 f_D} (\sigma ' +\sqrt 2 {\zeta_c} ' \pm \delta ') + \Big [- \frac {1}{f_D} (\sigma ' +\sqrt 2 {\zeta_c} ' \pm \delta ') +\frac {d_1}{2 f_D ^2} ({\rho}_p^s +{\rho}_n^s\\ &+{\rho}_{\Lambda^{0}}^s+{\rho}_{\Sigma^+}^s +{\rho}_{\Sigma^{0}}^s+{\rho}_{\Sigma^-}^s +{\rho}_{\Xi^{0}}^s+{\rho}_{\Xi^-}^s) +\frac {d_2}{4 f_D ^2} \Big (({\rho}_p^s +{\rho}_n^s) \pm ({\rho}_p^s -{\rho}_n^s)+\frac{1}{3}{\rho}_{\Lambda^{0}}^s \\ &+({\rho} _{\Sigma^+}^s +{\rho} _{\Sigma^-}^s) \pm ({\rho}_{\Sigma^+}^s -{\rho}_{\Sigma^-}^s) +{\rho} _{\Sigma^{0}}^s \Big ) \Big ] (\omega ^2 - {\vec k}^2), \end{aligned} $

(28) where
$ \pm $ refers to$ \bar{D^0} $ and$ D^- $ , respectively. The self-energy for strange-charmed mesons is expressed as$ \begin{aligned}[b] \Pi_{D_s}(\omega,|\vec{k}|)=&\left[\left(\frac{d_{1}}{2 f_{D_{S}}^{2}}\left(\rho_{p}^{s}+\rho_{n}^{s}+\rho_{\Lambda}^{s}+\rho_{\Sigma^+}^{s}+\rho_{\Sigma^{0}}^{s}+\rho_{\Sigma^-}^{s}+\rho_{\Xi^{0}}^{s}+\rho_{\Xi^-}^{s}\right)\right)\right. +\left(\frac{d_{2}}{2 f_{D_{S}}^{2}}\left(2\left(\rho_{\Xi^{0}}^{s}+\rho_{\Xi^-}^{s}\right)+\rho_{\Lambda}^{s}+\rho_{\Sigma^+}^{s}+\rho_{\Sigma^{0}}^{s}+\rho_{\Sigma^-}^{s}\right)\right)\\& \left.-\left(\frac{\sqrt{2}}{f_{D_{S}}}\left(\zeta^{\prime}+\zeta_{c}^{\prime}\right)\right)\right]\left(\omega^{2}-\vec{k}^{2}\right) \pm\left[\frac{1}{2 f_{D_{S}}^{2}}\left(2\left(\rho_{\Xi^{0}}+\rho_{\Xi^-}\right)+\rho_{\Lambda}+\rho_{\Sigma^+}+\rho_{\Sigma^{0}}+\rho_{\Sigma^-}\right)\right] \omega +\left[\frac{m_{D_{S}}^{2}}{\sqrt{2} f_{D_{S}}}\left(\zeta^{\prime}+\zeta_{c}^{\prime}\right)\right]. \end{aligned} $

(29) Here, the
$ \pm $ signs in the co-efficient of ω refer to$ {D_S}^+ $ and$ {D_S}^- $ mesons, respectively. In Eqs. (27), (28), and (29),$ \sigma^\prime $ = ($ \sigma - \sigma_0 $ ),$ \zeta^\prime_c $ = ($ \zeta_c - \zeta_{c0} $ ),$ \delta^\prime $ = ($ \delta - \delta_0 $ ), and$ \zeta^\prime $ = ($ \zeta - \zeta_0 $ ) denote the fluctuations of scalar fields from their vacuum values. The fluctuation$ \zeta^\prime_c $ has been observed to be negligible [106], and its contribution to the in-medium masses of open charm mesons is neglected in this investigation. The charged open charm mesons (j=$ D^+ $ ,$ D^- $ ,$ {D_S}^+ $ ,$ {D_S}^- $ ) have an additional positive mass modification in magnetic fields, which, retaining only the lowest Landau level, is given by$ \begin{array}{*{20}{l}} m^{\rm eff}_{j} = \sqrt[]{m_{j}^{*2} + |eB|}. \end{array} $

(30) In the above equation,
$ m_{j}^{*} $ are solutions of the dispersion relations given by Eq. (26) for ω at$ |\overrightarrow{k}| $ = 0. For the neutral open charm mesons (j=$ D^0 $ ,$ \bar{D^0} $ ), there is no contribution from the Landau quantization effects, and their effective mass in the medium is given by$ \begin{array}{*{20}{l}} m^{\rm eff}_{j} = {m_{j}}^{*}. \end{array} $

(31) -
In this section, we describe the mass shifts of charmonia
$ (c\bar{c}) $ such as$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ ,$ \chi_{c0} $ ,$ \chi_{c2} $ , which are the 1S, 2S, 1D,$ 1^3P_0 $ , and$ 1^3P_2 $ states, respectively, in strange hadronic matter in the presence of strong magnetic fields. The heavy quarkonium states are modified in a hadronic environment due to modifications of gluon condensates [79–83]. The trace anomaly in QCD indicates that the trace of the energy-momentum tensor is non-zero when the scale symmetry is broken. A non-zero trace of the energy-momentum tensor in QCD originates from the gluon condensates and finite quark mass contributions. This scale invariance breaking is simulated in the chiral effective Lagrangian given by Eq. (1) at the tree level through the scale breaking term:$ \begin{aligned}[b] {\cal L}_{\rm scalebreak}=& -\frac{1}{4} \chi^{4} {\rm ln} \frac{\chi^{4}}{\chi_{0}^{4}} + \frac{d}{3} \chi^{4} \\&\times{\rm ln} \Bigg( \frac{\left( \sigma^{2} - \delta^{2}\right)\zeta } {\sigma_{0}^{2} \zeta_{0}} \left( \frac{\chi}{\chi_{0}}\right) ^{3}\Bigg). \end{aligned} $

(32) Comparing the expressions for the trace of energy-momentum tensor from QCD, and from the scale-breaking Lagrangian given by Eq. (32), we obtain [107, 108]
$ \begin{equation} \theta_{\mu}^{\mu} = \langle \frac{\beta_{\rm QCD}}{2g} G_{\mu\nu}^{a} G^{\mu\nu a} \rangle + \sum\limits_i m_i \bar {q_i} q_i \equiv -(1 - d)\chi^{4}. \end{equation} $

(33) The second term in the trace accounts for the finite quark masses, with
$ m_i $ being the current quark mass for the quark of flavor,$ i=u,d,s $ . Here, parameter d originates from the second term in$ {\cal L}_{\rm scalebreak} $ given by Eq. (32). The QCD β function at one-loop level is given by$ \begin{equation} \beta_{\mathrm{QCD}}(g)=-\frac{11 N_{c} g^{3}}{48 \pi^{2}}\left(1-\frac{2 N_{f}}{11 N_{c}}\right). \end{equation} $

(34) Here,
$ N_c=3 $ is the number of colors, and$ N_f $ is the number of quark flavors. In the above equation, the first term in the parentheses results from the antiscreening contribution of the gluons, and the second term results from the screening contribution of quark pairs. Using Eqs. (33) and (34), we obtain the scalar gluon condensate that is related to the dilaton field as$ \begin{equation} \langle\frac{\alpha_{s}}{\pi} G_{\mu \nu}^{a} G^{\mu \nu a}\rangle=\frac{24}{\left(33-2 N_{f}\right)}\left[(1-d) \chi^{4}+\sum\limits_{i} m_{i} \bar{q}_{i} q_{i}\right]. \end{equation} $

(35) The second term,
$ \sum_i m_i \bar q_i q_i $ , which is related to the explicit chiral symmetry breaking term$ {\cal L}_{\rm SB} $ in Eq. (1), is given by [27]$ \sum_i m_i \bar {q_i} q_i = \Big[ m_{\pi}^{2} f_{\pi} \sigma + \left( \sqrt{2} m_{k}^{2}f_{k} - \frac{1}{\sqrt{2}} m_{\pi}^{2} f_{\pi} \right) \zeta \Big]. $

(36) In the chiral effective model, the leading order mass shift formula of the charmonium states is given by [65, 66]
$ \begin{aligned}[b] \Delta m_{\psi}=& \frac{1}{18} \int {\rm d}k^{2} \langle \vert \frac{\partial \psi (\vec k)}{\partial {\vec k}} \vert^{2} \rangle \frac{k}{k^{2} / m_{c} + \epsilon} \\&\times \bigg ( \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle - \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle _{0} \bigg ), \end{aligned} $

(37) where
$ \begin{equation} \langle \vert \frac{\partial \psi (\vec k)}{\partial {\vec k}} \vert^{2} \rangle =\frac {1}{4\pi}\int \vert \frac{\partial \psi (\vec k)}{\partial {\vec k}} \vert^{2} {\rm d}\Omega. \end{equation} $

(38) In Eq. (37),
$ m_{c} $ is the mass of the corresponding heavy quark, and$ \epsilon $ =$ 2m_{c}- m_{\Psi} $ represents the binding energy of the corresponding charmonium state. Here,$ \langle \dfrac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle $ and$ \langle \dfrac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle_{0} $ are the expectation values of the scalar gluon condensates in the magnetized medium and vacuum, respectively.$ \psi(k) $ is the wave function in the momentum space normalized as$ \int \dfrac{{\rm d}^{3} k}{(2 \pi)^{3}}|\psi(k)|^{2}=1 $ . The wave functions for these heavy quarkonium states are considered to be harmonic oscillator wave functions and are given by [90]$ \psi_{N,l} =N {Y_{l}}^m ( \theta, \phi)(\beta ^2r^2)^{l/2} {\rm e}^{-({1}/{2}) \beta ^2r^2} L_{N-1}^{l+({1}/{2})} (\beta ^2r^2). $

(39) Here,
$ {L_{p}}^{k}(z) $ is the associated Laguerre polynomial, and$ \beta^2 $ =Mω/h characterizes the strength of the harmonic potential, where$ M = m_{c}/2 $ . The β values for$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ are obtained by fitting their root mean squared radii [83, 84]. The β values for$ \chi_{c0} $ and$ \chi_{c2} $ are obtained using the linear extrapolation of the β vs. vacuum mass of the charmonium states [94]. For$ N_f $ =3, the difference in the value of scalar gluon condensate in the medium and vacuum is given by$ \begin{aligned}[b]& \bigg ( \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle - \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle _{0} \bigg )\\=&\frac{8}{9}\left[(1-d)\left(\chi^{4}-\chi_{0}^{4}\right)+m_{\pi}^{2} f_{\pi} \sigma^{\prime}+\left(\sqrt{2} m_{K}^{2} f_{K}-\frac{1}{\sqrt{2}} m_{\pi}^{2} f_{\pi}\right) \zeta^{\prime}\right]. \end{aligned} $

(40) In the above equation, the terms proportional to
$ \sigma ' $ and$ \zeta ' $ originate from the finite quark mass term$ \sum_i m_i \bar {q_i} q_i $ . When the mass of light quarks is neglected, the terms proportional to$ \sigma ' $ and$ \zeta ' $ vanish. The change in the gluon condensates in the limit of massless light quarks is given by$ \bigg ( \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle - \langle \frac{\alpha_{s}}{\pi} G_{\mu\nu}^{a} G^{\mu\nu a}\rangle _{0} \bigg )=\frac{8}{9}\left[(1-d)\left(\chi^{4}-\chi_{0}^{4}\right)\right]. $

(41) Under this limit, the mass shift of charmonia given by Eq. (37) reduces to [93]
$ \begin{equation} \Delta m_{\psi}^{(m_i=0)}= \frac{4}{81} (1 - d) \int {\rm d}k^{2} \langle \vert \frac{\partial \psi (\vec k)}{\partial {\vec k}} \vert^{2} \rangle \frac{k}{k^{2} / m_{c} + \epsilon} \left( \chi^{4} - {\chi_0}^{4}\right). \end{equation} $

(42) Hence, when the masses of light quarks are neglected, the mass shift for the charmonium states is observed to be proportional to the modification of the dilaton field.
-
In this section, we present the results of the modifications of the scalar fields and the masses of open charm mesons and charmonium states in isospin asymmetric magnetized strange hadronic matter. The parameters in the chiral model are phenomenologically constrained to reproduce the vacuum and nuclear-matter saturation properties [71]. Such a choice of parameters enables the chiral model to predict the properties of hadronic matter. The vacuum expectation values (VEV) of the scalar fields are determined through the relation
$ \sigma_0= -f_\pi $ ,$ \zeta_0=-({1}/{\sqrt{2}})(2f_k-f_\pi) $ [71]. Here,$ f_\pi $ is the pion decay constant, and$ f_k $ is the kaon decay constant. The expectation value of scalar isovector field δ vanishes in the vacuum. The coupling constants of the scalar fields with the nucleons are determined through Eq. (3), using the experimentally known vacuum values of the nucleon masses and the VEV of these scalar fields. Similarly, the couplings of the scalar fields with the hyperons can be determined using Eq. (3) by fitting the known values of the vacuum masses of hyperons when the VEVs of scalar fields are fixed [65, 71, 72]. The vacuum values of scalar fields are$ \sigma_0 $ =$ -93.3 $ MeV and$ \zeta_0 $ =$ -106.6 $ MeV. Thus, the couplings of scalar mesons to nucleons (i= N = p, n in Eq. (3)) are set as$ g_{\sigma N} $ = 10.6 and$ g_{\zeta N} $ =$ -0.47 $ . The couplings of the δ meson with nucleons in Eq. (3) are determined by fitting to the saturation properties of asymmetric nuclear matter in the mean-field theory. Hence, we obtain$ g_{\delta p} $ = 2.5 and$ g_{\delta n} $ =$ -2.5 $ . The values of the couplings of scalar fields with hyperons in Eq. (3) are$ g_{\sigma\Lambda} $ = 7.52,$ g_{\zeta\Lambda} $ = 5.8,$ g_{\delta\Lambda} $ = 0,$ g_{\sigma\Sigma} $ = 6.13,$ g_{\zeta\Sigma} $ = 5.8,$ g_{\delta{\Sigma}^+} $ = 6.79,$ g_{\delta{\Sigma}^-} $ =$ -6.79 $ ,$ g_{\delta{\Sigma}^0} $ = 0,$ g_{\sigma\Xi} $ = 3.78,$ g_{\zeta\Xi} $ = 9.14,$ g_{\delta{\Xi}^0} $ = 2.36, and$ g_{\delta{\Xi}^-}= -2.36 $ . The masses of scalar mesons are set at$ m_\zeta $ = 1024.5 MeV,$ m_\sigma $ = 466.5 MeV, and$ m_\delta $ = 899.5 MeV.In Eq. (2), for nucleons (N= p, n), we obtain i=N; thus, the parameter
$ g_{\omega N} $ denotes the coupling of the ω vector meson with nucleons. The parameter$ g_{\omega N} $ and the VEV of the dilaton field denoted as$ \chi_0 $ in Eq. (4) are selected to fit the binding energy of nuclear matter$ \epsilon/\rho_B-m_N $ =$ -16 $ MeV at the saturation density$ \rho_0 $ = 0.15$ {\rm fm}^{-3} $ [71, 72]. The coupling$ g_4 $ in Eq. (4) is fitted such that the compressibility of the nuclear matter lies in the desired region between 200−300 MeV in the mean-field approximation [71, 72]. These parameters in the mean-field approximation assume the following values:$ g_{\omega N} $ = 13.3,$ g_4 $ = 79.7, and$ \chi_0 $ is determined to be 409.8 MeV. The coupling constants of vector mesons with baryons are fixed using symmetry relations when$ g_{\omega N} $ is fixed [71, 72]. Hence, in asymmetric nuclear matter, the coupling of the ρ meson with a proton in Eq. (2) is determined to be$ g_{\rho p} $ = 5.5, and that with a neutron is determined to be$ g_{\rho n} $ = −5.5. The values of couplings of hyperons with the vector mesons in Eq. (2) are$ g_{\omega\Lambda}= $ $ g_{\omega\Sigma}= $ $ ({2}/{3}) g_{\omega N} $ ,$ g_{\rho{\Sigma}^+}= $ $ ({2}/{3}) g_{\omega N} $ ,$ g_{\rho{\Sigma}^-}= $ $ -({2}/{3}) g_{\omega N} $ ,$g_{\rho{\Sigma}^0} = 0$ ,$ g_{\omega\Xi}= $ $ ({1}/{3}) g_{\omega N} $ ,$ g_{\rho\Lambda}=0 $ ,$ g_{\rho{\Xi}^0}= $ $ ({1}/{3}) g_{\omega N} $ ,$ g_{\rho{\Xi}^-}= $ $ -({1}/{3}) g_{\omega N} $ ,$ g_{\phi\Lambda}= $ $ g_{\phi\Sigma}= $ $ -({\sqrt{2}}/{3}) g_{\omega N} $ ,$ g_{\phi\Xi} $ =$ -({2\sqrt{2}}/{3}) g_{\omega N} $ . The parameters$ k_0 $ ,$ k_2 $ , and$ k_4 $ in Eq. (5) are fixed by demanding that the thermodynamical potential (Ω) has an extremum with respect to scalar fields σ, ζ, and χ in the vacuum [71]. The parameter$ k_3 $ in Eq. (5) is constrained by the mass difference of η and$ \eta' $ mesons, and$ k_1 $ is fitted to provide the σ meson a mass of the order of$ m_\sigma \simeq $ 500 MeV. The values of these parameters are set at$ k_0 $ =2.54,$ k_1 $ =1.35,$ k_2=-4.78 $ ,$ k_3 =-2.77 $ , and$ k_4=-0.22 $ [65, 71]. The parameter d in Eq. (5), which is closely related to the one-loop beta function, is set at d= 0.064 [66].In Figs. 1 and 2, the scalar fields σ, ζ, δ, and χ in isospin asymmetric (η=0.5) hadronic matter are plotted as a function of
$ \rho_{B} $ /$ \rho_{0} $ . Here,$ \rho_{0} $ is the nuclear matter saturation density, and$ \rho_{B} $ is the baryon density. These scalar fields are plotted at magnetic fields eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for various values of the strangeness fraction$ f_{s} $ =0, 0.3, 0.5. In each subplot,$ f_{s} $ =0 corresponds to pure nuclear matter, and$ f_{s} \neq $ 0 corresponds to strange hadronic matter. The effects of the AMMs of the baryons are included in these plots. They are compared with the case in which the effects of the AMMs are ignored (shown as dotted lines). The magnitude of the scalar fields σ and ζ decreases as the baryon density increases in the magnetized medium. This behavior is due to the increase in the scalar density of the baryons with an increase in baryon density. The strange scalar field ζ at high baryon densities exhibits a saturation behavior for$ f_{s} $ =0. This saturation behavior is less pronounced in hyperonic matter, where ζ exhibits a larger variation as a function of density owing to its stronger coupling with hyperons. Since the equation of motion of χ is coupled with that of other scalar fields, the magnitude of χ also decreases with an increase in baryon density. In contrast, the magnitude of δ initially increases with density and then tends to a saturation behavior at high densities. For nuclear matter, this saturation behaviour of δ is observed at densities above$ \rho_{B} $ =2.5$ \rho_{0} $ .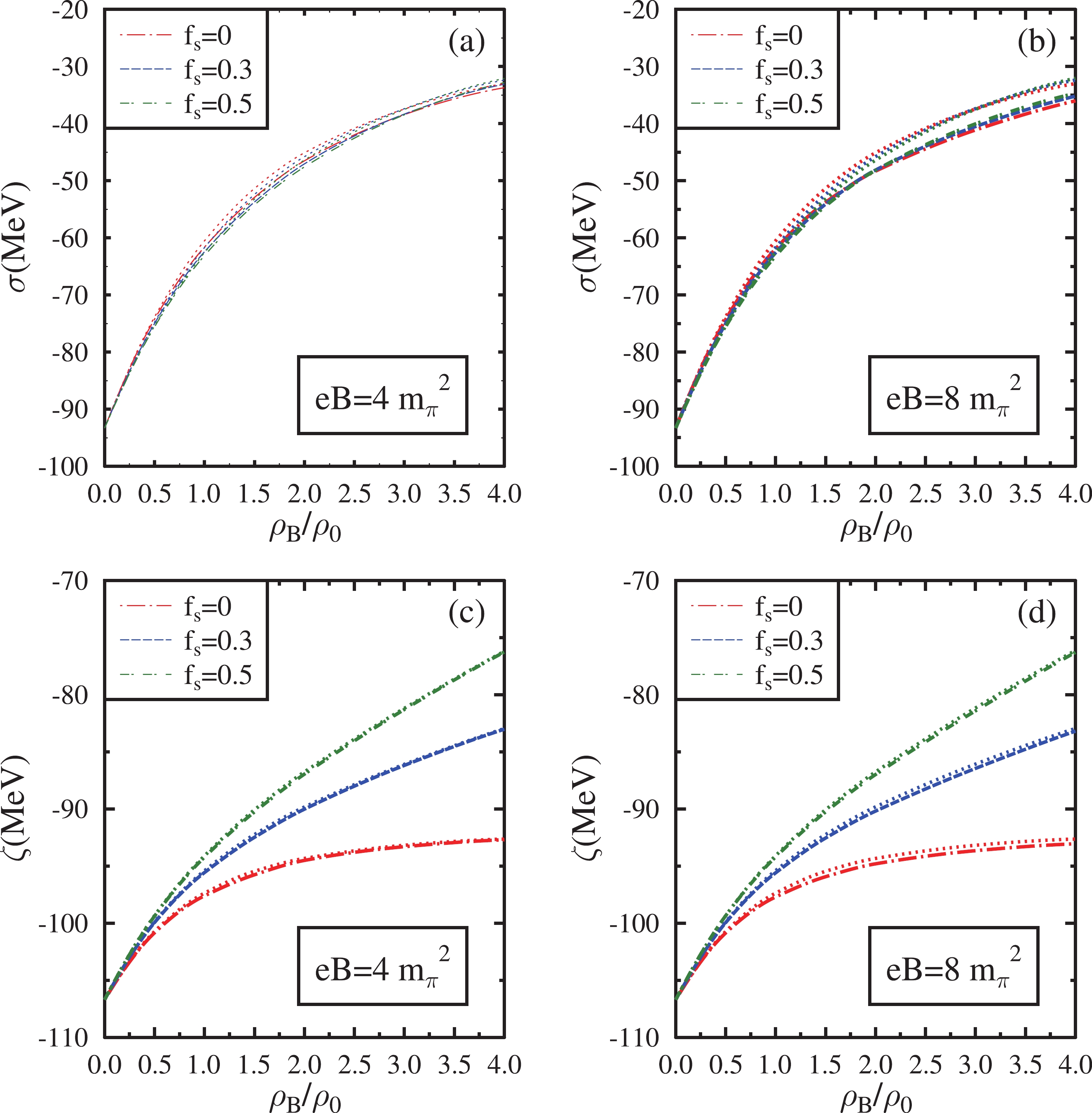
Figure 1. (color online) Scalar fields σ and ζ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of the baryon density
$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at magnetic fields eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for different values of strangeness fraction$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines).
Figure 2. (color online) Scalar fields δ and χ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of
$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines).At small baryon densities and at a fixed magnetic field, as
$ f_s $ increases, the magnitude of σ increases. However, at higher densities, the magnitude of σ instead decreases as$ f_s $ increases. This change in the dependence of σ on$ f_s $ occurs at approximately$ \rho_B $ =3.3$ \rho_0 $ for$ eB=4m_{\pi}^2 $ and at approximately$ \rho_B $ =1.9$ \rho_0 $ for$ eB=8m_{\pi}^2 $ when AMM effects are considered. When AMM effects are neglected, the change in the dependence of σ on$ f_s $ occurs at approximately$ \rho_B $ =3.2$ \rho_0 $ for$ eB=4m_{\pi}^2 $ and$ eB=8m_{\pi}^2 $ . This behavior occurs because the sum of the scalar densities of baryons for$ f_s\neq0 $ is larger than the scalar density of neutrons for$ f_s=0 $ at$ \eta=0.5 $ and at large baryon densities. We observe that the magnitude of ζ significantly decreases as$ f_s $ increases, particularly at large baryon densities. However, the magnitude of δ is observed to increase with an increase in$ f_s $ . The onset of saturation behavior of δ is observed at relatively higher densities for$ f_s \neq $ 0 compared with$ f_s $ = 0. The dilaton field χ decreases as$ f_s $ increases owing to its coupling with the other scalar fields. The effects of$ f_s $ on σ and δ are larger when the magnetic fields are stronger.For charged baryons, the expression of scalar density given by Eq. (9) contains the summation over the Landau energy levels and contributions from their AMMs. In the expression for the scalar densities of neutral baryons given by Eq. (12), the effects of the magnetic field are in terms of their AMMs only. Hence, in the absence of AMMs, the neutral baryons are not subjected to the effect of the magnetic field. When the AMM effects are incorporated, the scalar density of nucleons is modified more than that of hyperons because the values of the gyromagnetic ratio corresponding to the AMMs of the nucleons are slightly larger [98, 99]. For η=0.5, the AMM effects result in slightly smaller values of the cumulative scalar densities of the baryons compared with the case when AMM effects are neglected. Hence, the magnitude of σ with AMM effects is larger than that of the case in which AMM effects are neglected. The effects of AMMs on σ are observed to be larger at large densities and magnetic fields. The effect of AMMs on the ζ field are qualitatively similar to that of σ, but the variation is marginal. In the strange hadronic medium, the magnitude of δ increases at large baryon densities when AMM effects are considered. The dependence of δ on AMM effects is elevated at stronger magnetic fields.
The effects of the magnetic field on the scalar fields are less dominant than the effects of density. For a given value of
$ f_s $ , at small baryon densities, the magnitude of σ and χ increases marginally with the increase in the magnetic field when AMM effects are considered. At$ \rho_B=4\rho_0 $ , the magnitude of σ increases by$ \sim $ 2 MeV, and that of χ increases by$ \sim $ 1 MeV as the magnetic field increases from eB=$ 4m_\pi^2 $ to eB=$ 8m_\pi^2 $ . The variation in ζ as a function of the magnetic field is smaller than that of σ. The change in δ is marginal as a function of the magnetic field at small densities. For strange hadronic matter, at higher densities (above 3$ \rho_0 $ ), the magnitude of δ is observed to increase with an increase in the magnetic field. When AMM effects are neglected, the effect of the magnetic field on scalar fields is minimal for hyperonic matter. In this case, only the charged baryons are affected by the variation in the magnetic field.For
$ \eta=0.5 $ ,$ f_s=0.3 $ , and eB=$ 4m_\pi^2 $ , the values of σ (in MeV) at$ \rho_B $ =$ \rho_0 $ , 2$ \rho_0 $ , 3$ \rho_0 $ , and 4$ \rho_0 $ with (without) AMM effects are observed to be$ -62.42\; (-61.68) $ ,$ -47.02\; (-45.77) $ ,$ -38.31\; (-37.37) $ , and$ -33.08 $ ($ -32.36 $ ), respectively. For eB=$ 8m_\pi^2 $ , they are modified to$ -62.57 \;(-61.66) $ ,$ -48.11\; (-45.76) $ ,$ -40.49 (-37.35) $ , and$ -35.17 \;(-32.35) $ , respectively. For eB=$ \ 4m_\pi^2 $ , the values of ζ (in MeV) at$ \rho_B $ =$ \rho_0 $ , 2$ \rho_0 $ , 3$ \rho_0 $ , and 4$ \rho_0 $ with (without) AMM effects are observed to be$ -95.55\; (-95.40) $ ,$ -90.01\; (-89.82) $ ,$ -86.17\; (-86.08) $ , and$ -83.01\;(-82.96) $ respectively. For eB=$ \ 8m_\pi^2 $ , the values of ζ become$ -95.58\; (-95.39) $ ,$ -90.18 $ ($ -89.81 $ ),$ -86.44 (-86.06) $ , and$ -83.18\; (-82.94) $ , respectively. For δ, the values in the same order are$ -3.10\; (-3.16) $ ,$ -4.92\; (-4.97) $ ,$ -5.68\; (-5.65) $ , and$ -5.94\; (-5.86) $ for eB=$ 4m_\pi^2 $ . As the magnetic field is increased to eB=$ 8m_\pi^2 $ , the values of δ are modified to$ -3.10\; (-3.16) $ ,$ -4.86\; (-4.98) $ ,$ -5.67 (-5.66) $ , and$ -6.05\; (-5.87) $ . For eB=$ 4m_\pi^2 $ , the values of χ under the same medium conditions are 406.78 (406.65), 403.11 (402.76), 399.96 (399.61), 397.46 (397.14) at$ \rho_B $ =$ \rho_0 $ , 2$ \rho_0 $ , 3$ \rho_0 $ , and 4$ \rho_0 $ respectively with (without) AMM effects. For eB=$ 8m_\pi^2 $ , they become 406.80 (406.65), 403.41 (402.75), 400.73 (399.60), 398.34 (397.14), respectively.The in-medium masses of the open charm mesons
$ D(D^0,D^+) $ ,$ \bar{D}(\bar{D^0},D^-) $ , and$ D_s({D_s}^+,{D_s}^-) $ in the presence of magnetic fields are plotted in Figs. 3, 4, and 5, respectively. They are calculated using the dispersion relations for these mesons. The values of parameters$ d_1 $ and$ d_2 $ in Eqs. (24) and (25) are$ d_1 $ = 2.56/$ m_K $ and$ d_2 $ =0.73/$ m_K $ . The D meson decay constant in Eq. (24) is set as$ f_D $ =135 MeV [109] and their vacuum masses are$ m_{D^+} $ =$ m_{D^-} $ = 1869 MeV and$ m_{D^0} $ =$ m_{\bar{D^0}} $ = 1864.5 MeV. For the$ D_s $ meson, the decay constant in Eq. (25) is set as$ f_{D_s} $ = 235 MeV [70] and their vacuum masses are$ m_{{D_s}^+} $ =$ m_{{D_s}^-} $ = 1968.5 MeV. The mass modifications of these mesons are due to the Weinberg-Tomozawa term, scalar meson-exchange term, and range terms. For charged mesons, there is an additional contribution of the magnetic field through Landau quantization according to Eq. (30).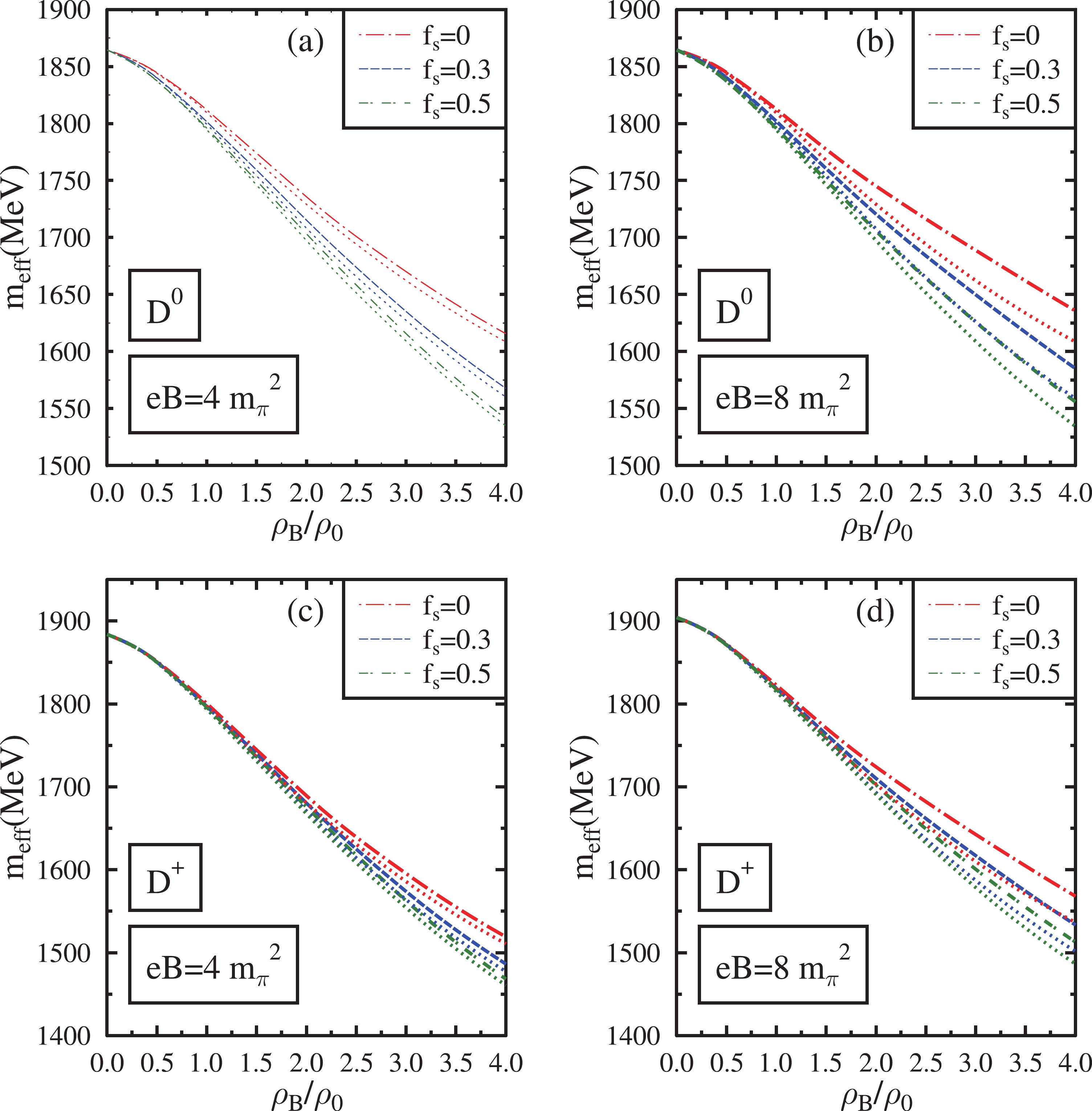
Figure 3. (color online) Effective masses of
$ D(D^0,D^+) $ mesons in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines).
Figure 4. (color online) Effective masses of
$ \bar{D}(\bar{D^0},D^-) $ mesons in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines).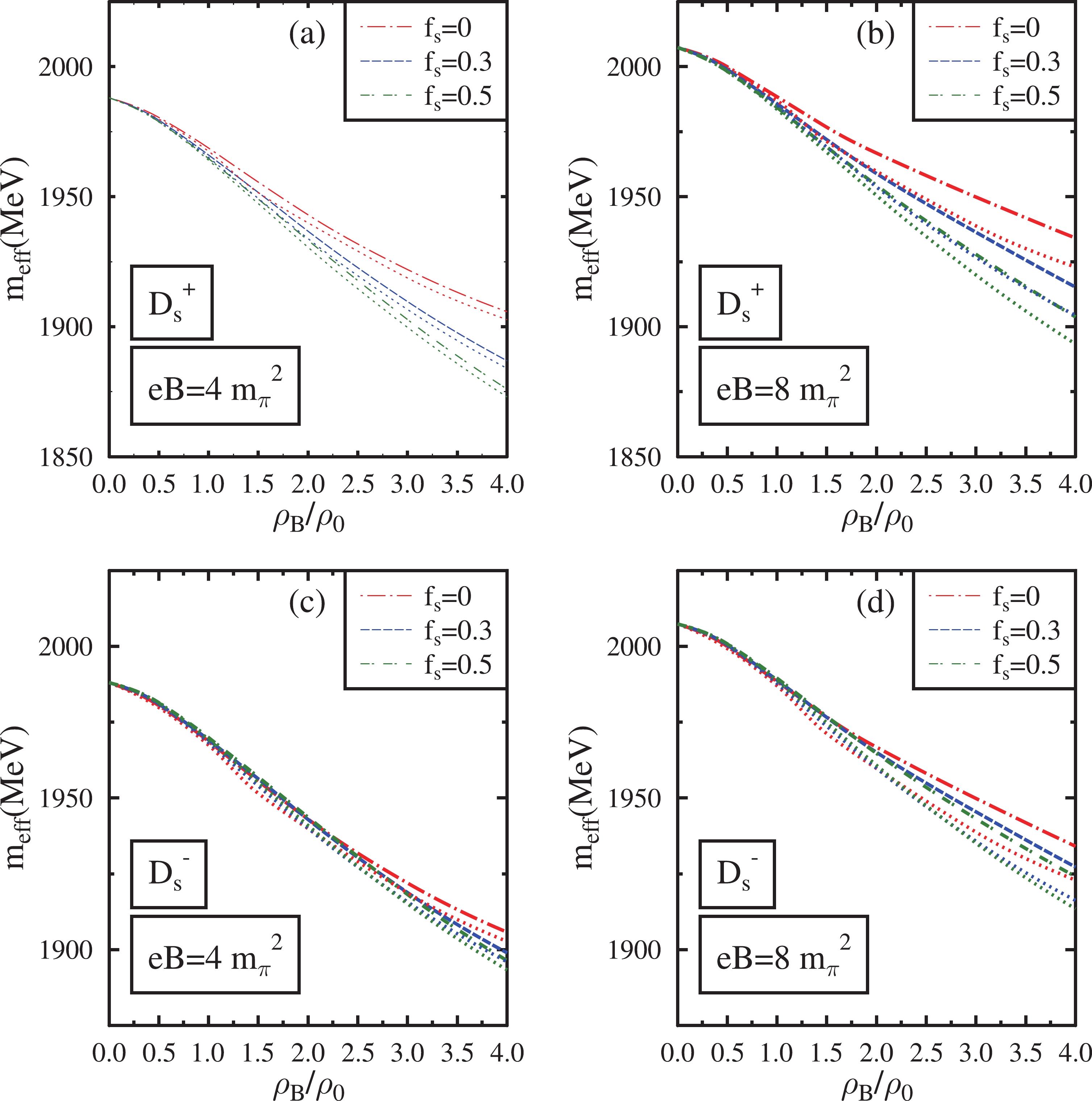
Figure 5. (color online) Effective masses of
$ ({D_s}^+,{D_s}^-) $ mesons in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines).The isospin symmetric part of the Weinberg-Tomozawa term is attractive for D mesons (results in a mass decrease for
$ D^0 $ and$ D^+ $ ) and repulsive for$ \bar{D} $ mesons (results in an increase in the mass of$ \bar{D^0} $ and$ D^- $ ). The isospin asymmetric part ($ \sim $ ($ \rho_p-\rho_n $ ), ($ \rho_{\Sigma^+}-\rho_{\Sigma^-} $ ), ($ \rho_{\Xi^0}-\rho_{\Xi^-} $ )) of the Weinberg-Tomozawa term distinguishes the isospin pairs of mesons. Hence, in an isospin asymmetric medium, the Weinberg-Tomozawa term results in the mass splitting of mesons in the isospin doublets. This term positively contributes to the mass of$ D^0 $ and negatively contributes to the mass of$ D^+ $ . Similarly, the mass of$ D^- $ increases, whereas the mass of$ \bar{D^0} $ decreases due to this term. Hence,$ D^+ $ and$ D^0 $ , as well as$ D^- $ and$ \bar{D^0} $ mesons, have non-degenerate masses in asymmetric matter. Even in magnetized symmetric matter, the non-zero value of δ contributes to the scalar meson exchange and range terms, which marginally breaks the mass degeneracy.Because δ is negative in asymmetric nuclear matter (
$ \eta=0.5 $ ), the δ term makes the scalar-meson exchange term more attractive for$ D^+ $ and$ D^- $ mesons compared with symmetric matter. In contrast, the contribution of δ makes the scalar-meson exchange term less attractive for$ D^0 $ and$ \bar{D^0} $ mesons than for symmetric matter. The contribution of δ makes the first range term more repulsive for$ D^+ $ ,$ D^- $ mesons and less repulsive for$ D^0 $ ,$ \bar{D^0} $ mesons in asymmetric nuclear matter. The$ d_1 $ range term is attractive for all mesons. For$ \eta=0.5 $ nuclear matter, while the$ d_2 $ term contributes to the mass decrease of$ D^+ $ ,$ D^- $ mesons, it does not contribute to$ D^0 $ and$ \bar{D^0} $ mesons. The modifications of D and$ \bar{D} $ mesons in the magnetized nuclear medium are discussed further in Ref. [91].The masses of the D and
$ \bar{D} $ mesons decrease from their vacuum masses as the baryon density increases for a fixed values of the magnetic field and$ f_s $ . This decrease in mass is due to the attractive scalar meson exchange term and$ d_1 $ and$ d_2 $ range terms, which dominate over the repulsive first range term at large densities. The$ d_1 $ and$ d_2 $ terms contain scalar densities of baryons whose magnitude increases with baryon density. The scalar meson exchange term contains the fluctuations of scalar fields denoted as$ \sigma^\prime $ and$ \delta^\prime $ , which also increases with density. For$ \bar{D} $ mesons, the attractive contributions of the scalar meson exchange term and$ d_1 $ ,$ d_2 $ range terms also dominate over the repulsive contributions of the Weinberg-Tomozawa term at high densities. For D mesons, the Weinberg-Tomozawa term is attractive. Hence, the masses of D ($ D^0 $ ,$ D^+ $ ) mesons decrease more than those of$ \bar{D} $ ($ \bar{D^0} $ ,$ D^- $ ) mesons in magnetized media. Among$ D^0 $ and$ D^+ $ mesons, the mass of$ D^+ $ decreases more owing to the cumulative contributions of isospin asymmetric terms in the interaction Lagrangian. When AMM effects are incorporated, for$ f_s $ =0.3 and eB=$ \ 4m_\pi^2 $ ,$ D^0 $ ,$ D^+ $ ,$ \bar{D^0} $ , and$ D^- $ experience decreases in mass of 63, 72, 35, and 11 MeV, respectively, at$ \rho_B $ =$ \rho_0 $ . At$ \rho_B $ = 4$ \rho_0 $ , the decreses in mass of$ D^0 $ ,$ D^+ $ ,$ \bar{D^0} $ , and$ D^- $ are 297, 383, 205, and 168 MeV respectively.For a given value of the magnetic field and density, as we increase the value of
$ f_s $ , D and$ \bar{D} $ mesons experience a larger mass decrease. At eB=$ \ 4m_\pi^2 $ , incorporating the AMM effects,$ D^0 $ and$ D^+ $ mesons have a mass decrease of 10 and 3 MeV more for$ f_s $ =0.3 than for$ f_s $ =0 at$ \rho_B $ =$ \rho_0 $ . Under the same conditions, the mass decreases of$ \bar{D^0} $ and$ D^- $ mesons are 16 and 9 MeV more for$ f_s $ =0.3 than for$ f_s $ =0. When the baryon density increases to$ \rho_B $ = 4$ \rho_0 $ ,$ D^0 $ ,$ D^+ $ ,$ \bar{D^0} $ , and$ D^- $ mesons have additional mass decreases of 48, 33, 58, and 62 MeV, respectively, for$ f_s $ =0.3 than for$ f_s $ =0. This larger mass decrease in the strange medium is due to the larger value of cumulative scalar densities of baryons with an increase in$ f_s $ , particularly at large densities. The$ d_1 $ and$ d_2 $ range terms depend on the scalar densities of baryons. These terms become more attractive as$ f_s $ increases and ensure a large decrease in the masses of D and$ \bar{D} $ in the magnetized hyperonic medium. Moreover, the contribution of the Weinberg-Tomozawa term to the mass of the D and$ \bar{D} $ mesons become weaker when the medium is populated with hyperons [65]. For D mesons, the Weinberg-Tomozawa term is attractive and becomes weaker in the presence of hyperons. For$ \bar{D} $ mesons, the repulsive Weinberg-Tomozawa term becomes weaker and further contributes to the mass decrease of$ \bar{D} $ in the strange hadronic medium. Hence, the mass decrease of$ \bar{D} $ mesons is more sensitive to the change in$ f_s $ compared with that of D mesons.The isospin asymmetric contributions in the Weinberg-Tomozawa term and
$ d_2 $ range term are dominantly responsible for the difference in the mass decrease of the mesons in isospin doublets as$ f_s $ increases. The scalar meson exchange term and first range term rely on the fluctuations$ \sigma^\prime $ and$ \delta^\prime $ . As discussed earlier, the scalar field σ does not behave in a monotonic manner with the increase in$ f_s $ . However, the magnitude of δ increases with an increase in$ f_s $ at all baryon densities. Hence, the magnitude of the scalar meson exchange and first range terms depends on the interplay of$ \sigma^\prime $ and$ \delta^\prime $ in strange hadronic media.The magnetic field introduces mass modifications of D and
$ \bar{D} $ mesons by modifying the scalar fields and the scalar densities of baryons. For a fixed value of$ f_s $ , when AMM effects are considered, the mass of D and$ \bar{D} $ mesons increases with an increase in the magnetic field, particulary at large densities. For isospin asymmetric matter, the cumulative scalar density of the baryons and the fluctuation$ \sigma^\prime $ decrease as$ eB $ increases. Hence, in the presence of a magnetic field, the attractive contributions from the$ d_1 $ ,$ d_2 $ range terms and the scalar meson exchange term decrease. This decrease in the cumulative scalar density of baryons with an increase in the magnetic field is more pronounced in a nuclear medium compared with a strange hadronic medium. Moreover, the fluctuation$ \sigma^\prime $ induced by an increase in the magnetic field is also smaller in the nuclear medium. Hence, the magnitude of the$ d_1 $ ,$ d_2 $ range terms, and scalar meson exchange term weaken further in magnetized nuclear media compared with magnetized hyperonic media. The neutral D mesons are subjected to less modification from the magnetic field compared with charged D mesons. The magnetic field induces additional positive mass modifications for$ D^+ $ and$ D^- $ mesons through Landau quantization according to Eq. (30). At$ \rho_B=\rho_0 $ ,$ D^0 $ and$ \bar{D^0} $ mesons exhibit only a marginal mass modification as a function of the magnetic field. For$ f_s=0.3 $ , incorporating the AMM effects, as the magnetic field is increased from eB=$ \ 4m_\pi^2 $ to eB=$ \ 8m_\pi^2 $ ,$ D^0 $ and$ \bar{D^0} $ experience an increase in mass of 17 and 18 MeV, respectively, at$ \rho_B $ = 4$ \rho_0 $ . Under the same conditions,$ D^+ $ and$ D^- $ experience an increase of 47 and 49 MeV, respectively, in their in-medium masses.When the AMM effects are ignored, only the charged baryons are subjected to the change in the magnetic field. For
$ \eta=0.5 $ and$ f_s=0 $ , the nuclear matter is composed of only neutrons. When AMM effects are neglected, neutrons, which are electrically neutral, will not undergo modifications in the magnetic field. In the strange hadronic medium, the variation in scalar densities and scalar fields with an increase in the magnetic field is small when AMM effects are ignored. This variation increases with an increase in$ f_s $ . The effect of the magnetic field on neutral$ D^0 $ and$ \bar{D^0} $ mesons are marginal in this case. They experience a mass decrease of less than 1–2 MeV as the magnetic field increases from eB =$ \ 4m_\pi^2 $ to eB =$ \ 8m_\pi^2 $ . The in-medium mass of D and$ \bar{D} $ mesons are observed to be smaller when AMM effects are neglected compared with the case in which these effects are included. This behavior is due to the larger value of scalar density and the smaller magnitude of σ when AMM effects are neglected, thereby increasing the attractive contributions from the total range and scalar meson exchange terms.The in-medium masses of
$ D_s $ mesons decrease as the baryon density increases when the magnetic field is fixed. In a nuclear medium, the interaction Lagrangian of$ D_s $ mesons has no contribution from the Weinberg-Tomozawa term and$ d_2 $ range terms. These terms depend only on the number density and scalar density of hyperons, respectively. Hence, the net mass decrease in$ D_s $ mesons in nuclear matter is primarily due to the$ d_1 $ range term, which depends on the scalar density of the nucleons. When$ \eta=0.5 $ and$ f_s=0 $ , the$ d_1 $ range term depends on the scalar density of only neutrons. The attractive contribution of the scalar meson exchange term proportional to the fluctuation$ \zeta^\prime $ becomes saturated at large densities owing to the saturation behavior of ζ in the nuclear matter, as shown in Fig. 1. The repulsive first range term, which is also proportional to$ \zeta^\prime $ , becomes surpassed by the dominant$ d_1 $ range term at relatively large densities. Moreover, because of the vanishing Weinberg-Tomozawa term in nuclear matter, the self-energy expression given by Eq. (29) becomes identical for both$ {D_s}^+ $ and$ {D_s}^- $ mesons. Hence, their in-medium masses are degenerate in the nuclear matter at a fixed magnetic field. In an asymmetric ($ \eta=0.5 $ ) nuclear medium, at eB =$ 4m_\pi^2 $ , the masses of$ {D_s} $ mesons are 1968.70, 1943.03, 1921.98 and 1905.80 MeV at$ \rho_0 $ , 2$ \rho_0 $ , 3$ \rho_0 $ , and$ 4\rho_0 $ , respectively, incorporating the AMM effects.In the strange hadronic medium, the contributions of the Weinberg-Tomozawa term and
$ d_2 $ range term are non-vanishing in the interaction Lagrangian of$ D_s $ mesons. The Weinberg-Tomozawa term, which is attractive for$ {D_s}^+ $ mesons and repulsive for$ {D_s}^- $ mesons, breaks their mass degeneracy when hyperons are present in the medium. This breaking of mass degeneracy becomes aggravated with an increase in baryon density. The variation in ζ as a function of baryon density is more pronounced in the hyperonic matter. Hence, the magnitude of the scalar meson exchange and first range terms is larger in the hyperonic medium compared with that in the nuclear medium. The overall attractive contributions from the total range and scalar meson exchange terms are more dominant than the Weinberg-Tomozawa term. Hence, a net mass decrease for$ D_s $ mesons is observed in the magnetized hyperonic medium. For the$ {D_s}^+ $ meson, the attractive Weinberg-Tomozawa term contributes to the mass decrease. However, for$ {D_s}^- $ meson, the repulsive Weinberg-Tomozawa term reduces the net attractive contributions. Hence, the mass of$ {D_s}^+ $ meson decreases more than that of$ {D_s}^- $ mesons in the magnetized strange hadronic medium. For$ \eta=0.5 $ ,$ f_s=0.3 $ , and eB =$ 4m_\pi^2 $ , the masses of$ {D_s}^+ $ mesons are 1966.02, 1936.72, 1909.66, and 1886.81 MeV at$ \rho_0 $ , 2$ \rho_0 $ , 3$ \rho_0 $ , and$ 4\rho_0 $ , respectively, incorporating the AMMs of baryons. Under the same conditions, the masses of$ {D_s}^- $ mesons are 1969.16, 1942.92, 1918.83, and 1898.98 MeV, respectively.At a fixed baryon density and magnetic field, the
$ {D_s}^+ $ meson experiences a significant mass decrease in the strange hadronic matter compared with that in the nuclear matter. This behavior is due to the attractive Weinberg-Tomozawa term and$ d_2 $ range term, which are absent in the nuclear matter. The magnitude of the attractive scalar meson exchange term is larger in the hyperonic matter, which further aids in the mass decrease of the$ {D_s}^+ $ meson. The mass drop of the$ {D_s}^- $ meson is smaller in the hyperonic matter than that in the nuclear matter at small to intermediate densities (up to 1.9$ \rho_0 $ -2$ \rho_0 $ ). This behavior is due to the non-vanishing repulsive contributions of the Weinberg-Tomozawa term for$ {D_s}^- $ mesons in the hyperonic matter. The Weinberg-Tomozawa term is dominant at small to intermediate densities. However, at higher densities (above 2$ \rho_0 $ ), the magnitude of the attractive contributions from$ d_1 $ ,$ d_2 $ range terms and scalar meson exchange term dominates over the repulsive Weinberg-Tomozawa term. Hence, the$ {D_s}^- $ mass decreases more in the hyperonic matter compared with that in nuclear matter at large baryon densities. As$ f_s $ increases, the mass decrease becomes greater at high densities.The masses of
$ {D_s}^+ $ and$ {D_s}^- $ mesons increase with an increase in the magnetic field due to the Landau quantization effect according to Eq. (30). At small densities (up to$ 1.5\rho_0 $ ), this positive mass modification of charged$ {D_s} $ mesons is dominant over the mass decrease owing to the attractive terms in the expression of self-energy. The modification of the scalar field ζ and scalar densities of baryons as a function of the magnetic field also contribute to the medium mass of$ {D_s} $ mesons. As the magnetic field is increased from eB =$ \ 4m_\pi^2 $ to eB =$ \ 8m_\pi^2 $ , the mass of$ D_s $ mesons increases by 20 MeV at$ \rho_B $ =$ 1\rho_0 $ when AMM effects are considered. At$ \rho_B $ =$ 4\rho_0 $ , the mass of$ D_s $ mesons increases by 28 MeV as the magnetic field is increased from eB =$ \ 4m_\pi^2 $ to eB =$ \ 8m_\pi^2 $ . At a fixed magnetic field, the in-medium masses of$ {D_s} $ mesons are smaller when AMM effects are neglected compared with the case when these effects are incorporated. This behavior is due to the larger values of scalar densities and a smaller value of ζ in the absence of AMM effects, making the$ d_1 $ ,$ d_2 $ range terms and scalar meson exchange term more attractive. The effects of AMMs on the masses of these mesons become significant at larger magnetic fields and larger densities. From Figs. 3, 4, and 5, we can observe that the mass modification of$ {D_s} $ mesons as a function of baryon density is smaller than that of$ D(\bar{D}) $ mesons. Hence, the effect of Landau quantization has relatively more significance in the overall mass modifications of$ {D_s} $ mesons, particularly at small baryon densities.We have investigated the modifications of charmonium states in strange hadronic matter under strong magnetic fields. The mass shifts of
$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ ,$ \chi_{c0} $ , and$ \chi_{c2} $ in isospin asymmetric ($ \eta=0.5 $ ) magnetized hadronic matter are shown in Figs. 6−10. The mass shifts are plotted as a function of baryon density at magnetic fields eB =$ \ 4m_\pi^2 $ and eB =$ \ 8m_\pi^2 $ for various values of the strangeness fraction ($ f_s $ ). The effects of the AMMs of baryons are also incorporated into these plots, represented by dashed lines. In these figures, subplots (a) and (c) correspond to the mass shifts when the medium modification of gluon condensates is calculated by neglecting the finite quark mass term given by Eq. (41). Subplots (b) and (d) show the mass shifts incorporating the quark mass term in the modification of gluon condensates given by Eq. (40).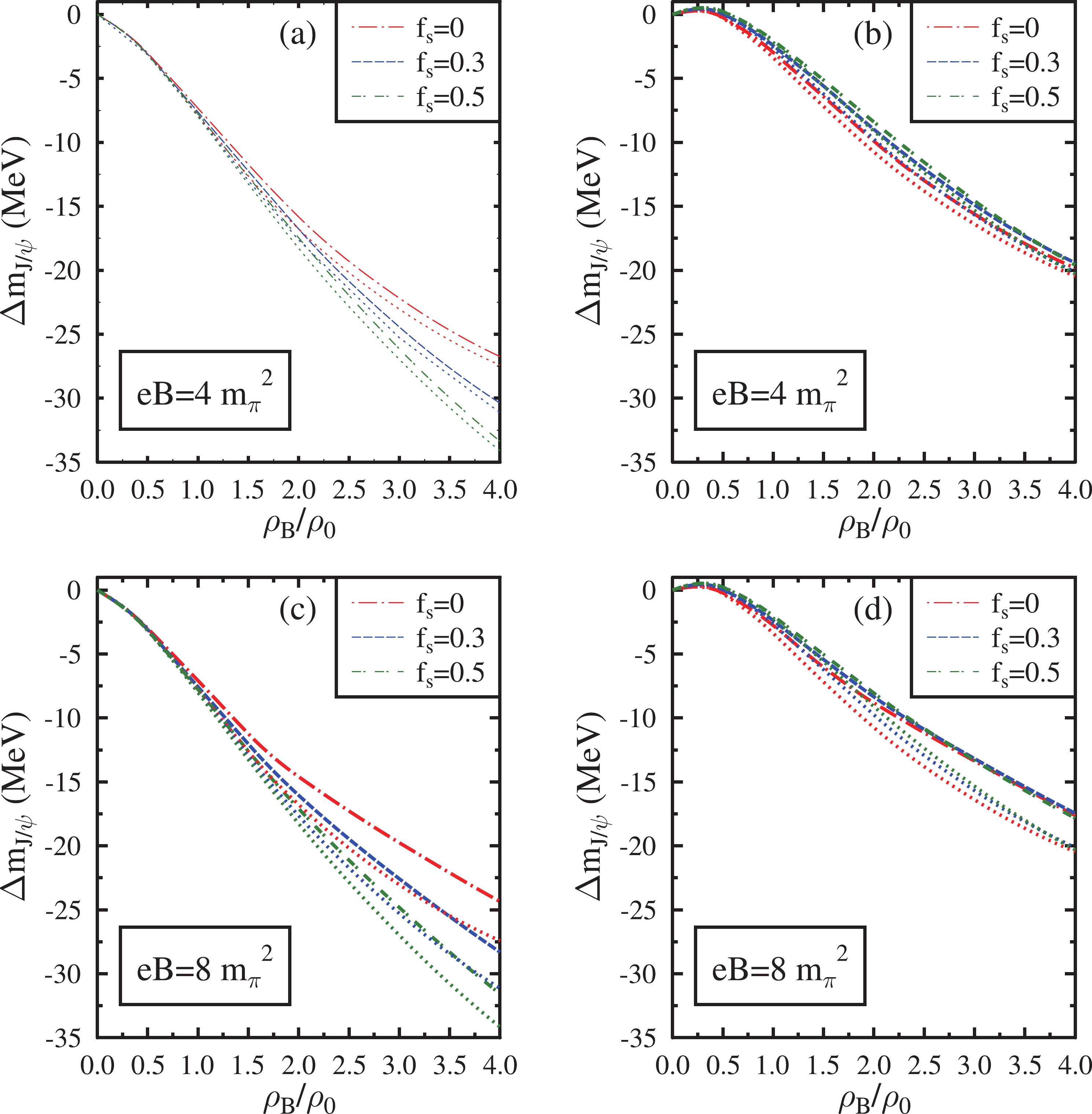
Figure 6. (color online) Mass shift of
$ J/\psi $ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines). In subplots (a) and (c), the mass shifts are shown when the modification of gluon condensates is calculated by neglecting the finite quark mass term. In subplots (b) and (d), the mass shifts are shown incorporating the quark mass term.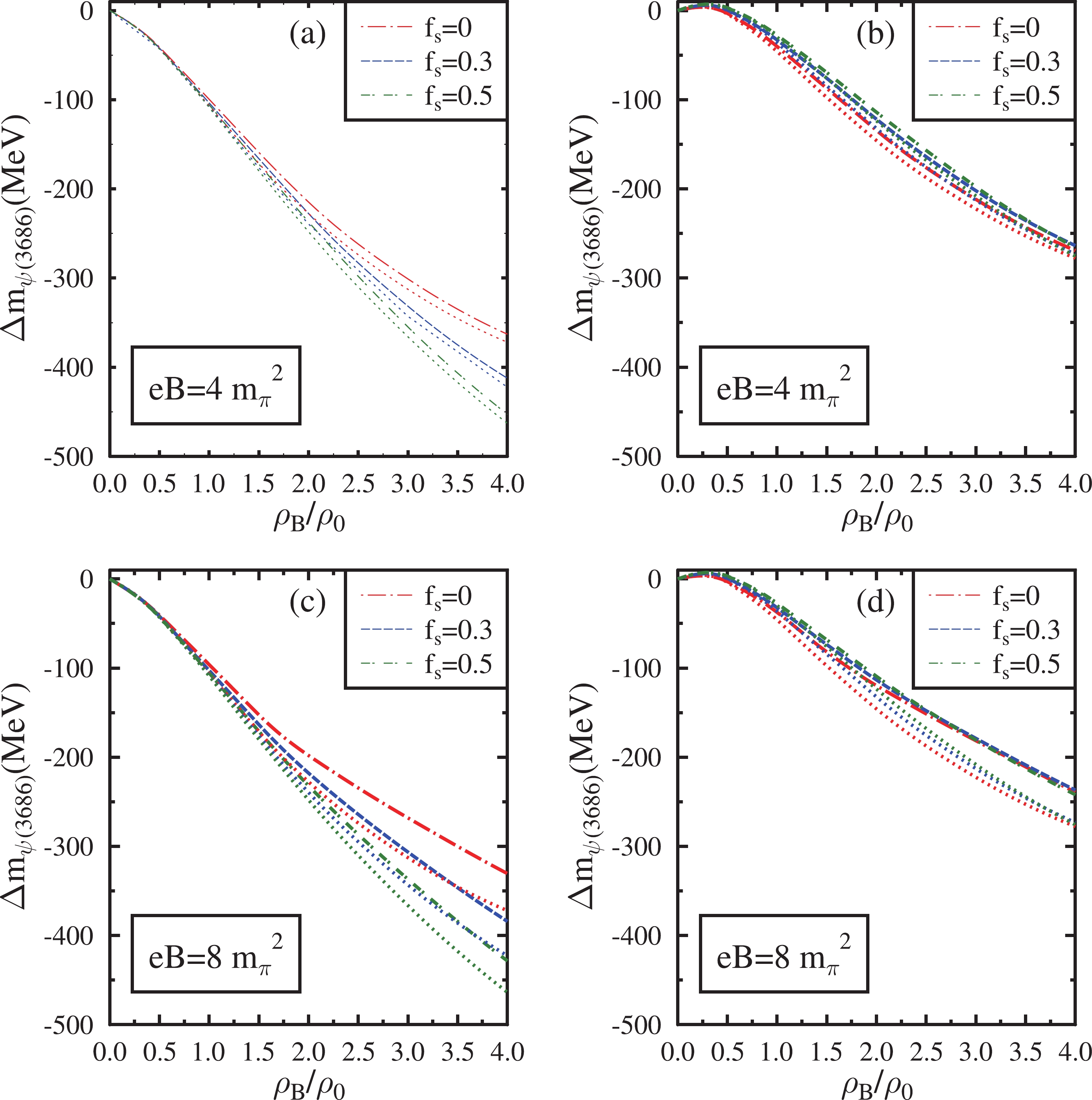
Figure 7. (color online) Mass shift of
$ \psi(3686) $ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines). In subplots (a) and (c), the mass shifts are shown when the modification of gluon condensates is calculated by neglecting the finite quark mass term. In subplots (b) and (d), the mass shifts are shown incorporating the quark mass term.
Figure 8. (color online) Mass shift of
$ \psi(3770) $ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines). In subplots (a) and (c), the mass shifts are shown when the modification of gluon condensates is calculated by neglecting the finite quark mass term. In subplots (b) and (d), the mass shifts are shown incorporating the quark mass term.
Figure 9. (color online) Mass shift of
$ \chi_{c0} $ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of the baryon density$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB =$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines). In subplots (a) and (c), the mass shifts are shown when the modification of gluon condensates is calculated by neglecting the finite quark mass term. In subplots (b) and (d), the mass shifts are shown incorporating the quark mass term.
Figure 10. (color online) Mass shift of
$ \chi_{c2} $ in isospin asymmetric (η=0.5) hadronic matter plotted as a function of the baryon density$ \rho_{B} $ /$ \rho_{0} $ . These are plotted at eB=$ 4{m_{\pi}}^2 $ ,$ 8{m_{\pi}}^2 $ for$ f_{s} $ = 0, 0.3, 0.5. The effects of the anomalous magnetic moment of baryons are incorporated into these plots (dashed lines) and compared with the case in which these effects are neglected (dotted lines). In subplots (a) and (c), the mass shifts are shown when the modification of gluon condensates is calculated by neglecting the finite quark mass term. In subplots (b) and (d), the mass shifts are shown incorporating the quark mass term.The value of the mass of the charm quark is set as
$ \ m_c=1.95 $ GeV in this investigation. Such a choice can reproduce the mass difference of the charmonium states$ J/\psi $ and$ \psi(3686) $ in a vacuum [82, 83]. In this investigation, the wave functions of the charmonium states are considered to be harmonic oscillator wave functions. The values of the parameter β, which characterizes the strength of the harmonic potential (in GeV) for$ J/\psi $ ,$ \psi(3686) $ , and$ \psi(3770) $ are 0.51, 0.38, and 0.37, respectively. They are calculated using the mean square radii of these charmonium states, which assume the values of$ 0.47^2 $ ,$ 0.96^2 $ , and$ 1 fm^2 $ , respectively [82, 83]. For the$ \chi_{c0} $ and$ \chi_{c2} $ states, the values of β in GeV are determined as 0.44 and 0.41 using the linear extrapolation of the vacuum mass versus β graph of the charmonium states$ J/\psi $ ,$ \psi(3686) $ , and$ \psi(3770) $ [94].The mass shifts for each charmonium state are proportional to the magnitude of the integral given in Eq. (37). The integral is calculated from their respective momentum wave functions. Among all the charmonium states,
$ \psi(3770) $ experiences the largest mass decrease because the integral calculated for this particular state amplifies the density dependence of the mass shift. The mass shift of$ J/\psi $ is small compared with that of other excited charmonium states. The dominant medium effect on the mass modification of the charmonium states is observed to be the effect of density. At a fixed value of the magnetic field and strangeness fraction, the value of χ decreases from its vacuum value as the baryon density increases. Hence, under the massless quark limit, the mass shifts of all charmonium states, which are proportional to$ \chi^4-{\chi_0}^4 $ (Eq. (42)), are negative. The magnitude of mass shifts steadily increases with an increase in baryon density. Since the dilaton field χ decreases with an increase in$ f_s $ , the mass shifts of charmonia calculated in the limit of massless quark are larger in a hyperonic medium than in a nuclear medium. As the magnetic field increases, charmonium states undergo marginal mass shifts at lower densities (up to 2$ \rho_0 $ ) when the AMM effects are considered. However, at large densities, the mass drop of charmonium states decreases with an increase in the magnetic field. This behavior is due to the increase in the value of χ as a function of the magnetic field. Moreover, the mass shift is more significant in magnetized nuclear matter than in hyperonic matter. When the AMMs of baryons are neglected, the effects of the magnetic field on the mass shifts of charmonium states are marginal in the strange hadronic medium. Hence, in the strange medium, the mass shift of charmonia is larger when AMM effects are ignored compared with the case in which these effects are incorporated. This effect becomes prominent with an increase in the strength of the magnetic field.When the finite quark mass term is incorporated in the modification of gluon condensates as given by Eq. (40), the terms proportional to
$ \sigma ' (=\sigma-\sigma_0) $ and$ \zeta ' (=\zeta-\zeta_0) $ also contribute along with the term proportional to$ \chi^4-{\chi_0}^4 $ . At finite baryon densities,$ \chi < \chi_0 $ , with χ and$ \chi_0 $ both being positive. Hence, the term proportional to$ \chi^4-{\chi_0}^4 $ in Eq. (40) is negative. At finite densities,$ \sigma > \sigma_0 $ ($ |\sigma| < |\sigma_0| $ ), with σ and$ \sigma_0 $ both being negative. Similarly$ \zeta > \zeta_0 $ ($ |\zeta| < |\zeta_0| $ ), with ζ and$ \zeta_0 $ both being negative. Hence, the terms proportional to$ \sigma '(=\sigma-\sigma_0) $ and$ \zeta '(=\zeta-\zeta_0) $ in Eq. (40) are positive. Thus, the modification of gluon condensates in the finite quark mass limit depends on the interplay of these positively and negatively contributing terms. The resulting mass shift of charmonia in the finite quark mass limit will also be dependent on these three terms via Eq. (37).In the limit of finite quark masses, a slight positive mass shift for charmonia is observed up to small baryon densities (0.4−0.55
$ \rho_0 $ ). This positive mass shift is due to the more considerable modification of σ and ζ at small densities compared with χ. Hence, the positive contribution of the terms proportional to$ \sigma '(=\sigma-\sigma_0) $ and$ \zeta '(=\zeta-\zeta_0) $ are dominant at small baryon densities. However, as the baryon density increases, the term proportional to$ \chi^4-{\chi_0}^4 $ dominates, and a negative mass shift is observed thereafter. The density at which the mass shift becomes negative for a particular charmonium state depends on the value of$ f_s $ and the magnetic field. Moreover, the terms proportional to$ \sigma ' $ and$ \zeta ' $ saturates at large densities. Hence, the magnitude of the negative mass shifts of charmonia increases with an increase in baryon density. When finite quark masses are incorporated, at small densities, the mass shifts calculated in the hyperonic medium are smaller than those in the nuclear medium. However, at large densities, the mass shifts of charmonia are observed to be larger in hyperonic medium than that in the nuclear medium.When the quark masses are incorporated, the terms proportional to
$ \sigma ' $ and$ \zeta ' $ oppose the contribution of the term proportional to$ \chi^4-{\chi_0}^4 $ in the modification of gluon condensates. Hence, the net mass shift of the charmonia calculated in the finite quark mass limit is relatively small compared with the mass shift calculated by neglecting the quark mass term. Because the ζ field undergoes marginal modifications in the nuclear medium, the contribution of the term proportional to$ \zeta ' $ in the modification of gluon condensates is also marginal. Hence, the contribution of finite quark mass term to the mass shift of charmonia is less significant in the magnetized nuclear medium ($ f_s $ =0). Although the magnitude of the terms proportional to$ \sigma ' $ and$ \zeta ' $ increase with baryon density, the term proportional to$ \chi^4-{\chi_0}^4 $ is dominant at densities above 0.55$ \rho_0 $ . The qualitative behavior of the mass shifts above this density is governed by the term proportional to$ \chi^4-{\chi_0}^4 $ . When the quark mass term is neglected, the mass shift of$ J/\psi $ in the nuclear matter is −26.74 MeV at$ \rho_B $ =$ 4\rho_0 $ for eB =$ 8m_\pi^2 $ . When the quark mass term is incorporated, the corresponding mass shift has the value −19.83 MeV. Hence, from a qualitative perspective, the omission of quark masses in calculating the mass shift is reasonable, particularly in magnetized nuclear matter at large densities. Nevertheless, the mass shifts calculated by incorporating the finite quark mass term in the modification of gluon condensates are more realistic. Such a term is also quantitatively significant in magnetized strange hadronic matter.When the quark mass term is neglected, under a magnetic field of eB=
$ \ 4m_\pi^2 $ incorporating the AMM effects, the mass shifts (in MeV) of$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ ,$ \chi_{c0} $ ,$ \chi_{c2} $ are$ -7.63 \;(-30.38) $ ,$ -103.59 \;(-412.36) $ ,$ -127.68 (-508.26) $ ,$ -27.25 \;(-108.48) $ , and$ -42.15\; (-167.80) $ , respectively, at$ \rho_B $ =$ \rho_0 $ (4$ \rho_0 $ ) and$ f_s $ =0.3. At eB=$ 8m_\pi^2 $ the mass shifts of charmonia under similar medium conditions in the same order are$ -7.57 \;(-28.30) $ ,$ -102.76 (-384.11) $ ,$ -126.66\; (-473.45) $ ,$ -27.03 \;(-101.05) $ ,$ -41.81 (-156.30) $ , respectively. When the effects of AMM of baryons are ignored, under a magnetic field of eB=$ \ 4m_\pi^2 $ , the mass shifts are observed to be$ -7.94\; (-31.12) $ ,$ -107.81\; (-422.43) $ ,$ -132.89\; (-520.67) $ ,$ -28.36\; (-111.13) $ , and$ -43.87\; (-171.89) $ , respectively, at$ \rho_B $ =$ \rho_0 $ (4$ \rho_0 $ ) and$ f_s $ =0.3. In the absence of AMM effects, when the magnetic field is increased to eB=$ \ 8m_\pi^2 $ , the mass shifts of charmonia become$ -7.95\; (-31.13) $ ,$ -107.93\; (-422.57) $ ,$ -133.03 (-520.84) $ ,$ -28.39\; (-111.17) $ , and$ -43.92\; (-171.95) $ , respectively.When the quark mass term is incorporated, under a magnetic field of eB=
$ \ 4m_\pi^2 $ , incorporating the effects of AMMs, the mass shifts (in MeV) of$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(3770) $ ,$ \chi_{c0} $ ,$ \chi_{c2} $ are$ -2.43 \;(-19.42) $ ,$ -32.99 \;(-263.60) $ ,$ -40.67\; (-324.91) $ ,$ -8.68\; (-69.35) $ , and$ -13.42\; (-107.26) $ , respectively, at$ \rho_B $ =$ \rho_0 $ (4$ \rho_0 $ ) and$ f_s $ =0.3. At eB=$ \ 8m_\pi^2 $ the mass shifts of charmonia under similar medium conditions in the same order are$ -2.38\; (-17.45) $ ,$ -32.35 (-236.84) $ ,$ -39.87 \;(-291.92) $ ,$ -8.51\; (-62.31) $ , and$ -13.16 (-96.37) $ , respectively. When the effects of AMMs of baryons are ignored, under a magnetic field of eB=$ \ 4m_\pi^2 $ , the mass shifts are observed to be$ -2.66 \;(-20.13) $ ,$ -36.15\; (-273.20) $ ,$ -44.56 \;(-336.73) $ ,$ -9.51\; (-71.87) $ , and$ -14.71\; (-111.17) $ , respectively, at$ \rho_B $ =$ \rho_0 $ (4$ \rho_0 $ ) and$ f_s $ =0.3. In the absence of AMMs, when the magnetic field is increased to eB =$ \ 8m_\pi^2 $ , the mass shifts of charmonia become$ -2.66 \; (-20.13) $ ,$ -36.20\; (-273.27) $ ,$ -44.62\; (-336.82) $ ,$ -9.52 (-71.89) $ , and$ -14.73\; (-111.20) $ .In Refs. [82, 83], the mass shifts of
$ J/\psi $ ,$ \psi(3686) $ , and$ \psi(3770) $ in the nuclear matter without considering the magnetic field were calculated to be$ -8 $ ,$ -100 $ , and$ -140 $ MeV, respectively, at$ \rho_B $ =$ \rho_0 $ . The above calculations were performed using the QCD second-order Stark effect in the linear density approximation. The mass shift of$ J/\psi $ was investigated within the QCD sum rules in Ref. [26] without considering the magnetic field. In the investigation, the mass shift of$ J/\psi $ at nuclear saturation density was observed to be$ -7 $ MeV. Neglecting the quark mass term and the magnetic field, the chiral model predicted mass shifts of$ -8.6 $ ,$ -117 $ ,$ -155 $ MeV for$ J/\psi $ ,$ \psi(3686) $ , and$ \psi(3770) $ , respectively, in symmetric ($ \eta=0 $ ) nuclear matter and$ -8.4 $ ,$ -114 $ ,$ -150 $ MeV, respectively, in asymmetric ($ \eta=0.5 $ ) nuclear matter [65]. In symmetric hyperonic media ($ f_s=0.5 $ ), the mass shifts of the above charmonium states calculated within the chiral model were$ -8.41 $ ,$ -114 $ , and$ -151 $ MeV, respectively, at$ \rho_B $ =$ \rho_0 $ , using$ N_f $ = 3 in the beta function [65]. In Ref. [93], the masses of charmonia were investigated in isospin symmetric and asymmetric magnetized nuclear matter.In this investigation, we have focused on the effect of baryon density, strangeness fraction, magnetic field, and AMMs of the baryons on the mass modifications of the open charm mesons and charmonia. This study has not considered the effects of finite temperature and magnetically induced spin mixing of pseudoscalar and vector mesons. The effects of temperature can be introduced through Fermi distribution functions in the expressions of scalar and number densities of baryons [37−39, 99]. The scalar and vector fields, which depend on the scalar density and number density of baryons, respectively, will be modified as a function of temperature. Because the mass modification of the mesons depends on the modification of scalar density, number density, and scalar fields, the effects of temperature get reflected on their in-medium masses. The effects of temperature on the masses of the open charm mesons and charmonium states were observed to be marginal compared with the effects of density within the chiral effective model [65, 70]. In Refs. [37, 39], the effects of temperature on the masses of the D mesons and charmonium states in the magnetized nuclear matter were calculated using QCD sum rules. In the study, the effects of the magnetic field on the scalar fields and meson masses in neutron matter were qualitatively different at high temperatures. Such behavior is expected in magnetized asymmetric strange hadronic matter. Nevertheless, the effects of temperature were observed to be marginal in magnetized nuclear matter compared with the effects of the density [37−39]. In this paper, as a first-step calculation, the mass modifications have been studied without considering the effects of temperature.
Moreover, the pseudoscalar (P) mesons can mix with the longitudinal component of the corresponding vector mesons (V) in a magnetic field [32, 34, 35, 40, 41]. The spin mixing results in a significant positive mass shift of the longitudinal component of the vector mesons and a negative mass shift for the pseudoscalar mesons. In these studies, the effect of spin mixing was considered through a phenomenological interaction Lagrangian
$ {\cal L}_{PV\gamma}= \dfrac{g_{PV}}{m_{av}} e {\tilde F}_{\mu \nu} (\partial ^\mu P) V^\nu $ [32, 34, 35, 40, 41]. Here,$ {\cal L}_{PV\gamma} $ introduces the corresponding three-point vertex interaction;$ m_{av}=(m_V+m_P)/2 $ , where$ m_P $ and$ m_V $ are the masses for the pseudoscalar and vector mesons, respectively;$ {\tilde F}_{\mu \nu} $ is the dual electromagnetic field, and e is the unit electric charge. The mixing coupling parameter$ g_{PV} $ is calculated from the observed value of the radiative decay width$ \Gamma(V\rightarrow P +\gamma) $ . The same phenomenological Lagrangian$ {\cal L}_{PV\gamma} $ can be used to study the contributions of spin mixing on the masses of open charm mesons and charmonium states in the magnetized strange hadronic matter.Ref. [40] investigated the effect of spin mixing on the properties of pseudoscalar and vector D mesons, as well as charmonium states in the vacuum. Ref. [41] investigated the effect of spin mixing on the masses of charmonium states
$ \eta_c(1S) $ ,$ \eta_c(2S) $ ,$ J/\psi $ ,$ \psi(2S) $ ,$ \psi(1D) $ , and the partial decay widths of charmonium states to$ D\bar{D} $ in the magnetized nuclear matter. The in-medium masses of these mesons were calculated using the chiral model, and the effect of spin mixing was considered using the phenomenological Lagrangian$ {\cal L}_{PV\gamma} $ . The contributions of spin mixing on these mesons were significant when magnetic fields were stronger, and they were investigated at a nuclear matter saturation density. In Ref. [41], the mass splitting between$ J/\psi $ and$ \eta_c(1S) $ in the symmetric nuclear matter increased from 111 to 132 MeV when the spin mixing effect was included at$ \rho_B=\rho_0 $ and eB =$ 5m_{\pi}^2 $ . The magnitude of the mass splitting due to spin mixing depended on the in-medium masses of the particles involved in mixing. In our investigation, the effect of$ f_s $ on the in-medium masses of open charm mesons and charmonia is marginal at$ \rho_B=\rho_0 $ . Consequently, the effect of$ f_s $ on the spin mixing contributions in the medium is also marginal. Hence, at small densities, the mass splitting due to spin mixing in the strange hadronic matter is expected to be similar to that in the magnetized nuclear matter given in Ref. [41]. In a future study, we will incorporate the effects of spin mixing and finite temperature on the masses of these heavy flavor mesons in magnetized strange hadronic matter. -
The mass modifications of open charm mesons (D,
$ \bar{D} $ ,$ D_{s} $ ) and charmonium states in magnetized strange hadronic matter are investigated using a chiral effective Lagrangian model. In heavy-ion collision experiments, where strong magnetic fields are created, the study of mass modifications of hadrons is necessary as they affect the experimental observables. The magnetic field distinguishes charged baryons from neutral baryons in the medium owing to differences in their charge and AMMs. The number and scalar densities of charged baryons have contributions from Landau energy levels. We have studied magnetized strange hadronic matter by solving the equations of motion to obtain the values of scalar fields as a function of baryon density for various strangeness fractions and magnetic fields. The effects of the AMMs of baryons are also included in this investigation. The magnitude of scalar fields σ, ζ, and χ decrease as baryon density increases, whereas δ exhibits a saturation behavior under similar conditions. The obtained values of scalar fields are used to determine the mass modifications of open charm mesons and charmonium states. Generally, the masses of all these mesons decrease with an increase in the baryon density. At large densities, D,$ \bar{D} $ ,$ {D_{s}}^+ $ mesons and the charmonium states experience a larger mass modification in hyperonic matter compared with that in nuclear matter. At small densities, the$ {D_{s}}^- $ meson experiences a smaller mass decrease in hyperonic matter compared with that in nuclear matter. The effect of the magnetic field on the mass shifts of charmonia is negligible when AMM effects are neglected. The excited charmonium states experience a larger mass shift than$ J/\psi $ . The charged open charm mesons$ {D}^+ $ ,$ {D}^- $ ,$ {D_{s}}^+ $ , and$ {D_{s}}^- $ have an additional positive mass modification owing to the Landau quantization effect in the presence of a magnetic field. For$ {D_{s}} $ mesons, the Landau quantization effect has a significant role at low densities. In this investigation of the open charm mesons and charmonium states, the dominant medium effect is due to the density. These medium effects should have observable consequences in the$ {D}^+ $ /$ {D}^0 $ ,$ {D}^- $ /$ \bar{D^0} $ , and$ {D_{s}}^+ $ /$ {D_{s}}^- $ ratios, as well as in the partial decay widths of the charmonium states to$ {D}^+ $ $ {D}^- $ and$ {D}^0 $ $ \bar{D^0} $ pairs, in asymmetric heavy-ion collisions in compressed baryonic matter (CBM) experiments at FAIR at the future GSI facility. -
A.J.C.S is grateful to Ankit Kumar, Manju Soni, Jaswant Singh, and Arjun Kumar for fruitful discussions.
Open charm mesons and charmonia in magnetized strange hadronic matter
- Received Date: 2022-02-07
- Available Online: 2022-08-15
Abstract: We investigate the in-medium masses of open charm mesons (D(






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













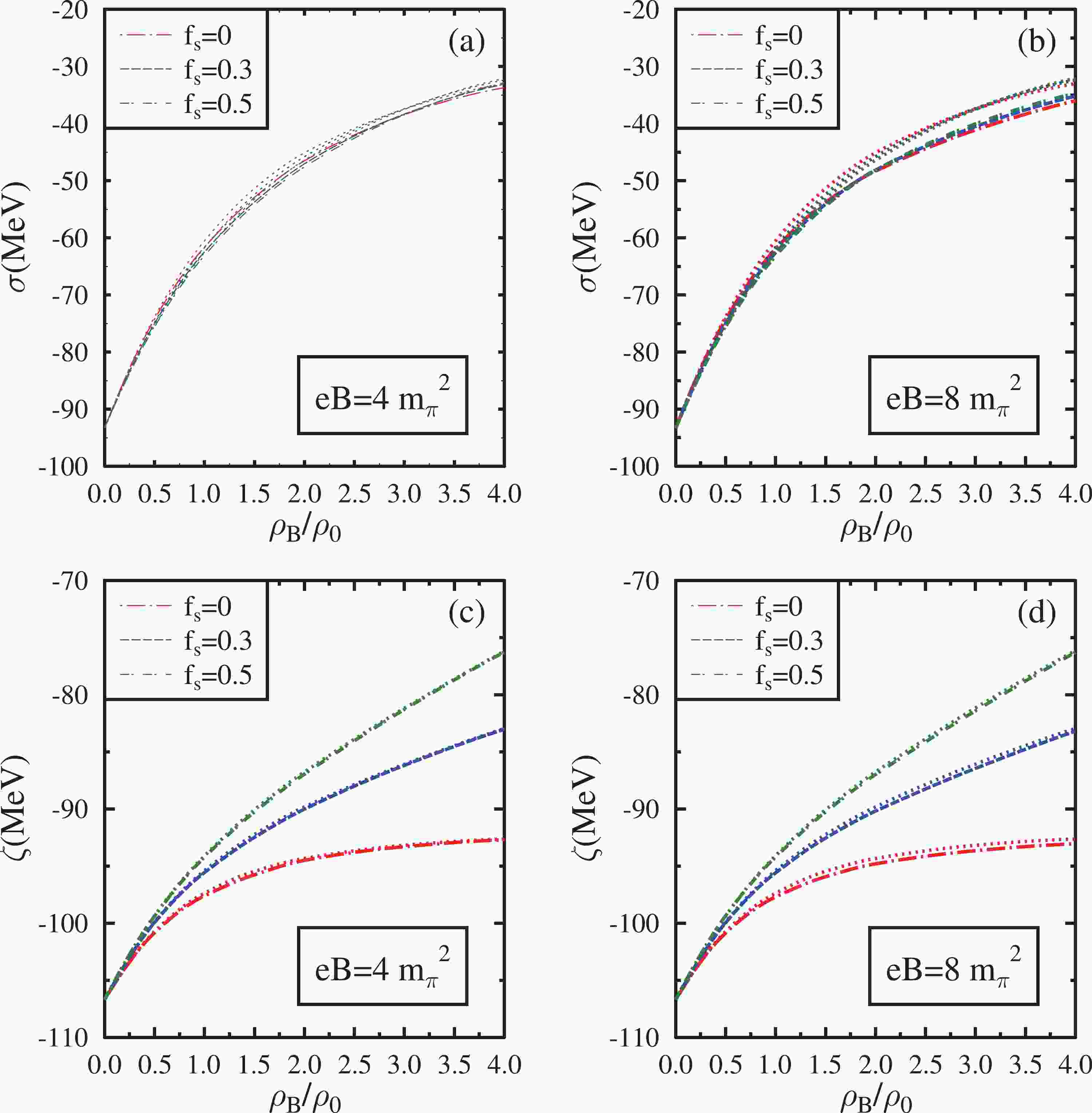













 DownLoad:
DownLoad: