Constraints on cosmic-ray boosted dark matter in CDEX-10

Compelling astrophysical and cosmological evidence points to the existence of dark matter (DM) [1, 2], yet very little is known about particle nature of DM. If DM particles could annihilate or decay into standard model particles, then observations of gamma rays, antiprotons and positrons in cosmic ray telescopes and neutrinos in related detectors will provide clues for DM properties and indirectly even for its origin [3–6]. In addition, several decades have been spent searching for DM directly with low-background detectors in deep underground laboratories on Earth that seek to turn DM–nucleus or DM–electron recoiled energy into light, heat and ionization signals. DM direct detection experiments intend to distinguish nuclear recoils (NRs) and electronic recoils (ERs) with noble gas liquid detectors such as PandaX [7], Xenon1T [8] and LUX [9] using liquid Xenon, DEAP-3600 [10] and DarkSide [11] using liquid Argon, while a few complementary experiments with crystals register DM energy deposits only, such as CoGeNT [12] and CDEX [13] using Germanium. Rapid progress has been made, but we are confronted more often than not with null results. As a result, stringent exclusion limits have be placed in the plane of the DM mass $ m_\chi $ and the DM coupling strength $ \sigma_{\chi0} $, given the weakly interacting massive particle (WIMP) as a DM candidate in the standard halo model (SHM) [14, 15].

In the high DM mass region, the neutrino floor caused by coherent elastic neutrino–nucleus scatterings (CEνNS) is close at hand and leads to intrinsic neutrino backgrounds for the next-generation large scale DM detectors [16–22]. Due to the energy threshold in current detector technology, a relatively large space remains unexplored in the light DM scheme. Tremendous efforts are still underway, aiming at the ultra-low threshold with large-scale detectors to reach better sensitivities. Novel experimental detection strategies and a number of new theoretical ideas to probe low mass DM have been proposed and actively discussed very recently [23], including better detection techniques to overcome the energy-recoil threshold barrier [24, 25], the Migdal effect to observe electrons dissociated from the atom through the nuclear scattering [26–30], and boosted DM from heavy-generation annihilations in a multi-component DM model in order to surpass the detector threshold limitation [31]. One of the interesting topics in the exploration of low-mass DM is the cosmic ray boosted DM (CRBDM) mechanism proposed in recent studies [32–38]. In the galaxy, there must be an isotropic and relativistic cosmic-ray stream [39, 40] consisting of protons ($ \sim $86%), helium nuclei ($ \sim $11%), some other heavier nuclei and electrons ($ \sim $3%). DM can generate nuclear recoils in direct detection experiments to offer observable signals. It is likely that DM is scattered and boosted by relativistic cosmic rays in the expanding universe. Several studies have already investigated CRBDM and offered relatively tight constraints on light DM, including the diurnal effect [41], DM–nucleon interactions propagated by various mediators [42–45] and the so-called reverse direct detection method [46]. There are cosmological constraints from Big Bang Nucleisynthesis (BBN) and the DM relic density. Previous studies show that CRBDM with a large enough cross section is expected to achieve thermal equilibrium with SM particles before the BBN epoch and would affect the prediction of BBN. Consequently, the current observation of BBN excludes the DM mass below a few MeV, which still leaves a viable parameter region to be probed [47]. In addition, the DM relic density puts constraints on low mass DM, but this largely depends on model assumptions [48, 49].

As we noticed in previous CRBDM studies, the attenuation effect results in the upper bound of the exclusion region for CRBDM. Both MiniBooNE and XENON1T provide lower bounds on CRBDM, despite the dependence of DM and cosmic ray distribution in the galaxy. The attenuation effect in XENON1T cuts into the exclusion region of CRBDM. Therefore, there exists a gap in the parameter space between MiniBooNE and XENON1T constraints [32]. Compared with other types of detector, Germanium detectors with a lower energy threshold and better energy resolution are an effective means of setting limits on the scattering cross section for GeV-scale DM in the standard WIMP detection. As a consequence, the CDEX experiment, located 2.4 km underground using a point contact high purity germanium detector, might be able to close the gap due to its lower level of backgrounds and lower energy threshold compared to MiniBooNE and XENON1T. Based on the CRBDM mechanism, it must be valuable to re-analyze the 102.8 kg$ \times $day data of the CDEX-10 experiment, and provide constraints on spin-independent DM–nucleon cross section for $ m_\chi < 1 $ GeV.

This article is organized as follows. In Sec. II, we review the mechanism of CRBDM and derive the theoretical energy recoil spectrum with the Earth attenuation effect taken into account. In Sec. III, we re-analyze the CDEX-10 data in the CRBDM hypothesis. Finally, we summarize and make conclusions in Sec. IV.

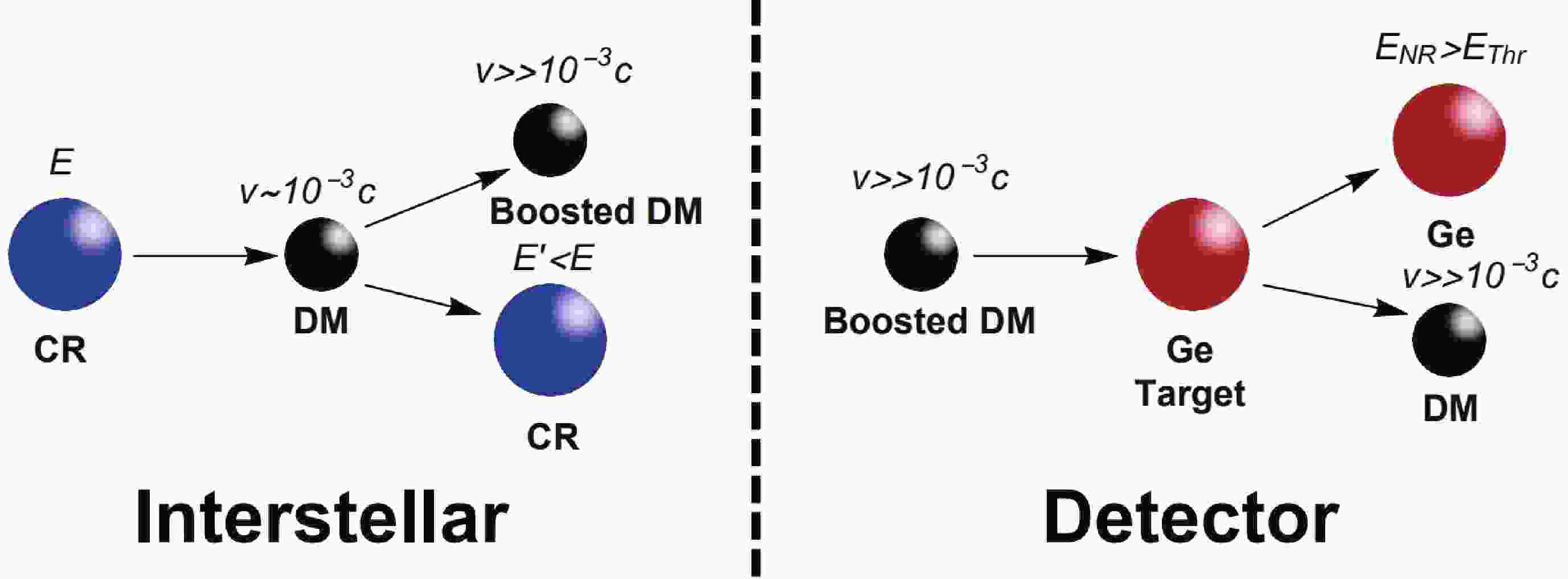
In a CRBDM mechanism, cosmic rays and DM exchange their energy and momentum by the process of collisions, so that the boosted DM would become almost relativistic. Then, boosted DM particles traveling toward the detector on the Earth and scattering off the target nuclei, could generate enough recoil energy to exceed the threshold energy. A schematic diagram to illustrate the acceleration and detection processes is given in Fig. 1. To study a scattering process, we need to know information about the incident particle, the target, and the collision process. The local density of DM near the solar system is $ \rho_{\chi 0} \sim 0.4 \; \rm{GeV/cm}^3 $ according to cosmological observations [2]. The velocity distribution of DM in the standard halo model (SHM) [14] approximates to the Maxwell–Boltzmann distribution where the most probable velocity $ v_0 $ is about 220 km/s. In the following, we will discuss the CRs and review the collision process between CRs and DM.

Figure 1.  (color online) Schematic diagram for the acceleration and detection processes in a CRBDM mechanism.

CRs might originate from some of the supernova remnants (SNR) in the Galactic Disk [50]. Fermi pointed out that CRs from SNR bounce constantly between the shock surface and the magnetic field behind the wave surface. To explain the highly isotropic distributions for energetic charged particles, the concept of CR diffusion was proposed, in which the Galactic magnetic field plays an important role [40]. To calculate the differential CR flux, two main components (protons and helium nuclei) are considered and marked with subscript i in the following formula. With the data from PAMELA, the fitting formula for the Local Interstellar Spectra (LIS) of CRs are parameterized [51] as follows:

where R is the rigidity of each nucleus. For a particle with a proton number Z, the relationship between the rigidity R and the kinetic energy of CR particle $ T_i $ is: $ \dfrac{T_i}{R} = Z e $. The differential CR flux obeys a power law with an index $ \sim -2.7 $. As shown in Eq. (1), $ a,\; b,\; c,\; d,\; e,\; f,\; g $ are the numerical coefficients [51, 52] and we show the coefficients of the proton and helium nucleus in Table 1. Considering that CRs are isotropic in the interstellar, we integrate the volume to obtain the differential CR flux $\dfrac{{\rm d}\Phi_i}{{\rm d}T_i}$: $\dfrac{{\rm d}\Phi_i}{{\rm d}T_i} = 4 \pi \dfrac{{\rm d}\Phi_i}{{\rm d}R} \dfrac{{\rm d}R}{{\rm d}T_i}$.

	$ a_0 $	$ a_1 $	$ a_2 $	$ a_3 $	$ a_4 $	$ a_5 $	b	c
p	94.1	−831	0	16700	−10200	0	10800	8500
He	1.14	0	−118	578	0	−87	3120	−5530
	$ d_1 $	$ d_2 $	$ e_1 $	$ e_2 $	$ f_1 $	$ f_2 $	g
p	−4230000	3190	274000	17.4	−39400	0.464	0
He	3370	1.29	134000	88.5	−1170000	861	0.03

Table 1.  Parameters of the analytical fits to the proton and He LIS [52].

Compared with the relativistic velocity of CRs, DM at a velocity of $ \sim 10^{-3}\; c $ in the SHM can be safely treated as at rest. Considering the collision of DM and CRs, although inelastic scattering occurs due to the high energy of CRs, it only contributes a negligible portion to the DM fluxes boosted by CRs compared to elastic scattering, and the signals of γ rays and neutrinos from inelastic scattering are beyond our topic [53]. Consequently, it is reasonable for us to consider only the elastic scattering process. With the assumption that the collision is elastic and isotropic, we relate the kinetic energy of DM at $ T_\chi $ to that of CRs at $ T_i $ by energy and momentum conservation in the following:

where θ is the scattering angle in the center of momentum frame, and $ m_i $ is the mass for CR particle i. According to Eq. (2), $ T_\chi $ tends to decrease and is proportional to $ m_\chi $ if $ m_\chi \ll m_i $, while DM would gain more energy if $ m_\chi $ is close to $ m_i $. DM gets the maximimal kinetic energy $ T_\chi^\mathrm{max}(T_i) $ when the CR direction is completely reverted after such a collision ($ \theta=0 $). The minimum energy of the incident particle $ T_i^\mathrm{min}(T_\chi) $ is given in Eq. (3):

Note that the signs $ +/- $ apply to the cases with $ T_\chi > 2 m_i $ and $ T_\chi < 2 m_i $ respectively.

When momentum transfer occurs in the scattering process, the internal structure of the nuclei would give an effect. Therefore, the cross section varies with the exchange of momentum described by the form factor $ G_i $: $ \sigma_{\chi i} = \sigma_{\chi i}^0 G_i^2(2m_\chi T_\chi) $, where $ \sigma_{\chi i}^0 $ is the cross section for zero momentum transfer. In a collision process with large momentum transfer, such as the case where DM is boosted by CRs, we adopt the dipole form to describe the effect of nonpoint-like structure of the nucleon. Note that for small momentum transfer, the Helm model is preferred. The dipole form factor for protons and helium is given by [54]:

where $ \Lambda_i $ is inversely proportional to the charge radius, and we set $ \Lambda_p = 770 $ MeV for the proton and $\Lambda_{\rm He} = 410$ MeV [55] for the helium nucleus. It is generally believed that the DM couplings to the proton and nucleon are the same, so the cross section can be written as Eq. (5) with a dependence on the mass number A for the incident particle i:

It is worth mentioning that the factor $ A^2 $ in Eq. (5) is 16 for the helium nucleus and 1 for the proton. The helium nucleus and the proton make contributions at the same order of magnitude to the differential flux for DM (helium nuclei account for 10% of CRs).

Based on the above information, we start to calculate the differential flux for boosted DM. Inside a volume ${\rm d}V$, the collision rate with energy exchange ${\rm d} T_i$ for CRs and ${\rm d} T_\chi$ for DM is given by:

where $\dfrac{{\rm d}\Phi_i}{{\rm d} T_i}$ is the differential flux for CRs. Without a loss of generality, we make an energy-independent assumption here with such a form factor that energy transfer is uniformly distributed as $\dfrac{{\rm d}\sigma_{\chi i}^0}{{\rm d}T_\chi} = \dfrac{\sigma_{\chi i}^0}{T_\chi^{\max}}$. By integrating the volume and the energy $ T_i $, we obtain the differential flux for the boosted DM in Eq. (7). In addition, the volume integral requires the distribution of DM and CRs in the galaxy. Note that the integral needs to be divided by the factor $ 4 \pi d^2 $ to obtain the DM flux boosted by CRs, where d is the distance between the collision point and the Earth. We introduce the effective distance $ D_{\rm{eff}} $ to represent the volume integral, into which we put the results of different assumptions on the CR spatial distribution. The CR spatial distribution is considered a homogeneous and spherical distribution as given in reference [33] and results in $ D_{\rm{eff}}=1 $ kpc conservatively. Other researchers assume that CRs are uniformly distributed in a cylindrical distribution with a radius $ R = 10 $ kpc and a half-height $ h = 1 $ kpc [34, 35], which results in $ D_{\rm{eff}}=3.7 $ kpc. Also, the CR distribution can be simulated with the GALPROP code [41]. Therefore, the CR distribution is worth further investigation in future work. We now take two benchmark examples of $ D_{\rm{eff}} $ for analysis:

where $ T_i^\mathrm{min} $ and $ T_\chi^\mathrm{max}(T_i) $ are given in Eq. (3) and Eq. (2) with $ \theta=0 $. Following uncertainty analyses on the DM local density and the DM spatial distribution [35], we take 50% uncertainty for analysis. To further study the boosted DM, we can make a comparison between the boosted DM flux induced by CRs and the DM flux under the SHM in the same reference frame:

where $ f(v) $ is the Maxwellian velocity distribution with the most probable velocity at $ v_0=220 \; \rm{km/s} $ and the galactic escape velocity at $v_{\rm escape}=540 \; \rm{km/s}$ [56]. Here the velocity distribution in SHM is taken as follows:

where k is the normalization factor. The numerical results for the CRBDM fluxes are compared and shown in Fig. 2. As the DM density in space is fixed, the smaller DM mass results in a larger number density of DM. Compared with the DM flux under the SHM hypothesis, the flux intensity boosted by CRs is a small portion of the total flux. Only a small portion of CRs lose energy, so that the CRBDM mechanism can survive in the current constraints from astrophysical experiments. This provides a clue for reverse direct detection of DM [46].

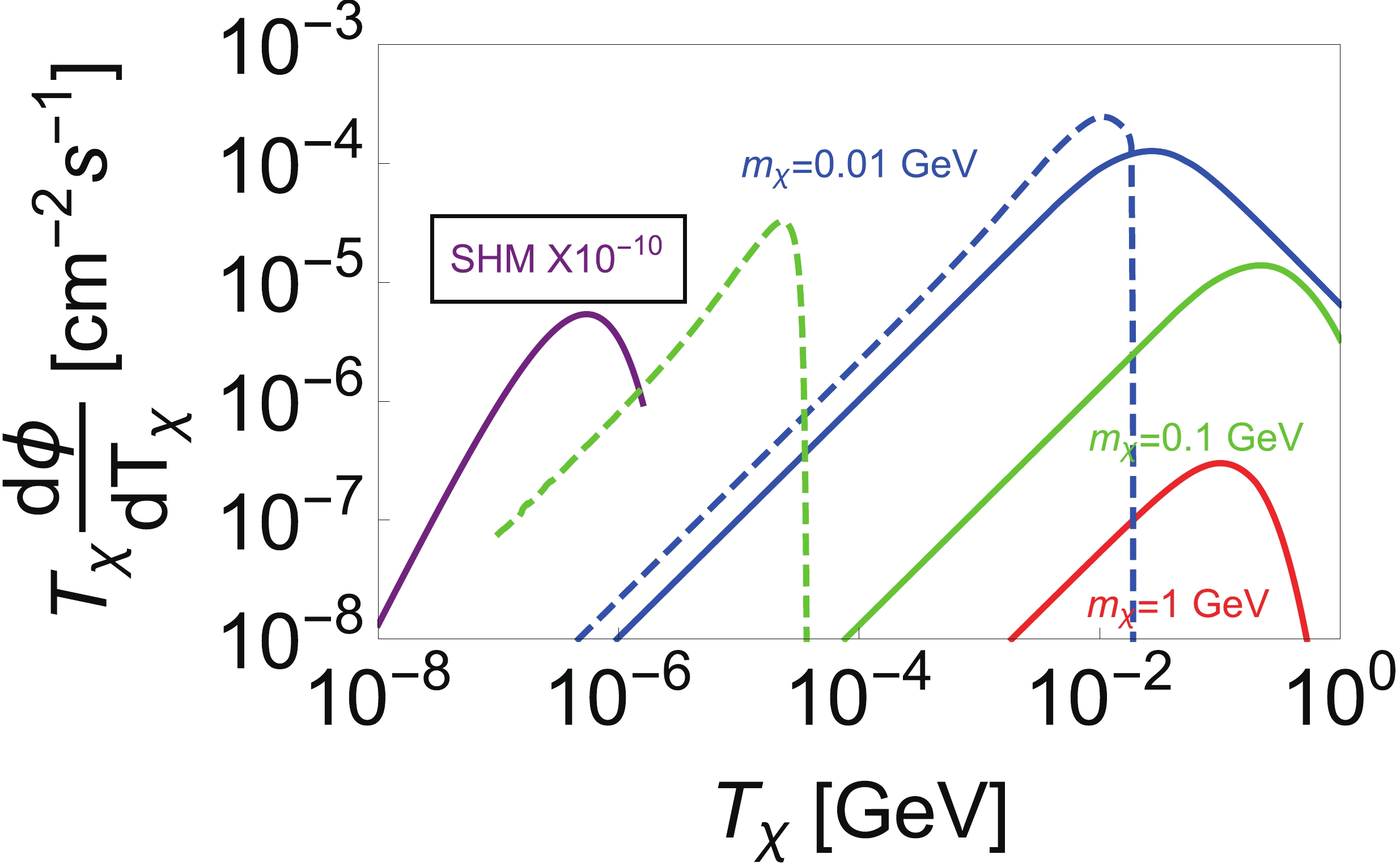
Figure 2.  (color online) Fluxes of CRBDM. Solid lines show the flux with DM mass $ m_\chi = 0.01 $ GeV (blue), $ m_\chi = 0.1 $ GeV (green) and $ m_\chi = 1 $ GeV (red), assuming $ \sigma_{\chi 0} = 10^{-28} \; \rm{cm}^2 $ and D$ _ \rm{eff} $ =1 kpc. The purple solid line is the DM flux with $ m_\chi = 1 $ GeV for SHM normalized by $ 10^{-10} $. Dashed lines represent fluxes of CRBDM with the Earth attenuation effect taken into account.

As DM particles could collide with ordinary matter, the DM flux from space to the detector would be blocked by the atmosphere and the rock, which causes energy loss or de-acceleration for the DM. We estimate the mean free path for DM as $\lambda = 1/\sigma_{\chi N} n_{N}$ where $\sigma_{\chi N}$ stands for the DM–nucleus scattering cross section. Taking as parameters the mean mass number $ \overline{A} = 20 $ , the mean density $\rho_{\rm crust} = 2.7$ g/cm³ [57] and the cross section $ \sigma_{\chi 0} = 10^{-30} $ cm², we get the the mean free path: $ \lambda \sim 0.1 $ km. In order to suppress backgrounds from cosmic rays, direct detection experiments are usually located deep underground. For example, China Jinping Underground Laboratory that hosts the CDEX experiment has a rock overburden of $ z \sim 2.4 $ km. Next we establish a model to analyze the Earth attenuation effect and adopt the ballistic trajectory approximation.

Under the assumption of energy independence, $\dfrac{{\rm d} \sigma_{\chi N}}{{\rm d} T_{r}} = \dfrac{\sigma_{\chi N}}{T_{r}^{\max }}$, we obtain the energy loss for DM crossing the crust:

where $ T_{r}^{\max } $ is the maximal recoil energy between the DM particle and the nucleus N. Here the form $ T_{r}^{\max} $ is similar to Eq. (2) with $ \theta=0 $ by a replacement of $ m_\chi \rightarrow m_N $ and $ m_i \rightarrow m_\chi $. We have to solve the differential equation in Eq. (10) to establish the relationship between DM energy in the space and detector: $ T_\chi^z = T_\chi^z (T_\chi^0) $. However, recent studies [58, 59] involve the form factor in the energy loss calculations and make necessary modifications on Eq. (10), which leads to a different constraint on the parameter space of DM. In the following section, we will make a comparison of these effects in the exclusion plots. After that, we obtain the attenuated DM flux spectrum as follows:

Adopting the nuclear composition of the Earth's crust given in reference [57] and the crust thickness as 2400 m, we present the DM flux with and without the Earth attenuation effect in Fig. 2. The comparison of different line colors shows us the interesting features associated with the DM mass, while the dashed/solid lines highlight the cases with/without the attenuation effect, respectively. Under the same assumption for the cosmic ray acceleration mechanism, we see the low mass DM gets boosted into the higher flux intensity region. However, the high mass DM tends to be bounced towards the low kinetic energy region by rock as the Eartch attenuation effect is taken into account. If such a bounce on Earth for CRBDM is too strong, the DM particle might not be able to reach the detector. The energy loss of DM particles crossing the crust depends on the maximal recoil energy, which also depends on the DM mass. As a result, lighter DM will lead to less recoil energy of particles in the crust and suffer less from attenuation. It is noted that the total number of DM should be normalized in two scenarios related to the Earth attenuation in order to verify the correctness in numerical calculations. Therefore, one cannot neglect the attenuation effect in sensitivity studies. As shown in the following section, we will see the ceiling limit caused by the Earth attenuation effect in re-analyzing experimental data.

To obtain the recoil spectrum from CRBDM, we focus on the elastic and isotropic collision of DM and the target particle in the detector. Neglecting energy dependence, we get the recoil spectrum by integrating the kinetic energy of DM particle ${\rm d} T_\chi$:

where $ T_\chi^z $ and $\dfrac{{\rm d} \Phi_{\chi}}{{\rm d} T_\chi^z} = \dfrac{{\rm d} T_\chi}{{\rm d} T_\chi^z} \dfrac{{\rm d} \Phi_{\chi}}{{\rm d} T_\chi}$ are the kinetic energy of DM and the DM flux in the detector with depth of z, respectively. Here $ \sigma_{\chi N} $ is given by $ \sigma_{\chi N}=\sigma_{\chi N}^0 F^2(E_R) $, where $ F(E_R) $ is the form factor [15]. Since the momentum transfer is small in the process of DM–nucleus scattering, we adopt the Helm model which describes the nucleon distribution of the target nucleus with two parameters: the effective nuclear radius and the surface thickness [60, 61]. We follow a similar expression to Eq. (3) and Eq. (2) with $ \theta=0 $ to calculate $ T_\chi^\mathrm{min} $ and $ E_R^{\max} $. For scintillation and ionization detectors calibrated with γ sources, the observable nuclear recoil energy $ E_v $ differs from the true recoil energy $ E_R $: $ E_v = f_n(E_R) E_R = F(E_R) $, where $ f_n $ is called the quenching factor and is a function of $ E_R $ calculated by the TRIM software package [62–64]. $ F(E_R) $ is more convenient for the derivation. Furthermore, because of finite detector energy resolution and electronic noise, recoils at energy $ E_R' $ would be observed as a Gaussian distribution. Consequently, we obtain the modified recoil spectrum:

where $ \Delta E_v $ is the energy resolution. As a demonstration, Fig. 3 shows the energy recoil spectrum from CDEX-10 data, and the predicted recoil spectrum for DM with $ m_\chi = 1 $ MeV and $ \sigma_{\chi 0} $. Note that the quenching factor and the energy resolution are included in the calculation of theoretical predictions. The effect of the detector efficiency has been included in the experimental data so that we can directly compare the experimental data with the theoretical expectation from Eq. (13) [65].

Figure 3.  (color online) Measured energy recoil spectrum in CDEX-10 as black data points plus error bars [13]; flat background assumption as blue dashed line; predicted CRBDM recoil spectrum as red solid line for $ m_\chi = 1\; \rm{MeV} $ and $ \sigma_{\chi0}=7\times10^{-30} $ cm². Here "eVee" represents electron equivalent energy derived from a charge calibration.

Future DM direct detection experiments will encounter an irreducible background from solar, atmospheric and diffusive supernovae neutrinos through the CEνNS process [16, 18, 22, 66], which will hinder our searches for CRBDM. Whether DM direct detection experiments will see neutrino events, and how to evaluate the impact of neutrino backgrounds on DM detection, are questions of statistics. The neutrino floor is defined as the discovery limit: when the true DM model lies above the limit, a given experiment has a 90% probability of obtaining more than $ 3\sigma $ DM signals.

CEνNS [67] is the dominant channel of neutrino background due to the coherent enhancement. The differential cross section of the neutrino–nucleus scattering is given by:

where $ Q_{W}=N-\left(1-4 \sin \theta_{W}^{2}\right) Z $ is the weak charge, $ \theta_{W} $ is the weak mixing angle, and $ F\left(E_{r}\right) $ is the Helm form factor. By analogy with Eq. (12), one can obtain the CEνNS event rates in a DM detector. Then we construct a likelihood function $ \mathscr{L}\left(\sigma_{\chi 0}, \vec{\phi}\right) $ based on the Monte Carlo data, where $ \vec{\phi} $ stands for nuisance parameters including uncertainties of different neutrino sources. In order to obtain the discovery limit, we take the background-only case as the null hypothesis $ H_0 $ and the alternative hypothesis $ H_1 $ includes both DM signals and backgrounds. Thus, the test statistic $ q_0 $ can be written as following:

where $ \hat{\hat{\vec{\phi}}} $ is the value of ϕ which maximizes $ \mathscr{L} $ for $ H_0 $, while $\hat{\sigma}_{\chi 0} ~\rm{ and } ~ \hat{\vec{\phi}}$ globally maximize $ \mathscr{L} $ for $ H_1 $. Because $ q_0 $ asymptotically follows a $ \chi^2 $ distribution with one degree of freedom, according to Wilk's theorem, a $ 3\sigma $ statistical significance means the test statistics of an observation $ q_\mathrm{obs} $ must be larger or equal to 9. Finally, we carry out Monte Carlo experiments 500 times with the same $ m_\chi $ and $ \sigma_{\chi 0} $ and apply the statistical principle to obtain the neutrino floor.

The CDEX-10 experiment located at China Jinping Underground Laboratory (CJPL) with about 2400 m of rock overburden makes use of p-type point contact Germanium (pPCGe) to reconstruct the ionization signals generated by collisions between DM and target particles [68]. With an energy threshold as low as 160 eVee, CDEX-10 improves limits on $ \sigma_{\chi 0} $ down to $ m_\chi $ of 2 GeV. To obtain the constraints, we adopt the minimum-$ \chi^2 $ analysis as the statistical method. Considering that high energy $\gamma$-rays from ambient radioactivity produce flat electron-recoil backgrounds at low energy [63, 69], two free and positive parameters $ \sigma_{\chi0} $ and b, which characterize the flat backgrounds and the spin-independent DM–nucleon scattering cross section $ \sigma_{\chi0} $, are used to construct the statistical measure:

where $S_k^{\rm Ex}$ is the experimental data with the uncertainty $ \sigma_k $, and $S_k^{\rm Th}$ stands for the theoretical predictions in each bin. Note that we add a pull term accounting for astrophysical uncertainty, where ρ is treated as a nuisance parameter with the central value $\hat{\rho} = 0.4 \rm{GeV/cm}^3$ and uncertainty $ \sigma_\rho = 0.2\; \rm{GeV/cm}^3 $. To assess the exclusion limit, we calculate the probability in the likelihood analysis for background-only data $ H_b $ with respect to the null hypothesis $ H_0=H_s+H_b $ where CRBDM is taken into account [70]. We assume that the data in each bin follow a Guassian distribution when we construct the likelihood function, and $ \Delta \chi^2 $ asymptotically follows a $ \chi^2 $ distribution with two degrees of freedom. The explicit distribution on $ \Delta \chi^2 $ could be obtained by Monte Carlo, which needs more inputs from the detector response beyond our current study. In a likelihood analysis, the excluded parameter space is obtained by $ \chi^2 $ as follows:

where $\chi^2_{\min}$ is the minimum value of $ \chi^2 $ and $ \Delta \chi^2 $ is associated with the number of considered parameters. When $ \Delta \chi^2 $ exceeds 4.61 for two degrees of freedom, we reject the hypothesis $ H_0 $ at a 90% confidence level and obtain an exclusion limit in the parameter space. To be conservative, the DM mass and maximally allowed cross section that satisfy the conditions in Eq. (17) are represented as a point in the parameter space in Fig. 3. Scanning over the interesting low-mass DM range, we then figure out the exclusion limit for the spin-independent cross section as a lower bound. Nevertheless, the Earth attenuation effect will dilute the strong exclusion limit since the bounced CRBDM might not be able to reach the detector threshold. This caveat will offer the upper ceiling limit. The eventual constraints on the DM parameter space will be obtained by a combination of exclusion limits for the lower bound from an analysis of recoil spectrum in the DM direct detection experiment and the upper bound from the Earth attentuation effect.

Following this strategy, we take the CDEX-10 experiment as a demonstration and reanalyze their data to obtain constraints on the DM mass $ m_\chi $ and the cross section $ \sigma_{\chi0} $ in the CRBDM hypothesis at a 90% C.L. with two benchmark examples: $ D_{\rm{eff}}=1 $ kpc and $ D_{\rm{eff}}=3.7 $ kpc as shown in Fig. 4. Compared with the Migdal effect, the CRBDM framework will reach a much lower mass region but suffers from the Earth attenuation effect. However, cosmological constraints like the cosmic microwave background (CMB) [71] and the gas cloud cooling [72] help to exclude the parameter space above the reach of DM direct detection experiments. For the DM mass range 1 keV $ <m_\chi < $ 1 MeV and $ D_{\rm{eff}}=1 $ kpc, we reach an almost flat floor limit at $ 8.32\times10^{-30} $ cm² on the spin-independent DM–nucleon scattering cross section, while this limit turns upwards for $ m_\chi >1 $ MeV and converges towards the ceiling limit caused by Earth attenuation. Here, we emphasize that the energy threshold also plays a crucial role for the attenuation effect. The low threshold of the CDEX detector somehow compensates for the sensitivity loss caused by the attenuation, though the CDEX experiment might suffer a stronger attenuation effect due to the thicker overburden. Therefore, the ceiling of the CDEX constraint can be higher than that of the XENON1T constraint. As shown in Fig. 4, the gray region enclosed by solid and dashed black lines stand for the constraints under the ballistic trajectory approximation with and without considering the form factor, respectively. We notice that the constraint without the form factor suppression in the attenuation calculations is more conservative, except for a minor difference around the right endpoint. Next we come to the question of why the form factor helps to extend the ceiling limit. DM particles with higher energies suffer less energy loss when going through the crust due to the form factor suppression. Then more DM particles can reach the underground detector and the attenuation effect is relieved. The current result from CDEX-10 is one order of magnitude better than the neutrino experiment MiniBooNE but not comparable to the XENON1T data. Due to the attenuation, there will be a narrow gap between the excluded parameter regions from MiniBooNE and XENON1T. Given a larger $ D_{\rm{eff}} $, the floor limit for each experiment will become stronger, while the ceiling limit induced from Earth attenuation will hardly change. In a word, our analysis is more conservative compared with the previous study. The effective distance can enlarge the excluded regions for MiniBooNE and XENON1T to narrow the gap or even close it. It is then valuable to make a further study on $ D_{\rm{eff}} $ in detail, especially for the uncertain CR spatial distribution. With the current CRBDM hypothesis, the CDEX-10 result can close the gap in a nice manner. This fact highlights the importance of multiple detection technologies and combined analysis to examine the CRBDM mechanism.

Figure 4.  (color online) Constraints on spin-independent cross section of DM–nucleon interactions from CDEX-10 (gray), XENON1T (purple) and MiniBooNE (blue) [33] in the framework of CRBDM at a 90% C.L. The gray region enclosed by solid and dashed black lines stand for constraint from CDEX-10 under the ballistic trajectory approximation with and without considering the form factor, respectively. As a comparison, we also include the exclusion limit from EDELWEISS [29] based on the Migdal effect (red) and from the CMB [71] (green) as well as gas cloud cooling [72] (orange). The neutrino floor (brown) is obtained with an exposure of 1 ton$ \cdot $year and a recoil energy threshold of 1 keV for the Germanium detector.

Distinct from the ballistic trajectory assumption we take in deriving the attenuation effect, several studies performed a Monte Carlo (MC) simulation on the scattering process in the crust in detail [58, 59, 73–75]. MC simulation is able to calculate the deflection of DM going through the Earth crust, which results in fewer DM particles reaching the underground detector. Thus, compared with the ballistic trajectory approach considering the form factor in the attenuation calculation, the MC simulation provides a slightly more conservative constraint. In addition, in the ballistic approach without considering the form factor, there is a suppression at the higher energy range ($ \sim 0.1 $ GeV). Due to the suppression, DM can not generate enough recoil energy and be detected when the cross section climbs over the ceiling limit. Since DM with higher energies can go through the crust for form factor suppression, both the MC method and the ballistic approach in this case lead to too many recoil events. Thus, in order to be consistent with experimental results, it is needed to enhance the attenuation effect in terms of a larger DM cross section.

As for a smaller DM cross section, the floor limit suffers less from Earth attenuation compared with the ceiling bound. Therefore, the differences among the floor limits derived from various approaches should be smaller than those between the ceiling limits. However, for a larger cross section or thicker crust leading to a stronger attenuation effect, the differences become larger and more careful treatment is needed to calculate the Earth attenuation. See Appendix A for more details. The data analyses in different experiments based on MC simulation set complementary constraints on the parameter space, and the global floor limit comes down to about $ 3 \times 10^{-32} $ cm² on the spin-independent DM–nucleon scattering cross section for a DM mass below 0.1 GeV. For the upper bound, the constraint derived from MC simulation can exclude the parameter space between the floor limit and excluded regions from the CMB and gas cloud cooling constraints.

Coherent neutrino–neucleus scatterings will become intrinsic backgrounds of future DM direct detection experiments as soon as they make non-negligible contributions to nuclear recoils in the detector. Compared to the Xenon-based experiment, a Germanium detector can obtain more energy transferred from neutrinos with tiny masses and has a lower energy threshold, which leads to more neutrino backgrounds. Taking neutrino backgrounds into account, we calculate the sensitivity of future germanium detectors on CRBDM with an exposure of about 1 ton$ \cdot $year and an energy threshold as low as 160 eVee in case of CDEX upgrades. The corresponding result for the neutrino floor is shown at the bottom area in Fig. 4. For the DM mass range 1 keV $ <m_\chi < $ 1 MeV and $ D_{\rm{eff}}=1 $ kpc, it is found that we reach the neutrino floor at a cross section of about $ 3 \times10^{-32} $ cm² in future Germanium-based DM experiments. In other words, a large-scale Germanium-based detector with a lower threshold might observe CEνNS events and simultaneously facilitate the study of astrophysical neutrino physics.

Given that DM could elastically scatter with target nuclei in detectors, it is straightforward to think of collisions between relativistic cosmic rays and low-speed DM in the galaxy. In this way, CRBDM would become more energetic, taking the recoil energy above the threshold in detectors, especially for DM in the low mass range. Previous studies were conducted to constrain CRBDM for various experiments including MiniBooNE and XENON1T. There exists a gap in the excluded parameter regions between MiniBooNE and XENON1T partially due to the fact that the Earth attenuation effect will dilute the experimental constraints. Such a gap strongly depends on the effective distance determined by CR models, for which we need further investigation of the CR spatial distribution. We have reviewed the theoretical framework for CRBDM, including modified DM fluxes, the Earth attenuation effect from overburden and the energy recoil spectrum for the general detector target nuclei. Taking the CDEX-10 experimental results, we have re-analyzed 102.8 kg$ \times $day data to constrain CRBDM, and obtained constraints on the spin-independent DM–nucleon cross section in the low mass range 1 keV $ <m_\chi < $ 1 GeV, surpassing the detector energy threshold limitation in a classical analysis. The Migdal effect can also constrain light DM but is still not comparable to the CRBDM mechanism. We have found that the CDEX-10 result is able to close the gap unambiguiously regardless of the assumed effective distance in the parameter space between MiniBooNE and XENON1T constraints.

For future direct detection experiments, the same strategy to constrain CRBDM could be applied. Note that it is still necessary to include careful treatment of uncertainties from astrophysical and nuclear physics inputs as well as the detector response in order to give more rigorous results on CRBDM. In addition, we also quantitiviely provide the neutrino floor on searching for CRBDM in future direct detection experiments using Germanium. Our work should encourage experimental collaborations to press forward with development of the next generation Germanium detectors and joint analysis with other experiments using different detection technologies. Recently, the XENON1T collaboration reported the low-energy ER excess [76]. CRBDM might be able to explain the observed ER excess in the LXe detector [77]. We look forward to further examination by next-generation low-threshold DM direct detection experiments.

We appreciate Dr. Li-Tao Yang for communications and useful discussions. Thanks to Dr. Cheng-Cheng Han and Dr. Sampsa Vihonen for careful reading of the manuscript.

To explicitly present the differences in calculating the attenuation effect with the ballistic approach and the MC method, we choose three benchmark points located on the floor limits in Fig. 4 and show the corresponding DM fluxes and recoil spectra as shown in Fig. A1. The simulation code Darkprop is utilized for calculations of the attenuation effect [58]. From the upper plots of Fig. A1, one can see that the fluxes in the MC case have a tail distribution in the higher energy range due to the form factor suppression. As for the smaller cross section or DM mass, the attenuation effect gets weaker so that the differences between the ballistic approach and the MC method eventually diminish. From the lower plots of Fig. A1, we find that the recoil spectrum of the MC method is a bit more conservative than that of the ballistic approach for the longer effective distance with $ D_\rm{eff}=3.7\; \rm{kpc} $. Note that whether the form factor is considered in the ballistic approach or not, the recoil spectra are almost the same. For the closer collision location with $ D_\rm{eff}=1\; \rm{kpc} $ and a larger cross section, the spectrum discrepancy increases in a comparison of the MC method and ballistic approach. Consequently, the floor limit would be lifted if the MC method is adopted, while a larger $ D_\rm{eff} $ can dilute the relevant modification.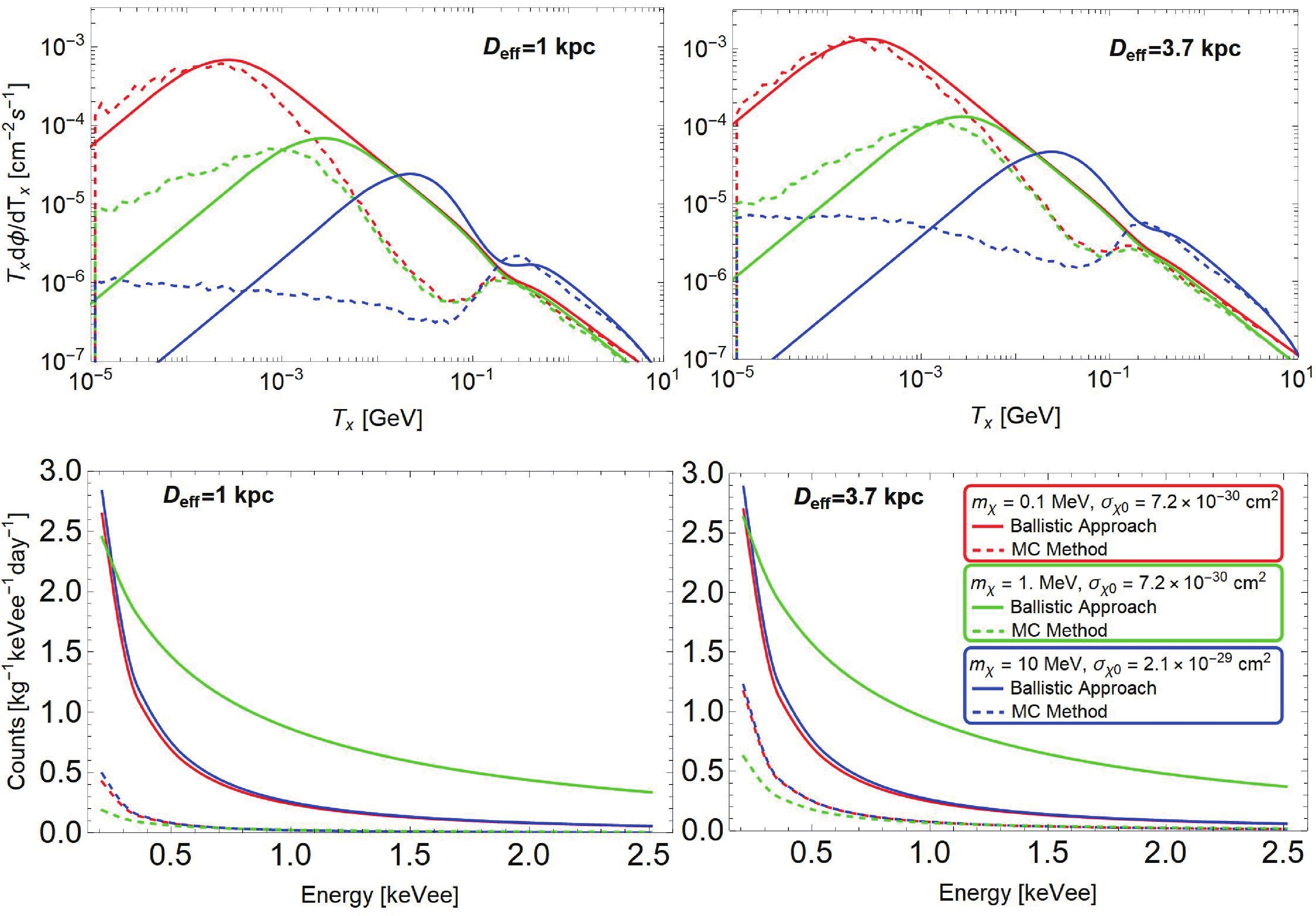

Figure A1.  (color online) CRBDM fluxes and theoretical spectra derived from the ballistic approach (solid line) and the MC method (dashed line). Form factor effects are included here in all panels.

A larger cross section or thicker crust would lead to a stronger attenuation effect. Thus, we strongly advise that a more careful treatment is needed to judge the Earth attenuation effect.