-
In the context of extended general relativity, the consistency of quantum behavior, including the understanding of gravity, may be related to the possible mass of graviton, which is a long-standing basic physical question of classical field theory. In general, adding a mass term to the action of a given background leads to various instabilities in gravity theories, sometimes even to the non-linearity. Recently, the authors (in the dRGT large-scale theory) in Refs. [1–4] constructed a non-linear generalization for all orders, in which a higher-order interaction term was introduced into the Boolean function to eliminate the Boulware-Deser ghost [5–7]. There are also many interesting results in the cosmological behavior and the black hole solution [8–14] for the three-dimensional dRGT. Subsequently, the spherically symmetric solution was also discussed in [15–17].
The recent study on the thermodynamic characteristics of an AdS black hole in massive gravity has attracted great interest [18–22], and the method [23–56] to study AdS black hole was extended such that the cosmological constant is regarded as the state parameter of a black hole thermodynamic system: pressure.
$ P=\frac{n(n-1)}{16 \pi l^{2}},\; \; \; \; \Lambda=-\frac{n(n-1)}{2 l^{2}}, $

(1) and the corresponding thermodynamic volume is
$V= \left(\dfrac{\partial M}{\partial P}\right)_{S,Q,c_{i}}$ . The critical behavior of an AdS black hole in massive gravity was studied (the conjugate variables were selected to be$ P\sim V $ ). The thermodynamic properties of AdS black holes in massive gravity were simulated. These properties are similar to that in a Van de Waals (VdW) system. However, the studies on the first-order phase transition of an AdS black hole in massive gravity have not been paid much attention. Furthermore, up to now, the statistical mechanics background of black holes as a thermodynamic system has not been made clear. Therefore, it is important to find the relationship between the thermodynamic properties of various AdS black holes, to explore the internal connection between different AdS black hole thermodynamic quantities, and to discuss the thermodynamic properties of AdS black holes. This would facilitate further understanding on entropy, temperature, and heat capacity; it would also significantly improve the self-consistent black hole thermodynamic geometry theory.In Refs. [30, 57–60], the phase diagram of
$ P-v $ for the charged topological Dilaton AdS black holes was analyzed. It was found that when the temperature of black hole is low, there exists a region in which the pressure increases with the volume and the system is mechanically unstable. This phenomenon is similar to the result of the Van der Waals-Maxwell (VdWM) system. In order to solve this problem, Maxwell proposed the famous Maxwell equal-area law. For the Topological AdS black hole in massive gravity, we also face the same problem as a VdWM gas-liquid phase diagram. This research extends Maxwell's equal-area law and applies it to study the topological AdS black hole in massive gravity. In this paper, we not only solved the problem in the mechanically unstable region but also present the coexistent curve and its slope. Furthermore we discuss the effect of various parameters on the phase transition.As is well known, the phase transition point of thermodynamical systems in the canonical ensemble is independent of the selection of the conjugate variables (such as
$ P\sim V $ and$ T\sim S $ ). This conclusion is also true for black holes. The conjugate variables obtained from the first law of thermodynamic are$ P\sim V $ ,$ T\sim S $ ,$ C_1\sim c_1 $ and$ C_2\sim c_2 $ [21] for the AdS black hole with a fixed charge in massive gravity. Thus it is necessary to select different conjugate variables to study the phase transition's condition of the AdS black hole in massive gravity to prove that selected conjugate variables are the state parameters of the system. From our discussion, topological AdS black hole in massive gravity not only has second-order phase transition but also has the coexistent curve of$ P\sim T $ . What we want to point out is that all the first-order phase transition's points with the conjugate variables of$ P,\; V,\; T,\; S,\; C_1,\; c_1,\; C_2,\; c_2 $ are the same, so these variables can be regarded as the state parameters of a topological AdS black hole in massive gravity. We look forward to studying the thermodynamic system phases, phase transition, and other characteristics of the topological AdS black hole in massive gravity, as well as providing more insightful information on understanding the properties and behavior of quantum gravity.This paper is arranged as follows: the topological AdS black holes in massive gravity is briefly introduced in Sec. II. Maxwell's equal-area law is applied to topological AdS black hole in massive gravity thermodynamic system in Sec. III. The different conjugate variables are selected to obtain the relationship between the boundary points and parameters of the coexistent zone in the system and to display the effect on the boundary points. We analyze the relationship between temperature and pressure in the coexistence zone of two-phase as well as present the coexistent curve and its slope of
$ P\sim T $ in Sec. IV. Then we introduce a new order parameter to probe the microstructure of a black hole in Sec. V. Finally the conclusion is summarized in Sec.VI. -
For the AdS topological static charged black hole in massive gravity, we consider the metric of five-dimensional spacetime in the following form [8]
$ {\rm d} s^2 = -f(r){\rm d}t^2+f^{-1}(r){\rm d}r^2+r^2 h_{ij} {\rm d}x^i {\rm d} x^j, $

(2) $ f(r) = k-\frac{m_0}{r}+\frac{q^2}{r^2}-\frac{\Lambda}{3}r^2+m^2A, $

(3) $ A = \frac{cc_1}{2}r+c^2c_2+\frac{c^3c_3}{r}, $

(4) where
$ i,j=1,2,3. $ and$h_{ij}{\rm d}x^i{\rm d}x^j$ is a spatial metric in a three-dimensional space. The constant k characterizes the geometric property of black hole horizon hypersurface, which takes values$ k=0 $ for flat,$ k=-1 $ for negative curvature, and$ k=1 $ for positive curvature. The letter q is an integration constant, and it is related to the electrical charge;$ m_0 $ is an integration constant that is related to the total mass of black hole; m is the graviton mass; c is a positive constant; and$ c_i $ are constants. For the parameters$ c_i $ , we should give the following explanation. In a self-consistent massive gravity theory, all these coefficients might be required to be negative if$ m^2>0 $ . However, in this paper we do not impose this limit, since in AdS space the fluctuations of some fields with negative squared masses could still be stable if the squared mass obeys the corresponding Breitenlohner-Freedman bounds.Denoting
$ r_+ $ as the position of the event horizon of a black hole, it satisfies the expression:$ f(r_+)=0 $ . Hence, in this black hole system the radiation temperature T, pressure P, entropy S, charge Q, energy M, and electric potential Φ are:$ T = \frac{k}{4\pi r_+}-\frac{r_+\Lambda}{4\pi}-\frac{q^2}{4\pi {r_+}^3}+\frac{m^2}{4\pi r_+}(cc_1r_+ +c^2c_2), $

(5) $ P = \frac{4 \pi T-m^{2} c c_{1}}{8 \pi r_+}-\frac{k+m^{2} c^{2} c_{2}}{8 \pi r_+^{2}}+\frac{q^{2}}{8 \pi r_+^{4}}, $

(6) $ S = \frac{v_2{r_+}^2}{4},\; \; \; \; Q=\frac{v_2q}{4\pi},\; \; \; \; M=\frac{v_2m_0}{8\pi},\; \; \; \; \Phi=\frac{q}{r_+}, $

(7) where
$ v_2 $ is the area of a unit volume of constant$ (t,r) $ space ($ v_2=4\pi $ for$ k=0 $ ). With the above expressions, we find that these quantities obey the first law of black hole thermodynamics in an extended phase space$ {\rm d}M=T{\rm d}S+\Phi {\rm d}Q+V{\rm d}P+C_1{\rm d}c_1+C_2{\rm d}c_2+C_3{\rm d}c_3. $

(8) Therefore, we can give the related thermodynamic quantities as
$ \begin{aligned}[b] T =& \left(\frac{\partial M}{\partial S}\right)_{Q, P, c_{i}},\quad \Phi=\left(\frac{\partial M}{\partial Q}\right)_{S, P, c_{i}}, \\ V =& \left(\frac{\partial M}{\partial P}\right)_{S, Q, c_{i}}=\frac{v_{2} r_+^{3}}{3},\; \; \; \; P=-\frac{\Lambda}{8 \pi},\\ C_{1} =& \left(\frac{\partial M}{\partial c_{1}}\right)_{Q, P, Q, c_{2,3}}=\frac{v_{2} c m^{2} r_+^{2}}{16 \pi},\\ C_{2} =& \left(\frac{\partial M}{\partial c_{2}}\right)_{Q, P, Q, c_{1,3}}=\frac{v_{2} c^{2} m^{2} r_+}{8 \pi}, \\ C_{3} =& \left(\frac{\partial M}{\partial c_{1}}\right)_{Q, P, Q, c_{1,2}}=\frac{v_{2} c^{3} m^{2}}{8 \pi}. \end{aligned} $

(9) One can calculate the critical value of the second-order phase transition for the topological AdS black hole in massive gravity [21] by
$ \left(\dfrac{\partial P}{\partial r_{+}}\right)_{T}=\left(\dfrac{\partial^{2} P}{\partial r_{+}^{2}}\right)_{T}=0 $ . We find the critical position of the event horizon$ r_{+c} $ , critical temperature$ T_{c} $ , and critical pressure$ P_{c} $ to be$ \begin{aligned}[b] r_{+c} =& \frac{\sqrt{6}|q|}{\sqrt{k+m^{2} c^{2} c_{2}}},\\\;\; T_{c} =& \frac{\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{3 \sqrt{6} \pi q}+\frac{m^{2} c c_{1}}{4 \pi},\\ \;\; P_{c} = &\frac{\left(k+m^{2} c^{2} c_{2}\right)}{96 \pi q^{2}}. \end{aligned} $

(10) By adopting the conjugate variables
$ P\sim V $ , the critical value that is acquired by solving the expressions$ \left(\dfrac{\partial P}{\partial V}\right)_{T}=\left(\dfrac{\partial^{2} P}{\partial V^{2}}\right)_{T}=0 $ has the same form as Eq. (10). -
For the topological AdS black hole in massive gravity under the same condition, does the selection of conjugate variables influence the first-order phase transition point in the canonical ensemble? We select the different conjugate variables to construct the equal-area law and to study the the phase transition's condition of the AdS black in massive gravity.
-
For the topological AdS black hole in massive gravity with a given charge q at a first-order phase transition point, we denote the temperature and pressure as
$ T_0,\; P_0 $ . In the$ P-V $ diagram, the abscissas corresponding to the boundary of the two-phase coexistence area are$ V_2 $ and$ V_1 $ . One constructs Maxwell's equal-area law as follows$ P_{0}\left(V_{2}-V_{1}\right)=\int_{V_{1}}^{V_{2}} P {\rm d} V, $

(11) the
$ P_0 $ derived from Eq. (6) read as$ \begin{aligned}[b] P_{0} =& \frac{4 \pi T-m^{2} c c_{1}}{8 \pi r_{1}}-\frac{k+m^{2} c^{2} c_{2}}{8 \pi r_{1}^{2}}+\frac{q^{2}}{8 \pi r_{1}^{4}}\\ =&\frac{4 \pi T-m^{2} c c_{1}}{8 \pi r_{2}}-\frac{k+m^{2} c^{2} c_{2}}{8 \pi r_{2}^{2}}+\frac{q^{2}}{8 \pi r_{2}^{4}}, \\ 2 P_{0} =& \frac{3\left(4 \pi T_{0}-m^{2} c c_{1}\right)(1+x)}{8 \pi r_{2}\left(1+x+x^{2}\right)}-\frac{3\left(k+m^{2} c^{2} c_{2}\right)}{4 \pi r_{2}^{2}\left(1+x+x^{2}\right)}\\&+\frac{3 q^{2}}{4 \pi r_{2}^{4} x\left(1+x+x^{2}\right)}, \end{aligned} $

(12) where
$ x=r_1/r_2 $ . From the above equations, we can obtain$\begin{aligned}[b] r_{2}^{2}\left(k+m^{2} c^{2} c_{2}\right) =& \frac{q^{2}}{x^{2}} \frac{\left(1+2 x-6 x^{2}+2 x^{3}+x^{4}\right)}{(1-x)^{2}}\\=&\frac{q^{2}}{x^{2}}\left(1+4 x+x^{2}\right)\equiv q^{2} f_{q}(x), \end{aligned} $

(13) $ \frac{\left(4 \pi T_{0}-m^{2} c c_{1}\right)}{4 \pi\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}} = \frac{(1+x)}{4 \pi x q f_{q}^{1 / 2}(x)}-\frac{(1+x)\left(1+x^{2}\right)}{4 \pi q f_{q}^{3 / 2}(x) x^{3}}. $

(14) With the following definition
$ T_{0}=\chi \frac{\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{3 \sqrt{6} \pi q}+\frac{m^{2} c c_{1}}{4 \pi},\; 0<\chi\leq1, $

(15) Eq. (14) can be rewritten as
$ \chi x^{2} f_{q}^{3 / 2}(x) \frac{1}{3 \sqrt{6}}=(1+x). $

(16) Obviously, when the temperature is given (χ is a fixed value), the ratio between the charge and the black hole event horizon is a fixed value. It means the black hole event horizons of two coexistent phases (
$ r_{2},\; r_{1} $ ) are determined when the charge$ q,\; \left(k+m^{2} c^{2} c_{2}\right) $ is given. According to the Ehrenfest phase transition classification, the position of the event horizon that satisfies Eq. (13) is the first-order phase transition position. We plot the$ P-V $ diagrams with different temperatures and k in Fig. 1.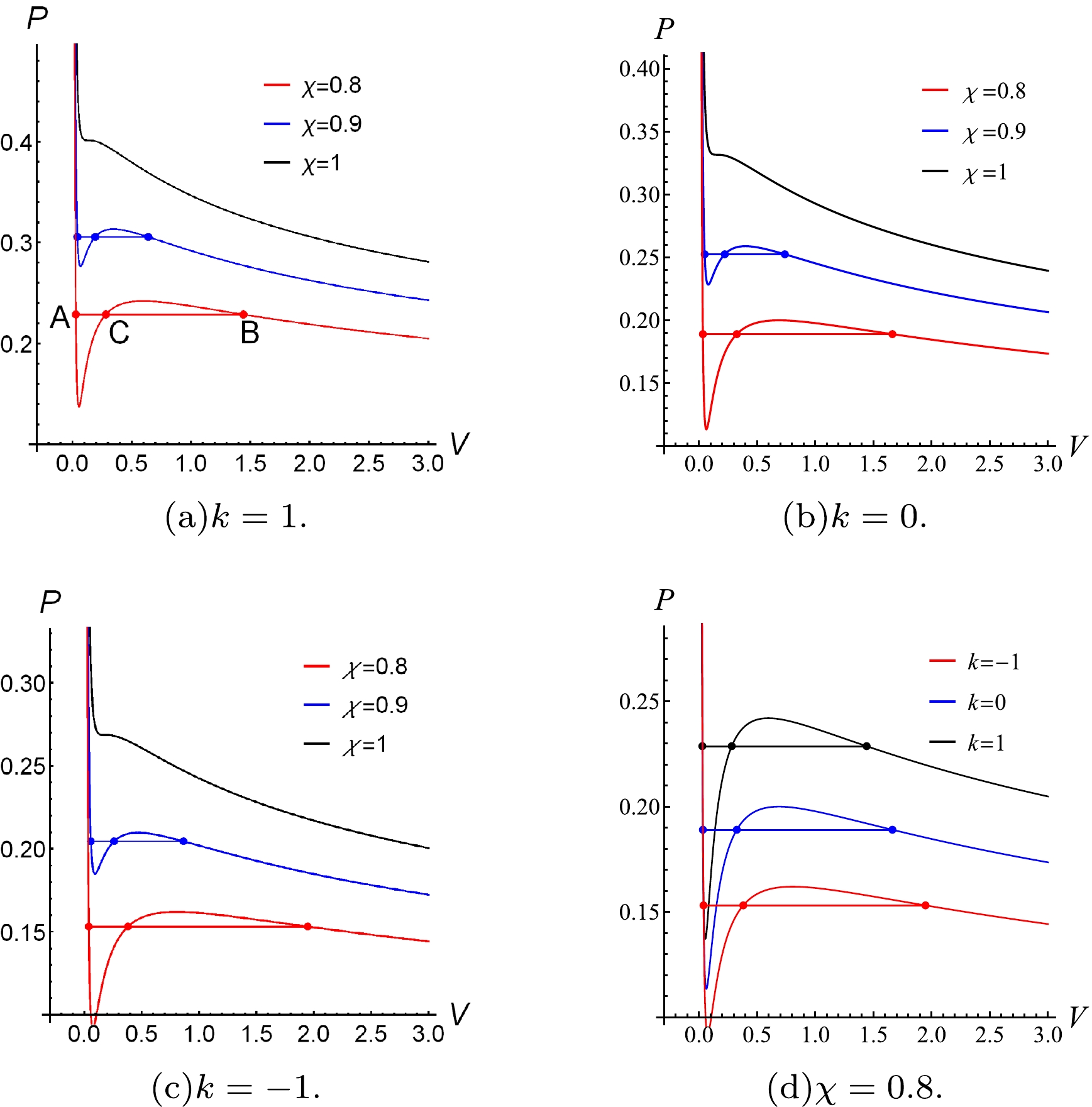
Figure 1. (color online) The
$ P-V $ diagrams for the different k and χ with$ m=1,\; q=1,\; c_1=1,\; c_2=10,\; v_{2}=1 $ .As can be seen from Fig. 1, the isothermal curve
$ P-V $ of spacetime is similar to that of the VdW system. When the temperature of spacetime is below the critical temperature, the first-order phase transition occurs, and the isotherm consists of three segments. The segment on the left, which is parallel to the P axis (with a small equal-compression coefficient), represents the liquid phase (α phase) in the VdW system. The right segment represents the gas phase (β phase) in the VdW system. For the middle segment, which is parallel to the V axis, the line from point A to B represents the coexistence state of the two-phases. The proportion of each phase changes with the temperature. The geometric properties of black hole horizon hypersurfaces at the two coexistent phases are different while the spacetime parameters are same. The coexistence area of positive curvature ($ k=1 $ ) is less than that of negative curvature ($ k=-1 $ ); this means the parameter k has influence on the pressure corresponding to the coexistence region of two-phases. -
When pressure is a constant and is less than the critical value, in the
$ T-S $ diagram the boundary abscissa of the coexistence region of two-phases are$ S_1 $ ,$ S_2 $ . The temperature at a phase transition point is denoted by$ T_0 $ . One can construct the Maxwell's equal-area law as follows:$ \begin{aligned}[b] T_{0}\left(S_{2}-S_{1}\right)=&\int_{S_{1}}^{S_{2}} T {\rm d} S=\frac{v_{2}}{8 \pi} \int_{r_{1}}^{r_{2}}\left(k-r_+^{2} \Lambda-\frac{q^{2}}{r_+^{2}}\right.\\&\left.+\frac{m^{2}}{4 \pi}\left(c c_{1} r_++c^{2} c_{2}\right)\right) {\rm d} r_+, \end{aligned}$

(17) the
$ T_{0} $ derived from Eq. (5) read as$ \begin{aligned}[b] T_{0}=&\frac{k+m^{2} c^{2} c_{2}}{4 \pi r_{1}}-\frac{r_{1} \Lambda}{4 \pi}-\frac{q^{2}}{4 \pi r_{1}^{3}}+\frac{m^{2} c c_{1}}{4 \pi}\\=&\frac{k+m^{2} c^{2} c_{2}}{4 \pi r_{2}}-\frac{r_{2} \Lambda}{4 \pi}-\frac{q^{2}}{4 \pi r_{2}^{3}}+\frac{m^{2} c c_{1}}{4 \pi},\\ &\frac{4 \pi T_{0}-m^{2} c c_{1}}{2} r_{2}^{2}\left(1-x^{2}\right)\\=&r_{2}\left(k+m^{2} c^{2} c_{2}\right)(1-x)\\&-\frac{r_{2}^{3}}{3} \Lambda\left(1-x^{3}\right)-q^{2} \frac{1-x}{r_{2} x}. \end{aligned} $

(18) From the above equations, we have
$ r_{2}^{2}\left(k+m^{2} c^{2} c_{2}\right)=\frac{q^{2}}{x^{2}}\left(1+4 x+x^{2}\right)\equiv q^{2} f_{q}(x) $

(19) $ \begin{aligned}[b] 2 x q f_{q}^{3 / 2}(x) \frac{\left(4 \pi T_{0}-m^{2} c c_{1}\right)}{\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}=&(1+x) f_{q}(x)\\&-\frac{\left(1+3 x+3 x^{2}+x^{3}\right)}{x^{2}} . \\[-10pt]\end{aligned}$

(20) Substituting Eq. (15) into Eq. (20), one find that it has the same form as Eq. (16). Noting
$ \begin{aligned}[b] T_{0}=\chi \dfrac{\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{3 \sqrt{6} \pi q}+ \dfrac{m^{2} c c_{1}}{4 \pi}\ {\rm and} \end{aligned}$

$ \begin{aligned}[b]r_{+}=\dfrac{\sqrt{6}|q|}{\sqrt{k+m^{2} c^{2} c_{2}}} , \end{aligned}$

we plot the
$ T-S $ curves with the different pressures and k in Fig. 2.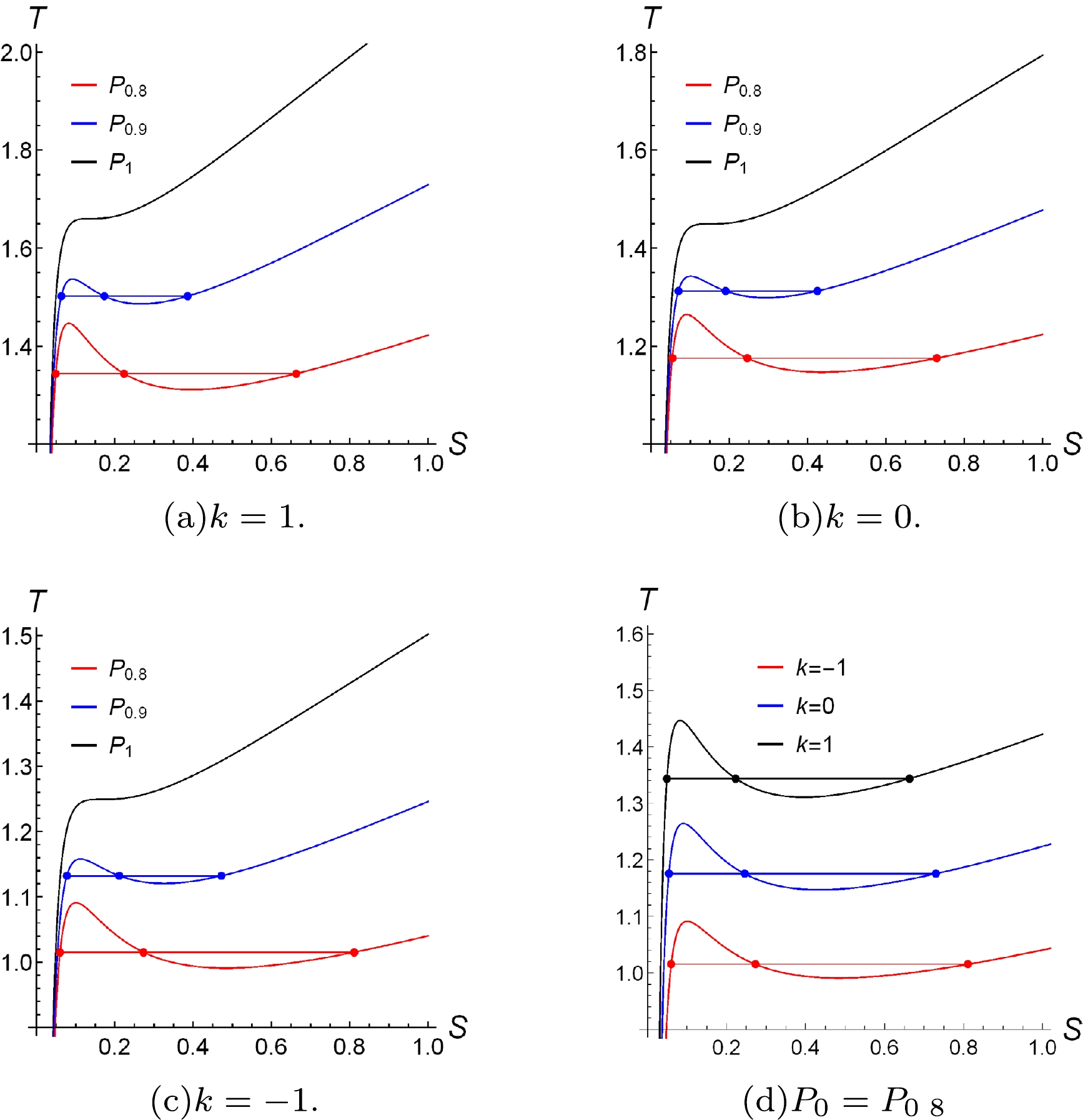
Figure 2. (color online) The
$ T-S $ diagrams for the different k and pressure with$ m=1,\; q=1,\; c_1=1,\; c_2=10,\; v_{2}=1 $ .The pressure
$ P_0 $ corresponding to the different χ and k are given in Table 1. Fig. 2 shows the different$ T-S $ curves with the different χ and k and the region of the coexistent area, in which the intersection points A, C, and B, respectively. The results indicate that the pressure is less than the critical one; in different phases, the temperatures varying with entropy have different behaviors. From A to B, each point of the curve does not meet the requirement of equilibrium stability of the thermodynamic system. According to Maxwell's equal-area law, the curve between A and B is replaced by the line. Figure 2 shows that when the parameters of spacetime keep invariant, the geometric property of black hole horizon hypersurface is different, and the coexistence area of two-phases is also different. The spacetime coexistence region for$ k=1 $ is less than$ k=-1 $ . It also shows the effect of k on the temperature corresponding to the coexistence region of two-phases.k $ P_{0.8} $ 

$ P_{0.9} $ 

$ P_1 $ 

−1 0.153136 0.204521 0.268574 0 0.189057 0.252496 0.331573 1 0.228759 0.30552 0.401203 Table 1. The value of
$ P_0 $ corresponding to the different χ and k. -
aWhen the pressure P and temperature T are constants, the abscissas of a topological AdS black hole in coexistence region of two-phases in massive gravity are
$ C_{12} $ and$ C_{11} $ , and the ordinate temperature is$ c_1 $ . We construct the Maxwell's equal-area law as$ \begin{aligned}[b] c_{10}\left(C_{12}-C_{11}\right)=&\int_{C_{11}}^{C_{12}} c_{1} {\rm d} C_{1}=\int_{C_{11}}^{C_{12}}\Bigg[4 \pi T_{0}-P_{0} 8 \pi r_+\\&-\frac{k+m^{2} c^{2} c_{2}}{r_+}+\frac{q^{2}}{r_+^{3}}\Bigg] \frac{v_{2} c m^{2} r_+}{8 \pi} {\rm d} r_+. \end{aligned}$

(21) From the first law of black hole thermodynamics, one can give the following:
$ \begin{aligned}[b] m^{2} c c_{1} =& 4 \pi T_{0}-8 \pi P_{0} r_+-\frac{k+m^{2} c^{2} c_{2}}{r_+}+\frac{q^{2}}{r_+^{3}}, \\ 2 m^{2} c c_{10} =& 8 \pi T_{0}-8 \pi P_{0} r_{2}(1+x)\\&-\frac{k+m^{2} c^{2} c_{2}}{r_{2} x}(1+x)+\frac{q^{2}\left(1+x^{3}\right)}{r_{2}^{3} x^{3}}, \end{aligned} $

(22) $ 0 = -8 \pi P_{0} r_{2}(1-x)+\frac{k+m^{2} c^{2} c_{2}}{r_{2} x}(1-x)-\frac{q^{2}\left(1-x^{3}\right)}{r_{2}^{3} x^{3}}. $

(23) From the above equations, we have
$ \begin{aligned}[b]& r_{2}^{2}\left(k+m^{2} c^{2} c_{2}\right) \\=& \frac{q}{x^{2}} \frac{(1+2 x-0 x+2 x+x)}{(1-x)^{2}}\\=&\frac{q}{x^{2}}\left(1+4 x+x^{2}\right)\equiv q^{2} f_{q}(x), \end{aligned} $

(24) $\begin{aligned}[b] & \frac{k+m^{2} c^{2} c_{2}}{4 \pi r_{2}^{2} x}-\frac{q^{2}\left(1+x+x^{2}\right)}{4 \pi r_{2}^{4} x^{3}} \\=& \frac{3\left(4 \pi T_{0}-m^{2} c c_{1}\right)(1+x)}{8 \pi r_{2}\left(1+x+x^{2}\right)}-\frac{3\left(k+m^{2} c^{2} c_{2}\right)}{4 \pi r_{2}^{2}\left(1+x+x^{2}\right)}\\&+\frac{3 q^{2}}{4 \pi r_{2}^{4} x\left(1+x+x^{2}\right)} . \end{aligned} $

(25) Taking
$ P=P_c $ s and Eq. (15) into Eq. (25), one get the same form as Eq. (16). We plot$ m^2cc_1-C_1 $ curve under an isobaric condition with different temperatures corresponding to$ \chi=1,\; \chi=0.9,\; \chi=0.8 $ .As can be seen from Fig. 3, the influence of k on the two-phases' coexistence zone is similar to that on the isothermal
$ P-V $ and isobaric$ T-S $ . However, under the conditions of different temperature and pressure, the parameter$ c_1 $ that corresponds to the coexistence of two-phases is not influenced by k. -
When the pressure P and temperature T are constants, the abscissas of a topological AdS black hole in the coexistence region of two-phases in massive gravity are
$ C_{22} $ and$ C_{21} $ , and the ordinate temperature is$ c_2 $ . One can construct the Maxwell's equal-area law as$ \begin{aligned}[b] c_{20}\left(C_{22}-C_{21}\right)=&\int_{C_{21}}^{C_{22}} c_{2} {\rm d} C_{2}=\int_{C_{21}}^{C_{22}}\Bigg[\left(4 \pi T_{0}-m^{2} c c_{1}\right) r_+\\&-k-8 \pi r_+^{2} P_{0}+\frac{q^{2}}{r_+^{2}}\Bigg] \frac{v_{2} c^{2} m^{2}}{8 \pi} {\rm d} r_+. \\[-13pt] \end{aligned}$

(26) From the first law of black hole thermodynamics, we obtain
$ \frac{8 \pi r_{2}^{3} P_{0}}{3}(1-x)^{2} = \frac{q^{2}(1-x)^{2}}{r_{2} x^{2}}, $

(27) $ \left(4 \pi T_{0}-m^{2} c c_{1}\right) r_{2} = \frac{4 q^{2}(1+x)}{r_{2}^{2} x^{2}}, $

(28) $ r_{2}^{2}\left(k+m^{2} c^{2} c_{2}\right) = \frac{q^{2}}{x^{2}}\left(1+4 x+x^{2}\right)\equiv q^{2} f_{q}(x). $

(29) Substituting Eqs. (27) and (29) into Eq. (12), one gets the same form as Eq. (16). Noting
$ P=P_c $ and$ T_{0}= \chi \dfrac{\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{3 \sqrt{6} \pi q}+\dfrac{m^{2} c c_{1}}{4 \pi} $ . we plot the$ m^2c c_2-C_2 $ curve under an isobaric condition with different temperatures corresponding to$ \chi=1,\; 0.9,\; 0.8 $ .Figure 4 shows that the curves of
$ C_2-c_2 $ and$ C_1-c_1 $ are similar, and the influence of k on the size of the coexistence region is similar to that in the$ P-V $ and$ T-S $ diagrams under the same parameters. However, the parameter$ c_2 $ that corresponds to the two-phase coexistent state for different phase transition points is independent of k.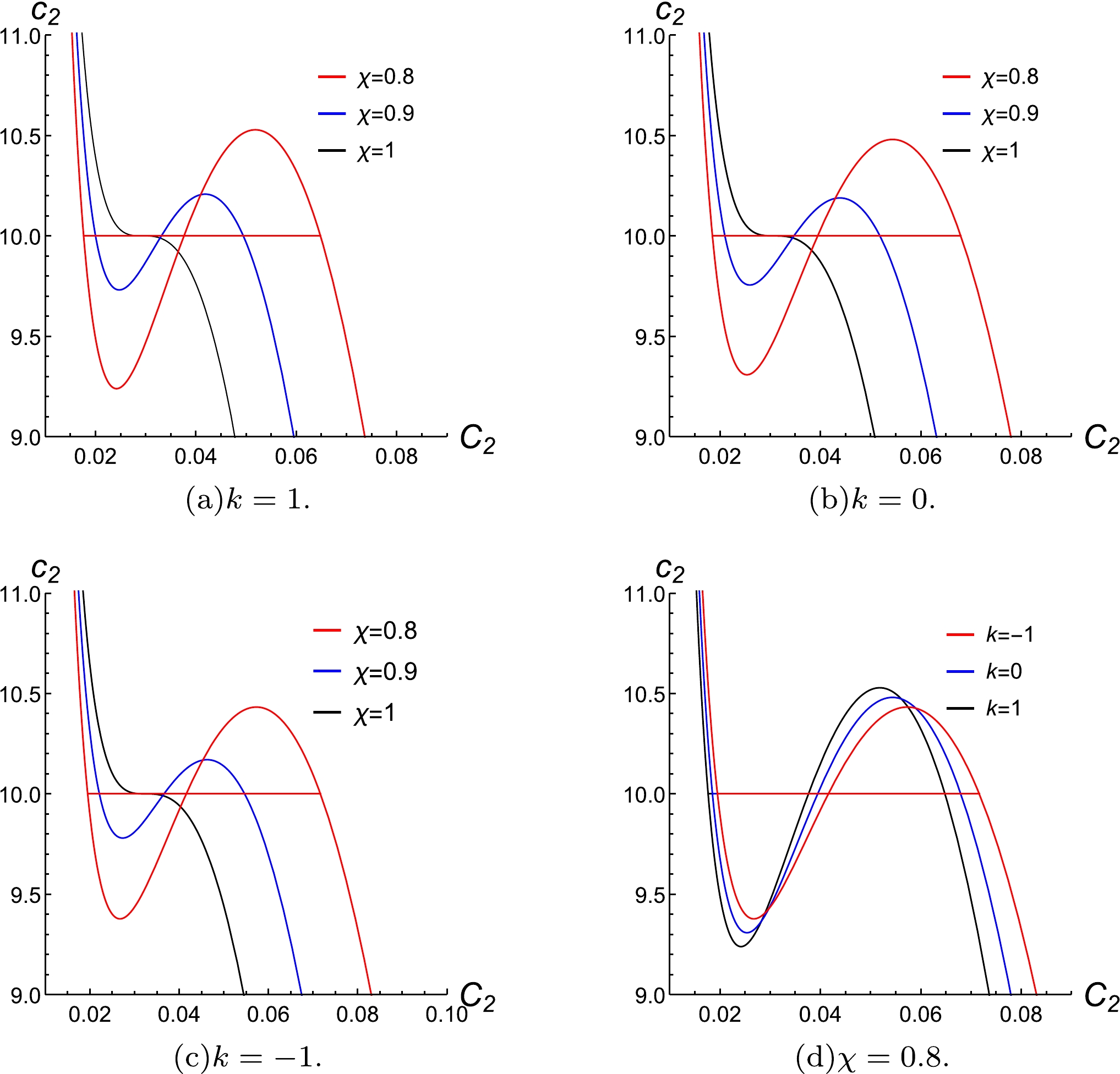
Figure 4. (color online) The isothermal-isobaric
$ C_2-c_2 $ diagram with$ c_1=1,\; m=1,\; c=1,\; q=1,\; v_{2}=1 $ .Comparing Figs. 1 and 2 with 3 and 4, we find that the phase transition curve of a black hole followed the law of the Van's system phase transition curve. However in the diagrams of
$ C_1-c_1 $ and$ C_2-c_2 $ , the parameters of$ c_1 $ and$ c_2 $ at different phase transition points (i.e., different values of χ) are both fixed. This is different from an isotherm$ P-V $ curve or an isobaric$ T-S $ curve. It means$ c_1 $ and$ c_2 $ are fixed when a phase transition happens despite different temperatures.When we select the different conjugate variables, it is known from Eq. (16) that if the black hole radiation temperature is given (χ is given), x satisfies the equation and does not change due to the difference of independent conjugate variables. Instead, from Eqs. (13), (19), (24), and (29) when the temperature
$ T_0 $ is given, the ratio of$ r_2 $ to the charge q carried by the topological AdS black hole is$ \sqrt{\left(k+m^{2} c^{2} c_{2}\right) / f_{q}(x)} $ when$ \left(k+m^{2} c^{2} c_{2}\right) $ is set to be a constant. Therefore, the phase transition point of the topological AdS black hole in massive gravity with a given temperature$ T_0 $ is not only affected by the black hole's horizon radius$ r_2 $ but also related to the charge q and$ \left(k+m^{2} c^{2} c_{2}\right) $ . Namely, it is not only just a large/small black holes phase transition. When$ T_0 $ and$ \left(k+m^{2} c^{2} c_{2}\right) $ are fixed, the system with a given charge q is in α phase if$ r_{+}<r_{1} $ , which corresponds to the liquid phase of the VdW system. The topological AdS black hole in massive gravity is in β phase when$ r_{+}>r_{2} $ , which corresponds to the vapor phase of the VdW system. And the system will be in a two-phase coexistent state when$ r_{2} \geq r_{+} \geq r_{1} $ , which is corresponds to the Vapor-liquid coexistence area of the VdW system. According to the ratio between the charge and the radius of the black hole horizon, we call the three states the high potential phase (α phase), medium potential phase (coexistent phases), and low potential phase (β phase).From Eqs. (13), (19), (24), and (29), we know that when the temperature is given, the horizon radius of the topological AdS black hole in massive gravity undergoing a phase transition is related to the charge q and
$ \left(k+m^{2} c^{2} c_{2}\right) $ ; it is independent of the parameters$ c_1 $ and$ c_2 $ . Furthermore when the black hole horizon is given, the temperature and pressure of the topological AdS black hole in massive gravity are both related to the charge q and$ \left(k+m^{2} c^{2} c_{2}\right) $ but are irrelevant to$ c_3 $ .As well as the Maxwell's equal-area law, Gibbs free energy is an important thermodynamic quantity to study phase transition. It exhibits a swallow tail behavior at the first-order phase transition point and is continuous but not smooth at a second-order phase transition. These two methods are thermodynamically equivalent. Therefore, we do not present the swallow tail behavior and only give the relation of Gibbs free energies for two coexistent phases in the following. Gibbs free energy can be written as [21]
$\begin{aligned}[b] G=&M-T S=-v_{2} P \frac{r_+^{3}}{6}\\&+v_{2} \frac{m^{2} r_+\left(c^{2} c_{2} r_++2 c^{3} c_{3}\right)+\left(k r_+^{2}+3 q^{2}\right)}{16 \pi r_+}.\end{aligned} $

At a phase transition, the Gibbs free energy for two coexistent phases are
$ \begin{aligned}[b] \;G_{2}=&-v_{2} \frac{r_{2}^{2}\left(4 \pi T-m^{2} c c_{1}\right)}{48 \pi}\\&+v_{2} \frac{r_{2}\left(k+m^{2} c^{2} c_{2}\right)}{12 \pi}+v_{2} \frac{q^{2}}{6 \pi r_{2}}+v_{2} \frac{m^{2} c^{3} c_{3}}{8 \pi} \end{aligned} $

$ \begin{aligned}[b] G_{1}=&-v_{2} \frac{r_{1}^{2}\left(4 \pi T-m^{2} c c_{1}\right)}{48 \pi}+v_{2} \frac{r_{1}\left(k+m^{2} c^{2} c_{2}\right)}{12 \pi}\\&+v_{2} \frac{q^{2}}{6 \pi r_{1}}+v_{2} \frac{m^{2} c^{3} c_{3}}{8 \pi}, \end{aligned} $

and their difference reads
$ \begin{aligned}[b] G_{2}-G_{1}=&v_{2} \frac{(1-x)}{48 \pi}\Bigg[-r_{2}^{2}\left(4 \pi T-m^{2} c c_{1}\right)(1+x)\\&+4 r_{2}\left(k+m^{2} c^{2} c_{2}\right)-8 \frac{q^{2}}{r_{2} x}\Bigg]. \end{aligned} $

(30) Substituting Eqs. (15), (16), and (19) into Eq. (30), we find
$ G_{2}-G_{1}=0. $

(31) When the horizon radius and pressure (or temperature) of a topological AdS black hole in massive gravity are given, we know that the Gibbs free energy of a black hole is related to
$ c_2 $ and$ c_3 $ . That is, the Gibbs free energy at two points A and B is a function of$ c_2 $ and$ c_3 $ , and the Gibbs free energy of the two points A and B are always equal, satisfying the condition of the first-order phase transition. -
For an ordinary thermodynamic system, due to the lack of knowledge regarding the chemical thermal potential, the coexistent curve is directly determined by experiment in fact. The slope of the
$ P-V $ curve is given by the Clapeyron equation:$ \frac{{\rm d} P}{{\rm d} T}=\frac{L}{T\left(V_{\beta}-V_{\alpha}\right)}. $

(32) Here,
$ L=T\left(S_{\beta}-S_{\alpha}\right) $ is the latent heat;$ V_{\alpha} $ and$ V_{\beta} $ are the volumes corresponding to α and β phases. The Clapeyron equation of an ordinary thermodynamic system is in good agreement with the experimental results, providing a direct experimental verification for the correctness of thermodynamics.For the topological AdS black hole in massive gravity, substituting Eq. (29) into Eqs. (14) and (18), we have
$ \begin{aligned}[b] P =& \frac{3\left(k+m^{2} c^{2} c_{2}\right)^{2}}{8 \pi x^{2} q^{2} f_{q}^{2}(x)}=\frac{3 x^{2}\left(k+m^{2} c^{2} c_{2}\right)^{2}}{8 \pi q^{2}\left(1+4 x+x^{2}\right)^{2}},\\ T =& \frac{(1+x) x\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{\pi q\left(1+4 x+x^{2}\right)^{3 / 2}}+\frac{m^{2} c c_{1}}{4 \pi}. \end{aligned} $

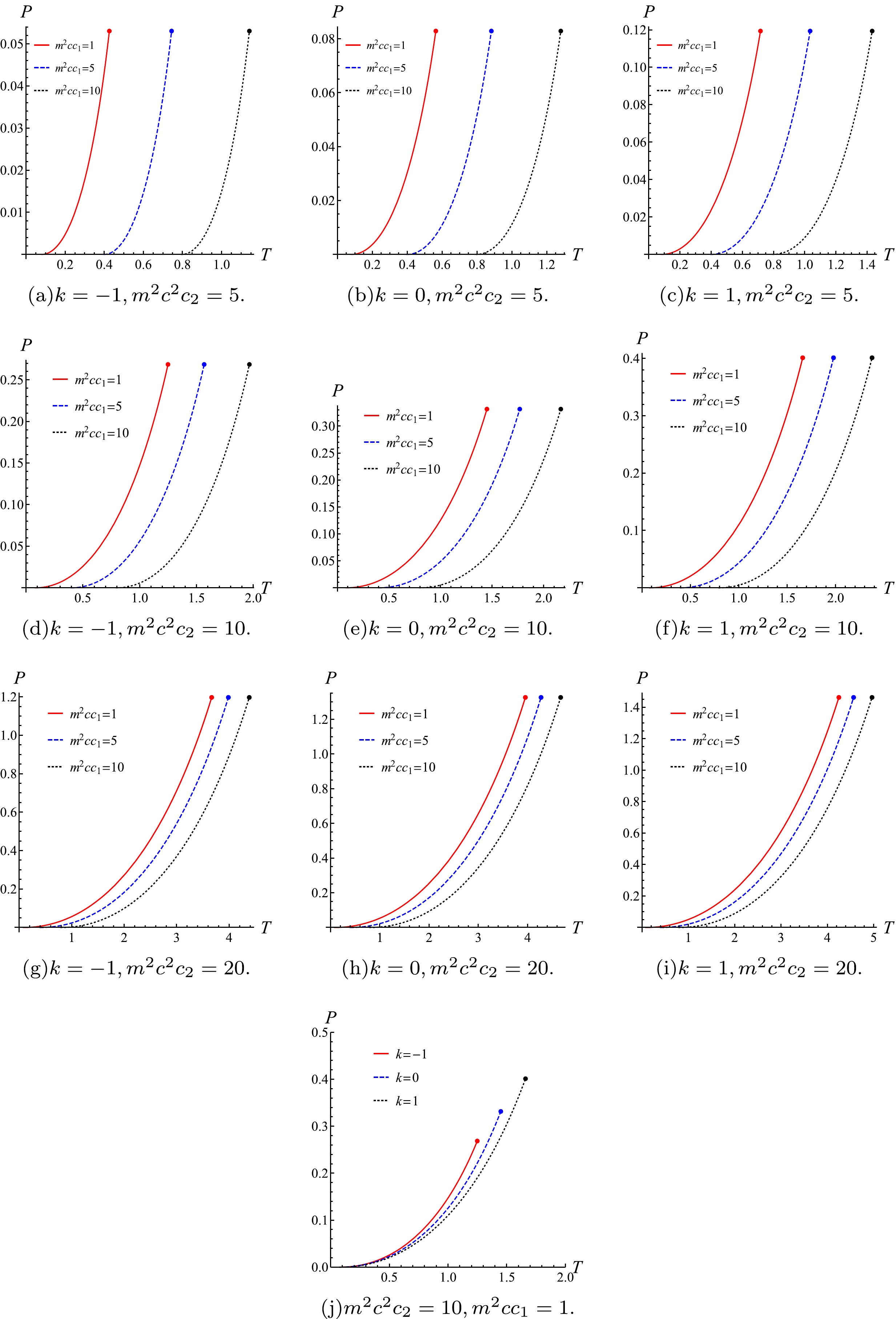
(33) From the above equations, we can see that P and T can be obtained for a given value of x. The coexistent curve of
$ P-T $ with different parameters are presented in Fig. 5.Figure 5 shows the influence of parameters on the coexistent curve when the black hole undergoes a first-order phase transition. The end of the coexistent curve is the second-order phase transition point (i.e., the critical point). Therefore, the curve also shows the influence of different parameters on phase transition.
The slope of the coexistent curve of
$ P-T $ is given by$ \begin{aligned}[b]\frac{{\rm d} P}{{\rm d} T}=&\frac{3 x\left(1-x^{2}\right)\left(k+m^{2} c^{2} c_{2}\right)^{1 / 2}}{4 q\left(1+4 x+x^{2}\right)^{1 / 2}\left(1-x^{3}\right)}\\=&\frac{3 x(1+x)\left(k+m^{2} c^{2} c_{2}\right)^{1 / 2}}{4 q\left(1+4 x+x^{2}\right)^{1 / 2}\left(1+x+x^{2}\right)}.\nonumber\end{aligned} $

In an ordinary thermodynamic system, the slope of the coexistent curve of
$ P-T $ is given by Eq. (28). So the latent heat of phase transition for the topological AdS black hole in massive gravity can be written as$\begin{aligned}[b] L=&\frac{q^{2} x\left(1-x^{2}\right)\left(1+4 x+x^{2}\right)}{4\left(k+m^{2} c^{2} c_{2}\right)}\\&\times\left[\frac{4(1+x) x\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{q\left(1+4 x+x^{2}\right)^{3 / 2}}+m^{2} c c_{1}\right], \end{aligned}$

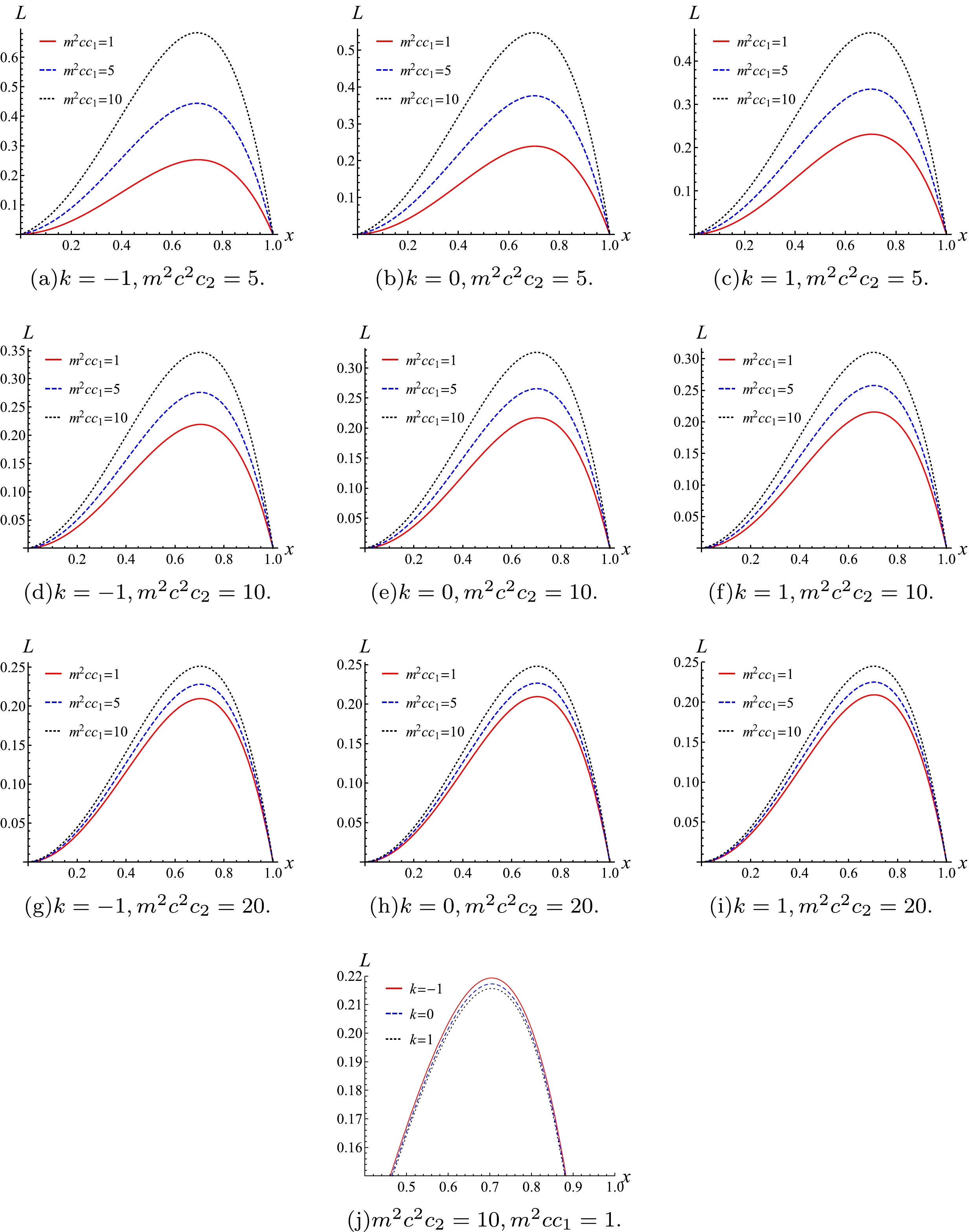
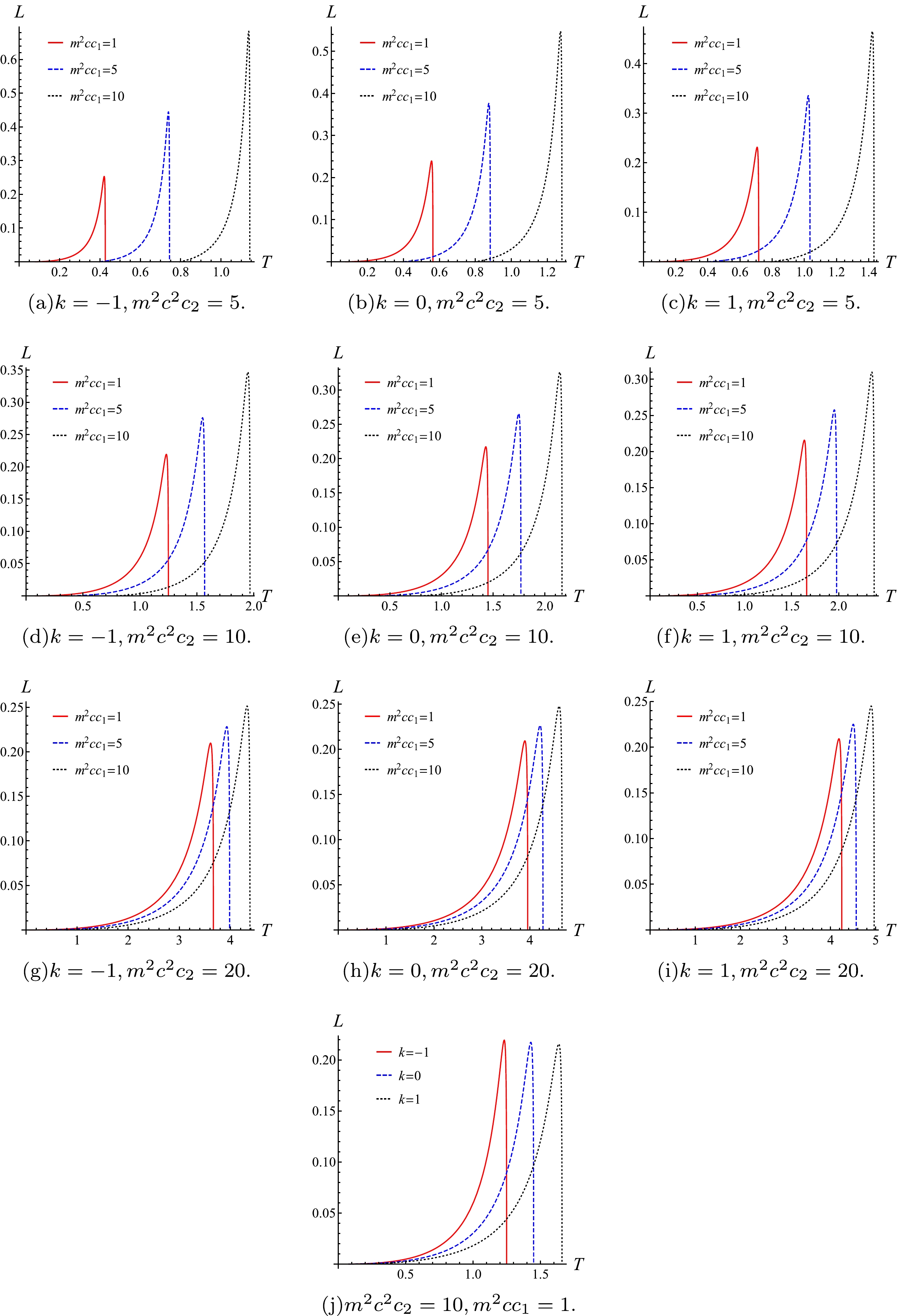
(34) which is a function of x. In order to present the influence of different parameters on the latent heat of phase transition, we plot the
$ L-x $ diagram in Fig. 6.For the topological AdS black hole in massive gravity, we have from Eq. (34):
$ \frac{{\rm d} L}{{\rm d} T}=\frac{{\rm d} L}{{\rm d} x} \frac{{\rm d} x}{{\rm d} T}=\frac{{\rm d} L}{{\rm d} x} \frac{\pi q\left(1+4 x+x^{2}\right)^{5 / 2}}{\left(1-x^{3}\right)\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}} $

(35) with
$ \begin{aligned}[b] \frac{{\rm d} L}{{\rm d} x}=\frac{q^{2}\left(1+8 x-16 x^{3}-5 x^{4}\right)}{4\left(k+m^{2} c^{2} c_{2}\right)} \end{aligned} $

$ \begin{aligned}[b] &\times\left[\frac{4(1+x) x\left(k+m^{2} c^{2} c_{2}\right)^{3 / 2}}{q\left(1+4 x+x^{2}\right)^{3 / 2}}+m^{2} c c_{1}\right] \\& +\frac{q x\left(1-x^{2}\right)\left(1-x^{3}\right)\left(k+m^{2} c^{2} c_{2}\right)^{1 / 2}}{\left(1+4 x+x^{2}\right)^{3 / 2}}, \end{aligned} $

(36) whose pictures are shown in Fig. 7.
Figure 7 shows that the phase transition latent heat changes has an extreme value with increasing temperature and the different parameters of the black hole influence on this extreme value, but the extreme value has nothing to do with the constant k that characterizes the geometric property of the black hole horizon hypersurface.
-
A growing number of research efforts show that black holes have thermodynamic properties that are similar to that of an ordinary thermodynamical system. To more clearly understand the thermodynamic properties of black holes, it is necessary to have a reasonable explanation for the origin of black hole's entropy from a micro perspective, although a lot of work has been done on this topic [61–77]. However, the microstructures of a black hole is still unclear. In order to make sense of physical properties at the critical point, it is required to
$ \left(k+m^{2} c^{2} c_{2}\right)>0 $ . When taking$ (T, P, V),\; (P, T, S),\; \left(T, C_{1},\; c_{1}\right) $ , and$ \left(T, C_{2}, c_{2}\right) $ as state functions, the conditions at the second-order and the first-order phase transition points, which all satisfy Eqs. (13), (19), (24), and (29), are the same. Therefore, for the phase transition of the topological AdS black hole in massive gravity, we can choose any set of conjugate variables$ P\thicksim V,\; T\thicksim S,\; C_1\thicksim c_1 $ , and$ C_2\thicksim c_2 $ according to different conditions. These results indicate that, when the temperature is given, the phase transition of this system is independent of the conjugate variable, and from a micro persective, it is the change of the order for the black hole molecules. According to the reference [68], the black hole molecule itself carries the microscopic freedom degree of black hole entropy.From Figs. 1, 2, 3, and 4, we know that when the temperature is given, the black hole can be in three different states. And the phase transition is determined by the electric potential at the black hole's horizon for the given temperature and pressure. The system at point A stands for a high potential, low symmetry of the effective molecules, and high degree of order state. While at point B, it becomes a low potential, high symmetry of the effective molecules, and low degree of order state. For any point between A and B, it is a medium potential, mixed orderly, and disorderly sate. This is analogous to the electromagnetic polarization in electromagnetics. When a media is under a strong electrical field, the molecules in the media are translated, polarized, and reorientated. As a result, they are orderly arranged. These similarities indicate that the black hole molecules have a tendency to align after being affected by the electric field, and they are more orderly than without the electric field. In order to illustrate this issue, with the help of the electric potential concept we can define an order parameter, which is the difference between the high potential and low potential
$ \phi(T)=\frac{\phi_{1}-\phi_{2}}{\phi_{c}}=\frac{\sqrt{6}(1-x)}{f_{Q}^{1 / 2}(x) x}. $

(37) Here
$ \phi_1 $ and$ \phi_2 $ stands for the potentials of two coexistent phases$ \phi_{2}=\frac{q}{r_{2}}=\frac{\left(k+m^{2} c^{2} c_{2}\right)^{1 / 2}}{f_{Q}^{1 / 2}(x)}, \; \; \; \; \; \; \phi_{1}=\frac{q}{r_{1}}=\frac{\left(k+m^{2} c^{2} c_{2}\right)^{1 / 2}}{x f_{Q}^{1 / 2}(x)}, $

(38) where x is given by Eq. (16). We take the order parameter as
$ \phi(T) $ , and plot the$ \phi(T)-\chi $ curve in Fig. 8 when$ 1 / \sqrt{2} \leq \chi \leq 1 $ .As shown in Fig. 8, we know that the order parameter has a non-zero value when the system passes through the first-order phase transition of high potential and low potential, the value decreases with increasing temperature. When the temperature takes the critical temperature, that is
$ x \rightarrow 1 $ , this value is zero. Figure 6 shows that the phase transition heat of a black hole is zero at the critical point. It indicates that when the black hole is below the critical temperature, the high-potential and low-potential black holes have different microstructures. However, the black hole microstructure tends to be consistent if the black hole temperature is above the critical point. -
In this manuscript, we have presented the properties of phase transition for the five-dimensional AdS black hole in massive gravity through Maxwell's equal-area law, Gibbs free energy, and Clapeyron equation. And by introducing a new order parameter, we also discussed the maybe microstructure of this system.
Firstly, considering topological AdS black hole in massive gravity as a thermodynamic system, the system's equation of state does not satisfy the equilibrium and stability requirements in some regions. When analyzing the phase transition of the system, we found there exists a certain region in which the system does not meet the equilibrium and stability conditions. As shown in Fig. 1, when the temperature is lower than the critical temperature in the
$ P\sim V $ phase diagram, a part of it was replaced by an isotherm-isobaric straight line. This straight line means that the system has the same temperature and pressure in this interval, but its volume changed at different points, i.e., the black hole horizon radius has changed. On the other hand, the potential of AdS black hole in massive gravity is different on the straight line. Therefore, this interval is the one of the high-potential and low-potential coexistence. The phase transition of the system, which occurs at the phase transition point$ r_1 $ and point$ r_2 $ , is a first-order phase transition based on the Ehrenfest classification.Since the topological AdS black hole in massive gravity is a multi-parameter thermodynamic system, there are many adoptions of the independent conjugate state function for the five-dimensional topological AdS black hole. At the first-order phase transition point, this system should meet the thermal equilibrium condition
$ T_{\alpha}=T_{\beta} $ , the mechanical equilibrium condition$ P_{\alpha}=P_{\beta} $ , and the phase transition equilibrium condition$ G_{\alpha}=G_{\beta} $ , which have nothing to do with the adoption of independent conjugate state functions. Through the discussion in the third part, we also proved that the second-order and first-order phase transition points were the same for different adoption of independent conjugate state functions ($P\sim V $ ,$T\sim S $ ,$ C_{1}\sim c_{1}, $ and$ C_2\sim c_2 $ ). Furthermore, for an ordinary thermodynamic system, Clapeyron equation is in good agreement with the experimental results, providing a direct experimental verification for the correctness of the thermodynamics. On this issue, we have shown the coexistent curve of$ P\sim T $ , its slope, and the latent heat of the first-order phase transition. The provided conditions can help seek ordinary thermodynamic systems similar to the thermodynamic properties of black holes, and provide a theoretical basis for various experimental studies of black holes.Due to the similarity between the topological AdS black holes in massive gravity and the VdW system, it can be assumed that an AdS black hole may have a similar microstructure. From a microscopic point of view, the VdW fluid is composed of fluid molecules, and it can be assumed that black holes are also composed of black hole molecules, which themselves carry the microscopic degree of freedom for black hole entropy. Since the phase transition of this system is between the high-potential and low-potential black holes, we introduced a new order parameter associated with the electric potential and discussed the microstructure of five-dimensional topological AdS black holes in massive gravity from a different perspective. These conclusions provide an insight for exploring the microstructure of black holes. In particular, the further study of black hole microstructure will help with the understanding of the basic properties of the gravity of black holes and provide important value for the establishment of quantum gravity.
Phase equilibrium and microstructure of topological AdS black holes in massive gravity
- Received Date: 2022-03-08
- Available Online: 2022-08-15
Abstract: In order to clearly understand the gravitational theory through the thermal properties of the black hole, it is important to further investigate the first-order phase transition of black holes. In this paper, we adopt different conjugate variables (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: