-
The normally deformed (ND) and super deformed (SD) states of
$ ^{36} $ Ar have been the research topics of several theoretical models [1, 2] since the discovery of the SD rotational band [3]. In recent years, properties of the hypernuclear system,$ ^{37}_{\; {\Lambda}} $ Ar, have often been discussed [4–7], although this hypernuclear system has not been experimentally observed. The most popular topics associated with$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar are the SD states; the ground states are ND. For the$ {\Lambda} $ hyperon occupying the s-shell orbital, the relativistic mean field (RMF) model [4] and beyond-RMF calculations [7] indicate that the SD state of$ ^{37}_{\; {\Lambda}} $ Ar gives a larger$ {\Lambda} $ separation energy,$ S_{\Lambda} $ , than the ground state. However, antisymmetrized molecular dynamics (AMD) [5] and the Skyrme-Hartree-Fock (SHF) model [6] show that the$ S_{\Lambda} $ of the SD state is smaller than that of the ground state. Compared to AMD [5] and the beyond-RMF calculations [7], the SHF model [6] merely provides mean-field results, which breaks rotational symmetry and thus hinders further uses of the rotational bands and the transition probabilities observed in laboratories. Since 2015, the beyond-mean-field SHF model for$ {\Lambda} $ hypernuclei has gradually improved [8–12]. The angular momentum projection (AMP) technique is used to restore rotational symmetry, and the generator coordinate method (GCM) is employed to deal with shape mixing. Therefore, the beyond-mean-field SHF model is used to research the rotational bands corresponding to the configuration$ ^{36} $ Ar$ \otimes $ s $ _{\Lambda} $ , which is the first of the three motivations of this paper.Beside the s-shell orbital, the
$ {\Lambda} $ hyperon may be excited onto the p-shell orbitals, and such a$ {\Lambda} $ hyperon coupled with an ND or SD nuclear core can provide various configurations. These configurations correspond to low-lying energy levels with negative parity, and the beyond-mean-field SHF model can be used to predict them. For example, in a previous study [10], the rotational energy levels corresponding to the configurations$ ^{8} $ Be$ \otimes $ p$ _{{\Lambda}}^{\parallel} $ and$ ^{8} $ Be$ \otimes $ p$ _{{\Lambda}}^{\perp} $ [13, 14] were precisely reproduced. Therefore, the second motivation of this paper is to obtain predictions for configurations such as$ ^{36} $ Ar$ \otimes $ p$ _{\Lambda} $ , which will help identify the negative-parity energy levels of$ ^{37}_{\; {\Lambda}} $ Ar in future experiments.For several typical hypernuclear systems such as
$ ^{9}_{{\Lambda}} $ Be,$ ^{13}_{\ \,{\Lambda}} $ C,$ ^{21}_{\ {\Lambda}} $ Ne, and$ ^{25}_{\; {\Lambda}} $ Mg,$ {\Lambda} $ hyperons on the s-shell orbital or excited onto the p-shell orbitals have been studied using various theoretical models [10–12,15–18] in recent years. However, the sd-shell$ {\Lambda} $ hyperon in these hypernuclei does not provide a bound state because they are too light to bind such a$ {\Lambda} $ hyperon. Some (K$ ^{-} $ ,$ \rm{\pi}^{-} $ ) and ($ \rm{\pi}^{+} $ , K$ ^{+} $ ) reactions [19–21] reveal that the configuration$ ^{39} $ Ca$\otimes {sd}_{\Lambda}$ gives bound energy levels (that is, energy levels below the separation threshold of$ ^{39} $ Ca+$ {\Lambda} $ ), whereas$ ^{31} $ S$\otimes {sd}_{\Lambda}$ gives unbound energy levels.$ ^{37}_{\; {\Lambda}} $ Ar is between$ ^{32}_{{\Lambda}} $ S and$ ^{40}_{{\Lambda}} $ Ca in the hypernuclear chart, which is probably to provide bound states for configurations such as$ ^{36} $ Ar$ \otimes $ sd$ _{\Lambda} $ . Hence, the third motivation of this paper is to theoretically investigate the existence of bound states for$ ^{36} $ Ar$ \otimes $ sd$ _{\Lambda} $ and obtain the corresponding configurations with Nilsson quantum numbers.In this paper, a beyond-mean-field SHF model that considers AMP techniques and the GCM is employed to study the low-lying energy levels corresponding to various configurations of
$ ^{37}_{\; {\Lambda}} $ Ar. These configurations include an ND or SD nuclear core coupled to a$ {\Lambda} $ hyperon onto the orbitals of s, p, or sd shells. This paper is organized as follows. In Sec. II, the formalism of the beyond-mean-field calculation is introduced. Sec. III presents the results and discussions. In Sec. IV, we draw conclusions about the study. -
In a hypernuclear system, the physical quantities we are most concerned with are its eigenstates, eigenenergies, and transition rates. To obtain these physical quantities, the beyond-mean-field SHF model begins with a mean-field state of the
$ {\Lambda} $ hypernucleus in the intrinsic frame of reference [22]$ \begin{equation} \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle = \big| {\Phi^N (\beta)} \big\rangle \otimes \big| \Phi^{{\Lambda}} \big\rangle \:, \end{equation} $

(1) where
$ \big| {\Phi^N (\beta)} \big\rangle $ represents a nuclear core with the deformation parameter β, and$ \big| \Phi^{{\Lambda}} \big\rangle $ denotes the single-particle wave function of a$ {\Lambda} $ hyperon.A general eigenstate of the
$ {\Lambda} $ hypernuclear system is given by linear superposition:$ \begin{eqnarray} \big| \Psi^{JM}_{\alpha}\big\rangle = \sum_\beta F^J_{\alpha}(\beta) \hat{P}^J_{MK} \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle \:, \end{eqnarray} $

(2) where β plays the role of the generator coordinate, and the AMP operator,
$ \hat{P}^J_{MK} $ , restores the rotational symmetry of the system. The mean-field state in the intrinsic frame of reference,$ \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle $ , is derived by a constrained SHF model [6], and a density-dependent delta interaction (DDDI) [23] is considered for the nucleons as$ \begin{equation} G( {r})=V_0\left[1-\frac{\rho( {r})}{\rho_0}\right]. \end{equation} $

(3) The weight function
$ F^J_{\alpha}(\beta) $ in Eq. (2) and the eigenenergies are determined by the Hill-Wheeler-Griffin (HWG) equation [24],$ \begin{equation} \sum_{\beta'} \Big[ H'^J_{KK}(\beta,\beta') - E^J_{\alpha} N^J_{KK}(\beta,\beta') \Big] F^J_{\alpha}(\beta') = 0 \:, \end{equation} $

(4) in which the Hamiltonian and norm elements are given by
$ \begin{eqnarray} H'^J_{KK}(\beta,\beta') = \big\langle {\Phi^{(N{\Lambda})} }(\beta') \big| \hat{H'}\hat{P}^J_{KK} \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle \:, \end{eqnarray} $

(5) $ \begin{eqnarray} N^J_{KK}(\beta,\beta') = \big\langle {\Phi^{(N{\Lambda})} }(\beta') \big| \hat{P}^J_{KK} \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle \:. \end{eqnarray} $

(6) The corrected Hamiltonians
$ \hat{H'} $ is$ \begin{equation} \hat{H'} = \hat{H} - \lambda_p(\hat{N}_p-Z)-\lambda_n(\hat{N}_n-N) \:, \end{equation} $

(7) where the final two terms on the right-hand side account for the fact that the projected wave function does not provide the correct number of particles on average [25–27], and
$ \hat{H} $ is given by the energy density functional (EDF) in Ref. [28].For a certain configuration determined by the intrinsic state
$ \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle $ , the projected energy is derived as$ \begin{equation} E(\beta,J,K)=\frac{H'^J_{KK}(\beta,\beta)}{N^J_{KK}(\beta,\beta)}. \end{equation} $

(8) Given two general eigenstates,
$ |\alpha;J\rangle $ and$ |\alpha';J'\rangle $ , the reduced$ E2 $ transition rate between them is derived as$ \begin{equation} B(E2,J{\alpha} \to J'{\alpha}') = \frac{1}{2J+1} \left|\langle {\alpha}';J' || \hat{Q}_2 || {\alpha};J \rangle\right|^2 \:, \end{equation} $

(9) where
$ \begin{aligned}[b] \langle {{\alpha}'};J' || \hat{Q}_2 || {{\alpha}};J \rangle = & \sqrt{2J'+1} \sum_{M\mu \beta\beta'} {F^{J'}_{{\alpha}'}}^* (\beta') F^J_{\alpha}(\beta) \\&\times C^{J'K'}_{J M 2\mu} \big\langle {\Phi^{(N{\Lambda})} }(\beta') \big| \hat{Q}_{2\mu}\hat{P}^J_{MK} \big| {\Phi^{(N{\Lambda})} }(\beta) \big\rangle \:. \end{aligned} $

(10) In the above equation,
$ \hat{Q}_{2\mu} = r^2Y_{2\mu}(\varphi,\theta) $ is the electric quadrupole operator [29], and$ C^{J'K'}_{JM2\mu} $ denotes the Clebsh-Gordon coefficients.Parameters: In this paper, the SLy4 force is used for the
$ NN $ interaction, and the strength of the pairing force is$ V_0=-410 $ MeV fm$ ^3 $ for both protons and neutrons [30], with a smooth pairing energy cutoff of 5 MeV around the Fermi level [31, 32]. For the$ N{\Lambda} $ interaction, we use the SLL4 force [28], which offers the best fit for the$ {\Lambda} $ separation energy in the spherical SHF model [28].Notations: Single-particle orbitals of the
$ {\Lambda} $ hyperon are denoted by Nilsson quantum numbers$ [Nn_3m_l]\Omega^{\pi} $ ; the same notation is also adopted in Ref. [4]. Then, a certain configuration of the$ {\Lambda} $ hypernuclear system is given as$ ^{A-1} $ Z$ \otimes{\Lambda}[Nn_3m_l]\Omega^{\pi} $ , in which$ ^{A-1} $ Z is the nuclear core, and$ {\Lambda}[Nn_3m_l]\Omega^{\pi} $ represents a$ {\Lambda} $ hyperon occupying the orbital$ [Nn_3m_l]\Omega^{\pi} $ . To emphasize the deformation,$ ^{36} $ Ar$ ^{{\rm{N}}} $ and$ ^{36} $ Ar$ ^{{\rm{S}}} $ are used to represent the ND and SD nuclear cores of$ ^{37}_{\; {\Lambda}} $ Ar, respectively. For example, the configuration$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ denotes an SD nuclear state of$ ^{36} $ Ar coupled with a$ {\Lambda} $ hyperon occupying the orbital$ {\Lambda} $ [110]$ \frac{1}{2}^{-} $ .Model space: Because intrinsic wave functions are kept axially symmetric, the quadrupole deformation parameter β of the nuclear core is the exclusive generator coordinate. If the
$ {\Lambda} $ orbital is specified, the range of β and the number of basis functions determine the model space jointly. In this paper, β is between$ -1.4 $ and$ 2.8 $ , and 90 basis functions are evenly spaced over this range for both$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar. -
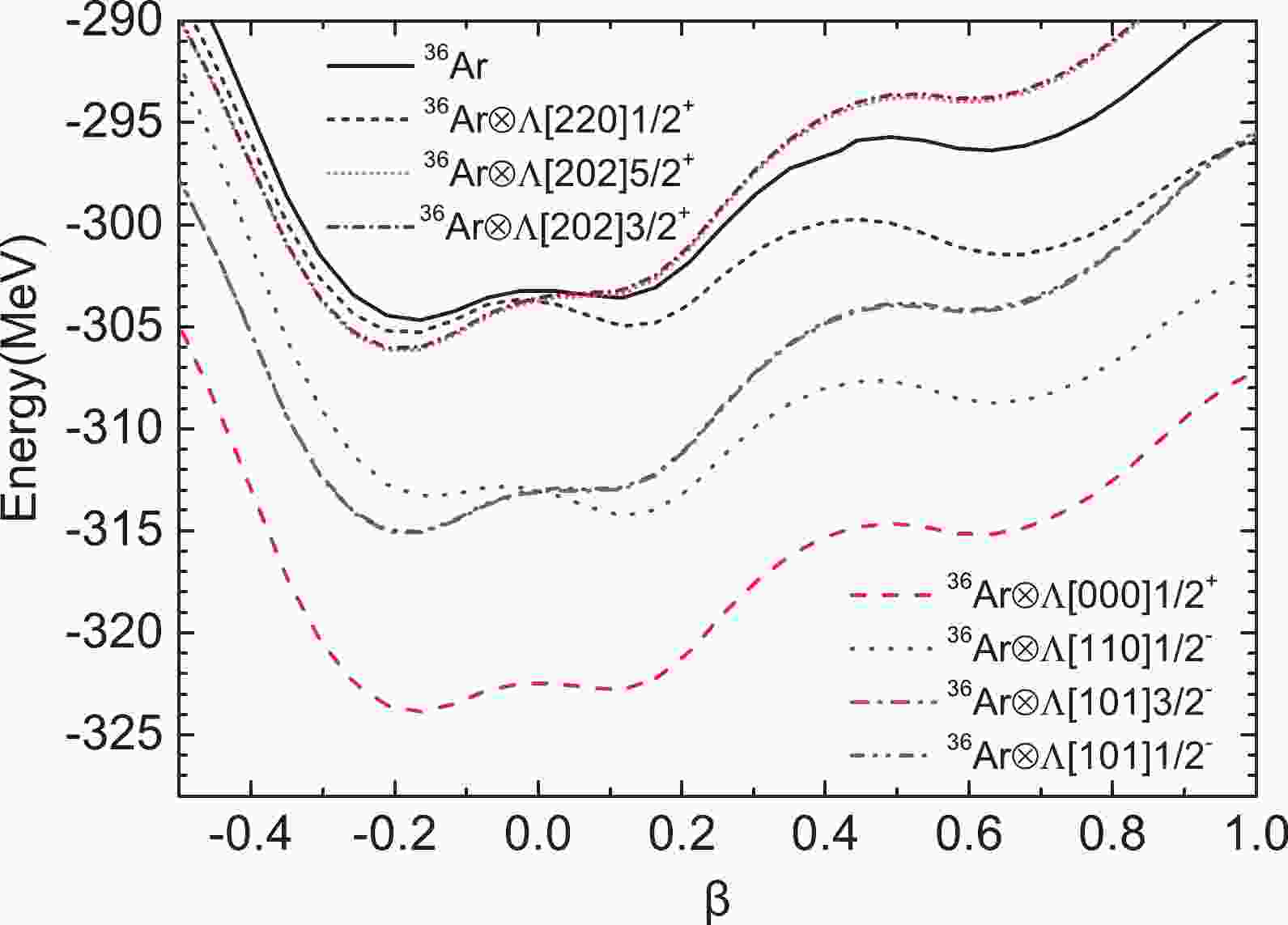
The potential energy surfaces (PESs) of
$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar derived using the mean-field calculation are shown in Fig. 1, and we can see that there are three energy minima for$ ^{36} $ Ar. Two of these minima, located at$ \beta=-0.16 $ and$ \beta=0.12 $ , both give ND configurations, whereas the third, located at$ \beta=0.63 $ , exhibits an SD prolate shape. For$ ^{37}_{\; {\Lambda}} $ Ar, the addition of one$ {\Lambda} $ hyperon onto the orbitals of thes, p, or sd shells causes various impurity effects. In our current mean-field calculation, the hyperon $ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ makes$ |\beta| $ of the three energy minima slightly smaller, which is already known from early research [33]. Such a reduction in deformation is not clear in Fig. 1 because the nuclear core$ ^{36} $ Ar is sufficiently heavy against the$ N{\Lambda} $ attraction. For the p-shell$ {\Lambda} $ hyperon, Fig. 1 clearly shows that$ {\Lambda} $ [110]$ \frac{1}{2}^{-} $ in$ ^{37}_{\; {\Lambda}} $ Ar makes the prolate minima significantly deeper and nearly eliminates the oblate minimum, whereas$ {\Lambda} $ [101]$ \frac{3}{2}^{-} $ and$ {\Lambda} $ [101]$ \frac{1}{2}^{-} $ make the prolate energy minima shallower and enhance the oblate minimum. These opposite phenomena are due to the density distributions of the p-shell$ {\Lambda} $ orbitals. Fig. 2 shows the density distributions of several p-shell and sd-shell$ {\Lambda} $ s. It must be emphasized that the density distributions of$ {\Lambda} $ [101]$ \frac{3}{2}^{-} $ and$ {\Lambda} $ [101]$ \frac{1}{2}^{-} $ are nearly identical and share the same contour map in Fig. 2, and$ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ and$ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ do the same. In the top-right panel of Fig. 2, we can see that$ {\Lambda} $ [110]$ \frac{1}{2}^{-} $ is prolately distributed; thus, its coupling to a prolate nuclear core leads to a lower binding energy. However, the top-left panel of Fig. 2 shows that$ {\Lambda} $ [101]$ \frac{3}{2}^{-} $ and$ {\Lambda} $ [101]$ \frac{1}{2}^{-} $ are oblately distributed; hence, they prefer oblate nuclear cores. For the sd-shell$ {\Lambda} $ hyperon, Fig. 1 shows the PESs of configurations$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [220]$ \frac{1}{2}^{+} $ ,$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ , and$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ because only these three configurations give bound states, the properties of which will be discussed in detail in the final two paragraphs of this section.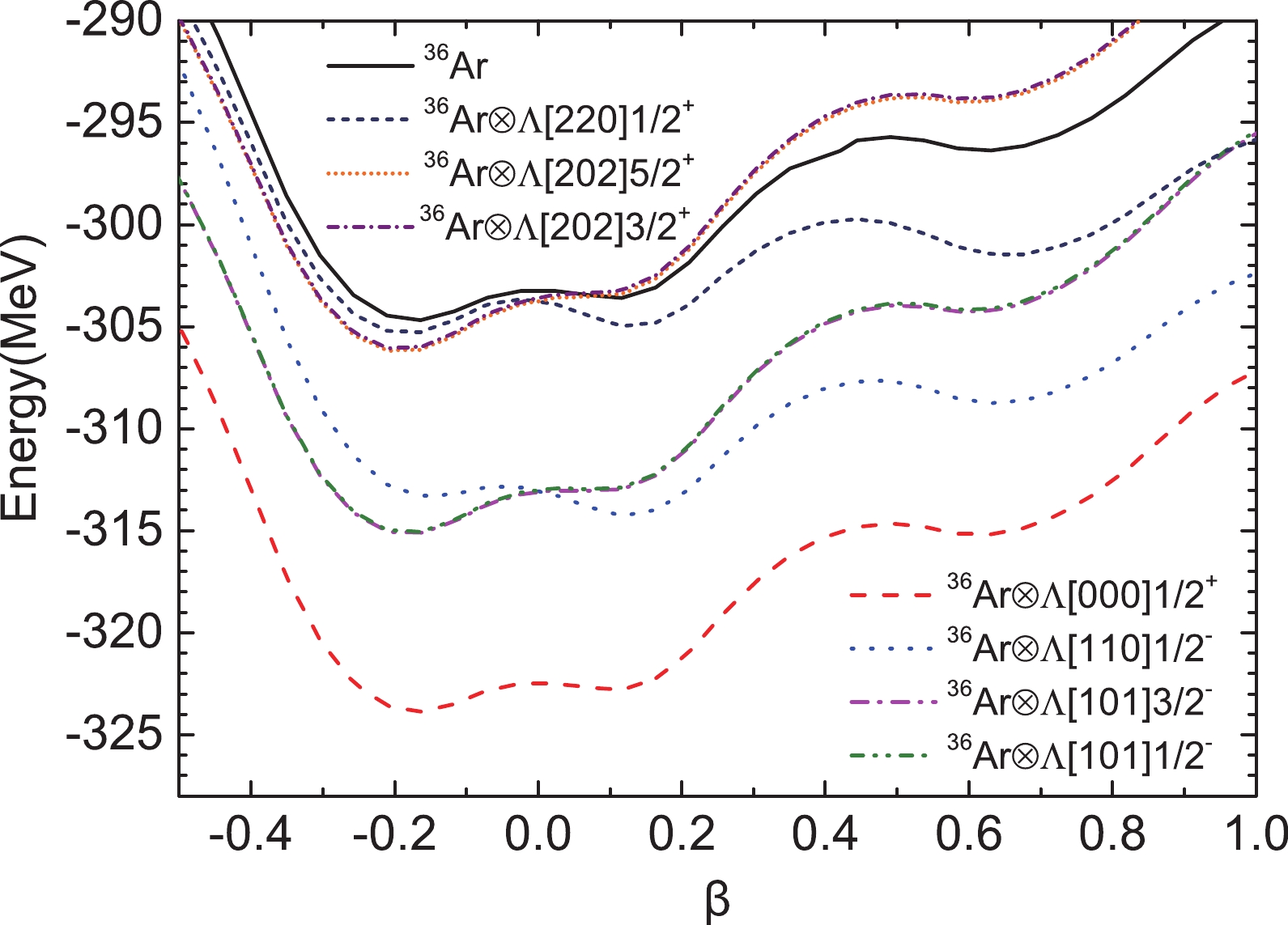
Figure 1. (color online) PESs obtained from the mean-field calculations for certain configurations indicated in the legend. The horizontal axis represents the quadrupole deformation parameter β.
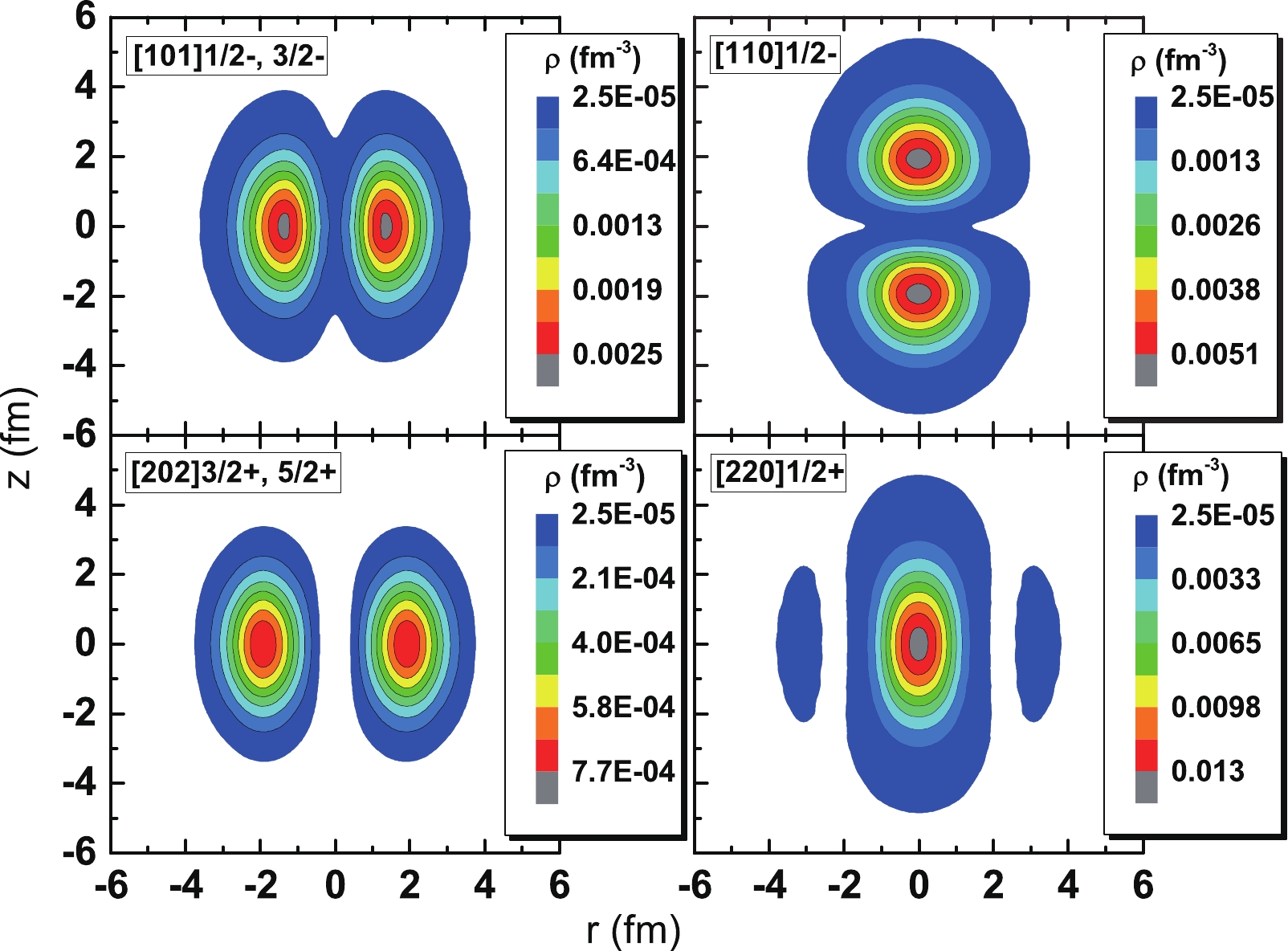
Figure 2. (color online) Density distributions of the
$ {\Lambda} $ hyperon on the orbitals$ {\Lambda} $ [101]$ \frac{3}{2}^{-} $ or$ {\Lambda} $ [101]$ \frac{1}{2}^{-} $ (top-left pannel),$ {\Lambda} $ [110]$ \frac{1}{2}^{-} $ (top-right panel),$ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ or$ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ (bottom-left panel), and$ {\Lambda} $ [220]$ \frac{1}{2}^{+} $ (bottom-right pannel). The deformation parameter β of each corresponding nuclear core is constrained to the average,$ \bar{\beta} $ , of the bandhead given by the GCM calculation.Figure 3 gives the projected PESs,
$ E(\beta,J,K) $ , on each angular momentum J for$ ^{36} $ Ar. In this figure, all the ND and SD energy minima of the$ J^{\pi}=0^{+} $ PES are more obvious than those of the mean-field PES, which is due to the energy gained from the restoration of rotational symmetry. The energy levels derived by the GCM are also given in the same figure, and we can clearly see that there are two rotational bands for the ND states and the SD states of$ ^{36} $ Ar. In this current calculation, the bandhead of the ND band corresponds to the ground state (g.s.), whereas that of the SD band is the 4th$ 0^{+} $ state. The bandheads of the ND and SD bands are located at –308.02 MeV and –300.96 MeV, respectively, which indicate the binding energy of these two states. Figure 3 also shows that the g.s. and SD bands cross at$ J^{\pi}=6^{+} $ , and these calculated results agree with the observed data in Ref. [3]. Besides the ND and SD rotational bands, there are other observed low-lying energy levels such as the 4.4 MeV 2$ ^{+} $ level [3]; however, these levels may involve two-quasi-particle (2-qp) excitations [2]. 2-qp excitations are beyond the basis space of this current model; therefore, only the properties of the g.s. and SD bands are discussed hereafter.
Figure 3. (color online) Projected PESs,
$ E(\beta,J) $ , and the GCM energy levels of$ ^{36} $ Ar. The angular momentum and parity for each projected PES are given in the legend, and the mean-field PES labeled by 'MF' is also shown for comparison. The solid bullets and horizontal bars indicate the GCM energy levels, which are plotted at their average deformation$ \bar{\beta} $ .The projected PESs of
$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ are given in Fig. 4, and the GCM energy levels of the g.s. and SD bands are also shown in the same figure. The addition of$ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ turns the$ J^{\pi}=0^{+} $ states of$ ^{36} $ Ar into those with$ J^{\pi}=\frac{1}{2}^{+} $ and turns the other states into spin doublets. The band-head energies of the g.s and SD bands are –327.22 MeV and –319.79 MeV, respectively. Therefore, we can deduce that the$ {\Lambda} $ separation energy,$ S_{\Lambda} $ , for the ground state is 19.20 MeV, whereas$ S_{\Lambda} $ for the$ J^{\pi}=\frac{1}{2}^{+} $ SD state is 18.83 MeV, which indicates that$ S_{\Lambda} $ of the SD state is smaller than that of the ground state. This is in agreement with the mean-field SHF calculation using the SKI4 parameters [6] but conflicts with the RMF calculations [4, 7]. This conflict stems from the fact that the RMF calculations give an SD state with a localized density, which leads to a larger overlap between$ {\Lambda} $ and the SD nuclear core. This does not occur in the SHF calculation.
Figure 4. (color online) Same as Fig. 3, but for
$ ^{37}_{{\Lambda}{\rm s}} $ Ar. The notation${\Lambda}{ s}$ denotes a$ {\Lambda} $ hyperon on the s-shell orbital, that is,$ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ , and only the GCM energy levels of the g.s. and SD bands are preserved for simplification.Figures 5 and 6 give the collective wave functions
$ g_{\alpha}^{J}(\beta) $ of the ND-band and SD-band states for$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar, respectively. These two figures reproduce the observed features of the ND and SD bands qualitatively. For each state of the ND band, it is shown that the maximum of$ g_{\alpha}^{J}(\beta) $ corresponds to β within the ND region; for the SD-band states, all the collective wave functions reach their maxima at$ \beta\approx0.65 $ , which indicates an SD shape. It is also shown that, compared to those of$ ^{36} $ Ar, the s-shell$ {\Lambda} $ slightly pulls the$ g_{\alpha}^{J}(\beta) $ of the hypernuclear states in$ ^{37}_{\; {\Lambda}} $ Ar toward the spherical shape, which leads to a reduction in deformation.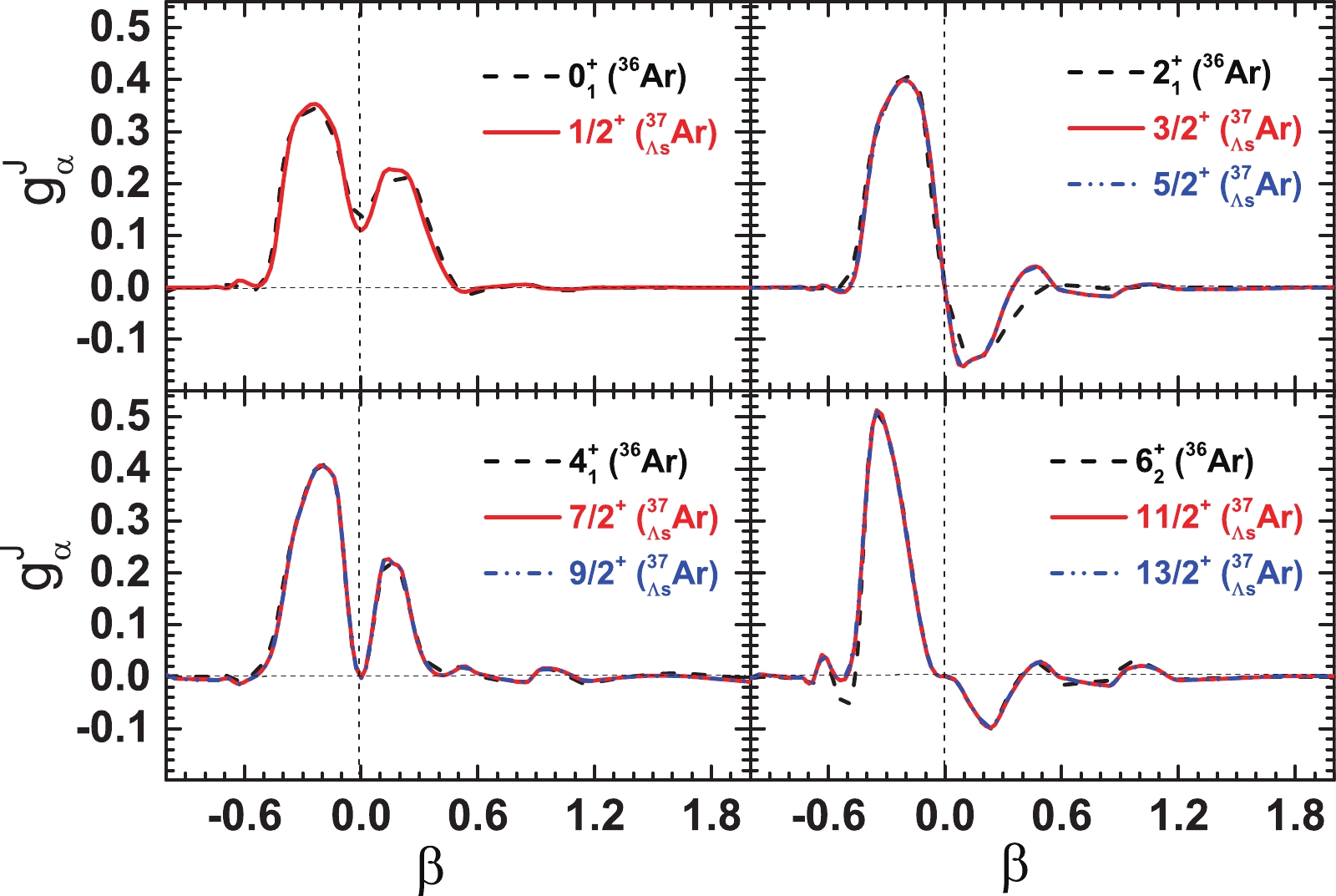
Figure 5. (color online) Collective wave functions
$ g_{\alpha}^{J}(\beta) $ for ND-band states in$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar. The angular momenta, J, are shown in the legend of each panel.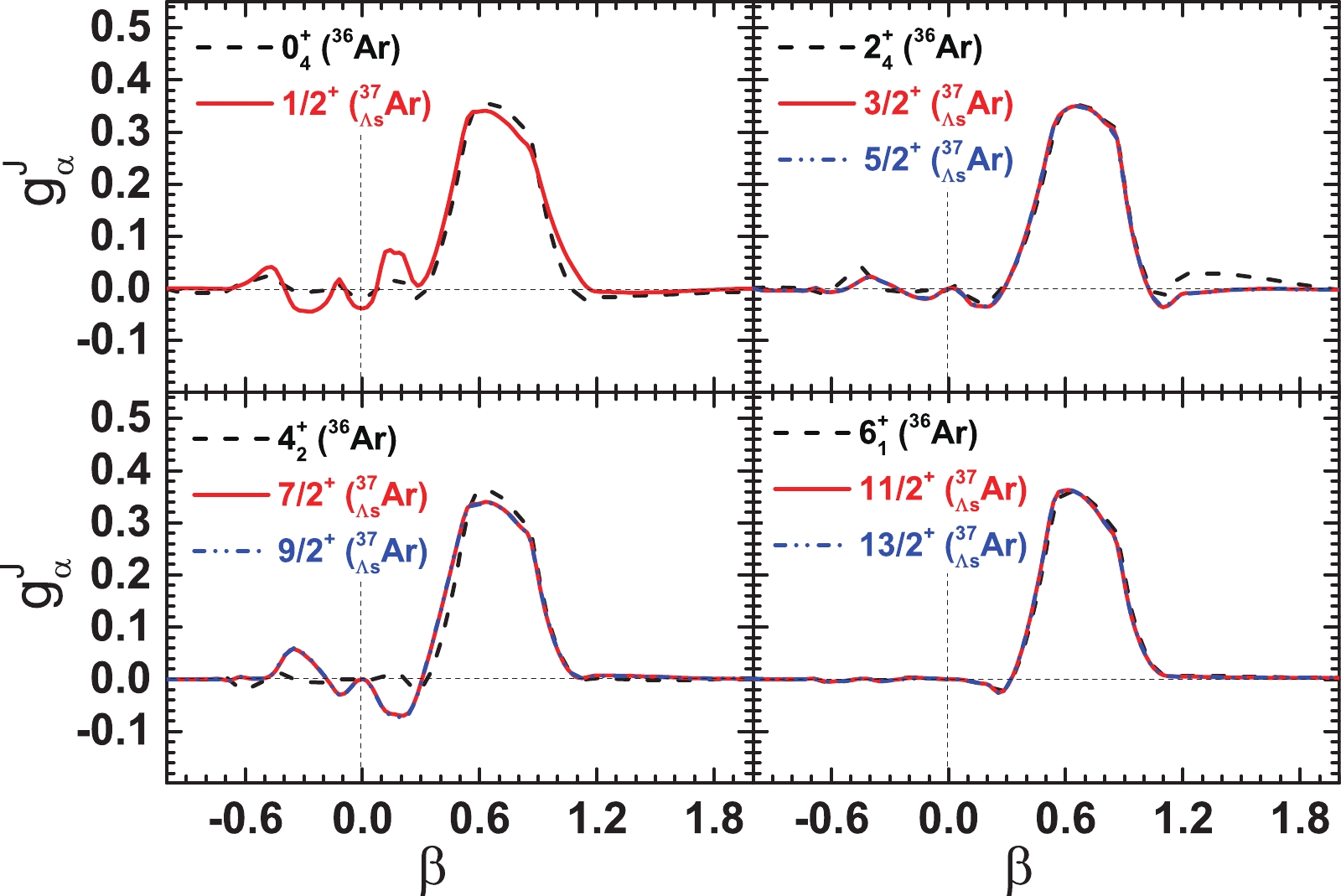
Figure 6. (color online) Same as Fig. 5, but for the SD-band states in
$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar.To discuss the reduction in deformation more comprehensively, the g.s. and SD bands of
$ ^{36} $ Ar and$ ^{37}_{\; {\Lambda}} $ Ar in Figs. 3 and 4 are extracted and shown in Fig. 7, where the observed data [34, 35] on$ ^{36} $ Ar are also given for comparison. Until$ J^{\pi}=4^{+} $ , the current model reproduces the observed g.s. band of$ ^{36} $ Ar very well. Moreover, the intervals between the energy levels of the calculated SD band are in good agreement with the observed data. However, the current model gives a significantly higher$ J^{\pi}=6^{+} $ energy level for the g.s. band than the observed value, and the predicted SD band is nearly 3 MeV greater than the experimental data. This disagreement with the observed data likely stems from the fact that quasi-particle excitations are absent in the GCM space of our model. In Fig. 7, it is also shown that the addition of$ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ shifts the excited energy levels of$ ^{37}_{\; {\Lambda}} $ Ar slightly upward compared to those of$ ^{36} $ Ar because the moment of inertia of the nuclear core is reduced owing to the reduction in defromation. The reduction in deformation is also indicated by the intra-band$ B(E2) $ values of$ ^{37}_{\; {\Lambda}} $ Ar in comparison with those of$ ^{36} $ Ar. As shown in Fig. 7,$ B(E2,\frac{5}{2}^{+}\rightarrow \frac{1}{2}^{+}) $ in the g.s. band of$ ^{37}_{\; {\Lambda}} $ Ar is reduced by$ 9\% $ compared to$ B(E2,2^{+}\rightarrow0^{+}) $ in the g.s. band of$ ^{36} $ Ar, whereas for the SD band of$ ^{37}_{\; {\Lambda}} $ Ar,$ B(E2,\frac{5}{2}^{+}\rightarrow \frac{1}{2}^{+}) $ is reduced by approximately$ 5\% $ . The contrast between the reductions in the$ B(E2) $ values of the g.s. band and those of the SD band indicates that deformation of the SD band is more stable than that of the g.s. band. For the g.s. band, the stability of deformation is also indicated by the PESs given in Fig. 1, which show that there are two ND energy minima and the barrier between them is less than 1.5 MeV. Furthermore, the collective wave functions in Fig. 5 show that the two ND energy minima compete with each other. Finally, it is deduced that shape deformation in the g.s. band is relatively soft and unstable. Note that the beyond-mean-field RMF calculation provides a clearer reduction in the$ B(E2) $ values in$ ^{37}_{{\Lambda}} $ Ar [7]. This is because the relativistic$ N\Lambda $ interaction is stronger than the nonrelativistic interaction, as verified in Refs. [6, 9].Besides
$ {\Lambda} $ [000]$ \frac{1}{2}^{+} $ , the ND and SD nuclear cores, denoted as$ ^{36} $ Ar$ ^{{\rm{N}}} $ and$ ^{36} $ Ar$ ^{{\rm{S}}} $ in this paper, may couple with a$ {\Lambda} $ hyperon on the p- or sd-shell orbitals, and each specific combination corresponds to a certain configuration of$ ^{37}_{\; {\Lambda}} $ Ar. Energy levels corresponding to these configurations, which are lower than the separation threshold of$ ^{36} $ Ar$ +{\Lambda} $ , are given in Fig. 8. It is shown that the configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ ,$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [101]$ \frac{3}{2}^{-} $ , and$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [101]$ \frac{1}{2}^{-} $ give three rotational bands with bandheads at 11.13 MeV, 9.02 MeV, and 8.80 MeV, respectively. Because the ground state of$ ^{36} $ Ar is oblate, the configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [101]$ \frac{3}{2}^{-} $ and$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [101]$ \frac{1}{2}^{-} $ give lower energies than the configuration$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ . However, for the SD state, the configuration$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ gives a rotational band with the bandhead at 13.70 MeV, which is approximately 5 MeV lower than the energy levels given by the configurations$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [101]$ \frac{3}{2}^{-} $ and$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [101]$ \frac{1}{2}^{-} $ . This is because the SD state of$ ^{36} $ Ar is prolately deformed, and its coupling with$ {\Lambda} $ [110]$ \frac{1}{2}^{-} $ produces lower energies. Figure 8 also shows that, although the configurations$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [101]$ \frac{3}{2}^{-} $ and$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [101]$ \frac{1}{2}^{-} $ both give bound states, their energy levels are near the separation threshold of$ ^{36} $ Ar$ +{\Lambda} $ . In our earlier research [10], the beyond-mean-field SHF model successfully reproduced the negative-parity energy levels of$ ^{9}_{{\Lambda}} $ Be, which were denoted as a genuine hypernuclear state and$ ^{9} $ Be-analogue. Furthermore, the same model predicted the negative-parity levels of$ ^{13}_{\ \,{\Lambda}} $ C, which was in good agreement with the observed values [11]. Therefore, the beyond-mean-field SHF model is powerful, and the predicted energy levels in Fig. 8 for the p-shell$ {\Lambda} $ are reliable and can help identify the negative-parity levels of$ ^{37}_{\; {\Lambda}} $ Ar in future experiments.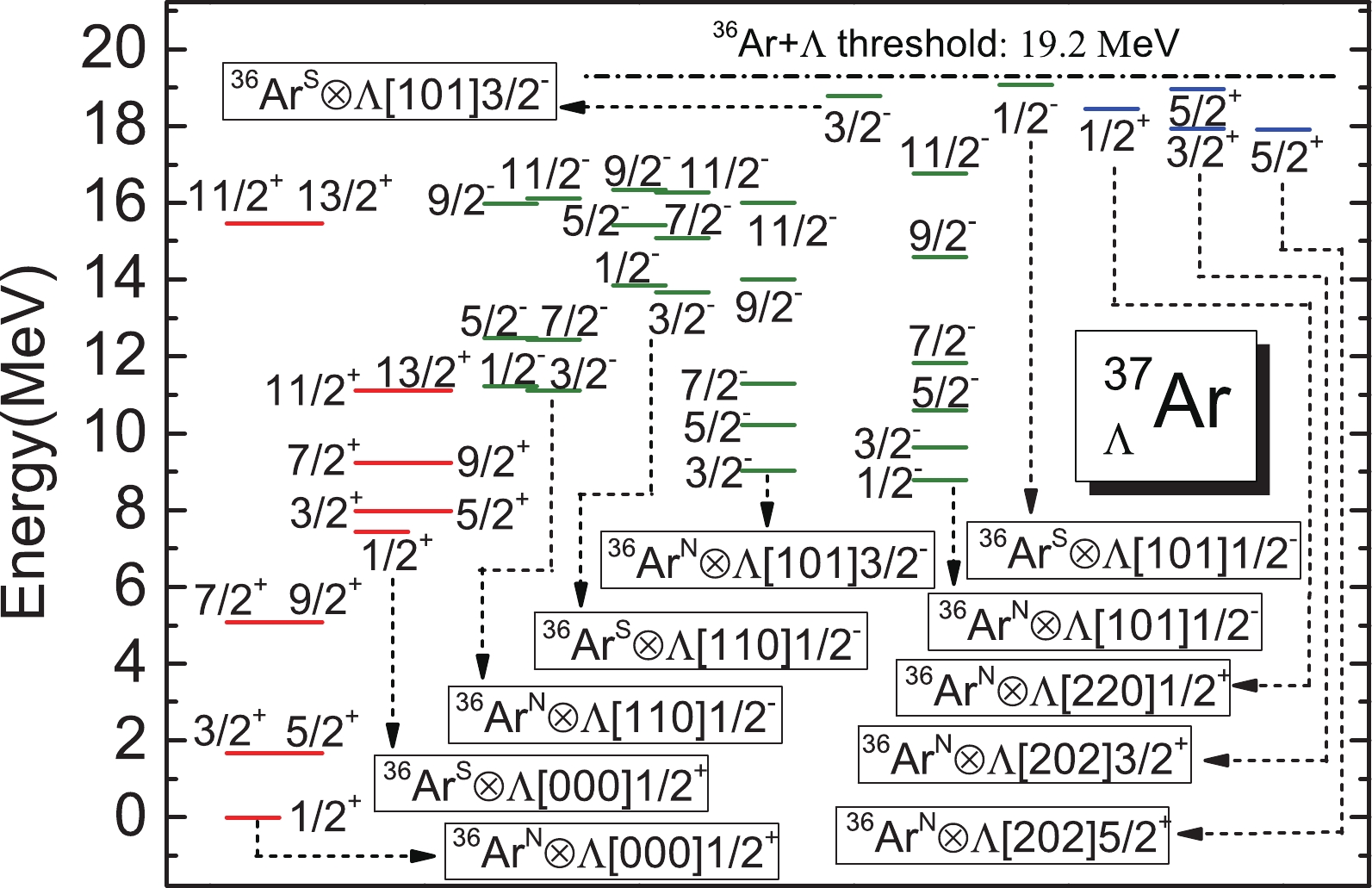
Figure 8. (color online) Comprehensive energy spectra for
$ ^{37}_{\; {\Lambda}} $ Ar. Configurations corresponding to each rotational band are indicated by the solid box and dashed arrow. Energy levels higher than the separation threshold of$ ^{36} $ Ar +$ {\Lambda} $ are neglected for simplification.As deduced in Sec. I,
$ ^{37}_{\; {\Lambda}} $ Ar may provide bound states for configurations such as$ ^{36} $ Ar$ \otimes $ sd$ _{\Lambda} $ . Thus, in future experiments, theoretical predictions for the energy levels of$ ^{36} $ Ar$ \otimes $ sd$ _{{\Lambda}} $ are crucial for identifying the bound state near the separation threshold of$ ^{36} $ Ar$ +{\Lambda} $ . The current calculation finds bound states for configurations$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [220]$ \frac{1}{2}^{+} $ ,$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ , and$ ^{36} $ Ar$\otimes$ $ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ , the energy levels of which are shown in the top right corner of Fig. 8. For$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [220]$ \frac{1}{2}^{+} $ and$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{5}{2}^{+} $ , only the bandheads with$ J^{\pi}=\frac{1}{2}^{+} $ and$ \frac{5}{2}^{+} $ are lower than the separation threshold, and their energies are 18.45 MeV and 17.91 MeV, respectively. For$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{3}{2}^{+} $ , the bandhead is with$ J^{\pi}=\frac{3}{2}^{+} $ , and its energy is 17.94 MeV. For the same configuration, there is another bound state with$ J^{\pi}=\frac{5}{2}^{+} $ ; however, the energy level is only 0.24 MeV lower than the separation threshold.The mean-field PESs of the three configurations discussed above are shown in Fig. 1. It is found that
$ {\Lambda} $ [220]$ \frac{1}{2}^{+} $ enhances the energy minima on the prolate side of the PES and weakens the oblate one, whereas$ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ and$ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ exhibit opposite effects. Similar to cases of the p-shell$ {\Lambda} $ , impurity effects of those in the sd-shell mainly stem from their density distributions, which are shown in Fig. 2. For$ {\Lambda} $ [220]$ \frac{1}{2}^{+} $ , the main component of its wave function is$ Y_{2,0}(\theta,\varphi) $ and it is elongated along the symmetry axis (shown in the bottom-right panel of Fig. 2); hence, it prefers a prolate nuclear core. Conversely, for$ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ and$ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ , the main components of their wave functions are$ Y_{2,\pm2}(\theta,\varphi) $ ; therefore, they are both compressed in the direction of the symmetry axis (shown in the bottom-left panel of Fig. 2) and prefer oblate nuclear cores. As shown in Fig. 8, this type of effect also causes the GCM energy levels of the configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{5}{2}^{+} $ and$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{3}{2}^{+} $ to be approximately 0.5 MeV lower than that of$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [220]$ \frac{1}{2}^{+} $ . This is because, for all three configurations, the nuclear core$ ^{36} $ Ar$ ^{{\rm{N}}} $ is oblately distributed, and its coupling with$ {\Lambda} $ [202]$ \frac{5}{2}^{+} $ or$ {\Lambda} $ [202]$ \frac{3}{2}^{+} $ leads to relatively lower energies. -
In summary, a beyond-mean-field SHF model that includes AMP techniques and the GCM is introduced in this paper. Based on this model, a comprehensive energy spectrum of
$ ^{37}_{\; {\Lambda}} $ Ar is given and researched in detail. Attention is mainly paid to the bound states that are formed by an ND or SD nuclear core coupled with a$ {\Lambda} $ hyperon occupying one of the s-, p-, or sd-shell orbitals. For the s-shell$ {\Lambda} $ hyperon, ND and SD bands corresponding to the configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [000]$ \frac{1}{2}^{+} $ and$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [000]$ \frac{1}{2}^{+} $ are given. The intra-band$ B(E2) $ values of these two bands decreased compared to those of$ ^{36} $ Ar, which is due to the reduction in deformation. For the p-shell$ {\Lambda} $ hyperon, three ND bands and one SD band are shown, which correspond to the configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ ,$ ^{36} $ Ar$ ^{{\rm{N}}} \otimes {\Lambda} $ [101]$ \frac{3}{2}^{-} $ ,$ ^{36} $ Ar$ ^{{\rm{N}}} \otimes {\Lambda} $ [101]$ \frac{1}{2}^{-} $ , and$ ^{36} $ Ar$^{{\rm{S}}} \otimes {\Lambda}$ [110]$ \frac{1}{2}^{-} $ , respectively. Moreover, the configurations$ ^{36} $ Ar$ ^{{\rm{S}}} \otimes {\Lambda} $ [101]$ \frac{3}{2}^{-} $ and$ ^{36} $ Ar$ ^{{\rm{S}}} \otimes {\Lambda} $ [101]$ \frac{1}{2}^{-} $ give two bound states, the energy levels of which are below the separation threshold of$ ^{36} $ Ar+$ {\Lambda} $ within 0.5 MeV. For the sd-shell$ {\Lambda} $ hyperon, three configurations$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [220]$ \frac{1}{2}^{+} $ ,$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{5}{2}^{+} $ , and$ ^{36} $ Ar$^{{\rm{N}}} \otimes {\Lambda}$ [202]$ \frac{3}{2}^{+} $ give bound states with energy levels lying at 18.45 MeV, 17.91 MeV, and 17.94 MeV above the ground state, respectively. Finally, it is expected that the predictions in this paper will aid future experiments in identifying the observed states of$ ^{37}_{\; {\Lambda}} $ Ar. -
One of the authors thanks Xian-Ye Wu for informative discussions.
Beyond-mean-field study of ${{} ^{\bf 37}_{\; {\bf\Lambda}}} $ Ar based on the Skyrme-Hartree-Fock model
- Received Date: 2022-01-10
- Available Online: 2022-07-15
Abstract: We present the hypernuclear states of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: