-
In the extensive nuclide chart, most nuclei are observed to be deformed. In these nuclei, shape evolution and possible shape coexistence, which was first introduced by Morinaga in 1956 [1], have attracted considerable attentions. Later, Heyde and Wood revealed that shape coexistence is ubiquitous and may appear across the entire nuclide chart [2–4]. Moreover, triple and multiple shape coexistences have been observed or predicted [5, 6]. As one evidence of the appearance of shape coexistence, exploring the delicate interplay between the single-particle and collective behavior of nucleons, which exhibit opposite trends in nuclei, could promote understanding of nuclear collectivity and the nuclear shell structure [7].
Investigations on hypernuclear systems provide invaluable information for exploring many-body hadronic physics with "strangeness" utilized as a new degree of freedom [8–13]. In hypernuclei, hyperons have the advantage of being free from the Pauli exclusion principle for nucleons, and as a result, they can move deep into the nuclear interior as an impurity to probe nuclear structures and properties. Numerous studies have been performed on single-Λ hypernuclei both experimentally [14–17] and theoretically [18–24]. The interesting impurity effects of hyperons have been studied from various aspects, such as the nuclear size and binding energies [25, 26], nuclear cluster structures [18, 19, 27], neutron drip line [28–30], nucleon and hyperon skin or halo [30–33], and pseudospin symmetry of nucleons [34].
The impurity effects of Λ hyperons may also be observed from drastic changes in nuclear shape and deformation. Various studies have shown that s-wave and p-wave hyperons have significantly different impurity effects. By including a spherical
$ s_\Lambda $ hyperon, the deformation of nuclei can be reduced, and the corresponding core nucleus becomes more spherical. For instance, as shown in Ref. [35], research using the axially deformed RMF model for$ ^{29}_{\Lambda} $ Si and$ ^{13}_\Lambda $ C revealed that the oblate nuclei 28Si and 12C became spherical after adding an$ s_\Lambda $ hyperon. A similar conclusion was obtained in Ref. [36], where the triaxially-deformed RMF model was used to study the potential energy surfaces$ E\sim(\beta,\gamma) $ , which found that the additional$ s_\Lambda $ hyperon drove the ground state of light C, Mg, and Si isotopes to a point with a small β and soft γ. In contrast with the$ s_\Lambda $ hyperon, a$ p_\Lambda $ hyperon exhibits strong polarization effects, which may enhance nuclear deformation [37]. In Ref. [38], the study using the deformed Skyrme-Hartree-Fock (DSHF) model showed that$ p_\Lambda $ hyperons in the$ 1/2^-[110] $ and$ 3/2^-[101] $ states had different effects on nuclear deformation, which resulted in more prolate and oblate nuclear shapes, respectively. In recent years, shape-driven effects induced by a valence nucleon(s) in high-spin states have been extensively researched [39–41]. The nucleon occupying the high-j and low-Ω orbital can cause the nucleus to be more prolate. A similar hyperon effect has been confirmed that polarizes nuclear shapes [37, 42].To describe nuclear deformation with various shape degrees of freedom, it is better to reduce the symmetric restrictions imposed when solving the equations of motion. In CDFT, we can do this with a harmonic oscillator (HO) basis [43, 44] or three-dimensional lattice space [45–48]. Recently, Zhou et al. developed the multidimensionally constrained covariant density functional theories (MDC-CDFTs) [49–52], which can accommodate various shape degrees of freedom. They applied this model to a series of investigations on, for example, the fission barriers of actinides [50, 51, 53–56], nonaxial octupole
$ Y_{32} $ correlation in$ N= 150 $ isotones [57], the third minima and triple-humped barriers in light actinides [58], and potential energy curves (PECs) in the superheavy nucleus 270Hs [59]. Subsequently, by including Λ hyperons, the MDC-CDFTs have been extended to study hypernuclei. Shape evolution in the C, Mg, and Si isotopes and the possible polarization effects of the Λ hyperon [36], the superdeformed states in Ar isotopes [42], the$ \Lambda\Lambda $ pairing correlations [60], and the new effective$ \Lambda N $ interactions [61] have been either studied or developed. Recently, we used the MDC-CDFTs to explore shape evolution and possible shape coexistence in even-even Ne isotopes [62]. By exploring the PECs, possibilities for shape coexistence were found in nuclei$ ^{24,26,28} $ Ne. Furthermore, the impurity effects of the$ s_{\Lambda} $ and$ p_{\Lambda} $ hyperons on the nuclear shape, size, and binding energies were studied.In this paper, following our previous study in Ref. [62], shape evolution and possible shape coexistence in odd-A Ne isotopes are explored with the MDC-RMF model by including the blocking effect for the unpaired odd neutron and the impurity effects are investigated by adding a single-Λ hyperon occupying the lowest s or p orbitals. For shape coexistence in odd-A Ne isotopes, in Ref. [63], constrained RMF+BCS calculations with the NL075 force has been performed and possible shape coexistence was predicted in
$ ^{25,27} $ Ne. The paper is organized as follows: In Sec. II, the MDC-RMF model for single-Λ hypernuclei including the blocking effect is briefly presented. In Sec. III, numerical details are provided. After the results and discussions in Sec. IV, a summary and perspectives are provided in Sec. V. -
In the meson-exchange MDC-RMF model for single-Λ hypernuclei, the covariant Lagrangian density is composed of two parts:
$ \mathcal{L}=\mathcal{L}_0+\mathcal{L}_\Lambda, $

(1) where
$ \mathcal{L}_0 $ is the standard RMF Lagrangian density for nucleons. For details, see Refs. [64–68]. In the case of the Lagrangian density for the Λ hyperon$ \mathcal{L}_\Lambda $ , considering the neutral and isoscalar particle properties, only couplings with scalar-isoscalar σ and vector-isoscalar ω mesons are included, and$ \mathcal{L}_\Lambda $ is expressed as$ \begin{aligned}[b] \mathcal{L}_\Lambda =&\bar{\psi}_\Lambda\left[{\rm i}\gamma^\mu \partial_\mu-m_\Lambda-g_{\sigma\Lambda}\sigma-g_{\omega\Lambda}\gamma^\mu \omega_\mu\right]\psi_\Lambda\\ & +\frac{f_{\omega\Lambda\Lambda}}{4m_\Lambda}\bar{\psi}_\Lambda\sigma^{\mu\nu}\Omega_{\mu\nu}\psi_\Lambda, \end{aligned} $

(2) where the mass of the Λ hyperon,
$ m_\Lambda=1115.6 $ MeV, the coupling constants of the Λ hyperon with the σ and ω meson fields,$ g_{\sigma\Lambda} $ and$ g_{\omega\Lambda} $ , and the parameter$ f_{\omega\Lambda\Lambda} $ in the tensor coupling term between the Λ hyperon and ω field, which is strongly related to small single-Λ spin-orbit splitting [69], constitute the$ \Lambda N $ interaction. The field tensor of the ω field,$ \Omega_{\mu \nu}=\partial_{\mu} \omega_{\nu}-\partial_{\nu} \omega_{\mu} $ .In the framework of the RMF model, using the variational procedure, the Dirac equations for baryons as well as the Klein-Gordon equations for mesons and photons can be obtained under the mean-field and no-sea approximations. The Λ hyperon satisfies the following Dirac equation:
$ \left[\mathit{\boldsymbol{\alpha}} \cdot {{\boldsymbol p}}+\beta\left(m_{\Lambda}+S_{\Lambda}\right)+V_{\Lambda}+T_{\Lambda}\right] \psi_{\Lambda }=\epsilon \psi_{\Lambda }, $

(3) where
$ \mathit{\boldsymbol{\alpha}} $ and β are the Dirac matrices, and$ S_\Lambda $ ,$ V_\Lambda $ , and$ T_\Lambda $ represent the scalar, vector, and tensor parts, respectively, of the mean-field potentials for the Λ hyperon,$ S_\Lambda = g_{\sigma\Lambda}\sigma, $

(4) $ V_\Lambda = g_{\omega\Lambda}\omega, $

(5) $ T_\Lambda = -\frac{f_{\omega\Lambda\Lambda}}{2 m_{\Lambda}}\beta(\mathit{\boldsymbol{\alpha}} \cdot {\boldsymbol{p}}) \omega. $

(6) In odd-A nuclei, the blocking effect for the unpaired nucleon should be treated, which is of a crucial importance [70–72]. The ground state of an odd system is a one-quasiparticle state, and in the BCS approach, it could be described by the following wave function [70, 71]:
$ \hat{\alpha}_{k_1}^+|{\rm{BCS}}\rangle=\hat{a}_{k_1}^+\prod\limits_{k>0,k\neq k_1}(u_k+v_{k}\hat{a}_{k}^+\hat{a}_{\bar k}^+)|0\rangle, $

(7) where
$ |{\rm{BCS}}\rangle $ is the BCS vacuum state,$ \hat{\alpha}_{k_1}^{+} $ and$ \hat{a}_{k_1}^{+} $ are the creation operators for the quasiparticle and single-particle, respectively, and$ k_1 $ denotes the blocked orbital occupied by the unpaired particle.To determine the nuclear ground state and low-lying excited states in an odd-A nucleus, a variety of calculations are performed with the odd nucleon blocked in different single-particle states k around the Fermi surface. As a result, the state with the lowest total binding energy is considered the ground state, while others form the low-lying excited energy spectra.
To obtain potential energy curves (PECs), constraint calculations [70] with a modified linear constraint method [50, 51] are performed, which has been effectively demonstrated in MDC-RMF calculations compared to the quadratic constraint method [36]. The Routhian is calculated as
$ E'=\langle\hat{H}\rangle+\sum\limits_{\lambda\, \mu} \frac{1}{2} C_{\lambda \,\mu} Q_{\lambda \,\mu}, $

(8) where
$ \hat{H} $ is the RMF Hamiltonian, and$ C_{\lambda\,\mu} $ are variables that change their values in different iteration steps as follows:$ C_{\lambda \,\mu}^{(n+1)}=C_{\lambda \,\mu}^{(n)}+k_{\lambda\, \mu}\left(\beta_{\lambda\, \mu}^{(n)}-\beta_{\lambda\, \mu}\right), $

(9) where
$ C_{\lambda\,\mu}^{(n+1)} $ and$ C_{\lambda\,\mu}^{(n)} $ are values obtained in the$ (n+1) $ th and nth iterations, respectively,$ \beta_{\lambda\,\mu} $ is the desired nuclear deformation, and$ \beta^{(n)}_{\lambda\,\mu} $ is the calculated value in the nth iteration. Changes in$ C_{\lambda\,\mu} $ and$ \beta_{\lambda\, \mu} $ are linked by a constant$ k_{\lambda\,\mu} $ .The intrinsic multipole moment
$ Q_{\lambda \,\mu} $ in Eq. (8) can be calculated with the vector density$ \rho_{V}({\boldsymbol r}) $ and spherical harmonics$ Y_{\lambda\,\mu}(\Omega) $ by$ Q_{\lambda\, \mu}=\int {\rm d}^{3} {\boldsymbol{r}} \rho_{V}({\boldsymbol{r}}) {\boldsymbol r}^{\lambda} Y_{\lambda \,\mu}(\Omega). $

(10) Subsequently, with the multipole moment, the corresponding deformation parameter
$ \beta_{\lambda\,\mu} $ can also be calculated using$ \beta_{\lambda \,\mu}=\frac{4 \pi}{3 B R^{\lambda}} Q_{\lambda \,\mu}, $

(11) where
$ R = 1.2 A^{1/3} $ fm is the radius of the nucleus, with A as the total number of nucleons, and B represents the number of protons, neutrons, Λ hyperons, or total baryons.In an axially symmetric system, we only have the good quantum numbers of parity and the z component of the angular momentum. In this case, calculations with only a single-constraint on the quadrupole deformation
$ \beta_2 $ will be performed. -
Shape evolution and possible shape coexistence are explored in odd-A Ne isotopes with
$ A=19-33 $ using the self-consistent MDC-RMF model. Moreover, the impurity effects of Λ hyperons occupying the s or p orbitals are investigated. As a continuation of our previous study on even-even Ne isotopes [62], the same numerical details are used.In the RMF functional, the PK1 [73] parameter set is used for the
$ NN $ interaction. For the$ \Lambda N $ interaction, the PK1-Y1 [74] parameter set is adopted, where the scalar-isoscalar coupling constant$ g_{\sigma\Lambda}=0.580 g_\sigma $ and vector-isoscalar coupling constant$ g_{\omega\Lambda}=0.620 g_\omega $ , which were determined by fitting the experimentally observed single-Λ binding energies, and the tensor coupling constant$ f_{\omega\Lambda\Lambda}=-g_{\omega\Lambda} $ , which was determined by reproducing$ p_\Lambda $ spin-orbit splittings in$ ^9_\Lambda $ Be and$ ^{13}_\Lambda $ C.To solve the RMF equations, an axially deformed harmonic oscillator (ADHO) basis [43, 44] is taken with the truncation parameters
$ N_{{\rm{F}}}=14 $ for fermion shells and$ N_{{\rm{B}}}=20 $ for boson shells, as in Ref. [36]. With these parameters, the truncation error in the binding energy of the nucleus 26Si is less than$ 30 $ keV.In the mean-field approximation, the translational symmetry is broken. To remedy this, the following microscopic center-of-mass (c.m.) correction [75] is employed:
$ E_{{\rm{c.m.}}}=-\frac{1}{2 M}\langle\hat{{\boldsymbol{P}}}^{2}\rangle, $

(12) where M is the total nuclear mass.
The BCS approach is used to treat the pairing effects with a finite-range separable pairing force [76–78].
$ V\left({\boldsymbol{r}}_{1}-{\boldsymbol{r}}_{2}\right)=-G \delta\left(\tilde{{\boldsymbol{R}}}-\tilde{{\boldsymbol{R}}}^{\prime}\right) P(\tilde{{\boldsymbol r}}) P\left(\tilde{\boldsymbol r}^{\prime}\right) \frac{1-\hat{P}_{\sigma}}{2}, $

(13) where G is the strength of the pairing force,
$ \tilde{{\boldsymbol{R}}} $ and$ \tilde{{\boldsymbol{r}}} $ are the center of mass and relative coordinates between the paired particles, respectively, and$ P(\tilde{\boldsymbol r}) $ is a Gaussian shaped function.$ P(\tilde{\mathit{\boldsymbol{r}}})=\frac{1}{\left(4 \pi a^{2}\right)^{3 / 2}} {\rm e}^{-\tilde{r}^{\,2} / a^{2}}, $

(14) where a is the effective range of the pairing force. Here, the strength G and range a are taken as
$ G=728.0\; {\rm{MeV\cdot fm}}^{3}, \quad a=0.644\; {\rm{fm}}, $

(15) which can be used to obtain the same momentum dependency of the pairing gap in nuclear matter as that of the D1S Gogny force [76].
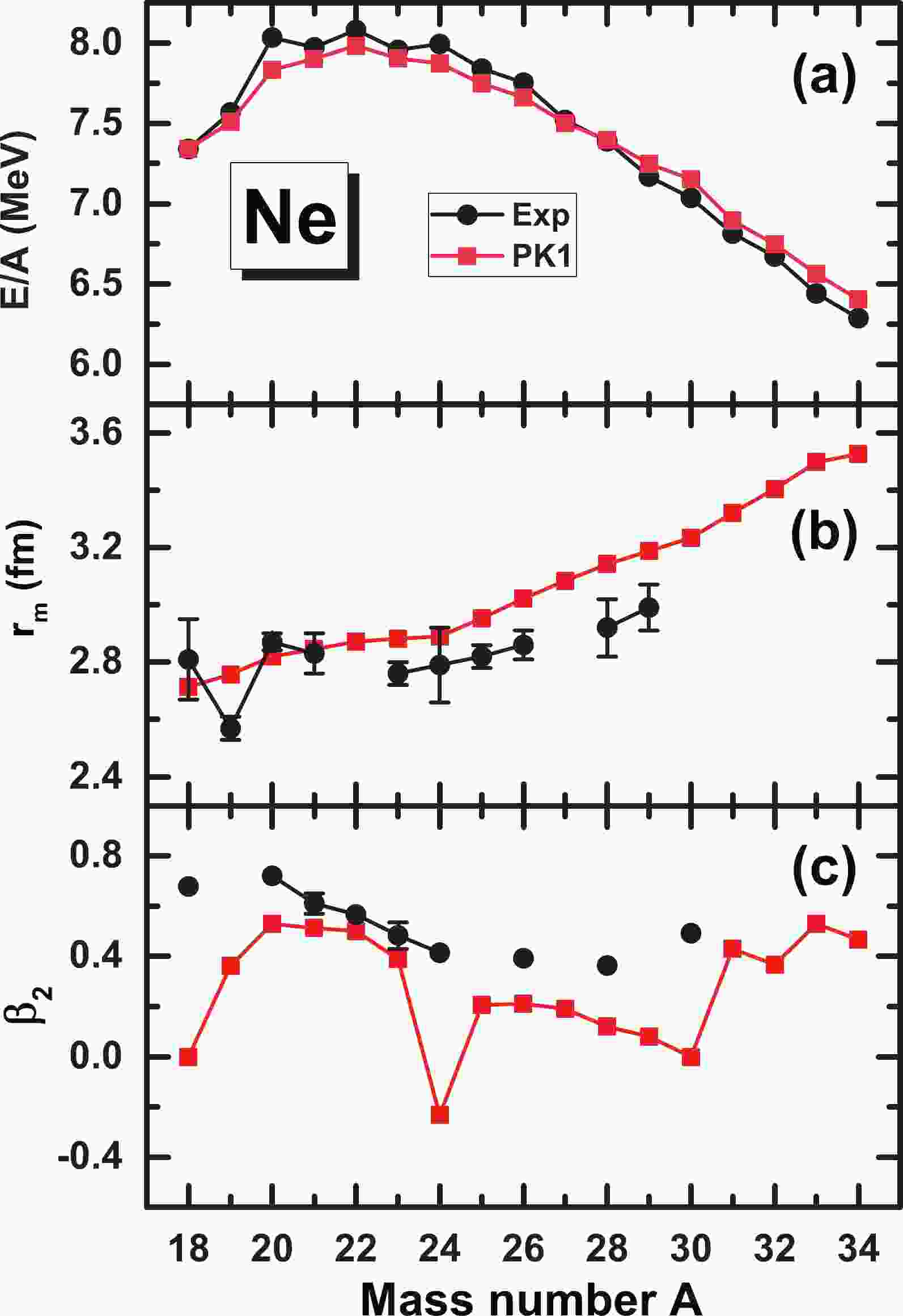
In Fig. 1, the binding energy per nucleon
$ E/A $ , matter radius$ r_m $ , and quadrupole deformation$ \beta_2 $ in the ground states of Ne isotopes determined by unconstrained RMF calculations with the PK1 parameter set are compared with the available experimental data [79]. In general, good consistency with the experimental results is revealed, indicating that the choice of the PK1 parameter set for the description of Ne isotopes is suitable.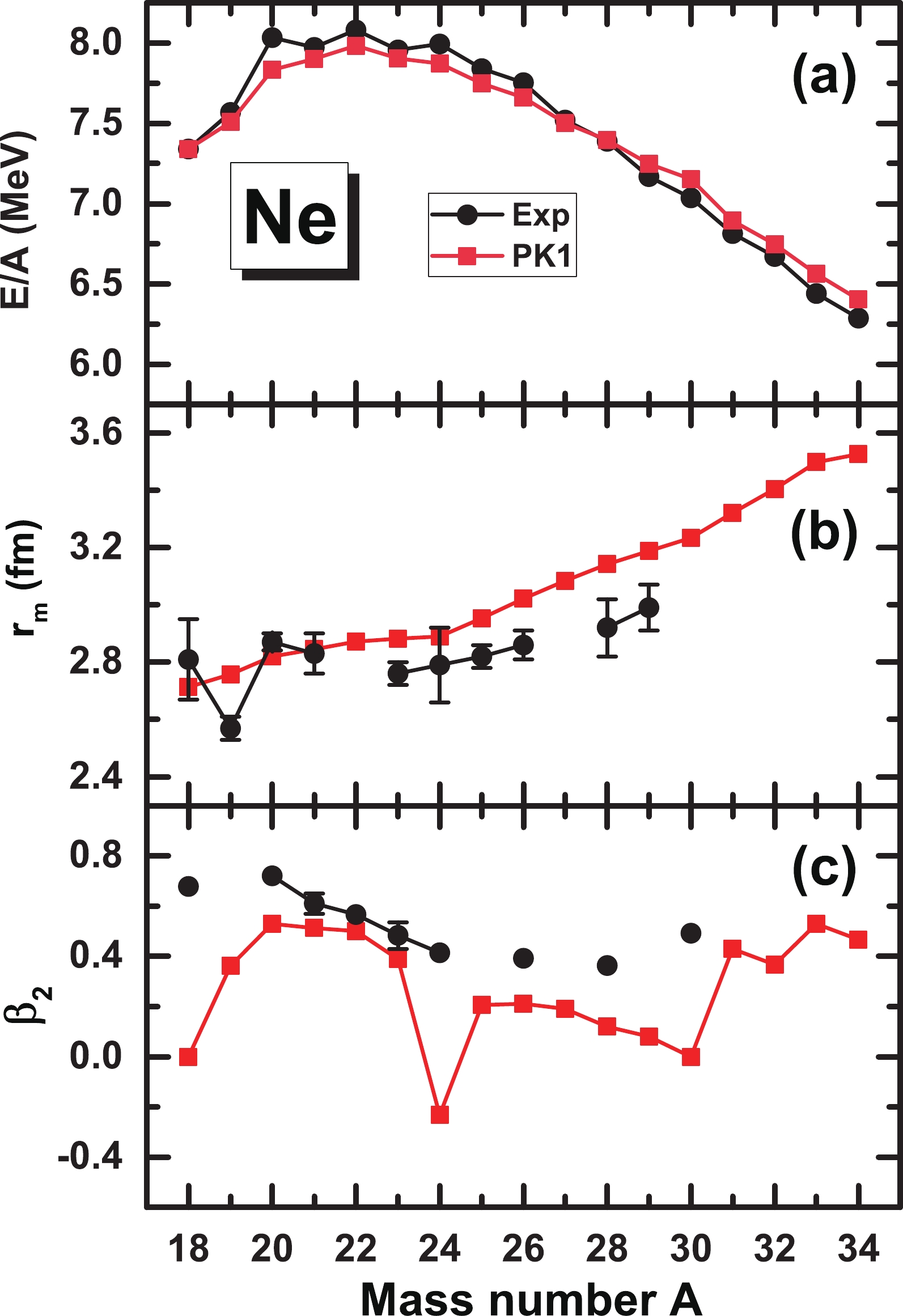
Figure 1. (color online) Binding energy per nucleon
$ E/A $ , matter radius$ r_m $ , and quadrupole deformation$ \beta_2 $ as a function of the mass number A in the ground states of Ne isotopes in comparison with the available experimental data [79]. -
To explore shape coexistence on the mean field level, the PECs are mainly analyzed. If two close-lying energy minima with a difference of a few hundred keV that own prolate and oblate quadrupole deformations are observed in combination with a pronounced barrier between them, possible shape coexistence is indicated because their ground states may have two competing configurations.
In Fig. 2, the PECs for odd-A Ne isotopes from
$ A=19 $ to$ 33 $ are plotted as functions of the quadrupole deformation$ \beta_2 $ , which are obtained using constrained calculations with the self-consistent MDC-RMF model. The unpaired odd neutron is blocked in different orbitals around the Fermi surface, and the state with the lowest binding energy is deemed the ground state while others form the local minima.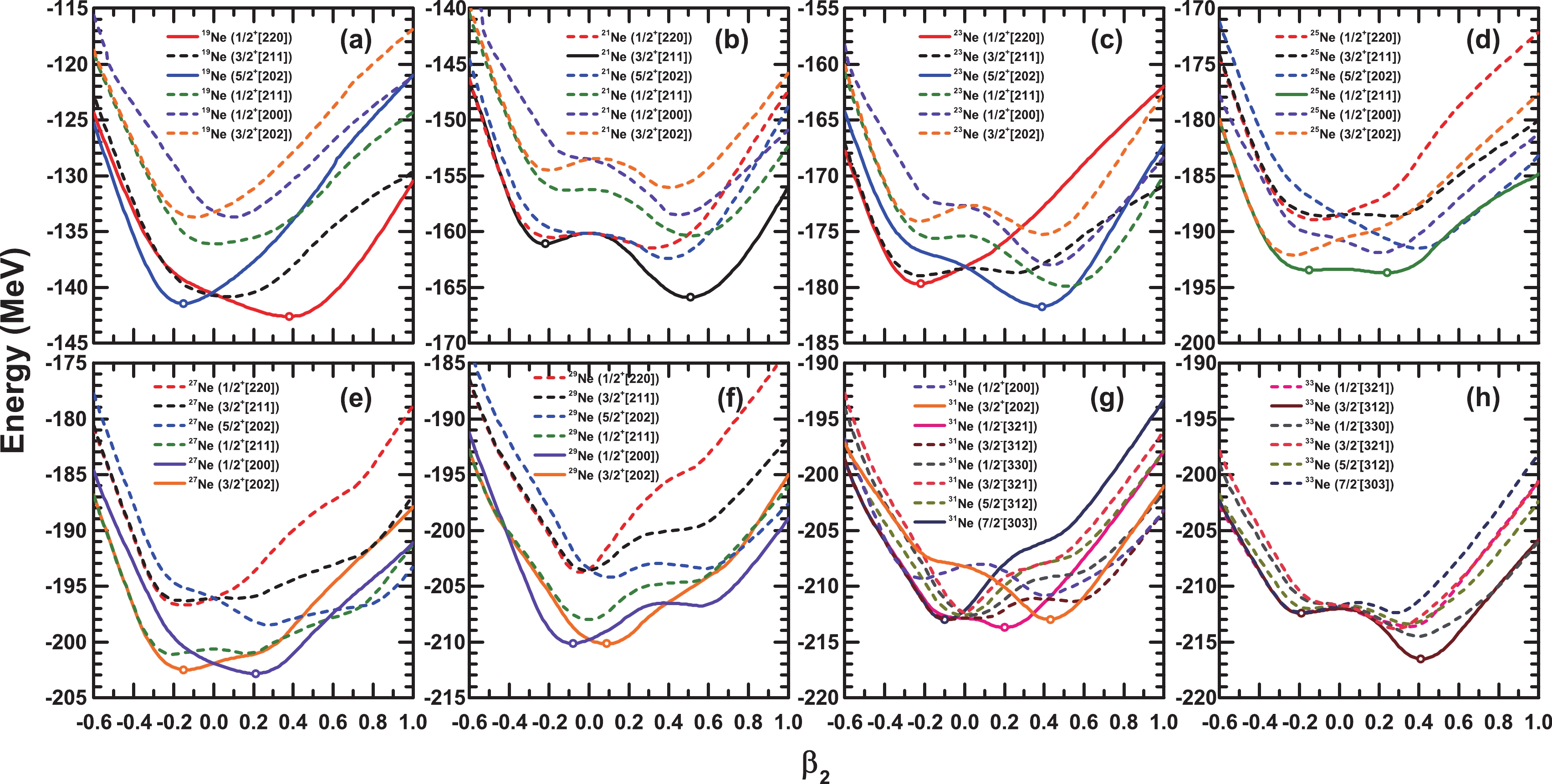
Figure 2. (color online) Potential energy curves (PECs) as a function of the deformation parameter
$ \beta_2 $ in odd-A Ne isotopes, with the odd neutron blocked in different orbitals around the Fermi surface denoted by the Nilsson quantum numbers$ \Omega^{\pi}[Nn_3m_l] $ . The open circles denote local energy minima.In Fig. 3, to observe the level structures in the Ne isotopes, the single-neutron levels
$ \Omega[Nn_3m_l] $ obtained using the constrained MDC-RMF calculations are plotted for the even-even nucleus 30Ne, where the solid lines represent levels with positive parity, and the dashed lines represent those with negative parity. At a spherical shape with the deformation$ \beta_2=0 $ , we observe the neutron shell closures$ N=8 $ and$ N=20 $ , whereas the shell closure$ N=28 $ vanishes owing to the inversion of the$ 1f_{7/2} $ and$ 2p_{3/2} $ levels. Referring to this single-neutron level structure, the odd neutron in$ ^{19-29} $ Ne most likely occupies the$ 2s,1d $ orbitals and$ 2p, 1f $ orbitals in$ ^{31,33} $ Ne. Calculations have been performed with all these configurations, and the obtained PECs are presented in Fig. 2, where the local energy minima are marked by open circles. The values of the quadrupole deformations, binding energies, and blocked orbitals of the unpaired odd neutron corresponding to the local energy minima are listed in Table 1.Nucleus Quadrupole deformation Energy $ \beta_2 $ 

$ \beta_{2n} $ 

$ \beta_{2p} $ 

$ ^{19}{\rm{Ne}} (1/2^{+}[220]) $ 

0.361 0.303 0.413 $ - $ 142.612

$ ^{19}{\rm{Ne}}^*(5/2^{+}[202]) $ 

$ - $ 0.145

$ - $ 0.138

$ - $ 0.151

$ - $ 141.477

$ ^{21}{\rm{Ne}} (3/2^{+}[211]) $ 

0.512 0.515 0.509 $ - $ 165.917

$ ^{21}{\rm{Ne}}^*(3/2^{+}[211]) $ 

$ - $ 0.201

$ - $ 0.209

$ - $ 0.193

$ - $ 161.081

$ ^{23}{\rm{Ne}} (5/2^{+}[202]) $ 

0.388 0.370 0.411 $ - $ 181.759

$ ^{23}{\rm{Ne}}^*(1/2^{+}[220]) $ 

$ - $ 0.223

$ - $ 0.236

$ - $ 0.205

$ - $ 179.701

$ ^{25}{\rm{Ne}} (1/2^{+}[211]) $ 

0.206 0.193 0.225 $ - $ 193.711

$ ^{25}{\rm{Ne}}^*(1/2^{+}[211]) $ 

$ - $ 0.131

$ - $ 0.131

$ - $ 0.130

$ - $ 193.487

$ ^{27}{\rm{Ne}} (1/2^{+}[200]) $ 

0.190 0.177 0.213 $ - $ 202.836

$ ^{27}{\rm{Ne}}^*(3/2^{+}[202]) $ 

$ - $ 0.130

$ - $ 0.135

$ - $ 0.120

$ - $ 202.503

$ ^{29}{\rm{Ne}} (3/2^{+}[202]) $ 

0.080 0.068 0.103 $ - $ 210.166

$ ^{29}{\rm{Ne}}^*(1/2^{+}[200]) $ 

$ - $ 0.075

$ - $ 0.073

$ - $ 0.079

$ - $ 210.144

$ ^{31}{\rm{Ne}} (1/2^{-}[321]) $ 

0.191 0.196 0.181 $ - $ 213.707

$ ^{31}{\rm{Ne}}^*(7/2^{-}[303]) $ 

$ - $ 0.090

$ - $ 0.089

$ - $ 0.091

$ - $ 213.022

$ ^{31}{\rm{Ne}}^*(3/2^{+}[202]) $ 

0.429 0.439 0.408 $ - $ 212.986

$ ^{33}{\rm{Ne}} (3/2^{-}[312]) $ 

0.419 0.428 0.397 $ - $ 216.533

$ ^{33}{\rm{Ne}}^*(3/2^{-}[312]) $ 

$ - $ 0.162

$ - $ 0.182

$ - $ 0.116

$ - $ 212.418

Table 1. Quadrupole deformations and binding energies (in MeV) for ground states and local energy minima (labeled with asterisks) in
$ ^{19-33}{\rm{Ne}} $ .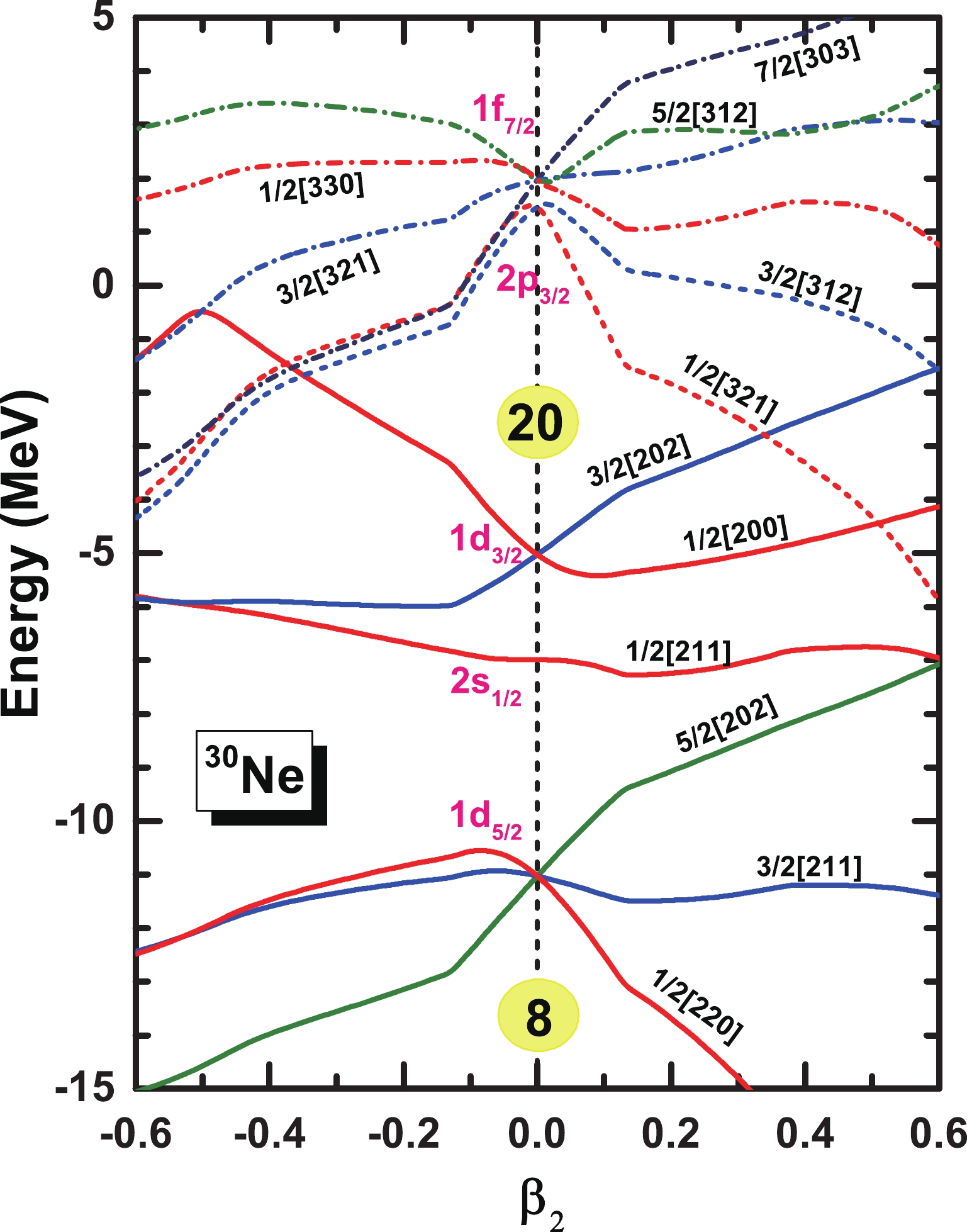
Figure 3. (color online) Single-neutron levels
$ \Omega[Nn_3m_l] $ as a function of the deformation parameter$ \beta_2 $ in 30Ne.Regarding the nucleus 19Ne with a neutron number just exceeding an
$ N=8 $ shell closure, it is optimal that the odd neutron occupies the$ 1d_{5/2} $ orbital, which can be splitted into the$ \Omega^{\pi}[Nn_3m_l]=1/2^{+}[220] $ ,$ 3/2^{+}[211] $ , and$ 5/2^{+}[202] $ orbitals with axially symmetric quadrupole deformation. Further analysis, shown in Fig. 2(a), demonstrates that the odd neutron blocked in the$ 1/2^{+}[220] $ orbital corresponds to the ground state with a prolate deformation of$ \beta_2=0.361 $ , whereas the odd neutron blocked in$ 5/2^{+}[202] $ contributes to the second energy local minimum, which exhibits an oblate shape at$ \beta_2=-0.145 $ . In the case of the unpaired neutron occupying other orbitals, the obtained PECs (denoted by dashed lines) are significantly higher. Hereafter, we focus our attention on the configurations for the ground state and other local energy minima that may generate shape coexistence. With two more neutrons in 21Ne, the odd neutron occupying the$ 3/2^{+}[211] $ orbital results in both the ground state and second local energy minimum, which are located at the prolate deformation of$ \beta_2=0.512 $ and oblate deformation of$ \beta_2=-0.201 $ , respectively. As for 23Ne, the configurations of the ground state and the second local minimum are opposite to those in 19Ne, that is, the odd neutron occupying the$ 5/2^{+}[202] $ orbital leads to the prolate ground state observed at$ \beta_2=0.388 $ , while the odd neutron blocked in the$ 1/2^{+}[220] $ orbital corresponds to the second local energy minimum identified at the deformation$ \beta_2=-0.223 $ . Because the corresponding energy differences between the ground state and second local energy minimum in$ ^{19,21,23} $ Ne are as large as$ 1.135, \;4.836,\; 2.058 $ MeV, possible shape coexistence is excluded in those nuclei. With regard to the nucleus 25Ne, the configuration of the unpaired neutron blocked in$ 1/2^{+}[211] $ from the spherical$ 2s_{1/2} $ orbital contributes to the lowest PEC, on which the ground state with the prolate deformation$ \beta_2=0.206 $ and the second local energy minimum with an oblate shape at$ \beta_2=-0.131 $ are obtained. Although the energy difference between them is as small as$ 0.224 $ MeV, the circumjacent PEC is flat, where different deformations within a limited scope correspond to similar binding energies. In this case, the occurrence of shape coexistence is believed to be difficult. Moving further to the nuclei 27Ne and 29Ne, odd neutrons have great possibilities of occupying the$ 1d_{3/2} $ ($ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ ) orbital. For 27Ne, when the odd neutron is blocked in the$ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ orbitals, the ground state with prolate deformation at$ \beta_2=0.190 $ and second energy local minimum exhibiting an oblate shape at$ \beta_2=-0.130 $ are observed, respectively. A small energy difference of$ 0.333 $ MeV in combination with a barrier of$ 0.984 $ MeV in height between them are observed, providing great potential for shape coexistence in 27Ne. In the case of 29Ne, with the odd neutron blocked in$ 3/2^{+}[202] $ , the prolate ground state is identified at a deformation of$ \beta_2=0.080 $ , whereas the configuration with the odd neutron occupying$ 1/2^{+}[200] $ leads to an oblate second local minimum with a deformation of$ \beta_2=-0.075 $ . Similar to 27Ne, owing to the small energy difference of$ 0.022 $ MeV coupled with a barrier of$ 0.4 $ MeV between the two local energy minima, possible shape coexistence is expected in 29Ne. Far from the$ N=20 $ shell closure, the unpaired neutron in the nuclei 31Ne and 33Ne is likely to occupy the$ 2p_{3/2} $ ($ 1/2^-[321] $ ,$ 3/2^-[312] $ ) and$ 1f_{7/2} $ ($ 1/2^-[330] $ ,$ 3/2^-[321] $ ,$ 5/2^-[312] $ ,$ 7/2^-[303] $ ) orbitals. For the nucleus 31Ne, a possible triple shape coexistence is observed, which is comprised of the prolate ground state at$ \beta_2=0.191 $ with the odd neutron blocked in$ 1/2^-[321] $ , a second oblate local energy minimum at$ \beta_2=-0.090 $ with the odd neutron in$ 7/2^-[303] $ , and a third prolate local minimum at$ \beta_2=0.429 $ with the odd neutron in$ 3/2^+[202] $ . The corresponding excitation energies are$ 0.685 $ and$ 0.721 $ MeV with respect to the ground state, which together with a proper barrier between them, guarantees the appearance of shape coexistence. In the case of 33Ne, with the odd neutron occupying$ 3/2^-[312] $ , both the ground state and the second local minimum are observed owing to a prolate shape at$ \beta_2=0.419 $ and an oblate shape at$ \beta_2=-0.162 $ , respectively. Because of the large energy difference of$ \Delta E= 4.1 $ MeV, the appearance of shape coexistence is difficult.To explore the impurity effects of Λ hyperons, taking the single-Λ hypernucleus
$ ^{28}_{\Lambda} $ Ne (or denoted by$ ^{27}{\rm{Ne}}\otimes\Lambda $ ) as an example, PECs are plotted in Fig. 4 where the s-wave ($ \Omega^\pi[N n_3 m_l]=1/2^+[000] $ ) and three p-wave ($ 1/2^-[110] $ ,$ 1/2^-[101] $ , and$ 3/2^-[101] $ ) single-Λ hyperons are considered (denoted by dashed lines). In panels (a) and (b), the odd neutron is blocked in the$ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ orbitals, respectively.
Figure 4. (color online) PECs as a function of deformation
$ \beta_2 $ in$ ^{27}{\rm{Ne}} $ and the single-Λ hypernucleus$ ^{28}_{\Lambda} $ Ne (27Ne$ \otimes\Lambda $ ). The odd neutron is blocked in the (a)$ 1/2^+[200] $ and (b)$ 3/2^+[202] $ orbitals, and the single-Λ hyperon is injected into the lowest s or p orbitals. The open circles denote the local energy minima.Generally, after injecting an
$ s_\Lambda $ hyperon, the PEC shapes remain almost unchanged, while the depths deepen significantly owing to the attractive$ \Lambda N $ interaction. Moreover, a clear "glue-like" effect of the$ s_{\Lambda} $ hyperon is observed, which results in smaller nuclear deformations and a more spherical nuclear shape. For example, in Fig. 4(a), the reduced deformation of the prolate ground state changes from$ \beta_2=0.190 $ to$ \beta_2=0.165 $ , and in Fig. 4(b), the deformation of the oblate second local minimum reduces to$ \beta_2=-0.115 $ from$ \beta_2=-0.130 $ .Regarding single-
$ p_\Lambda $ hypernuclei, PECs obtained with the Λ hyperon injected into the$ 1/2^-[101] $ orbital from the$ 1p_{1/2} $ orbital and the$ 3/2^-[101] $ orbital from the$ 1p_{3/2} $ orbital are almost degenerate owing to small spin-orbit splitting; however, they exhibit significant differences from those obtained by injecting the$ p_\Lambda $ hyperon into the$ 1/2^-[110] $ orbital. Hereafter, considering that the$ p_\Lambda $ hyperon occupying the$ 1/2^-[101] $ and$ 3/2^-[101] $ orbitals exhibit similar effects, we only discuss the latter case. In general, after injecting a$ p_\Lambda $ hyperon, the PEC shapes as well as the locations of the local energy minima clearly change. Furthermore, different polarization effects are exhibited by$ p_\Lambda $ hyperons occupying the$ 1/2^-[110] $ and$ 3/2^-[101] $ orbitals. For instance, in Fig. 4(a), with the Λ hyperon blocked in the$ 1/2^-[110] $ orbital, the prolate deformation of$ \beta_2=0.190 $ corresponding to the nuclear ground state in 27Ne is driven to$ \beta_2=0.265 $ , whereas it is reduced to$ \beta_2=0.126 $ when the$ p_\Lambda $ hyperon is blocked in the$ 3/2^-[101] $ orbital. Similar effects by the$ p_\Lambda $ hyperon have been observed in Fig. 4(b), where the unpaired neutron in the core nucleus is blocked in the$ 3/2^+[202] $ orbital, which corresponds to the second local minimum. In detail, the$ p_{\Lambda} $ hyperon in the$ 1/2^-[110] $ state drives the nucleus toward a spherical shape, and the oblate deformation of$ \beta_2=-0.130 $ corresponding to the second local energy minimum decreases to$ \beta_2=-0.044 $ . Meanwhile, the$ p_{\Lambda} $ hyperon occupying the$ 3/2^-[101] $ orbital causes the hypernucleus to become more oblately deformed with$ \beta_2=-0.162 $ .Similar investigations as those of
$ ^{28}_{\Lambda} $ Ne shown in Fig. 4 have also been performed for other Ne hypernuclei. The same impurity effects of single-Λ hyperons on nuclear deformations and binding energies are obtained. As a result of the introduced Λ hyperons, the nuclear PECs are significantly deepened; however, their increments are varied at different deformations$ \beta_2 $ . Therefore, the energy difference$ \Delta E $ between different local energy minima might change, which may influence the possibility of shape coexistence. In Table 2, the values of$ \Delta E $ in the nuclei$ ^{19-33} $ Ne are presented in comparison with values after injecting a single-Λ hyperon into the$ 1/2^+[000] $ ,$ 1/2^-[110] $ , and$ 3/2^-[101] $ orbitals. With the additional$ s_\Lambda $ hyperon, the energy difference$ \Delta E $ decreases significantly in all the hypernuclei. As a result, possible shape coexistence in$ ^{27,29,31} $ Ne can persist well in$^{28,30,32}_{\phantom{28,30,3}\Lambda}$ Ne. For example, the value of$ \Delta E $ between the ground state and second local energy minimum reduces to$ 0.238 $ MeV in$ ^{28}_{\Lambda} $ Ne from$ 0.333 $ MeV in 27Ne. Moreover, the hypernucleus$ ^{20}_{\Lambda} $ Ne becomes a new candidate for possible shape coexistence because$ \Delta E $ therein is reduced to$ 0.924\; $ MeV. With the addition of a$ p_\Lambda $ hyperon, the influence on the value of$ \Delta E $ becomes complex. With the addition of a single-$ p_\Lambda $ hyperon occupying the$ 1/2^-[110] $ orbital, there is a significant increase in$ \Delta E $ in all hypernuclei, which reduces the possibility of shape coexistence. For instance, the energy difference$ \Delta E $ in$ ^{28}_\Lambda{\rm{Ne}} $ increases to$ 1.811\; {\rm{MeV}} $ from$ 0.333\; $ MeV. Furthermore, one of the local energy minima disappears in$^{22,26}_{\phantom{22,2}\Lambda}$ Ne with the addition of a$ p_\Lambda $ hyperon. Similarly, by including a$ p_{\Lambda} $ hyperon in the state of$ 3/2^-[101] $ , the values of$ \Delta E $ increase in most of the nuclei, and the probabilities of shape coexistence decrease. This differs from those in even-even Ne isotopes [62], where the additional$ p_{\Lambda} $ occupying the$ 3/2^-[101] $ orbital provides a higher possibility of shape coexistence.Core nuclei $ \Lambda(1/2^+[000]) $ 

$ \Lambda(1/2^-[110]) $ 

$ \Lambda(3/2^-[101]) $ 

19Ne $ \otimes\Lambda $ 

1.135 0.924 2.916 0.138 21Ne $ \otimes\Lambda $ 

4.836 4.434 − 3.188 23Ne $ \otimes\Lambda $ 

2.058 1.831 4.804 0.502 25Ne $ \otimes\Lambda $ 

0.224 0.113 − − 27Ne $ \otimes\Lambda $ 

0.333 0.238 1.811 $ - $ 0.443

29Ne $ \otimes\Lambda $ 

0.022 0.020 0.902 $ - $ 0.356

31Ne $ \otimes\Lambda $ 

0.685 0.602 1.934 $ - $ 0.019

33Ne $ \otimes\Lambda $ 

4.115 3.955 6.218 2.834 Table 2. Energy difference
$ \Delta E $ (in MeV) between the two local energy minima in$ ^{19-33} $ Ne (core nuclei) and the corresponding single-Λ hypernuclei$ ^{19-33} $ Ne$ \otimes\Lambda $ with the Λ hyperon injected into the$ 1/2^+[000] $ ,$ 1/2^-[110] $ , and$ 3/2^-[101] $ orbitals.To study the impurity effects of
$ s_\Lambda $ and$ p_\Lambda $ hyperons on the nuclear quadrupole deformations$ \beta_2 $ , nuclear root mean square (r.m.s.) radii r, and binding energies E, we take the hypernucleus$ ^{28}_{\Lambda} $ Ne as an example and list the corresponding values in Table 3. The single-Λ separation energies$ S_{\Lambda}=E(^{A+1}_\Lambda{\rm{Ne}})-E(^{A}{\rm{Ne}}) $ are also given. Configurations with the odd-neutron blocked in the$ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ (denoted by asterisks) orbitals, which correspond to the ground state and the second local minimum of the core nucleus 27Ne, are considered. In general, the$ s_\Lambda $ hyperon is more deeply bound than the$ p_{\Lambda} $ hyperon, which results in a relatively small nuclear size$ r_{\Lambda} $ and a large single-Λ separation energy$ S_\Lambda $ . Moreover, the$ s_\Lambda $ and$ p_{\Lambda} $ hyperons induce different impurity effects. The$ s_{\Lambda} $ hyperon exhibits a significant shrinkage effect, which makes the nuclei more bound with a smaller size. For example, with the addition of the$ s_{\Lambda} $ hyperon, the nuclear r.m.s. radius in the ground state 27Ne$ (1/2^+[200]) $ decreases from$ 3.083 $ fm to$ 3.074 $ fm, the total binding energy E becomes$ 16.546 $ MeV deeper, and the nuclear shape tends to be more spherical. For the quadrupole deformation$ \beta_2 $ of 27Ne$ \otimes\Lambda(1/2^+[000]) $ , it maintains the same sign as the core nucleus. In the case of the$ s_\Lambda $ hyperon, its deformation$ \beta_{2\Lambda} $ is influenced in turn by the core nucleus. For instance, in the hypernucleus 27Ne$ (1/2^+[200])\otimes s_\Lambda $ , the Λ hyperon is slightly prolate with a deformation$ \beta_{2\Lambda}=0.053 $ , the sign of which is the same as that of the core nucleus 27Ne$ (1/2^+[200]) $ . The same behavior is found in 27Ne$ ^*(3/2^+[202])\otimes s_\Lambda $ . In contrast with the$ s_\Lambda $ hyperon, the$ p_{\Lambda} $ hyperon may enhance the nuclear size slightly. Additionally,$ p_{\Lambda} $ hyperons in the states of$ 1/2^-[110] $ and$ 3/2^-[101] $ exhibit significantly different effects on nuclear deformation. For the$ p_{\Lambda} $ hyperon occupying$ 1/2^-[110] $ , which is a prolate shape, the core nucleus becomes more prolate. Conversely, for the hyperon occupying$ 3/2^-[101] $ or$ 1/2^-[101] $ , which is oblate, the core nucleus becomes more oblate or less prolate. For instance, in 27Ne$ (1/2^+[200])\otimes p_\Lambda(1/2^-[110]) $ , because both the$ p_{\Lambda} $ hyperon and core nucleus are prolate, the$ p_{\Lambda} $ hyperon enhances the nuclear prolate deformation from$ \beta_2=0.190 $ to$ \beta_2=0.265 $ , while shape decoupling occurs in 27Ne$ (1/2^+[200])\otimes p_\Lambda(3/2^-[101]) $ , where the$ p_{\Lambda} $ hyperon and core nucleus have different shapes, which leads to a reduction in the total nuclear deformation from$ \beta_2=0.190 $ to$ \beta_2=0.126 $ . In Refs. [80, 81], shape decoupling in the deformed halo nuclei$ ^{42,44} $ Mg are discussed, in which the shapes of the core and outside halo are different.Nucleus Quadrupole deformation r.m.s. radii/fm Energy/MeV $ \beta_2 $ 

$ \beta_{2n} $ 

$ \beta_{2p} $ 

$ \beta_{2\Lambda} $ 

$ r_m $ 

$ r_{\rm{core}} $ 

$ r_\Lambda $ 

E $ S_\Lambda $ 

$ ^{27}{\rm{Ne}}(1/2^{+}[200]) $ 

0.190 0.177 0.213 3.083 $ - $ 202.836

$ ^{27}{\rm{Ne}}\otimes\Lambda(1/2^{+}[000]) $ 

0.165 0.157 0.188 0.053 3.056 3.074 2.511 $ - $ 219.382

16.546 $ ^{27}{\rm{Ne}}\otimes\Lambda(1/2^{-}[110]) $ 

0.265 0.217 0.262 1.087 3.105 3.091 3.461 $ - $ 210.693

7.857 $ ^{27}{\rm{Ne}}\otimes\Lambda(1/2^{-}[101]) $ 

0.128 0.140 0.162 $ - $ 0.414

3.093 3.079 3.443 $ - $ 209.133

6.297 $ ^{27}{\rm{Ne}}\otimes\Lambda(3/2^{-}[101]) $ 

0.126 0.138 0.161 $ - $ 0.429

3.092 3.079 3.431 $ - $ 209.317

6.481 $ ^{27}{\rm{Ne}}^*(3/2^{+}[202]) $ 

$ - $ 0.130

$ - $ 0.135

$ - $ 0.120

3.077 $ - $ 202.503

$ ^{27}{\rm{Ne}}^*\otimes\Lambda(1/2^{+}[000]) $ 

$ - $ 0.115

$ - $ 0.124

$ - $ 0.109

$ - $ 0.033

3.051 3.069 2.505 $ - $ 219.144

16.641 $ ^{27}{\rm{Ne}}^*\otimes\Lambda(1/2^{-}[110]) $ 

$ - $ 0.044

$ - $ 0.082

$ - $ 0.061

0.774 3.088 3.075 3.432 $ - $ 208.882

6.379 $ ^{27}{\rm{Ne}}^*\otimes\Lambda(1/2^{-}[101]) $ 

$ - $ 0.162

$ - $ 0.155

$ - $ 0.139

$ - $ 0.509

3.094 3.080 3.444 $ - $ 209.625

7.122 $ ^{27}{\rm{Ne}}^*\otimes\Lambda(3/2^{-}[101]) $ 

$ - $ 0.162

$ - $ 0.154

$ - $ 0.139

$ - $ 0.530

3.094 3.080 3.439 $ - $ 209.760

7.257 Table 3. Quadrupole deformation parameters, root mean square (r.m.s.) radii, binding energies, and Λ separation energies in the odd-A nucleus
$ ^{27}{\rm{Ne}} $ and the corresponding single-Λ hypernuclei$ ^{27}{\rm{Ne}}\otimes \Lambda $ with the Λ hyperon injected into the lowest s orbital or three p orbitals. The odd neutron is blocked in the$ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ orbitals, which correspond to the ground state and the second local energy minimum (denoted by asterisks), respectively.In Fig. 5, the density distributions
$ \rho(r,z) $ in the r-z plane with the symmetric axis along the z-axis are shown for the nucleus 27Ne (a) and the corresponding hypernucleus$ ^{28}_{\Lambda}{\rm{Ne}} $ (b,c,d). Cases with the core nucleus 27Ne in the ground state and the second local minimum (denoted by asterisks) as well as the single-Λ hyperon occupying the$ 1/2^+[000] $ (b),$ 1/2^-[110] $ (c), and$ 3/2^-[101] $ (d) orbitals are studied. In the upper and lower parts of panels (b–d), densities are plotted for the total hypernucleus and single-Λ hyperon, respectively. In Fig. 5(a), a prolate shape is observed for the ground state of 27Ne, while an oblate shape is observed for the second energy minimum. After introducing an$ s_{\Lambda} $ hyperon, in Fig. 5(b), the nuclear shapes remain almost unchanged but with an increment of inner density. Meanwhile, the injected$ s_{\Lambda} $ hyperon is slightly deformed and has the same shape as the core nucleus. In Fig. 5(c), a "dumbbell" shape is observed for the prolate$ p_{\Lambda} $ hyperon in the state of$ 1/2^-[110] $ , the addition of which increases (reduces) the prolate (oblate) deformation of the core nucleus in the ground state (second energy minimum). At the same time, owing to the coupling of the$ p_{\Lambda} $ hyperon and nuclear core, slight differences in the density distributions of the$ p_{\Lambda} $ hyperon are observed in the two cases (panel c). In Fig. 5(d), a "ring" shape is observed for the oblate$ p_{\Lambda} $ hyperon in the state of$ 3/2^-[101] $ . As a result, deformation of the prolate ground state decreases, and the oblate deformation of the second energy minimum is enhanced. A similar analysis of the impurity effects of the$ p_{\Lambda} $ hyperon on the nuclear density can be found in Refs. [38, 62].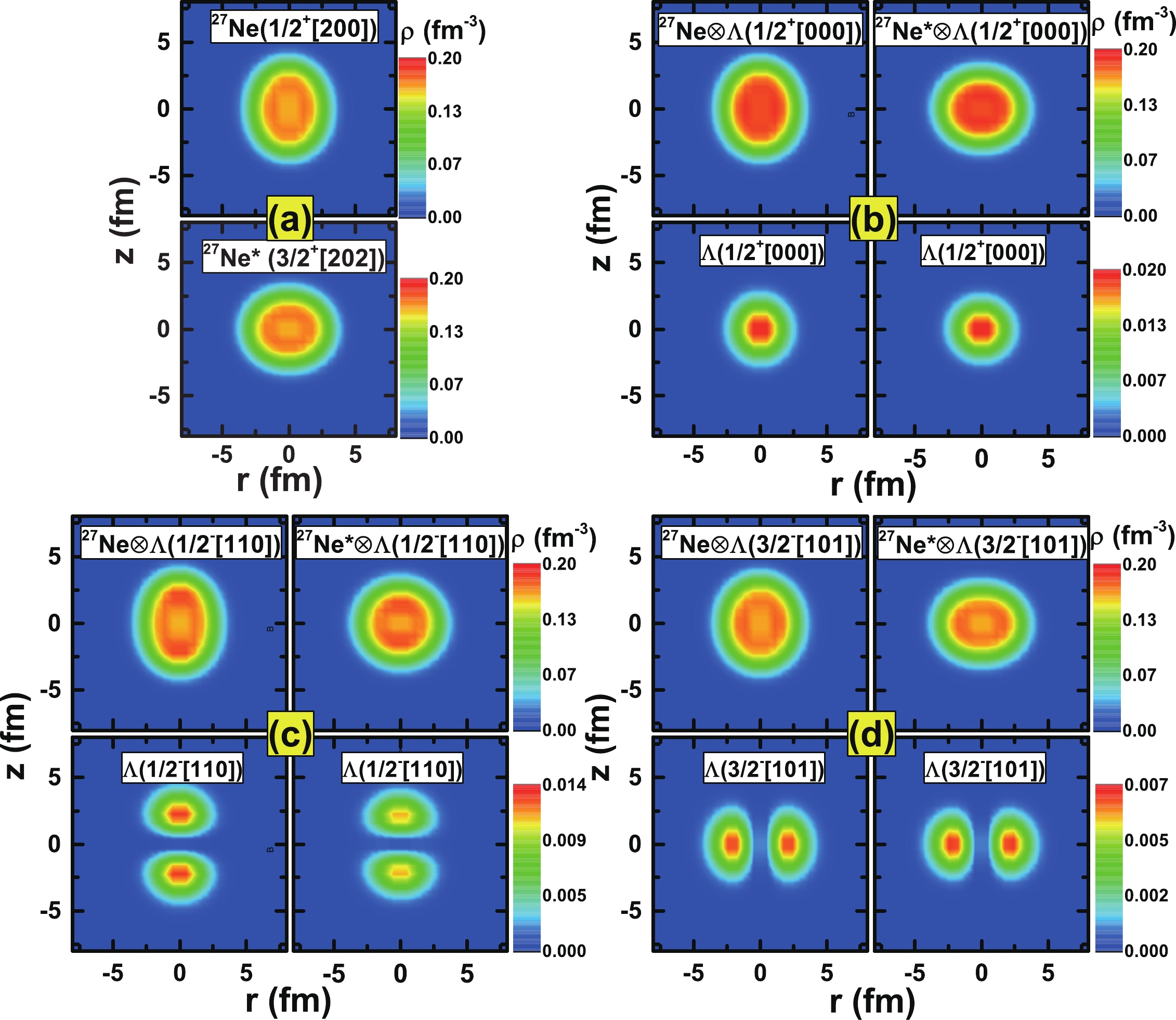
Figure 5. (color online) Two-dimensional density distributions in the r-z plane for (a) the core nucleus 27Ne and (b), (c), (d) the corresponding single-Λ hypernuclei with the Λ hyperon injected into the (b)
$ 1/2^+[000] $ , (c)$ 1/2^-[110] $ , and (d)$ 3/2^-[101] $ orbitals, respectively. The odd neutron in the ground state and the second local minimum (denoted by asterisks) occupies the$ 1/2^+[200] $ and$ 3/2^+[202] $ orbitals, respectively. The upper and lower parts of panels (b), (c), and (d) are the densities of the entire hypernuclei and the single-Λ hyperon, respectively.To explain the mechanism behind the effects of
$ s_{\Lambda} $ and$ p_{\Lambda} $ hyperons on nuclear densities and shapes in an intuitive way, taking$ ^{27}{\rm{Ne}}\otimes\Lambda $ with the core nucleus in the ground state an example, we presentdensity distributions ρ along the r- and z-axes in Fig. 6. For the$ s_{\Lambda} $ hyperon, almost the same density distributions (red dashed lines in the lower part of each panel) are found along the r- and z-axes; however, the distribution is slightly extended along the z-axis, which suggests the$ s_{\Lambda} $ hyperon has a weakly prolate shape. With the addition of an$ s_{\Lambda} $ hyperon to 27Ne, the nuclear density clearly increases in the inner part ($ r<3\; $ fm,$ z<2.5 $ fm) both in the directions of the r- and z-axes. However, for the densities on the outer nuclear side, different influences are found, that is,$ \rho(r) $ becomes slightly more extended while$ \rho(z) $ shrinks. These cause 27Ne$ \otimes\Lambda $ to become more spherical compared to the core nucleus. In the case of the$ p_{\Lambda} $ hyperon occupying$ 1/2^-[110] $ ,$ \rho(r) $ vanishes and a visible distribution is presented along the z-axis with a maximum at$ z=2.5 $ fm. As a result, a clear increment in the nuclear density along the z-axis is induced, and the nuclear shape becomes more prolate. For the$ p_{\Lambda} $ hyperon in the state of$ 3/2^-[101] $ , the nuclear density is enhanced in the direction of the r-axis and prolate deformation is weakened.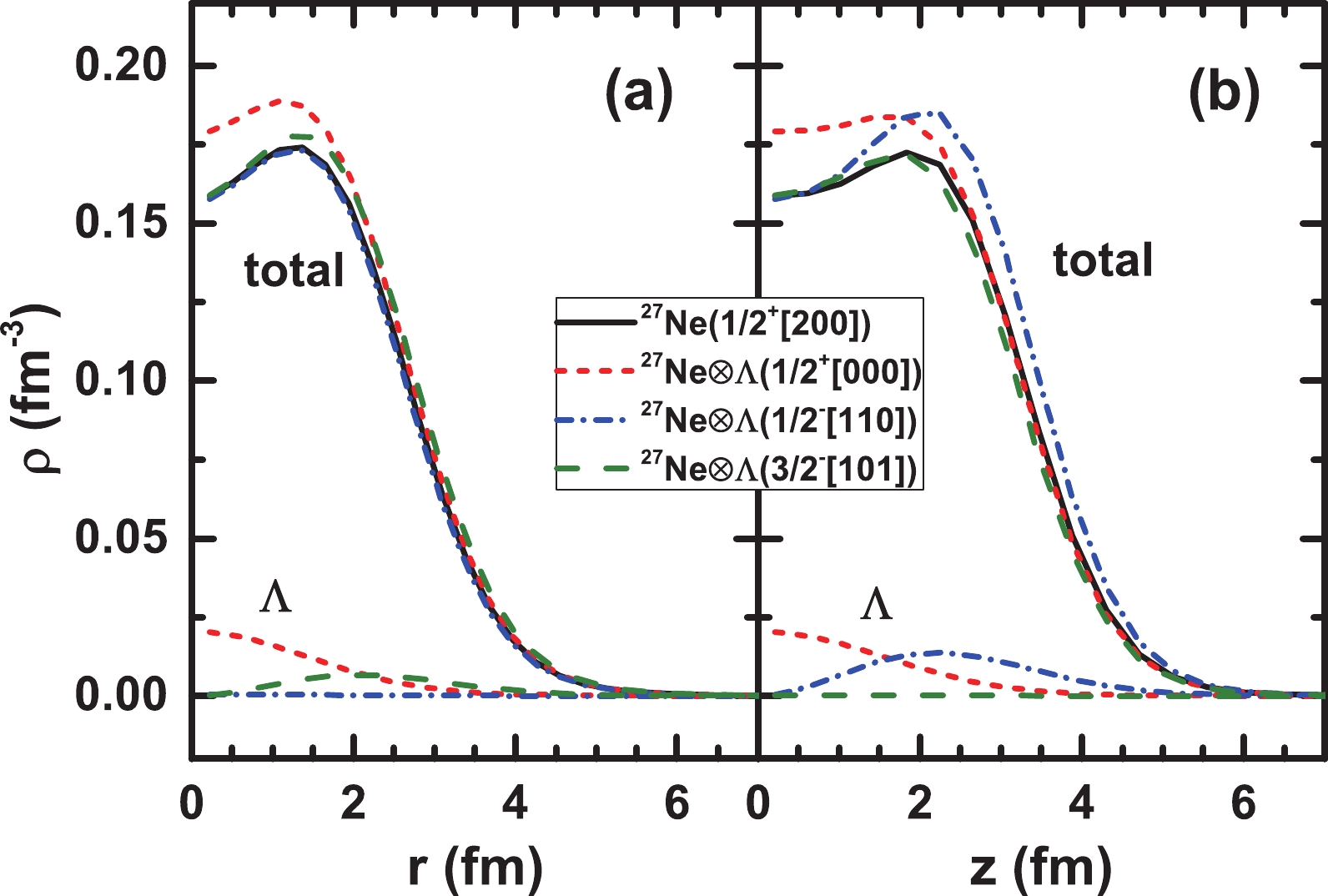
Figure 6. (color online) Density distributions
$ \rho(r,z) $ along the r-axis (a) and z-axis (b) in 27Ne with the odd neutron occupying$ 1/2^+[200] $ (solid lines) and the corresponding single-Λ hypernuclei (dashed lines) with the Λ hyperon injected into the$ 1/2^+[000] $ (red short dashed line),$ 1/2^-[110] $ (blue dash-dotted line), and$ 3/2^-[101] $ (olive dashed line) orbitals. In the upper and lower parts of each panel, density distributions contributed by the total nuclei and the Λ hyperon are plotted, respectively. -
In this study, following our previous research [Sci. China-Phys. Mech. Astron. 64, 282011(2021)], shape evolution and possible shape coexistence in odd-A Ne isotopes are explored using the MDC-RMF model, which has achieved great success in describing nuclear deformations. Moreover, by introducing s- or p-wave Λ hyperons, the impurity effects on nuclear shape, energy, size, and density distribution are discussed. For
$ NN $ and$ \Lambda N $ interactions in the RMF functional, the PK1 and PK1-Y1 parameter sets are adopted, respectively.By blocking the unpaired odd neutron in different orbitals around the Fermi surface, the nuclear ground state and other local energy minima are determined, and by examining the PECs, possible shape coexistences in
$ ^{27,29} $ Ne and a possible triple shape coexistence in 31Ne are predicted. For 27Ne, with the odd neutron blocked in the$ 1/2^{+}[200] $ and$ 3/2^{+}[202] $ orbitals, the ground state is observed in a prolate shape at a deformation of$ \beta_2=0.190 $ and the second energy minimum exhibits an oblate shape at$ \beta_2=-0.130 $ , respectively. A small energy difference of$ 0.333 $ MeV and a barrier with a height of$ 0.984 $ MeV between them are observed, supporting possible shape coexistence in 27Ne. Similarly, in 29Ne, with the odd neutron blocked in the$ 3/2^{+}[202] $ orbital, the prolate ground state is identified at$ \beta_2=0.080 $ , while the configuration with the odd neutron occupying$ 1/2^{+}[200] $ leads to an oblate second local minimum at$ \beta_2=-0.075 $ . In the case of 31Ne, possible triple shape coexistence, including the ground state at$ \beta_2=0.191 $ with the odd neutron blocked at$ 1/2^-[321] $ , the second local energy minimum at oblate deformation$ \beta_2=-0.090 $ with the odd neutron at$ 7/2^-[303] $ , and the third local minimum at prolate deformation$ \beta_2=0.429 $ with the odd neutron at$ 3/2^+[202] $ , is predicated.To discuss the impurity effects of
$ s_\Lambda $ and$ p_\Lambda $ hyperons, nuclear quadrupole deformations, r.m.s. radii, binding energies, and density distributions are compared in detail for 27Ne and the corresponding hypernuclei$ ^{28}_\Lambda $ Ne in cases where the odd neutron occupies the$ 1/2^+[200] $ and$ 3/2^+[202] $ orbitals. The$ s_{\Lambda} $ hyperon exhibits clear shrinkage effects, which reduces the nuclear size and deformation. In contrast, the$ p_\Lambda $ hyperon exhibits strong polarization effects, which may enhance the nuclear deformation. Meanwhile, the$ p_{\Lambda} $ hyperons occupying different orbitals exhibit different effects: the hyperon from the$ 1/2^-[110] $ orbital drives the nuclear shape to become more prolate, and the hyperon in the$ 3/2^-[101] $ or$ 1/2^-[101] $ state results in a more oblate nuclear shape. These conclusions are consistent with those for even-even Ne isotopes [62]. Furthermore, with the addition of the$ s_{\Lambda} $ hyperon, the energy difference$ \Delta E $ between the ground state and second local energy minimum decreases, which may increase the probability of shape coexistence. However, introducing a$ p_\Lambda $ hyperon results in a distinct disadvantage for shape coexistence in most of hypernuclei.In the present study, we investigate shape evolution and possible shape coexistence at the mean-field level by analyzing PECs. This is the first step in our research. Recently, in Refs. [82, 83], the angular momentum and parity projected multidimensionally constrained relativistic Hartree-Bogoliubov model was developed. In the future, we aim to go beyond the mean-field to perform studies [84–87]. Quantities such as electric quadrupole transitions
$ B(E2) $ will also be analyzed to study the shape coexistence and impurity effects of Λ hyperon, as conducted in Refs. [38, 88]. -
The authors thank Prof. Shan-Gui Zhou for providing the MDC-RMF code and helpful discussions. The theoretical calculation was supported by the nuclear data storage system at Zhengzhou University.
Possible shape coexistence in odd-A Ne isotopes and the impurity effects of Λ hyperons
- Received Date: 2022-01-26
- Available Online: 2022-07-15
Abstract: In this study, shape evolution and possible shape coexistence are explored in odd-A Ne isotopes in the framework of the multidimensionally constrained relativistic-mean-field (MDC-RMF) model. By introducing





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: