-
Experimental observation of neutrino oscillations has shown that neutrinos are large and lepton flavors are mixed, which clearly indicates the existence of new physics beyond the standard model. The natural method of accommodating the tiny neutrino masses is to introduce the unique Weinberg dimension-five operator
$ LLHH/\Lambda $ [1], where L and H denote the lepton and Higgs doublet, respectively, and Λ is the cut-off scale of new physics. After spontaneous gauge symmetry breaking, the Weinberg dimension-five operator gives rise to Majorana neutrino masses$ m_{\nu} \sim \langle H \rangle^2/\Lambda $ , with$ \langle H \rangle $ being the vacuum expectation value (vev) of the Higgs doublet; thus, the small size of the neutrino masses can be ascribed to the existence of a large new scale Λ. At tree-level, there are only three generic ways of obtaining the Weinberg dimension-five operator: the type-I [2–6], type-II [7–11], and type-III [12,13] seesaw mechanisms, in which three$SU(2)_{L}$ singlet right-handed neutrinos, an$SU(2)_{L}$ Higgs triplet, and three$SU(2)_{L}$ triplet fermions are added to the standard model, respectively. The key to testing these seesaw mechanisms is to search for the existence of the introduced heavy states. Because all three seesaw mechanisms violate the lepton-number in their own unique ways, we can probe the production signal of the relevant heavy particles via the lepton-number violating processes during ongoing and forthcoming experiments, if the mass of the heavy particles is in the TeV scale. In this study, we investigate the collider phenomenology of the Higgs triplet introduced in the type-II seesaw mechanism at future$ e^{-}p $ colliders.A typical feature of the type-II seesaw mechanism is that the introduced Higgs triplet can be produced directly through gauge interactions with electroweak bosons. In the framework of the type-II seesaw mechanism, there are seven physical Higgs bosons (that is,
$ H^{++} $ ,$H^{--}$ ,$ H^{+} $ ,$ H^{-} $ ,$ H^{0} $ ,$ h^{0} $ , and$ A^{0} $ ), and searches for new triplet scalars have been extensively conducted in various collider experiments (see Ref. [14] for recent reviews). In hadron colliders, new triplet scalars are mainly produced in pairs because single production and the associated production with gauge bosons are highly suppressed by the small Higgs triplet vev. Specifically, the most relevant production channels are the Drell-Yan processes via s-channel$ \gamma^\ast/Z^\ast $ or$ W^\ast $ exchange [15–27]. A pair of triplet scalars can also be produced via the vector boson fusion process [28, 29], among which charged Higgs pair production via the photon fusion process is of particular interest owing to the contribution from collinear photons, including both elastic and inelastic processes [30–32]. In addition, the pair production of triplet scalars via the gluon fusion process is found to be sub-leading with respect to the Drell-Yan process [33, 34]. At$ e^{+}e^{-} $ colliders, the most widely studied mode for triplet scalars is pair production via s-channel$ \gamma^\ast/Z^\ast $ exchange [35–38]. At$ e^{-}p $ colliders, the single production of triplet scalars with signal rates directly proportional to the Yukuwa coupling between the lepton doublet and Higgs triplet has been discussed in several earlier studies [39–41].$ ep $ colliders are hybrids of$ e^+e^- $ and$ pp $ colliders, which provide cleaner environments than$ pp $ colliders and higher center-of-mass energies than$ e^+e^- $ colliders. While one could search for triplet scalars at$ e^+e^- $ and$ pp $ colliders, it remains necessary to conduct studies at$ ep $ colliders because this may provide important complementary information. In this study, we investigate the production and decay of triplet scalars via the vector boson fusion process at future$ e^{-}p $ colliders, such as the FCC-ep [42] and ILC$ \otimes $ FCC [43]. Because the single production of triplet scalars via the vector boson fusion process is also highly suppressed by the small Higgs triplet vev, we focus on the production of a pair of triplet scalars. The dominant production channel considered here is the pair production of the doubly charged Higgs, which may decay into same-sign dileptons ($ \ell^{\pm}\ell^{\pm} $ ) or same-sign dibosons ($ W^{\pm}W^{\pm} $ ) depending on the size of the Higgs triplet vev. To explore the discovery potential of the doubly charged Higgs at future$ e^{-}p $ colliders, we discuss both of these decay scenarios in this paper.The remainder of the paper is organized as follows. The main properties of the type-II seesaw model are briefly reviewed in Section II, and the various constraints on the model parameters are summarized in Section III. In Section IV, the dominant production channels of triplet scalars via the vector boson fusion process and their decay properties are studied. The signal observability at future
$ e^{-}p $ colliders for both the lepton decay mode and gauge boson decay mode is discussed in Section V. Finally, we summarize our study in Section VI. -
In the type-II seesaw model, the Higgs sector is composed of the standard model Higgs doublet H with hypercharge
$ Y_{H}=1 $ and an$SU(2)_{L}$ Higgs triplet Δ with hypercharge$ Y_{\Delta}=2 $ , which can be expressed in matrix form as$ H = \left(\begin{array}{c} \phi^+ \\ \phi^{0} \end{array}\right) \; , \quad \Delta = \left(\begin{array}{cc} \delta^+/\sqrt{2} & \delta^{++} \\ \delta^{0} & -\delta^+/\sqrt{2}\end{array}\right) \; , $

(1) where
$ \phi^{+} $ ,$ \phi^{0} $ ,$ \delta^{++} $ ,$ \delta^{+} $ , and$ \delta^{0} $ are all complex scalar fields; therefore, there is a total of 10 degrees of freedom in the Higgs sector. The most general gauge-invariant Lagrangian relevant for the Higgs sector can be given by$ \begin{aligned}[b] {\cal L}_{\rm{type-II}} =& (D_{\mu}H)^{\dagger}(D^{\mu}H) + {\rm{Tr}}\left[(D_{\mu}\Delta)^{\dagger}(D^{\mu}\Delta)\right] \\&-V(H,\Delta)+{\cal L}_{\rm{Yukawa}} \; . \end{aligned} $

(2) Here, the covariant derivatives are defined as
$ \begin{aligned}[b] D_{\mu}H \equiv& \partial_{\mu}H + {\rm i} g \tau^{k} W_{\mu}^{k}H + {\rm i} g^{\prime} \frac{Y_{H}}{2} B_{\mu}H \; , \\ D_{\mu}\Delta \equiv& \partial_{\mu}\Delta + {\rm i} g \left[\tau^{k} W_{\mu}^{k},\Delta\right] + {\rm i} g^{\prime} \frac{Y_{\Delta}}{2} B_{\mu}\Delta \; , \end{aligned} $

(3) where
$ W_{\mu}^{k} $ ($ k=1,2,3 $ ) and$ B_{\mu} $ are the$SU(2)_{L}$ and$ U(1)_Y $ gauge fields, respectively. g and$ g^{\prime} $ are the corresponding gauge couplings, respectively, and$ \tau^{k}=\sigma^{k}/2 $ ($ k=1,2,3 $ ) represents the$SU(2)_{L}$ generator with$ \sigma^{k} $ being the Pauli matrices.There are seven large physical Higgs bosons in the model: doubly charged
$ H^{++} $ and$H^{--}$ , singly charged$ H^{+} $ and$ H^{-} $ , CP-even neutral$ H^{0} $ and$ h^{0} $ , and CP-odd neutral$ A^{0} $ , where$ h^{0} $ is marked as the SM-like Higgs boson and the remainder of the Higgs states are Δ-like. To derive the Higgs mass spectrum, a detailed study on the Higgs potential should be performed. In the framework of the type-II seesaw mechanism, the complete gauge invariant Higgs potential can be given by$ \begin{aligned}[b] V(H, \Delta)=&-m_{H}^{2} H^{\dagger} H+\frac{\lambda}{4}\left(H^{\dagger} H\right)^{2} +M_{\Delta}^{2} {\rm{Tr}} \left(\Delta^{\dagger} \Delta\right)\\& +\left(\mu H^{T} {\rm i} \sigma^{2} \Delta^{\dagger} H+{\rm{h.c.}}\right) +\lambda_{1}\left(H^{\dagger} H\right){\rm{Tr}} \left(\Delta^{\dagger} \Delta\right) \\&+\lambda_{2}\left({\rm{Tr}}\Delta^{\dagger} \Delta\right)^2 +\lambda_{3}{\rm{Tr}}\left(\Delta^{\dagger} \Delta\right)^2 +\lambda_{4}H^{\dagger}\Delta\Delta^{\dagger}H \; . \end{aligned} $

(4) Here,
$ m_{H} $ and$ M_{\Delta} $ are the mass parameters, and λ and$ \lambda_{i} $ $ (i= 1, 2, 3, 4) $ are five independent dimensionless couplings [20, 22]. Because we will simply consider a quasi-degenerate mass spectrum for the Δ-like Higgs states and be mainly interested in a heavy Higgs triplet, contributions from the terms proportional to$ \lambda_{i} $ can be safely neglected. It is worth noting that the term proportional to the μ parameter in Eq. (4) represents mixing between the Higgs doublet and triplet. When the neutral components of H and Δ acquire their vevs$ \langle H \rangle= \left(\begin{array}{c} 0 \\ v_{H}/\sqrt{2} \end{array}\right) \quad {\rm{and}} \quad \langle \Delta \rangle = \left(\begin{array}{cc} 0 & 0 \\ v_{\Delta}/\sqrt{2} & 0\end{array}\right) \; , $

(5) the gauge symmetry is spontaneously broken down. After minimizing the minimal Higgs potential in Eq. (4), we can easily obtain
$ v_{H} = \sqrt{\frac{4m_{H}^{2}M_{\Delta}^{2}}{\lambda M_{\Delta}^{2}-4\mu^{2}}} \; , \quad v_{\Delta} = \frac{\mu v_{H}^{2}}{\sqrt{2}M_{\Delta}^{2}} \; , $

(6) with
$ \sqrt{v_{H}^{2}+v_{\Delta}^{2}}\approx 246\; {\rm{GeV}} $ , where$ \lambda M_{\Delta}^{2}-4\mu^{2}>0 $ has been assumed. Note that the Higgs triplet vev$ v_{\Delta} $ contributes to the electroweak gauge boson masses and hence the ρ-parameter at tree-level. According to Eq. (5), the Higgs doublet and triplet can be redefined respectively as$\begin{aligned}[b] H =& \left(\begin{array}{c} \phi^+ \\ (v_{H} + \xi + {\rm i} \chi)/\sqrt{2} \end{array}\right) \; , \\ \Delta =& \left(\begin{array}{cc} \delta^+/\sqrt{2} & \delta^{++} \\ (v_{\Delta} + \zeta + {\rm i} \eta)/\sqrt{2} & \; -\delta^+/\sqrt{2}\; \end{array}\right) \; . \end{aligned}$

(7) Here, ξ, χ, ζ, and η are real scalar fields with zero vevs. Inserting Eq. (7) into Eq. (4), we have
$ \begin{aligned}[b] V(H, \Delta)&\supset M_{\Delta}^{2}\delta^{++}\delta^{--} + \sqrt{2}\mu v_{\Delta}\phi^+\phi^- -\mu v_{H}\left(\phi^+\delta^-+\phi^-\delta^+\right)\\&+M_{\Delta}^{2}\delta^+\delta^- +\frac{1}{4}\lambda v_{H}^{2}\xi^{2}-\sqrt{2}\mu v_{H}\xi\zeta \\&+\frac{1}{2}M_{\Delta}^{2}\zeta^{2} +\sqrt{2}\mu v_{\Delta}\chi^{2} - \sqrt{2}\mu v_{H}\chi\eta+\frac{1}{2}M_{\Delta}^{2}\eta^{2} \; , \end{aligned} $

(8) where only the Higgs mass terms are retained and the relationships in Eq. (6) have been used. The doubly charged
$ \delta^{\pm\pm} $ are their mass eigenstates, while the singly charged$ (\phi^{\pm},\; \delta^{\pm}) $ , CP-even neutral$ (\xi,\; \zeta) $ and CP-odd neutral$ (\chi,\; \eta) $ mix with each other. Eq. (8) can be further rewritten as$ \begin{aligned}[b] V(H, \Delta)&\supset M_{\Delta}^{2}\delta^{++}\delta^{--} + \left(\begin{array}{cc} \phi^+ & \delta^+ \end{array}\right)M_{\pm}^{2} \left(\begin{array}{c} \phi^- \\ \delta^- \end{array}\right) \\ &+ \left(\begin{array}{cc} \xi & \zeta \end{array}\right)\frac{1}{2}M_{\rm{even}}^{2} \left(\begin{array}{c} \xi \\ \zeta \end{array}\right) + \left(\begin{array}{cc} \chi & \eta \end{array}\right)\frac{1}{2}M_{\rm{odd}}^{2} \left(\begin{array}{c} \chi \\ \eta \end{array}\right) \; , \end{aligned} $

(9) with the mass-squared matrices
$ M_{\pm}^{2} $ ,$ M_{\rm{even}}^{2} $ , and$ M_{\rm{odd}}^{2} $ given by$ \begin{aligned}[b] M_{\pm}^{2} =& \left(\begin{matrix} \sqrt{2}\mu v_{\Delta} & -\mu v_{H} \cr -\mu v_{H} & M_{\Delta}^{2} \end{matrix}\right) \; , M_{\rm{even}}^{2} = \left(\begin{matrix} \lambda v_{H}^{2}/2 & -\sqrt{2}\mu v_{H} \cr -\sqrt{2}\mu v_{H} & M_{\Delta}^{2} \end{matrix}\right) \; ,\\ M_{\rm{odd}}^{2}=& \left(\begin{matrix} 2\sqrt{2}\mu v_{\Delta} & -\sqrt{2}\mu v_{H} \cr -\sqrt{2}\mu v_{H} & M_{\Delta}^{2} \end{matrix}\right) , \end{aligned} $

(10) which are all real and symmetric and can be diagonalized by orthogonal transformations. To diagonalize the above mass-squared matrices, we introduce three orthogonal matrices to rotate the Lagrangian fields into their mass eigenstates in the following way:
$ \begin{aligned}[b] \left(\begin{matrix} \phi^{\pm} \cr \delta^{\pm} \end{matrix}\right) =& \left(\begin{matrix} \cos{\theta_{\pm}} & -\sin{\theta_{\pm}} \cr \sin{\theta_{\pm}} & \cos{\theta_{\pm}} \end{matrix}\right) \left(\begin{matrix} G^{\pm} \cr H^{\pm} \end{matrix}\right) \; , \quad {\rm{with}} \quad \tan{\theta_{\pm}}=\frac{\sqrt{2}v_{\Delta}}{v_{H}} \; , \\ \left(\begin{matrix} \xi \cr \zeta \end{matrix}\right) =& \left(\begin{matrix} \cos{\alpha} & -\sin{\alpha} \cr \sin{\alpha} & \cos{\alpha} \end{matrix}\right) \left(\begin{matrix} h^{0} \cr H^{0} \end{matrix}\right) \; , \; {\rm{with}} \; \tan{2\alpha}=\frac{4v_{\Delta}/v_{H}}{1-\lambda v_{\Delta}/\left(\sqrt{2}\mu\right)} \; , \\ \left(\begin{matrix} \chi \cr \eta \end{matrix}\right) =& \left(\begin{matrix} \cos{\beta} & -\sin{\beta} \cr \sin{\beta} & \cos{\beta} \end{matrix}\right) \left(\begin{matrix} G^{0} \cr A^{0} \end{matrix}\right) \; , \quad {\rm{with}} \quad \tan{\beta}=\frac{2v_{\Delta}}{v_{H}} \; . \end{aligned}$

(11) After diagonalization, the Higgs mass spectrum can be given by
$ \begin{aligned}[b] &M_{H^{\pm\pm}}^{2} = M_{\Delta}^{2} \; , \quad M_{H^{\pm}}^{2} = M_{\Delta}^{2}\left(1+\frac{2v_{\Delta}^{2}}{v_{H}^{2}}\right) \; , \\ &M_{h^{0}}^{2} = M_{\Delta}^{2}\left(\frac{\lambda v_{\Delta}}{\sqrt{2}\mu}\cos^{2}{\alpha}+\sin^{2}{\alpha}-\frac{2v_{\Delta}}{v_{H}}\sin{2\alpha}\right) \; , \\ &M_{H^{0}}^{2} = M_{\Delta}^{2}\left(\frac{\lambda v_{\Delta}}{\sqrt{2}\mu}\sin^{2}{\alpha}+\cos^{2}{\alpha}+\frac{2v_{\Delta}}{v_{H}}\sin{2\alpha}\right) \; , \\ &M_{A^{0}}^{2} = M_{\Delta}^{2}\left(1+\frac{4v_{\Delta}^{2}}{v_{H}^{2}}\right) \; , \quad M_{G^{\pm}}^{2} = M_{G^{0}}^{2} = 0 \; , \end{aligned} $

(12) where the doubly charged mass eigenstates
$ \delta^{\pm\pm} $ are replaced by$ H^{\pm\pm} $ .$ G^{\pm} $ and$ G^{0} $ correspond to the charged and neutral massless Goldstone bosons, which give masses to the electroweak gauge bosons$ W^{\pm} $ and Z. Taking the limit of$ v_{\Delta}\ll v_{H} $ , we can obtain a quasi-degenerate mass spectrum for the Δ-like Higgs states$ M_{H^{\pm}}^{2} \simeq M_{H^{0}}^{2} \simeq M_{A^{0}}^{2} \simeq M_{H^{\pm\pm}}^{2} = M_{\Delta}^{2} \; . $

(13) In this minimal setting, cascade decays between two heavy triplet Higgs bosons, such as
$ \begin{aligned}[b] & H^{\pm\pm} \rightarrow H^{\pm}H^{\pm} \; , \quad H^{\pm\pm} \rightarrow H^{\pm}W^{\pm} \; , \\& H^{\pm} \rightarrow H^{0}W^{\pm}/A^{0}W^{\pm} \; , \quad H^{0} \rightarrow A^{0}Z \; , \end{aligned} $

(14) are kinematically forbidden.
Furthermore, tiny neutrino masses can be generated from the Yukawa interaction between the lepton doublet
$ \ell^{}_{\rm{L}} $ and Higgs triplet Δ.$ {\cal L}_{\rm{Yukawa}}=-Y_{\nu} \overline{(\ell_{L})^{c}}\, {\rm i} \sigma^{2} \Delta \ell_{L}+{\rm{h.c.}} \; , $

(15) where
$ \overline{(\ell_{L})^{c}}=(\ell_{L})^{T}C $ . C is the charge-conjugation operator, and$ Y_\nu $ is the$ 3\times3 $ neutrino Yukawa coupling matrix. After spontaneous gauge symmetry breaking, the effective Majorana neutrino mass matrix can be given by$ M_{\nu}=\sqrt{2}Y_{\nu}v_{\Delta} = Y_{\nu}\frac{\mu v_{H}^{2}}{M_{\Delta}^{2}} \; . $

(16) Here, the cut-off scale Λ of new physics is replaced by
$ M_{\Delta}^{2}/\mu $ . If$ \mu\ll M_{\Delta} $ , the small size of neutrino masses can be explained by the seesaw spirit. In this paper, to search for the existence of the introduced Higgs triplet at future$ e^{-}p $ colliders, we explore the production and decay of triplet scalars from a phenomenological point of view. Assuming that the mass eigenstates of the charged leptons are identified with their flavor eigenstates, the effective neutrino mass matrix can be diagonalized by the so-called Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix [44, 45], for which standard parametrization [46] can be given by$ V_{\rm{PMNS}} = \left( \begin{array}{ccc} c^{}_{13} c^{}_{12} & c^{}_{13} s^{}_{12} & s^{}_{13} {\rm e}^{-{\rm i}\delta} \\ -s_{12}^{} c_{23}^{} - c_{12}^{} s_{13}^{} s_{23}^{} {\rm e}^{{\rm i}\delta}_{} & + c_{12}^{} c_{23}^{} - s_{12}^{} s_{13}^{} s_{23}^{} {\rm e}^{{\rm i}\delta}_{} & c_{13}^{} s_{23}^{} \\ + s_{12}^{} s_{23}^{} - c_{12}^{} s_{13}^{} c_{23}^{} {\rm e}^{{\rm i}\delta}_{} & - c_{12}^{} s_{23}^{} - s_{12}^{} s_{13}^{} c_{23}^{} {\rm e}^{{\rm i}\delta}_{} & c_{13}^{} c_{23}^{} \end{array} \right) \times {\rm{diag}}\left(1,e^{{\rm i}\alpha_{1}/2},{\rm e}^{{\rm i}\alpha_{2}/2}\right) , $ 
(17) where
$ c^{}_{ij} \equiv \cos \theta^{}_{ij} $ and$ s^{}_{ij} \equiv \sin \theta^{}_{ij} $ have been defined. δ is the Dirac CP-violating phase, while$ \alpha_{1} $ and$ \alpha_{2} $ are two Majorana CP-violating phases. Using Eq. (16), we can rewrite the neutrino Yukawa coupling matrix as$ Y_{\nu}=\frac{M_{\nu}}{\sqrt{2}v_{\Delta}} = \frac{V_{\rm{PMNS}}^{\ast}\widehat{M_{\nu}}V_{\rm{PMNS}}^{\dagger}}{\sqrt{2}v_{\Delta}} \; , $

(18) where
$ \widehat{M_{\nu}}={\rm{Diag}}\{m_{1}, m_{2}, m_{3}\} $ , with$ m_i $ ($ i=1,2,3 $ ) being the neutrino mass eigenvalues. The values of$ Y_{\nu} $ are thus governed by the neutrino oscillation parameters and Higgs triplet vev. It is also worth noting that due to the simultaneous existence of the μ term in Eq. (4) and the Yukawa interaction term in Eq. (15), the lepton number in this model is explicitly violated by two units; therefore, we can probe the production signal of the introduced Higgs triplet via lepton-number violating processes. -
The latest global analysis of neutrino oscillation data [47] yields the best-fit values of the neutrino oscillation parameters.
$ \begin{aligned}[b] & \sin^2 \theta^{}_{12} \simeq 0.310 \; , \quad \sin^2 \theta^{}_{23} \simeq 0.563 \; , \quad \sin^2 \theta^{}_{13} \simeq 0.02237 \; , \\ &\Delta m^2_{21} \simeq 7.39\times 10^{-5}\; {\rm{eV}}^2 \; , \quad \Delta m^2_{31} \simeq 2.528 \times 10^{-3}\; {\rm{eV}}^2 \; , \\& \delta = 221^\circ \; , \end{aligned} $

(19) where only the normal ordering of neutrino masses (that is,
$ m^{}_1 < m^{}_2 < m^{}_3 $ ) is considered for illustrative purposes. The absolute scale of neutrino masses has not yet been determined experimentally, and the updated upper limit on the sum of the neutrino masses reported by the Planck collaboration is$ m_{1} + m_{2} + m_{3} < 0.12\; {\rm{eV}} $ [48]. For simplicity, the mass of the lightest neutrino is set to zero (that is,$ m^{}_1=0 $ ) in our numerical analysis, which is consistent with the experimental constraint [47, 48]. Because the neutrino oscillation probabilities are independent of the Majorana CP-violating phases, we further neglect the effects of the Majorana phases (that is,$ \alpha_{1}=\alpha_{2}=0 $ ). -
The charged Higgs bosons introduced in this model may induce numerous rare lepton flavor violating decays, such as
$ \ell_{\alpha}\to\ell_{\beta}\ell_{\gamma}\ell_{\delta} $ and$ \ell_{\alpha}\to\ell_{\beta}\gamma $ [49–53]. The experimental limits on the branching ratios of these various lepton flavor violating processes can be used to set several stringent constraints on the neutrino Yukawa coupling, and the most stringent bounds can be derived from the$ \mu \rightarrow e\gamma $ (mediated by$ H^{\pm\pm} $ and$ H^{\pm} $ ) and$ \mu \rightarrow 3e $ (mediated by$ H^{\pm\pm} $ ) decays [54].● The branching ratio for
$ \mu \rightarrow e\gamma $ can be expressed as$ {\rm{BR}}\left(\mu \rightarrow e\gamma\right)\simeq\frac{27\alpha\left|\left(Y_{\nu}^{\dagger}Y_{\nu}\right)^{e\mu}\right|^2}{64\pi G^{2}_{\rm F}M_{\Delta}^{4}} \; , $

(20) where α is the fine structure constant, and
$G_{\rm F}$ is the Fermi coupling constant. The current experimental limit$ {\rm{BR}}\left(\mu \rightarrow e\gamma\right) < 4.2 \times 10^{-13} $ (90% C.L.) [55] requires that$ \left|\left(Y_{\nu}^{\dagger}Y_{\nu}\right)^{e\mu}\right|< 2.4 \times 10^{-6}\times\left(\frac{M_{\Delta}}{100\; {\rm{GeV}}}\right)^2 \; , $

(21) ● the branching ratio for
$ \mu \rightarrow 3e $ is given by$ {\rm{BR}}\left(\mu \rightarrow 3e\right)\simeq\frac{\left|Y_{\nu}^{\mu e}\right|^2 \left|Y_{\nu}^{ee}\right|^2}{4\pi G^{2}_{\rm F}M_{\Delta}^{4}} \; . $

(22) Making use of the current experimental bound
$ {\rm{BR}}\left(\mu \rightarrow 3e\right) < 1.0 \times 10^{-12} $ ($ 90 $ % C.L.) [56], we can easily find that$ \left|Y_{\nu}^{\mu e}\right| \left|Y_{\nu}^{ee}\right| < 2.3 \times 10^{-7}\times\left(\frac{M_{\Delta}}{100\; {\rm{GeV}}}\right)^2 \; . $

(23) The doubly charged Higgs boson also contributes to the anomalous magnetic moment of electrons and muons, muonium-antimuonium conversion, and
$ e^{}e^{}\rightarrow \ell^{}\ell^{} $ scattering, which give much weaker limits on the Yukawa coupling (see Refs. [57,58] for reviews). -
As mentioned above, the Higgs triplet vev can contribute to the electroweak gauge boson masses at tree-level through
$ M_{W}^{2}=\frac{g^{2}}{4}\left(v_{H}^{2}+2v_{\Delta}^{2}\right) \; , \quad M_{Z}^{2}=\frac{g^{2}}{4\cos^{2}{\theta_{W}}}\left(v_{H}^{2}+4v_{\Delta}^{2}\right) \; , $

(24) where
$ \theta_{W} $ is the Weinberg angle. Thus, the ρ parameter in this model can be expressed as$ \rho=\frac{M_{W}^{2}}{M_{Z}^{2}\cos^{2}{\theta_{W}}}= \frac{1+2v_{\Delta}^{2}/v_{H}^{2}}{1+4v_{\Delta}^{2}/v_{H}^{2}}. $

(25) The electroweak precision measurement of the ρ parameter requires that
$ v_{\Delta}/v_{H}\lesssim 0.03 $ or$ v_{\Delta}<8\; {\rm{GeV}} $ [59]. Apart from the ρ parameter, the triplet Higgs sector also contributes to the S, T, and U parameters. However, because the masses of the triplet scalars are assumed to be degenerate in our analysis, the constraints from the S, T, and U parameters can be neglected. As shown in the previous subsection, the neutrino Yukawa coupling is strongly constrained by the lepton flavor violating processes, which in turn gives a lower bound on the Higgs triplet vev with the help of Eq. (16). Given the lower bound on$ v_{\Delta} $ , the assumptions on the neutrino mass hierarchy and setting the lightest neutrino mass to zero in Subsection III.A have no impact on the following discussions. In the conservative case, the value of the Higgs triplet vev used in our numerical analysis is assumed to be$ 10\; {\rm{eV}} \lesssim v_{\Delta} \lesssim 1\; {\rm{GeV}} \; . $

(26) -
Direct searches for triplet scalars have been conducted at the LHC for various production and decay modes. No significant deviations from standard model predictions have been found, and lower limits on the triplet masses are derived at the 95% confidence level. At present, the most stringent constraints mainly originate from searches for the doubly charged Higgs. The ATLAS collaboration has recently searched for
$ H^{\pm\pm} $ via the Drell-Yan process and released its preliminary results with an integrated luminosity of 36.1$ {\rm{fb}}^{-1} $ collected at$ \sqrt{s}=13\; {\rm{TeV}} $ . For the$ \ell^{\pm}\ell^{\pm}\; (e^{\pm}e^{\pm}/\mu^{\pm}\mu^{\pm}/e^{\pm}\mu^{\pm}) $ channel, the observed lower limit on the mass of$ H^{\pm\pm} $ varies from 770 GeV to 870 GeV for$ {\rm{BR}}(H^{\pm\pm} \rightarrow \ell^{\pm}\ell^{\pm}) = 100 $ % and is greater than 450 GeV for$ {\rm{BR}}(H^{\pm\pm} \rightarrow \ell^{\pm}\ell^{\pm}) \geq 10 $ % [60]. For the$ W^{\pm}W^{\pm} $ channel, the observed lower limit on the mass of$ H^{\pm\pm} $ is 220 GeV [61]. The CMS collaboration has also searched for$ H^{\pm\pm} $ in the pair production mode$ pp\rightarrow H^{++}H^{–}\rightarrow \ell^{+}_{}\ell^{+}_{}\ell^{-}_{}\ell^{-}_{} $ and the associated production mode$ pp\rightarrow H^{\pm\pm}H^{\mp}\rightarrow \ell^{\pm}_{}\ell^{\pm}_{}\ell^{\mp}_{}\nu_{} $ with an integrated luminosity of 12.9$ {\rm{fb}}^{-1} $ collected at$ \sqrt{s}=13\; {\rm{TeV}} $ . The lower bounds on the$ H^{\pm\pm} $ mass are established between 535 GeV and 820 GeV in the 100% branching ratio scenarios and between 716 GeV and 761 GeV for four benchmark points of the type-II seesaw model [62]. For singly charged$ H^{\pm} $ and neutral$ H^{0}/A^{0} $ , the summary of current constraints from the LHC experiments can be found in Ref. [63]. In the type-II seesaw model, the decay rate of an SM Higgs boson to diphoton can be modified through one-loop diagrams involving charged Higgs bosons if the couplings to the SM Higgs are large and the charged Higgs are relatively light. Because all the couplings$ \lambda_{1,2,3,4} $ in Eq. (4) are set to zero in our analysis, the constraints from the decay rate of the SM Higgs to diphoton are ignored here. -
In this section, we first discuss the dominant production channels of triplet scalars via the vector boson fusion process at
$ e^{-}p $ colliders and subsequently study their decay properties. -
In the vector boson fusion process, triplet scalars can be produced by the fusion of two virtual vector bosons, such as W, Z, or γ. Because the single production of triplet scalars is highly suppressed by the small Higgs triplet vev, we only consider the production of a pair of triplet scalars through
$ e^- + p \rightarrow e^- + S + S^{\prime} + j \; , $

(27) and
$ e^- + p \rightarrow \nu_{e} + S + S^{\prime} + j \; , $

(28) with S and
$ S^{\prime} $ being$ H^{\pm\pm} $ ,$ H^{\pm} $ ,$ H^{0} $ , or$ A^{0} $ (see Fig. 1). Because photon-mediated processes receive contributions from collinear photons, they should be treated with great care. Specifically, for the photon emitted from the electron, we employ the following photon density function [64]: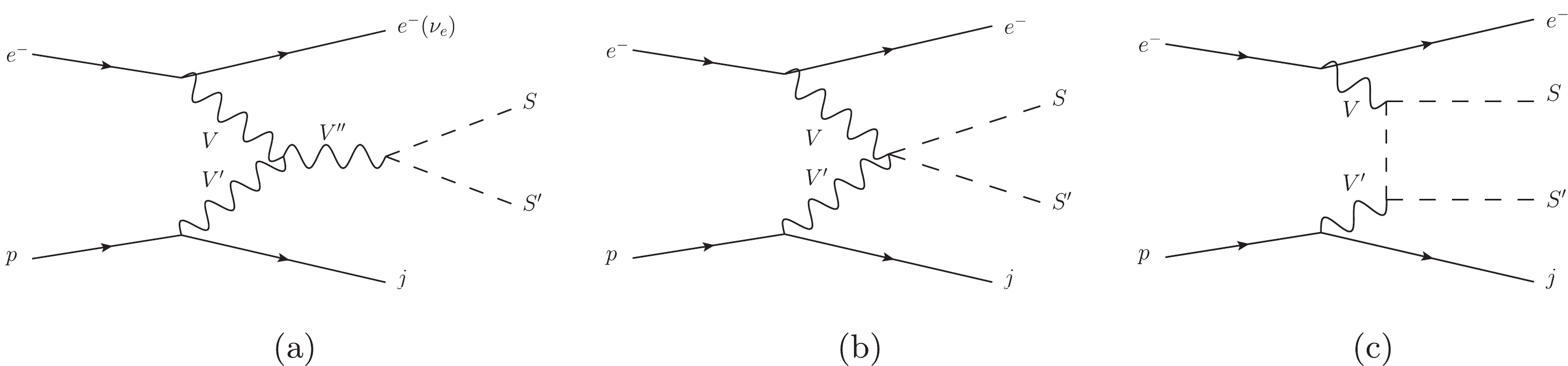
Figure 1. (color online) Feynman diagrams for the production of a pair of triplet scalars via the vector boson fusion process at
$ e^{-}p $ colliders, where the vector bosons V,$ V^{\prime} $ , and$ V^{\prime\prime} $ can be W, Z, or γ.$ \begin{aligned}[b] f_{\gamma/e^-}(x)=& \frac{\alpha}{2\pi}\left[\frac{1+(1-x)^2}{x}\ln{\frac{Q_{\rm{max}}^2}{Q_{\rm{min}}^2}}\right.\\&\left. + 2 m_e^2 x \left(\frac{1}{Q_{\rm{max}}^2}-\frac{1}{Q_{\rm{min}}^2}\right)\right] \; ,\end{aligned} $

(29) where
$ Q_{\rm{min}}^2=m_{e}^2 x^2/(1-x) $ ,$ Q_{\rm{max}}^2=(\theta_{c} E_{e})^2(1-x)+Q_{\rm{min}}^2 $ with x as the energy fraction of the photon and$ E_{e} $ as the energy of the electron,$ m_e=0.51\; {\rm{MeV}} $ as the mass of electron, and$ \theta_c=32\; {\rm{mrad}} $ as the cut of the electron scattering angle. As for the photon emitted from the proton, the photon parton distribution function$ f_{\gamma/p}(x, \mu^2_{f}) $ , which includes both elastic and inelastic contributions, is adopted, where$ \mu_{f} $ characterizes the factorization scale. Here, the CT14QED [65] parton distribution functions are employed in the calculation, and the factorization scale is set at$ \sqrt{\hat{s}} $ , where$ \hat{s} $ is the partonic center-of-mass energy.Before presenting the simulated results, we briefly summarize our simulation procedures. For the signal processes, we develop a package with the help of Form [66] to generate a Fortran code and take advantage of Vegas [67] to perform numerical integration. The backgrounds in the standard model are simulated using MadGraph [68].
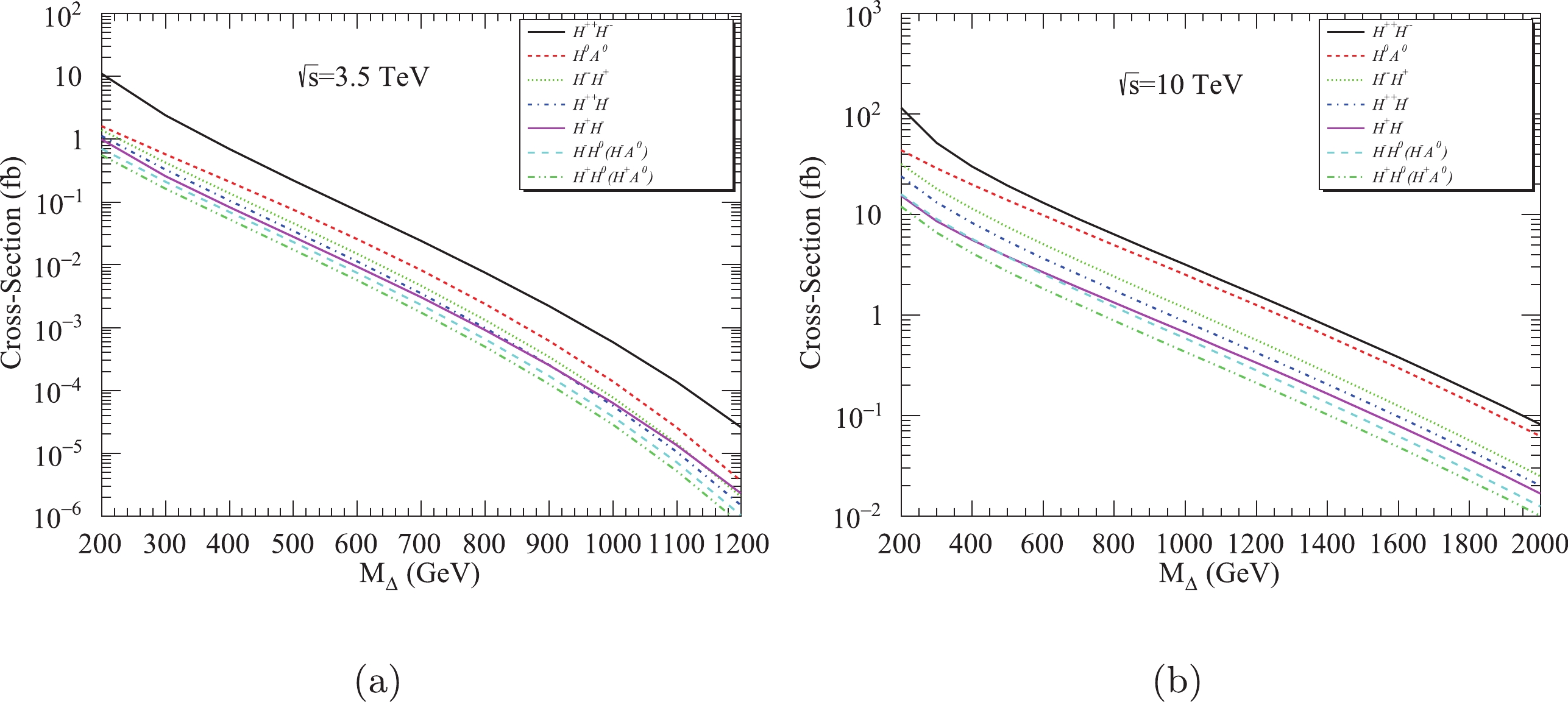
The total production cross sections of a pair of triplet scalars for the processes in Eq. (27) and Eq. (28) at the FCC-ep with
$ \sqrt{s}=3.5\; {\rm{TeV}} $ and the$ {\rm{ILC}}\otimes{\rm{FCC}} $ with$ \sqrt{s}=10\; {\rm{TeV}} $ are shown in Fig. 2 as a function of the triplet scalar mass. Here, our numerical results are presented only at leading order. Because we focus on the pair production of triplet scalars via the vector boson fusion process, NLO corrections can be approximately neglected [31]. The total production cross sections of a pair of triplet scalars via vector boson fusion processes depend on the couplings of triplet scalars to vector bosons. The detailed interactions of the Higgs triplet are presented in the Appendices of Refs. [20,22,26]. For example, the production cross section of$H^{++}H^{--}$ will be enhanced by a factor of 16 in the two photon channel with respect to$ H^{+}H^{-} $ . In Fig. 2, it is clear that the pair production of the doubly charged Higgs ($H^{++}H^{–-}$ ) has the largest production cross sections and will be used as the discovery channel to investigate the collider phenomenology of the Higgs triplet at future$ e^{-}p $ colliders in the next section. It is worth noting that the production cross sections of$H^{++}H^{--}$ considered here are independent of the values of the Yukawa couplings, which differs from the results of previous studies reported in Refs. [39–41]. -
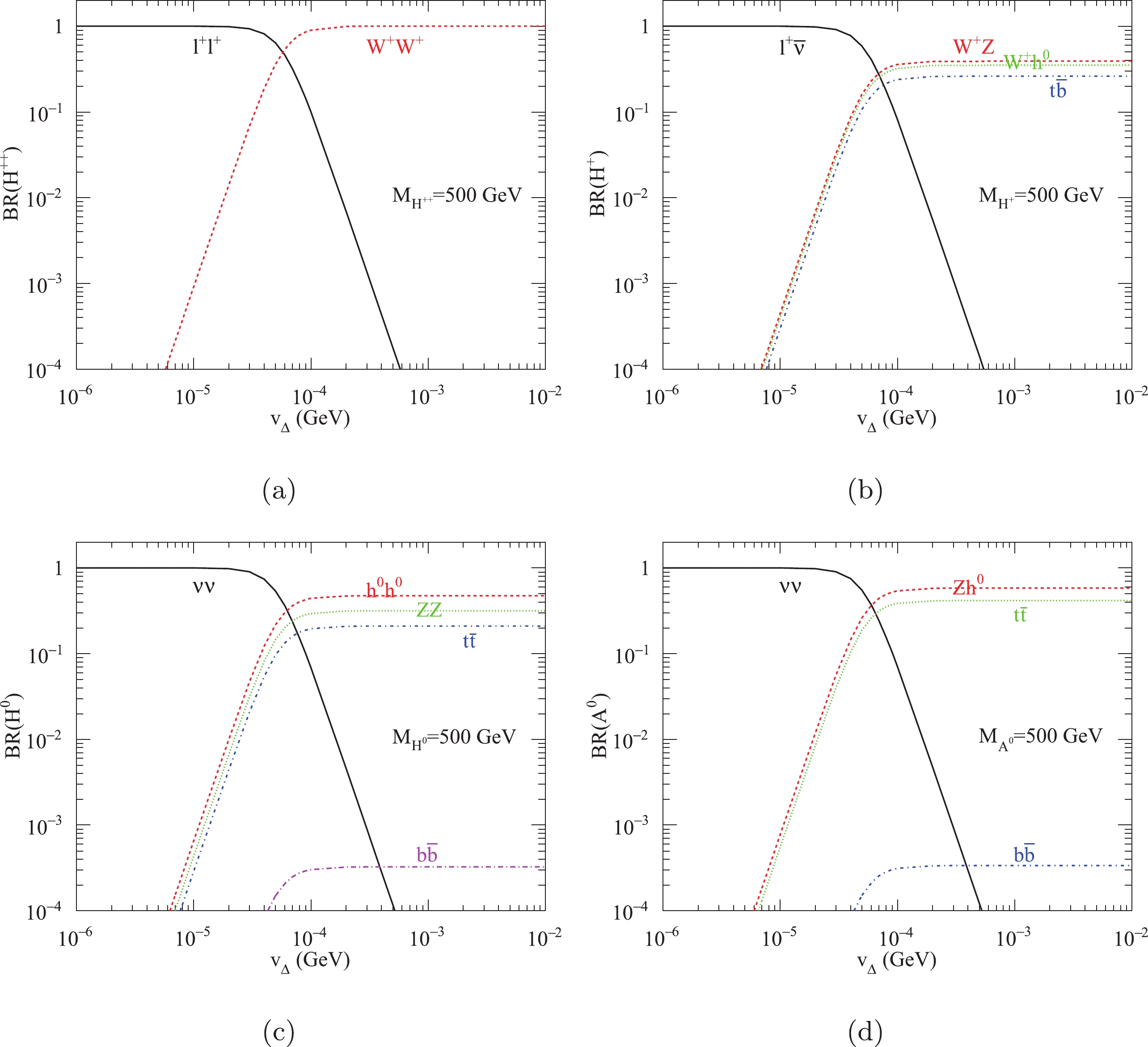
The decay rates of triplet scalars are sensitive to the Yukawa coupling and Higgs triplet vev, which are connected by the relation in Eq. (16). In Fig. 3, we plot the branching ratios of
$ H^{++} $ ,$ H^{+} $ ,$ H^{0} $ , and$ A^{0} $ as a function of$ v_{\Delta} $ for$ M_{\Delta}=500\; {\rm{GeV}} $ with the corresponding partial decay widths given in Ref. [20]. As shown in Fig. 3, the possible decays of$ H^{++} $ are$ H^{++} \rightarrow \ell^{+}\ell^{+} $ and$ H^{++} \rightarrow W^{+}W^{+} $ . For$ M_{H^{++}}=500\; {\rm{GeV}} $ , the same-sign dilepton decay dominates for small values of$ v_{\Delta} $ , while the same-sign diboson decay becomes important for large values of$ v_{\Delta} $ . In the case of$ H^{+} $ with$ M_{H^{+}}=500\; {\rm{GeV}} $ , the most relevant decay channel for small$ v_{\Delta} $ is$ H^{+} \rightarrow \ell^{+}\nu $ , while$ H^{+} \rightarrow W^{+}Z $ ,$ W^{+}h^{0} $ and$ H^{+} \rightarrow t\bar{b} $ are the dominant channels for large$ v_{\Delta} $ . For$ H^{0} $ and$ A^{0} $ with$ M_{H^{0},A^{0}}=500\; {\rm{GeV}} $ , the invisible decays$ H^{0} \rightarrow \nu\nu $ and$ A^{0} \rightarrow \nu\nu $ are the most important channels for small$ v_{\Delta} $ , while$ H^{0} \rightarrow h^{0}h^{0} $ ,$ ZZ $ ,$ t\bar{t} $ and$ A^{0} \rightarrow Zh^{0} $ ,$ t\bar{t} $ become dominant for large$ v_{\Delta} $ . All the decay properties of triplet scalars will provide useful information for the collider study in the next section. Note that the values of the Yukawa couplings in our numerical analysis are determined by the neutrino oscillation parameters and Higgs triplet vev, which are consistent with the constraints from lepton flavor violating measurements. -
As discussed in the previous section, the most important production channel for a pair of triplet scalars via the vector boson fusion process at
$ e^{-}p $ colliders is the pair production of doubly charged Higgs, and the produced doubly charged Higgs may decay into a pair of same-sign charged leptons or a pair of same-sign W bosons depending on the size of the Higgs triplet vev. To explore the discovery potential of the Higgs triplet at future$ e^{-}p $ colliders, we consider the inclusive production of the doubly charged Higgs through$e^{-}p\rightarrow H^{++} H^{--} + X$ with$H^{++}/H^{--}\rightarrow \ell^{+}\ell^{+}/\ell^{-}\ell^{-}$ and$H^{++}/H^{--}\rightarrow W^{+}W^{+}/W^{-}W^{-}$ . -
We first consider the case of a doubly charged Higgs decaying dominantly into a pair of same-sign charged leptons:
$ \begin{aligned}[b] & e^- + p \rightarrow e^- + H^{++} + H^{--} + j \; , \quad {\rm{with}} \\& H^{++} \rightarrow \ell^+\ell^+ \; , \quad H^{--} \rightarrow \ell^-\ell^- \; , \\& e^- + p \rightarrow \nu_{e} + H^{++} + H^{--} + j \; , \quad {\rm{with}} \\& H^{++} \rightarrow \ell^+\ell^+ \; , \quad H^{–} \rightarrow \ell^-\ell^- \; . \end{aligned} $

(30) The signal in this case consists of at least two same-sign dilepton pairs. The decay branching ratios of the doubly charged Higgs to different flavors can be easily computed using the best-fit values of the neutrino oscillation parameters in Eq. (19) with the assumption of
$ {\rm{BR}}(H^{\pm\pm}\rightarrow \ell^{\pm}\ell^{\pm})=100 $ % for small values of$ v_{\Delta} $ ; the numerical results are listed in Table 1. Note that this choice is also in agreement with the experimental constraints discussed in Section III. For illustration, we only concentrate on the cleanest dimuon production mode. By considering the decay branching ratios, the total cross sections for the inclusive process$e^{-}p\rightarrow $ $ H^{++} H^{--} + X\rightarrow $ $ 2\mu^{+}2\mu^{-}+ X$ at the FCC-ep and${\rm{ILC}}\otimes {\rm{FCC}}$ are shown in Fig. 4 as a function of$ M_{H^{\pm\pm}} $ . The shaded regions represent the uncertainties from the PDF with an energy scale varying from$ \sqrt{s}/2 $ to$ 2\sqrt{s} $ . It is clear that the uncertainties are 3% at most with respect to the tree-level results at the 3.5 TeV FCC-ep and up to 8% at the 10 TeV$ {\rm{ILC}}\otimes{\rm{FCC}} $ .$ ee $ 

$ e\mu $ 

$ e\tau $ 

$ \mu\mu $ 

$ \mu\tau $ 

$ \tau\tau $ 

BR 0.34% 1.28% 4.08% 36.2% 35.2% 22.9% Table 1. Decay branching ratios of doubly charged Higgs to different flavors.

Figure 4. (color online) Inclusive production cross sections for
$e^{-}p\rightarrow H^{++} H^{--} + X\rightarrow 2\mu^{+}2\mu^{-}+ X$ at the (a) FCC-ep and (b)$ {\rm{ILC}}\otimes{\rm{FCC}} $ as a function of$ M_{H^{\pm\pm}} $ . The shaded regions represent the uncertainties from the PDF with an energy scale varying from$ \sqrt{s}/2 $ to$ 2\sqrt{s} $ .To simulate the detector effects, we smear the lepton and jet energies according to the assumption of the Gaussian resolution parametrization
$ \frac{\delta(E)}{E} = \frac{a}{\sqrt{E}}\oplus b, $

(31) where
$ \delta(E)/E $ is the energy resolution, a is a sampling term, b is a constant term, and$ \oplus $ denotes the sum in quadrature. We take$ a=12.4 $ % and$ b=1.9 $ % for leptons and$ a=51.8 $ % and$ b=5.4 $ % for jets [69].For the processes in Eq. (30), the four muons originating from the
$ H^{\pm\pm} $ decay are labeled as$ \mu_{i} $ ($ i=1,2,3,4 $ ) and are ranked by$ p_{T} $ with$ p_{T}^{\mu_{1}}>p_{T}^{\mu_{2}}>p_{T}^{\mu_{3}}>p_{T}^{\mu_{4}} $ . To investigate the transverse momentum distributions of the final state particles, it is useful to define the differential distribution of the four muons as$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu}_{{T}}= $ $ 1/\sigma({\rm{d}}\sigma/{\rm{d}}p^{\mu_{1}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{\mu_{2}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{\mu_{3}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{\mu_{4}}_{{T}})/4$ . In Fig. 5, we plot the normalized transverse momentum distributions$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu,e,j}_{{T}}$ for$ M_{H^{\pm\pm}}=500\; {\rm{GeV}} $ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ . We observe that the transverse momentum of electrons is significantly softer than that of muons, and the transverse momentum of the final state particles becomes harder with increasing collider energy. The kinematical distributions displayed in these figures can provide useful information for setting basic acceptance cuts.
Figure 5. (color online) Normalized transverse momentum distributions (a)
$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu,e}_{{T}}$ and (b)$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{j}_{{T}}$ for$ M_{H^{\pm\pm}}=500\; {\rm{GeV}} $ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ .To identify the isolated lepton or jet, we define the angular separation between particle i and particle j as
$ \Delta R_{ij} = \sqrt{\Delta \phi^2_{ij}+\Delta\eta^2_{ij}}\; , $

(32) where
$ \Delta \phi_{ij}=\phi_{i}-\phi_{j} $ and$ \Delta\eta_{ij}=\eta_{i}-\eta_{j} $ , with$ \phi_{i} $ ($ \eta_{i} $ ) being the azimuthal angle (rapidity) of the related lepton or jet.According to the above distributions, we apply the basic acceptance cuts
$ p_{T}^{\ell} > 20\; {\rm{GeV}} , |\eta^{\ell}| < 2.5 , p_{T}^{j} > 20\; {\rm{GeV}} , |\eta^{j}| < 5 \; , $

(33) $ \min\{\Delta R_{\ell\ell},\; \Delta R_{\ell j},\; \Delta R_{jj}\} > 0.4 \; . $

(34) The dominant backgrounds in the standard model for the signal process are
$ e^{-}p \rightarrow e^{-}(\nu_{e})ZZjX $ and$e^{-}p \rightarrow $ $ e^{-}(\nu_{e})ZW^{\pm}W^{\mp}jX$ with$ Z \rightarrow \mu^{+}\mu^{-} $ and$ W^{\pm} \rightarrow \mu^{\pm}\nu_{\mu} $ , which are simulated using MadGraph [68]. To reduce the intermediate Z boson backgrounds, any opposite-sign dimuon pairs with an invariant mass close to$ M_{Z} $ are rejected.$ \left|M_{\mu^+\mu^-}-M_{Z}\right| > 20\; {\rm{GeV}} \; . $

(35) With an integrated luminosity of
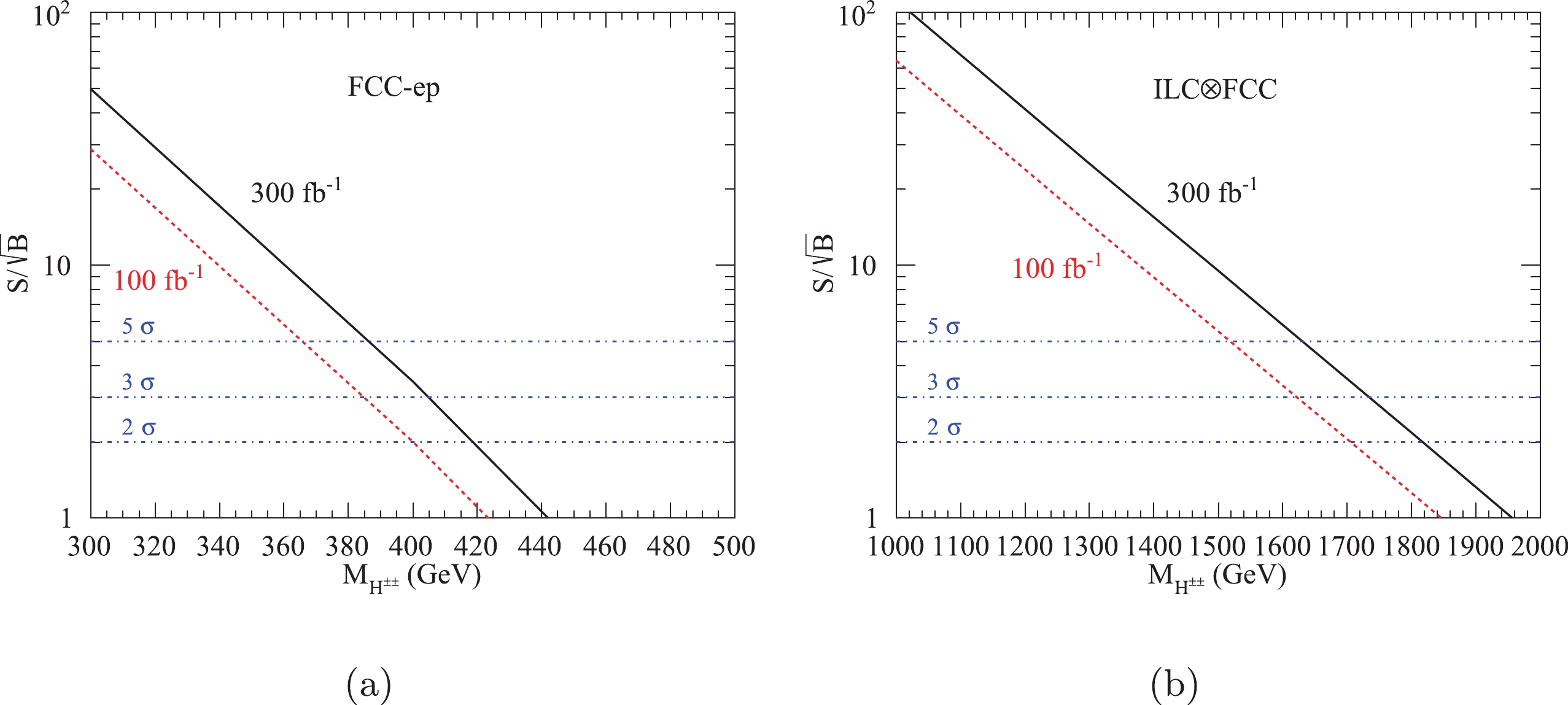
$ 100\; {\rm{fb}}^{-1} $ and$ 300\; {\rm{fb}}^{-1} $ , we display the statistical significance as a function of the doubly charged Higgs mass at the FCC-ep and ILC$ \otimes $ FCC in Fig. 6, where the statistical significance is defined as$S/\sqrt{B}$ with S(B) being the signal (background) event numbers after cuts. This reveals that, at the FCC-ep, the upper limit of the doubly charged Higgs mass is 400 GeV (418 GeV) with an integrated luminosity of$ 100\; {\rm{fb}}^{-1} $ ($ 300\; {\rm{fb}}^{-1} $ ) for 2σ discovery, which has already been ruled out by LHC experiments. At the ILC$ \otimes $ FCC, with an integrated luminosity of$ 100\; {\rm{fb}}^{-1} $ ($ 300\; {\rm{fb}}^{-1} $ ), the doubly charged Higgs mass can reach 1708 GeV (1818 GeV) at 2σ significance, 1622 GeV (1734 GeV) at 3σ significance, and 1518 GeV (1630 GeV) at 5σ significance. -
As mentioned previously, for large values of
$ v_{\Delta} $ , doubly charged Higgs decays will be dominated by a pair of same-sign W bosons. In this case, we focus on investigating the doubly charged Higgs in the following processes:$ \begin{aligned}[b] & e^- + p \rightarrow e^- + H^{++} + H^{--} + j \; , \quad {\rm{with}} \quad \\&\left\{ \begin{array}{ll} H^{++} \rightarrow W^+W^+ \; , \; H^{--} \rightarrow W^-W^- \; , \\ W^+W^+ W^-W^- \rightarrow \ell^{\pm}\ell^{\pm}{\notE}_{T} + 4j \; , \end{array} \right. \\ & e^- + p \rightarrow \nu_{e} + H^{++} + H^{--} + j \; , \quad {\rm{with}} \\& \left\{ \begin{array}{ll} H^{++} \rightarrow W^+W^+ \; , \; H^{--} \rightarrow W^-W^- \; , \\ W^+W^+ W^-W^- \rightarrow \ell^{\pm}\ell^{\pm}{\notE}_{T} + 4j \; . \end{array} \right. \end{aligned} $

(36) For the processes in Eq. (36), we demand two same-sign W bosons in their leptonic decays, and the remaining two decay hadronically. As before, we only concentrate on the muon production mode. Including the decay branching ratios, we display the total cross sections for the inclusive process
$e^{-}p\rightarrow H^{++} H^{--} + X\rightarrow $ $ \mu^{\pm}\mu^{\pm}{\notE}_{T}4j+ X$ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ in Fig. 7 as a function of$ M_{H^{\pm\pm}} $ . The uncertainties from the PDF estimated by scaling the energy scale from$ \sqrt{s}/2 $ to$ 2\sqrt{s} $ are also given as shaded regions.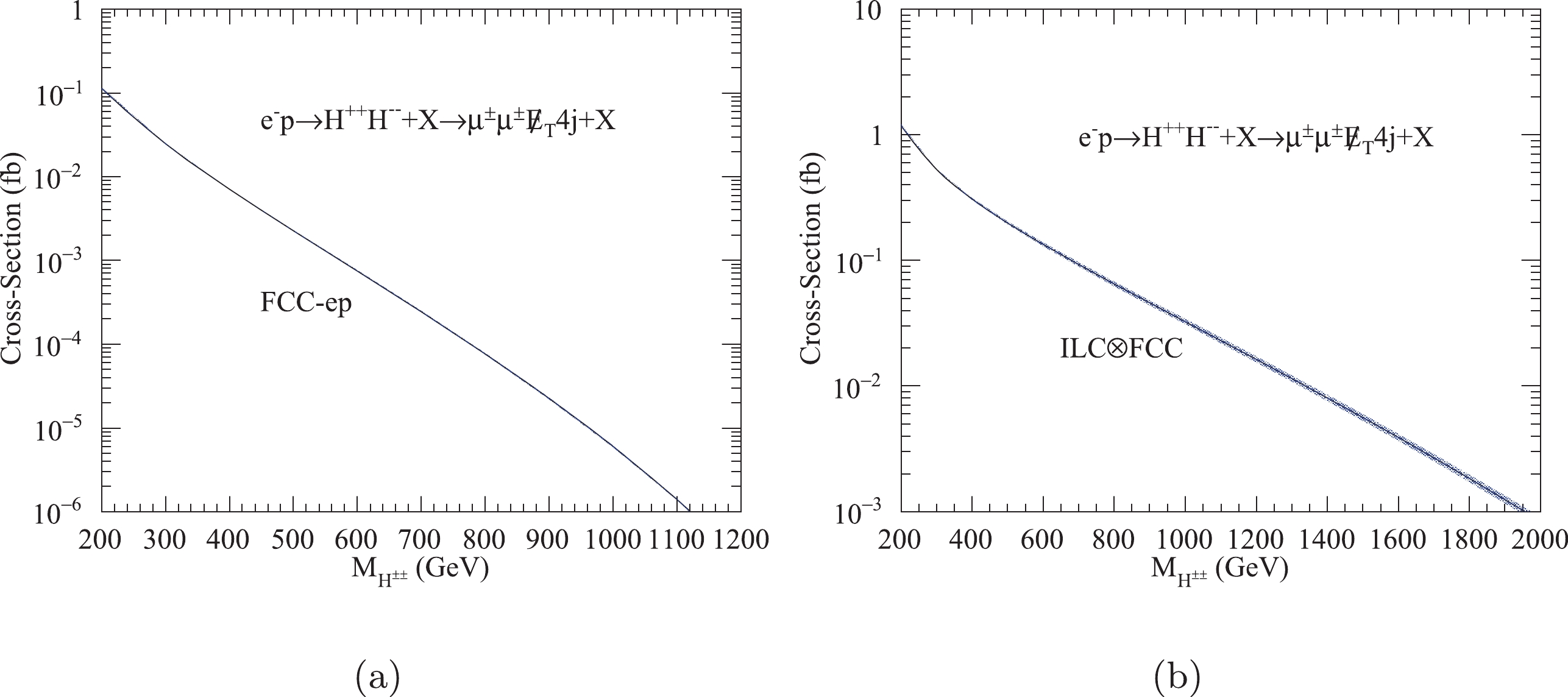
Figure 7. (color online) Inclusive production cross sections for
$e^{-}p\rightarrow H^{++} H^{--} + X\rightarrow \mu^{\pm}\mu^{\pm}{\notE}_{T}4j+ X$ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ as a function of$ M_{H^{\pm\pm}} $ . The shaded regions represent the uncertainties from the PDF with an energy scale varying from$ \sqrt{s}/2 $ to$ 2\sqrt{s} $ .After smearing the lepton and jet energies with the help of Eq. (31), we investigate the transverse momentum distributions of the final state particles for the processes in Eq. (36). The two muons in the final states are labeled as
$ \mu_{i} $ ($ i=1,2 $ ) and are ranked by$ p_{T} $ with$ p_{T}^{\mu_{1}}>p_{T}^{\mu_{2}} $ . Analogously, the transverse momentum differential distribution of the two muons is defined as$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu}_{{T}}=1/\sigma({\rm{d}}\sigma/{\rm{d}}p^{\mu_{1}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{\mu_{2}}_{{T}})/2$ . For jets, the four jets$ j_{i} $ ($ i=1,2,3,4 $ ) that possess an invariant mass closest to$ M_{H^{\pm\pm}} $ are selected and are ranked by$ p_{T} $ with$ p_{T}^{j_{1}}>p_{T}^{j_{2}}>p_{T}^{j_{3}}>p_{T}^{j_{4}} $ . We define the transverse momentum differential distribution of the four selected jets as$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{j}_{{T}}=1/\sigma({\rm{d}}\sigma/{\rm{d}}p^{j_{1}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{j_{2}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{j_{3}}_{{T}}+{\rm{d}}\sigma/{\rm{d}}p^{j_{4}}_{{T}})/4$ . The remaining jet produced in association with$H^{++}H^{--}$ is denoted by$ j_5 $ . In Fig. 8, we plot the normalized transverse momentum distributions$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu,e,j,j_5}_{{T}}$ for$M_{H^{\pm\pm}}= $ $ 500\; {\rm{GeV}}$ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ . The tendency of the transverse momentum of the final state leptons is similar to that in Fig. 5, but becomes more moderate. As for the jets, we find that the transverse momentum of the jet produced in association with$H^{++}H^{--}$ is softer than that from the$ H^{\pm\pm} $ decay. The kinematical features of the final state particles can provide useful information for setting basic acceptance cuts.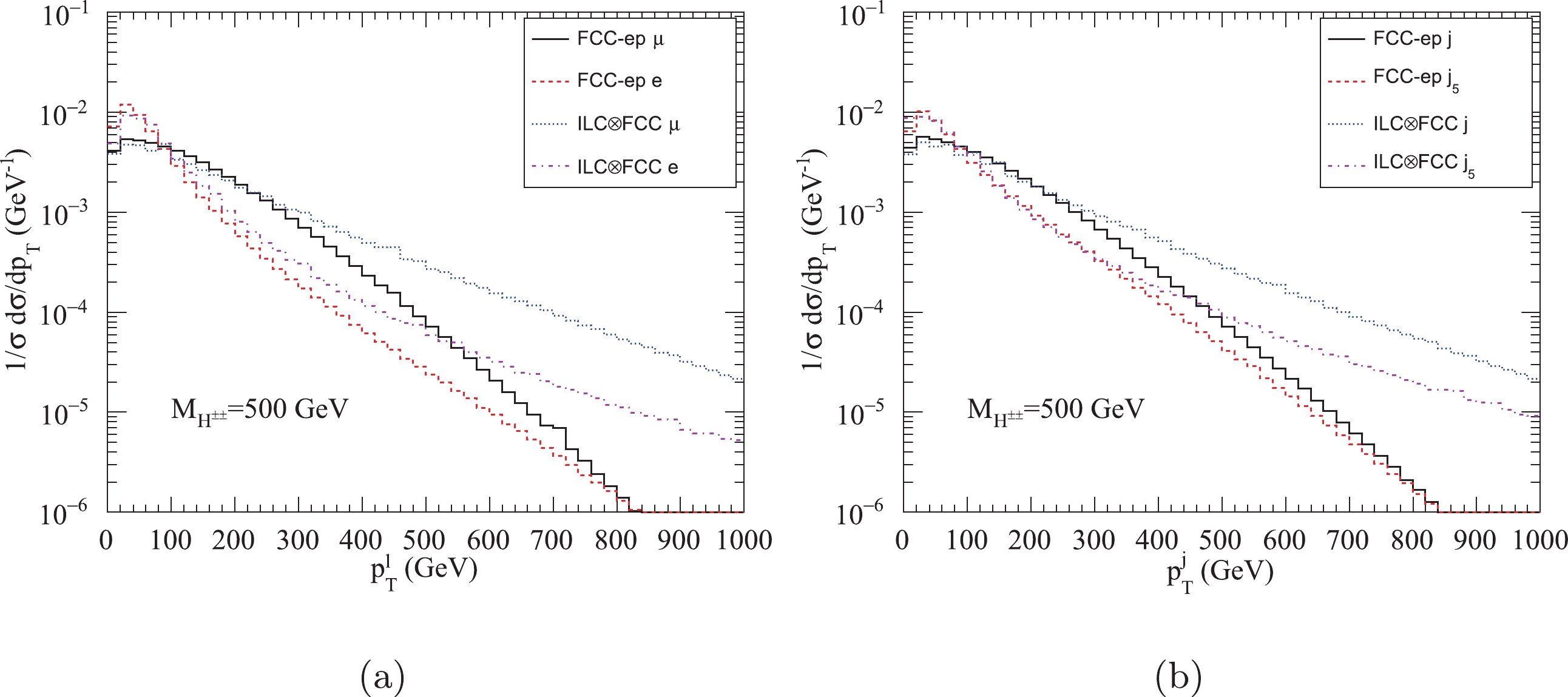
Figure 8. (color online) Normalized transverse momentum distributions (a)
$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{\mu,e}_{{T}}$ and (b)$1/\sigma{\rm{d}}\sigma/{\rm{d}}p^{j}_{{T}}$ for$ M_{H^{\pm\pm}}=500\; {\rm{GeV}} $ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ .Using the above distributions, we begin with the following basic cuts:
$\begin{aligned}[b] p_{T}^{\ell} > 20\; {\rm{GeV}} \; , \;\; |\eta^{\ell}| < 2.5 \; ,\;\; p_{T}^{j} > 20\; {\rm{GeV}} \; , \;\; |\eta^{j}| < 5 \; , \end{aligned} $

(37) $ \min\{\Delta R_{\ell\ell},\; \Delta R_{\ell j},\; \Delta R_{jj}\} > 0.4 \; , \quad {\notE}_{T} > 30\; {\rm{GeV}} \; , $

(38) as in Eq. (33) and Eq. (34), but with an additional cut on the missing transverse energy. The leading background to the signal is
$\begin{aligned}[b] e^-p& \rightarrow e^-(\nu_e) t\bar{t}W^{\pm}j \rightarrow e^-(\nu_e) b\bar{b}W^+W^-W^{\pm}j\\& \rightarrow e^-(\nu_e) \mu^{\pm}\mu^{\pm} b\bar{b}jjj\nu_{\mu}\nu_{\mu} \; . \end{aligned} $

(39) To further purify the signal, the invariant mass of
$ j_1,j_2,j_3,j_4 $ close to$ M_{H^{\pm\pm}} $ is required.$ |M_{j_{1}j_{2}j_{3}j_{4}} - M_{H^{\pm\pm}}| < 30\; {\rm{GeV}} \; . $

(40) In Fig. 9, we display the statistical significance as a function of the doubly charged Higgs mass with integrated luminosities of
$ 100\; {\rm{fb}}^{-1} $ and$ 300\; {\rm{fb}}^{-1} $ at the FCC-ep and ILC$ \otimes $ FCC, respectively. It is found that, at 2σ significance, the upper limit of the doubly charged Higgs mass is 216 GeV (251 GeV) at the FCC-ep with the integrated luminosity of$ 100\; {\rm{fb}}^{-1} $ ($ 300\; {\rm{fb}}^{-1} $ ), which is difficult to probe. At the ILC$ \otimes $ FCC, with the integrated luminosity of$ 100\; {\rm{fb}}^{-1} $ ($ 300\; {\rm{fb}}^{-1} $ ), the doubly charged Higgs mass up to 386 GeV (482 GeV) can be probed for 2σ discovery, while the upper limit is 321 GeV (418 GeV) for 3σ discovery and 252 GeV (328 GeV) for 5σ discovery. -
To explain the tiny neutrino masses, an
$SU(2)_L$ Higgs triplet Δ is introduced to the standard model in the framework of the type-II seesaw mechanism. A typical feature of the type-II seesaw mechanism is that the introduced Higgs triplet can be produced directly through gauge interactions with electroweak bosons. In this study, we explore the pair production of the doubly charged Higgs via the vector boson fusion process at future$ e^- p $ colliders. Depending on the size of the Higgs triplet vev, the doubly charged Higgs may decay into a pair of same-sign charged leptons or a pair of same-sign W bosons. We investigate these two decay scenarios in detail. The total cross sections for the inclusive processes$e^{-}p\rightarrow H^{++} H^{--} + $ $ X\rightarrow 2\mu^{+}2\mu^{-}+ X$ and$e^{-}p\rightarrow H^{++} H^{--} $ $ + X\rightarrow \mu^{\pm}\mu^{\pm}{\notE}_{T}4j+ $ $ X$ at the FCC-ep and$ {\rm{ILC}}\otimes{\rm{FCC}} $ are predicted. Furthermore, the transverse momentum distributions of the final state particles for the signal processes are studied. Finally, we derive the discovery potential of the doubly charged Higgs at future$ e^- p $ colliders. We found that it is difficult to probe the doubly charged Higgs at the FCC-ep. However, it is possible to conduct the study at the ILC$ \otimes $ FCC. Specifically, with an integrated luminosity of$ 100\; {\rm{fb}}^{-1} $ ($ 300\; {\rm{fb}}^{-1} $ ), the doubly charged Higgs mass can reach 1708 GeV (1818 GeV) at 2σ significance, 1622 GeV (1734 GeV) at 3σ significance, and 1518 GeV (1630 GeV) at 5σ significance for the dilepton decay mode, while the upper limit is 386 GeV (482 GeV) at 2σ significance, 321 GeV (418 GeV) at 3σ significance, and 252 GeV (328 GeV) at 5σ significance for the diboson decay mode. The production of doubly charged Higgs at the ILC$ \otimes $ FCC is an important complement to that at current and future hadron colliders. As discussed in Ref. [14], the doubly charged Higgs mass can reach$ 0.75\; (1.1)\; {\rm{TeV}} $ at the$ 2\sigma $ level for the lepton decay mode with$ {\cal L} = 300\; (3000)\; {\rm{fb}}^{-1} $ at the$ 14\; {\rm{TeV}} $ LHC. Meanwhile, statistically significant signals up to$ 600\; {\rm{GeV}} $ can be achieved for the boson decay mode with$ {\cal L} = 300\; {\rm{fb}}^{-1} $ at the$ 14\; {\rm{TeV}} $ LHC. Comparing the above projected results, we conclude that the ILC$ \otimes $ FCC can probe significantly larger values of$ M_\Delta $ for the lepton decay mode. -
The authors would like to thank Profs. Yi Jin, Hong-Lei Li, Shi-Yuan Li, and Zong-Guo Si for their helpful discussions.
Doubly charged Higgs production at future ep colliders
- Received Date: 2022-01-07
- Available Online: 2022-06-15
Abstract: The Higgs sector of the standard model can be extended by introducing an






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: