-
The generation of unstable exotic nuclei, which is a crucial subject pertaining to the technology upgrade in producing radioactive isotope (RI) beams (see Refs. [1, 2] and references therein), has made great progress in recent times. Exotic features of nuclear structure, such as neutron halos [3] and new magic numbers [4–6], have been confirmed in present laboratories. However, most of the neutron-rich nuclei far from the stability valley will remain beyond experimental access for the foreseeable future. Therefore, universal and unified theoretical models are required. Particularly, precise predictions for very neutron-rich nuclei and the limits of nuclear binding are responsible for understanding r-process nucleosynthesis [7, 8] and neutron star crusts [9, 10].
Within the nonrelativistic framework, many well-calibrated mass models have been developed and can be primarily separated into two categories. The macroscopic-microscopic models, such as the finite range droplet model (FRDM) [11, 12], the WS4 model [13], and others [14–16], contain both macroscopic and microscopic terms in the expression of nuclear energy and thus can account for most of physics. The microscopic mean-field models rely on various energy density functionals constrained by fitting experimental data, such as the Skyrme Hartree-Fock-Bogoliubov (HFB) model within diverse parametrizations [17, 18] and Gogny HFB with D1S [19] and D1M [20, 21] interactions. In these calculations [19–21], the dynamical correlation energies (DCEs) have been taken into account self-consistently by using a five-dimensional collective Hamiltonian (5DCH) based on the constrained mean-field calculations [22, 23], and the root-mean-square (rms) deviation with respect to the measured nuclear masses has been reduced significantly from several MeV to a few hundred keV [24, 25]. The DCEs have also been systematically studied by the generator coordinate method (GCM) for the ground-state properties of even-even nuclei by imposing axial symmetry [26–31]. Very recently, the two-dimensional GCM with both the quadrupole and octupole deformations as generator coordinates was used to calculate the DCEs for a set of Xe, Ba, Ce, and Nd isotopes [32]. Comparing to other beyond-mean-field calculations, 5DCH model with parameters determined by the mean-field calculations is much cheaper in numerical realization.
Covariant density functional theory (CDFT) has proven to be a powerful theory in nuclear physics which has been used to describe successfully a variety of nuclear phenomena [33–41]. Based on CDFT, lots of efforts have been made to develop self-consistent mass tables [42–47], such as the axially symmetric deformed relativistic mean-field plus Bardeen-Cooper-Schrieffer (RMF+BCS) approach [43] and relativistic Hartree-Bogoliubov (RHB) [45], with an accuracy as
$ \sim $ 2 MeV. Containing the deformation and continuum effects simultaneously, the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) was developed [48–51]. DRHBc has been applied to a variety of investigations, including the interpretaton of deformed halo nuclei [48, 49, 52–57], the deformation effects on neutron drip line and shape coexistence in nuclei [58–60], and the possible peninsulas beyond the two-neutron drip line [61–63]. Very recently, our DRHBc Mass Table Collaboration has performed a global mass table calculation using the PC-PK1 functional [64] for even-even nuclei with$ 8 \leq Z \leq 120 $ [65, 66]. The rms deviations of binding energies are 2.744 MeV and 1.518 MeV without and with a rotational correction, respectively.The present version of the DRHBc mass table is within the mean-field frame and only contains a simplified rotational correction energy in the cranking approximation, which cannot treat the weakly deformed nuclei properly, e.g.,
$ |\beta|\le0.05 $ , and cannot take into account large shape fluctuations for transitional nuclei. Therefore, even though the rms deviation for binding energies is lowered significantly, the two-nucleon separation energies are almost unchanged or even worse. To reduce the rms deviation further, especially for the separation energies, one needs to take into account the beyond-mean-field dynamical correlation energies. Recently, some attempts to calculate the DCEs systematically using the 5DCH [67, 68] based on the triaxial RMF+BCS [69] and triaxial RHB [70] calculations have been performed. After taking into account DCEs, the rms deviation of nuclear masses is reduced significantly down to 1.14 MeV in the former calculation [69], and down to 1.31 MeV in the latter one [70]. In addition, the DCEs and their effects on$ S_{2n} $ and$ \Delta S_{2n} $ for the neutron-rich Er, Yb, Hf, and W isotopes have been analyzed using the GCM method based on axially symmetric RMF+BCS [71].In this work, we will extend the DRHBc theory to go beyond mean-field framework by performing a two-dimensional collective Hamiltonian (2DCH). This model can describe the axially symmetric deformed quadrupole vibration and rotation and allow one to examine the influence of the dynamical correlations on the ground-state properties, including the binding energies, two-neutron separation energies, and quadrupole deformations for Se, Nd, and Th isotopes, which locate in different nuclear mass regions. Moreover, the effect of pairing correlations on the DCEs will be discussed. This work provides the first investigation on the dynamical correlations in the relativistic framework containing the continuum effect in the coordinate space, which is crucial for the description of nuclei in the vicinity of neutron drip line.
The theoretical framework for DRHBc+2DCH is presented in Sec. II. Numerical details and the results are presented in Sec. III, in comparison with the results of DRHBc without and with
$ E_{\rm{rot}} $ and available data [72]. A summary is provided in Sec. IV. -
The relativistic Hartree-Bogoliubov (RHB) equation [73] can provide a unified and self-consistent treatment of both the mean-field and the pairing correlation, and describe the exotic nuclei properly in the Dirac Woods-Saxon basis [74]. The RHB equation reads
$ \begin{equation} \begin{pmatrix} h_{D}-\lambda_{\tau} & \Delta \\ -\Delta^{*} & -h^{*}_{D}+\lambda_{\tau} \end{pmatrix} \begin{pmatrix} U_{k} \\ V_{k} \end{pmatrix} = E_{k} \begin{pmatrix} U_{k} \\ V_{k} \end{pmatrix}, \end{equation} $

(1) where
$ \lambda_{\tau} $ is the nucleon Fermi energy, and$ E_{k} $ and$ (U_{k}, V_{k})^{\mathsf{T}} $ are the quasiparticle energy and wave function, respectively. The Dirac Hamiltonian in the coordinate space is$ \begin{equation} h_{D}({\boldsymbol{r}}) = {\boldsymbol{\alpha}} \cdot {\boldsymbol{p}}+V({\boldsymbol{r}})+\beta[M+S({\boldsymbol{r}})], \end{equation} $

(2) with the scalar potential
$ S({\boldsymbol{r}}) $ and the vector potential$ V({\boldsymbol{r}}) $ . For axially symmetric deformed nuclei with spatial reflection symmetry, the potentials are expanded in terms of the Legendre polynomials,$ \begin{equation} f({\boldsymbol{r}}) = \sum\limits_{\lambda}f_{\lambda}(r)P_{\lambda}(\mathrm{cos}\theta),\ \ \ \lambda = 0,2,4,\cdots. \end{equation} $

(3) The pairing potential reads
$ \begin{equation} \Delta({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}) = V^{PP}({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}) \kappa({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}), \end{equation} $

(4) where
$ \kappa({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}) $ is the pairing tensor [75]. A density-dependent zero-range pairing force is adopted as$ \begin{align} V^{PP}({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}) = V_{0}\frac{1}{2}(1-P^{\sigma})\delta({\boldsymbol{r}}_{1}-{\boldsymbol{r}}_{2}) \left(1-\frac{\rho({\boldsymbol{r}}_{1})}{\rho_{\rm sat}}\right), \end{align} $

(5) with the pairing strength
$ V_{0} $ and the saturation density of nuclear matter$\rho_{\rm sat}$ .$ \dfrac{1}{2}(1-P^{\sigma}) $ is the projector for the spin$ S = 0 $ component in the pairing channel. The details of the DRHBc theory with meson-exchange and point-coupling density functionals can be found in Refs. [49] and [65], respectively.By solving the DRHBc equations self-consistently, one obtains the static mean-field solution which is characterized by the breaking of translational and rotational symmetries. To determine the beyond-mean-field ground-state energy
$ E(0^{+}_{1}) $ , it is necessary to extend the DRHBc scheme to include collective dynamical correlations that arise from symmetry restoration and shape fluctuations around the mean-field minima.The beyond-mean-field ground-state energy
$ E(0^{+}_{1}) $ can be described using a collective Hamiltonian, with deformation-dependent collective parameters determined from constrained DRHBc calculations. The 2DCH Hamiltonian takes the following form:$ \begin{aligned}[b] \hat{H}_{\mathrm{coll}} = &\hat{T}_{\mathrm{vib}}+\hat{T}_{\mathrm{rot}}+V_{\mathrm{coll}}\\ = &-\frac{\hbar^{2}}{2}\frac{1}{\sqrt{\mathscr{I}B_{\beta\beta}}}\frac{\partial}{\partial\beta}\sqrt{\frac{\mathscr{I}}{B_{\beta\beta}}} \frac{\partial}{\partial\beta}+\frac{ \hat{J}^{2}}{2\mathscr{I}}+V_{\mathrm{coll}} , \end{aligned} $

(6) where
$ \hat{T}_{\mathrm{vib}} $ and$ \hat{T}_{\mathrm{rot}} $ are the vibrational and rotaitonal kinetic-energy terms, respectively.$ V_{\mathrm{coll}} $ is the collective potential. In the second line of Eq. (6),$ \hat{J} $ denotes the total angular momentum in the intrinsic frame, and$ \mathscr{I} $ denotes the moment of inertia, which is calculated by the Inglis-Belyaev formular [75–77]:$ \begin{equation} \mathscr{I} = \sum_{i,j}\frac{(u_{i}v_{j}-v_{i}u_{j})^2}{E_{i}+E_{j}}|\langle i|\hat{J}|j\rangle|^{2}, \end{equation} $

(7) where
$ |i\rangle $ and$ |j\rangle $ denote the single-particle states in the canonical basis, while$ v_{i} $ ($ u_{i} $ ) and$ E_{i} $ represent the occupation probabilities and the quasi-particle energies, respectively. The collective mass$ B_{\beta\beta} $ is calculated in the cranking approximation [78],$ \begin{align} B_{\beta\beta} = \frac{9r_{0}^{4}A^{10/3}}{5\pi}\hbar^{2}\left[M_{(1)}^{-1}M_{(3)}M_{(1)}^{-1}\right], \end{align} $

(8) with
$ \begin{align} M_{(n)} = \sum\limits_{ij}\frac{\langle i|\hat{Q}_{20}|j\rangle\langle j|\hat{Q}_{20}|i\rangle}{(E_{i}+E_{j})^{n}}(u_{i}v_{j}+v_{i}u_{j})^{2} , \end{align} $

(9) where the quadrupole moment operator
$\hat{Q}_{20} = $ $ \sqrt{16\pi/5}r^{2}Y_{20}(\theta,\varphi)$ ,$ r_0 = 1.2 $ fm, and A is the mass number. The collective potential$ V_{\mathrm{coll}} $ is calculated from the DRHBc total energy$ E_{\mathrm{tot}} $ by subtracting the zero-point energy (ZPE) corrections [78], mainly including the rotational correction energy$ E_{\mathrm{rot}} $ and the vibrational correction energy$ E_{\mathrm{vib}} $ ,$ \begin{aligned}[b] V_{\mathrm{coll}} = &E_{\mathrm{tot}}-E_{\mathrm{rot}}-E_{\mathrm{vib}}\\ = &E_{\mathrm{tot}}-\frac{\langle \hat J^{2}\rangle}{2\mathscr{I}}-\frac{1}{4}\left[M_{(2)}M_{(3)}^{-1}\right] . \end{aligned} $

(10) By diagonalizing the 2DCH Hamiltonian in Eq. (6), one can obtain the beyond-mean-field ground-state energy
$ E(0^{+}_{1}) $ . The dynamical correlation energy is defined as the difference between the global minimum of the total energy curve and$ E(0^{+}_{1}) $ :$ \begin{align} \mathrm{DCE} = E_{\mathrm{tot}}^{\mathrm{min}}-E(0^+_{1}) . \end{align} $

(11) -
Numerical details for the mean-field calculations are the same as suggested in Ref. [65]. The density functional PC-PK1 [64] is adopted, which is considered to be one of the best relativistic density functionals for the description of nuclear masses [61, 69, 70, 79, 80]. The pairing strength
$ V_{0} = -325 $ MeV fm$ ^{3} $ together with a pairing window of 100 MeV is adopted, which can accurately reproduce the odd-even mass differences for calcium and lead isotopes [65]. The Legendre expansion truncations in Eq. (3) are chosen as$ \lambda = 6 $ for Se and Nd isotopes and$ \lambda = 8 $ for Th isotopes [81].For the 2DCH calculation, we choose a transitional nucleus
$ ^{148} $ Nd as an example in Fig. 1 to present the deformation dependence of the collective parameters in Eq. (6) and the beyond-mean-field DCE. We first carry out a constrained calculation to generate the mean-field total energies (blue dashed line in Fig. 1(a)) and wave functions of the axially symmetric quadrupole deformed shapes. The single-particle wave functions, occupation probabilities, and quasiparticle energies are used to calculate the collective potential, collective mass, and moment of inertia (red solid lines in Fig. 1), all of which are functions of the deformation β. The collective potential around the global minimum is lowered by$ \approx 3 $ MeV compared with the mean-field total energy due to the ZPE corrections. The collective mass fluctuates slightly within 130$ \hbar^{2} $ MeV$ ^{-1} $ in the prolate side but increases sharply at$ \beta \approx -0.45 $ due to the proton pairing collapse [82, 83]. The moment of inertia grows rapidly with increasing deformation$ |\beta| $ and saturates as$ \approx38 ~~ \hbar^{2} $ MeV$ ^{-1} $ ($ \approx33 ~~ \hbar^{2} $ MeV$ ^{-1} $ ) for the prolate (oblate) side when$ |\beta|>0.4 $ . By solving the 2DCH (c.f. Eq. (6)) constructed from the three collective parameters, we can obtain the ground state$ 0_{1}^{+} $ shown as a triangle in Fig. 1(a). Finally, the DCE is calculated as the difference between the global minimum of total energy (blue circle) and$ E(0^+_1) $ , displayed by the green segment, and its value is 1.91 MeV.
Figure 1. (color online) The collective potential
$V_{\rm coll}$ together with the constrained mean-field total energy curve$E_{\rm tot}$ (a), the collective mass$B_{\beta\beta}$ (b), and the moment of inertia$\mathscr{I}$ (c) for$^{148}$ Nd as functions of the deformation parameter β calculated by the DRHBc+2DCH. The circle and triangle in panel (a) denote the global minimum of the total energy curve and the ground-state energy$E(0^+_1)$ .Figure 2(a) displays the evolution of DCEs for Nd isotopes from the two-proton drip line to the two-neutron drip line calculated by DRHBc+2DCH. For the nuclei with the magic number, the DCEs are almost zero as expected, whereas they increase rapidly to
$ \approx 2.0\sim3.0 $ MeV when moving away from the neutron shells. It is remarkable that peaks appear at$ N \approx 70,106 $ , and$ 116 $ . This can be attributed to the large shape fluctuation characterized by a very soft potential around the global minima, which can be seen clearly in Fig. A2 in the Appendix. The DCEs of$ ^{120,152} $ Nd exhibit conspicuous non-physical jumps. This is because the pairing collapse of both neutron and proton around the global minimum causes relatively larger non-physical vibrational correction energies in the collective potential (c.f. Eq. (10)). Compared with the rotational correction energies$ E_{\rm rot} $ , the DCEs present similar behavior for most of well-deformed nuclei as expected, while they are generally enhanced for the near spherical and transitional nuclei. This plays a vital role in improving the description of nucleon separation energies (c.f. Fig. 4).
Figure 2. (color online) (a) The dynamical correlation energies in Eq. (11) and rotational correction energies obtained from the cranking approximation
$E_{\rm rot} = \langle \hat J^{2}\rangle/2\mathscr{I}$ , as functions of the neutron number in Nd isotopes. (b) The differences between the experimental binding energies [72] and those from DRHBc with DCE for Nd isotopes versus the neutron number. The results of DRHBc without and with$E_{\rm{rot}}$ are also shown for comparison.Figure 2(b) shows the differences between the calculated binding energies and the available data [72]. In general, the deviations for binding energies including either DCEs or
$ E_{\mathrm{rot}} $ are significantly reduced, within$ \pm1.7 $ MeV, compared to those of DRHBc. However, it is emphasized that the inclusion of DCEs can give a better description for the near-spherical nuclei with$ N = 80, 84 $ , and thus reduces the rms deviation slightly from 0.90 MeV to 0.87 MeV.In Fig. 3, systematic DRHBc+2DCH calculations are also performed for Se and Th isotopes to further examine the evolution of DCEs and their effect on the binding energies in different mass regions. In Figs. 3(a) and (c), the evolutions of DCEs in these two isotopic chains are similar to that in the Nd isotopes except for the Se nuclei at
$ N = 50, 70 $ where the (sub-) shell effect is eroded away due to the very soft potential around the global spherical minima. The consistency between$ E_{\rm rot} $ and DCE for well-deformed nuclei is also noted in the light and heavy mass regions. Moreover, it is found that the trend of the correction energies as a whole decreases slightly for heavier nuclei in one isotopic chain, and it also applies for the case from light to heavy isotopic chains. In Figs. 3(b) and (d), we find that the DCE and$ E_{\mathrm{rot}} $ have almost equivalent effect on reducing the deviations of binding energies in both Se and Th isotopes except for the near spherical nuclei close to the neutron shells. For Se isotopes, the rms deviation is reduced from 2.86 MeV in the DRHBc calculations to 0.95 MeV by including$ E_{\mathrm{rot}} $ and to 0.77 MeV by including DCE. For Th isotopes, it is reduced from 2.76 MeV to 1.80 MeV and 1.99 MeV by including the$ E_{\mathrm{rot}} $ and DCE, respectively. The over-binding for$ N \sim 126 $ nuclei found in the Th isotopes also arises in a number of other DFT calculations [20, 24, 25, 45], and it remains as an open question, which has not been explained.
Figure 3. (color online) The same as in Fig. 2, but for Se and Th isotopes.
Figure 4 shows the two-neutron separation energies of Se, Nd, and Th isotopes from two-proton drip line to two-neutron drip line calculated from DRHBc without and with correction energies, in comparison with the available data [72]. In general,
$ S_{2n} $ decreases smoothly along the isotopic chains except at magic numbers, e.g.,$ N = 28 $ , 50, 82, and 126, where$ S_{2n} $ drops significantly. It is interesting to find the disappearance of the$ N = 82 $ shell in the very neutron-rich Se isotopes and the emergence of a possible new magic number$ N = 184 $ in the neutron-rich Th isotopes. One notes that the inclusion of dynamical correlations reduces the$ N = 82 $ and$ 126 $ shell gaps characterized by the$ \Delta S_{2n} $ , e.g., from 6.08 to 5.25 MeV and from 5.91 to 4.95 MeV for the$ N = 126 $ shell in Nd and Th isotopes, respectively. This is consistent with the findings in the GCM calculations based on the axially symmetric HFB [31] and RMF+BCS [71]. Kinks of$ S_{2n} $ in some isotopes, e.g.,$ ^{104} $ Se and$ ^{180,192} $ Nd, are found in the DRHBc calculations with$ E_{\rm rot} $ . This is due to the quenching of$ E_{\rm rot} $ for the nuclei in the vicinity of the (sub-) shells (c.f. Figs. 2 and 3). The theoretical results agree well with the available data, especially for the nuclei away from the neutron shells. The rms deviations of$ S_{2n} $ in Se, Nd, and Th isotopic chains are respectively 0.79, 1.23, and 1.16 MeV for the DRHBc calculations without correction energies, and 1.01, 1.15, and 1.02 MeV for the calculations with$ E_{\rm rot} $ . One notes that the inclusion of DCEs can improve the description of$ S_{2n} $ , and the corresponding rms deviations of$ S_{2n} $ for the three isotopic chains are reduced respectively to 0.69, 1.02, and 0.88 MeV, with an overall decline of$\approx$ 17% compared to that with$E_{\rm rot}$ . Furthermore, it is found that the neutron drip lines of Se and Nd isotopic chains are extended respectively from$^{126}$ Se to$^{128}$ Se and from$^{216}$ Nd to$^{218}$ Nd by including the DCEs.
Figure 4. (color online) The two-neutron seperation energies of Se, Nd, and Th isotopes calculated from the DRHBc with DCE. The experimental data and the results of DRHBc without and with
$ E_{\mathrm{rot}} $ are also shown for comparison. Detailed predictions of$S_{{2n}}$ for the nuclei close to the drip lines are illustrated in the inserted panels.It is interesting to further study the effect of dynamical correlations on the quadrupole deformations, which can be seen in Fig. 5. The deformations in DRHBc+ 2DCH model are calculated as the expectation values of β in the ground state
$ 0^+_1 $ . It is found that the results of DRHBc+2DCH calculations are similar to those of mean-field calculations for the nuclei away from the (sub-) shells, and both well reproduce the data. In contrast, for the nuclei close to the neutron (sub-) shells, the DRHBc+ 2DCH gives nonzero or even rather large deformations, e.g.,$ |\beta|\approx 0.15 $ in$ ^{84} $ Se due to the shape fluctuation, and the calculated deformations agree well with the data, which are extracted from the measured$ B(E2; 0^+_1\to 2^+_1) $ [84].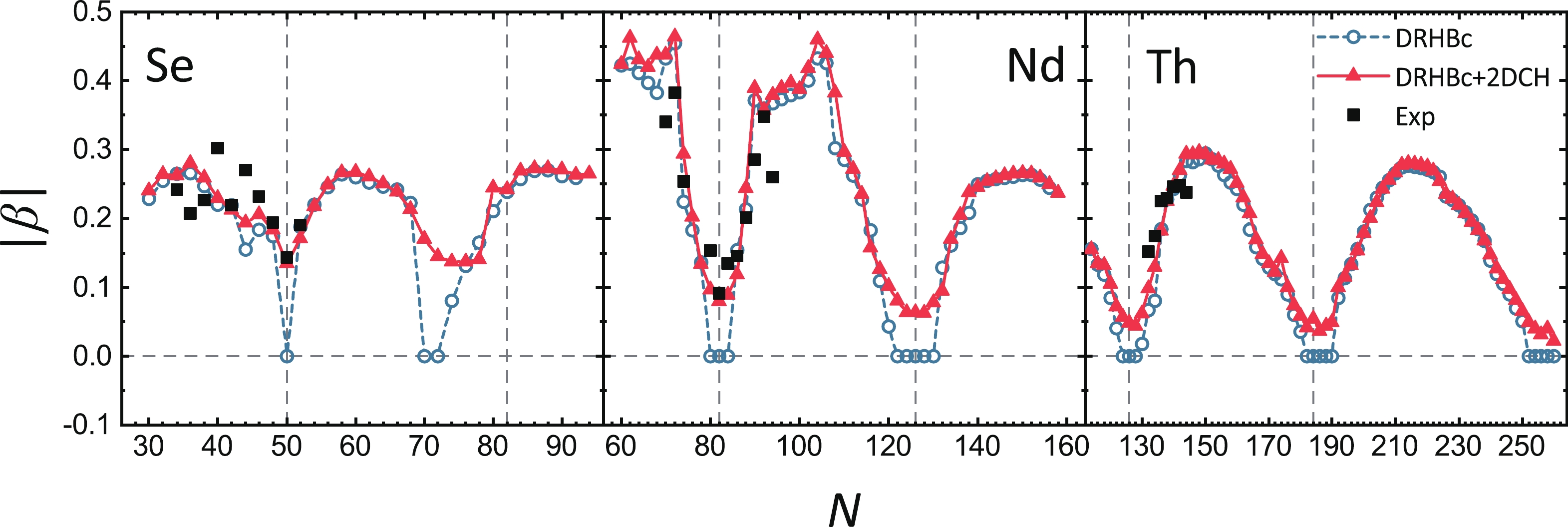
Figure 5. (color online) Absolute values of the quadrupole deformations
$ |\beta| $ of Se, Nd, and Th isotopes calculated by DRHBc and DRHBc+2DCH, compared with the available data [84].The collective parameters of the collective Hamiltonian have a rather strong dependence on the pairing correlations [82, 83] and thus affect the ground state energy
$ E(0^+_1) $ as well as the DCE. Therefore, it is necessary to quantify the relation between DCE and pairing correlation to further improve the description of nuclear masses and separation energies based on the beyond mean-field collective Hamiltonian. To this end, we choose three different values of pairing strength in the DRHBc+2DCH for the case$ ^{148} $ Nd: –309, –325, and –341 MeV fm$ ^{3} $ , corresponding to 95%, 100%, and 105%, respectively, of the original pairing strength that was determined in the DRHBc mass table. Figure 6(a) shows that by increasing the pairing strength, both total energy curves and collective potential curves move downwards as expected, and it is interesting to note that the latter ones lower faster due to the enhancement of the ZPE correction energies plotted in Fig. 6(b). As the pairing strength$ V_{\mathrm{0}} $ increases gradually from −309 to −341 MeV fm$ ^{3} $ , the$ E_{\mathrm{rot}} $ grows from 1.56 to 1.79 MeV, and finally reaches 2.19 MeV, while the$ E_{\mathrm{vib}} $ changes very slightly. This results in the rise of DCE from 1.67 to 2.29 MeV with an enhancement of$ \approx 37 $ %.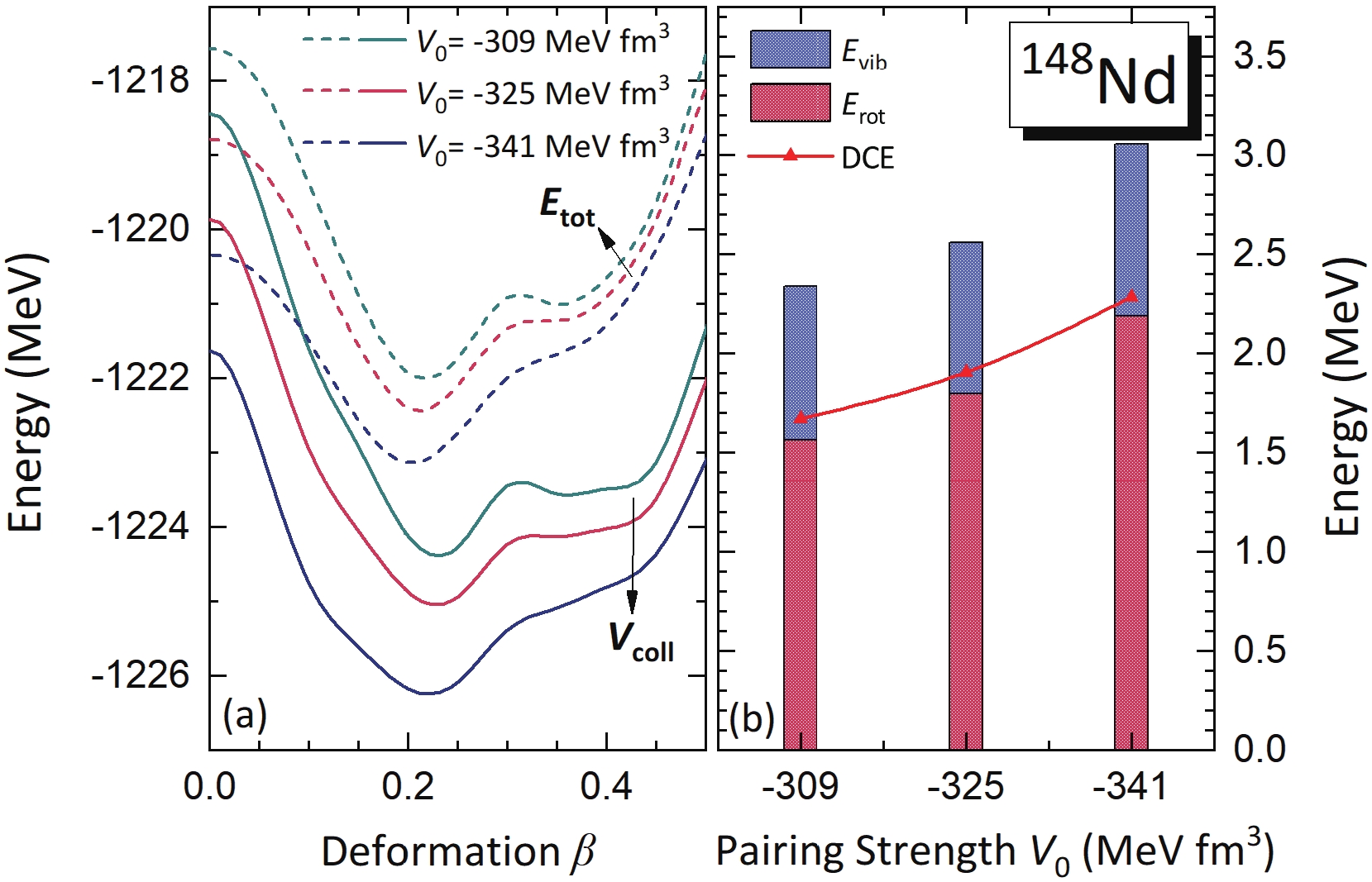
Figure 6. (color online) (a) The mean-field total energies
$E_{\mathrm{tot}}$ (dashed lines) and the collective potentials$V_{\mathrm{coll}}$ (solid lines) of$^{148}$ Nd calculated using three different pairing strengths: −309, −325, and −341 MeV fm$^{3}$ , denoted by the colors green, red, and blue, respectively. (b) The vibrational and rotational correction energies corresponding to the global minima of the total energy curves for different pairing strengths. Red triangles indicate the DCEs. -
In summary, we extend the DRHBc theory to go beyond mean-field framework by performing the 2DCH with parameters determined by constrained mean-field calculations for quadrupole deformed shapes. The influence of the dynamical correlations on the ground-state properties was examined, including the binding energies, two-neutron separation energies, and quadrupole deformations, for Se, Nd, and Th isotopes, which are located in different nuclear mass regions. It is found that the DCEs and
$ E_{\mathrm{rot}} $ have an almost equivalent effect on the description of binding energies for most of deformed nuclei, and the DCEs can provide a significant improvement for the (near) spherical nuclei close to the neutron shells and thus reduce the rms deviations of$ S_{2n} $ . After taking into account DCEs, the rms deviations of binding energies for Se, Nd and Th isotopic chains are reduced respectively to 0.77, 0.87, and 1.99 MeV, and the corresponding rms deviations of$ S_{2n} $ are improved to 0.69, 1.02, and 0.88 MeV in comparison with those including$ E_{\mathrm{rot}} $ (1.01, 1.15, and 1.02 MeV). The quadrupole deformations are also calculated by the DRHBc+2DCH, and the results are similar to those of mean-field calculations for the nuclei away from the (sub-) shells. However, for the (near) spherical nuclei in the mean-field calculations, the DRHBc+2DCH gives nonzero or even rather large deformations, which agree well with the available data. Furthermore, it is found that the DCEs are quite sensitive to the pairing correlations. For the case of$ ^{148} $ Nd, the DCE grows by$ \approx $ 37%, from 1.67 to 2.29 MeV, as the pairing strength increases by 10%.This study provides a comprehensive analysis of the beyond-mean-field effects of the dynamical correlations and demonstrates that the DRHBc+2DCH constructed in the coordinate space is an effective and efficient model to improve the present relativistic mass model. This encourages us to perform a global calculation for the DCEs and other properties of the ground and excited states. Moreover, our systematic 5DCH calculation based on triaxial RHB with harmonic oscillator basis revealed that a number of neutron-rich nuclei, in particular, the nuclei on the path of r-process and those in the vicinity of neutron drip line, exhibit transitional properties characterized by triaxial soft potentials [70]. Therefore, it would be interesting to extend our present axially symmetric DRHBc to include triaxial degree of freedom, i.e., to construct the triaxial relativistic Hartree-Bogoliubov theory in continuum (TRHBc), and such studies are in progress. Furthermore, the 5DCH based on TRHBc is planned and expected to provide relatively more convincing predictions for very neutron-rich nuclei.
-
Helpful discussions with members of the DRHBc Mass Table Collaboration, Mr. Jing Geng, and Dr. Jian Xiang are highly appreciated.
-
The convergence checks for the total energies and the collective masses in
$ ^{148} $ Nd with respect to the energy cutoff$ E_{\mathrm{cut}}^{+} $ and angular momentum cutoff$ J_{\mathrm{max}} $ are shown in Fig. A1, and$ E_{\mathrm{cut}}^{+} = 300 $ MeV and$J_{\mathrm{max}} = $ $ 23/2 \hbar$ are adopted.Figure A2 displays the evolution of total energy curves for
$ ^{120-216} $ Nd calculated by constrained DRHBc with PC-PK1 functional. Very soft potentials around the global minima can be seen clearly in the nuclei around the mass numbers$ A = 130,166 $ , and$ 176 $ , which correspond to the peaks of DCEs in Fig. 2.
Beyond-mean-field dynamical correlations for nuclear mass table in deformed relativistic Hartree-Bogoliubov theory in continuum
- Received Date: 2022-01-07
- Available Online: 2022-06-15
Abstract: We extend the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) to go beyond-mean-field framework by performing a two-dimensional collective Hamiltonian. The influences of dynamical correlations on the ground-state properties are examined in different mass regions, picking Se, Nd, and Th isotopic chains as representatives. It is found that the dynamical correlation energies (DCEs) and the rotational correction energies





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: