-
As one of the densest forms of matter in the observable universe, the neutron star is proven to have a strong magnetic field by the observation of soft-gamma repeaters (SGRs) and anomalous X-ray pulsars (AXPs) [1]. The surface magnetic field strength of neutron stars generally ranges from
$ 10^{9} $ G to 10$ ^{13} $ G [2]. For some neutron stars, which are called magnetars, the surface magnetic field could reach as high as$ 10^{14}-10^{15} $ G [3]. The strong magnetic field can significantly affect both the composition and the maximum mass of neutron stars [4,5]. In the crust of a neutron star, there exist abundant nuclei ranging from$ ^{56} $ Fe to heavy nuclei with mass number$ A\sim200 $ [6], and the$ \beta^- $ decay in the crust plays a key role in the neuron star cooling process [7–9]. Interestingly, the$ \beta^- $ decay rates could be changed correspondingly as the electron transverse momentum components are quantized into Landau levels in the magnetic field [10]. A few theoretical works have been carried out to discuss this magnetic field effect on$ \beta^- $ decay [10–13]. For example, the$ \beta^- $ decay of a neutron in a strong quantizing magnetic field is studied by Fassio by making use of the wave function for the electron [11]. The influence of the strong magnetic field on$ \beta^- $ decay in the stellar surroundings is also discussed using the improved Fuller–Flower–Newman (FFN) technique [12,13].Previous research has been devoted to the studies of the magnetic field effect on the stellar
$ \beta^- $ decay with fixed electron density, temperature and decay energy [10–13]. Little attention has been paid to the dependence of$ \beta^- $ decay rates on these variables in the magnetic field. The main purpose of this paper is to present a systematic analysis of the$ \beta^- $ decay rates in the magnetic field under different stellar environments. By considering the electron spectrum modified by the presence of Landau levels, we improve the Takahashi–Yokoi model in order to calculate the$ \beta^- $ decay rates in the presence of strong magnetic field. This model was originally proposed in 1983 to perform calculations of$ \beta^- $ decay rates for highly-ionized heavy atoms in a plasma of electrons and ions at high temperature and high density [14]. Very recently, we have successfully applied this model to investigate the bound state$ \beta^- $ decays of a number of nuclei [15]. The behavior of$ \beta^- $ decay rates in the magnetic field with different temperature, electron density, and decay energy is considered to be helpful for the understanding of late evolution and crust composition of neutron stars.The paper is organized as follows. In Sec. II, the formulas of the electron chemical potential and the improved Takahashi–Yokoi model for calculating the
$ \beta^- $ decay rates in the magnetic field are given. In Sec. III, we calculate the$ \beta^- $ decay rates of Ni isotopes in the magnetic field, and discuss the$ \beta^- $ decay rates under the conditions of different electron density, temperature and decay energy. Sec. IV gives a short summary. -
In the stellar environment, the
$ \beta^- $ decay rate λ in the framework of Takahashi–Yokoi model is [14,16]:$ \lambda = [(\ln2)/(ft)]\, f_m \,\,\,\,\,\,\,\, m = a, nu, u, $

(1) where m = a,
$ nu $ , and u represent allowed, non-unique first-forbidden and unique first-forbidden transitions, respectively.$ ft $ is the comparative half-life which is directly related to the square of nuclear transition matrix element, and the$ ft $ values are taken from the experimental data [17].$ f_m $ is the lepton phase volume part. For the non-magnetic stellar environment,$ f_m $ can be described as below [14],$ \begin{aligned}[b] f_m =& \int_{1}^{W_0}\sqrt{W^2-1}W(W_0-W)^2F(Z,W)(1-G_-)S_{m}(Z,W){\rm d}W \\ m =& a, nu,u, \end{aligned} $

(2) where
$ W_0 $ is the decay energy in the unit of$ m_ec^2 $ [17]. The term$ F(Z,W) $ is the Fermi function [18]:$ \begin{array}{*{20}{l}} F(Z,W) = \begin{cases} F_0(Z,W) & \rm{for }m = a, nu \\ F_1(Z,W) & \rm{for }m = u, \end{cases} \end{array} $

(3) where
$ \begin{aligned}[b] F_0(Z,W) =& \frac{4}{\left|\Gamma(1+2\sqrt{1-\alpha^2Z^2})\right|^2}\\&\times\left(2R\sqrt{W^2-1}\right)^{2\left(\sqrt{1-\alpha^2Z^2}-1\right)}\exp{\left[\frac{\pi\alpha ZW}{\sqrt{W^2-1}}\right]}\\ &\times\left|\Gamma\left(\sqrt{1-\alpha^2Z^2}+{\rm i}\frac{\alpha ZW}{\sqrt{W^2-1}}\right)\right|^2, \end{aligned} $

(4) $ \begin{aligned}[b] F_1(Z,W) =& \frac{(4!)^2}{\left|\Gamma(1+2\sqrt{4-\alpha^2Z^2})\right|^2}\\ &\times\left(2R\sqrt{W^2-1}\right)^{2(\sqrt{4-\alpha^2Z^2}-2)}\exp{\left[\frac{\pi\alpha ZW}{\sqrt{W^2-1}}\right]}\\ &\times\left|\Gamma\left(\sqrt{4-\alpha^2Z^2}+{\rm i}\frac{\alpha ZW}{\sqrt{W^2-1}}\right)\right|^2. \end{aligned} $

(5) Z represents the proton number of daughter nucleus, and
$ \alpha = 1/137 $ is the fine structure constant. Γ is the gamma function.$ S_{m}(Z,W) $ are the spectral shape factors [14]:$ S_{m}(Z,W) = \begin{cases} L_{0} & \rm{for }m = a, nu \\ (W_0-W)^2L_0+9L_1 & \rm{for }m = u. \end{cases} $

(6) $ L_0 $ and$ L_1 $ are certain combinations of electron radial wave functions evaluated at an appropriately chosen nuclear radius R [18,19]:$ L_0 = \frac{1+\sqrt{1-\alpha^2Z^2}}{2}, $

(7) and
$ L_1 = \frac{F_1(Z,W)}{F_0(Z,W)}\left(\frac{W^2-1}{9}\right)\frac{2+\sqrt{4-\alpha^2Z^2}}{4}. $

(8) $ G_- $ is the Fermi–Dirac distribution function of electrons:$ G_- = \frac{1}{1+{\rm e}^{\frac{W-1-U_F}{kT}}}. $

(9) $ U_F $ is the electron chemical potential, which is associated with the number density of electrons$ \rho Y_e $ [20,21]$ \rho Y_e = \frac{1}{\pi^2N_{\rm A}}\left(\frac{m_ec}{\hbar}\right)^3\int_{0}^{\infty}(G_-G_+)p^2 {\rm d} p. $

(10) ρ represents the baryon density, and
$ Y_e $ is the mean electron fraction [22].$N_{\rm A}$ is Avogadro's number, and$ p = \sqrt{W^2-1} $ is the electron momentum.$ G_+ $ is Fermi–Dirac distribution function of positrons:$ G_+ = \frac{1}{1+{\rm e}^{\frac{W+1+U_F}{kT}}}. $

(11) The density of electron–position pairs has been removed by subtracting
$ G_+ $ from$ G_- $ in Eq. (10).In the magnetic field, the electron density is modified by the presence of Landau levels [13]:
$ \rho Y_e = \frac{\varTheta}{2\pi^2N_{\rm A}}\left(\frac{m_ec}{\hbar}\right)^3\sum\limits_{n = 0}^{\infty}g_{n0}\int_{0}^{\infty}(G^M_--G^M_+){\rm d}p_z, $

(12) where
$ \varTheta = \frac{eB\hbar}{m_e^2c^3} = 0.0227B_{12}. $

(13) B is the magnetic field strength, and
$ B_{12} $ is the magnetic field strength in units of$ 10^{12} $ G.$ g_{n0} = 2-\delta_{n0} $ is the spin degeneracy of electron [23]. The electron and positron distribution functions$ G^M_- $ and$ G^M_+ $ become$ G^M_- = \frac{1}{1+{\rm e}^{\frac{W_n-1-U_F}{kT}}},\quad G^M_+ = \frac{1}{1+{\rm e}^{\frac{W_n+1+U_F}{kT}}}, $

(14) where the electron energy
$ W_n = \sqrt{p_z^2+1+2n\varTheta} $ .$ n = $ $ 0, 1, 2,... $ corresponds to the Landau levels, and$ p_z $ is the electron momentum along the field [23].In the magnetic field, the electrons are not distributed in the Fermi sphere, but in the Landau cylinder [24]. The state density of electron
$ {\rm d}\nu_e $ and that of neutrino$ {\rm d}\nu_{\nu} $ can be written respectively as [12,25]:$ {\rm d}\nu_e = \frac{\varTheta V}{4\pi^2\lambda_e^3}{\rm d}p_z,\quad {\rm d}\nu_{\nu} = \frac{V}{8\pi^3\lambda_e^3}q^2dq{\rm d}\Omega_{\nu}, $

(15) where V is the normalized volume and
$ \lambda_e $ is the reduced Compton wavelength. q and$ {\rm d}\Omega_{\nu} $ are the momentum and the solid angle of neutrino emission, respectively. With the inclusion of the electron spectrum modified by the existence of Landau levels, the lepton phase volume$ f^M_m $ in the magnetic field can be rewritten as [10,12]:$ \begin{aligned}[b] f^M_m =& \frac{\varTheta}{2}\sum\limits_{n = 0}^{n_{\max}}g_{n0}\int_{0}^{\sqrt{W_0^2-Q_n^2}}(W_0-W_n)^2F_0(Z,W_n)\\&\times(1-G^M_-)S_{m}(Z,W_n){\rm d} p_z \\ m =& a, nu, u, \end{aligned} $

(16) where
$ W_0 $ is the$ \beta^- $ decay energy, and$ Q_n = \sqrt{1+2n\varTheta} $ ,$ n = 0,1,2,... $ .$n_{\max}$ is the highest Landau energy level that the emitted electron can occupy [24]:$ n_{\max} = \frac{W_0^2-1}{2\varTheta}. $

(17) The
$ \beta^- $ decay rate$ \lambda^M $ in the magnetic field can be written as$ \lambda^M = [(\ln2)/(ft)]\, f^M_m \,\,\,\,\,\,\,\, m = a, nu, u. $

(18) -
The r-process involves long chains of neutron-capture reactions and β decays, which are responsible for the synthesis of roughly half of the isotopes of elements above iron in binary neutron-star mergers and other extremely neutron-rich environments [26–31]. As one of the important isotopic chains participating in the r-process, research on neutron-rich Ni isotopes has significant astrophysical applications [32–35]. For instance, the measurements of the β-decay feeding intensity distribution and the Gamow–Teller transition strength distribution of
$ ^{71,73} $ Ni could provide constraints to theoretical calculations for the r-process [34]. Furthermore, the doubly magic nucleus$ ^{78} $ Ni is an important waiting point in the r-process, which plays a key role in the synthesis of heavier elements [35]. We define an enhancing factor C in order to describe the magnetic field effect on the$ \beta^- $ decay rates :$ C = \frac{\lambda^M}{\lambda^N}, $

(19) where
$ \lambda^M $ and$ \lambda^N $ are the$ \beta^- $ decay rates with and without the magnetic field, respectively. Taking the allowed$ \beta^- $ decay branching of nucleus$ ^{70} $ Ni as an example, the enhancing factor C of its$ \beta^- $ decay rate as a function of magnetic field is given in Fig. 1. Note that the electron density$ \rho Y_e $ in Fig. 1 is chosen as$ 10^6 $ g/cm3 with baryon density ρ and electron fraction$ Y_e $ both being in the range of the outer crust of the neutron star. Based on the Baym–Pethick–Sutherland model [36], the estimated baryon density ρ in the outer crust ranges from about$ 10^{6} $ g/cm3 to$ 10^{11} $ g/cm3, and electron fraction$ Y_e $ is calculated to be ranging from 0.46 to 0.31 [6,37]. The temperature$ T = 10^8 $ K in Fig. 1 is a typical value used in the stellar environment [16,20]. For a relatively weak magnetic field ($ B<10^{13} $ G), the Landau level spacing factor$ \varTheta $ is much smaller than the decay energy$ Q_{\beta^-} $ ($ Q_{\beta^-} = W_0\cdot m_ec^2 $ ), and the created electron can be emitted into any of a large number of Landau levels with energies less than the electron energy [10]. Due to the fact that Landau levels are so dense, the state density of electrons in the magnetic field approaches that without the magnetic field. Thus, the enhancing factor C is approximately equal to 1, implying that the effect of the weak magnetic field on the$ \beta^- $ decay rates is negligible. With the magnetic field strength in the range$ 10^{13} $ G$ <B< 10^{15} $ G, there are fewer Landau levels contributing to the lepton phase volume$ f^{M}_{m} $ as the Landau level spacing is quite large, resulting in a decreased$ \beta^- $ decay rate with the increase of magnetic field strength. It is emphasized that the degree of degeneracy of Landau levels is directly proportional to the magnetic field strength B [25], and the reduction of the$ \beta^- $ decay rate is a result of complicated interactions between the number of Landau levels and its degree of degeneracy in the environment with a given temperature and electron density. Under the different conditions of temperature, electron density and decay energy, oscillation of the$ \beta^- $ decay rate could occur due to this complicated relationship (see Fig. 2(d) and Fig. 3). When the magnetic field strength is larger than$ 1.35\times10^{15} $ G (labeled by the vertical dashed line in Fig. 1), the created electron can only be emitted into the Landau energy level with$ n = 0 $ . The degree of degeneracy of the$ 0 $ th Landau level increases with the increase of B. Thus, there are more unoccupied quantum states in the$ 0 $ th Landau level for emitted electrons and the$ \beta^- $ decay rate increases correspondingly with$ B>1.35\times10^{15} $ G.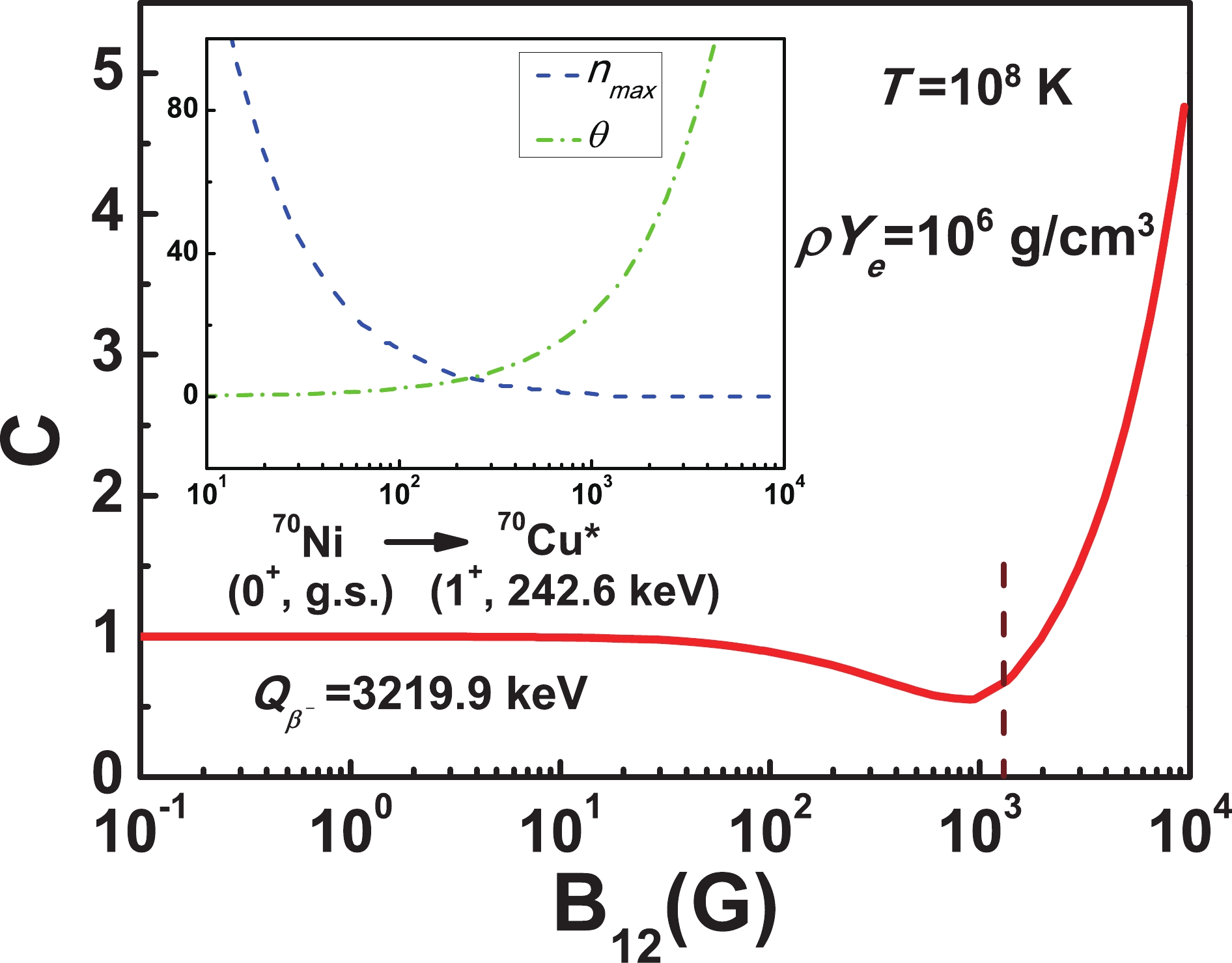
Figure 1. (color online) Enhancing factor C of
$ \beta^- $ decay rates from the ground state of$ ^{70} $ Ni into the excited state of$ ^{70} $ Cu, with decay energy$ Q_{\beta^-} $ = 3219.9 keV. Vertical dashed line labels the minimum magnetic field strength at which only the$ n = 0 $ Landau level is included in the calculation. Blue and green dashed lines represent the highest Landau energy level$n_{\max}$ for emitted electron and the Landau level spacing factor$ \varTheta $ , respectively.
Figure 2. (color online) (a)
$ \beta^- $ decay rates$ \lambda^{M} $ from the ground state of$ ^{70} $ Ni into the excited state of$ ^{70} $ Cu in the magnetic field with different temperatures T ($ \rho Y_e = 10^6 $ g/cm3). (b) Corresponding enhancing factor C as a function of magnetic field with different temperatures T. (c)$ \beta^- $ decay rates$ \lambda^{M} $ from the ground state of$ ^{70} $ Ni into the excited state of$ ^{70} $ Cu in the magnetic field with different electron density$ \rho Y_e $ ($ T = 10^8 $ K). (d) Corresponding enhancing factor C as a function of magnetic field with different electron density$ \rho Y_e $ .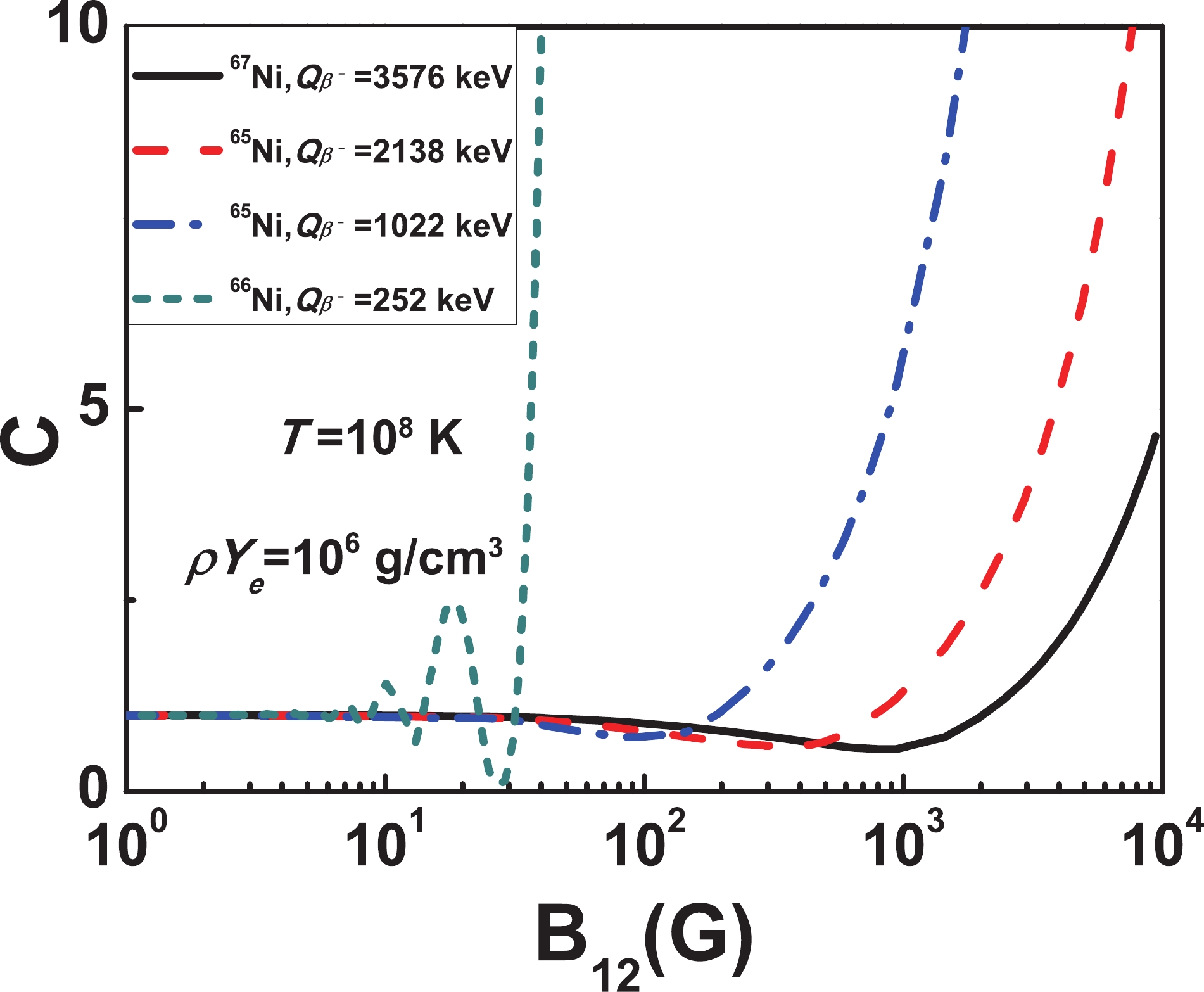
Figure 3. (color online) Enhancing factor C of
$ \beta^- $ decay rates for Ni isotopes with different decay energies as a function of magnetic field.In Fig. 2, we plot the variations of the
$ \beta^- $ decay rates$ \lambda^M $ and the corresponding enhancing factor C of$ ^{70} $ Ni under the conditions of different temperatures T and electron densities$ \rho Y_e $ , respectively. It is known that the$ \beta^- $ decay rate is directly related to the number of quantum states that the emitted electron can occupy. With the increase of temperature T, the thermal electron Fermi–Dirac distribution$ G^{M}_{-} $ has more electrons at higher energy and the drop-off in the distribution becomes less sharp. Therefore, the emitted electrons are hindered by the Pauli blocking effect due to the thermal electrons at higher energies ($ E> 0.511$ MeV), leading to a decrease of$ \beta^- $ decay rates at high temperatures in Fig. 2(a). The effect of temperature T is considered to be irrelevant to the magnetic field strength in our calculations, thus the curves in Fig. 2(b) are almost coincident. The effects of electron density on the$ \beta^- $ decay rates and the enhancing factor are shown in Fig. 2(c) and Fig. 2(d), respectively. It can be seen that the$ \beta^- $ decay rate in Fig. 2(c) decreases with the increase of electron density ($ \rho Y_e = 10^5,10^6,10^7,10^8 $ g/cm3). This is because the electron chemical potential is increased with the increase of environmental electron density, and the integrand of the decay rate is cut off at the chemical potential [13]. The corresponding changes of the enhancing factor C at different densities are shown in Fig. 2(d). An interesting feature in Fig. 2(d) is the oscillation of C with environmental electron density$ \rho Y_e = 10^8 $ g/cm3. This is not surprising as the$ \beta^- $ decay rate is relevant to both the state density of electrons at each Landau level and the number of Landau levels involved. With the magnetic field strength in the range$ 10^{13} $ G$ <B< 10^{15} $ G, the increase of states at each Landau level competes with the decrease of Landau levels participating in the decay (see blue and green dashed lines in Fig. 1), resulting in the oscillation of enhancing factor.In Fig. 3, we plot the dependence of enhancing factor C on decay energy
$ Q_{\beta^-} $ for the isotopic chain of Ni. Let us take$ ^{67} $ Ni as an example. It is clearly seen from Fig. 3 that the enhancing factor C of$ ^{67} $ Ni first decreases and then increases rapidly with the magnetic field strength. The enhancing factor of$ ^{67} $ Ni with the decay energy$ Q_{\beta^-} $ = 3576 keV reaches its minimum at$ B = 10^{15} $ G. Similar behavior of the enhancing factor exists also for the two decay channels of$ ^{65} $ Ni. In contrast, an oscillation feature of the enhancing factor C occurs for$ ^{66} $ Ni, which has the smallest decay energy$ Q_{\beta^-} $ = 252 keV. The reason for this oscillation feature is quite similar to the above discussions and we do not repeat here. Note that the present calculations are performed by considering the changes of electron spectrum with the appearance of Landau levels in the outer crust of neutron stars. Several improvements might be considered in future. (1) The outer crust of a neutron star consists of nuclei in a Coulomb lattice and electron gas, and the involved density is smaller than neutron drip density$ \rho_d\sim4.3\times10^{11} $ g/cm3 [37]. On the contrary, in the inner crust the nuclei are so closely packed that they are almost touching, and the density could reach as high as$ 10^{14} $ g/cm3 [6,37]. The nuclear medium effect is considered to be non-negligible if one extend the calculation of$ \beta^- $ decay rates in the inner crust [38]. (2) The electron screening effect in the outer crust of a neutron star is ignored here, which might have impact on the$ \beta^- $ decay threshold energy and the chemical potential [39]. Note that the electron screening effect could be investigated by using approaches such as the linear-response theory model [40]. (3) The Landau levels are obtained by solving the Schrödinger equation in a constant uniform magnetic field in the non-relativistic limit, which might be further improved by solving the corresponding Dirac equation [41]. -
Within the improved Takahashi–Yokoi model, a systemic analysis has been performed to explore the
$ \beta^- $ decay rates in different stellar environments. It is found that both the electron density and decay energy are important in determining the$ \beta^- $ decay rates, whereas the effect of temperature in the range of$ 10^{7} $ K$ <T<10^{10} $ K is negligible in present analysis. When the magnetic field strength is larger than$ 10^{15} $ G, the$ \beta^- $ decay rates of Ni isotopes are found to increase significantly owing to the intriguing properties of Landau levels. In contrast, the$ \beta^- $ decay rates decrease with the increasing of environmental electron densities ($ \rho Y_e = 10^5,10^6,10^7,10^8 $ g/cm3). An oscillation phenomenon of the enhancing factor is found to occur under specific electron densities and decay energies for the Ni isotopes. It is thus concluded that the influence of different stellar environments on the$ \beta^- $ decay rates is non-trivial, especially in strong magnetic field ($ B>10^{15} $ G).
Influence of electron density, temperature and decay energy on β– decay rates in a stellar environment
- Received Date: 2021-12-03
- Available Online: 2022-05-15
Abstract: In this paper, the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: