-
With the operation of the Large Hadron Collider (LHC), the exploration of heavy resonance, such as the additional Higgs boson, neutral gauge boson (
$ Z^\prime $ ), and charged bosons ($ W^{\prime \pm} $ ), we have currently reached the Tera-eV era. The Standard Model (SM) Higgs particle was discovered in 2012 at the LHC [1, 2], which confirmed the prediction of the SM for fundamental particles and the role of the Higgs particle in electroweak symmetry breaking. Further precision measurements on the Higgs particles have been proposed for future Higgs factories, including the Circular Electron Positron Collider (CEPC) [3], the electron-positron stage of the Future Circular Collider (FCC-ee) [4, 5], and the International Linear Collider (ILC) [6]. It is attractive to study the new physics effects in Higgs production at future Higgs factories.A simple extension of the SM is possible by including an additional
$ U(1) $ group that may result in models derived from grand unified theories (GUT). Additional$ U(1) $ groups can also result from higher dimensional constructions such as string compactifications. In many models of GUT symmetry breaking,$ U(1) $ groups survive at relatively low energies, resulting in corresponding neutral gauge bosons, commonly referred to as$ Z^\prime $ bosons [7]. Such$ Z^\prime $ bosons typically couple to SM fermions via the electroweak interaction and are observed at hadron colliders as narrow resonances. This extra gauge boson$ Z^\prime $ has been searched for many years at the Tevatron, Large Electron-Positron Collider (LEP), and LHC [8-15]. Another interesting motivation is that the$ Z^\prime $ boson is a mediator or candidate for dark matter sectors, which is beyond the scope of this study.Many experimental searches have been conducted for the extra gauge boson
$ Z^\prime $ and the strong constraints on the mass of$ Z^\prime $ . The primary studied mode for a$ Z^\prime $ at a hadron collider is the Drell-Yan production of a dilepton resonance$ pp ~~ (p\bar{p}) \to Z^\prime \to l^+ l^- $ , where$ l = e $ or μ. Other channels, such as$ Z^\prime \to jj $ , where j is the jet,$ Z^\prime \to t\bar{t} $ ,$ Z^\prime \to e \mu $ , or$ Z^\prime \to \tau^+ \tau^- $ , are also possible. The forward-backward asymmetry for$ pp ~~ (p\bar{p}) \to l^+ l^- $ due to γ, Z, and$ Z^\prime $ interference below the$ Z^\prime $ peak is also important. Today, the collider phenomenology of the$ Z^\prime $ boson has been extensively studied (see, for example [16-28]). The phenomenological implications of the$ Z^\prime $ boson in an additional$ U(1) $ extended model are significant. They can be explored in fermion-pair production processes in$ e^-e^+ $ collisions [29-31]. With the accumulated events increasing on the Higgs particle, the interaction of$ Z^\prime $ and Higgs boson is an interesting phenomenon. An important process to study the$ Z^\prime $ boson is an associated production of the SM Higgs boson (H) with the SM Z boson, such as$ p p \to Z^\prime \to ZH $ at the LHC [32-35] and$ e^+ e^- \to Z^\prime \to ZH $ at future$ e^+ e^- $ linear colliders [36]. In our previous research, we investigated the process of$ p p \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ at 14 TeV LHC and proposed methods to enhance the signal-background ratio [32].In this study, to investigate the properties of
$ Z^\prime $ , including one additional$ U(1)_{\rm X} $ extension of the SM, we investigate the$ Z^\prime $ signal via the process of$ e^+e^- \to Z^\prime/Z \to ZH $ at the electron-positron collision. The cross section is calculate to include the$ Z^\prime $ -Z mixing effects. As the leptonic decay of Z boson can be a good trigger for the signal process, we demonstrate the final lepton angular distribution with the subsequent decay of$ Z \to l^+ l^- $ and$ H \to b \bar{b} $ . The correlation of the final lepton angular distribution with the$ Z^\prime ZH $ interactions is investigated at the unpolarized/polarized electron-positron collision.The remainder of this paper is organized as follows. In Section II, the theoretical framework is described in detail, and the current experimental status on
$ Z^\prime $ is summarized. In Section III, we investigate the$ ZH $ production via$ Z^\prime/Z $ mediators and present the final angular distributions of leptons with various parameter sets. A forward-backward asymmetry is proposed as an observable for$ Z^\prime $ -Z mixing. Finally, a summary and discussion are presented. -
The gauge group structure of the SM,
$ SU(3)_{\rm C} \times $ $ SU(2)_{\rm L} \times U(1)_{\rm Y} $ , can be extended with an additional$ U(1)_{\rm X} $ group. We follow the notations in reference [37] to depict the interactions and mass relations. The new gauge sector$ U(1)_{\rm X} $ is only coupled with the SM through kinetic mixing with a hypercharge gauge boson$ B_\mu $ . The kinetic energy terms of the$ U(1)_{\rm X} $ gauge group are$ \begin{align} \begin{split} \mathcal{L}_K & = - \frac{1}{4} \hat{X}_{\mu\nu} \hat{X}^{\mu\nu} + \frac{\chi}{2} \hat{X}_{\mu\nu} \hat{B}^{\mu\nu}, \end{split} \end{align} $

(1) where
$ \chi \ll 1 $ is useful to keep the precision electroweak predictions consistent with experimental measurements. Additionally, the Lagrangian for the gauge sector is given by$ \begin{aligned}[b] \mathcal{L}_G =& - \frac{1}{4} \hat{B}_{\mu\nu} \hat{B}^{\mu\nu} - \frac{1}{4} \hat{W}_{\mu\nu}^a \hat{W}^{a\mu\nu} \\&- \frac{1}{4} \hat{X}_{\mu\nu} \hat{X}^{\mu\nu} + \frac{\chi}{2} \hat{X}_{\mu\nu} \hat{B}^{\mu\nu} , \end{aligned} $

(2) where
$ W_{\mu\nu}^a $ ,$ B_{\mu\nu} $ , and$ X_{\mu\nu} $ are the field strength tensors for$ SU(2)_{\rm L} $ ,$ U(1)_{\rm Y} $ , and$ U(1)_{\rm X} $ , respectively. We can diagonalize the 3$ \times 3 $ neutral gauge boson mass matrix and express the mass eigenstates as$ \begin{align} \begin{split} \begin{pmatrix} B \\ W^3 \\ X \end{pmatrix} & = \begin{pmatrix} \cos \theta_W & -\sin \theta_W \cos \alpha & \sin \theta_W \sin \alpha\\ \sin \theta_W & \cos \theta_W \cos \alpha & -\cos \theta_W \sin \alpha\\ 0 & \sin \alpha & \cos \alpha \\ \end{pmatrix} \begin{pmatrix} A \\ Z \\ Z^\prime \end{pmatrix}, \end{split} \end{align} $

(3) where the usual weak mixing angle and new gauge boson mixing angle are
$ \begin{align} \begin{split} \sin \theta_W & = \frac{g^\prime}{\sqrt{g^2 + g^{\prime2}}}, \quad \ \ \tan 2\alpha = \frac{-2 \eta \sin \theta_W}{1- \eta^2 \sin^2 \theta_W - \Delta z}, \ \end{split} \end{align} $

(4) with
$ \Delta z $ =$ {m_X^2}/{m_{Z_0}^2} $ ,$ m_{Z_0}^2 $ =${((g^2 + g^{\prime2})v^2})/{4}$ ,$ \eta = {\chi}/{\sqrt{1-\chi^2}} $ .$ m_{Z_0} $ and$ m_X $ are the masses before mixing. The two heavier boson mass eigenvalues are$ \begin{aligned}[b] m_{Z,\;Z^\prime}^2 = &\frac{m_{Z_0}^2}{2} \Bigg[ \left( 1 + \eta^2 \sin^2 \theta_W + \Delta Z \right) \\&\left.\pm \sqrt{\left(1 - \eta^2 \sin^2 \theta_W - \Delta Z \right)^2 + 4 \eta^2 \sin^2 \theta_W } \right] . \end{aligned} $

(5) With the assumption of
$ \eta \ll 1 $ , we can set the mass eigenvalues as$ m_Z \approx m_{Z_0} = 91.19 $ GeV and$ m_{Z^\prime} \approx m_X $ . Therefore, the Z and$ Z^\prime $ coupling to SM fermions are$ \begin{aligned}[b] \begin{split} \bar{\psi} \psi Z =& \frac{{\rm i}g}{\cos \theta_W} \left[ \cos \alpha \left( 1 - \eta \sin \theta_W \tan \alpha \right) \right]\\&\times \left[T_{\rm L}^3 - \frac{\left(1 - \eta \tan \alpha / \sin \theta_W \right)}{\left(1 - \eta \sin \theta_W \tan \alpha \right)} \sin^2 \theta_W Q \right] \end{split} , \end{aligned} $

(6) $ \begin{aligned}[b] \begin{split} \bar{\psi} \psi Z^\prime =& \frac{-{\rm i}g}{\cos \theta_W} \left[ \cos \alpha \left(\tan \alpha + \eta \sin \theta_W \right) \right] \\&\times\left[T_{\rm L}^3 - \frac{\left(\tan \alpha + \eta / \sin \theta_W \right)}{\left(\tan \alpha + \eta \sin \theta_W \right)} \sin^2 \theta_W Q \right] \end{split} , \end{aligned} $

(7) and the
$ Z^\prime ZH $ interaction can be expressed as$ \begin{align} \begin{split} Z^\prime ZH & = 2{\rm i} \frac{m_{Z_0}^2}{v} \left(-\cos \alpha + \eta \sin \theta_W \sin \alpha \right) \left( \sin \alpha + \eta \sin \theta_W \cos \alpha \right). \end{split} \end{align} $

(8) The above is a very common model that includes the
$ Z^\prime $ boson. Such types of models that differ from the coupling strength exist, e.g.,$ Z^\prime_{\rm SSM} $ and$ Z^\prime_{\psi} $ , which have been studied extensively at high energy colliders. The branching ratio of$ Z^\prime $ is depicted in Fig. 1 for$ \sin\alpha = 0.01 $ . The main decay channels are$ Z^\prime \to q \bar{q} $ and$ Z^\prime \to l^+l^- $ . The corresponding branching ratios are close to 40$ \% $ . The branching ratio of$ Z^\prime \to ZH $ is close to 2$ \% $ for$ m_{Z^\prime} = 400 $ GeV.The processes of
$ pp \to Z^\prime \to e^+ e^- $ and$ pp \to Z^\prime \to $ $ \mu^+ \mu^- $ have been studied by the D0 [9] and CDF collaborations [38], respectively, and lower limit on the mass of the Sequential Standard Model (SSM)$ Z^\prime $ boson of 1023 GeV was given by D0. The CDF excludes the mass region of 100 GeV$ < m_{Z^\prime} < $ 982 GeV for a$ Z^\prime_{\eta} $ boson in the E6 model.For the SSM, the
$ Z^\prime $ boson decaying to a pair of τ-leptons with$ m_{Z^\prime} < $ 2.42 TeV was excluded at the 95$ \% $ confidence level by the ATLAS experiment, while$ m_{Z^\prime} < $ 2.25 TeV was excluded for the non-universal$ G(221) $ model that exhibits enhanced couplings to third-generation fermions [39]. Moreover, searches are performed for high-mass resonances in the dijet invariant mass spectrum.$ Z^\prime $ gauge bosons are excluded in the SSM with$ Z^\prime \to b\bar{b} $ for masses up to 2.0 TeV and excluded in the leptophobic model with SM-value couplings to quarks for masses up to 2.1 TeV [40].This shows that the results imply a lower limit of 4.5 (5.1) TeV on
$ m_{Z^\prime} $ for the E6-motivated$ Z^\prime_\psi $ ($ Z^\prime_{\rm SSM} $ ) boson in the dilepton channel [41]. Upper limits are set on the production cross section times branching fraction for the$ Z^\prime $ boson in the top color-assisted-technicolor model, resulting in the exclusion of$ Z^\prime $ masses up to 3.9 and 4.7 TeV for decay widths of 1$ \% $ and 3$ \% $ , respectively [42]. The heavy$ Z^\prime $ gauge bosons decay into$ e\mu $ final states in proton-proton collisions were excluded for masses up to 4.4 TeV by the CMS experiment [43]. By analyzing data of proton-proton collisions collected by the CMS experiment from 2016 to 2018, the limit of$ Z^\prime $ mass was obtained for the combination of the dielectron and dimuon channels. The limits are 5.15 TeV for the$ Z^\prime_{\rm SSM} $ and 4.56 TeV for the$ Z^\prime_\psi\; $ [44].Studies have also been conducted on the
$ Z^\prime $ boson at the lepton colliders, particularly in the small mass regions. The experiments of ALEPH and OPAL at the LEP limited the mass of the$ Z^\prime $ boson with the process of$ e^+e^- \to ff $ , where f is a τ lepton or b quark. The lower limits of$ Z^\prime $ from τ-pair production were 365 GeV at ALEPH and 355 GeV at OPAL, and those from$ b\bar{b} $ production were 523 GeV at ALEPH and 375 GeV at OPAL [44]. With the proposal of the future lepton colliders, the mass region and coupling strength of the$ Z^\prime $ boson can be significantly extended, particularly in the process of Higgs boson production. -
In this section, we consider the process of
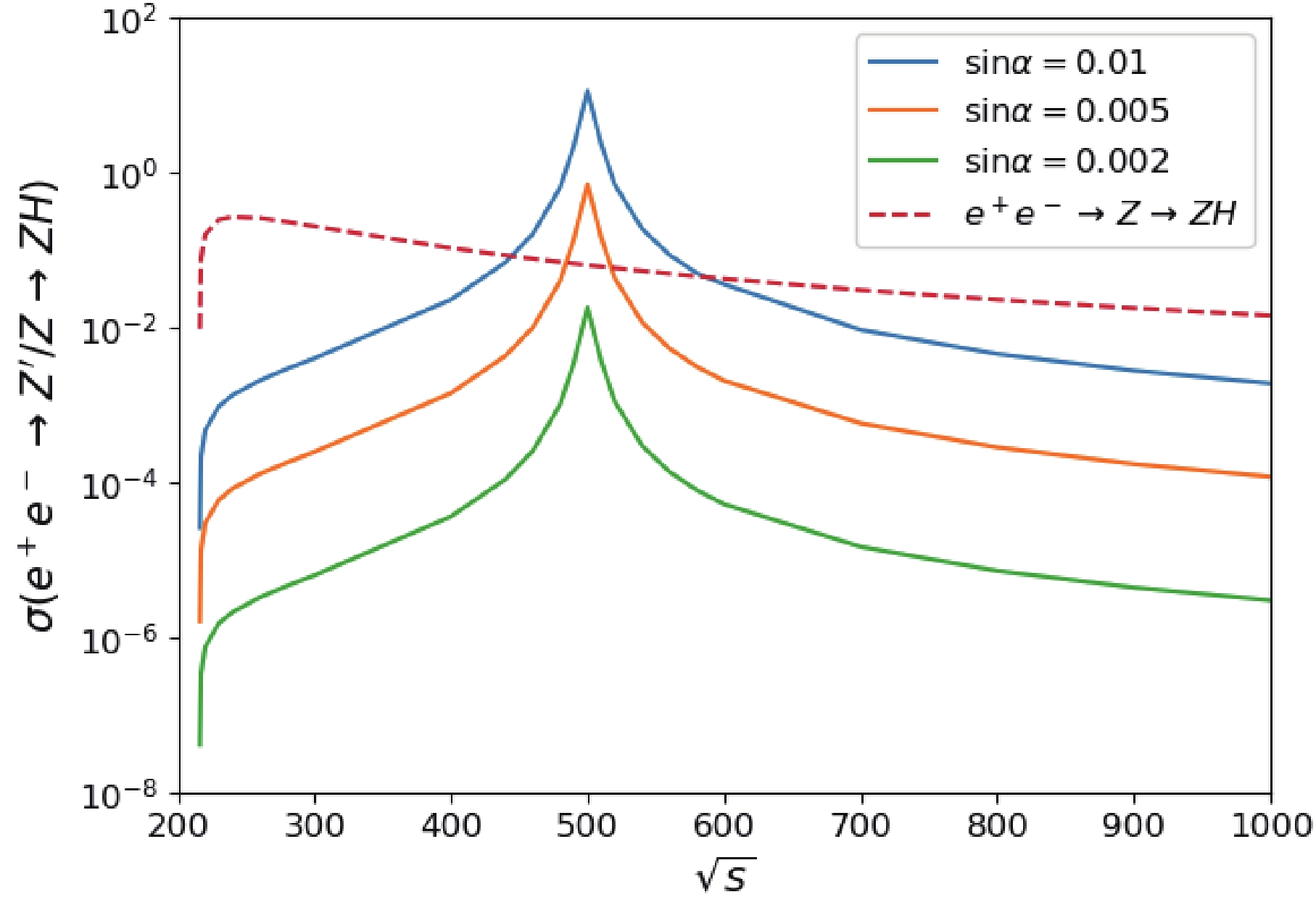
$ e^+e^- \to Z^{\prime}/Z \to ZH $ at future lepton colliders. The cross sections are shown in Fig. 2 as a function of$ \sin\alpha $ for$ Z^\prime $ masses of 300, 400, 500, and 600 GeV, respectively. The cross section for$ m_{Z^\prime} = 500 $ GeV is the largest one owing to resonance enhanced effects with the center-of-mass-system (C.M.S.) energy$ \sqrt{s} = 500 $ GeV. We observe that the cross section is 11.33 pb with$ m_{Z^\prime} = 500 $ GeV when$ \sin\alpha $ is 0.01. The cross section of$ e^+e^- \to Z \to ZH $ is closed to 0.1 pb with a slight decrease when$ \sin\alpha $ increases; this is because the interaction of Z and Higgs boson has a slight dependence on the mixing angle. The resonance threshold effects are apparent with the$ \sqrt{s} = m_{Z^\prime} $ from the lines in the right panel compared with those on the left. Fig. 3 shows the cross section distribution for various C.M.S. energies for$ m_{Z^\prime} = 500 $ GeV. With the increase in$ \sin\alpha $ , the cross section of$ e^+e^- \to Z^\prime \to ZH $ increases. If the C.M.S. energy is set at approximately the value of$ m_{Z^\prime} $ , the cross section of$ e^+e^- \to Z^\prime \to ZH $ will be three or four orders larger than that without resonance effects. -
With the cascaded decay of
$ H \to b \bar{b} $ and$ Z \to l^+ l^- $ , we select the final state of$ b\bar{b} l^+l^- $ as the final signature at the collider. Following the discussion in reference [45], we adopt the angular distribution of the final leptons to investigate the$ Z^\prime ZH $ interaction. The angle can be expressed from the following formula:$ \begin{align} \begin{split} \cos\theta & = \frac{ \boldsymbol{p}^*_{l^-} \cdot \boldsymbol{p}_{e^-} }{ \lvert \boldsymbol{p}^*_{l^-} \rvert \cdot \lvert \boldsymbol{p}_{e^-} \rvert}\ , \end{split} \end{align} $

(9) where
$ \boldsymbol{p}^*_{l^-} $ is the three-momentum of the negative charged lepton in the Z boson rest frame and$ \boldsymbol{p}_{e^-} $ is the three-momentum of the electron in the$ e^+e^- $ rest frame.Figure 4 shows the angular distribution
$1/\sigma{\rm d}\sigma /{\rm d}\cos\theta$ for the charged lepton$ l^- $ in the process of$ e^+e^- \to $ $ Z^\prime /Z\to ZH \to l^+l^- b \bar{b} $ with$ \eta = 0.1 $ . The distributions with pure$ Z^\prime $ contributions are well separated from those with both$ Z^\prime $ and Z-boson mediators effects in Fig. 4 (a) for$ \sqrt{s} = 500 $ GeV. The angular distributions are not very sensitive to the mass of$ Z^\prime $ bosons. Comparing the distributions with different C.M.S. energies from Fig. 4 (a) and Fig. 4 (b), the discrepancy decreases with the increase in collision energy. A forward-backward asymmetry can be defined as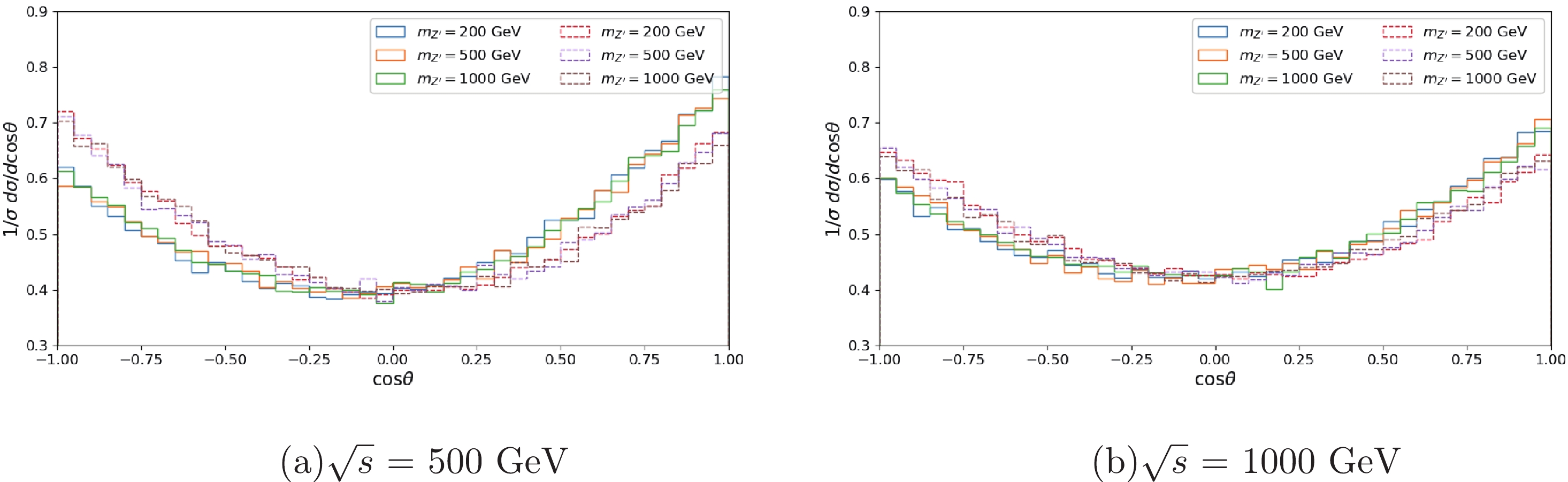
Figure 4. (color online) Angular distribution for the charged lepton
$ l^- $ with$ \eta = 0.1 $ for C.M.S. energies of (a) 500 GeV and (b) 1000 GeV. The solid lines are the distributions for the process$ e^+e^- \to Z^\prime \to ZH \to l^+l^- b \bar{b} $ and the dashed lines are for$ e^+e^- \to Z^\prime /Z\to ZH \to l^+l^- b \bar{b} $ with$ m_{Z^\prime} $ setas 200, 500, and 1000 GeV, respectively.$ \begin{align} \begin{split} A_{\rm FB} & = \frac{ \sigma(\cos \theta \ge 0 ) - \sigma(\cos \theta < 0) }{ \sigma(\cos \theta \ge 0) + \sigma(\cos \theta < 0)} \ . \end{split} \end{align} $

(10) Corresponding to the results in Fig. 4, the asymmetries are listed in Table 1. The forward-backward asymmetry is 0.0726 with
$ \sqrt{s} = m_{Z^\prime} = 500 $ GeV for the pure$ Z^\prime $ contribution, while it changes to$ -0.0136 $ after considering the Z-boson contributions.$ \sqrt{s}=500 $ GeV

$ \sqrt{s}= $ 1000 GeV

$ m_{Z^\prime} $ 

200 GeV 500 GeV 1000 GeV 200 GeV 500 GeV 1000 GeV $ Z^\prime $ 

$ 8.51 \times 10^{-2} $ 

$ 7.26\times 10^{-2} $ 

$ 7.14\times 10^{-2} $ 

$ 4.94\times 10^{-2} $ 

$ 4.02\times 10^{-2} $ 

$ 3.83\times 10^{-2} $ 

$ Z/Z^\prime $ 

$ -2.09\times 10^{-2} $ 

$ -1.36\times 10^{-2} $ 

$ -2.47\times 10^{-2} $ 

$ -1.05\times 10^{-2} $ 

$ -6.69\times 10^{-3} $ 

$ -4.98\times 10^{-3} $ 

Table 1. Forward-backward asymmetry for the processes
$ e^+ e^- \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ and$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with$ \eta = 0.1 $ .The angular distributions of the charged lepton
$ l^- $ are shown in Fig. 5 with$ \sin\alpha = 0.01 $ . The distributions with$ \cos\theta ~~ < $ 0 are lower than those with$ \cos\theta \ge 0 $ for$ e^+ e^- \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ in Fig. 5 (a) and (b). Moreover, the distributions are noticeably separated with various$ m_{Z^\prime} $ in Fig. 5 (c) compared with those in Fig. 5 (a), where the contribution from Z-boson and$ Z^\prime $ -Z interference are included in Fig. 5 (c). With increase in the C.M.S. energy (Fig. 5 (d)), the discrepancies decrease but the asymmetries are observed with the resonance effects when$ m_{Z^\prime} = \sqrt{s} = 1000 $ GeV for$ e^+e^- \to Z^\prime/Z \to $ $ ZH \to l^+l^- b \bar{b} $ . The corresponding forward-backward asymmetries are listed in Table 2.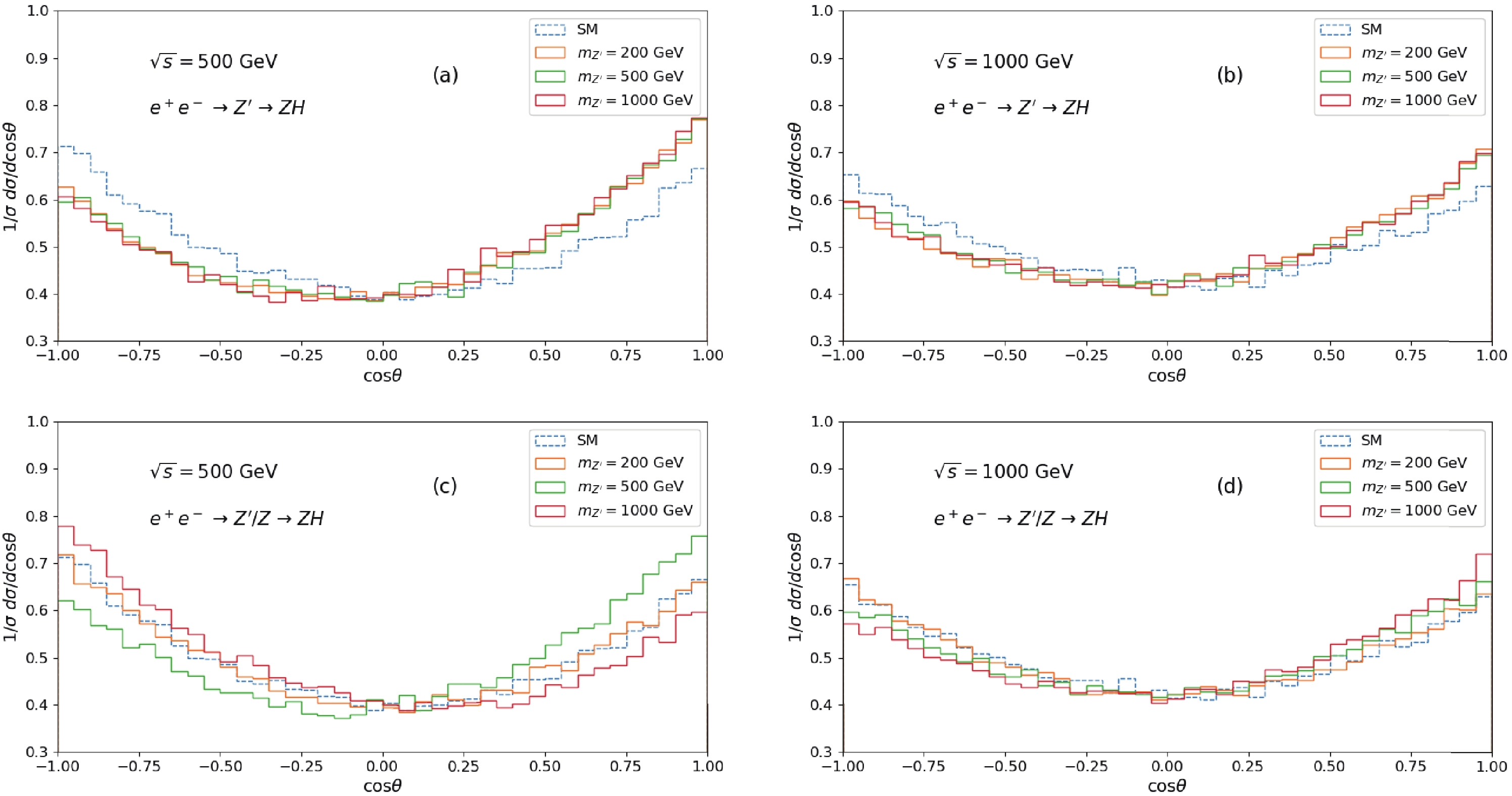
Figure 5. (color online) Angular distribution for the charged lepton
$ l^- $ with$ \sin\alpha = 0.01 $ . The solid lines are the distributions for process$ e^+e^- \to Z^\prime \to ZH \to l^+l^- b \bar{b} $ or$ e^+e^- \to Z^\prime/Z \to ZH \to l^+l^- b \bar{b} $ with$ m_{Z^\prime} $ set as 200, 500, and 1000 GeV, respectively, and the dashed lines are the SM process$ e^+e^- \to Z \to ZH \to l^+l^- b \bar{b} $ .$ m_{Z^\prime} $ 

$ \sqrt{s}=500 $ GeV

$ \sqrt{s}= $ 1000 GeV

$ m_{Z^\prime} $ 

200 GeV 500 GeV 1000 GeV 200 GeV 500 GeV 1000 GeV $ Z^\prime $ 

$ 8.29 \times 10^{-2} $ 

$ 7.43\times 10^{-2} $ 

$ 9.00\times 10^{-2} $ 

$ 4.34\times 10^{-2} $ 

$ 4.20\times 10^{-2} $ 

$ 4.84\times 10^{-2} $ 

$ Z/Z^\prime $ 

$ -2.47\times 10^{-2} $ 

$ 7.50\times 10^{-2} $ 

$ -8.78\times 10^{-2} $ 

$ -1.37\times 10^{-2} $ 

$ 2.67\times 10^{-3} $ 

$ 5.14\times 10^{-3} $ 

Table 2. Forward-backward asymmetry for process of
$ e^+ e^- \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ and$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with$ \eta = 0.1 $ .In Fig. 6, we show the angular distributions of
$ e^+e^- \to $ $ Z^\prime \to ZH \to l^+l^-b\bar{b} $ and$ e^+e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ for different$ Z^\prime $ -Z mixing angles. With the increase in the mixing angle, the asymmetry increases for$ m_{Z^\prime} = $ $ \sqrt{s} = 500 $ GeV. The asymmetry for$ e^+e^- \to $ $ Z^\prime \to ZH $ is larger than the SM process of$ e^+e^- \to Z \to $ $ ZH $ , as shown in Fig. 6 (a) and (b). In particular, the discrepancies increase with the C.M.S energy close to the mass of$ m_{Z^\prime} $ . The asymmetry of the process$ e^+ e^- \to Z^\prime/Z \to ZH \to $ $ l^+l^-b\bar{b} $ with$ \sin\alpha = 0.001 $ is hardly distinguished from the asymmetry of pure Z-boson contribution from Fig. 6 (c). With the collision energy being apart from the value of$ m_{Z^\prime} $ , the distributions exhibit the same tendency as in Fig. 6 (b) and (d). The detailed values are listed in Table 3 with different collision energies and$ \sin\alpha $ . The asymmetry is 0.0715 (0.0741) with$ \sin\alpha = 0.001 $ ($ \sin\alpha = 0.01 $ ) for the$ e^+e^- \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ process with$ \sqrt{s} = 500 $ GeV. For both the Z and$ Z^\prime $ effects, the asymmetry is$ -0.0257 $ (0.0754) with$ \sin\alpha = 0.001 $ ($ \sin\alpha = 0.01 $ ) for$ e^+e^- \to Z^\prime /Z \to ZH \to l^+l^-b\bar{b} $ process with$ \sqrt{s} = 500 $ GeV.
Figure 6. (color online) Angular distribution for the charged lepton
$ l^- $ with$ m_{Z^\prime} = 500 $ GeV. The solid lines are the distributions for process$ e^+e^- \to Z^\prime \to ZH \to l^+l^- b \bar{b} $ or$ e^+e^- \to Z^\prime/Z \to ZH \to l^+l^- b \bar{b} $ with$ \sin\alpha $ are set as 0.001, 0.005, and 0.01, respectively, and the dashed lines are for SM process$ e^+e^- \to Z \to ZH \to l^+l^- b \bar{b} $ .$ \sqrt{s}=500 $ GeV

$ \sqrt{s}=1000 $ GeV

$ \sin\alpha $ 

$ 0.001 $ 

$ 0.005 $ 

$ 0.01 $ 

$ 0.001 $ 

$ 0.005 $ 

$ 0.01 $ 

$ Z^\prime $ 

$ 7.15 \times 10^{-2} $ 

$ 7.24\times 10^{-2} $ 

$ 7.43\times 10^{-2} $ 

$ 3.88\times 10^{-2} $ 

$ 3.73\times 10^{-2} $ 

$ 4.20\times 10^{-2} $ 

$ Z/Z^\prime $ 

$ -2.57\times 10^{-2} $ 

$ 7.16\times 10^{-2} $ 

$ 7.50\times 10^{-2} $ 

$ -1.31\times 10^{-2} $ 

$ -3.89\times 10^{-3} $ 

$ 2.67\times 10^{-2} $ 

Table 3. Forward-backward asymmetry for process of
$ e^+ e^- \to Z^\prime \to ZH \to l^+l^-b\bar{b} $ and$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with$ m_{Z^\prime} $ set at 500 GeV. -
The lepton colliders have an advantage in the polarization of electron/positron beams, and this may affect the measurement of the final particles' distribution to a certain extent. We consider the production of
$ e^+e^- \to Z^\prime \to ZH $ with beam polarization. The cross sections for the studied process are shown in Fig. 7 with various polarizations of the positron and a fixed value of the electron.$ P_{e^{\pm}} $ denotes the longitudinal polarization of$ e^{\pm} $ .$ P_{e^{+}} = 100 $ corresponds to purely right-handed$ e^+ $ . The cross sections decrease when the positron's polarization changes from$ -100 $ to 100 when the electron is right-handed, while the inverse trend occurs when the electron is left-handed. An interesting point occurs at$ P_{e^+}\sim 62 $ where the lines cross each other. This is due to the dependence on the polarization being cancelled at this point. Moreover, the cross section decreases when the positron and electron have the same sign polarizations.
Figure 7. (color online) Cross section of
$ e^+e^- \to Z^\prime \to ZH $ with polarized electron and positron beam.The angular distribution is depicted in Fig. 8 for the process
$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with various beam polarizations. The parameters are set as$ m_{Z^\prime} = \sqrt{s} = 500 $ GeV and$ \sin\alpha = 0.01 $ . Compared with the unpolarized condition, the distributions change significantly, particularly for the right-handed positron and left-handed electron collisions. Assuming the initial state as the right-handed polarized positron and unpolarized electron, the distinctions in distribution are significant (Fig. 8 (b)). The forward-backward asymmetries are listed in Table 4. The asymmetry can reach$ -0.124 $ with one hundred percent polarization of the right-handed positron and left-handed electron.
Figure 8. (color online) Angular distribution for the process
$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with$ m_{Z^\prime} = \sqrt{s} = 500 $ GeV and$ \sin\alpha = 0.01 $ . The colored lines correspond to various polarization values ($ P_{e^+} $ ,$ P_{e^-} $ ).( $ P_{e^+} $ ,

$ P_{e^-} $ )

$ A_{FB} $ 

( $ P_{e^+} $ ,

$ P_{e^-} $ )

$ A_{FB} $ 

$ (100,-100) $ 

$ -1.24 \times 10^{-1} $ 

$ (100,0) $ 

$ -1.23 \times 10^{-1} $ 

$ (80,-80) $ 

$ -1.10 \times 10^{-1} $ 

$ (80,0) $ 

$ -4.51 \times 10^{-2} $ 

$ (60,-60) $ 

$ -6.90 \times 10^{-2} $ 

$ (60,0) $ 

$ 2.70 \times 10^{-3} $ 

$ (-100,100) $ 

$ 1.27 \times 10^{-1} $ 

$ (-100,0) $ 

$ 1.24 \times 10^{-1} $ 

$ (-80,80) $ 

$ 1.22\times 10^{-1} $ 

$ (-80,0) $ 

$ 1.18 \times 10^{-1} $ 

$ (-60,60) $ 

$ 1.19\times 10^{-1} $ 

$ (-60,0) $ 

$ 1.10 \times 10^{-1} $ 

Table 4. Forward-backward asymmetry for process of
$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ with$ m_{Z^\prime} = \sqrt{s} = 500 $ GeV and$\sin\alpha = 0.01 .$ -
The extensions of the SM have been studied extensively at the frontier of energy and luminosity of high energy collision experiments. The
$ Z^\prime $ boson as a new gauge boson has been proposed in many new physics models. As a proton-proton collider, the LHC has reported the search results of$ Z^\prime $ with a mass of a few TeV. The interactions for$ Z^\prime $ coupling to fermions have been investigated in detail. The next generation of high energy colliders possibly focuses on the Higgs physics, i.e., Higgs factory, which provides an opportunity to study the interaction of$ Z^\prime $ coupling to Higgs boson.In this paper, we have investigated the process of
$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ . The interactions and couplings are adopted following the models proposed by Wells et al. The$ Z^\prime $ couplings to the SM are related to$ Z^\prime $ -Z mixing. We investigate the$ e^+ e^- \to $ $ Z^\prime \to ZH $ production cross section. The cross section is at the same order as the SM process$ e^+ e^- \to Z \to ZH $ with the mixing angle$ \sin\alpha\sim10^{-2} $ . The angular distributions of the leptons decaying from the Z-boson rely on the mixing angle and$ Z^\prime $ mass; we have investigated the distributions with the parameters variation of$ 0.001 < \sin\alpha < 0.01 $ ,$ 200\; \text{GeV} < m_{Z^\prime} < 1000 $ GeV and$ \sqrt{s} = 500, 1000 $ GeV. The forward-backward asymmetry can reach 0.0743 for$ \sin\alpha = 0.01 $ and$ m_{Z^\prime} = \sqrt{s} = 500 $ GeV. The beam polarization effects have been investigated for the signal process$ e^+ e^- \to Z^\prime/Z \to ZH \to l^+l^-b\bar{b} $ . The final particles distributions change noticeably with some special polarization compared with the unpolarized condition. As the enhancement of the precision measurement on the Higgs boson, these observations will promote the understanding of the interactions between Higgs and new physics particles.
Investigating the Z' gauge boson at future lepton colliders
- Received Date: 2022-01-01
- Available Online: 2022-05-15
Abstract:






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: