-
One of the most important questions in the study of unstable neutron-rich nuclei is the evolution of shell structures, such as a rapid change of the 1
$ s_{1/2} $ orbit relative to the 0$ d_{5/2} $ and 0$ p_{1/2} $ orbits in the nuclei around N = 8 [1, 2]. This variation can lead to the disappearance of conventional magic number N = 8 and the appearance of new magic number N = 14 or N = 16. Our experimental results obtained from the single-nucleon transfer reactions of 11Be on proton and deuteron targets imply the breakdown of the magic number N = 8 and the strong intrusion of the$ sd $ -shell in 11Be and 12Be [3-9]. As another well-known example, a systematic comparison of the energies of the 2$ ^+ $ states in neutron-rich oxygen and carbon isotopes and the study of the evolution of single-particle levels in 17C suggests that the N = 14 sub-shell is absent for Z = 6 [10, 11]. In 13C, 15C, and 17C, the excitation energies of the 5/2$ ^+ $ states are higher than the 1/2$ ^+ $ states [12], demonstrating the inversion of 1$ s_{1/2} $ and 0$ d_{5/2} $ orbitals in comparison with the conventional shell model.For the neutron-rich nucleus 16C, its bound excited states and high-lying unbound states have been intensively studied by various experiments; see Refs. [13-16] and references therein. However, apart from one 2n transfer reaction [17, 18] and one knockout experiment of 17C on a proton target [19], the experimental studies of low-lying unbound states at
$ E_x $ = 5–10 MeV, which are important to well understand the shell gap between$ sd $ - and p-shell as well as the ordering of s- and d-shells [20], are scarce. One resonant state at$ E_x $ = 6.11 MeV was firstly observed in the 14C(t, p)16C reaction [17, 18, 21]. The larger 2n transfer cross sections for this state suggested that its spin-parity was either of 2$ ^+ $ , 3$ ^- $ , or 4$ ^+ $ [17, 18]. Three unbound states at$ E_x $ = 5.45, 6.11, 6.28 MeV in 16C were observed by Satou$ et ~al $ in a 1n knockout reaction [19]. The 5.45 and 6.28 MeV states decay predominately via 1n to the first excited state of 15C (5/2$ ^+ $ , d-wave), while the 6.11 MeV state decays to the ground state (g.s.) of 15C (1/2$ ^+ $ , s-wave). The spin-parity of 2$ ^- $ was assigned to the 5.45 MeV state because both the excitation energy and the cross section were consistent with theoretical calculations. The negative-parity assignment to this state was further confirmed by the fact that its parallel momentum angular distribution agreed well with a p-wave neutron knockout from 17C [19]. For the 6.11 MeV state, comparing with theoretical calculations, its excitation energy and the 1n knockout cross section preferred the$ J^{\pi} $ assignment of 2$ ^+ $ /3$ ^- $ rather than 4$ ^+ $ [19]. Fortune suggested that the 6.11 MeV state was not 3$ ^- $ , but probably 1$ ^- $ (0$ ^- $ ) according to the shell model and a simple weak-coupling model [22]. However, Fortune recently concluded that its$ J^{\pi} $ was 2$ ^+ $ after investigating its width (32.6(5) keV) from the 14C(t, p)16C reaction [23]. For the 6.28 MeV state, Satou$ et ~al $ suggested that the spin-parities of 1$ _2^- $ and 2$ _2^- $ were candidates [19], and lately Fortune concluded that its$ J^{\pi} $ was 2$ ^- $ [22]. These studies are summarized in Table 1.Table 1. Summary of spin-parity assignments for the negative-parity states in 16C.
In this paper, we report on a new measurement of the low-lying unbound states in 16C, which were populated by the deuteron inelastic scattering using a radioactive beam 16C at about 23.5 MeV/nucleon in inverse kinematics. Details of this experiment has been published in Refs. [14-16], and in this paper we only focus on the inelastic scattering of 16C to its unbound states.
-
A 16C secondary beam was produced from a 59.6-MeV/nucleon 18O primary beam impinging on a 4.5-mm-thick 9Be target. The secondary beam was purified and transmitted by the Radioactive Ion Beam Line in Lanzhou (RIBLL), Institute of Modern Physics (IMP), China. The time-of-flight (TOF) provided by two plastic scintillator detectors and energy losses (
$ \Delta E $ ) in a large-surface silicon detector (SSD) were used to identify the secondary beam. The average beam intensity and the purity of 16C were up to about 10$ ^4 $ particles per second (pps) and 90%, respectively. The beam energy was ~23.5 MeV/nucleon.The experimental setup is given in Refs. [14, 15]. Three parallel-plate avalanche chambers (PPACs) were placed upstream of the physical targets to provide beam tracking information. The resolution of the hit position on the target was ~1.0 mm (FWHM, full width at half maximum) in both x and y directions. A 9.53
$ \pm $ 0.12 mg/cm$ ^2 $ (CD$ _2 $ )$ _n $ target was used to measure the inelastic scattering data. A 13.73$ \pm $ 0.13 mg/cm$ ^2 $ carbon target was employed to subtract the background coming from carbon atoms in the (CD$ _2 $ )$ _n $ target. An empty target was also applied to measure random or accidental coincidence events. Several sets of telescopes were installed in a large vacuum chamber to detect and identify charged particles using a standard$ \Delta E $ - E method. The telescope T$ _0 $ and T$ _2 $ were placed 156 and 157 mm away from the target to distinguish the carbon isotopes at forward angles and the recoil deuterons emitting to backward angles, respectively. The telescope T$ _0 $ installed at around 0$ ^{\circ} $ is made up of three 1000-μm-thick double-sided silicon strip detectors (DSSDs), three 1500-μm-thick SSDs, and a layer of 4-cm-thick CsI(Tl) crystals read out by photodiodes. The telescope T$ _2 $ , which consists of a 300-μm-thick DSSD, a 1500-μm-thick SSD, and a layer of CsI(Tl) crystals, was placed at$ \sim 69 ^{\circ} $ relative to the beam direction. Each DSSD with an active area of$ 63.96 \;\;{\rm mm}\times 63.96 $ mm is divided into 32 strips on both sides. The angular coverage of the telescopes T$ _0 $ and T$ _2 $ are$ \theta_{\rm{lab}}^{T_0} $ = 0$ \sim 12 ^{\circ} $ and$ \theta_{\rm{lab}}^{T_2} $ = 57$ ^{\circ} $ $ \sim $ 82$ ^{\circ} $ , respectively. The overall angular resolution of the telescope T$ _2 $ was$ \sim 0.92^{\circ} $ (FWHM).The particle identification (PID) spectra detected by the telescope T
$ _0 $ in coincidence with the recoil light-charged particles measured by the telescope T$ _2 $ are presented in Fig. 2 (a) of Ref. [14]. The carbon isotopes 16C, 15C, and 14C are discriminated clearly. 16C ions were from the elastic or inelastic scattering to the bound states at$ E_x $ = 1.766(2$ _1^+ $ ), 3.986, 4.088 and 4.142 MeV in 16C, while 15C and 14C particles came from the inelastic scattering to unbound states in 16C which subsequently decay via 1n and 2n, respectively. Note that the second 0$ ^+ $ state at around$ E_x $ = 3.027 MeV was hardly populated by the inelastic scattering [14, 24].With a gate of all carbon isotopes, including 16C, 15C, and 14C, the recoil deuterons detected by the telescope T
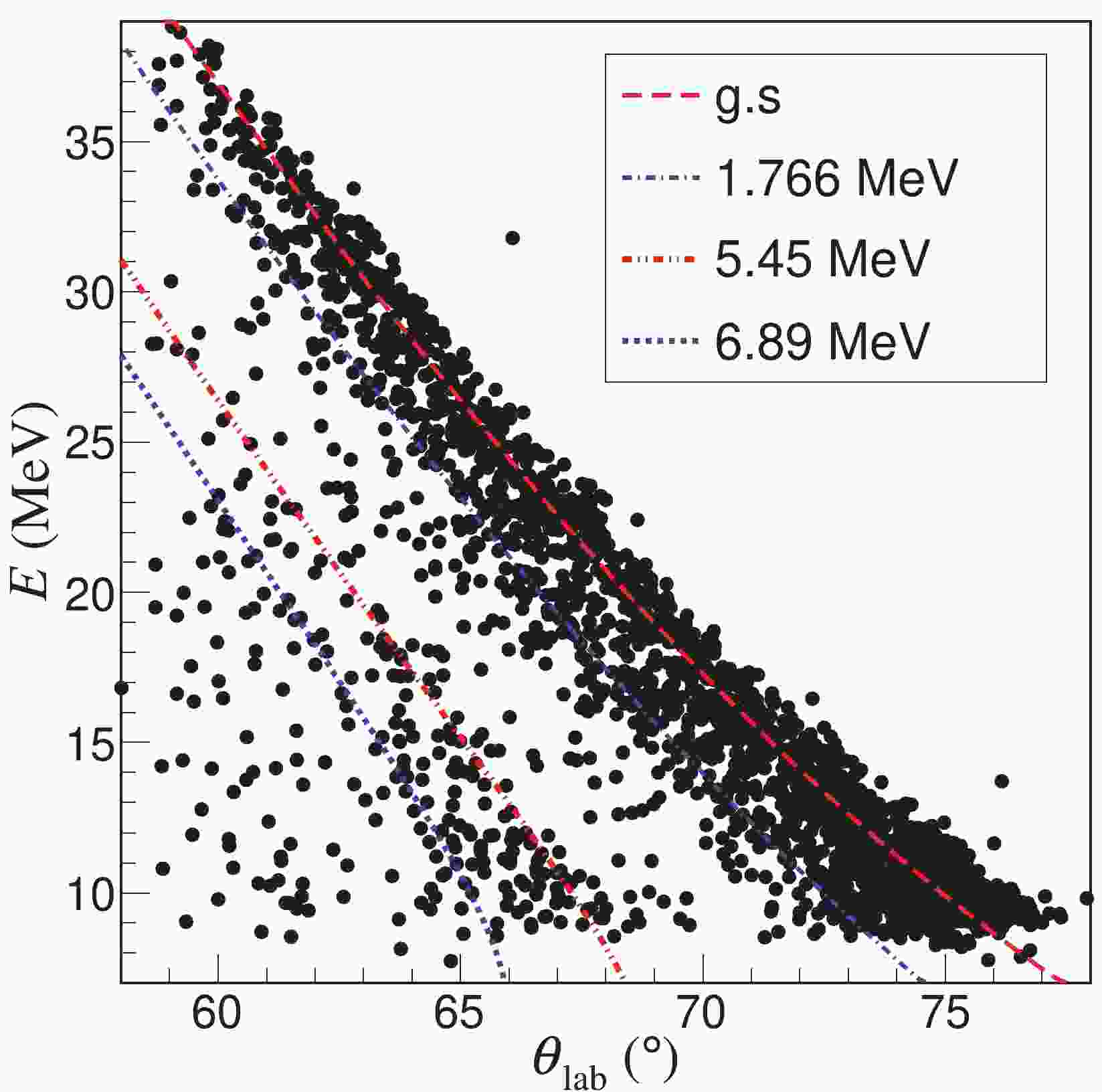
$ _2 $ were used to analyze the elastic and inelastic scattering differential cross sections (DCSs). The energies of the recoil deuterons as a function of their angles in the laboratory frame are displayed in Fig. 1. Most data points agree well with the calculated kinematic curves, indicating that these events are indeed from elastic or inelastic scattering of 16C + d. Although the statistics are limited, the 1.766 and 5.45 MeV states are clearly seen. Within the angular range of 60°$ \sim$ 66° in the laboratory frame, some events are also in line with the blue dotted curve, which stands for the calculated kinematics of a new unbound state at$ E_x $ = 6.89 MeV.
Figure 1. (color online) Kinematics for the recoil deuterons in coincidence with
$^{14,15,16}$ C. The curves are calculated for the elastic scattering and the inelastic scatterings of 16C + d to the 1.766, 5.45, and 6.89 MeV states in 16C.Figure 2 displays the Q-value spectra deduced from the energies and angles of the recoil deuterons emitted in the angular range between 60°
$ \sim $ 68° in the laboratory frame. The g.s., and the 1.766, ~4.0, 5.45 MeV excited states in 16C are clearly observed. A new resonant state centered at around 6.89 MeV is measured experimentally for the first time. In coincidence with 15C, the Q-value spectrum is illustrated as the grey histograms. Note that the high-energy portion for 15C is prone to be contaminated by the secondary beam 16C, therefore the cut of 15C should be gated not only on the PID spectrum measured by the telescope T0 but also on the two-dimensional (energies versus angles) spectrum of carbon isotopes according to the kinematics of 16C + d inelastic scattering. Comparing to the spectra gated by all carbon isotopes (white histograms), the events at around the 6.89 MeV state reduce slightly, indicating that this state predominantly decays via 1n to the bound states in 15C rather than via 2n to 14C even though its excitation energy is higher than the 2n separation threshold ($ S_{2n} $ = 5.468 MeV). However, its specific decay path, namely to the g.s. or to the first excited state in 15C, can not be determined just from the present experiment.
Figure 2. (color online) Excitation energy spectra reconstructed from the energies and angles of the recoil deuterons in coincidence with 14,15,16C (white histograms) or with 15C (grey histograms).
As shown in Fig. 3, four excitation energy spectra were constructed within an angular bin of 2
$°$ in the laboratory frame. The 5.45 MeV state is clearly measured in each spectrum. However, the 6.89 MeV resonance is hardly seen in Fig. 3 (d) because the recoil deuterons inelastically scattered from this state can not reach 66°–68°$°$ according to the kinematics, as seen in Fig. 1. In Fig. 2 and Fig. 3, the events at around 3.5 MeV correspond to the mixture of the excited states at 3.03(0$ _2^+ $ ), 3.98(2$ ^+ $ ), 4.088($ 3^+ $ ) and 4.142($ 4^+ $ ) MeV in 16C. However, the statistics are too low to fix the excitation energy spectrum with so many states. Their effect on the differential cross sections of unbound states was estimated to be negligible.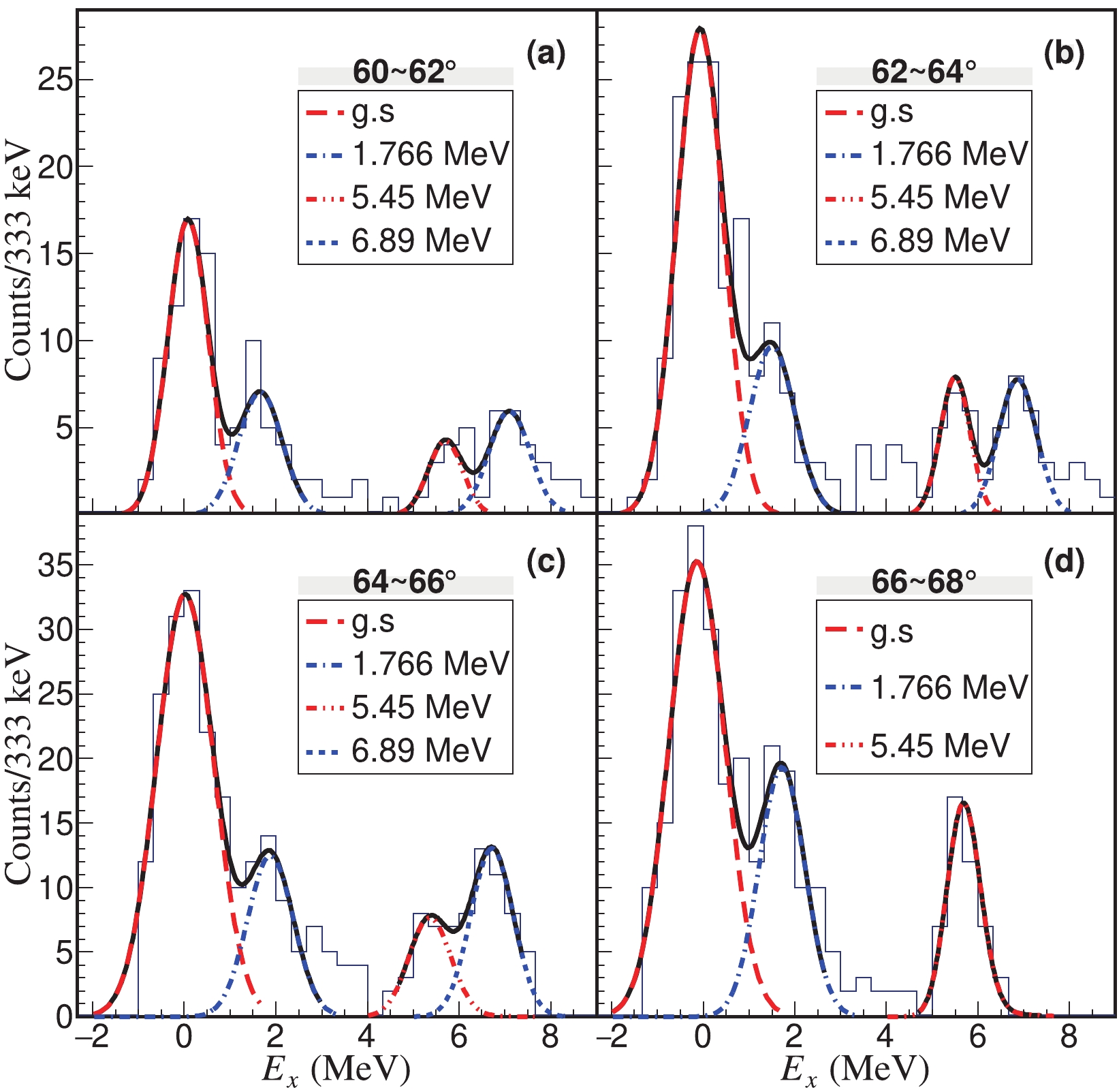
Figure 3. (color online) With a gate of all carbon isotopes (14,15,16C), excitation energy spectra deduced from the energies and angles of the recoil deuterons emitted at (a) 60°–62°, (b) 62°–64°, (c) 64°–66°, and (d) 66°–68°.
The Gaussian and Breit–Wigner functions [25] were convoluted with the response function of the whole detection system to fit the bound and unbound states, respectively, in the excitation energy spectra (Figs. 2 and 3). The Breit–Wigner function with the energy-dependent width
$ \Gamma(E_r) $ is defined as [25]:$ F(E_r) = \frac{\Gamma(E_r)}{(E_x-E_0)^2+\Gamma^2(E_r)/4}, $

(1) where
$ E_r $ is the relative energy of the decay particles,$ E_0 $ and$ E_x $ are the centroid energy and the excitation energy of the resonant peak, respectively. The relationship between$ E_r $ and$ E_x $ is$ E_x $ =$ E_r $ +$ S_n $ , where$ S_n $ = 4.25 MeV is the 1n separation energy of 16C [26]. Note that the 5.45 MeV state predominantly decays by 1n to the first excited state at$ E_{\rm{1st}} $ = 0.74 MeV in 15C rather than to its g.s. [19], therefore the equation$ E_r =E_x - S_n - E_{\rm 1st}$ is used here. The energy-dependent width is defined as$ \Gamma(E_r)\equiv g \sqrt{E_r} $ , where g is a free parameter during the fitting procedure. We assumed that the 6.89 MeV state has the same decay path as the 5.45 MeV state, as they have the same excitation mode (see below). The response function was simulated using the GEANT4 package [27], taking into account the energy spread of the secondary beam (2.0%), the energy losses of the recoil deuterons in the CD$ _2 $ target, the energy and angular resolution of the actual experimental setup and so on [14]. The simulated resolutions for the 5.45 and 6.89 MeV states are 952 and 1050 keV (FWHM), respectively, which are not good enough to discriminate these two states from the 6.11 and 6.28 MeV states. By comparing the experimental excitation energy spectra to the simulation results with different mixture portion of the 6.11 and 6.28 MeV states, we found that the mixture of these two states is smaller than 20%. Therefore, we assumed that they are pure 5.45 and 6.89 MeV states in this paper. The intrinsic width of the 5.45 MeV resonance is deduced to be 3.5 keV ($ g \sqrt{E_r} $ ), which is consistent with the conclusion from the 1n knockout reaction [19]. How should we understand such a narrow intrinsic 1n-decay width of the 5.45 MeV state? This near-threshold state is only 30 keV below the 2n emission threshold. Therefore, its wave function is coupled by the imprint of the 2n-decay channel, which leads to a very narrow decay width [28, 29]. The intrinsic width of the newly measured state is determined to be 10.2 keV.The elastic scattering DCSs of 16C + d have been published in Ref. [14]. The systematic optical potential (OP) parameters obtained from Daehnick et al. [30], An et al. [31], Han et al. [32], and Zhang et al. (DA1p) [33] were applied to describe the DCSs of 16C + d. In order to best fit the experimental data, the well depths of real (
$ V_V $ ) and imaginary parts ($ W_V $ +$ W_S $ ) [4] were searched. The searching process were performed with the code SFRESCO [34] using the$ \chi^2 $ minimization method. The best OP parameters are listed in Table 2.$V_0\; {\rm{/MeV} }$ 

$r_0\; {\rm{/fm}}$ 

$a_0\; {\rm{/fm}}$ 

W/MeV $r_W\; {\rm{/fm}}$ 

$a_W\; {\rm{/fm}}$ 

$W_D\; {\rm{/MeV}}$ 

$r_{W_D}\; {\rm{/fm}}$ 

$a_{W_D}\; {\rm{/fm}}$ 

$\delta_d\; {\rm{/fm}}\;5.45\;{\rm{MeV}}$ 

$\delta_d\; {\rm{/fm}}\;6.89\;{\rm{MeV}}$ 

DA1 p [33] 82.397 1.067 0.776 9.557 1.699 0.744 0.006 1.699 0.744 0.58 0.55 Daehnick et al. [30] 72.405 1.170 0.792 2.496 1.325 0.692 9.196 1.325 0.692 0.55 0.51 An et al. [31] 73.881 1.149 0.751 3.363 1.345 0.603 7.542 1.394 0.687 0.56 0.52 Han et al. [32] 74.017 1.174 0.809 6.787 1.563 0.813 6.346 1.328 0.578 0.56 0.53 Table 2. Parameters of the optical model potentials extracted from the elastic scattering of 16C + d [14]. The corresponding deformation lengths extracted from the inelastic scattering DCSs for the 5.45 and 6.89 MeV states are listed in the last two columns.
The counts of the inelastically scattered deuterons were determined by fitting each Q-value spectrum displayed in Fig. 3. Comparing with the theoretical calculations, the DCSs for inelastic scattering to the two unbound states are plotted in Fig. 4. Only statistical errors are shown. The systematic errors are estimated to be about 10%, including the contributions from different cuts on the PID spectra to choose the recoil deuterons and carbon isotopes, the uncertainties in target thickness and in the simulation of solid angles. The background contribution from carbon in the CD
$ _2 $ target was found to be negligible after analyzing the data from the carbon and the empty targets. It should be noted that the data points at 60°–62°$°$ in the laboratory frame for the 5.45 MeV state were discarded for two reasons. First, the energies of deuterons are close to the threshold of the CsI(Tl) detector, leading to the loss of some events in this detector. Second, some recoil deuterons punch through the detectors sideways at the edges, resulting in incorrect measurement of their energies.
Figure 4. (color online) Angular distributions of inelastic scatterings to the (a) 5.45 and (b) 6.89 MeV states in 16C in comparison with the DWBA calculations using different OPs and the corresponding deformation lengths. See text for more details. Note that the DWBA calculations have been averaged over an angular range, which corresponds to the angular acceptance for each data point (2 degrees in the laboratory frame).
Distorted-wave Born approximation (DWBA) calculations were performed using the code FRESCO [34] in the framework of rotational model to extract the deformation length. The method is similar to that used in the inelastic scattering to the 2
$ ^+ $ state in 16C [14]. Using the OP parameters obtained from the elastic scattering data and deformation length δ = 1.0 as the starting points, the best δ values were searched using the code SFRESCO [34] with the minimum$ \chi^2 $ method. With different OP parameters, different δ values are extracted and listed in Table 2. In Fig. 4, the black solid and the black dot-dot-dashed curves stand for the DWBA calculations using the same systematic OP parameters obtained from An$ et ~al $ [31] but with an l = 1 and an l = 2 excitation, respectively. It is clear that the l = 1 result gives a better reproduction of the experimental DSCs. In the rotational model, they assume an intrinsic shape that is common to the initial and final states. Thus, only the natural parity transitions with (-1)$ ^l $ (l is parity change) are allowed. In the case of an l = 1 transition, only the assumption of 1$ ^- $ state is valid. For the 5.45 MeV state, the valid assumption of J$ ^\pi $ = 1$ ^- $ is different from the spin-parity assignment of 2$ ^- $ in Ref. [19], which needs more discussion (below) and studies to clarify.The average δ values are 0.56
$ \pm $ 0.05 (statistics)$ \pm $ 0.06 (systematics) fm and 0.53$ \pm $ 0.05 (statistics)$ \pm $ 0.05 (systematics) fm for the 5.45 and 6.89 MeV state, respectively. The statistical errors were obtained from the experimental DCSs, while the systematic errors were deduced from the results with different OPs used in the calculations. The deformation lengths for the 5.45 and 6.89 MeV states (an l = 1 excitation) are consistent with each other within the error bar, but are different from that of 1.18$ \pm $ 0.15 for the 1.776 MeV state (an l = 2 excitation). This kind of difference was also found in 12Be, where deformation lengths of 0.24 and 1.56 fm were extracted for the E1 and E2 cases, respectively [35]. This phenomenon demonstrates that 16C has reduced deformation when being excited from the g.s. to the negative excited states, similar to the excitation of$ ^9 $ Li [36]. The integrated cross sections are 6.42 and 5.41 mb for the 5.45 and 6.89 MeV states, respectively. -
For 16C, shell model calculations were performed using the original and the modified YSOX interaction in the 3
$ \hbar\omega $ model space [12, 37, 38]. Figure 5 plots the calculated results compared with the experimental data. The calculated results for the negative-parity states using the WBT interaction are also displayed [19]. The bound excited states are reasonably well reproduced by the calculations with the original model (YSOX1), but most of the calculated excitation energies are higher than the experimental data, especially for the unbound states above the 1n separation energy. The calculations with a decrease of 200 keV of$ 0d5/2 $ -orbital (YSOX2) give a better description of the excited states. Note that such reduction in the YSOX interaction leads to a decrease of the$ 5/2^+ $ state in 15C and an increase of the$ 1/2^+ $ and$ 5/2^+ $ states in 17C, but does not change the energy level sequence of the low-lying states in both 15C and 17C.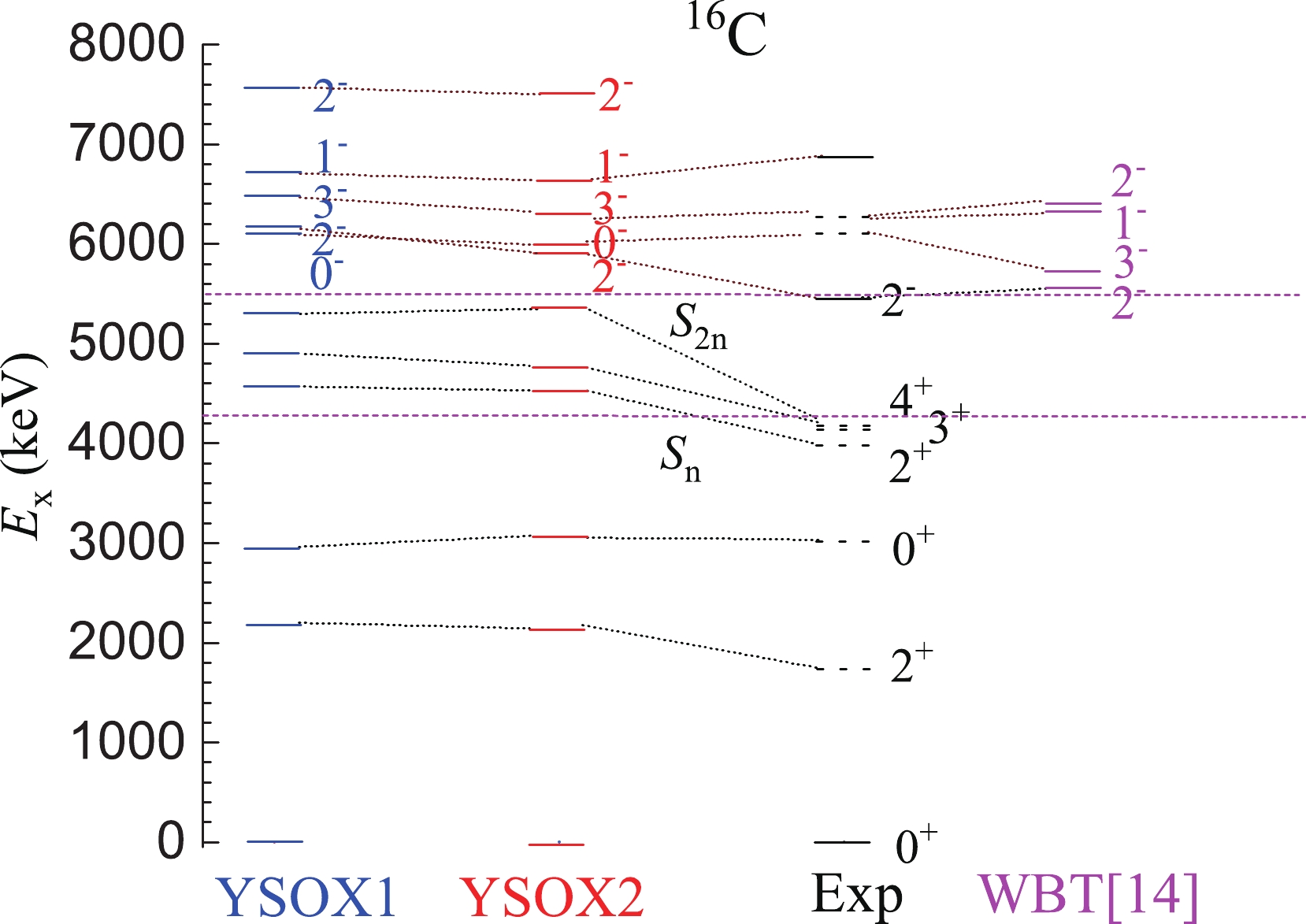
Figure 5. (color online) Energy level scheme of 16C compared with the shell model calculations using the original (YSOX1, blue) and modified (YSOX2, red) YSOX interaction [12], and the WBT interaction (WBT, purple) [19]. For the experimental results, the black solid and dotted lines stand for the states observed in the present and previous experiments, respectively.
The lowest two negative-parity states, 0
$ ^- $ and 2$ ^- $ , are inverted if we use YSOX2 instead of YSOX1. Considering an l = 1 excitation for the 5.45 MeV state, both the spin-parities of 0$ ^- $ and 2$ ^- $ are possible. The configurations and neutron occupations of the unbound negative-parity states with excitation energies lower than 8000 keV are listed in Table 3. Calculations from YSOX2 give a predominant 1$ \hbar\omega $ configuration for all these negative-parity states, demonstrating that the major excitation mode is the single-particle cross-shell excitation. The 0$ ^- $ state has an obviously large s-shell neutron occupation number, while the 2$ ^- $ state has a relatively large d-shell neutron occupation number. Thus, the assignment of 2$ ^- $ is more appropriate than 0$ ^- $ for the 5.45 MeV state because it decays predominantly to the first excited state of 15C [19], in which state the valence neutron dominantly populates the d-orbital. This spin-parity assignment is consistent with Refs. [19, 22]. With more d-orbital components, 3$ ^- $ and 1$ _2^- $ are possible candidates for the 6.89 MeV state, which has the same decay path or the same excitation mode and excitation cross sections as the 5.45 MeV state [19]. The 2$ _2^- $ state with more s-orbital neutrons is ruled out. Taking into account the DWBA calculation results, its spin-parity is most likely 1$ _2^- $ . Note that, here, using the standard shell model instead of the continuum shell model for the description of resonances is not completely appropriate, thus the spin-parity assignment is very preliminary. The new tentative assignments are summarized in Table 1, where controversial spin-parity results for these negative-parity states are clearly seen. Thus, in the future, more experiments with better resolution are required to clarify these divergences.spin-parity $1 \hbar\omega\;({\text{%}})$ 

$3 \hbar\omega\;({\text{%}})$ 

$N _{p1/2}$ 

$N _{p3/2}$ 

$N _{d3/2}$ 

$N _{d5/2}$ 

$N _{s1/2}$ 

$2 ^-$ 

92.4 7.6 1.169 3.279 0.260 2.147 0.635 $0 ^-$ 

92.7 7.3 1.185 3.772 0.173 1.925 0.945 $3 ^-$ 

92.2 7.8 1.178 3.784 0.264 2.009 0.765 $1 ^-$ 

92.8 7.2 1.291 3.666 0.195 2.091 0.757 $2 _2^-$ 

92.4 7.6 1.225 3.737 0.223 1.778 1.037 Table 3. Configurations and the neutron occupancies of the low-lying negative-parity states in 16C, with YSOX2 in the
$3 \hbar\omega$ model space. -
In summary, two negative-parity states at
$ E_x $ = 5.45, 6.89 MeV in 16C were studied by deuteron inelastic scattering in inverse kinematics. The former is consistent with the previous experimental result from the 1n knockout from 17C [19], while the latter resonance is newly observed in our experiment. The angular distributions of these two states were well reproduced by the DWBA calculations with an l = 1 excitation. The shell model calculations with the modified YSOX interaction in the 3$ \hbar\omega $ model space support the negative-parity assignment for these two states. -
We gratefully thank the IMP accelerator group for providing 18O primary beam and the RIBLL collaboration for supplying a lot of electronics.
Investigation of negative-parity states in 16C via deuteron inelastic scattering
- Received Date: 2021-12-28
- Available Online: 2022-05-15
Abstract: Two low-lying unbound states in 16C are investigated by deuteron inelastic scattering in inverse kinematics. Besides the 2





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: