-
A recent observation by the LHAASO cooperative team has opened a new window for exploring ultra-high-energy (UHE) cosmic rays and challenged our current understanding on the origin of such UHE gamma radiation as well as theories on high energy physics. The LHAASO experiment has detected a large number of gamma-ray photons with energies exceeding 100 TeV from twelve gamma-ray sources in our galaxy [1]. The highest energies of up to 1.42 PeV reveal the coming of a new age of Galactic PeVatrons in extremely-high-energy astronomy. Previously, the photon spectra of galactic sources with energies beyond 100 TeV have been detected by the Tibet-ASγ [2, 3], HAWC [4, 5], and Carpet-2 [6].
In theory, the observation of UHE cosmic rays introduces two fundamental problems. The first involves the origin of UHE gamma radiation [7]. The types of galactic sources that can provide the extreme physical conditions required to accelerate particles to such high energy levels remain a mystery [8]. The second concerns the propagation of UHE cosmic rays in the universe or galaxy, which is involved in various interactions between cosmic rays and backgrounds such as CMB or interstellar radiation fields (ISRF). One outstanding problem is on the fate of Lorentz symmetry at these high energy levels, which determines the threshold value of the possible interactions and leads to different energy cutoffs that can be observed on Earth. The possibility of using UHE cosmic rays as a probe for Lorentz symmetry violation has been extensively investigated in literature [9-13]; on the theoretical side, this may be treated as a sign of quantum gravity effects [14-19].
A discussion on Lorentz symmetry violation based on LHAASO data is presented in [20-24]. Additionally, the constraints on the mass scale of Lorentz symmetry violation has been discussed based on the LHAASO data. In particular, Lorentz violation due to the subluminal scenario seems to be preferred, and the constraints on the mass scale are stronger in comparison with those that appear in literature [25-29]. One of the main reasons for considering Lorentz symmetry violation arises from the fact that the observed energy of gamma ray photons is significantly higher than the threshold value of pair-production interactions. In the universe, high-energy cosmic rays interact with the background. One typical process for gamma rays is the interaction with CMB photons:
$ \gamma \gamma \rightarrow e^{+} e^{-} $ . Obtaining the threshold energy for gamma-ray photons from the threshold theorem in standard special relativity is straightforward and reads as$ m^2_e/\epsilon_{b} $ , where$ \epsilon_{b} $ is the energy of the background photons and$ m_e $ is the mass of an electron. Substituting the energy of CMB photons into this expression, the threshold energy for gamma ray photons is calculated to be approximately$ 400 $ TeV. Because the energy of some gamma-ray photons detected by the LHAASO is significantly higher than this threshold value, the theoretical value of the threshold energy must be increased by modifying the ordinary dispersion relations in special relativity; this introduces the possibility of Lorentz symmetry violation, which has been investigated in Ref. [22]. However, inspired by [22], we intend to understand the LHAASO data from an alternative point of view. Although the energy of gamma-ray photons detected by the LHAASO is significantly higher than the threshold value of pair production, which means the gamma-ray photons must interact with background photons and thus decay during propagation, the key point to consider is how many photons would survive during propagation and finally reach the Earth; this depends on the number density of the background photons as well as the distance between the gamma-ray sources and Earth. This problem is addressed by considering the transparency of the universe to gamma rays [30-33]. The average distance that gamma rays can propagate through the background is described by the optical depth τ. Roughly speaking, if τ is less than one, the gamma rays can penetrate the medium between the source and Earth.The attenuation of galactic gamma-rays due to the interaction with photons from the CMB and ISRF is briefly discussed in an original paper by the LHAASO team; the opacity for four gamma sources is presented in Figure 6 of that paper [1]. In this study, we are concerned with the fate of Lorentz symmetry; thus, we investigate what the lowest value may be for the survival probability among eleven gamma ray sources①. Therefore, following the suggestion from [22], we intend to elaborate upon the investigation on gamma ray photons with the background based on LHAASO data. In particular, we will compute the optical depth, mean free path, and survival probability for photons from all gamma-ray sources in the LHAASO and then find the lowest survival probability for the observed gamma ray photons. Our key result is that among the eleven gamma ray sources, the optical depth is always less than one, and the lowest survival probability is approximately 0.60, which is a high value and implies that a high quantity photons with energies above the threshold value may reach the Earth without Lorentz symmetry violation. We conclude that it is unreasonable to argue that Lorentz symmetry will be violated from current observations at the LHAASO.
-
In this section, we present the main process for computing the optical depth and survival probability of gamma ray photons; a detailed derivation and discussion can be found in Ref. [32]. Because photons detected by the LHAASO are galactic and in the range of 100 TeV to 10 PeV, we only consider the interaction process with CMB photons, which is dominant in comparison with the ISRF photon process, as shown in Refs. [32, 33].
Usually, during a propagation process, the survival probability of photons is defined as
$ P_{\gamma \rightarrow \gamma}\left(E_{0}, z_{s}\right) = {\rm e}^{-\tau_{\gamma}\left(E_{0}, z_{s}\right)}, $

(1) where
$ E_{0} $ is the observed energy, and$ z_{s} $ is the redshift. The key quantity$ \tau_{\gamma}\left(E_{0}, z_{s}\right) $ is the optical depth which characterizes the dimming of the source at$ z_{s} $ . During propagation in the universe,$ \tau_{\gamma}\left(E_{0}, z_{s}\right) $ is given by [30, 32]$ \begin{aligned}[b] \tau_{\gamma}\left(E_{0}, z_{s}\right) =& \int_{0}^{z_{s}} \mathrm{\; d} z \frac{\mathrm{d} l(z)}{\mathrm{d} z} \int_{-1}^{1} \mathrm{\; d}(\cos \varphi) \frac{1-\cos \varphi}{2} \\ &\times \int_{\epsilon_{\mathrm{thr}}(E(z), \varphi)}^{\infty} \mathrm{d} \epsilon(z) n_{\gamma}(\epsilon(z), z) \sigma_{\gamma \gamma}(E(z), \epsilon(z), \varphi), \end{aligned} $

(2) where φ is the scattering angle,
$ n_{\gamma} $ is the number density of the background photons,$ \sigma_{\gamma \gamma} $ is the cross-section of the pair production interaction,$ \epsilon_{\mathrm{thr}} $ is the threshold energy of the background photons in the interaction, and$ \epsilon(z) $ and$ E(z) $ are the energy of background photons and gamma ray photons at a certain redshift z, respectively. In standard special relativity with Lorentz symmetry,$ \epsilon_{\mathrm{thr}}(E, \varphi) = \dfrac{2 m_{e}^{2} c^{4}}{E(1-\cos \varphi)} $ . In addition,$ \mathrm{d} l(z)/\mathrm{d} z $ is the distance travelled by a photon per unit redshift at redshift z, which is given within the standard ΛCDM cosmological model as$ \frac{\mathrm{d} l(z)}{\mathrm{d} z} = \frac{c}{H_{0}} \frac{1}{(1+z)\left[\Omega_{\Lambda}+\Omega_{M}(1+z)^{3}\right]^{1 / 2}}, $

(3) where
$ H_{0}\simeq 7 \times 10^3 \mathrm{cm} \ \mathrm{s^{-1} \ kpc}^{-1} $ is the Hubble-Lemaitre constant,$ \Omega_{\Lambda}\simeq0.7 $ is the dark energy density, and$ \Omega_{M}\simeq 0.3 $ is the matter energy density.As mentioned above, for the galactic sources presented in Ref. [1], the background photons are dominated by CMB photons, and the effect of the redshift z on the quantities in (2) is ignored throughout the paper because the redshift is small. In this context, the number density of CMB photons
$ n_{\gamma}(\epsilon(z), z) $ can be approximately expressed as$ n_{\gamma}(\epsilon) = \frac{8 \pi \epsilon ^2}{c^3 h^3 \left({\rm e}^{\frac{\epsilon }{k T}}-1\right)}, $

(4) where k is Boltzmann constant and T is the temperature of the background. The cross-section
$ \sigma_{\gamma \gamma}(E(z), $ $ \epsilon(z), \varphi) $ is given by [32, 33]$ \sigma_{\gamma \gamma}(E, \epsilon, \varphi) = \frac{2 \pi \alpha^{2}}{3 m_{e}^{2}} W(\beta) \simeq 1.25 \cdot 10^{-25} W(\beta) \; \mathrm{cm}^{2}, $

(5) with
$ W(\beta) = \left(1-\beta^{2}\right)\left[2 \beta\left(\beta^{2}-2\right)+\left(3-\beta^{4}\right) \ln \left(\frac{1+\beta}{1-\beta}\right)\right], $

(6) where α is the fine-structure constant, and
$\beta = (1- $ $ \epsilon_{\mathrm{thr}}/\epsilon)^{1/2}$ .Furthermore, the distance D is more appropriate than the redshift
$ z_{s} $ for galactic sources, and their relationship is given by$ \begin{array}{*{20}{l}} &D = c z_{s}/H_0. \end{array} $

(7) Thus, for the leading order of D, Eq. (2) is replaced by the following expression:
$ \tau_{\gamma}\left(E_0, D\right) = D \int_{-1}^{1} \mathrm{\; d}(\cos \varphi) \frac{1-\cos \varphi}{2} \int_{\epsilon_{\mathrm{thr}}(E, \varphi)}^{\infty} \mathrm{d} \epsilon \; n_{\gamma}(\epsilon) \sigma_{\gamma \gamma}(E, \epsilon, \varphi), $

(8) which is the main formula used in this paper. Additionally, note that for the source distance corresponding to the small redshift,
$ E_0\approx E $ .Once the optical depth is computed, the mean free path of the gamma ray photons can be obtained using the following relation [32]:
$ \lambda_{\gamma}(E_0,D) = \frac{D}{\tau_{\gamma}(E_0,D)}, $

(9) where
$ \lambda_{\gamma}(E_0,D) $ denotes the mean free path of photons with energy$ E_0 $ . -
In this section, we apply the above theoretical analysis to LHAASO data. The optical depth, mean free path, and survival probability are computed for the eleven LHAASO sources, and the main results are summarized in Table 1. To explicitly demonstrate the relationship between these quantities, we choose five LHAASO sources to depict in each figure, four of which (LHAASO J2032+4102, J0534+2202, J1843-0338 and J2226+6057) have a definite distance②. For the remaining one (LHAASO J1929+1745), we choose a possible location with a maximum distance of
$ 6.3 \,\rm{kpc} $ . First, we demonstrate the relationship between the mean free path and observed energy for different LHAASO sources, as illustrated in Fig. 1. Unsurprisingly, the mean free path continues to decrease as the energy increases, because the gamma ray photons interact with the CMB photons more easily. In addition, we plot the optical depth and survival probability as a function of energy for different LHAASO sources, as illustrated in Fig. 2. In general, the optical depth increases with the gamma ray photon energy. It is also evident that the survival probability decreases with increasing gamma-ray photon energy. Nevertheless, as a whole, we find that the survival probability remains at a high level, even after considering the statistical uncertainties, which can be seen directly from Table 1. This result is qualitatively the same as depicted in Fig. 6 of Ref. [1].LHAASO Source Distance/kpc Observed energy/PeV Optical depth Mean free path/kpc Survival probability LHAASO J2032+4102 1.40 $ \pm 0.08 $ 

1.42 $ \pm 0.13 $ 

$ 0.18_{-0.02}^{+0.02} $ 

$ 7.68_{-0.19}^{+0.25} $ 

$ 0.83_{-0.01}^{+0.01} $ 

LHAASO J0534+2202 2.0 0.88 $ \pm 0.11 $ 

$ 0.20_{-0.02}^{+0.02} $ 

$ 10.00_{-0.87}^{+1.30} $ 

$ 0.82_{-0.02}^{+0.02} $ 

LHAASO J1825-1326 3.1 $ \pm 0.2 $ 

0.42 $ \pm 0.16 $ 

$ 0.11_{-0.08}^{+0.10} $ 

$ 29.07_{-13.03}^{+91.85} $ 

$ 0.90_{-0.08}^{+0.08} $ 

1.6 0.42 $ \pm 0.16 $ 

$ 0.06_{-0.04}^{+0.04} $ 

$ 29.07_{-13.03}^{+91.85} $ 

$ 0.95_{-0.04}^{+0.04} $ 

LHAASO J1839-0545 4.8 0.21 $ \pm 0.05 $ 

$ 0.02_{-0.01}^{+0.02} $ 

$ 305.60_{-184.67}^{+1116.01} $ 

$ 0.98_{-0.02}^{+0.01} $ 

1.3 0.21 $ \pm 0.05 $ 

$ 0.00_{-0.00}^{+0.01} $ 

$ 305.60_{-184.67}^{+1116.01} $ 

$ 1.00_{-0.01}^{+0.00} $ 

LHAASO J1843-0338 9.6 $ \pm 0.3 $ 

$ 0.26_{-0.10}^{+0.16} $ 

$ 0.08_{-0.07}^{+0.26} $ 

$ 120.92_{-91.85}^{+1300.68} $ 

$ 0.92_{-0.21}^{+0.07} $ 

LHAASO J1849-0003 7 0.35 $ \pm 0.07 $ 

$ 0.15_{-0.08}^{+0.09} $ 

$ 45.71_{-16.64}^{+46.23} $ 

$ 0.86_{-0.07}^{+0.07} $ 

5.5 0.35 $ \pm 0.07 $ 

$ 0.12_{-0.06}^{+0.07} $ 

$ 45.71_{-16.64}^{+46.23} $ 

$ 0.89_{-0.06}^{+0.06} $ 

LHAASO J1908+0621 2.4 0.44 $ \pm 0.05 $ 

$ 0.09_{-0.02}^{+0.02} $ 

$ 26.28_{-4.98}^{+8.25} $ 

$ 0.91_{-0.02}^{+0.02} $ 

3.4 0.44 $ \pm 0.05 $ 

$ 0.13_{-0.03}^{+0.03} $ 

$ 26.28_{-4.98}^{+8.25} $ 

$ 0.88_{-0.03}^{+0.03} $ 

LHAASO J1929+1745 4.6 $ 0.71_{-0.07}^{+0.16} $ 

$ 0.37_{-0.04}^{+0.08} $ 

$ 12.31_{-2.21}^{+1.67} $ 

$ 0.69_{-0.05}^{+0.03} $ 

6.2 $ 0.71_{-0.07}^{+0.16} $ 

$ 0.50_{-0.06}^{+0.11} $ 

$ 12.31_{-2.21}^{+1.67} $ 

$ 0.60_{-0.06}^{+0.04} $ 

$ 6.3_{-0.7}^{+0.8} $ 

$ 0.71_{-0.07}^{+0.16} $ 

$ 0.51_{-0.11}^{+0.19} $ 

$ 12.31_{-2.21}^{+1.67} $ 

$ 0.60_{-0.10}^{+0.07} $ 

LHAASO J1956+2845 2 0.42 $ \pm 0.03 $ 

$ 0.04_{-0.01}^{+0.01} $ 

$ 29.07_{-3.99}^{+5.45} $ 

$ 0.93_{-0.01}^{+0.01} $ 

2.3 $ \pm 0.2 $ 

0.42 $ \pm 0.03 $ 

$ 0.08_{-0.02}^{+0.02} $ 

$ 29.07_{-3.99}^{+5.45} $ 

$ 0.92_{-0.02}^{+0.02} $ 

LHAASO J2018+3651 $ 1.8_{-1.4}^{+1.7} $ 

0.27 $ \pm 0.02 $ 

$ 0.02_{-0.01}^{+0.03} $ 

$ 104.88_{-23.49}^{+36.22} $ 

$ 0.98_{-0.03}^{+0.01} $ 

3.3 $ \pm 0.3 $ 

0.27 $ \pm 0.02 $ 

$ 0.03_{-0.01}^{+0.01} $ 

$ 104.88_{-23.49}^{+36.22} $ 

$ 0.97_{-0.01}^{+0.01} $ 

4.0 $ \pm 0.5 $ 

0.27 $ \pm 0.02 $ 

$ 0.04_{-0.01}^{+0.02} $ 

$ 104.88_{-23.49}^{+36.22} $ 

$ 0.96_{-0.02}^{+0.01} $ 

LHAASO J2226+6057 0.8 0.57 $ \pm 0.19 $ 

$ 0.05_{-0.03}^{+0.02} $ 

$ 16.48_{-5.03}^{+20.37} $ 

$ 0.95_{-0.02}^{+0.03} $ 

Table 1. The optical depth and survival probability of gamma ray photons detected by the LHAASO.
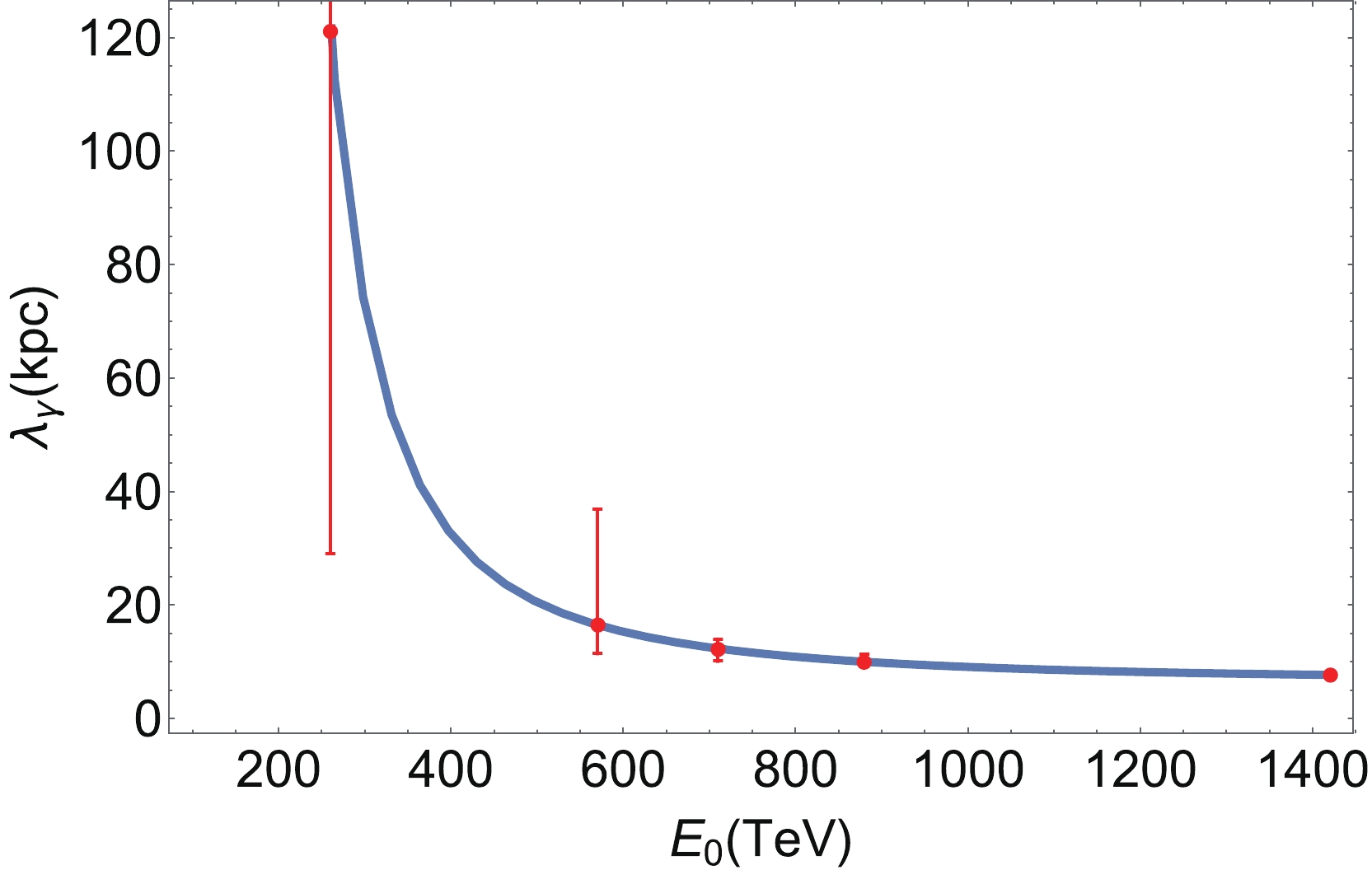
Figure 1. (color online) The relationship between the mean free path and energy of observed photons, where the gamma ray photons detected by the LHAASO are marked as red dots.
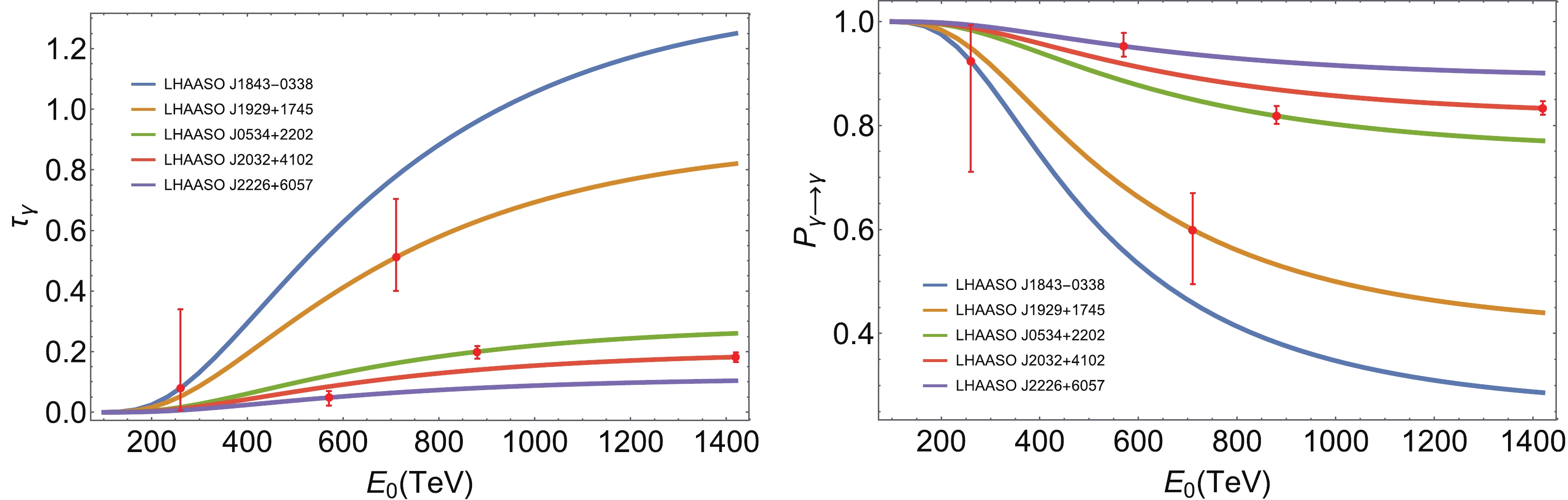
Figure 2. (color online) The optical depth (left) and survival probability (right) as a function of energy, where the gamma ray photons detected by the LHAASO are marked as red dots.
Similarly, we plot the optical depth and survival probability as a function of source distance, as shown in Fig. 3. Note that the optical depth increases with increasing source distance, whereas the survival probability decreases. This trend is reasonable because UHE gamma rays from the source farthest from the Earth are more likely to interact with the background. In addition, for galactic sources, the mean free path is not influenced by the source distance to the leading order of D, which is evident if (8) is substituted into (9). This indicates that the mean free path is only sensitive to energy for galactic sources in this context.

Figure 3. (color online) The optical depth (left) and survival probability (right) as a function of source distance, where the gamma ray photons detected by the LHAASO are marked by red dots.
Finally, we turn to the main results summarized in Table 1, which lists the optical depth, mean free path, and survival probability of the eleven LHAASO sources. First, from the fourth column in Table 1, we note that the optical depth of all the LHAASO sources is significantly less than one, that is
$ \tau_{\gamma} \ll 1 $ , which indicates that a large quantity of gamma-ray photons emitted from the source can reach the Earth without being absorbed. Furthermore, from the final column in Table 1, we note that the majority of the survival probabilities of gamma ray photons are above 0.8. In Ref. [1], the gamma rays from LHAASO J2032+4102 have an energy of 1.42 PeV, and the survival probability of these high-energy photons reaching the Earth is$ P_{\gamma \rightarrow \gamma}\left(E_{0}, z_{s}\right)\simeq83.3\ $ %. The lowest survival probability for observed gamma ray photons originates from LHAASO J1929+1745 and is approximately 0.60. This further shows that although the energy of gamma ray photons is 0.71 PeV and beyond the threshold value of pair production, a large number of gamma-ray photons can still reach the Earth without Lorentz symmetry violation.Therefore, we intend to conclude that it is still unreasonable to argue that Lorentz symmetry will be violated from current observations at the LHAASO.
-
We computed the optical depth, mean free path, and survival probability of photons from all gamma-ray sources detected by the LHAASO in Ref. [1]. The cross-section of pair production due to interaction with CMB photons is obtained within standard special relativity, and we find that the survival probability is high for galactic gamma ray photons, even though the energy of those photons may exceed the threshold value of pair production. Thus, the violation of Lorentz symmetry need not be considered. This should be true for general galactic pevatrons because, in comparison with the cosmic scale, the distance between galactic sources and the Earth remains too close to provide sufficient opportunities to collide with CMB photons during propagation.
To be more specific, current data from [1] are not sufficient to result in a subluminal correction constrained by the pair-production reaction
$ \gamma \gamma \rightarrow e^{+} e^{-} $ . The superluminal corrections constrained by the photon decay reaction do not conflict with our results because the distances from the possible origins shown in [1] are sufficient for photons to decay [34].Nevertheless, we may wonder what type of observations on UHE cosmic rays would trigger the need to consider Lorentz symmetry violation. For gamma-ray photons, such a condition would be reached once the optical depth is close to, or larger than, one. From Fig. 3, and also suggested in [21, 22], one would expect that if PeV photons with significantly higher source distances are detected by the LHAASO in the future, Lorentz symmetry violation would require consideration.
Of course, it is entirely possible to consider corrections on the survival probability due to Lorentz symmetry violation. For instance, one may modify the dispersion relations of photons, obtain the threshold energy with corrections, and plot the optical depth with Lorentz symmetry violation, as performed in Ref. [33].
-
We are very grateful to Zhe Chang, Yu-Chen Ding, Chao-guang Huang, and Qinghua Zhu for helpful discussions on the LHAASO project and relevant topics. We would also like to thank the anonymous referees for helpful comments and suggestions.
Implications of gamma-ray photon measurements at the LHAASO on Lorentz symmetry
- Received Date: 2021-08-04
- Available Online: 2022-05-15
Abstract: The Large High Altitude Air Shower Observatory (LHAASO) has reported the measurement of photons with high energies of up to 1.42 PeV from twelve gamma-ray sources. We are concerned with the implications of the LHAASO data on the fate of Lorenz symmetry at such high energy levels; thus, we consider the interaction between gamma rays and photons in the cosmic microwave background (CMB) and compute the optical depth, mean free path, and survival probability of photons from these gamma-ray sources. Employing the threshold value predicted by standard special relativity, the lowest survival probability for observed gamma ray photons is found to be approximately 0.60, which is fairly high and implies that abundant photons with energies above the threshold may reach the Earth without Lorentz symmetry violation. We conclude that it is unreasonable to argue that Lorentz symmetry would be violated using current observations at the LHAASO.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: