-
Cluster decay is a relatively recent known mode of nuclear radioactivity compared with other types of emissions, and it is an important topic in nuclear physics. Different microscopic and macroscopic formalisms with various types of interaction potentials and empirical formulas, have been introduced to calculate the half-life [1-10]. Nuclear and Coulomb potentials construct the effective potential among interacting nuclei and can include different physical parameters based on the type of adopted model. Hence, the evaluation of the role of these factors in half-life calculation can be useful. Nuclear matter and charge density distributions are essential constituents of double-folding nuclear and Coulomb potentials. The two parameter Fermi (2pF) distribution is a well-known phenomenological form of densities with two adjustable parameters: half-density radii and surface diffuseness. The constant values of these parameters are prevalent in proton, alpha, cluster decay, and fusion cross section calculations [11-14]. Nuclear asymmetry,
$ I = \dfrac{N-Z}{A} $ , is an intrinsic factor of any nucleus that can be explicitly or indirectly included in density distributions.In Ref. [15], the asymmetry dependent parameters of the neutron and proton densities have been given by fitting these densities to the corresponding microscopically calculated densities through the energy density functional method. Using these densities, we adopted the 2pF-fit densities and investigated the role of asymmetry in proton radioactivity [16]. In contrast to proton emitters, cluster emitters have notable neutron excess. Therefore, we were motivated to adopt the 2pF-fit densities in cluster decay calculations and to compare it with the commonly used 2pF densities with constant parameters.An alternative approach to handling the neutron and proton density parameters as a function of asymmetry involves the neutron skin-type or neutron halo-type assumption of the nucleus, employing the asymmetry dependent skin thickness and experimental root mean square (rms) charge radii. This formalism was used in Refs. [17-20] to evaluate the role of nuclear asymmetry in alpha decay calculations. Becasue cluster emitters have neutron excess, this formalism may be used in cluster decay calculations. Therefore, another aim of this study was to test the applicability of the skin/halo-type assumption in cluster decay and to investigate the role of the different sets of 2pF parameters, the 2pF-fit, and the skin/halo-type assumption. A theoretical model for calculating the cluster decay half-lives is given in Sec. II, the obtained results are given in Sec. III, and a summary and conclusion are presented in Sec. IV.
-
Analogous to alpha decay, the cluster decay half-life can be calculated via the well-known Gamow decay formula
$ T_{1/2} = \frac{\ln2}{\nu P_c P}, $

(1) where the assault frequency ν and tunneling probability P are expressed in the framework of the semiclassical WKB method:
$ \nu\simeq\frac{\hbar}{2\mu}\left[\frac{1}{2}\int^{r_2}_{r_1}\dfrac{{\rm d}r}{\sqrt{\frac{2\mu}{\hbar^2}|Q-V_{\rm eff}(r)}|} \right]^{-1},\nonumber $

$ P = \left[1+\exp{\left(\frac{2\sqrt{2\mu}}{\hbar}\int^{r_3}_{r_2}{\rm d}r \sqrt{V_{\rm eff}(r)-Q}\right)}\right]^{-1}, $

(2) where Q,
$ r_i $ , and μ are the released energy in the cluster decay, turning points, and reduced mass of the cluster-daughter system, respectively. In Eq. (1),$ P_c $ is the cluster preformation probability. An empirical formula to estimate this important quantity was introduced in [21] as a function of cluster mass number:$ P_c = P_{\alpha}^{(A_c-1)/3}, $

(3) where
$ P_{\alpha} $ is a constant value, which is determined using the linear fit of the logarithm of$ P_c^{\rm exp} $ with mass number.$ P_c^{\rm exp} $ is the experimental preformation probability and is determined as$ P_c^{\rm exp} = \ln 2 / T_{1/2}^{\rm exp}\nu P $ . The consistency of the empirical preformation formula, Eq. (3), with statistical physics has been investigated in Ref. [22], and new updated values of$ P_{\alpha}^{(\rm e-e)} $ for even-even and$ P_{\alpha}^{(\rm A-odd)} $ for odd-A parent nuclei have been presented. The constant value of the preformation formula is model dependent and may vary with the number of studied cases and type of nuclear potential. Similar studies [23, 24] have confirmed the capability of this formula and obtained comparable results for this constant.The effective internuclear potential, as a sum of the nuclear
$ V_N $ , Coulomb$ V_{\rm C} $ , and modified centrifugal$ V_{\rm cf}(r) = \dfrac{\hbar^2 (l+1/2)^2}{2\mu r^2} $ potentials, is given as$ V_{\rm eff}(r) = V_N(r)+V_{\rm C}(r)+V_{\rm cf}(r). $

(4) The modified centrifugal term guarantees the presence of the first turning point for zero values of the orbital angular momentum l of the cluster nucleus. The double-folding nuclear potential
$ V_N $ , assuming a separate and equivalent contribution of neutrons and protons, is expressed as$ \begin{aligned}[b]V_N(r) =& V_N^n(r)+V_N^p(r) = \int {\rm d}\vec{r}_1 {\rm d}\vec{r}_2 \rho_d^n(\vec{r}_1) v(s) \rho_c(\vec{r}_2)\\&+\int {\rm d}\vec{r}_1 {\rm d}\vec{r}_2 \rho_d^p(\vec{r}_1) v(s) \rho_c(\vec{r}_2),\end{aligned} $

(5) where
$ s = |\vec{r}_2-\vec{r}_1+\vec{r}| $ is the relative distance between the interacting nucleon pair, v is the nucleon-nucleon interaction potential, and the subscripts d and c denote the daughter and cluster, respectively. The effective nucleon-nucleon potential Yukawa (M3Y)-Reid-type interaction with a zero-range exchange contribution is given as [25]$ v^{\rm M3Y}(s) = 7999 \frac{{\rm e}^{-4s}}{4s}-2134 \frac{{\rm e}^{-2.5s}}{2.5s}-276\delta(s), $

(6) A well-known phenomenological density distribution is the two parameter Fermi (2pF) density distribution, which is used as an analytic formula for nuclear matter and charge density distributions. This distribution for neutron or proton matter,
$ i = n,p $ , is written as$ \rho^i(r) = \frac{\rho_0^i}{1+\exp\left[\dfrac{r-R^i}{a^i}\right]}, $

(7) where
$ \rho_0^i $ is the saturation density and is determined by mass number or charge conservation,$ A^i = \int {\rm d}^3r \rho^i(r) $ .$ R^i = r^i_0 A^{1/3} $ and$ a^i $ are the half-density radii, referred to as radii, and diffuseness parameter of the neutron (proton) density. Using Fourier transformations, the six-fold double-folding nuclear potential in Eq. (5) can be converted to the three-fold integral and integrated numerically. Analogous to the nuclear potential, the Coulomb potential can be determined by the double-folding integration of the charge density distributions of daughter and cluster nuclei and the point charge proton-proton potential$ v(s) = \dfrac{e^2}{4\pi\epsilon_0}\dfrac{1}{s} $ $ V_{\rm C}(r) = \int {\rm d}\vec{r}_1 {\rm d}\vec{r}_2 \rho_d^p(\vec{r}_1) v(s) \rho_c^p(\vec{r}_2). $

(8) The adjustable parameters of the matter and charge densities,
$ r_0 $ and a, may have a noticeable effect on the calculated half-lives. For this purpose, we used three sets of data: i) constant values,$ r_0 = 1.07 \;{\rm fm} $ and$ a = 0.54\; {\rm fm} $ , referred to as 2pF in following sections, ii) explicitly asymmetry dependent fitted parameters based on the energy density functional method [15], referred to as the 2pF-fit, and iii) experimental rms charge radii with the skin/halo-type assumption of the daughter nuclei. The third set includes two asymmetry dependent sets, skin and halo-type, and two asymmetry independent sets, skin and halo-type with zero thickness.For the second set, the asymmetry dependent formulas for the proton and neutron radii,
$ R^p $ and$ R^n $ , and their corresponding surface diffuseness,$ a^p $ and$ a^n $ , are given as [15]$ \begin{aligned}[b] R^p =& 1.249 A^{1/3}-0.5401-0.9582\;I, \\ R^n = &1.2131 A^{1/3}-0.4415+0.8931 \;I, \\ a^p =& 0.4899-0.1236 \;I, \\ a^n =& 0.4686+0.0741 \; I, \end{aligned} $

(9) where
$ I = \dfrac{N-Z}{A} $ is the nuclear asymmetry parameter.The neutron or proton rms radii are defined as
$R^i_{\rm rms} = \langle r^2\rangle ^{1/2} = \left[\frac{\int \rho^i(r)r^4 {\rm d}r}{\int \rho^i(r)r^2 {\rm d}r}\right]^{1/2}, $

(10) and hence, the density parameters can be determined from the known values of
$ {\rm{R}}^i_{\rm rms} $ . In the third set, by considering two assumptions, neutron skin-type and neutron halo-type, for the nuclei, one can obtain the$ r_0^p $ from the experimental rms charge radii$ {\rm{R}}^p_{\rm rms} $ . The experimental data are adopted from Ref. [26]. Furthermore, the fitted formula for the rms charge radii$ R^p_{\rm rms} = (r_0+r_1 A^{-2/3}+r_2 A^{-4/3})A^{1/3}, $

(11) with parameters
$ r_0 = 0.891\;{\rm{fm}} $ ,$ r_1 = 1.52\;{\rm{fm}} $ , and$ r_2 = -2.8 $ $ {\rm{fm}} $ , can be used for unavailable data in Ref. [27].Based on the neutron skin-type assumption, similar to skin nuclei [28], the largest neutron radii are considered in comparison with those of proton. Hence,
$ r_0^n > r_0^p $ and$ r_0^n $ can be determined from$ {\rm{R}}^n_{\rm rms} $ through the neutron skin thickness$ \Delta r_{np} $ radii$ R^n_{\rm rms} = R^p_{\rm rms}+\Delta r_{np}, $

(12) where
$ \Delta r_{np} $ , which is the difference between the neutron and proton rms, is presented in Ref. [29] as a linear function of the nuclear asymmetry I,$ \Delta r_{np} = (-0.04\pm 0.03)+(1.01\pm0.15)I. $

(13) In contrast with the latter assumption for the same value of the proton and neutron surface diffuseness,
$ a^p = a^n $ , the parameters in the neutron halo-type assumption are not equal; a larger density diffuseness is considered for neutrons,$ a^n>a^p $ , and$ a^p $ is fixed [17, 29]. Moreover, the proton and neutron radii are fixed. Therefore,$ r_0^p $ , and consequently$ r_0^n $ , is determined from$ R^p_{\rm rms} $ . Finally, the neutron diffuseness$ a^n $ is obtained from Eq. (10) ($ R^n_{\rm rms} = R^p_{\rm rms}+\Delta r_{np} $ ). A brief description of the two skin/halo-type nuclei assumptions for determining the density parameters is presented in Table 1.$ r_0^n $ 

$ r_0^p $ 

$ a^n $ 

$ a^p $ 

Skin-type Eq. (12) Eq. (10) fixed $ a^p=a^n $ 

Halo-type $ r_0^n=r_0^p $ 

Eq. (10) Eq. (12) fixed Table 1. Neutron skin/halo-type assumption to determine the neutron/proton density distribution parameters.
Owing to the adoption of the WKB method, the centrifugal potential with Langer modification has been used for the effective potential, Eq. (4). The corresponding orbital angular momentum quantum number l was determined based on the spin-parity selection rule. Another requirement of the WKB method is the normalized nuclear potential based on the Bohr-Sommerfeld quantization condition. Here, the same parameters as in our previous paper [30] have been employed.
-
To calculate the ground state-ground state cluster decay half-lives of thirty six cluster emitters, density parameters were adopted based on Table 1. Additionally, the value of
$ 0.54 \;{\rm fm} $ was used for the fixed values of diffuseness. The constant values of$ r_0 = 1.07 \;{\rm fm} $ and$ a = 0.54\; {\rm fm} $ were adopted for the cluster densities. Because of the comparative aim of this study, and to reveal the distinctive role of the asymmetry dependency of the density parameters, the cluster preformation probability was set equal to unit$ P_c = 1 $ in the initial part of the results. For a comparison of the calculated half-lives with experiments, the different values of$ P_{\alpha} $ in Eq. (3) for different potentials were determined via fitting to the experimental half-lives. The second and third datasets, 2pF-fit and skin/halo-type, are nuclear asymmetry dependent; the former explicitly accounts for the asymmetry parameter, whereas the latter involves the asymmetry indirectly through neutron skin thickness. Because of the neutron excess nature of the cluster emitters and daughter nuclei and the increase in the asymmetry for heavier isotopes, as can be seen in Fig. 1 for a variety of daughter nuclei, the asymmetry may affect the density parameter sets and consequently the decay half-lives.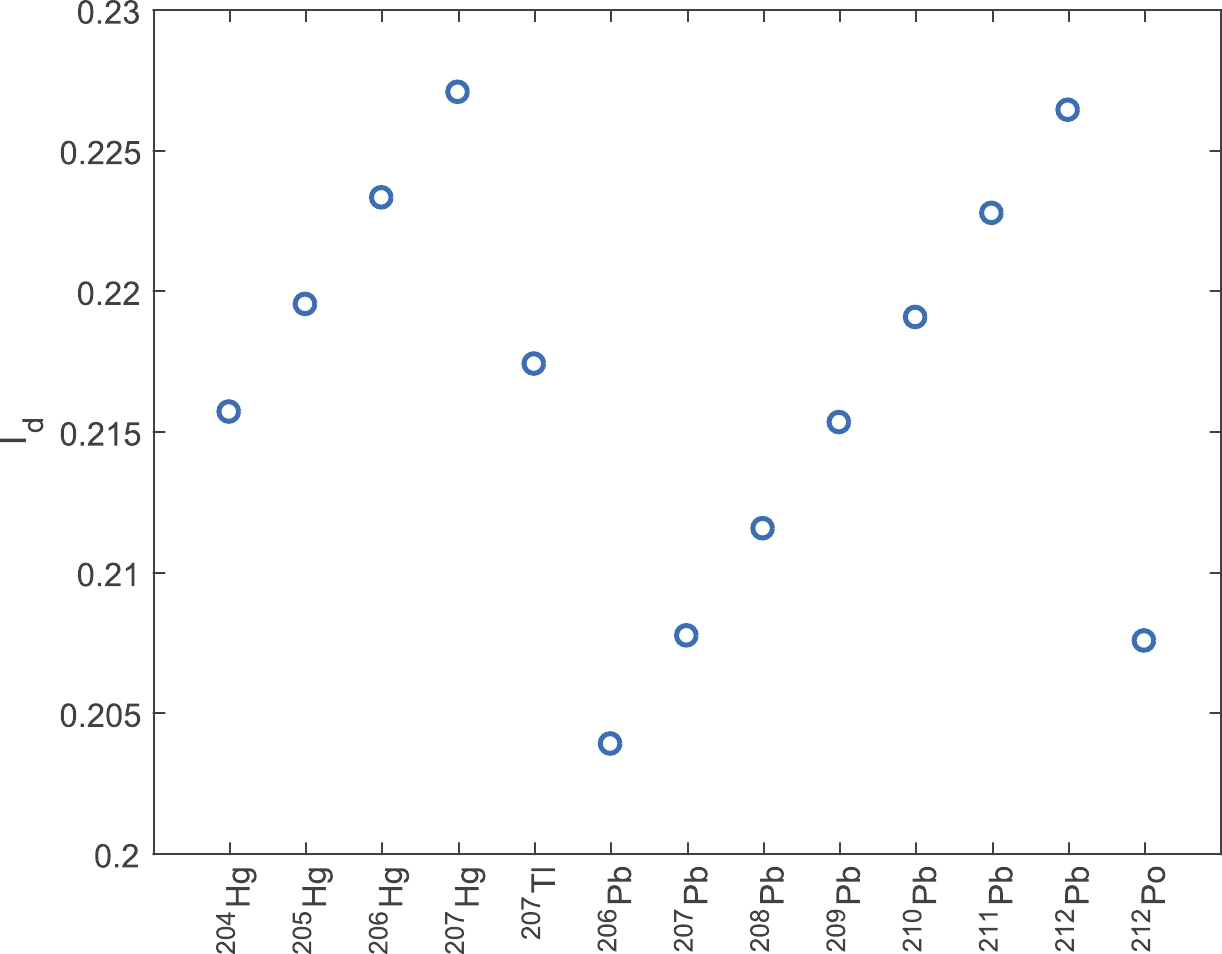
Figure 1. (color online) Nuclear asymmetry of the daughter nuclei. As a result of the occurrence of daughter nuclei about the double-magic 208Pb nucleus, the asymmetry variation is small and can be observed at approximately 0.21.
The variation in the asymmetry parameter of the daughter nuclei of the studied cluster emitters is presented in Fig. 1. The daughter nuclei of various cluster decays, nuclei of the isotopes of Hg, Pb, 207Tl, and 212Po, are generally located around the double-closure nucleus 208Pb. This is why the nuclear asymmetry shown in Fig. 1 exhibits negligible changes.
The calculated density parameters for daughter nuclei,
$ r_0 $ and a, based on the 2pF-fit and skin/halo-type assumption were plotted in Fig. 2 (a) and (b). The parameters$ r^{n/p}_0 $ -2pF-fit correspond to the$ R^i = r^i_0 A^{1/3} $ relation of the 2pF-fit formula. For different daughter nuclei,$ r^n_0 $ -skin and the$ r^n_0 $ -2pF-fit provide the same trends with similar results at approximately 1.17 fm. Similar results are observed for$ r^p_0 $ -skin/halo and the$ r^p_0 $ -2pF-fit around 1.12 fm. The difference between the$ r^n_0 $ -2pF-fit and$ r^p_0 $ -2pF-fit reveals the explicit role of asymmetry. The variations in the diffuseness of$ a_n $ -halo and the$ a_n $ -2pF-fit in Fig. 2 (b) presents the same trends but with different values around 0.730 fm and 0.475 fm, respectively. Based on Eq. (9) and the small variation in the asymmetry of the daughter nuclei around I$ \sim 0.21 $ , adjacent results with contrasting behaviors are observed for the$ a_n $ -2pF-fit and$ a_p $ -2pF-fit.
Figure 2. (color online) Density parameters of the daughter nuclei from both the 2pF-fit and skin/halo-type assumption. The parameters
$ r^n_0/r^p_0- $ 2pF-fit correspond to the$ R^i = r^i_0 A^{1/3} $ relation. Figures (a) and (b) show the variation in$ r_0 $ and a for all daughter nuclei. The differences among the results originate from the inclusion of asymmetry.The calculated half-lives of thirty six cluster emitters with
$ P_c = 1 $ are listed in Table 2. The experimental Q-values and half-lives are the same as cited in our recent paper [30]. The values of the employed minimum angular momentum in calculations are those listed in Table 1 of Ref. [30]. The calculated half-lives with 2pF-fit, skin-type, and halo-type are denoted with superscripts (I), (II), (III). The data in lower rows correspond to the asymmetry independent half-lives of 2pF, skin/halo with$ \Delta_{np} = 0 $ .No. Cluster decay Q/MeV $R^p_{\rm rms}/{\rm fm}$ 

$\log T_{1/2}^{\rm (I)}$ 

$\log T_{1/2}^{\rm (II)}$ 

$\log T_{1/2}^{\rm (III)}$ 

$\log T_{1/2}^{\rm exp}$ 

1 221Fr (14C) 31.29 5.485 8.106 7.880 7.882 14.52 9.584 8.619 8.613 2 221Ra (14C) 32.40 5.494 6.957 6.712 6.706 13.42 8.429 7.404 7.417 3 222Ra (14C) 33.05 5.501 5.584 5.331 5.284 11.0 7.029 5.997 5.991 4 223Ra (14C) 31.84 5.510 7.311 7.040 6.998 15.21 8.775 7.754 7.748 5 224Ra (14C) 30.54 5.521 9.576 9.290 9.268 15.87 11.098 10.035 10.030 6 226Ra (14C) 28.20 5.540 14.591 14.275 14.255 21.24 16.168 15.062 15.074 7 226Th (14C) 30.55 5.554 10.697 10.403 10.353 > 15.30 12.221 11.053 11.058 8 226Th (18O) 45.73 5.501 10.529 10.233 10.224 > 15.30 12.418 11.121 11.115 9 228Th (20O) 44.73 5.501 13.067 12.741 12.729 20.87 15.031 13.672 13.666 10 230Th (24Ne) 57.76 5.484 14.214 13.780 13.760 24.64 16.509 14.962 14.953 11 232Th (26Ne) 55.97 5.484 17.741 17.285 17.249 > 29.20 20.107 18.503 18.494 12 231Pa (23F) 51.86 5.501 14.370 13.989 13.961 > 24.61 16.541 15.037 15.028 13 231Pa (24Ne) 60.42 5.485 11.494 11.138 11.108 22.89 13.766 12.267 12.259 14 230U(22Ne) 61.40 5.501 10.837 10.460 10.459 > 18.20 13.080 11.534 11.527 15 230U (24Ne) 61.36 5.490 11.542 11.132 11.102 > 18.20 13.789 12.183 12.175 16 232U (24Ne) 62.31 5.501 10.010 9.612 9.573 20.40 12.279 10.699 10.707 17 232U (28Mg) 74.33 5.474 12.730 12.191 12.145 > 22.65 15.265 13.462 13.452 18 233U (24Ne) 60.51 5.510 11.551 11.130 11.031 24.83 13.785 12.223 12.227 19 233U (25Ne) 60.75 5.501 12.603 12.197 12.158 23.30 14.925 13.320 13.310 20 233U (28Mg) 74.25 5.478 12.770 12.266 12.216 > 27.59 15.348 13.561 13.551 Continued on next page Table 2. Calculated cluster decay half-lives with
$ P_c = 1 $ . The$ R^p_{\rm rms} $ is the rms charge radii. The superscripts (I), (II), (III) are the calculated half-lives with 2pF-fit (Eq. (9)), skin type (Eq. (10)), and halo type (Eq. (10)). The data in lower rows correspond to the asymmetry independent 2pF and skin/halo type with$ \Delta_{np} = 0 $ .To evaluate the obtained data in Table 2 in further detail, the difference between the determined half-lives with
$ P_c $ = 1 from the skin-type assumption with and without skin-thickness ($ T_{1/2}^{\rm skin} $ and$ T_{1/2}^{{\rm skin},\Delta = 0} $ ), skin/halo type assumption ($ T_{1/2}^{\rm skin} $ and$ T_{1/2}^{\rm halo} $ ), 2pF-fit and skin-type assumption ($T_{1/2}^{\rm 2pF-fit}$ and$ T_{1/2}^{\rm skin} $ ), and 2pF and 2pF-fit ($ T_{1/2}^{\rm 2pF} $ and$ T_{1/2}^{\rm 2pF-fit} $ ) have been plotted for all emitters in Fig. 3 (a)-(d), respectively. A direct comparison among the calculated half-lives with$ P_c $ = 1 can reveal the role of the asymmetry parameter of daughter nuclei in calculations. Fig. 3 (a) shows that the difference$ \log T_{1/2}^{{\rm skin},\Delta = 0} $ -$ \log T_{1/2}^{\rm skin} $ lies in a range from 0.6 to 1.5. This difference may be justified by the notable role of nuclear asymmetry in the determination of skin-type parameters. The obtained half-lives with the skin-type or halo-type assumption are extremely similar. Additionally, similar results have been obtained for$ \log T_{1/2}^{{\rm halo},\Delta = 0} $ -$ \log T_{1/2}^{\rm halo} $ . Fig. 3 (b) shows the trivial difference in the range of$ 0< \log T_{1/2}^{\rm skin}- \log T_{1/2}^{\rm halo}< $ $ 0.12 $ ; this result is inconsistent with a similar investigation on alpha decay [17]. Fig. 3 (c) displays the role of the density parameters in half-life calculations. The 2pF-fit gives larger half-lives than the skin-type assumption in the range of$ 0.2< \log T_{1/2}^{\rm 2pF-fit}- \log T_{1/2}^{\rm skin} < 0.6 $ . 2pF provides the largest half-life values and, as can be seen in Fig. 3 (d), its notable difference to the 2pF-fit is located in the range of$ 1.4< \log T_{1/2}^{\rm 2pF}- \log T_{1/2}^{\rm 2pF-fit}<3 $ . Fig. 3(a) and (d) show the remarkable effect of the asymmetry parameter in calculations. The asymmetry parameter was explicitly included in$ T_{1/2}^{\rm skin} $ ; hence, its comparison with$ T_{1/2}^{{\rm skin},\Delta = 0} $ (Fig. 3(a)) reveals the direct role of asymmetry in calculations. The indirect effect of asymmetry can be seen in Fig. 3(b) through a comparison of the calculated half-lives with the 2pF density with constant radii and diffuseness parameters and the 2pF fit with corresponding asymmetry dependent parameters.
Figure 3. (color online) Difference among the calculated half-lives with different asymmetry dependent and independent datasets of neutron and proton densities. The small difference between the obtained half-lives based on the skin and halo assumptions and the direct role of the asymmetry parameter in calculations are observed.
Table 2-continued from previous page No. Cluster decay Q/MeV $R^p_{\rm rms}/{\rm fm}$ 

$\log T_{1/2}^{\rm (I)}$ 

$\log T_{1/2}^{\rm (II)}$ 

$\log T_{1/2}^{\rm (III)}$ 

$\log T_{1/2}^{\rm exp}$ 

21 234U (24Ne) 58.84 5.521 14.025 13.560 13.502 25.07 16.322 14.706 14.697 22 234U (26Ne) 59.47 5.501 14.820 14.411 14.363 25.07 17.177 15.539 15.540 23 234U (28Mg) 74.13 5.484 12.854 12.348 12.304 25.54 15.432 13.675 13.666 24 235U (24Ne) 57.36 5.529 16.293 15.817 15.753 27.44 18.675 17.007 16.999 25 235U (25Ne) 57.73 5.521 16.171 15.690 15.572 27.44 18.494 16.825 16.817 26 235U (28Mg) 72.21 5.494 14.217 13.664 13.560 > 28.45 16.711 15.019 15.002 27 236U (24Ne) 55.96 5.540 18.578 18.066 18.023 > 26.28 20.977 19.284 19.275 28 236U (26Ne) 56.75 5.521 18.015 17.533 17.433 > 26.28 20.388 18.705 18.714 29 236U (30Mg) 72.48 5.484 15.518 14.997 14.937 27.58 18.168 16.361 16.351 30 237Np (30Mg) 74.99 5.485 13.472 13.037 12.975 > 27.57 16.069 14.362 14.352 31 236Pu (28Mg) 79.67 5.501 8.570 8.107 8.038 21.67 11.113 9.338 9.327 32 238Pu (28Mg) 75.93 5.521 11.975 11.435 11.335 25.69 14.549 12.722 12.731 33 238Pu (30Mg) 77.00 5.501 12.190 11.716 11.659 25.69 14.826 12.987 12.978 34 238Pu (32Si) 91.21 5.484 11.257 10.70 10.623 25.30 14.104 12.157 12.147 35 240Pu (34Si) 91.05 5.484 11.507 10.919 10.833 > 24.20 14.396 12.416 12.405 36 241Am (34Si) 93.94 5.485 9.597 9.106 9.016 > 25.32 12.504 10.565 10.571 The comparison between cases (3) and (33), 222Ra(14C) and 238Pu(30Mg), in Fig. 3(a) reveals a considerable difference despite the same daughter nucleus, 208Pb. The value of
$ \delta^I = \log T_{1/2}^{\rm skin}-\log T_{1/2}^{{\rm skin},\Delta = 0} $ is approximately 0.65 for case (3) and 1.25 for case (33). The values of 226Th(16O), (9) 228Th(18O), (12) 231Pa(23F), (14) 230U(22Ne), (16) 232U(24Ne), (19) 233U(25Ne), (22) 234U(26Ne), and (31) 236Pu(28Mg) with the same daughter nucleus 208Pb are approximately 0.90, 0.90, 1.05, 1.10, 1.10, 1.10, 1.15, and 1.20, respectively. These comparisons show the increasing role of the asymmetry factor of the daughter nuclei in interactions with heavier clusters. The remarkable difference$ \delta^I $ between cases with the same daughter nucleus, 208Pb, for the lightest and heaviest clusters, 14C and 30Mg, respectively, can be justified by focusing on the increase in nuclear interaction between a daughter nucleus and a heavier cluster rather than a lighter one.Owing to the same daughter nucleus, the nuclear density of the daughter nucleus is the same in both cases; however, the heavier cluster gives a larger cluster density, nuclear potential, and Coulomb potential. Therefore, inside the parent nucleus and near the barrier, where
$ V_N $ is dominant over$ V_{\rm C} $ , the effective potential$ V_{\rm eff} $ of the heavier nucleus has smaller values. In the outside region,$ V_{\rm C} $ is dominant and heavier nuclei has larger$ V_{\rm eff} $ . These comparisons have been displayed in Fig. 4 (a). In both cases, the near barrier and outside regions, which are important for determining the penetration probability, provide smaller values of skin-type effective potential with asymmetry factor$ V_{\rm eff}^{\rm Skin} $ than its asymmetry independent form$ V_{\rm eff}^{{\rm Skin},\Delta = 0} $ , as shown in Fig. 4 (b). This can be explained as a result of the increase in the asymmetry dependent radii$ R_{\rm rms}^n $ (Eq. (12)), increase in the range of nuclear potential, and decrease in the effective potential (potential barrier) for all cases. Therefore,$ V_{\rm eff}^{{\rm Skin},\Delta = 0} $ produces larger values than$ V_{\rm eff}^{\rm Skin} $ in both cases (3) and (33). Considering these comparisons, as shown in Fig. (b), larger$ V_{\rm eff}^{{\rm Skin},\Delta = 0}-V_{\rm eff}^{\rm Skin} $ differences are observed for the heavier cluster. Consequently, this notable difference can be observed in$ \delta^I = \log T_{1/2}^{\rm skin}-\log T_{1/2}^{{\rm skin},\Delta = 0} $ , and the heavier cluster has a larger value of$ \delta^I $ .
Figure 4. (color online) Effective potential (Eq. (4)) for decay cases (3) 222Ra(14C) and (33) 238Pu(30Mg) with the same daughter nucleus 208Pb.
$ Q(3) $ and$ Q(33) $ are the corresponding Q-values of these decays. Figure (a) shows the calculated effective potentials using the skin-assumption with and without the asymmetry parameter of the daughter nucleus.The difference between cases with the same daughter nuclei can be illustrated qualitatively by considering the fact that the heavier cluster has a larger half-life and is independent of daughter nucleus asymmetry. Considering the asymmetry factor of the daughter nucleus for each case increases the
$ R^n $ ,$ V_N $ range of the nuclear potential and decreases the potential barrier, causing a reduction in the half-life. As a result of the larger increase in$ V_N $ and its range and the decrease in the barrier for the heavier cluster, the decrease in the half-life is larger for the heavier cluster.To further analyze the direct role of the asymmetry of daughter nuclei in half-life calculations, the variation in
$ \delta^I = \log T_{1/2}^{\rm skin}-\log T_{1/2}^{{\rm skin},\Delta = 0} $ for different sets of decays with the same clusters were plotted in Fig. 5. As shown in each set with same clusters, the difference does not significantly change with increasing asymmetry factor of the daughter nuclei. Furthermore, the increase in$ \delta^I $ with the mass of the cluster can be observed for decays with the same and different daughter nuclei. A comparison between the first and fourth (second and fourth) series shows this result for different (same) daughter nuclei.
Figure 5. (color online) A comparison of the calculated half-lives using skin-type and skin-type with zero skin thickness for four sets of daughter nuclei with the same clusters. The numbers in the horizontal abscissa represent the different daughter nuclei in each set. The numbers for the first set (lightest cluster 14C) correspond to the (207Tl, 207,208,209,210,212Pb, 212Po) daughter nuclei. The second and third sets for the 24Ne and 28Mg clusters include (206Hg, 207Tl, 206,208,209,210,211,212Pb) and (204,205,206,207Hg, 208,210Pb), respectively. The fourth set, with the heaviest cluster 34Si includes the (206Hg,207Tl) nuclei.
To compare the calculated half-lives with experimental data, the value of
$ P_c $ should be determined for each case. The introduced method for determining$ P_{\alpha} $ in Eq. (3) shows the model dependency of this constant, where different potentials give different values. Adopting the fitted values of$ P_{\alpha} $ from one calculation model or one form of the potential and using it to compare the calculated half-lives of different forms of potentials or models with the experiment can give misleading results that offer better agreement of one model or potential with the experiment compared with another.The results of Table 2 and Fig. 3 (b) show similar values for the calculated half-lives with the skin and halo-type assumption. Therefore, the
$ P_{\alpha} $ values were determined for four assumptions: skin-type, skin-type with zero thickness (skin,$ \Delta = 0 $ ), 2pF-fit, and 2pF. To determine the$ P_{\alpha}^{\rm e-e} $ (for even-even parent nuclei) and$ P_{\alpha}^{\rm A-odd} $ (for odd-A parent nuclei) values for each of these potentials, data for twenty two experimental cluster decay half-lives with certain values, shown in the eighth column of Table 2, and four experimental alpha decay half-lives were used. The adopted alpha emitters are 212,213,214Po and 215Am. The Q-values and experimental half-lives of these decays are given in columns three and four of Table 1 in Ref. [23], with a Q-value of 8.54 MeV for 213Po. Because of the form of the empirical cluster preformation probability$ P_c $ formula in Eq. (3), the plot of the calculated experimental preformation probability$ P_c^{\rm exp} $ against cluster mass number$ A_c $ should be a straight line. Fig. 6(a) and (b) show the variation in the negative of$ \log P_c^{\rm exp} $ versus$ A_c $ for the potential with the 2pF-fit. Similar figures were also obtained for three other forms of potentials, which are displayed here. Fig. (a) and (b) show$ -\log P_c^{\rm exp, e-e} $ and$ -\log P_c^{\rm exp, A-odd} $ , respectively. From the best linear fit of$ -\log P_c^{\rm exp, e-e} $ and$ -\log P_c^{\rm exp, A-odd} $ with$ A_c $ , the values of$ P_{\alpha}^{\rm e-e} $ and$ P_{\alpha}^{\rm A-odd} $ were determined for these four potentials. The obtained results are presented in Table 3. The notable differences between the two forms of the asymmetry dependent/independent potentials with the skin-type assumption ('skin' and 'skin,$ \Delta = 0 $ ') and the two forms of asymmetry dependent/independent 2pF potentials ('2pF-fit' and '2pF') reflect the effect of neutron excess in daughter nuclei on cluster preformation.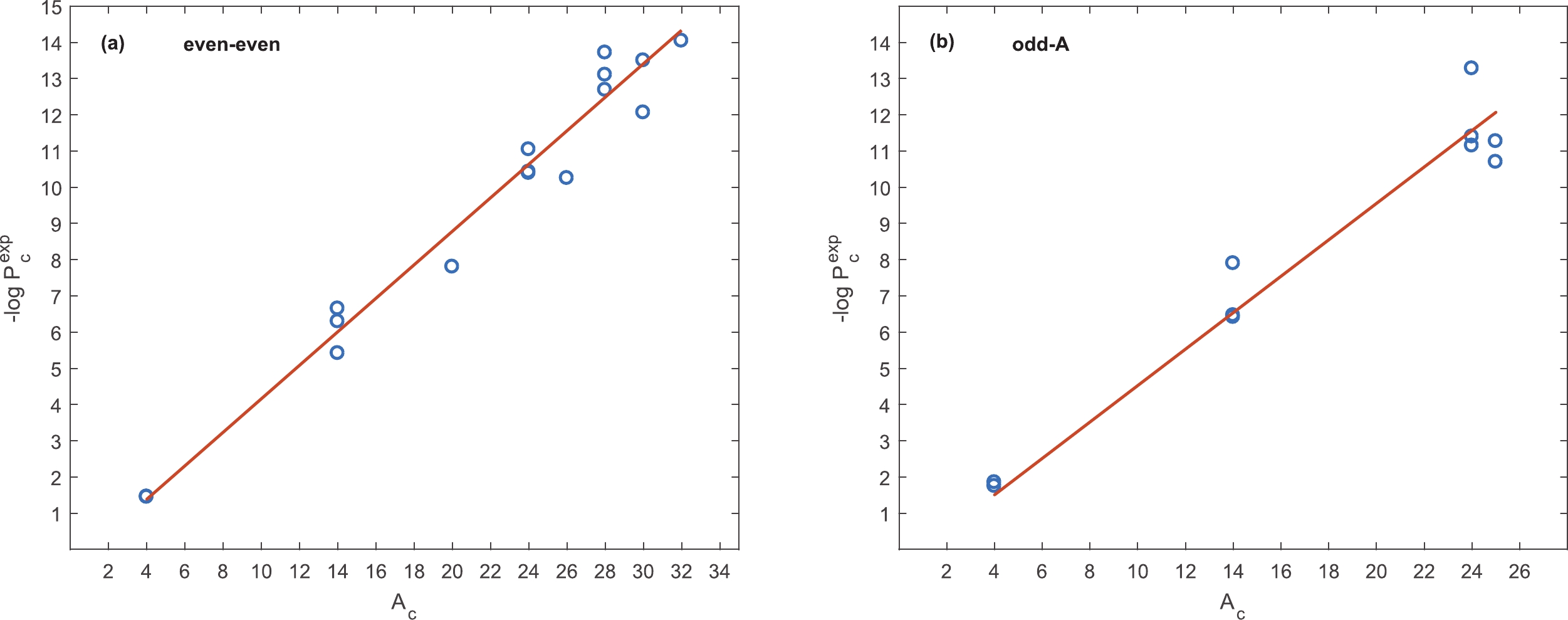
Figure 6. (color online) Negative logarithm of the calculated experimental preformation probability
$ P_c^{\rm exp} $ for the potential with the 2pF-fit as a function of cluster mass number$ A_c $ for (a) even-even and (b) odd-A parents.skin skin, $ \Delta=0 $ 

2pF-fit 2pF $P_{\alpha}^{\rm e-e}$ 

0.036 0.049 0.041 0.082 $P_{\alpha}^{\rm A-odd}$ 

0.027 0.038 0.031 0.062 Table 3. Best fitted values of
$ P_{\alpha} $ for four forms of potentials.Fig. 7 depicts the calculated half-lives with the parameters of skin-type (
$ T_{1/2}^{\rm skin} $ ), skin-type with zero skin thickness ($ T_{1/2}^{{\rm skin},\Delta = 0} $ ), 2pF ($ T_{1/2}^{\rm 2pF} $ ), and 2pF-fit ($ T_{1/2}^{\rm 2pF-fit} $ ), which were compared with the experimental data ($ T_{1/2}^{\rm exp} $ ). For each of these potentials, the cluster preformation probability$ \log P_c $ (Eq. (3) with the parameters in Table 3) was used for the thirty six cases in Table 2. As indicated by the similarities in the graphs, the bulk agreement between theory and experiment has been achieved. The systematic variations are almost the same for different potentials. However, the noticeable deviations from the experiment, for example, 230U (24Ne), may be related to uncertain experimental data. Because of the good agreement between theory and experiment for all potentials, the root-mean-square (rms) error on the decimal logarithm of the calculated half-lives for all potentials was obtained in same range, that is, approximately 0.8. The uncertain experimental half-lives were dropped in rms calculations.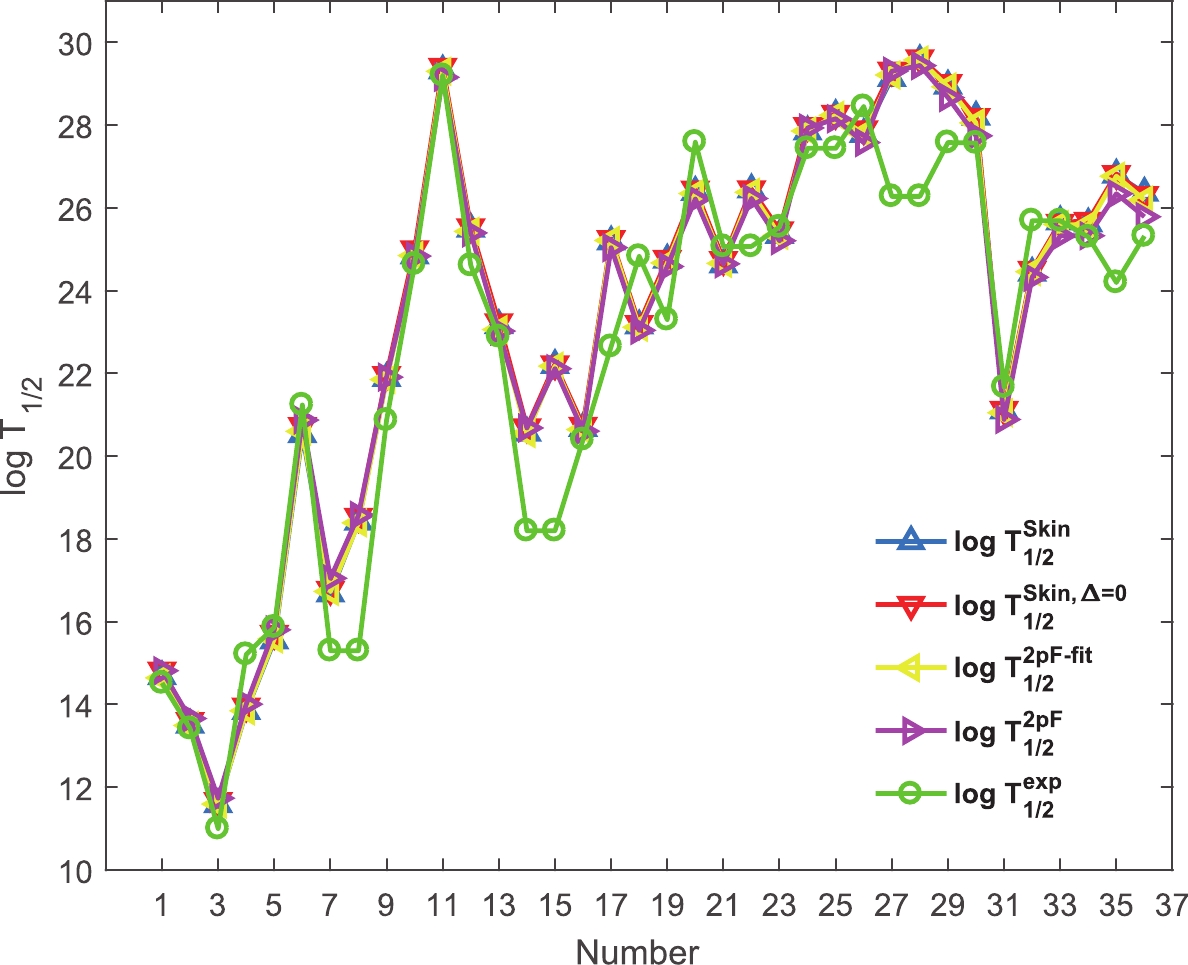
Figure 7. (color online) A comparison of the calculated half-lives using skin-type, skin-type with zero thickness, 2pF-fit, 2pF, and the experiment. Numbers in the horizontal axis correspond to the cluster emitters in Table 2.
-
In this theoretical study, we evaluated the role of nuclear asymmetry and different sets of neutron and proton density distribution parameters in the cluster decay half-lives of cluster emitters. By using the semiclassical WKB method and double-folding potentials, the assault frequency and tunneling probability were calculated. Two classes of asymmetry dependent parameters were used for neutron and proton density distributions; the first was obtained as fitted parameters of microscopic densities [15]. Experimental rms charge radii were used to determine the second class of parameters. Based on the neutron skin/halo-type assumption of the daughter nuclei, and by using skin thickness, the density parameters were calculated. The bulk agreement between the calculated half-lives and the experiment were observed for all cases by adopting the calculated cluster preformation probability. However, discrepancies may be related to the high sensitivity of the preformation probability to the cluster mass, rough estimation of the global quantum number, nuclear deformation, and densities with adjustable parameters. The obtained results show that the neutron skin or halo-type assumption gives a similar result and is a reliable method for determining neutron and proton density parameters in cluster decay calculations. The remarkable role of asymmetry parameters in half-life calculations was observed from the comparison between 2pF and all three asymmetry dependent sets and skin-type with and without an asymmetry parameter. The role of the adjustable parameters in calculations was revealed through the comparison between the 2pF-fit and skin-type parameters. Two sets gave similar results with a maximum difference
$ (\log T_{1/2}^{\rm 2pF-fit}-\log T_{1/2}^{\rm skin}) = 0.6 $ , which is less than the minimum of the difference in a prior comparison of nuclear asymmetry. As a continuation of this study, the neutron skin/halo-type assumption can also be evaluated in cluster decay calculations with the inclusion of nuclear deformations and microscopic neutron and proton densities. In addition, the role of the cluster asymmetry factor can be investigated in half-life calculations.
Cluster decay half-lives using asymmetry dependent densities
- Received Date: 2021-09-07
- Available Online: 2022-04-15
Abstract: By adopting different neutron and proton density distributions, cluster decay half-lives were investigated using double-folding potentials with constant and nuclear asymmetry dependent sets of nuclear density parameters. Two adopted asymmetry dependent sets of parameters were fitted based on microscopic calculations, and they were calculated based on the neutron skin/halo-type nuclei assumption and by employing experimental rms charge radii. A bulk agreement between theory and experiment was obtained for all sets of parameters using a calculated cluster preformation probability. Few differences were observed between the skin and halo-type assumptions. However, the notable role of the asymmetry parameter was observed in the relatively large differences between the skin and skin-type with zero thickness.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: