-
The LHAASO (Large High Altitude Air Shower Observatory) experiment, currently under design, is planned to be installed in the Sichuan Province (China) at 4410 m a.s.l. with the aim of studying the highest energy gamma-ray sources and cosmic rays in the wide energy range from hundreds of GeV to hundreds of TeV. Among its different components, optimized to study different energy regions, the WCDA (Water Cherenkov Detector Array) will be one of the most important detectors. Three ponds, for a total surface of 78000
$ {\rm m}^2 $ , will be equipped with 3120 PMTs to detect the Cherenkov light produced by ultra-relativistic particles. Each PMT will monitor a volume cell of 5 m$ \times $ 5 m$ \times $ 4.5 m. Data (signal amplitude, with a threshold set at 1 pe level, and arrival time) from each PMT are collected and sent to a DAQ system able to build and record events with all multiplicities starting from a single PMT fired. For small numbers, the primary energy for gammas corresponds to a few GeV, overlapping with the actual satellite detectors energy range. In this section, the scheme to calculate the expected rate and typology of GRBs detectable in follow-up mode with LHAASO is described and discussed. -
Gamma Ray Bursts are among the most powerful sources in the sky, with an energy spectrum extending from radio to gamma rays of tens of GeV (for a review see e.g. [1, 2]). They occur with a frequency of a few per day, and originate from the entire universe.
GRBs are divided into two classes depending on their duration. The short ones last up to 2 seconds and show a harder spectrum with a mean peak energy of 490 keV. It is believed that their origin is due to the merger of two compact objects such as neutron stars or blacks holes. Long GRBs have durations greater than 2 seconds with a softer spectrum and a peak at about 160 keV. In this case it is thought that the origin is due to the collapse of the nucleus of a type Ib/c Supernova, and in fact, the coincidence between these two phenomena has already been observed in many cases. The shape of the spectrum is well described in most cases by the Band function, characterized by two power laws smoothly connected. Although the majority of the ejection is concentrated in the energy region between keV and MeV, some photons have been observed up to tens of GeV using detectors in space on board the CGRO satellite and more recently Fermi and AGILE.
Until now all the experimental data in the MeV-GeV energy range were obtained from detectors onboard satellites, but due to their small size and the rapid fall of GRB energy spectra they hardly cover the energy region above 1 GeV. The detection on ground can be done by two kinds of detectors able to provide a much larger effective area: telescopes for the atmospheric Cherenkov light and EAS arrays.
With their enormous size, the Cherenkov telescope recently installed at HESS and those planned for the CTA observatory allow the detection of gamma rays with an energy threshold as low as 20 GeV. However, the necessity of working during nights with clear skies and no or few moon light limits the efficiency to 10%-15%. Furthermore, apart very seldom serendipitous observations or specific pointing strategies to cover a wider sky region, the field of view of less than about 5
$ ^{\circ} $ prevents the study of short GRBs and of the prompt phase of long GRBs, since the repointing requires a minimum time of about 100 seconds. So far, all major Cherenkov detectors (MAGIC, HESS, VERITAS) have tried to point the GRBs following the afterglow but without success. In the case of CTA it is expected a coincident detection of 0.5-2 GRBs per year [3] depending on the assumed high energy spectral features, satellite alert rate and array performance.The EAS arrays have on the contrary a large field of view (nominally 2 sr, limited only by the atmospheric absorption) and high efficiency (up to 100%), but the need to reveal enough secondary particles to reconstruct the arrival direction and energy of the primary increases the threshold to around 100 GeV.
An alternative mode consists in the measurement of the counting rates of the detectors at time intervals of the order of a fraction of second ("single particle technique") [4-6], and then in the search for an excess in coincidence with a GRB detected by a satellite. With this technique it is not possible to measure the arrival direction of the excess, but the threshold energy can be lowered to about 1 GeV. Both techniques have been used by various extensive air shower arrays, such as EASTOP, Chacaltaya, Milagro and more recently ARGO-YBJ which has studied the richest sample of GRBs ever analyzed by a detector on ground (over 200 events) [7]. Even in this case there has been no clear detection.
The HAWC experiment, an extensive air shower array with an area of 22000 m2 fully operating in Mexico since spring 2015 at an altitude of 4100 m a.s.l., has made a detailed study on the possibility of detecting GRBs with both techniques, estimating an overall detection rate of 1.55/y for short GRBs and 0.25/y for long ones [8, 9]. The shower technique was found to be preferred with the idea of lowering the threshold energy down to 50 GeV. In this paper a method similar to that used for CTA and HAWC to calculate the expected rate and features of detectable GRBs has been applied to LHAASO.
-
The LHAASO experiment, planned to be installed in the Sichuan Province (P. R. of China) at 4410 m a.s.l., is currently under design to study cosmic rays and photons in the energy range 0.1-1000 TeV. This very wide interval is obtained combining different air shower detection techniques covering different energy windows. At the lower end, from 100 to 30 TeV, the Water Cherenkov Detector Array (WCDA) is one of the major components of LHAASO. It is made of three ponds, covering a total surface of 78000 m2. Each pond is divided into 900 cells (5 m
$ \times $ 5 m each, with a depth of 4.5 m) seen by one PMT located at the cell floor centre and looking up to detect the direct Cherenkov light produced by the relativistic particles of the showers. In order to maximize the detector performance a large simulation campaign has been carried out to optimize both the cell dimensions and depth and the number of PMTs for each cell. The results show that a higher PMT density, obtained with both smaller cells and higher number of PMTs per cell gives a better performance in terms of angular resolution and sensitivity, but weighting these results with a cost estimate the 5 m$ \times $ 5 m cells seen by a unique PMT offer the most effective layout [10]. Besides simulations, a prototype water Cherenkov detector has been built and operated in Beijing and an engineering array corresponding to 1% of one pool (3$ \times $ 3 cells equipped with one 8'' Hamamatsu R5912 PMT each) has been implemented at the ARGO-YBJ site (Yangbajing Cosmic Ray Laboratory, 4300 m a.s.l., P.R. of China). The measured counting rate was about 35 kHz for each cell, with an expected minimum of 12.5 kHz given by cosmic rays. Since LHAASO will be located at a similar height, we foresee a counting rate close to this value. This very high single counting rate does not allow a simple majority but requires a topological one, with different trigger levels. The basic element is given by a 3$ \times $ 3 cells matrix, whose signal is collected by a custom FEE and sent to a station where a suitable trigger is generated and the corresponding data are recorded. This quite new approach is called "trigger-less" and allows the maximum DAQ flexibility. For example, overlapping the clusters (corresponding to 12$ \times $ 12 cells) by shifting them of 30 m and requiring a coincidence of at least 12 PMTs within 250 ns in any cluster, a trigger rate of 70 KHz is expected. In the search for GRBs, this approach is particularly effective. For very low multiplicities, starting from 3, the number of random coincidences does not allow the reconstruction of the arrival direction, and moreover the huge amount of events prevents the storage of data. However, if an on-line alert is provided by satellites, as for the case of Cherenkov telescopes, the DAQ can switch to this very low multiplicity mode for a limited amount of time ($ \sim $ minutes) and knowing the arrival direction the random coincidences can be strongly suppressed. Even if for these very low multiplicity events ($ \sim $ 3-10 hits) the angular resolution is very poor ($ \sim $ 10$ ^{\circ} $ -15$ ^{\circ} $ ) and the primary energy is very badly reconstructed, the background is highly reduced with respect to the single particle technique, where the contribution comes from the whole sky. Providing a buffer to store continuously some hundreds of seconds of low multiplicity data, the GRBs can be followed since the beginning covering the delay of the alert transmission. To sum up, the GRB search will be done by LHAASO using the WCDA data in three different ways, depending on multiplicity:● for n = 1, 2 or slightly higher number of particles, the DAQ will simply count the number of events in a fixed time window with the corresponding multiplicity and the search will be done in "scaler mode", looking for a statistical excess in the counting rate of all the PMTs in the detector;
● for n
$ \gtrsim $ 10 the events are reconstructed one by one and an excess is looked for in the GRB direction. Since all these data are recorded, this search can be done off-line with unlimited GRB duration;● for the intermediate multiplicities, data are recorded for a fixed time window before and after the real-time alert given by satellites. If successful, this technique will cover for the first time for EAS arrays the energy region between a few GeV and 100 GeV with some directional information.
In order to evaluate the rate and typology of GRBs detectable by LHAASO, several ingredients must be laid together and precisely a GRB model, a parametrization as a function of energy of the detector performance (effective area and angular resolution) and some hypotheses on the expected external trigger rate. All these items will be presented and discussed in the following sections.
-
To compare our results with CTA and mainly HAWC, we decided to use the same approach found in [3] and [11]. In these papers, a set of pseudo-GRBs has been simulated sampling their features from the experimental ones measured by Fermi (GBM and LAT) and Swift (BAT) satellites. At first, we assume that the external trigger will be given by Fermi-GBM. For each parameter, a different distribution has been considered for short (T
$ _{90}\leq $ 2 s) and long (T$ _{90}> $ 2 s) GRBs, and no correlation among them has been considered. -
We suppose a high energy emission in the 1-1000 GeV energy range as a simple power law with fixed spectral index and no intrinsic cutoff, that will be given exclusively by Extragalactic Background Light (EBL) absorption. To quantify this high energy contribution, we used the correlation between the fluencies measured by GBM and LAT, respectively in the low and high energy bands. Figure 1 shows this correlation, updated with all the 21 GRBs with fluence calculated in the same time window. The points are very scattered, and for short GRBs (red squares) only 3 events were measured by both detectors. Nevertheless we followed the assumptions made in [12] that the LAT fluence in the 100 MeV-10 GeV energy range is about 10% of the GBM fluence in the 10 keV-1 MeV energy range for long GRBs, while for short ones the amount is 100%.
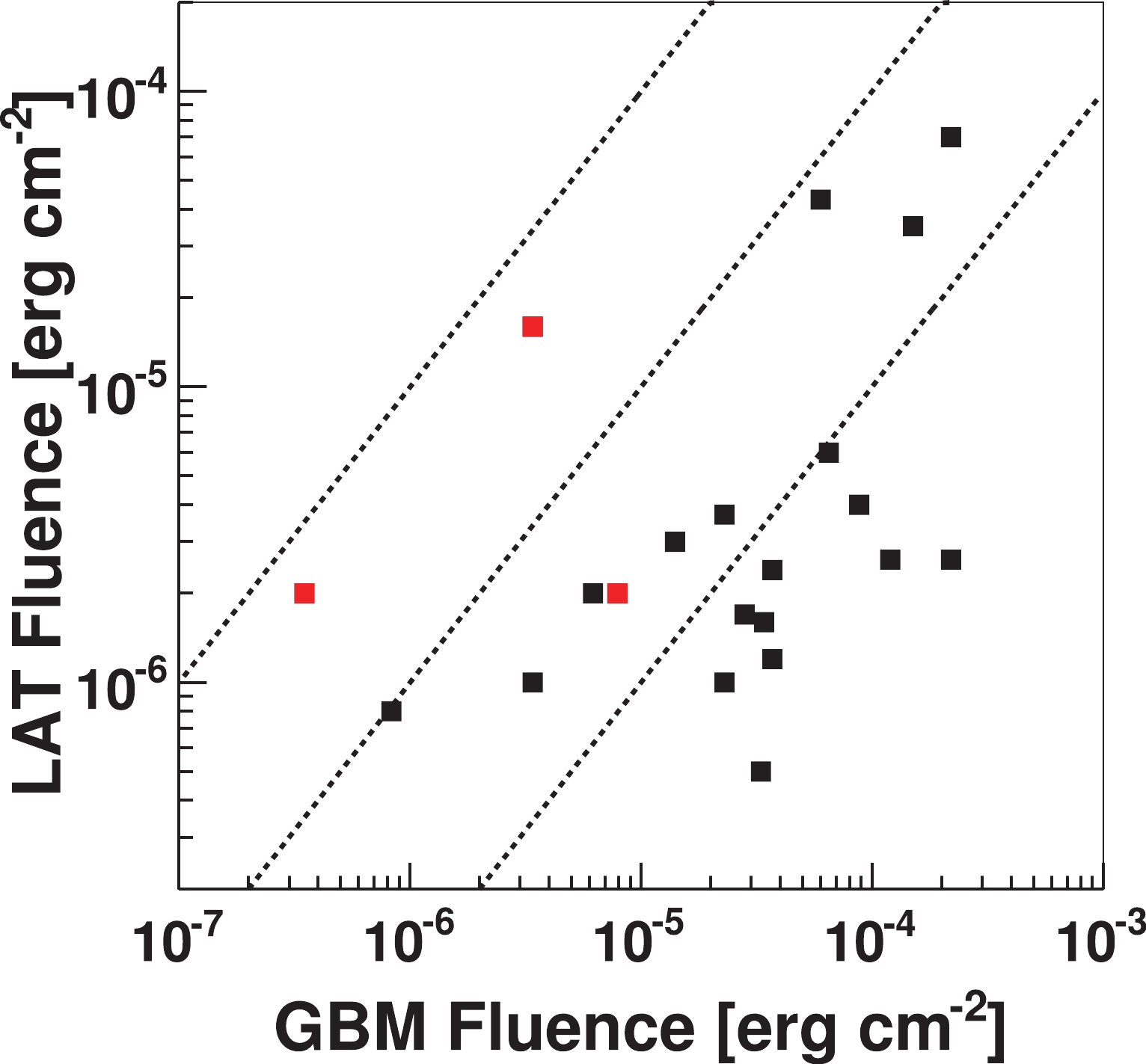
Figure 1. (color online) A comparison of the LAT and GBM fluencies in the [0.1-10] GeV and [10-1000] keV range respectively. Black (red) squares are for long (short) GRBs; dashed lines indicate LAT-GBM fluence ratio of 0.1, 1.0, 10.0 (bottom to top).
Figure 2 shows the low energy fluence measured by GBM (red: short GRBs; black: long GRBs). For the high energy emission of our pseudo-GRBs we sampled from these distributions a fluence that is reported to the 100 MeV-10 GeV energy region using the quoted percentages. Since the fluence distribution for long GRBs is shifted towards larger values by about a factor of 10 with respect to the short ones, the high energy scaling produces a close distribution for short and long GRBs. For the high energy spectrum we used a spectral index α = −2, since for long GRBs with an additional power law this is the mean value measured by LAT. For short GRBs we used α = −1.6, the same value used in [11]. The assumption that all short and long GRBs have an additional high energy power law with spectral index −1.6 and −2, respectively, and without any cutoff in all the considered energy range is quite raw and optimistic, but in any case it allows us to compare our results with the expected sensitivity of HAWC.
-
As pointed out by Ghisellini et al. in [13], the GRB light curve can be modeled as a constant flux during the T90 measured by GBM, followed by a power law fall-off with index γ = 1.5. Due to its expected higher sensitivity and to the fact that it will lose the prompt phase of most GRBs, CTA made this assumption in [3] to estimate the rate of detectable GRBs. We decided instead to follow the approach used for HAWC, i.e., we sampled the T90 distribution showed in Fig. 3 obtained by Fermi-GBM for long GRBs (black line), while we used a fixed GRB duration of 2 s for short GRBs.
-
The interaction of very high energy photons with the EBL produces e-pairs and thus a quite sharp spectral cutoff. This absorption depends on the redshift and GRBs are cosmological objects, with a mean value
$ z\simeq2 $ . Many models of EBL attenuation have been published in the last decades, with a general trend towards an increase of transparency due to the observation of very high energy photons at larger redshifts [14]. In this work we used the model by Kneiske et al. [15]. Since the energy resolution of the Fermi-GBM instrument does not allow the detection of clear spectral lines, the GRB distance is obtained sampling the redshift distributions measured by Swift-BAT. Figure 4 shows these distributions for long (black line) and short (red line) GRBs. We apply the EBL cutoff starting from z = 0.1 and up to 1 TeV, the maximum energy after which the source spectrum is totally absorbed. This choice is due to the fact that z = 0.1 corresponds roughly to a cutoff energy of 1 TeV in our model. An important point to be checked is that the higher sensitivity of Swift-BAT with respect to Fermi-GBM could distort the redshift distribution, so we selected the subsample of GRBs detected by both. The corresponding distribution (dashed black and red lines for long and short GRBs respectively) is also shown in Fig. 4 and does not show significant deviations from the whole data set. -
The sensitivity of an EAS array to any gamma-ray source and in particular to GRBs is given by the angular resolution and the effective area for primary photons. Both of these depend on the primary energy and on the zenith angle (however, the dependency of the angular resolution on the zenith angle is small). The expected performance of the detector is evaluated by means of a detailed Monte Carlo simulation that reproduces the development of gamma-ray showers in the atmosphere and the interaction of the secondary EAS particles with the detector. For each pseudo-GRB the expected signal S is calculated integrating from 1 GeV to 1 TeV:
$ S = \int_{1\; {\rm GeV}}^{1\; {\rm TeV}} S_{\gamma}(E) \times EBL(E,z) \times A^{\gamma}_{\rm eff}(E, \theta) \times T_{90}\; {\rm d}E , $

(1) where
$ S_{\gamma}(E) $ is the sampled GRB spectrum,$ EBL(E,z) $ the EBL absorption,$ A^{\gamma}_{\rm eff}(E, \theta) $ the photons effective area and$ T_{90} $ the burst duration. The peak energy$ E_{\rm peak} $ is defined as the energy corresponding to the maximum of the signal function before integration. For GRBs,$ E_{\rm peak} $ is typically less than 100 GeV.The zenith angle of the pseudo-GRB is randomly chosen in the range from 0 to 50 degrees, with a uniform distribution in the corresponding solid angle. To calculate the expected background B, the same Monte Carlo simulation is run for primary protons, obtaining an effective area
$ A^{p}_{\rm eff}(E, \theta) $ as a function of energy and zenith angle. The expected background B is calculated integrating in the same energy range 1GeV-1 TeV:$ B = \int_{1\; {\rm GeV}}^{1\; {\rm TeV}} S_p(E) \times A^{p}_{\rm eff}(E, \theta) \times T_{90} \times \Omega(E_{\rm peak})\; {\rm d}E , $

(2) where
$ S_p(E) $ is the cosmic ray spectrum and$ \Omega(E_{\rm peak}) $ the solid angle corresponding to the angular resolution for$ E = E_{\rm peak} $ . As angular resolution, we use the$ \Psi_{70} $ aperture that maximizes the signal to noise (i.e. S/$ \sqrt{(B)} $ ) ratio keeping 71.5% of the signal with an aperture of 1.58 σ.For the cosmic ray spectrum, all the primary nuclei from p to Fe have been simulated and then grouped into five mass sets (p, He, CNO, NeMgSi, Fe). As a first step, the effective area has been obtained considering a cosmic ray flux made by only protons, normalized to obtain a counting rate equivalent to that produced by all the five mass groups using the Hörandel primary composition [16]. For each primary particle (in our case photons and protons) this simulation procedure, that is very CPU-consuming requiring the generation of a huge amount of events, must be repeated for each trigger condition and several zenith angles. Figure 5 shows the angular resolution for internal events (
$ r< $ 160 m) and trigger multiplicity$ N_{\rm fit } \geq $ 20, where$ N_{\rm fit } $ corresponds to the total number of hits for each event after an iterative cleaning procedure to discard the random hits on the basis of the temporal features of the shower front. Figure 6 shows the effective areas for gammas (left) and protons (right) in steps of 15$ ^\circ $ for zenith angle from 0$ ^\circ $ to 60$ ^\circ $ and trigger multiplicity$ N_{\rm fit } \geq $ 10. These results have been obtained using CORSIKA [17] for the development of EASs from gamma rays and protons, and a custom software derived by the Milagro one for the detector response. The complete set of simulations for the different trigger conditions is currently undergoing. -
The confidence level of a detection is obtained requiring a signal greater than a given number of background fluctuations. A value of 5 s.d. has been set as the detector threshold, and to properly calculate the signal significance, equation (17) of [18] was used. Once the fraction of detectable GRBs has been derived, an external trigger rate must be provided. According to [19], Fermi/GBM detected GRBs with a mean detection rate of
$ \sim $ 250/y in its f.o.v. of 8.74 s. This corresponds to more than 700 GRBs yr-1 from the whole sky taking into account that GBM has a duty cycle of about 50%. The LHAASO angular acceptance up to 50$ ^{\circ} $ in zenith angle is 2.24 s, with a full sky coverage of 17.9%. The expected trigger rate in GBM follow-up observations is thus 45/y, while in independent mode we foresee$ \sim $ 130 "GBM-like" GRBs per year. These values will be used to normalize in time our pseudo-GRBs data set. -
CGRO/EGRET in the past and recently Fermi/LAT have clearly demonstrated the emission of GeV photons from GRBs. Nevertheless, this VHE emission is quite unusual and the presence of a hard power-law contribution to the spectrum has not been confirmed for all the GRBs seen by LAT. Moreover, the extrapolation to the GeV region is made over several orders of magnitude, with a fixed ratio between low and high energy fluencies that roughly fits reality. The expected fraction of detectable GRBs is largely dependent on the adopted GRB model, and for this reason we decided to use as much as possible the same assumptions made by CTA and mainly by HAWC to make the results comparable. Presently, our GRB model is defined together with all the calculation details. The determination of the effective area and angular resolution for gamma rays and protons and for the different trigger conditions is currently under way and the very first results on the GRBs detectability and typology for some trigger conditions by LHAASO-WCDA are under check.
-
Large High Altitude Air Shower Observatory (LHAASO) has been building the 2nd and 3rd water Cherenkov detectors, denoted as WCDA-2 and WCDA-3, using Multi Channel Plate (MCP) staffed 20" Photo Multiplier Tube (PMT) instead of the 8" traditional PMTs with dynodes as originally proposed. This will enhance its sensitivity at energies around 100 GeV. The effective area for gamma ray detection will reach to 1800 m2 and differential sensitivity to 0.2 Crab Unit (CU, the gamma ray flux from the Crab Nebula at corresponding energy) around 50 GeV. It will be the very useful survey detection for transient phenomena around 50 GeV in the northern sky. LHAASO is expected to play an important role in the multi-messenger astronomy after the WCDA-2 is put in operation by the end of 2019. WCDA-3 is expected to be finished by the end of 2020.
-
The first multi-messenger observation of Gravitational Wave (GW) event GW170817 by LIGO and VIRGO GW observatories together with many other Electro-Magnetic (EM) wave observations, such as FERMI [20] and the multi-wavelength campaign on the possible EM partner of the very high energy neutrino IC-170922A detected by the IceCube experiment [21] are very significant progresses in astroparticle physics in past years. They opened new windows for exploring the high energy phenomena in the universe. This, however, becomes a challenge to LHAASO with its original proposal which is designed to target the high energy (above several hundred GeV) gamma ray sources and charged particles at even higher energies up to a few EeV. At energies lower than 300 GeV, the gamma ray detection sensitivity is not sufficient to detect those sources which is typically faint. In order to enhance the sensitivity below 100 GeV, we proposed to enlarge the sensitive area of the photo cathode of the water Cherenkov detector in the LHAASO array. In this section, we are going to briefly describe the experiments with original WCDA as well as the upgrading plan in Sec. II.B, and the performance of WCDA in gamma ray astronomy with the the enhancement at low energy region in Sec. II.C The whole upgrading plan is briefly summarized in Sec. II.D
-
LHAASO is a multipurpose complex of Extensive Air Shower (EAS) detection observatory consisting of four major detector arrays. In the center of the observatory, the WCDA is divided into 3 independent water pools, namely two smaller pools with the area of
$ 150\ {\rm m} \times 150\ {\rm m} $ each, denoted as WCDA-1 and WCDA-2, and the larger one with the area of$300\ {\rm m} \times 110\ {\rm m}$ , denoted as WCDA-3. The layout and orientation of WCDA is shown in Fig. 7. WCDA-1, in south-west, is already put in scientific operation since April 2019.
Figure 7. (color online) The layout and orientation of the water Cherenkov detector array (WCDA, rectangle in the center) in LHAASO. In south-west, WCDA-1 of 150 m
$\times$ 150 m is put in operation. In south-east, WCDA-2 with the same size as WCDA-1 is illustrated with the pup-up square on the right-hand-side. It is divided into 900 detector units. 36 units form a cluster with a junction box with all Front-End Electronics (FEE), digitization, power suppliers and calibration LED-drivers in. The bigger one in north, WCDA-3, has 1320 units covering an area of 300 m$\times$ 110 m.WCDA-1 has 900 units, equipped by a large (8") PMT for timing and a small (1.5") PMT for pulse size in each unit. WCDA-1 measures shower directions with a resolution better than 0.2
$ ^\circ $ above 10 TeV and 1.0$ ^\circ $ above 600 GeV. The small PMTs enlarge the dynamic range of the detector very much. This enables the measurement of the detailed particle density distribution in the shower cores without saturation even for energetic showers up to 10 PeV and achievement of the core location resolution better than 3 m. This is designed for the identification of the primary particle species in the cosmic ray composition and spectrum measurements.Low energy showers are small in terms of total number of particles that reach to the pools, therefore the total Cherenkov signal generated by those secondary particles in every detector unit is faint, even for units being near the cores of the showers. In order to enhance the gamma ray detecting sensitivity at low energies, enlarging the sensitive photo-cathode area of the PMT in the same size unit could be one effective way to catch the faint signals. LHAASO has made a upgrading plan along with this approach, namely to replace the 8" PMTs by 20" PMTs in the rest WCDA-2 and WCDA-3 with the active area of 55500
$ {\rm m}^2 $ in total. To gain the enlarging factor of 6.25 in terms of the photo cathode area versus the 8" tube, the dynamic range is also shrunk by the same factor. This is the price to pay. In order to compensate the loss, a 3" PMT is installed beside the large PMT in each unit, read out only for the pulse size by a simplified version of the Front-End Electronics (FEE) covering 4 orders of magnitudes of number of photo-electrons. -
Gamma ray induced showers are different from showers induced by charged Cosmic Ray (CR) nuclei in terms of the hits distribution in the pool. In general, the later is more spread out than the former ones as shown in Fig. 8, where two Monte Carlo (MC) simulated events due to 1 TeV gamma ray and 2 TeV proton are compared with each other. Even more significantly, the CR events have many "hot spots", the populated hits, outside the core region, while the gamma ray events are much cleaner beyond some distance from the core. This enables us to identify the gamma events out of the CR background, nevertheless they are much more (104~5) than gamma ray signals even if within a very small angular region defined by the point-spread-function (PSF) near the sources. By eliminating the events which have the most populated hit in the outer region, 45 m from the core, greater than certain number of photoelectrons,
$ N_{\rm th} $ , the CR background will be suppressed to very low in the nearby region of sources. Making balancing between the elimination of the background CR events and the loss the γ-like signal events to maximize the sensitivity. It is found that$ N_{\rm th} $ increases with the number of hits that are involved in the shower front fit, denoted as$ N_{\rm fit} $ which measures the shower energy, i.e. proportional to$ N_{\rm fit}/{\rm log} N_{\rm fit} $ . Shown in the Fig. 8, one γ-like event from the Crab Nebula direction measured by WCDA-1 is selected according to the algorithm, together with a typical event that has similar number of hits to the γ-like event as a comparison. Other parameters characterize the distribution of hits in the whole pool area, such as hit density in the outer region, are used in the identification of gamma ray events. This results an effective area for gamma ray detection of about 230$ {\rm m}^2 $ at 50 GeV and 30000$ {\rm m}^2 $ at 1 TeV, respectively, if all 3 pools were equipped by 8" PMTs. The corresponding sensitivity of the gamma ray point-like source detection is plotted in Fig. 9 as a function of gamma ray energy.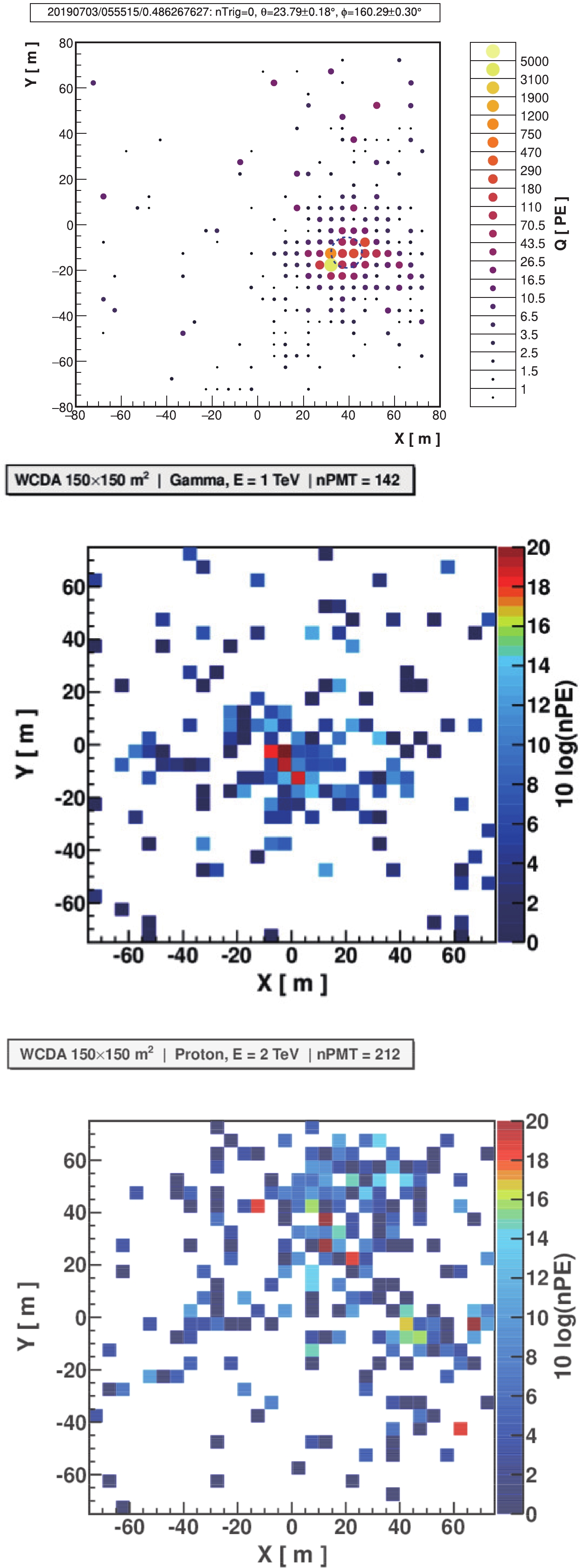
Figure 8. (color online) The top panel shows an event recorded by WCDA-1 representing γ-like from Crab Nebula direction according to the algorithm of
$\gamma/p$ discrimination. This algorithm was tested and optimized using simulated events. The middle panel shows a simulated event induced by 1 TeV gamma ray. As a comparison, a 2 TeV proton event is also showed in the bottom panel which looks much more spread out than the events induced by gamma rays.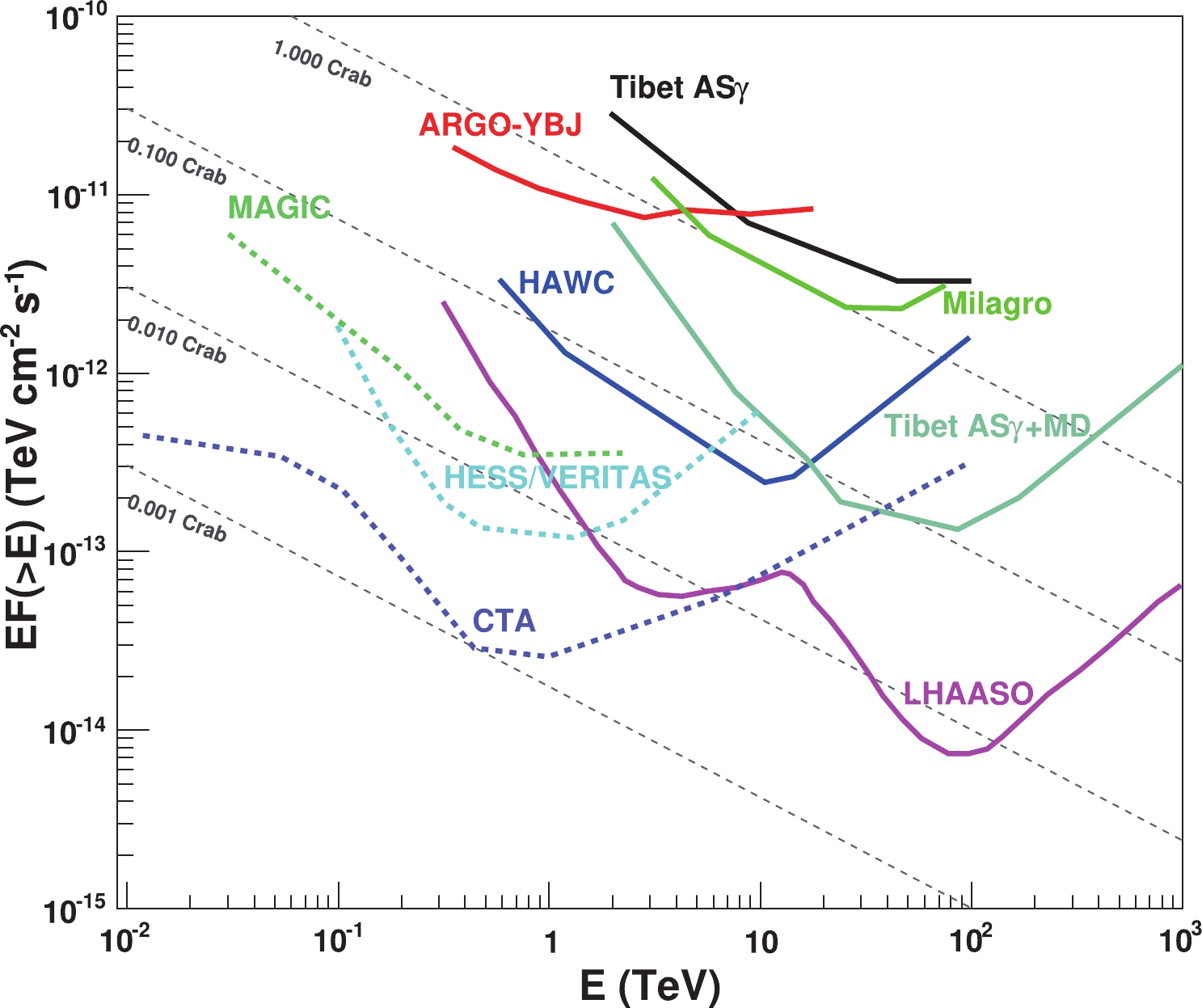
Figure 9. (color online) The integrated sensitivity of LHAASO (in pink) comparing with other experiments. The part of the curve below 10 TeV is the contribution of WCDA optimized with the cuts described in text.
With this configuration, LHAASO has a survey power for discovering all sources that are brighter than 7 mini crab unit above 1 TeV. Taking into account the wide field of view of
$ \sim 1/7 $ of the entire sky and the constant exposure time of 24 hours, LHAASO is very significant in finding new sources. It is actually estimated that about 40 new Active Galactic Nuclei (AGN) [21] could be discovered within one year after it is fully operated. It is also expected that LHAASO will make a deeper survey inside our galaxy comparing with what has been done by the HAWC experiment [22]. LHAASO will play as a wide FoV monitor for any kind of transient phenomena, such as AGN flares and Gamma Ray Bursts (GRB), as well. -
With the upgraded configuration using 20" PMTs in WCDA-2 and WCDA-3, the effective area at energies below 300 GeV is significantly enlarged, i.e. reaches to 1800
$ {\rm m}^2 $ at 50 GeV and 44000$ {\rm m}^2 $ at 1 TeV. The corresponding differential sensitivity around 50 GeV is expected to be 0.2 CU per a quart decade of energy which is compatible with the space borne detector FERMI-LAT, as shown in Fig. 10. The difference, however, is that the effective area is a factor of 1800 larger than the later. This means that more than 1000 photons are expected to be recorded if the gamma ray burst event GRB090510 happened again in the field of view of LHAASO. In event GRB130427A, FERMI-LAT recorded a single gamma photon at 95 GeV [23]. If such GRBs with high energy photons happened again, they should be detected by LHAASO given the LHAASO sensitivity. This opens a window for the multi-wavelength campaign in a much convenient way because of the clock-round operation of LHAASO. With any global alarm for transient phenomena, such as GRB, it is easy for LHAASO to recall the data in the window in which the alarm was ringing. Not only the status of the source at$ T_0 $ can be observed, but also it is in principle possible to find any pre-burst emission of gamma rays if there were.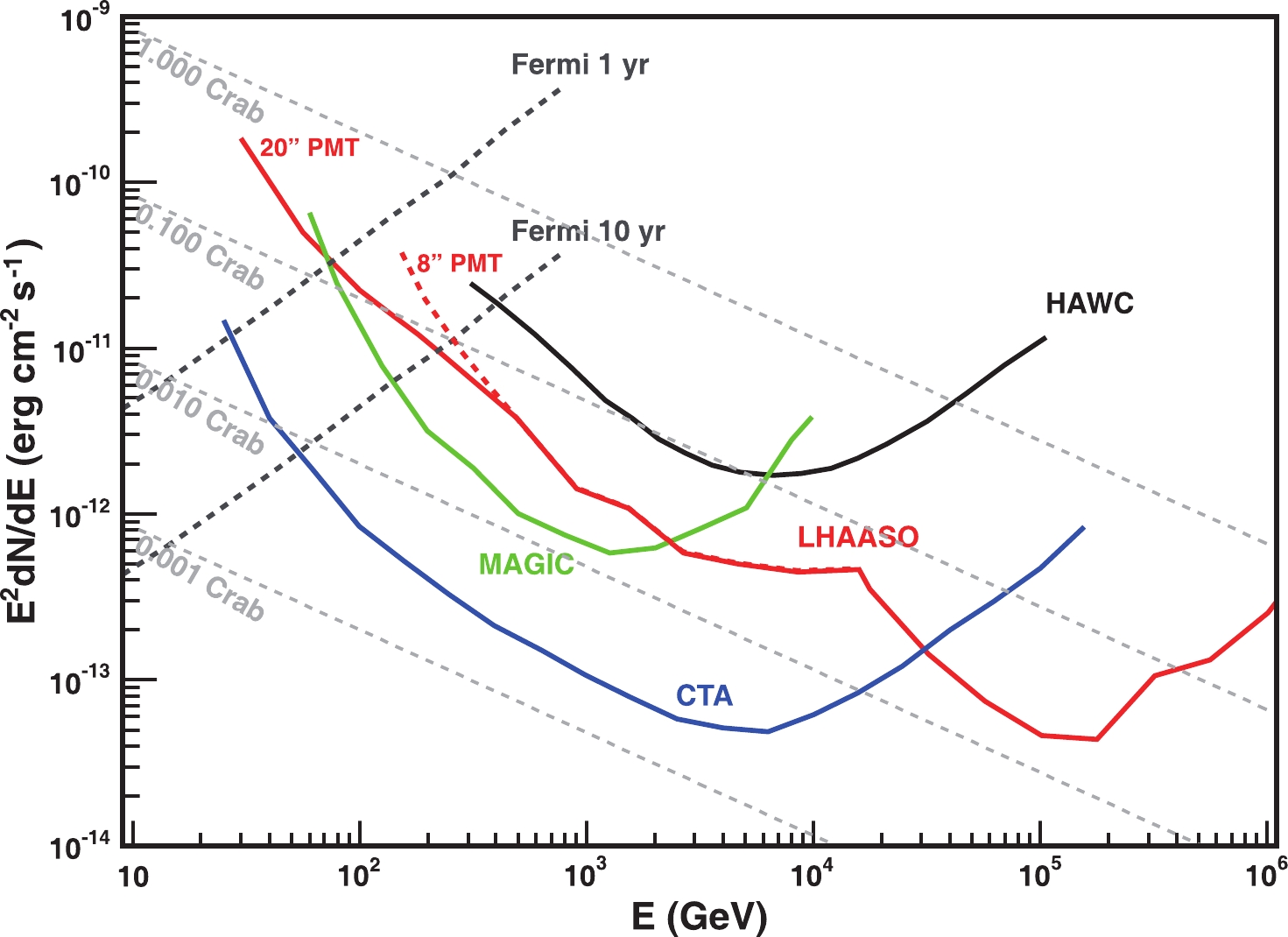
Figure 10. (color online) The differential sensitivity of LHAASO (in red) comparing with other experiments. Below 300 GeV, both estimates with 8" PMT configuration (dashed line) and 20" PMT configuration (solid line) are plotted. It is noticed that WCDA with 20" PMTs is almost as same sensitive as FERMI/LAT at 70 GeV.
With such a sensitivity, LHAASO will be a transient phenomenon finder as well. An alarm trigger algorithm is going to be operated to constantly watch all interested AGNs in LHAASO's Field of View (FoV) for any excess in various time windows, e.g. from few seconds to hours. It is useful for monitoring any AGN flare, e.g. if its emission level rises to be greater than 1 CU within a hour, an alarm will be broadcast to the whole community.
-
Investigating sources with multi-messengers is very powerful in viewing of inside mechanism of high energy phenomena in the universe, particularly for possible common origins of the messengers, such us neutrinos, gamma rays, charged particles and gravitational waves. However, to identify the sources and verify the association, all corresponding detectors are required for sufficient sensitivities. As an example, we investigated the possible association between the ultra high energy muon neutrino event IC-170922A detected by the IceCube experiment [21] and the blazer TXS 0506+056 which had a faint flare within 20 days after the neutrino event in multiple wavelength bands, including X-ray (SWIFT), gamma ray (FERMI-LAT) and very high energy gamma ray (MAGIC). The Spectral Energy Distribution (SED) of the blazer during the flare is reported in Ref. [21] and is quoted here in Fig. 11 over a very wide energy range. Also shown in the figure, sensitivity curves of several experiments, including HAWC, HESS, VERITAS and upgraded LHAASO. According to this, LHAASO will play a significant role in such multi-messenger observation by covering an important energy range starting from as low as 30 GeV to few hundred TeV.
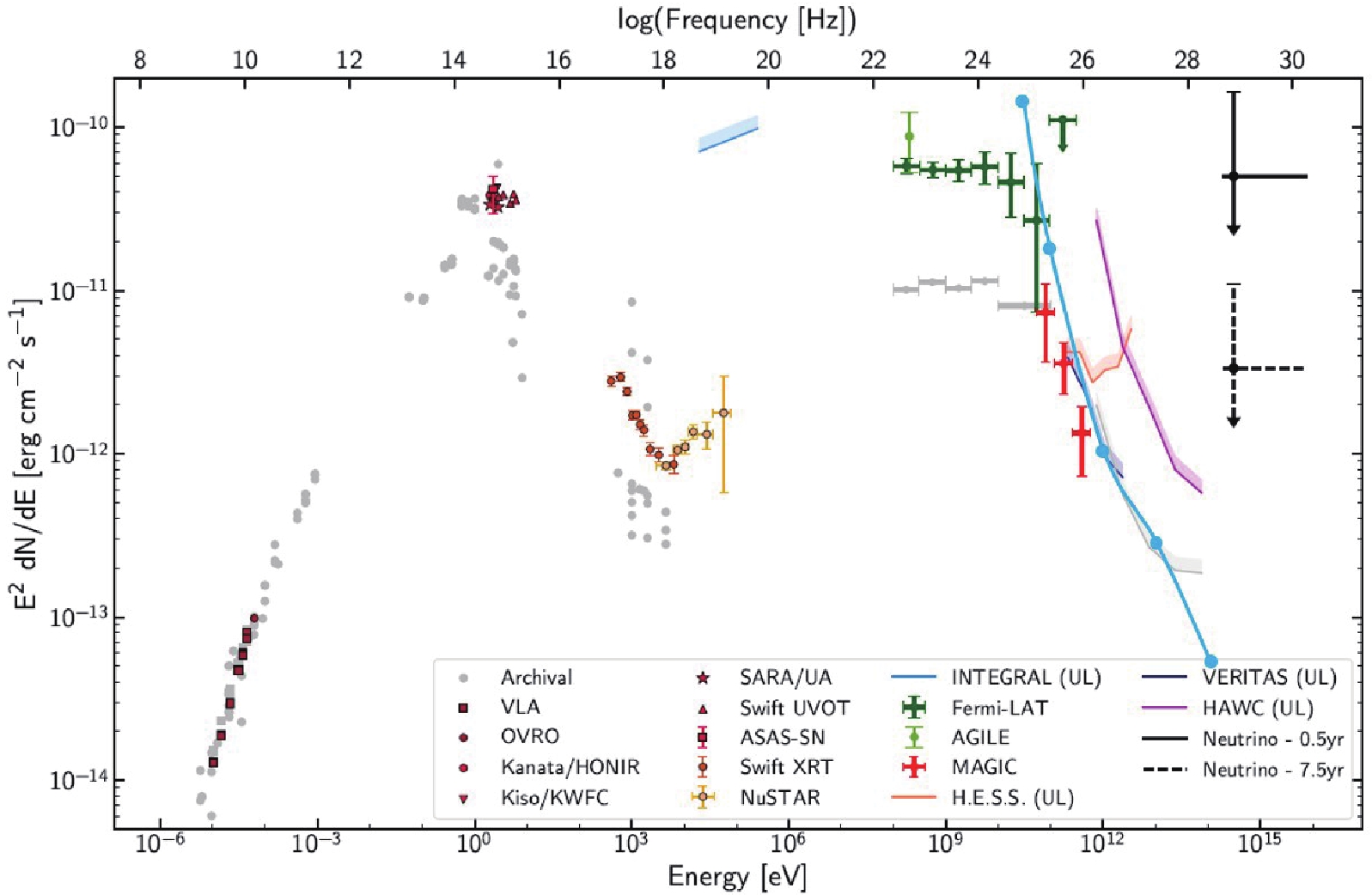
Figure 11. (color online) The SED of TXS 0506+056 during the flare within 20 days after the neutrino event IC-170922A. It is reported in Ref. [21] including sensitivity curves of HAWC, HESS and VERITAS experiments. The upgraded LHAASO sensitivity is also plotted in the same figure (light blue) from 30 GeV to 100 TeV.
For other blazars including BL Lac objects and flat-spectrum radio quasars, the most extreme subclass of AGNs, LHAASO has a full duty cycle and a large FoV to monitor flares of them continuously. In Fig. 12, the flare on Mrk501 for 35 days is measured by Swift, FERMI-LAT and ARGO-YBJ (See Ref. [24]). It clearly differs from the steady emission which fits well with the Synchrotron Self-Compton (SSC) model. Assuming the similar flare occurred again, the prediction for LHAASO's observation is plotted in Fig. 12 and LHAASO will give an accurate spectrum at TeV region which can be the key to explain the radiation mechanism of flare. LHAASO not only serves as a global alarm system for the high energy flares, but also opens a great opportunity to identify the emitting mechanism during the flares.
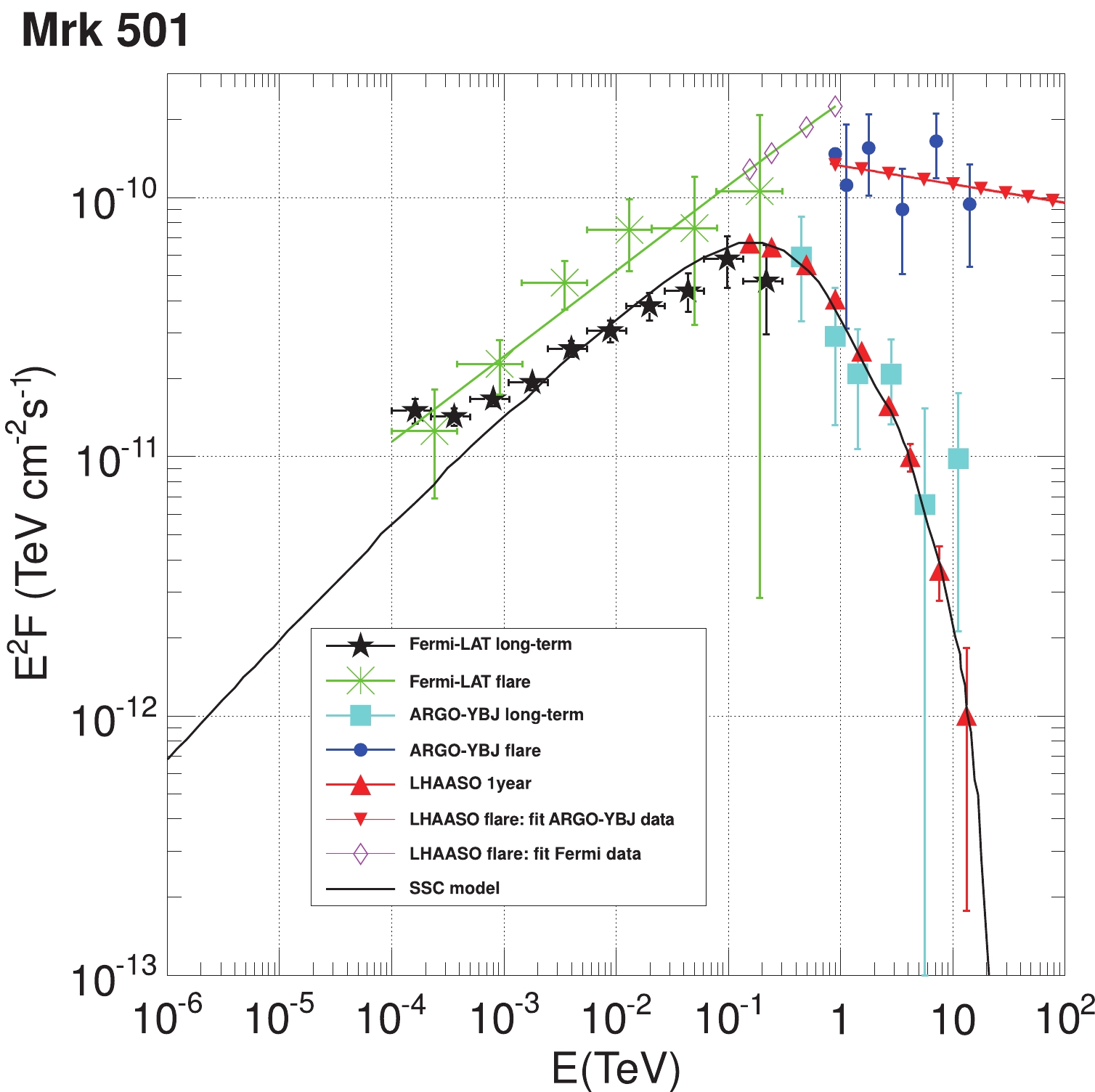
Figure 12. (color online) Expectation of the LHAASO project on Mrk501 (open diamonds and inverted filled triangles), comparing with the measurements by FERMI-LAT and ARGO-YBJ[24], respectively.
Beyond the traditional studies of the extra-galactic gamma ray emissions, the potential of LHAASO in exploring new physics such as intergalactic magnetic field detection and Lorentz invariance tests, has been discussed in depth elsewhere (See Ref. [25]).
-
LHAASO has started its upgrading plan by replacing the 8" PMTs with 20" PMTs in 70% of area of WCDA. WCDA-1, 30% of the total area of the detector and equipped with 8" PMTs, has been put in scientific operation since April 2019. Mrk-421 has been observed with a significance of 20σ within 173 days of observation. WCDA-2, same size as WCDA-1 but equipped with 20" PMTs, is under construction and going to be put in operation by the end of 2019. The whole array, including the scintillator counter array and muon detector array and Cherenkov telescopes, will be built up by 2021. With the upgraded configuration, the gamma ray detecting sensitivity below 300 GeV will be boosted to be about 0.2 crab unit per quarter decades of energy around 50 GeV [26] and as same sensitive as FERMI-LAT at 70 GeV. LHAASO therefore will play a significant role in surveying for new sources brighter than 7 milli-CU above 1 TeV in the northern sky and monitoring for transient phenomena in its FoV of the size of 1/7 sky at any moment. The LHAASO effective area of 1800
${\rm m}^2 $ around 50 GeV is going to be a useful tool in the multi-messenger astronomy involving in ultra high energy neutrino or gravitational wave detection. -
Detection of GeV photons from GRBs is crucial in understanding the most violent phenomenon in our universe. Due to the limited effective area of space-born experiment, only 29 GRBs above 10 GeV emission were detected at the time of writing. Large area EAS experiments at high altitude can reach a much larger effective area around 10 GeV, for which single particle technique is usually used to lower the threshold energy but its sensitivity is poor due to indistinguishable of direction. To reach an energy threshold as low as 10 GeV and guarantee the sensitivity at the same time, low multiplicity trigger is required, but random coincidences rather than cosmic ray showers overwhelms the signals, and it is a great challenge for traditional trigger logic and reconstruction algorithm to discriminate the signals from the noises. A new method is developed for LHAASO-WCDA(Large High Altitude Air Shower Observatory-Water Cherenkov Detector Array) to work under low multiplicity mode. With this technique, the LHAASO detector can even work below 100 GeV, the sensitivity and expectation of LHAASO-WCDA with low multiplicity technique to GRBs are presented.
-
Gamma Ray Bursts (GRBs) are among the most powerful events in the Universe, and have been the subject of observational studies from radio to multi-GeV energies. Satellites with instruments sensitive to hard gamma-rays, such as CGRO and Fermi LAT, have extended the observations from 30 MeV to tens of GeV. GRB130427A [27] that was observed up to 94 GeV, or 126 GeV once corrected for redshift, shows that GRBs are capable of producing very-high-energy photons. On the present, several GRBs have been observed above 10 GeV [12, 28-31]. It is unknown up to what energy the spectrum extends, as present-day observations are limited by effective area, in the case of space-based instruments, and by slewing constraints and energy threshold for ground-based Imaging Air Cherenkov Telescopes. Studying the spectrum beyond 10 GeV is crucial in understanding GRB mechanisms themselves, and also allows us to probe cosmological phenomena such as extra-galactic background light (EBL) and it may be used to constrain Lorentz invariance violation.
Currently three major classes of high-energy detectors exist: Satellite detectors, Imaging Atmospheric Cherenkov Telescopes (IACTs) and Extensive Air Shower (EAS) particle detector arrays. Satellites can observe very wide fields of view (e.g. 2.4 sr or
$ 19$ % of$ 4\pi $ sr for Fermi LAT) and have close to a$ 100$ % operational duty cycle. On the other hand, the limited physical size of satellites prevents them from obtaining enough statistics to reach energies greater than tens of GeV. Operating above 50 GeV IACTs that have been designed for fast slewing (1 min). EAS detector arrays, such as WCDA, benefit from a very large field of view (2 sr or$ 16$ % of$ 4\pi $ sr) and near$ 100$ % duty cycle that will allow for observations in the prompt phase. They are also sensitive to energies beyond those covered by satellites. EAS observatories, in particular WCDA, are thus useful high-energy GRB detectors that complement the observations by satellites such as Fermi.For EAS detectors, at present, two methods can be used to analysis the sensitivity and capabilities of detection of GRBs by WCDA: Shower mode method, Single particle technique (SPT) and Low multiplicity technique. Shower model method is a regular analysis method, threshold-energy is about 100 GeV, but GRBs with 100 GeV photons are very few. SPT can detect GRBs with 10 GeV photon but poor in sensitivity due to losing direction information. So taking advantage of characteristic of trigger mode of WCDA, a new method, low multiplicity technique is developed for GRBs detection, which can reach such energy like tens of GeV and reserve direction information at the same time. In this proceeding we will present the sensitivity and capabilities of low multiplicity technique for detection of GRBs by WCDA and show the observatory's ability to measure possible high-energy emission from GRBs.
-
Targeting gamma astronomy in energy band from 100 GeV to 30 TeV, the WCDA is one of the major components of the LHAASO, covering an area 90000
$ {\rm m}^{2} $ , has been proposed to be built at Daocheng County (4300 m a.s.l.), GanZizhou, SiChuan, China. Is is made of three ponds, two with area of$ 150 {\rm m}\times150 \ {\rm m} $ and another with an area of$ 300 \;{\rm m}\times110 \ {\rm m} $ . Total ($ 5 {\rm m}\times5 \ {\rm m} $ each partitioned by 0.5 mm-thick black curtains made of black polyethylene lines, with a effective water depth of 4 m) seen by one PMT located at the cell floor center and looking up to detect the direct Cherenkov light produced by the relativistic particles of the showers.The measured counting rate was about 36 kHz for each cell, which is much higher than the noise of PMT itself. So a new trigger technique based on "Trigger-less" is proposed for large area WCDA: each PMT will output a L1 (Level 1) single trigger signal of 250 ns after hit and over threshold, and if there is another over-threshold signal in the same 250 ns period, which will be taken as a new signal and trigger signal will extend 250 ns; namely the total array is divided into 81 trigger cluster (
$ 60 \ {\rm m} \times60 \ {\rm m} $ each, including$ 12\times12 = 144 $ PMTs) Horizontally and vertically, and then judge whether hit multiplicity is bigger than 12 at the falling edge of the clock of each trigger cluster. When any trigger cluster satisfies this selection, then output one L2 trigger signal and produce total trigger. In this trigger system, if single counting rate produced by cosmic ray is less than 50 kHz, random coincidence trigger rate produced by single counting can be controlled smaller than 1 kHz, and trigger rate of 70 kHz produced by air shower ($ > $ 10 GeV) is expected. -
In order to lower the threshold energy and reserve the primary direction information at the same time for GRBs detection, Low multiplicity technique is produced taking advantage of LHAASO-WCDA trigger technique based on "trigger-less", wide field of view and full duty cycle, only observatory array like LHAASO-WCDA with these three characteristics can do this. For WCDA1, total array is about
$ 10^{8} \ {\rm Hz} $ , corresponding to trigger rate of$ 10^{6} \ {\rm Hz} $ in the trigger window of 300ns, which is much higher than signal from cosmic ray, that means the random coincidence event rate is too high. Then how to discriminate the signals from the noise, it's a great challenge for traditional trigger logic and reconstruction algorithm, A new method is developed for LHAASO-WCDA to work under low multiplicity mode.Lowering down the huge background rate from single rate is crucial for this method. Three steps are take to realize this goal. firstly, we take the GRB alert as an "event" trigger for follow-up observation. As we know, typical delay of a GRB alert is about 1 minute, when a GRB alert comes, DAQ takes the GRB alert as an "event" trigger for low multiplicity technique and stores all the data in the pipeline and data of a certain time duration after the alert before reconstructing the shower core and direction for follow up observation. This implies that the GRB position is known from other observations. The time and duration of the burst are also assumed known, which allows one to efficiently reject the background by defining a restrictive time window. There is no any problem and hardware-free for WCDA. Secondly, we localize the shower, namely lower the total single rate. we can consider events with a distance from center of the array
$ < $ 50 m, and with zenith angle$ < 40^{\rm o} $ , after doing so, the total number of noise hits is reduced by a factor of 10, but it's still too high for a multiplicity as low as 3. At last, we shrink the trigger time window through hit time transformation. After this transformation, the coincidence time window can be reduced by a factor of$ \sim30 $ , in which the average number of noise hits can be reduced by a factor of$ \sim30 $ , from 3 to 0.1, it's good for low multiplicity trigger.In this method, all hits are to be saved, and the running time window should be applied on each hit, otherwise, shower hits can be separated into adjacent windows.
-
Gamma-ray showers are simulated with CORSIKA with an
$ E^{-2.0} $ spectrum at different energy. The detector response model developed for WCDA is used at an altitude of 4300 m using a GEANT4 based code. The lowest energy for primary gamma showers was set to 10 GeV. The signal rate in the low multiplicity technique is the number of PMT hit after detector response and before direction and position reconstruction.The signal rate S is given by:
$ S(\theta) = \int {\rm d}E \frac{{\rm d}N}{{\rm d}E}A^{\rm low\ multiplicity}_{\rm eff}(E,\theta) , $

(3) where
$ {\rm d}N/{\rm d}E $ is the photon spectrum and$ A^{\rm low \ multiplicity}_{\rm eff} $ is the detector effective area. Depends on several variables and here only energy E and zenith angle are treated. In this proceeding, only results of$ \theta = 0 $ are presented, and other direction will be considered later. The effective area of WCDA for gamma rays for different low multiplicity is shown in the Table 1.nhit $\geq$ 1 m2

nhit $\geq$ 2 m2

nhit $\geq$ 3 m2

10 GeV $3.7\times 10^4$ 

$4.7\times 10^3$ 

$1.7\times 10^3$ 

20 GeV $9.5\times 10^4$ 

$1.9\times 10^4$ 

$8.2\times 10^3$ 

50 GeV $3.0\times 10^5$ 

$8.9\times 10^4$ 

$4.6\times 10^4$ 

100 GeV $5.4\times 10^5$ 

$2.2\times 10^5$ 

$1.4\times 10^5$ 

Table 1. Effective area at different energy for low multiplicity.
-
Galactic cosmic rays are simulated with CORSIKA for multiple species with an
$ E^{-2.62} $ spectrum: protons, He, C, O, Ne, Mg, Si, Fe. The galactic cosmic ray spectrum is re-weighted to measurement by J. R. Hoerandel [32]. Background rate mainly includes occasional noise from cosmic rays and random coincidence noise. Fig. 13 is the distribution of hit number from cosmic ray background by simulation, from this figure, we can infer the occasional noise rate is$ 4.3\times10^{6} $ Hz for$ nhit\geq1 $ ,$ 1.6\times10^{6} $ Hz for$ nhit\geq2 $ and$ 8.4\times10^{5} $ Hz for$ nhit\geq3 $ by fitting the distribution of number of hits with a power law.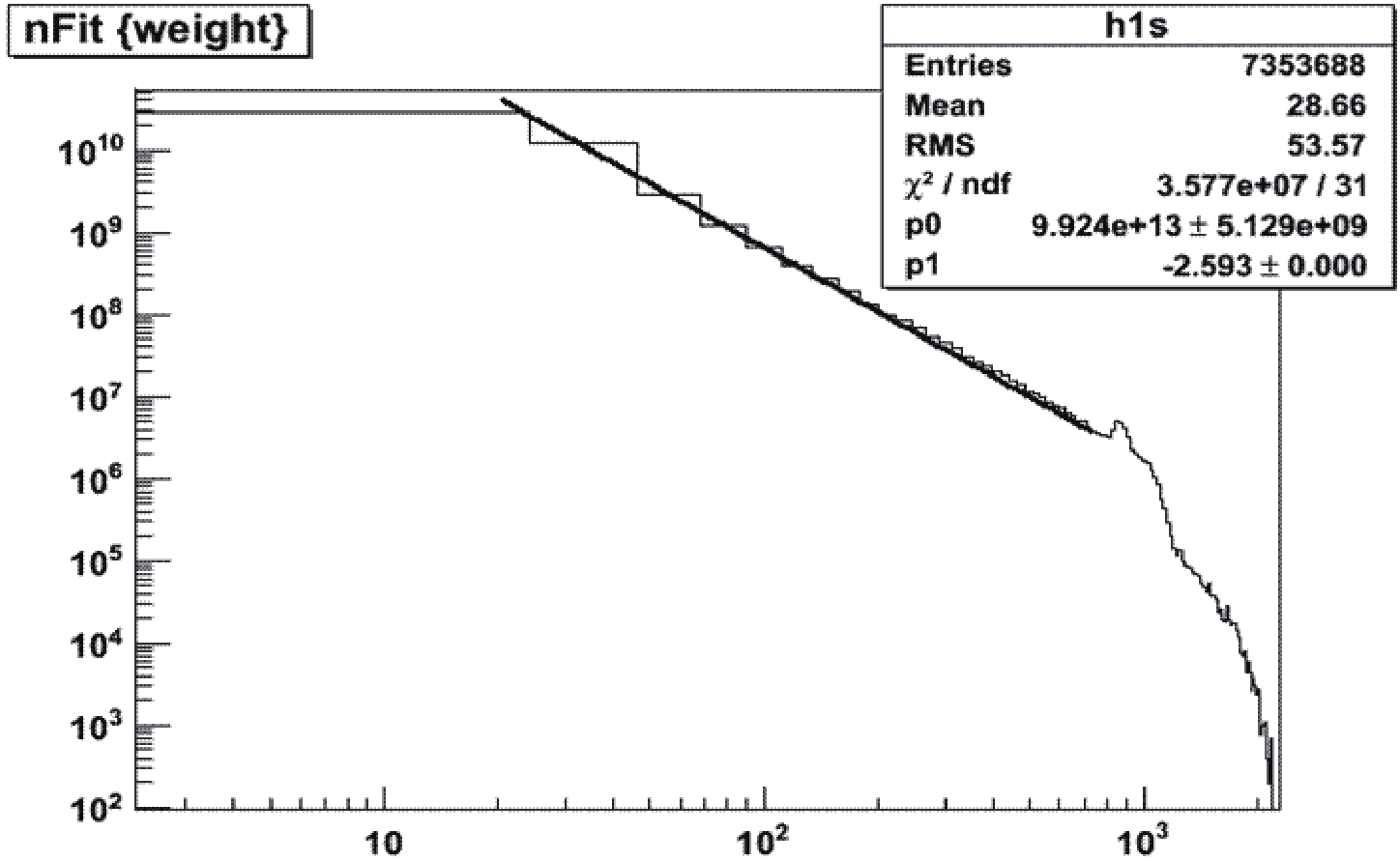
Figure 13. (color online) Distribution of number of hit. Solid line is a power law fit to the number of hits to infer low multiplicity due to threshold effect.
For random coincidence noise, firstly, we take the pipe line with a time duration of 200 seconds, to save all the data when a GRB alert comes and after the alert. Secondly, we localize the shower, considering events with a distance from the center of
$ < $ 50 m, then the total Number of noise hits is reduced by a factor of 10, i.e. from 30 hits ($ 10^{8} $ Hz$ \times 300\times10^{-9} $ s = 30 hits) reduced to 3 hits in trigger time window of 300 ns. The random coincidence noise rate is about 80 MHz for nhits$ \geq3 $ , about 300 times higher than shower rate (with direction information). Secondly, we shrink the trigger time window, namely perform hit time transformation: GRB direction cosines are (l,m,n), for each hit(x,y,z,t), we can define$ tr = t - (lx+my+nz)/C $ , where C is light velocity in vacuum, Automatically removed those far from GRB direction and shower direction information is obtained without direction reconstruction. After this transformation, the coincidence time window can be reduced from 300 to 10 ns, in which the average number of noise hits is reduced from 3 to 0.1, good for low multiplicity trigger. For low multiplicity trigger, the running time window was applied on each hit, then the random coincidence rate is about$ 0.5 $ MHz (nhits$ \geq3 $ for mean noise hit of 0.1), lowering down a factor of 100. For different low multiplicities, the random coincidence noise rate and the Background rate are presented in the following Table 2.occasional noise rate/Hz random coincidence noise rate/Hz background rate/Hz nhit $\geq$ 1

$4.3\times10^{6}$ 

$10^{8}$ 

$1.04\times10^{8}$ 

nhit $\geq$ 2

$1.6\times10^{6}$ 

$9.5\times10^{6}$ 

$1.11\times10^{7}$ 

nhit $\geq$ 3

$8.4\times10^{5}$ 

$4.6\times10^{5}$ 

$1.30\times10^{6}$ 

Table 2. Background rate at different low multiplicity.
-
For low multiplicity, the sensitivity of WCDA to GRBs depends on a number of factors, including the GRB emission time scale, emission spectrum and redshift, as well as on the signal and background estimation of the experiment. To calculate WCDA's sensitivity, we simulate gamma ray spectrum according to the power-law
$ {\rm d}N/{\rm d}E \propto E^{-2} $ with an arbitrary reference flux normalization. This injection spectrum can be weighted for any other spectral shapes. In which we take into account attenuation of VHE gamma rays due to interaction with extragalactic background light, the Franceschini et al. [33] model is used.Given a signal rate
$ S(\theta) $ , background rate B then the significance of a given observation is :$ \begin{aligned}[b] Sig = & S(\theta)T_{90}/\sqrt{BT_{90}} \\ = & \sqrt{T_{90}/B}\int {\rm d}E \frac{{\rm d}N}{{\rm d}E}A^{\rm low\ multiplicity}_{\rm eff}(E,\theta) .\end{aligned} $

(4) We have used various spectra of the type
$ {\rm d}N/{\rm d}E \varpropto E^{-\gamma} $ with sharp high-energy cutoffs to determine the sensitivity of the low multiplicity technique to GRBs. The sensitivity is defined as the flux detectable at$ 5\sigma $ significance. A range of spectral indices gamma between -3 and -1 and a range of cutoffs between 10 GeV and 10 TeV were tested, and effects of the EBL are also considered.Figure 14 shows WCDA's sensitivity curve of different GRB emission spectra on the expected sensitivity of WCDA using the low multiplicity (nhit
$ \geq3 $ ) calculated with equation compared to GRBs that have been detected by Fermi LAT. Assuming that the burst occurs at a zenith angle of$ 0^{\rm o} $ and lasts 1 second at a distance of redshift of$ z = 0.5 $ [33]. Data for GRBs 090510 and 090902b, extracted from [29] and [30] are shown for comparison. We conclude that the most promising cases for detection with high significance are GRBs such as GRB 090510 and GRB 090902b if the high-energy cutoff is above 30 GeV. Fermi LAT observations of these two GRBs were made up to 30 GeV without any indication of a cutoff. If high-energy emission from GRBs extends beyond 30 GeV, then WCDA will become even more significant due to limited physical size of Fermi LAT.
Figure 14. (color online) Sensitivity using the low multiplicity as a function of spectral index. The
$5\sigma$ discovery potential is shown as a function of spectral index for various values of a sharp high-energy spectral cutoff. The duration of the burst is fixed to 1s and the zenith angle is fixed to 0°. Data from 2 GRBs are corrected for duration and inserted for comparison [29, 30]. -
A new method was developed to detect GRBs at energy as low as 10 GeV and reserve source direction information using EAS array, like LHAASO-WCDA. From above analysis, we can conclude, WCDA, will have the capability of detecting GRBs at high energies. The simulations presented in this proceeding show that WCDA will be able to detect GRBs with characteristics similar to those of some of the brightest GRBs seen by Fermi LAT. As opposed to Fermi LAT, with a fixed physical size, the effective of the method of the low multiplicity increases with energy. Thus this method will expand upon the energy sensitivity of current detectors. Also WCDA is a wide field of view detector with near
$ 100$ % duty cycle, it will be able to make GRB observation in the prompt phase. WCDA, in union with satellite or other ground based detectors, will be able to measure the high-energy GRB components including a possible high-energy cutoff. Important astrophysical information will be deduced from spectral cutoffs such as the Lorentz boost factor of GRB jets, the effects of the EBL and the maximum energy to which GRBs accelerate particles.For low multiplicity technique, how to pick up the true events and analysis the data? This is still the question to be solved. In this proceeding, we present the result with GRBs alert information, at further step, we also can do without GRBs alert and work alone taking advantage of large field of view of WCDA, then CPU power maybe is a huge challenge.
-
We review the prospects for studies of active galactic nuclei (AGN) using the future Large High Altitude Air Shower Observatory (LHAASO). This review focuses on blazars, which constitute the vast majority of AGN detected at gamma-ray energies. We argue that LHAASO will enable substantial progress on searching for clear evidence of blazar releasing very high energy cosmic rays through its excellent flux sensitivity. We give two proposals: (a) searching for hard spectra
$ >10 $ TeV from the extreme blazars (e.g., 1ES 0229+200) and nearby blazars (e.g., Mrk 421); (b) searching for TeV photons from distant blazars with redshift$ z\sim1 $ . The surveys of LHAASO enable measurement of cosmic TeV background and construction of luminosity function of TeV blazars. These results will help us to understand the origins of Ultra-high energy cosmic rays (UHECRs). At last, we discuss the potential of LHAASO as a tool for probing new physics like Lorentz Invariance Violation (LIV) with the observatiosn of blazars. The traditional projects such as relativistic jet physics (including high-energy radiation mechanisms and acceleration of particles) and the extragalactic background light (EBL) determination are not discussed in this paper. However it should be pointed out that all these projects are interrelated. -
Active galactic nuclei (AGN) are the extragalactic sources of enhanced activity that are powered by the release of gravitational energy from the supermassive central black hole. Energy linked to the black hole spin [34] or rotating accretion disks [35] may be instrumental for forming prominent jets which transport the material with relativistic speed from the innermost region of the AGN to kpc-, sometimes even Mpc-scale distances. Such jets are usually identified through the detection of bright non-thermal radio emission as observed in radio-loud AGN. Only a small percentage (
$ \sim 10 $ %) of all AGN are known to be radio-loud. In the vicinity of the central region of an AGN, matter is accreted from a disk onto the black hole; line-emitting clouds (the so-called broad-line region, BLR, and narrow line region, NLR) form at pc to kpc distances from the central engine; and dusty material surrounding the accretion disk may imprint thermal signatures in the infrared part of the AGN spectrum [36].The radiation from the material which moves relativistically with speed
$ \beta_{\Gamma} c $ (with$ \Gamma = 1/\sqrt{1 - \beta_{\Gamma}^2} $ being the bulk Lorentz factor) along the jet axis is beamed into an angle$ \sim 1/\Gamma $ around the direction of propagation. Because of this beaming effect, mostly those AGN with jets pointing towards us (i.e., blazars) are favorably detected as gamma-ray sources. However, some mis-aligned AGN (i.e., radio galaxies) can be also detected, if they are sufficiently nearby. Blazars therefore offer an excellent opportunity to study jet physics in massive black hole systems and their evolution over cosmic time through population studies.Blazar emission is dominated by non-thermal radiation over all frequencies ranging from radio to TeV gamma-rays. Its typical multi-wavelength spectral energy distribution (SED) is characterized by two distinct humps (see Fig. 15). It is accepted that the first hump in the SED is the synchrotron emission radiated by relativistic electrons in the jet. The origin of the emission in the gamma-ray hump is still under debate.

Figure 15. (color online) One SED of Mrk 421, [from 37].
Different classes of blazars are defined according to various properties. BL Lac objects are typically defined if the equivalent width of the strongest optical emission line is
$ <5 $ Å. By contrast, flat spectrum radio quasars (FSRQs) have strong optical emission lines indicating the presences of dense BLR material and strong illuminating accretion-disk radiation. Blazars also can be divided into low, intermediate, and high synchrotron-peaked sources (LSPs, ISPs, and HSPs, respectively, defined by whether the peak frequency of the synchrotron component of the SED$ \nu^{\rm pk}_{\rm syn}<10^{14} $ Hz,$ 10^{14}<\nu^{\rm pk}_{\rm syn}\ (\rm Hz)<10^{15} $ , or$ \nu^{\rm pk}_{\rm syn}>10^{15} $ Hz) [38]. Most FSRQs are LSP blazars, whereas BL Lac objects include LSP, ISP, and HSP sources. Based on blazar SED and the emission variation, the relativistic jet physics (e.g., emission mechanisms and acceleration processes) can be investigated [e.g., 39], if the gamma-ray emissions are certainly produced in the jet.In this article, we review the prospects of LHAASO to understand the AGN high-energy phenomenon and its related physics including the origin of ultrahigh energy cosmic rays (UHECRs).
-
The origin of gamma-ray (GeV - TeV) emission from blazar is not resolved. Three kinds of models have been proposed to resolve this problem. In leptonic models, the gamma-ray emission is supposed to be inverse Compton (IC) emission from relativistic electrons in the jet that up-scatter either low-energy synchrotron photons emitted by the same population of electrons (synchrotron-self-Compton model, SSC), or photons originating from outside the jet (external inverse Compton, EIC). In hadronic models, the gamma-ray emission is attributed to synchrotron radiation of high-energy protons in the jet, or synchrotron radiation of secondary particles created in proton-photon interaction. In the third model, the gamma-ray emission is the secondary cascade gamma-ray photons produced in the propagation of UHECRs emitted by blazar [e.g., 40-42]. Since the gamma-ray photons in leptonic and hadronic models are produced in the jet, we classify the two kinds of models as jet model. Moreover, we refer to the model that produces gamma-ray photons in the interactions between the highest-energy cosmic rays and background photons in the Universe as cosmogenic model. The key issue of our attention is to disentangle the jet model and cosmogenic model from observations.
The observations of HESS found the non-variable and extremely hard TeV spectra of several blazars, e.g., 1ES 0229+200 and 1ES 1101-232 [43, 44]. The classical leptonic jet model is difficult to explain such hard TeV spectra (Modified leptonic jet models succeed in explaining the hard TeV spectra [e.g., 45, 46]). The hadronic jet models may account for the hard TeV spectra [e.g., 47]. Alternatively, [48] have proposed that the TeV spectrum of 1ES 0229+200 could be from the secondary gamma-ray produced in the propagation of UHECRs in the Universe. With the current TeV observation up to
$ \sim10\ $ TeV, we cannot disentangle the leptonic, hadronic and cosmogenic models. From [48], one can estimate that the energy flux of the UHECR-induced cascade gamma-rays calculated with a low EBL at 30 TeV is$ \simeq2\times10^{-13} $ $ \ {\rm{ erg}}\ $ cm−2 s−1. On the other hand, the one-year differential sensitivity of LHAASO at 30 TeV is also$ \simeq2\times10^{-13}\ \ {\rm{ erg}}\ $ cm−2 s−1. Therefore, LHAASO is capable of detecting the UHECR-induced cascade gamma-rays. By obtaining the good spectra of 1ES 0229+200 above 10 TeV, we could disentangle the jet models and cosmogenic models.Another interesting object is Mrk 421. The current IACTs observations show that the TeV emissions from Mrk 421 are strongly variable. This suggest that the steady UHECR-induced cascade gamma-rays cannot make a significant contribution to the observed TeV emissions. In Fig. 16, we show the spectrum of UHECR-induced cascade gamma-rays constrained by the current TeV data. In this case, LHAASO can detect the cascade gamma-rays in one year. LHAASO will detect 100 TeV photons from Mrk 421 if it really emits
$ > $ 1 EeV protons. The observations of LHAASO for these sources could provide strong evidence for UHECR origin.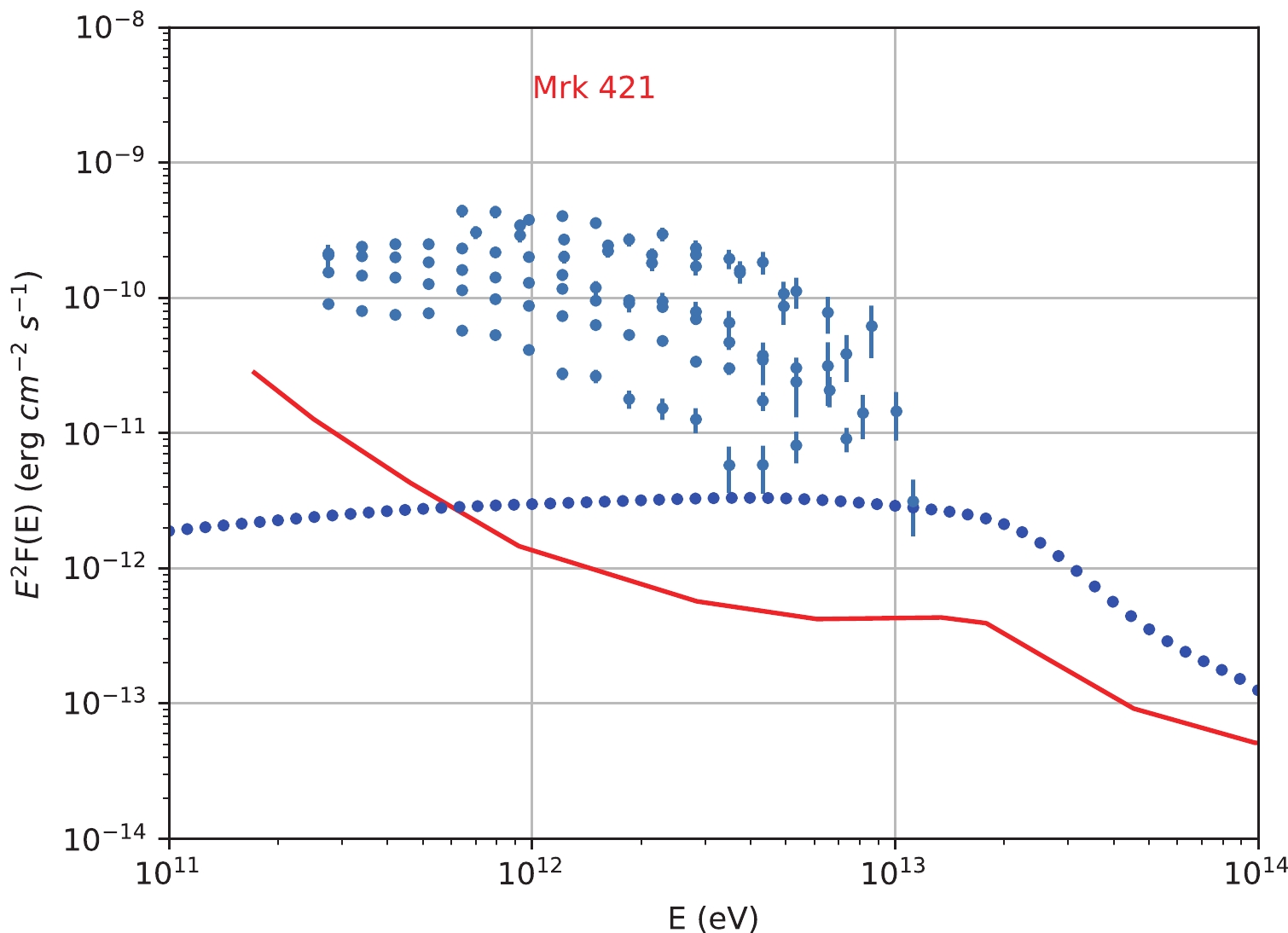
Figure 16. (color online) A spectrum of UHECR-induced cascade gamma-rays for Mrk 421 (dotted line) and the historical TeV data of Mrk 421 (points). The data are obtained through the SED Builder of ASDC (http://tools.asdc.asi.it). The cascade gamma-rays are calculated by using the TRANSPORTCR code [49]. The injection spectrum of protons is assumed to be a power-law with an exponential cutoff. We take the index of 2.6 and the cutoff energy of
$10^{19}$ eV. The EBL model of [33] is used in the calculation. The solid line is the one-year differential sensitivity of LHAASO.We also propose another strategy to find the clear evidence of blazar emitting UHECRs. Compared to the jet models, VHE photons produced by cosmogenic models suffer less absorption by extragalactic background light (EBL) because of the long energy-loss distance of UHECRs interactions with background lights. Therefore the VHE photons from the jet in high redshift blazars will suffer strong absorption by EBL. If LHAASO or CTA detect
$ >1\ $ TeV photons from very distant blazars, the observed gamma rays are the secondary photons produced in interactions of high-energy protons originating from the blazar jet and propagating over cosmological distances almost rectilinearly [e.g., 50-52]. In Fig. 17, we show the case for the distant TeV blazar PKS 1424+240. One can see that the cosmogenic model predicts harder spectrum above one TeV than the jet model.In the two topics mentioned above we do not seek to explain the observed cosmic ray spectrum above
$ 10^{18}\ $ eV (See the studies of [53] and [54] for the constraints on the origin of the observed$ >10\ $ EeV cosmic rays with the non-observation of 10 PeV neutrinos by IceCube). We focus on finding the evidence of UHECRs originating from the blazar jet through the observations of VHE gamma-rays by LHAASO. -
The Fermi gamma-ray space telescope has successfully measured the cosmic gamma-ray background (CGB) spectrum at 0.1-820 GeV [55]. It also provides an opportunity to explore and decipher the high-energy universe through a multi-messenger approach including the information from cosmic rays (CRs), gamma rays, and neutrinos [e.g., 56, 57]. However, the measurement of the cosmic TeV gamma-ray background radiation is still rare, although its upper and lower limits are given based on the current understandings of TeV sources (see Fig. 18).
Based on its good sensitivity and wide field of view, LHAASO will perform an unbiased sky survey of the Northern sky from TeV to 100 TeV. The high background rejection capability in the 10-00 TeV range will allow LHAASO to measure the cosmic TeV gamma-ray background radiation.
The GeV CGB are mainly contributed by the emission from blazars. Therefore, one can naturally speculate that blazars also contribute a substantial fraction of the TeV CGB. Under LHAASO extragalactic surveys, many TeV AGNs will be detected to build large and well-defined TeV AGN sample. We can construct the luminosity function of AGN at TeV band to study AGN evolution over cosmic time, and then to investigate the origin of the TeV CGB.
It is noted that the cosmogenic model mentioned in Sec. IV.B predicts a flat spectrum from TeV to a few tens TeV. The signature of the flat spectrum in the cosmic TeV gamma-ray background radiation will be also a key test on the UHECR-induced cascade emissions [e.g., 56, 57].
-
Astrophysical observations with gamma-ray experiments have proven to be a powerful tool of searching for physics beyond the Standard Model. For example, observations at gamma-ray energies can be used to search for the traces of axion-like particles (ALPs), in which blazars are abundantly observed sources. The photon-ALP oscillations may lead to two changes in the energy spectra: a) the gamma-ray source flux can be attenuated due to pair production with low energy background photons. ALPs produced in the vicinity of the source would mitigate this attenuation, and if they reconvert to gamma rays, leading to a significant boost of the observed photon flux, and b) the oscillations of the flux should be imprinted in the spectra around
$ E_{\rm crit} $ ③ and$ E_{\rm max} $ ④ [e.g., 59]. In the analysis of$ Fermi $ -LAT and IACT spectra of blazars, no ALP-induced spectral signature, which is a spectral hardening at high optical depths, was found [60, 61]. The LHAASO extragalactic survey with its good sensitivity could be used to search for a spectral hardening correlated with the photon-ALP oscillations.Lorentz Invariance (LI) is a basic component of Einstein's Special Relativity. It is strictly valid in Quantum Mechanics and has been verified in various accelerator experiments at the electro-weak scale. On the other hand, Lorentz Invariance Violation (LIV) has also been largely predicted in the framework of various classes of Quantum Gravity (QG) models. Tests of LIV with high-energy photons from distant sources have been proposed [e.g., 62, 63]. It is possible to utilize LHAASO for the detection of LIV through anomalies in the multi-TeV gamma-ray spectra of blazars [e.g, 64].
In Fig. 19, we show the predicted TeV spectrum of 1ES 0229+200 under the condition of LIV. One can see that this spectrum becomes harder at 10 TeV, and LHAASO cannot detect the concave shape around 10 TeV. But, it can detect the extremely hard spectrum (the photon index much less than 2) above 20 TeV, which is the evidence of LIV. The observed variability can also be used to probe LIV. Taking advantage of the wide energy-coverage of LHAASO, we can construct the energy-dependent light curves of blazars to search for a possible time lag between low- and high-energy photons, constraining an energy-dependent LIV [e.g., 66], i.e., an energy-dependent speed of light.

Figure 19. (color online) TeV spectrum of 1ES 0229+200 with the consideration of LIV (dotted line). The points are the HESS data of 1ES 0229+220. The EBL model of [65] is used in the calculation. The dashed line is the one-year differential sensitivity of LHAASO.
-
In this paper, we have proposed several projects for LHAASO. This is surely incomplete in the field of AGN research. The topics on the relativistic jets are not included. Although the EBL and intergalactic magnetic field (IGMF) are not specifically discussed, all the studies mentioned above are related to EBL and IGMF. All these questions are interrelated. To improve upon these constraints, we need a better understanding of the sources and emission mechanisms, including the relativistic jet physics. Actually the key issue is to determine the origin of the observed TeV photons. To better understand these questions, we need an overall emission model, e.g., a self-consistent jet+cosmogenic-propagation emission model [e.g., 50]. Combining the future measurement for the cosmic TeV background radiation and the observations on UHECRs and cosmic neutrinos, it is possible to improve the constraints on their origins. We believe that the observations of LHAASO will improve our understanding of the high-energy universe.
-
The extragalactic background light (EBL) contains important information about stellar and galaxy evolution. It leaves imprint on the very high energy γ-ray spectra from sources at cosmological distances due to the process of pair production. We have proposed a method to measure the EBL intensities by extracting the collective attenuation effects in a number of γ-ray sources at different redshifts. This method employs a Markov Chain Monte Carlo fitting algorithm to derive the EBL intensities and the intrinsic spectral parameters of γ-ray sources simultaneously, without prior assumption of the EBL shape. With larger sample of extragalactic sources, primarily blazars, and better spectral measurements by LHAASO, we expect to improve the measurement of EBL substantially.
-
The extragalactic background light (EBL) is the diffuse radiation from ultraviolet to far infrared wavelengths, spread isotropically in the universe (for a review of EBL, see [67, 68]). The EBL originates from the radiative energy releases of all the stars, other extragalactic sources and diffuse emissions since the epoch of recombination. Therefore its intensity and spectral shape hold crucial information about the formation and evolution of stellar objects and galaxies throughout the cosmic history. The EBL is one of the fundamental quantities in cosmology.
Direct measurement of EBL is, however, very difficult due to the contamination of the foreground emission from the solar system zodiacal light and the Galactic stellar and interstellar emissions [69]. Technically, it also requires the absolute calibration of the instruments, and the understanding all measurement uncertainties. Given the difficulties, direct measurements provide just lower and upper limits of EBL intensity. A strict lower limit on the EBL intensity is provided by the integrated light from resolved galaxies, e.g. in optical by the Hubble Space Telescope [70] and in infrared by the Spitzer telescope [71]. The upper limit can be derived from the uncertainties of the absolute measurement of EBL [67].
Another indirect, but effective way to study the EBL is through the observation of very high energy (VHE) γ-rays. The VHE γ-rays from extragalactic sources are attenuated by the process of electron/positron pair production,
$ \gamma_{\rm VHE}+ \gamma_{\rm EBL}\to e^+e^- $ , when propagating to the Earth [72]. With the rapid development of ground based γ-ray imagining atmospheric Cherenkov telescopes (IACT), quite a few VHE γ-ray sources from cosmological distances have been detected, most of which are blazars, a subgroup of active galactic nuclei (AGN), with relativistic jet pointing towards the observer. With reasonable assumption of the intrinsic blazar spectra we can set an upper limit of the EBL intensity by comparing the observed spectra with the intrinsic spectra [73]. The observations of blazars H 2356-309 and 1ES 1101-232 at redshifts$ z = 0.165 $ and$ z = 0.186 $ , respectively by HESS has set a strong upper limit of EBL, close to the lower limit set by galaxy counts, at the near infrared wavelength [74]. The MAGIC observation of 3C 279 at$ z = 0.536 $ set upper limit at the optical band [75]. In [76] Mazin and Raue gave a comprehensive study of EBL based on eleven blazars over a redshift range from$ 0.03 - 0.18 $ . They explored a large number of hypothetical EBL scenarios and set robust constraints on EBL over a wide wave-length range. With the Fermi observation of blazar spectra at GeV to$ \sim 100 $ GeV more stringent constraints on EBL are shown recently (e.g., [77-81]. These studies seem to indicate that the Universe is more transparent than we had expected.The power of this indirect method to study EBL is limited due to the fact that the intrinsic spectrum of each blazar is unknown. Therefore it is hard to disentangle the absorption effect by EBL from the intrinsic emission nature for a specific observation. The usual practice in the literature is to reconstruct the blazar intrinsic spectrum from the observation by first assuming an EBL model. The EBL model is rejected if it results in an unphysical intrinsic spectrum, for example, the reconstructed intrinsic spectrum follows a power law with an extremely hard spectral slope or even shows an exponential rise at the high energy end. Recently with large sample of γ-ray blazars, the EBL intensities were derived through a likelihood fit with given spectral template of the EBL [82, 83].
With the fast increasing number of γ-ray sources and better measurements of their spectra, we propose to measure the EBL intensities through extracting the collective absorption effects in a number of sources at different redshifts, using a global fitting method [84]. The method employs the Markov Chain Monte Carlo (MCMC) global fitting algorithm to fit the intrinsic source spectra and EBL simultaneously. Different from the previous studies in the literature, we make no assumption of the EBL spectral shape in the fitting. Instead the EBL intensities are approached as free parameters in a series of discrete energy bins, which are allowed to vary during the fitting. The application to a few sources by the current IACTs illustrate that this method can give effective measurement of both the intensities and shape of the EBL [84]. The derived results are consistent with the upper limits obtained with γ-ray observations as well as the theoretical modeling from galaxy evolution.
-
The observed VHE γ-ray spectrum after absorption by the EBL is commonly expressed as
$ F_{\rm{ obs}}(E) = {\rm e}^{-\tau(E,z)} F_{\rm int}(E)\ , $

(5) where
$ F_{\rm int}(E) $ is the intrinsic spectrum of the source at redshift z. The strength of the attenuation by EBL is described by the optical depth$ \tau(E,z) $ as a function of energy E and the source redshift z. The optical depth τ is expressed as [85]$ \tau(E,z) = \int_0^z {\rm d}l(z')\int_{-1}^{+1} {\rm d}\mu \frac{1-\mu}{2} \cdot\int_{\epsilon'_{\rm thr}}^\infty {\rm d}\epsilon' n'(\epsilon',z') \sigma(E',\epsilon',\mu) \ , $

(6) where the variables with prime are the quantities at redshift
$ z' $ ,$ {\rm d}l = c{\rm d}t = \dfrac{c}{H_0}\dfrac{{\rm d}z'}{(1+z') \sqrt{\Omega_M(1+z')^3+\Omega_{\Lambda}}} $ is tial path traveled by the VHE photon,$ \mu = \cos\theta $ with θ the angle between the momenta of VHE and EBL photons,$ n'(\epsilon',z') = n(\epsilon'/(1+z'),z = 0)(1+z')^3 $ is the EBL number density at redshift$ z' $ , and σ is the pair production cross section. Note that the VHE measurements mainly apply for low-redshift ($ z\lesssim 0.2 $ ) sources, and we neglect the late production of EBL photons and just consider its cosmological expansion and redshift effect.$ \epsilon'_{\rm thr} $ is the threshold energy for γ-ray energy$ E' = E(1+z') $ with an angle$ \cos\theta = \mu $ with the EBL photon. The cross section is peaked at a wavelength$ \lambda/\mu {\rm m} \sim 1.24 E/{\rm TeV} $ [86]. Therefore the observation of VHE γ-ray spectra can probe EBL at the wavelength from optical to far infrared, while it is not sensitive to UV band by the IACT data. The cosmological parameters used in this work are$ \Omega_M = 0.274 $ ,$ \Omega_{\Lambda} = 1-\Omega_M $ ,$ H_0 = 70.5 $ km s−1 Mpc−1 [87]. -
We assume the intrinsic spectrum of blazar,
$ F_{\rm int} $ , is of log-parabola shape ($ F\propto E^{-\alpha-\beta\log E} $ ). The blazar spectrum is commonly modeled by the synchrotron-self-Compton (SSC) scenario, which shows a concave γ-ray spectrum in general. If the measured energy range is not very wide, the simple power-law can actually give a quite good description to the observations. However, at least for some sources, deviation from single power-law distribution of the spectrum, even corrected for the absorption effect, has been observed [88]. Therefore we adopt the log-parabola form of the intrinsic spectrum. It has been tested that the log-parabola assumption of the intrinsic spectrum will give robust results of the EBL [84].No prior assumption about the EBL shape is adopted in this study. We divide the wavelength range of EBL from
$ 0.1 $ to$ 100 $ μm, which is relevant for γ-rays between 100 GeV and 100 TeV, into$ 10 $ bins logarithmically. Within each bin the intensity$ \nu I_{\nu} $ is assumed to be a constant$ \xi_i $ . Then we can fit the 10$ \xi_i $ s, as well as the intrinsic source parameters of each source (nuisance parameters), from a set of observed γ-ray spectra$ F_{\rm{ obs}}(E) $ . -
We explore the potential of LHAASO to measure the EBL intensities with this method. We first generate simulated observations of the blazar spectra with LHAASO-WCDA [89]. In [89] we studied the detectability of the blazars with LHAASO-WCDA, based on the Fermi AGN sample. The spectra of the Fermi AGNs, with known redshift measurements and within the field of view of LHAASO, are directly extrapolated to TeV energies based on the Fermi measurements. Then we apply the EBL absorption to the extrapolated spectra to derive the detected spectra of the sources. Comparing to the sensitivity of WCDA, we find that there will be about
$ 30-40 $ Fermi blazars, mostly BL Lacs, could be detectable by LHAASO-WCDA in a few years' survey. The actual number of sources may be higher, due to the unexpected flaring activities of the blazars and the sources without redshift measurements. However, the sources which do not have redshift measurements will not be able to be used to constrain the EBL.Taking the EBL model by Dominguez et al. (2011; [90]) as an example, we find that 45 sources with redshifts in the third LAT AGN catalog (3LAC; [91]) will be detectable by LHAASO-WCDA for one year sky survey. We simulate the spectral measurements of these sources following [89]. Fitting to these simulated spectra enables us to have a measurement of the EBL intensities, as shown in Fig. 20. We can see that the EBL intensities above
$ \sim1\;$ μm can be well constrained with the expected LHAASO data. At shorter wavelengths the constraints become weaker, due to the relatively high energy threshold of LHAASO. The fitting results reproduce the input EBL model well, illustrating the robustness of this method. Compared with the results obtained with the present (sub-)sample of blazars [84], we find that LHAASO will have significant potential to improve the measurements of the EBL intensities.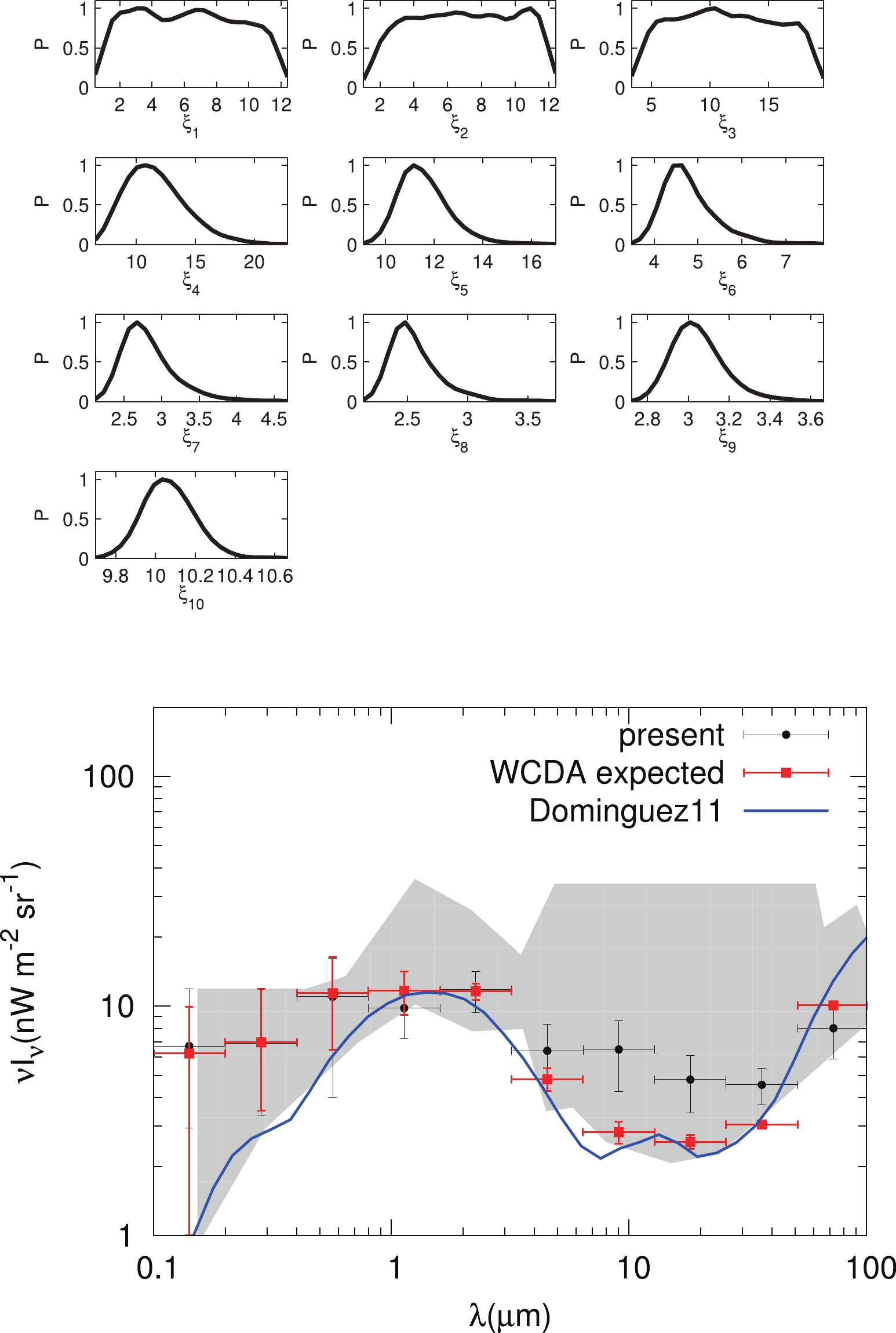
Figure 20. (color online) Upper: 1-dimensional marginalized probability distributions of the fitting parameters
$\xi_i$ . Lower: Fitting results of the EBL intensities with simulated LHAASO spectra of 45 blazars, compared with the input EBL model [90]. We also show the constraints with the current blazar data as derived in [84] for comparison. -
We propose to measure the EBL with a global fitting methods, based on the VHE γ-ray observations of extragalactic blazars by LHAASO. This method does not assume the spectral shape of EBL, but parameterizes the EBL intensities in different wavelength bins as a constant parameter. The intrinsic spectra of the sources and the EBL intensities are fitted simultaneously using an MCMC algorithm. With simulated observations of of blazars by LHAASO, we show that the EBL intensities can be well measured. A large sample of sources with good spectral measurements, which is the object of LHAASO, is very essential for improving our understanding of the EBL.
-
Detection of high-energy gamma-ray emission from star-forming and starburst galaxies by Fermi suggest that these galaxies are huge reservoirs of cosmic rays and these cosmic rays convert a significant fraction of their energy into gamma-rays by colliding with the interstellar medium. We propose that LHAASO observes nearby star-forming and starburst galaxies within about 20 Mpc. With its high sensitivity at energies above 10 TeV, LHAASO will be able to probe the acceleration and propagation of 0.1-1 PeV cosmic rays in these galaxies. As the processes producing VHE gamma-rays are accompanied by high energy neutrinos, the TeV-PeV gamma-ray flux of these galaxies can be used to study their contribution to the cosmic TeV-PeV neutrino background recently detected by IceCube.
-
It is generally believed that Galactic cosmic rays (CR) are accelerated by supernova remnant (SNRs) shocks. CR protons interact with the interstellar gas and produce neutral pions (schematically written as
$p+p\rightarrow \pi^0+ $ $ {\rm other \; products}$ ), which in turn decay into gamma-rays ($ \pi^0\rightarrow \gamma+\gamma $ ). The high SN rate in star-forming and starburst galaxies implies high CR emissivities, so they are predicted to be bright gamma-ray sources. Ackermann et al. [92] examined a sample of 69 dwarf, spiral, and luminous and ultraluminous infrared galaxies using 3 years of data collected by the Large Area Telescope (LAT) on the Fermi Gamma-ray Space Telescope (Fermi). They find further evidence for quasi-linear scaling relations between gamma-ray luminosity and and total infrared luminosity which apply both to quiescent galaxies of the Local Group and low-redshift starburst galaxies. Nearby star-forming and starburst galaxies, such as M82 and NGC 253 are also detected at very high-energy (VHE) gamma-rays by e.g. HESS, VERITAS [93, 94]. But so far only quite a few galaxies have been detected. Moreover, no starburst galaxies have been detected above 10 TeV. With LHAASO, which has much higher sensitivity at energies above$ 10 $ TeV, one may expect that much more star-forming and starburst galaxies can be detected above 10 TeV and even above 100 TeV, as long as the galaxies are within the distance where VHE photons have not been absorbed by extragalactic background light (EBL) (typically within about 10-20 Mpc). At such high energy photons can only be produced by PeV cosmic rays, so LHAASO can probe the acceleration of PeV cosmic rays in these galaxies.By extrapolating the TeV flux of M82 to the energy at
$ 10 $ TeV, we find that the predicted flux at is$ 2\times10^{-13}{\rm TeV cm^{-2} s^{-1}(E/10 TeV)^{-0.2}} $ . NGC253 has a similar predicted flux above 10 TeV. These fluxes are above the sensitivity of LHAASO, so we expected that M82 and NGC 253 may be detected by LHAASO above 10 TeV. Since these two starburst galaxies are at distances of$ 2-3 {\rm Mpc} $ , we expected that they may be detected even above 100 TeV by LHAASO. This will be useful to study whether these starburst galaxies host extragalactic PeVatrons.Recently, Tang et al. [95] reported the detection of gamma-ray emission above 200 MeV from a luminous infrared galaxy NGC 2146, which is at a distance of 15.2 Mpc. GeV gamma-rays have been also detected from some starburst galaxies hosting an obscured AGN, such as NGC 1068 and NGC 4945 [92], as well as from an ultra-luminous infrared galaxy, Arp 220 [96]. Using NGC 2146 as an example, we here estimate the detectability of these galaxies by LHAASO. Using the GeV flux and the spectrum of NGC 2146, we estimate the VHE flux assuming a simple power-law extrapolation. As can be seen from Fig. 21, the predicted energy flux is
$E^2 {\rm d}N/{\rm d}E\simeq $ $ 10^{-13}\;{\rm TeV cm^{-2} s^{-1} }(E/1\;{\rm TeV})^{-0.1}$ at TeV energies, which is within the reach of LHAASO sensitivity. Note that at a distance of 15.2 Mpc, the absorption by EBL is not severe even for 10-100 TeV photons. Therefore, we propose that LHAASO perform systematic observations of nearby star-forming and starburst galaxies within 10-20 Mpc. The main candidates include M 82, NGC 253, NGC 2146, NGC1068, which are within the field of view of LHAASO. -
The gamma-ray luminosity of starbursts depends not only on the CR intensity, but also on the efficiency of converting CR proton energy into pionic gamma-rays. This efficiency in turn depends on the ratio of the timescale of pion production to the escape time of protons. Protons escape by advection with galactic winds or by diffusion. The gamma-ray flux at 100 TeV will thus not only give us information about the acceleration of PeV cosmic rays, but also tell us physics about the transport of these cosmic rays in galaxies.
Proton-proton collisions in starbursts not only produce neutral pions, but also produce charged pions, which then decay and produce neutrinos. Loeb & Waxman [97] argued that supernova remnants in starburst galaxies accelerate CR protons and produce high-energy neutrinos. Chang et al. [98] calculated the accumulated neutrino flux by using the infrared luminosity function of star-forming galaxies recently obtained by the Herschel PEP/HerMES survey. Recently, the IceCube Collaboration reported 37 events ranging from 60 TeV to 3 PeV within three years of operation, corresponding to a
$ 5.7\sigma $ excess over the background atmospheric neutrinos and muons [99]. One attractive scenario for this excess is that they are produced by cosmic rays in starburst galaxies [97]. But whether neutrinos in starburst galaxies can extend to sub-PeV/PeV energies is uncertain, given that normal supernova remnants are usually believed to accelerate protons only to$ {\rm PeV} $ energy. It was suggested that hypernova remnants in starburst galaxies, by virtue of their fast ejecta, are able to accelerate protons to EeV energy [100] and produce sub-PeV/PeV neutrinos [101]. Future observations of nearby star-forming and starburst galaxies at 100 TeV will enable us to study the neutrino flux produced in such galaxies. One can then further study the total contribution to the cosmic neutrino background by all star-forming and starburst galaxies in the universe and hence pin down the starburst galaxy origin for IceCube neutrinos.
Chapter 3 Extra-galactic gamma-ray sources
- Received Date: 2021-12-02
- Available Online: 2022-03-15
Abstract: Extra-galactic gamma-ray sources, such as gamma-ray bursts, active galactic nuclei, starburst galaxies, are interesting and important targets for LHAASO observations. In this chapter, the prospects of detecting these sources with LHAASO and their physical implications are studied. The upgrade plan for the Water Cherenkov Detector Array (WCDA), which aims to enhance the detectability of relatively lower energy photons, is also presented. In addition, a study on constraining the extragalactic background light with LHAASO observation of blazars is presented.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF












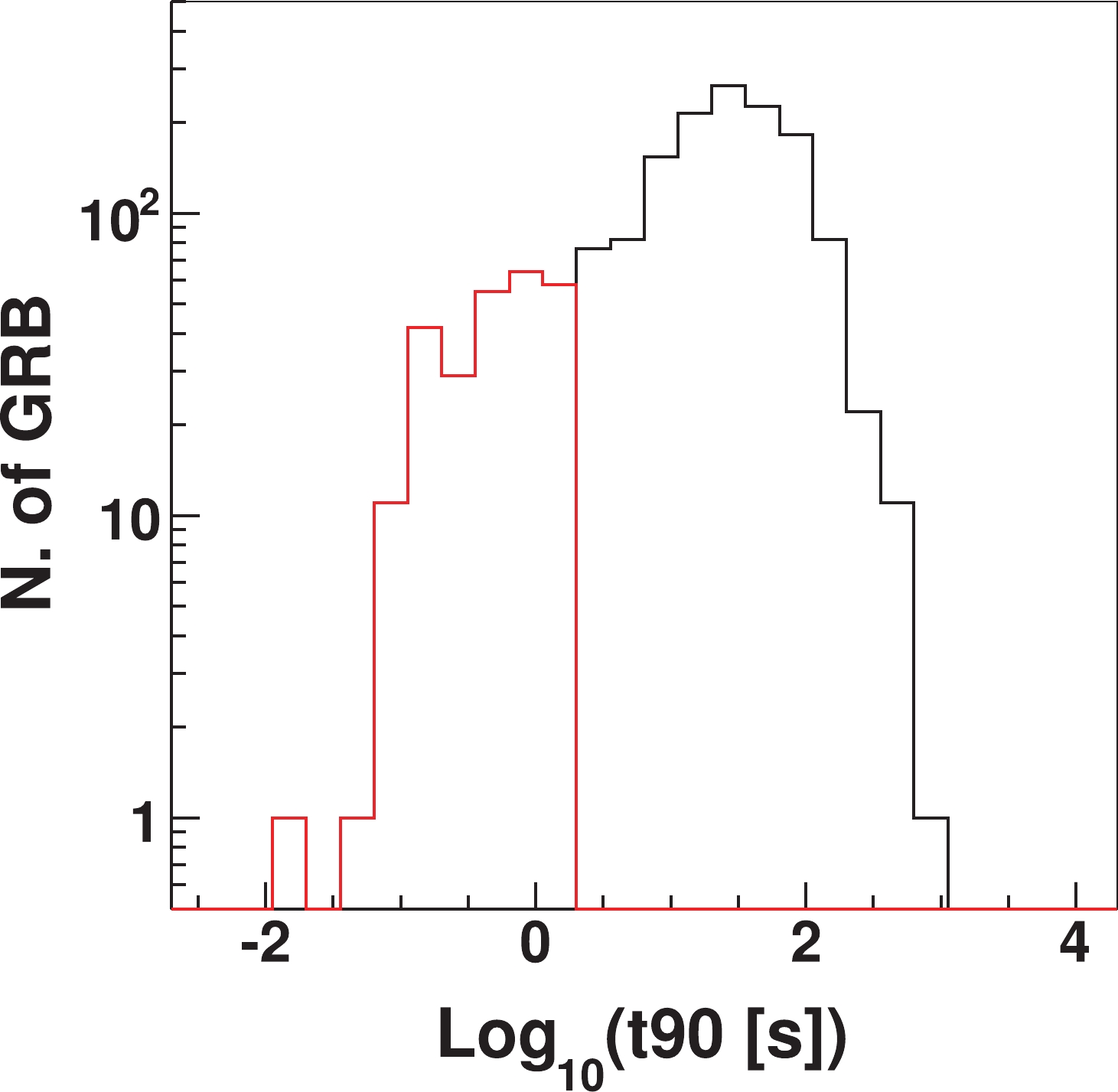

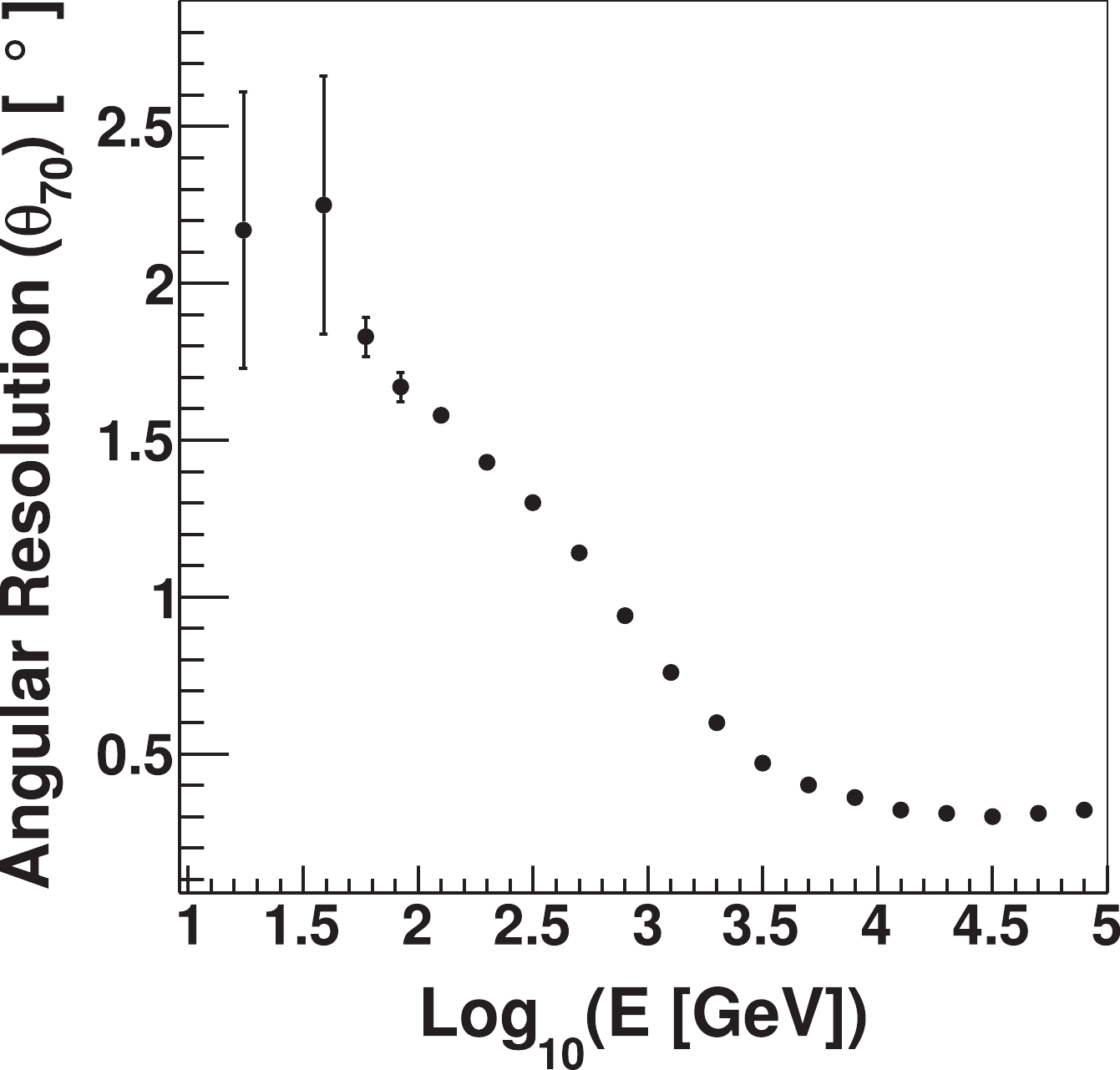






 DownLoad:
DownLoad: