-
In 2017, the LHCb collaboration observed five narrow excited
$ \Omega_{c} $ states, i.e.,$ \Omega_{c}(3000) $ ,$ \Omega_{c}(3050) $ ,$ \Omega_{c}(3066) $ ,$ \Omega_{c}(3090) $ , and$ \Omega_{c}(3119) $ , in the$ \Xi^{+}_{c}K^{-} $ mass spectrum [1]. Recently, they reported four excited$ \Omega_{b} $ states in the$ \Xi^{0}_{b}K^{-} $ mass spectrum [2]:$ \begin{aligned}[b] &\Omega_{b}(6316): m = 6315.64\pm0.31\pm0.07\pm0.50\;{\rm{MeV}},\quad\Gamma<2.8\;{\rm{MeV}},\\ &\Omega_{b}(6330): m = 6330.30\pm0.28\pm0.07\pm0.50\;{\rm{MeV}},\quad\Gamma<3.1\;{\rm{MeV}},\\ &\Omega_{b}(6340): m = 6339.71\pm0.26\pm0.05\pm0.50\;{\rm{MeV}},\quad \Gamma<1.5\;{\rm{MeV}},\\ &\Omega_{b}(6350): m = 6349.88\pm0.35\pm0.05\pm0.50\;{\rm{MeV}},\quad\Gamma = 1.4^{+1.0}_{-0.8}\pm0.1\;{\rm{MeV}}. \end{aligned} $ 
(1) Following this experimental progresses, there have been many theoretical works concerning various properties of these excited
$ \Omega_{Q} $ ($ Q = b,c $ ) states [3-26] and other excited heavy baryons [27-36].Two kinds of excitations, the ρ-mode and λ-mode, exist in these excited
$ \Omega_{Q} $ states. The ρ-mode excitation is the excitation between two strange quarks, while the λ-mode one is the excitation between the strange diquark and bottom (charm) quark. In Ref. [37], the authors systematically considered all possible baryon currents with a derivative for internal ρ- and λ-mode excitations and studied the P-wave charmed baryons using the QCD sum rule method in the framework of heavy quark effective theory. In Refs. [12, 22], the authors studied these excited states using the QCD sum rule method in the framework of QCD.In this paper, we construct the full QCD counterparts of the interpolating currents considered in Ref. [37] and study P-wave
$ \Omega_{b} $ excited states using the QCD sum rule method [38, 39]. The basic idea of the QCD sum rule method is that the correlation function of interpolating currents of hadrons can be represented in terms of hadronic parameters (the so-called hadronic side) and calculated at quark-gluon level by operator product expansion (OPE) (the so-called QCD side); then, by matching the two expressions, we can extract the physical quantities of the considered hadron.The rest of the paper is organized as follows. In Sec. II, we construct the interpolating currents and derive the required sum rules. Sec. III is devoted to numerical analysis, and a short summary is given in Sec. IV. In Appendix B, OPE results are shown.
-
Following Ref. [37], we introduce the symbols [
$ \Omega_{b},j_{l},s_{l},\rho/\lambda $ ] and$ J^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda} $ to denote the P-wave$ \Omega_{b} $ multiplets and the interpolating currents, respectively, where j is the total angular momentum; P is the parity;$ j_{l} $ and$ s_{l} $ are the total angular momentum and spin angular momentum of the light components, respectively; and ρ(λ) denotes the ρ(λ)-mode excitations. The general interpolating currents of$ \Omega_{b} $ baryons can be written as$ \begin{equation} J(x)\sim\epsilon^{abc}[s^{aT}(x)C\Gamma_{1}s^{b}(x)]\Gamma_{2}b^{c}(x), \end{equation} $

(2) where a, b, and c are color indices,
$ \epsilon^{abc} $ is the totally antisymmetric tensor, C is the charge conjugation operator, T denotes the matrix transpose on the Dirac spinor indices, and$ s(x) $ and$ b(x) $ are the strange and bottom quark fields, respectively. The state function corresponding to the diquark$ \epsilon^{abc}[s^{aT}(x)C\Gamma_{1}s^{b}(x)] $ can be written as$\rm |color\rangle\otimes $ $ \rm |flavor,\; spin,\; space\rangle$ and should be antisymmetric under the interchange of the two strange quarks. Now, the color part and flavor part are antisymmetric and symmetric, respectively. The spin part is antisymmetric for the scalar diquark$ \epsilon^{abc}[s^{aT}(x)C\gamma_{5}s^{b}(x)] $ and symmetric for the axial-vector diquark$ \epsilon^{abc}[s^{aT}(x)C\gamma_{\mu}s^{b}(x)] $ . The spatial wave function is antisymmetric and symmetric corresponding to the the ρ-mode and λ-mode excitation, respectively. For example, if the spin angular momentum of the diquark is 0, the excitation in the$ \Omega_{b} $ state should be the ρ-mode, and we have the baryon-multiplet [$ \Omega_{b} $ , 1, 0, ρ]. Consequently, the P-wave$ \Omega_{b} $ states can be classified into four multiplets, i.e., [$ \Omega_{b} $ , 1, 0, ρ], [$ \Omega_{b} $ , 0, 1, λ], [$ \Omega_{b} $ , 1, 1, λ], and [$ \Omega_{b} $ , 2, 1, λ], and the corresponding interpolating currents are● [
$ \Omega_{b} $ , 1, 0, ρ]:$ \begin{aligned}[b] J_{1/2,-,\Omega_{b},1,0,\rho}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{5}s^{b}(x)\\&- s^{T}(x)C\gamma_{5}[D_{\mu}s(x)]^{b}\}\gamma^{\mu}\gamma_{5}b^{c}(x),\\ J^{\alpha}_{3/2,-,\Omega_{b},1,0,\rho}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{5}s^{b}(x)\\&- s^{T}(x)C\gamma_{5}[D_{\mu}s(x)]^{b}\}\Gamma^{\alpha\mu}b^{c}(x), \end{aligned} $

(3) with
$ \Gamma^{\alpha\mu} = g^{\alpha\mu}-\frac{1}{4}\gamma^{\alpha}\gamma^{\mu} $ ,● [
$ \Omega_{b} $ , 0, 1, λ]:$ \begin{aligned}[b] J_{1/2,-,\Omega_{b},0,1,\lambda}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma^{\mu}s^{b}(x)\\&+ s^{T}(x)C\gamma^{\mu}[D_{\mu}s(x)]^{b}\}b^{c}(x), \end{aligned} $

(4) ● [
$ \Omega_{b} $ , 1, 1, λ]:$ \begin{aligned}[b] J_{1/2,-,\Omega_{b},1,1,\lambda}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{\nu}s^{b}(x)\\&+ s^{T}(x)C\gamma_{\nu}[D_{\mu}s(x)]^{b}\}\sigma^{\mu\nu}b^{c}(x),\\ J^{\alpha}_{3/2,-,\Omega_{b},1,1,\lambda}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{\nu}s^{b}(x)\\&+ s^{T}(x)C\gamma_{\nu}[D_{\mu}s(x)]^{b}\}\Gamma^{\alpha\mu\nu}_{1}b^{c}(x), \end{aligned} $

(5) with
$\Gamma^{\alpha\mu\nu}_{1} = \left(g^{\alpha\mu}\gamma^{\nu}-g^{\alpha\nu}\gamma^{\mu}- \dfrac{1}{4}\gamma^{\alpha}\gamma^{\mu}\gamma^{\nu}+\dfrac{1}{4}\gamma^{\alpha}\gamma^{\nu}\gamma^{\mu}\right)\gamma_{5}$ ,● [
$ \Omega_{b} $ , 2, 1, λ]:$ \begin{aligned}[b] J^{\alpha}_{3/2,-,\Omega_{b},2,1,\lambda}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{\nu}s^{b}(x)\\&+ s^{T}(x)C\gamma_{\nu}[D_{\mu}s(x)]^{b}\}\Gamma^{\alpha\mu\nu}_{2}b^{c}(x),\\ J^{\alpha_{1}\alpha_{2}}_{5/2,-,\Omega_{b},2,1,\lambda}(x) =& {\rm i}\epsilon_{abc}\{[D_{\mu}s^{T}(x)]^{a}C\gamma_{\nu}s^{b}(x)\\&+ s^{T}(x)C\gamma_{\nu}[D_{\mu}s(x)]^{b}\}\Gamma^{\alpha_{1}\alpha_{2}\mu\nu}b^{c}(x), \end{aligned} $

(6) where
$ \begin{equation} \Gamma^{\alpha\mu\nu}_{2} = \left(g^{\alpha\mu}\gamma^{\nu}+g^{\alpha\nu}\gamma^{\mu}-\frac{1}{2}g^{\mu\nu}\gamma^{\alpha}\right)\gamma_{5}, \end{equation} $

(7) $ \begin{aligned}[b] \Gamma^{\alpha_{1}\alpha_{2}\mu\nu} = &g^{\alpha_{1}\mu}g^{\alpha_{2}\nu}+g^{\alpha_{1}\nu}g^{\alpha_{2}\mu} -\frac{1}{3}g^{\alpha_{1}\alpha_{2}}g^{\mu\nu}\\&-\frac{1}{6}g^{\alpha_{1}\mu}\gamma^{\alpha_{2}}\gamma^{\nu} -\frac{1}{6}g^{\alpha_{1}\nu}\gamma^{\alpha_{2}}\gamma^{\mu}\\&-\frac{1}{6}g^{\alpha_{2}\nu}\gamma^{\alpha_{1}}\gamma^{\mu} -\frac{1}{6}g^{\alpha_{2}\mu}\gamma^{\alpha_{1}}\gamma^{\nu}. \end{aligned} $

(8) In the above equations,
$D_{\mu}(x) = \partial_{\mu}-{\rm i}g_{s}A_{\mu}(x)$ is the gauge-covariant derivative; a, b, and c are color indices; C is the charge conjugation operator; T denotes the matrix transpose on the Dirac spinor indices; and$ s(x) $ and$ b(x) $ are the strange and bottom quark fields, respectively. -
To obtain the mass sum rules for the P-wave excited
$ \Omega_{b} $ states, we begin with the following two-point correlation function of the interpolating currents constructed in the previous subsection,$ \begin{aligned}[b] \Pi^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}\beta_{1}\beta_{2}\cdots\beta_{j-\frac{1}{2}}}(p) =& {\rm i}\int {\rm d}x^{4}{\rm e}^{{\rm i}px}\langle0\mid {T}[J^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}(x)\\&\times \bar{J}^{\,\beta_{1}\beta_{2}\cdots\beta_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}(0)]\mid0\rangle. \end{aligned} $

(9) First, we need to phenomenologically represent the two-point correlation function (9) in terms of hadronic parameters. To this end, we insert a complete set of states with the same quantum numbers as the interpolating field, perform the integral over space-time coordinates, and finally obtain
$ \begin{aligned}[b] \Pi^{({\rm Phy})\alpha_{1}\cdots\alpha_{j-\frac{1}{2}}\beta_{1}\cdots\beta_{j-\frac{1}{2}}}(p) = & \frac{1}{m^{2}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}-p^{2}}\\&\times\langle0|J^{\alpha_{1}\cdots\alpha_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda} |j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda,p\rangle\\&\times\langle j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda,p| \bar{J}^{\beta_{1}\cdots\beta_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}|0\rangle\\& +{\rm{higher \;resonances}}. \end{aligned} $

(10) We parameterize the matrix element
$ \langle0|J^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda} $ $ |j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda,p\rangle $ in terms of the current-hadron coupling constant (pole residue)$ f_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda} $ and spinor$ u^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}(p) $ ,$ \begin{aligned}[b]& \langle0|J^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda} |j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda,p\rangle \\=& f_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}u^{\alpha_{1}\alpha_{2}\cdots\alpha_{j-\frac{1}{2}}}(p). \end{aligned} $

(11) As a result, we have
● for spin-
$ \dfrac{1}{2} $ baryon:$ \begin{equation} \Pi^{({\rm Phy})}(p) = \frac{f^{2}_{1/2}}{m^{2}_{1/2}-p^{2}}(\not{p}+m_{1/2})+{\rm{higher \;resonances}}, \end{equation} $

(12) ● for spin-
$ \dfrac{3}{2} $ baryon:$ \begin{aligned}[b] \Pi^{({\rm Phy})\alpha_{1}\beta_{1}}(p) = &\frac{f^{2}_{3/2}}{m^{2}_{3/2}-p^{2}}(\not{p}+m_{3/2})\Bigg(-g^{\alpha_{1}\beta_{1}} +\frac{\gamma^{\alpha_{1}}\gamma^{\beta_{1}}}{3}\\\\&+\frac{2p^{\alpha_{1}}p^{\beta_{1}}}{3m^{2}_{3/2}} -\frac{p^{\alpha_{1}}\gamma^{\beta_{1}}-p^{\beta_{1}}\gamma^{\alpha_{1}}}{3m_{3/2}}\Bigg) \\&+{\rm{higher \;resonances}}, \end{aligned} $

(13) ● for spin-
$ \dfrac{5}{2} $ baryon:$ \begin{aligned}[b] \Pi^{({\rm Phy})\alpha_{1}\alpha_{2}\beta_{1}\beta_{2}}(p) = &\frac{f^{2}_{5/2}}{m^{2}_{5/2}-p^{2}}(\not{p}+m_{5/2}) \Bigg[\frac{\tilde{g}^{\alpha_{1}\beta_{1}}\tilde{g}^{\alpha_{2}\beta_{2}}+\tilde{g}^{\alpha_{1}\beta_{2}}\tilde{g}^{\alpha_{2}\beta_{1}}}{2} -\frac{\tilde{g}^{\alpha_{1}\alpha_{2}}\tilde{g}^{\beta_{1}\beta_{2}}}{5}-\frac{1}{10}\left(\gamma^{\alpha_{1}}\gamma^{\beta_{1}} +\frac{\gamma^{\alpha_{1}}p^{\beta_{1}}-\gamma^{\beta_{1}}p^{\alpha_{1}}}{m_{5/2}}-\frac{p^{\alpha_{1}}p^{\beta_{1}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{2}\beta_{2}}\\&-\frac{1}{10}\left(\gamma^{\alpha_{2}}\gamma^{\beta_{1}} +\frac{\gamma^{\alpha_{2}}p^{\beta_{1}}-\gamma^{\beta_{1}}p^{\alpha_{2}}}{m_{5/2}}-\frac{p^{\alpha_{2}}p^{\beta_{1}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{1}\beta_{2}}-\frac{1}{10}\left(\gamma^{\alpha_{1}}\gamma^{\beta_{2}} +\frac{\gamma^{\alpha_{1}}p^{\beta_{2}}-\gamma^{\beta_{2}}p^{\alpha_{1}}}{m_{5/2}}-\frac{p^{\alpha_{1}}p^{\beta_{2}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{2}\beta_{1}}\\&-\frac{1}{10}\left(\gamma^{\alpha_{2}}\gamma^{\beta_{2}} +\frac{\gamma^{\alpha_{2}}p^{\beta_{2}}-\gamma^{\beta_{2}}p^{\alpha_{2}}}{m_{5/2}}-\frac{p^{\alpha_{2}}p^{\beta_{2}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{1}\beta_{1}}\Bigg]+{\rm{higher \;resonances}}, \end{aligned} $

(14) where we have used the following formulas
$ \begin{equation} \sum\limits_{s}u(p,s)\bar{u}(p,s) = \not{p}+m_{1/2}, \end{equation} $

(15) $ \sum\limits_{s}u^{\alpha_{1}}(p,s)\bar{u}^{\beta_{1}}(p,s) = (\not{p}+m_{3/2})\left(-g^{\alpha_{1}\beta_{1}} +\frac{\gamma^{\alpha_{1}}\gamma^{\beta_{1}}}{3}+\frac{2p^{\alpha_{1}}p^{\beta_{1}}}{3m^{2}_{3/2}} -\frac{p^{\alpha_{1}}\gamma^{\beta_{1}}-p^{\beta_{1}}\gamma^{\alpha_{1}}}{3m_{3/2}}\right), $

(16) $ \begin{aligned}[b] \sum\limits_{s}u^{\alpha_{1}\alpha_{2}}(p,s)\bar{u}^{\beta_{1}\beta_{2}}(p,s) = &(\not{p}+m_{5/2})\Bigg[\frac{\tilde{g}^{\alpha_{1}\beta_{1}}\tilde{g}^{\alpha_{2}\beta_{2}}+\tilde{g}^{\alpha_{1}\beta_{2}}\tilde{g}^{\alpha_{2}\beta_{1}}}{2} -\frac{\tilde{g}^{\alpha_{1}\alpha_{2}}\tilde{g}^{\beta_{1}\beta_{2}}}{5}-\frac{1}{10}\left(\gamma^{\alpha_{1}}\gamma^{\beta_{1}} +\frac{\gamma^{\alpha_{1}}p^{\beta_{1}}-\gamma^{\beta_{1}}p^{\alpha_{1}}}{m_{5/2}}-\frac{p^{\alpha_{1}}p^{\beta_{1}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{2}\beta_{2}}\\&-\frac{1}{10}\left(\gamma^{\alpha_{2}}\gamma^{\beta_{1}} +\frac{\gamma^{\alpha_{2}}p^{\beta_{1}}-\gamma^{\beta_{1}}p^{\alpha_{2}}}{m_{5/2}}-\frac{p^{\alpha_{2}}p^{\beta_{1}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{1}\beta_{2}}-\frac{1}{10}\left(\gamma^{\alpha_{1}}\gamma^{\beta_{2}} +\frac{\gamma^{\alpha_{1}}p^{\beta_{2}}-\gamma^{\beta_{2}}p^{\alpha_{1}}}{m_{5/2}}-\frac{p^{\alpha_{1}}p^{\beta_{2}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{2}\beta_{1}}\\&-\frac{1}{10}\left(\gamma^{\alpha_{2}}\gamma^{\beta_{2}} +\frac{\gamma^{\alpha_{2}}p^{\beta_{2}}-\gamma^{\beta_{2}}p^{\alpha_{2}}}{m_{5/2}}-\frac{p^{\alpha_{2}}p^{\beta_{2}}}{m^{2}_{5/2}}\right) \tilde{g}^{\alpha_{1}\beta_{1}}\Bigg], \end{aligned} $

(17) with
$ \tilde{g}^{\mu\nu} = g^{\mu\nu}-\dfrac{p^{\mu}p^{\nu}}{p^{2}} $ .Conversely, the correlation function (9) can be calculated theoretically via the OPE method at the quark-gluon level. We take the current
$ J_{1/2,-,\Omega_{b},1,0,\rho}(x) $ as an example to illustrate the involved technologies. Inserting the interpolating current$ J_{1/2,-,\Omega_{b},1,0,\rho}(x) $ (3) into the correlation function (9) and contracting the relevant quark fields using Wick's theorem, we find$ \begin{aligned}[b] \Pi^{(\rm OPE)}(p) = &-4{\rm i}\epsilon_{abc}\epsilon_{a^{\prime}b^{\prime}c^{\prime}}\int {\rm d}^{4}x {\rm e}^{{\rm i}px}\gamma_{\mu}\gamma_{5}S^{(b)}_{cc^{\prime}}(x)\gamma_{\mu^{\prime}}\gamma_{5}\\ & \times \Big\{{\rm Tr}\Big[\gamma_{5}S^{(s)}_{bb^{\prime}}(x)\gamma_{5}C\partial^{\mu}_{x}\partial^{\mu^{\prime}}_{y}S^{(s)T}_{aa^{\prime}}(x-y)C\Big]- {\rm Tr}\Big[\gamma_{5}\partial^{\mu}_{x}S^{(s)}_{bb^{\prime}}(x)\gamma_{5}C\partial^{\mu^{\prime}}_{y}S^{(s)T}_{aa^{\prime}}(x-y)C\Big]\Big\}_{y = 0}\\ &+4\epsilon_{abc}\epsilon_{a^{\prime}b^{\prime}c^{\prime}}\int {\rm d}^{4}x {\rm e}^{{\rm i}px}g_{s}A^{\mu ad}(x)\gamma_{\mu}\gamma_{5}S^{(b)}_{cc^{\prime}}(x)\gamma_{\mu^{\prime}}\gamma_{5}\\ & \times \Big\{{\rm Tr}\Big[\gamma_{5}\partial^{\mu^{\prime}}_{y}S^{(s)}_{bb^{\prime}}(x-y)\gamma_{5}CS^{(s)T}_{da^{\prime}}(x)C\Big]- {\rm Tr}\Big[\gamma_{5}S^{(s)}_{bb^{\prime}}(x)\gamma_{5}C\partial^{\mu^{\prime}}_{y}S^{(s)T}_{da^{\prime}}(x-y)C\Big]\Big\}_{y = 0}\\ &+\frac{\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{96}\epsilon_{abc}\epsilon_{a^{\prime}b^{\prime}c^{\prime}}\int {\rm d}^{4}x {\rm e}^{{\rm i}px}g_{s}\gamma_{\mu}\gamma_{5}S^{(b)}_{cc^{\prime}}(x)\gamma_{\mu^{\prime}}\gamma_{5}\\ & \times \left(\frac{\lambda_{n}}{2}\right)^{ad}\left\{\left(\frac{\lambda_{n}}{2}\right)^{da^{\prime}}x_{\nu} {\rm Tr}\Big[\gamma_{5}\partial^{\mu^{\prime}}_{y}S^{(s)}_{bb^{\prime}}(x-y)\gamma_{5}\sigma^{\mu\nu}\Big]-\left(\frac{\lambda^{n}}{2}\right)^{bb^{\prime}}x_{\nu} {\rm Tr}\Big[\gamma_{5}\partial^{\mu^{\prime}}_{y}S^{(s)}_{da^{\prime}}(x-y)\gamma_{5}\sigma^{\mu\nu}\Big]\right\}_{y = 0}, \end{aligned} $ 
(18) where a, b,
$ \cdots $ are color indices,$ \lambda^{n},n = 1,2,\cdots,8 $ are the Gell-Mann matrix,$ A^{\mu ad}(x) = A^{n\mu}(x)\left(\dfrac{\lambda_{n}}{2}\right)^{ad} $ is the gluon field,$ g_{s} $ is the strong interaction constant, and$ S^{(b)}(x) $ and$ S^{(s)}(x) $ are the full bottom- and strange-quark propagators, respectively, whose expressions are given in Appendix A. Inserting the expressions for the full quark propagators into (18) and performing the involved integrals, we have$ \Pi^{(\rm OPE)}(p) = \not{p}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}}, $

(19) where
$ \rho(s) $ is the QCD spectral density$ \begin{aligned}[b] \rho(s) = &-\frac{3}{64\pi^{4}}\int^{1}_{a_{\rm min}}{\rm d}a \frac{(1-a)^{3}}{a^{2}}(m^{2}_{b}-as)^{3}+\frac{3m^{2}_{s}}{16\pi^{4}}\int^{1}_{a_{\rm min}}{\rm d}a \frac{(1-a)^{2}}{a}(m^{2}_{b}-as)^{2}\\ &-\frac{3m_{s}\langle0|\bar{s}s|0\rangle}{4\pi^{2}}\int^{1}_{a_{min}}{\rm d}a (1-a)(m^{2}_{b}-as)-\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{256\pi^{4}}\int^{1}_{a_{\rm min}}{\rm d}a \frac{(1-a)^{3}}{a^{2}}\\ &-\frac{5\langle0|g^{2}_{s}GG|0\rangle}{256\pi^{4}}\int^{1}_{a_{\rm min}}{\rm d}a(1-a)(m^{2}_{b}-as) -\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{192\pi^{4}}(1-a_{\rm min})^{2} -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{96\pi^{2}M^{2}_{\rm B}}(1-a_{\rm min}), \end{aligned} $

(20) with
$a_{\rm min} = m^{2}_{b}/s$ ; here,$ m_{s} $ is the mass of the strange quark,$ m_{b} $ is the mass of the bottom quark. and$M^{2}_{\rm B}$ is the Borel parameter, introduced to make the Borel transform in the next step.Finally, we match the phenomenological side (12) and the QCD representation (19) for the Lorentz structure
$\not{p}$ ,$ \frac{f^{2}_{1/2,-,\Omega_{b},1,0,\rho}}{m^{2}_{1/2,-,\Omega_{b},1,0,\rho}-p^{2}}+{\rm{higher \;resonances}} = \int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12(m^{2}_{b}-p^{2})}, $

(21) According to the quark-hadron duality, the higher resonances can be approximated by the QCD spectral density above some effective threshold
$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} $ ,$ \frac{f^{2}_{1/2,-,\Omega_{b},1,0,\rho}}{m^{2}_{1/2,-,\Omega_{b},1,0,\rho}-p^{2}} +\int^{\infty}_{s^{1/2,-,\Omega_{b},1,0,\rho}_{0}}{\rm d}s\frac{\rho(s)}{s-p^2} = \int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12(m^{2}_{b}-p^{2})}. $

(22) Subtracting the contributions of the excited and continuum states, we obtain
$ \begin{equation} \frac{f^{2}_{1/2,-,\Omega_{b},1,0,\rho}}{m^{2}_{1/2,-,\Omega_{b},1,0,\rho}-p^{2}} = \int^{s^{1/2,-,\Omega_{b},1,0,\rho}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12(m^{2}_{b}-p^{2})}, \end{equation} $

(23) To improve the convergence of the OPE series and suppress the contributions from the excited and continuum states, it is necessary to make a Borel transform. As a result, we have
$ \begin{equation} f^{2}_{1/2,-,\Omega_{b},1,0,\rho}{\rm e}^{-m^{2}_{1/2,-,\Omega_{b},1,0,\rho}/M^{2}_{B}} = \int^{s^{1/2,-,\Omega_{b},1,0,\rho}_{0}}_{(m_{b}+2m_{s})^{2}} {\rm d} s\rho(s) {\rm e}^{-s/M^{2}_{B}} +\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12} {\rm e}^{-m^{2}_{b}/M^{2}_{B}}, \end{equation} $

(24) where
$M^{2}_{\rm B}$ is the Borel parameter. Applying the operator$-\frac{\rm d}{{\rm d}(1/M^{2}_{B})}$ to (24) and dividing the resulting equation with (24), we obtain the mass sum rule$ m^{2}_{1/2,-,\Omega_{b},1,0,\rho} = \frac{-\dfrac{\rm d}{{\rm d}(1/M^{2}_{B})}\left(\displaystyle\int^{s^{1/2,-,\Omega_{b},1,0,\rho}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho(s){\rm e}^{-s/M^{2}_{B}} +\dfrac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12}{\rm e}^{-m^{2}_{b}/M^{2}_{B}}\right)}{ \displaystyle\int^{s^{1/2,-,\Omega_{b},1,0,\rho}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho(s){\rm e}^{-s/M^{2}_{B}} +\dfrac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{12}{\rm e}^{-m^{2}_{b}/M^{2}_{B}}}. $

(25) In Sec. III, we will numerically analyze (25) and (24) and estimate the values of the mass
$ m_{1/2,-,\Omega_{b},1,0,\rho} $ and the pole residue$ f_{1/2,-,\Omega_{b},1,0,\rho} $ .For other interpolating currents, we do the same analysis, and the corresponding OPE results are given in Appendix B.
-
The sum rule (25) contains some parameters, various condensates, and quark masses, whose values are presented in Table 1. The values of
$ m_{b} $ and$ m_{s} $ are the$ \overline{MS} $ values. In addition to these parameters, we need to determine the working intervals of the threshold parameter$ s^{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}_{0} $ and the Borel mass$M^{2}_{\rm B}$ in which the masses and pole residues are stable. We take the continuum threshold to be approximately$m_{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}+ (0.7\pm $ $ 0.1)\; {\rm{GeV}}$ , while the Borel parameter is determined by demanding that both the contributions of the higher states and continuum are sufficiently suppressed and the contributions coming from higher dimensional operators are small.Parameter Value $ \langle\bar{s}s\rangle $ 

$ (0.8\pm0.1)\langle\bar{q}q\rangle $ 

$ \langle\bar{q}q\rangle $ 

$ -(0.24\pm0.01)^{3}{\rm{GeV}}^{3} $ 

$ \langle g_{s}\bar{s}\sigma Gs\rangle $ 

$ (0.8\pm0.1)\langle\bar{s}s\rangle {\rm{GeV}}^{2} $ 

$ \langle g^{2}_{s}GG\rangle $ 

$ 0.88\pm0.25\;{\rm{GeV}}^{4} $ 

$ m_{b} $ 

$ (4.18\pm0.03){\rm{GeV}} $ [40]

$ m_{s} $ 

$ (0.095\pm0.005){\rm{GeV}} $ [40]

Table 1. Input parameters required for calculations.
We define two quantities: the ratio of the pole contribution to the total contribution (Pole Contribution, abbreviated PC) and the ratio of the highest dimensional term in the OPE series to the total OPE series (Convergence, abbreviated CVG), as follows,
$ \begin{aligned}[b] {\rm{PC}}\equiv &\frac{\displaystyle\int^{s^{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho(s){\rm e}^{-\frac{s}{M^{2}_{B}}}} {\displaystyle\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho(s){\rm e}^{-\frac{s}{M^{2}_{B}}}}, \\{\rm{CVG}}\equiv &\frac{\displaystyle\int^{s^{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho^{(d = 7)}(s){\rm e}^{-\frac{s}{M^{2}_{B}}}} {\displaystyle\int^{s^{j,P,\Omega_{b},j_{l},s_{l},\rho/\lambda}_{0}}_{(m_{b}+2m_{s})^{2}}{\rm d}s\rho(s){\rm e}^{-\frac{s}{M^{2}_{B}}}}, \end{aligned} $

(26) where
$ \rho^{(d = 7)}(s) $ are the terms proportional to$ \langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle $ in the spectral density.For the current
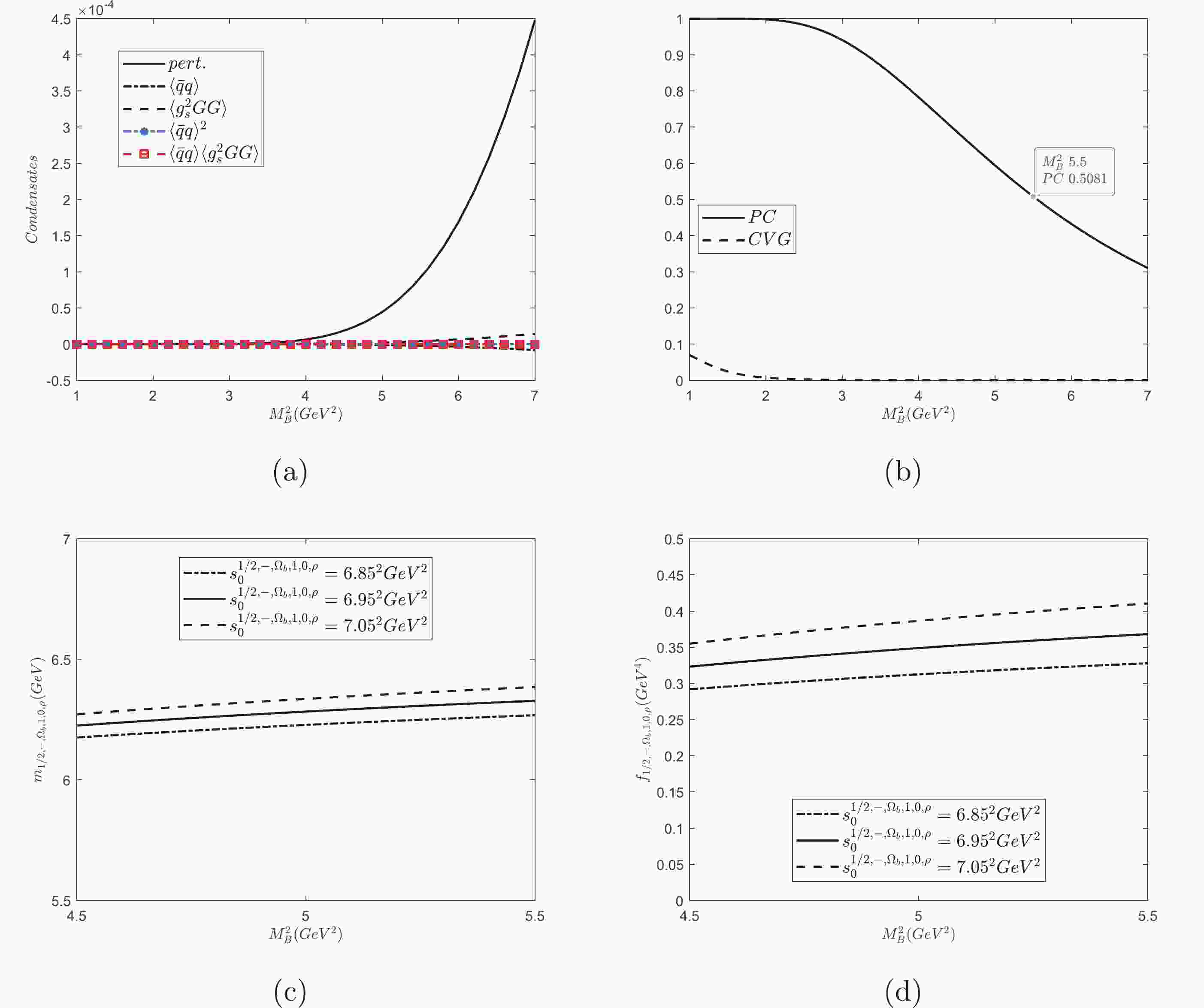
$ J_{1/2,-,\Omega_{b},1,0,\rho}(x) $ , the numerical results are shown in Fig. 1. In Fig. 1(a), we compare the various condensate contributions as functions of$M^{2}_{\rm B}$ with$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} = 6.95^{2}\;{\rm{GeV}}^{2} $ . From the figure, it is clear that the OPE has good convergence. Fig. 1(b) shows PC and CVG varying with$M^{2}_{\rm B}$ at$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} = 6.95^{2}\;{\rm{GeV}}^{2} $ . The figure shows that the requirement$ {\rm{PC}}\geqslant 50 $ % gives$M^{2}_{\rm B}\leqslant 5.5\;{\rm{GeV}}^{2}$ . The dependences of the mass$ m_{1/2,-,\Omega_{b},1,0,\rho} $ and the pole residue$ f_{1/2,-,\Omega_{b},1,0,\rho} $ on the Borel parameter$M^{2}_{\rm B}$ are depicted in Fig. 1(c) and (d) at three different values of$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} $ , respectively. It is obvious that the mass and the pole residue are stable in the interval$4.5\;{\rm{GeV}}^{2}\leqslant M^{2}_{\rm B}\leqslant 5.5\;{\rm{GeV}}^{2}$ . The mass and the pole residue are estimated to be$ m_{1/2,-,\Omega_{b},1,0,\rho} = (6.28^{+0.11}_{-0.10}){\rm{GeV}} $ and$ f_{1/2,-,\Omega_{b},1,0,\rho} = (0.35\pm0.06){\rm{GeV}}^{4} $ , respectively.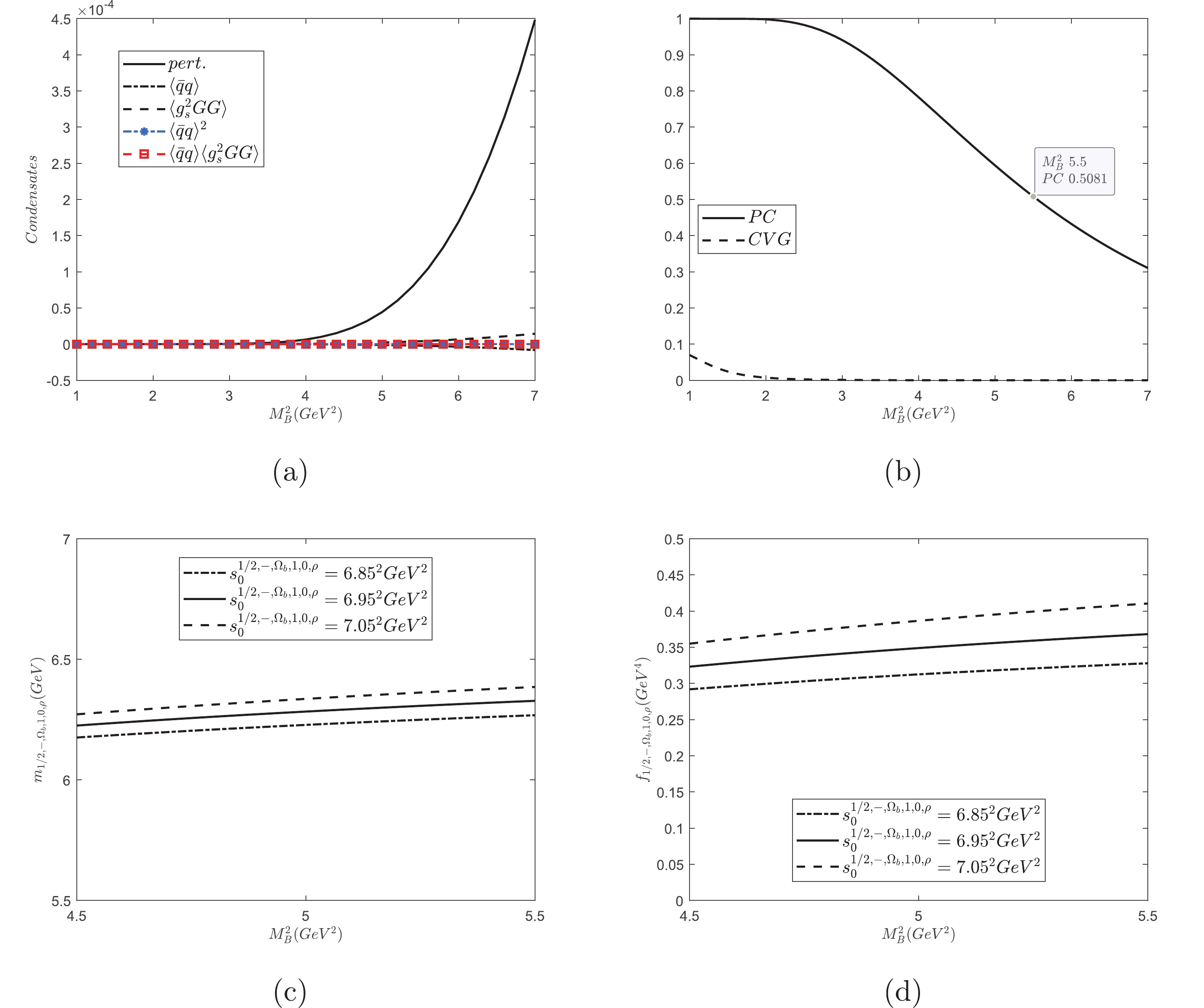
Figure 1. (color online) For the interpolating current
$ J_{1/2,-,\Omega_{b},1,0,\rho}(x) $ : (a) denotes the various condensate contributions as functions of$M^{2}_{\rm B}$ with$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} = 6.95^{2}\;{\rm{GeV}}^{2} $ ; (b) represents PC and CVG varying with$M^{2}_{\rm B}$ at$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} = 6.95^{2}\;{\rm{GeV}}^{2} $ ; (c) and (d) depict the dependence of the mass and the pole residue on$M^{2}_{\rm B}$ with three different values of$ s^{1/2,-,\Omega_{b},1,0,\rho}_{0} $ , respectively.For other interpolating currents, the same analysis can be performed. We summarize our results in Table 2 and compare the obtained masses with the results in Ref. [20] estimated using the QCD sum rule method in the framework of heavy quark effective theory. It is clear that they are in agreement with each other within the inherent uncertainties of the QCD sum rule method, except for the multiplet [
$ \Omega_{b} $ , 0, 1, λ]. We should provide some arguments regarding the result of the interpolating current$ J_{1/2,-,\Omega_{b},0,1,\lambda}(x) $ shown in Fig. 2. From Eqs. (B3) and (B4), we can see that all terms of the OPE series are proportional to the strange quark mass$ m_{s} $ or$ m^{2}_{s} $ , except for the second term in (B4). As a result, the gluon-condensate term is much larger than the other terms, and OPE is invalid in this case. Moreover, the corresponding mass and pole residue are much lower than the others. All in all, our model can not give reasonable results in this case.Multiples Baryons ( $ j^{P} $ )

Masses/ $ {\rm{GeV}} $ 

Pole residues/ $ {\rm{GeV}}^{4} $ 

This work Ref. [20] [ $ \Omega_{b} $ , 1, 0, ρ]

$ \Omega_{b} $ (

$ \frac{1}{2}^{-} $ )

$ 6.28^{+0.11}_{-0.10} $ 

$ 6.32^{+0.12}_{-0.10} $ 

$ 0.35\pm0.06 $ 

$ \Omega_{b} $ (

$ \frac{3}{2}^{-} $ )

$ 6.31^{+0.10}_{-0.11} $ 

$ 6.32^{+0.12}_{-0.10} $ 

$ 0.19\pm0.03 $ 

[ $ \Omega_{b} $ , 0, 1, λ]

$ \Omega_{b} $ (

$ \frac{1}{2}^{-} $ )

$ 5.75^{+0.05}_{-0.02} $ 

$ 6.34\pm0.11 $ 

$ 0.0183^{+0.0013}_{-0.0007} $ 

[ $ \Omega_{b} $ , 1, 1, λ]

$ \Omega_{b} $ (

$ \frac{1}{2}^{-} $ )

$ 6.33^{+0.10}_{-0.11} $ 

$ 6.34^{+0.09}_{-0.08} $ 

$ 0.62\pm0.10 $ 

$ \Omega_{b} $ (

$ \frac{3}{2}^{-} $ )

$ 6.37^{+0.10}_{-0.11} $ 

$ 6.34^{+0.09}_{-0.08} $ 

$ 0.36^{+0.06}_{-0.05} $ 

[ $ \Omega_{b} $ , 2, 1, λ]

$ \Omega_{b} $ (

$ \frac{3}{2}^{-} $ )

$ 6.34^{+0.09}_{-0.10} $ 

$ 6.35^{+0.13}_{-0.11} $ 

$ 0.71\pm0.11 $ 

$ \Omega_{b} $ (

$ \frac{5}{2}^{-} $ )

$ 6.54^{+0.07}_{-0.08} $ 

$ 6.36^{+0.13}_{-0.11} $ 

$ 0.15\pm0.02 $ 

Table 2. Masses and pole residues of the P-wave excited
$ \Omega_{b} $ states.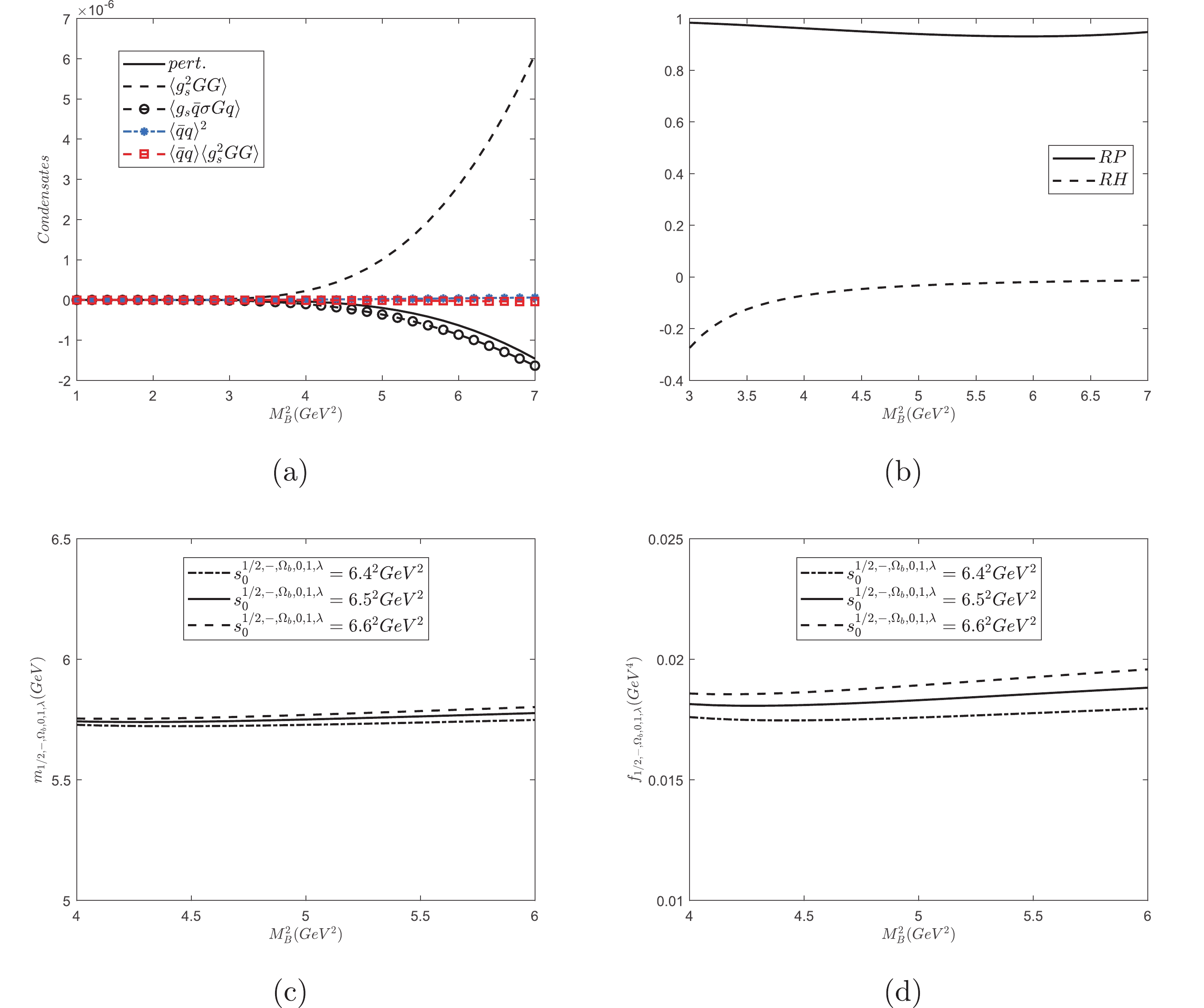
Figure 2. (color online) For the interpolating current
$ J_{1/2,-,\Omega_{b},0,1,\lambda}(x) $ : (a) denotes the various condensate contributions as functions of$ M^{2}_{\rm B} $ with$ s^{1/2,-,\Omega_{b},0,1,\lambda}_{0} = 6.5^{2}\;{\rm{GeV}}^{2} $ ; (b) represents$ RP $ and$ RH $ varying with$ M^{2}_{\rm B} $ at$ s^{1/2,-,\Omega_{b},0,1,\lambda}_{0} = 6.5^{2}\;{\rm{GeV}}^{2} $ ; (c) and (d) depict the dependence of the mass and the pole residue on$ M^{2}_{\rm B} $ with three different values of$ s^{1/2,-,\Omega_{b},0,1,\lambda}_{0} $ , respectively. -
In this paper, we consider all P-wave
$ \Omega_{b} $ states represented by interpolating currents with a derivative and calculate the corresponding masses and pole residues using the QCD sum rule method. The results are summarized in Table 2. Because of the large uncertainties in our calculation compared with the small difference in the masses of the excited$ \Omega_{b} $ states observed by the LHCb collaboration, it is necessary to study other properties of the P-wave$ \Omega_{b} $ states represented by the interpolating currents investigated in the present work to gain a better understanding of the four excited$ \Omega_{b} $ states observed by the LHCb collaboration. For example, we could study their decay widths. Our results in this paper are necessary input parameters when studying their decay widths using the QCD sum rule method or light-cone sum rule method. -
One of the authors, Yong-Jiang Xu, thanks Hua-Xing Chen for useful discussion on the construction of interpolating currents.
-
The full quark propagators are
$ \begin{aligned}[b] S^{q}_{ij}(x) = &\frac{i \not{x}}{2\pi^{2}x^4}\delta_{ij}-\frac{m_{q}}{4\pi^2x^2}\delta_{ij}-\frac{\langle\bar{q}q\rangle}{12}\delta_{ij} +{\rm i}\frac{\langle\bar{q}q\rangle}{48}m_{q}\not{x}\delta_{ij}-\frac{x^2}{192}\langle g_{s}\bar{q}\sigma Gq\rangle \delta_{ij}\\ &+{\rm i}\frac{x^2\not{x}}{1152}m_{q}\langle g_{s}\bar{q}\sigma Gq\rangle \delta_{ij}-{\rm i}\frac{g_{s}t^{a}_{ij}G^{a}_{\mu\nu}}{32\pi^2x^2}(\not{x}\sigma^{\mu\nu}+\sigma^{\mu\nu}\not{x})+\cdots \end{aligned} \tag{A1}$

for light quarks, and
$ \begin{aligned}[b] S^{Q}_{ij}(x) =& {\rm i}\int\frac{{\rm d}^{4}k}{(2\pi)^4}{\rm e}^{-{\rm i}kx}\Bigg[\frac{\not{k}+m_{Q}}{k^2-m^{2}_{Q}}\delta_{ij} -\frac{g_{s}t^{a}_{ij}G^{a}_{\mu\nu}}{4}\frac{\sigma^{\mu\nu}(\not{k}+m_{Q})+(\not{k}+m_{Q})\sigma^{\mu\nu}} {(k^2-m^{2}_{Q})^{2}}+\frac{\langle g^{2}_{s}GG\rangle}{12}\delta_{ij}m_{Q}\frac{k^2+m_{Q}\not{k}}{(k^2-m^{2}_{Q})^{4}}+\cdots\Bigg] \end{aligned}\tag{A2} $

for heavy quarks. In these expressions,
$ t^{a} = \dfrac{\lambda^{a}}{2} $ and$ \lambda^{a} $ are the Gell-Mann matrices,$ g_{s} $ is the strong interaction coupling constant, and$ i, j $ are color indices. -
We choose the Lorentz structures
$ {\not{p}} $ ,${ \not{p}}g^{\alpha\beta} $ , and${ \not{p}}g^{\alpha_{1}\alpha_{2}}g^{\beta_{1}\beta_{2}} $ to obtain the sum rules for spin-${1}/{2}$ , spin-${3}/{2}$ , and spin-${5}/{2}$ baryons, respectively. In this appendix, we will give the corresponding OPE results.For the interpolating current
$ J^{\alpha}_{3/2,-,\Omega_{b},1,0,\rho}(x) $ ,$ \begin{aligned}[b]\\[-3pt] \Pi^{(\rm OPE)\alpha\beta}(p) = {\not{p}}g^{\alpha\beta}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} -\frac{m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{24(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}},\end{aligned}\tag{B1} $

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &\frac{1}{384\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(4+a)}{a^{2}}(m^{2}_{b}-as)^{3}-\frac{m^{2}_{s}}{64\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{2}(2+a)}{a}(m^{2}_{b}-as)^{2}\\&+\frac{m_{s}\langle0|\bar{s}s|0\rangle}{8\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a a(1-a)(m^{2}_{b}-as)+\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{4608\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(4+a)}{a^{2}}\\&+\frac{\langle0|g^{2}_{s}GG|0\rangle}{512\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(2+a)(m^{2}_{b}-as) +\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{2304\pi^{4}}(1-a_{\min})^{2}(2+a_{\min})\\& +\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{24\pi^{2}}\int^{1}_{a_{\min}}{\rm d}aa(2-a)+\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{576\pi^{2}M^{2}_{\rm B}}a_{\min}(1-a_{\min}). \end{aligned}\tag{B2} $

For the interpolating current
$ J_{1/2,-,\Omega_{b},0,1,\lambda}(x) $ ,$ \Pi^{(\rm OPE)}(p) = {\not{p}}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{2m^{2}_{s}\langle0|\bar{s}s|0\rangle^{2}}{3(m^{2}_{b}-p^{2})}+\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{192\pi^{2}(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}}, \tag{B3} $

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &-\frac{3m^{2}_{s}}{32\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{2}}{a}(m^{2}_{b}-as)^{2}-\frac{\langle0|g^{2}_{s}GG|0\rangle}{128\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(m^{2}_{b}-as) \\&+\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{384\pi^{4}}(1-a_{\min})^{2} +\frac{3m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{16\pi^{2}}\int^{1}_{a_{\min}}{\rm d}aa. \end{aligned}\tag{B4} $

For the interpolating current
$ J_{1/2,-,\Omega_{b},1,1,\lambda}(x) $ ,$ \Pi^{(\rm OPE)}(p) = {\not{p}}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{192\pi^{2}(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}}, \tag{B5}$

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &-\frac{1}{8\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}}{a^{2}}(m^{2}_{b}-as)^{3}+\frac{27m^{2}_{s}}{32\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{2}}{a}(m^{2}_{b}-as)^{2}+\frac{3m_{s}\langle0|\bar{s}s|0\rangle}{\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a (1-a)(m^{2}_{b}-as)\\&-\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{96\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}}{a^{2}}-\frac{3\langle0|g^{2}_{s}GG|0\rangle}{128\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a\frac{(1-a)^{2}}{a}(m^{2}_{b}-as) +\frac{\langle0|g^{2}_{s}GG|0\rangle}{128\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(m^{2}_{b}-as)\\& -\frac{3m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{128\pi^{4}}(1-a_{\min})^{2}-\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{16\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a(4-7a) +\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{24\pi^{2}M^{2}_{B}}(1-a_{\min}) \\&-\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{96\pi^{2}s}a_{\min}. \end{aligned} \tag{B6}$

For the interpolating current
$ J^{\alpha}_{3/2,-,\Omega_{b},1,1,\lambda}(x) $ ,$ \Pi^{(\rm OPE)\alpha\beta}(p) = {\not{p}}g^{\alpha\beta}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{576\pi^{2}(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}}, \tag{B7}$

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &\frac{1}{96\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(3+a)}{a^{2}}(m^{2}_{b}-as)^{3}-\frac{3m^{2}_{s}}{32\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{2}(2+a)}{a}(m^{2}_{b}-as)^{2}\\&-\frac{m_{s}\langle0|\bar{s}s|0\rangle}{2\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a (1-a)(1+a)(m^{2}_{b}-as)+\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{1152\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(3+a)}{a^{2}}\\&-\frac{\langle0|g^{2}_{s}GG|0\rangle}{768\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a\frac{(1-a)^{2}(4-a)}{a}(m^{2}_{b}-as) -\frac{\langle0|g^{2}_{s}GG|0\rangle}{768\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(1+a)(m^{2}_{b}-as)\\& +\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{384\pi^{4}}(1-a_{\min})^{2}(2+a_{\min})-\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{48\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a(3-4a+4a^{2})\\& -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{144\pi^{2}M^{2}_{B}}(1-a_{\min})(1+a_{\min}) -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{288\pi^{2}s}a_{\min}(1-a_{\min}). \end{aligned}\tag{B8} $

For the interpolating current
$ J^{\alpha}_{3/2,-,\Omega_{b},2,1,\lambda}(x) $ ,$ \Pi^{(\rm OPE)\alpha\beta}(p) = {\not{p}}g^{\alpha\beta}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{5m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{576\pi^{2}(m^{2}_{b}-p^{2})}\right)+{\rm{other\; Lorentz\; structures}}, \tag{B9}$

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &\frac{1}{96\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(7+13a)}{a^{2}}(m^{2}_{b}-as)^{3}-\frac{3m^{2}_{s}}{32\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{2}(6+a)}{a}(m^{2}_{b}-as)^{2}\\&-\frac{m_{s}\langle0|\bar{s}s|0\rangle}{2\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a (1-a)(5-7a)(m^{2}_{b}-as)+\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{1152\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(7+13a)}{a^{2}}\\&-\frac{\langle0|g^{2}_{s}GG|0\rangle}{384\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(2+a)(m^{2}_{b}-as) +\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{384\pi^{4}}(1-a_{\min})^{2}(6+a_{\min})\\&+\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{48\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a(1-4a+18a^{2}) -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{144\pi^{2}M^{2}_{B}}(1-a_{\min})(5-7a_{\min})\\& -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{288\pi^{2}s}a_{\min}(1+3a_{\min}). \end{aligned}\tag{B10} $

For the interpolating current
$ J^{\alpha_{1}\alpha_{2}}_{5/2,-,\Omega_{b},2,1,\lambda}(x) $ ,$ \Pi^{(\rm OPE)\alpha_{1}\alpha_{2}\beta_{1}\beta_{2}}(p) = {\not{p}}g^{\alpha_{1}\alpha_{2}}g^{\beta_{1}\beta_{2}}\left(\int^{\infty}_{(m_{b}+2m_{s})^{2}}{\rm d}s\frac{\rho(s)}{s-p^2} +\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{1728\pi^{2}(m^{2}_{b}-p^{2})}\right) +{\rm{other\; Lorentz\; structures}}, \tag{B11} $

where
$ \rho(s) $ is the QCD spectral density,$ \begin{aligned}[b] \rho(s) = &\frac{1}{288\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(1+a)}{a}(m^{2}_{b}-as)^{3}-\frac{1}{288\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a\frac{(1-a)^{4}(1+2a)}{a}s(m^{2}_{b}-as)^{2}\\& -\frac{1}{144\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)^{5}s^{2}(m^{2}_{b}-as)-\frac{m^{2}_{s}}{32\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a (1-a)^{2}(m^{2}_{b}-as)^{2}\\&+\frac{m^{2}_{s}}{48\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a (1-a)^{3}s(m^{2}_{b}-as)-\frac{m_{s}\langle0|\bar{s}s|0\rangle}{18\pi^{2}}\int^{1}_{a_{\min}}{\rm d}a a(1-a)^{2}(3m^{2}_{b}-(a+1)s)\\&+\frac{m^{2}_{b}m_{s}\langle0|\bar{s}s|0\rangle}{18\pi^{2}}a_{\min}(1-a_{\min})^{3} +\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{3456\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a \frac{(1-a)^{3}(1+a)}{a}\\&-\frac{\langle0|g^{2}_{s}GG|0\rangle}{1152\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)(2-a^{2})(m^{2}_{b}-as) +\frac{\langle0|g^{2}_{s}GG|0\rangle}{6912\pi^{4}}\int^{1}_{a_{\min}}{\rm d}a(1-a)^{2}(3-4a^{2})s\\& +\frac{\langle0|g^{2}_{s}GG|0\rangle s}{3456\pi^{4}}(1-a_{\min})^{4}+\frac{m^{2}_{b}\langle0|g^{2}_{s}GG|0\rangle}{3456\pi^{4}}a_{\min}(1-a_{\min})^{3}\\& -\frac{\langle0|g^{2}_{s}GG|0\rangle s^{2}}{10368\pi^{4}M^{2}_{\rm B}}(1-a_{\min})^{5}-\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle}{3456\pi^{4}}(1-a_{\min})^{2}(1-4a_{\min})\\& +\frac{m^{2}_{s}\langle0|g^{2}_{s}GG|0\rangle s}{3456\pi^{4}M^{2}_{\rm B}}(1-a_{\min})^{3}-\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{72\pi^{2}}\int^{1}_{a_{\min}}{\rm d}aa^{2}(1-2a)\\&-\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{72\pi^{2}}\int^{1}_{a_{\min}}{\rm d}aa(1-a)-\frac{m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{432\pi^{2}}a_{\min}(1-a_{\min})(1-8a_{\min})\\&-\frac{m^{2}_{b}m_{s}\langle0|g_{s}\bar{s}\sigma\cdot Gs|0\rangle}{108\pi^{2}M^{2}_{\rm B}}a_{\min}(1-a_{\min})^{2} -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{1296\pi^{2}M^{2}_{\rm B}}(1-a_{\min})^{2}(4+a_{\min})\\& +\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle s}{1296\pi^{2}M^{4}_{\rm B}}(1-a_{\min})^{2}(5-4a_{\min})-\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle s^{2}}{1296\pi^{2}M^{6}_{\rm B}}(1-a_{\min})^{3}\\& -\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{5184\pi^{2}s}a_{\min} +\frac{m_{s}\langle0|\bar{s}s|0\rangle\langle0|g^{2}_{s}GG|0\rangle}{5184\pi^{2}M^{2}_{\rm B}}a_{\min}. \end{aligned}\tag{B12} $

In the above equations,
$a_{\min} = m^{2}_{b}/s$ , and$M^{2}_{\rm B}$ is the Borel parameter.
P-wave Ωb states: masses and pole residues
- Received Date: 2021-10-25
- Available Online: 2022-04-15
Abstract: In this study, we consider all P-wave






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: