-
The study of the nucleon resonances (
$ N^\ast $ 's) has always been a topic of great interest in hadron physics because a deeper understanding of the nucleon resonances is essential to obtain insights into the nonperturbative regime of quantum chromodynamics (QCD). Presently, our understanding of most of the$ N^\ast $ 's is mainly from the production reactions of$ \pi N $ ,$ \eta N $ ,$ K \Lambda $ , and$ K\Sigma $ channels. Recently, the photoproductions of vector mesons,$ \eta' $ meson, and$ KY^\ast \; (Y = \Lambda,\Sigma) $ have also been extensively investigated experimentally and theoretically to better understand the$ N^\ast $ 's [1-15].In this study, we focus on the photoproduction reaction
$ \gamma n \to K^{\ast 0} \Lambda $ . The threshold of the$ K^\ast\Lambda $ photoproduction is approximately the center-of-mass energy$ W\approx 2.0 $ GeV; thus, this reaction is more suitable to study the less-explored high-mass resonances. Further, the isospin$ I = 1/2 $ for the final states$ K^\ast\Lambda $ forbids the s-channel$ I = 3/2 \; \Delta $ resonance exchanges to contribute, thus providing facilities for the extraction of information on the$ I = 1/2 $ nucleon resonances.Unlike the reaction
$ \gamma p \to K^{\ast +} \Lambda $ for which the high-precision differential cross-section data [16] and the data on spin density matrix elements [17] are available, the only experimental data available for$ \gamma n \to K^{\ast 0} \Lambda $ are differential cross sections at three photon energies in the range$ 1.9 < E_\gamma < 2.5 $ GeV obtained from the CLAS Collaboration [18].The CLAS differential cross-section data for
$ \gamma n \to K^{\ast 0} \Lambda $ [18] have been thus far theoretically analyzed in two publications [19, 20]. In Ref. [19], the reaction$ \gamma n \to K^{\ast 0} \Lambda $ was studied using an effective Lagrangian approach; no resonance exchanges were considered and the data were described by adjusting the cutoff parameter of the t-channel form factor. The differential cross sections of$ \gamma n \to K^{\ast 0} \Lambda $ [18] were overwhelmingly dominated by the t-channel K exchange, while the contributions from all other terms were totally negligible. Although the cross-section data for$ \gamma n \to $ $ K^{\ast 0} \Lambda $ have been qualitatively described in Ref. [19], it is not clear whether the employed interactions, particularly the overwhelmingly dominated t-channel K exchange, works simultaneously for the reaction$ \gamma p \to K^{\ast +} \Lambda $ , of which not only the high-precision differential cross-section data but also the data on spin density matrix elements are available [16, 17]. In Ref. [20], the differential cross-section data for$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ [16, 18] were simultaneously analyzed by considering the t-channel K,$ K^\ast $ , and κ exchanges within a Regge model. The t-channel K exchange dominated the differential cross sections in both reactions. Nevertheless, owing to the lack of contributions from the s-channel nucleon resonance exchanges, the angular distribution data for the$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ reactions were only qualitatively described in Ref. [20]. Furthermore, the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ [17] was not considered in the analysis reported in Ref. [20].As the hadronic vertices and propagators are same in both
$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ except for certain possible isospin factors, and because most of the electromagnetic coupling constants can be determined by the radiative decays of the corresponding hadrons, a combined analysis of the available differential cross-section data for$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ and the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ is of great significance. It provides more constraints to the theoretical model and contributes to the reliability of the data analysis of$ \gamma n \to K^{\ast 0} \Lambda $ , for which only the differential cross-section data at three energy points are available so far.In Ref. [5], we have studied the photoproduction reaction
$ \gamma p \to K^{\ast +} \Lambda $ in an effective Lagrangian approach. Apart from the t-channel K,$ K^\ast $ , and κ exchanges, u-channel Λ, Σ, and$ \Sigma^\ast $ exchanges, s-channel N exchange, and interaction current, we considered as few as possible nucleon resonance exchanges in the s channel for constructing the reaction amplitudes to describe the data. The gauge invariance of the photoproduction amplitudes was fully implemented. It was found that by introducing the$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ resonance exchanges, the available data on both differential cross sections and spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ [16, 17] can be reasonably reproduced. The t-channel K exchange and s-channel$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ exchanges contributed predominantly for this reaction.In this study, we investigated the photoproduction reaction
$ \gamma n \to K^{\ast 0} \Lambda $ based on the same reaction mechanism as that of$ \gamma p \to K^{\ast +} \Lambda $ reported in our previous work [5]. Our aim was to obtain a unified description of all the available differential cross-section data for both$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ and the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ uisng the same reaction model.The paper is organized as follows. Sec. II briefly introduces the framework of our theoretical model. The numerical results are presented and discussed in Sec. III. The summary and conclusions are provided in Sec. IV.
-
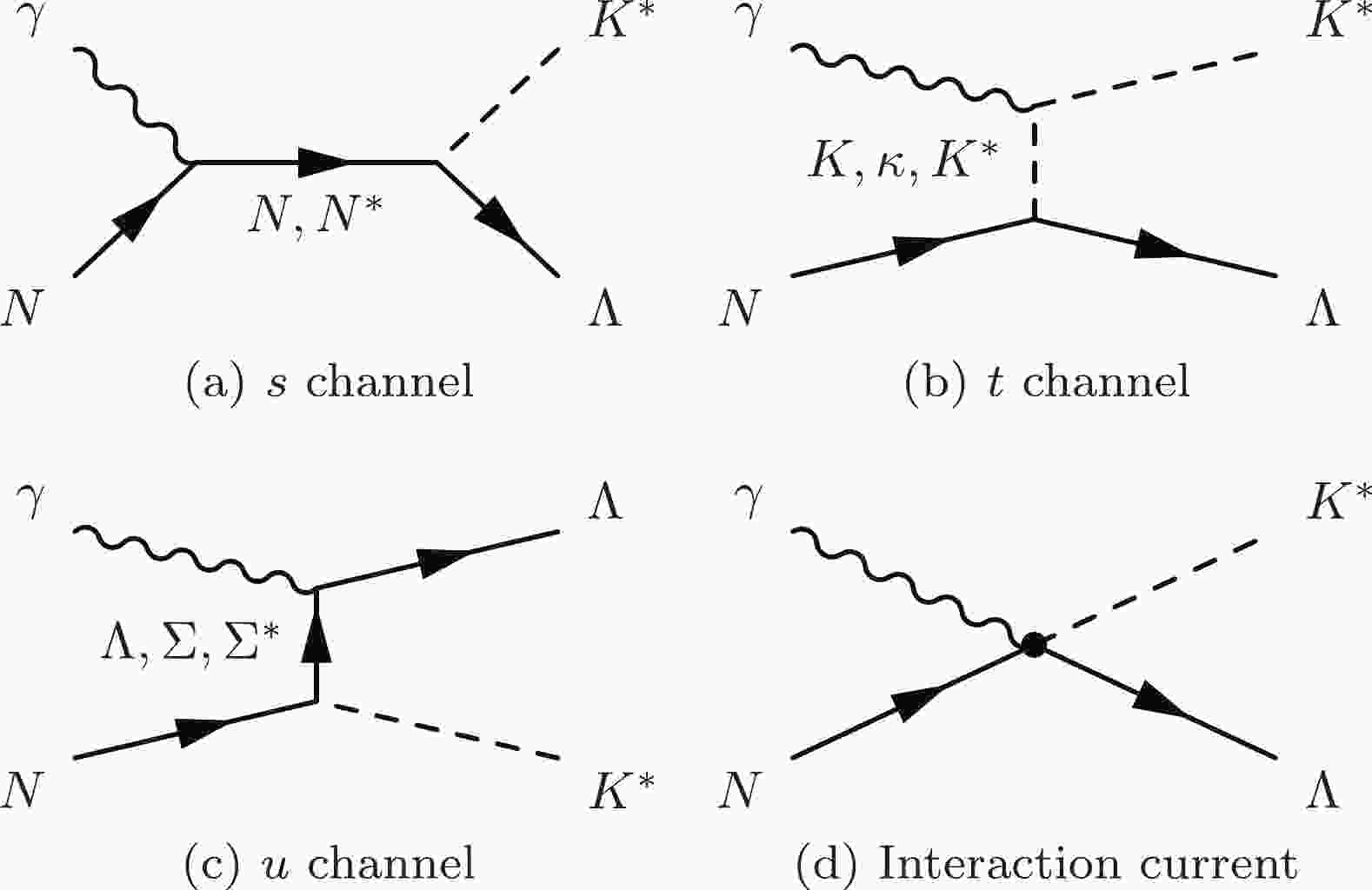
The generic structures of the photoproduction amplitudes for
$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ in our effective Lagrangian approach are illustrated in Fig. 1 [1, 4, 5]. Particularly, we considered the t-channel K,$ K^\ast $ , and κ exchanges, u-channel Λ, Σ, and$ \Sigma^\ast $ exchanges, s-channel N and$ N^\ast $ exchanges, and interaction current in constructing the reaction amplitudes for the$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ reactions. The s-, t-, and u-channel amplitudes can be obtained directly by calculating the corresponding Feynman diagrams. The interacting current consists of the conventional Kroll-Ruderman term and an auxiliary current; the latter was constructed for the full photoproduction amplitudes to satisfy the generalized Ward-Takahashi identity and thus becomes fully gauge invariant [1]. For the photoproduction reaction$ \gamma n \to K^{\ast 0} \Lambda $ , the interaction current and t-channel$ K^\ast $ exchange vanish owing to the neutral charges of$ K^{\ast 0} $ and n. Here, the reaction amplitudes are transverse; thus, the requirement of gauge invariance on the production amplitudes is already fulfilled.
Figure 1. Generic structures of the photoproduction amplitudes for
$\gamma p \to K^{\ast +} \Lambda$ and$\gamma n \to K^{\ast 0} \Lambda$ . Time proceeds from left to right. For$\gamma n \to K^{\ast 0} \Lambda$ , the interaction current and t-channel$K^\ast$ exchange vanish.The effective Lagrangians, resonance propagators, and phenomenological form factors for the photoproduction reaction
$ \gamma N \to K^{\ast} \Lambda $ have been reported in Ref. [1], where we analyzed the differential cross-section data for$ \gamma p \to K^{\ast +} \Lambda $ in an effective Lagrangian approach; we do not repeat them here for the sake of brevity. For the$ \gamma n \to K^{\ast 0} \Lambda $ reaction that we study in this paper, the hadronic coupling constants, form factor cutoffs, and resonance masses and widths remain the same as those of$ \gamma p \to K^{\ast +} \Lambda $ . We quote them from our recent work of Ref. [5], which was an update of the work of Ref. [1], where we simultaneously analyzed the differential cross-section data and data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ .In principle, the electromagnetic coupling constants in the reaction
$ \gamma n \to K^{\ast 0} \Lambda $ are different from those in$ \gamma p \to K^{\ast +} \Lambda $ when the N or$ K^{\ast} $ are involved in the electromagnetic vertices. For the t-channel κ exchange, the coupling constant$ g_{\gamma \kappa^0 K^{\ast 0}} = -0.428 $ is taken from Refs. [2, 3], determined using a vector-meson dominance model proposed by Black et al. [21]. For the t-channel K exchange, the coupling constant$ g_{\gamma K^0 K^{\ast 0}} = -0.631 $ is determined using the decay width of$ K^{\ast 0} \to K^0 \gamma $ reported by the Review of Particle Physics (RPP) [22] with the sign inferred from$ g_{\gamma \pi \rho} $ [23] via the flavor SU(3) symmetry considerations in conjunction with the vector-meson dominance assumption. In the s channel, apart from the N exchange, it was found in our previous work [5] that the$ N(2000)5/2^+ $ and$ N(2060)5/2^- $ exchanges are required to describe the available differential cross-section data and the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ . Here, the same resonances are considered in the reaction$ \gamma n \to K^{\ast 0} \Lambda $ , with their electromagnetic coupling constants being treated as fit parameters because there is no experimental information for the helicity amplitudes of the$ N(2000)5/2^+ \to n\gamma $ and$ N(2060)5/2^- \to n\gamma $ decays.In tree-level calculations as presented in this study and in Refs. [1, 4, 5], only the products of the electromagnetic and hadronic coupling constants
$ g_{RN \gamma}^{(1,2)} g_{R\Lambda K^\ast}^{(1,2,3)} $ of each resonance can be uniquely determined. As the ratios of$ g_{R\Lambda K^\ast}^{(2)}/g_{R\Lambda K^\ast}^{(1)} $ and$ g_{R\Lambda K^\ast}^{(3)}/g_{R\Lambda K^\ast}^{(1)} $ for both$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ exchanges have been determined in our previous study of$ \gamma p \to K^{\ast +} \Lambda $ [5], for the$ \gamma n \to K^{\ast 0} \Lambda $ reaction reported in this study, only the products$ g_{RN \gamma}^{(1)} g_{R\Lambda K^\ast}^{(1)} $ and$ g_{RN \gamma}^{(2)} g_{R\Lambda K^\ast}^{(1)} $ remain as adjustable parameters. They are determined using a fit to the available data for this reaction. -
The hadronic vertices and propagators in the
$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ reactions are the same except for some possible isospin factors, and the electromagnetic couplings in these two reactions, in principle, can be determined by the radiative decays of the corresponding hadrons. Therefore, a unified description of all the available data for both$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ is required. This would incorporate more constraints on the theoretical model and results in a more reliable understanding of the reaction mechanisms of$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ .In our previous work [5], we have investigated the photoproduction reaction
$ \gamma p \to K^{\ast +} \Lambda $ in an effective Lagrangian approach. By considering the t-channel K,$ K^\ast $ , and κ exchanges, u-channel Λ, Σ, and$ \Sigma^\ast $ exchanges, s-channel N,$ N(2060)5/2^- $ , and$ N(2000)5/2^+ $ exchanges, and interaction current in constructing the reaction amplitudes, we satisfactorily reproduced the high-precision differential cross section data and the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ . It was found that the t-channel K exchange and s-channel$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ exchanges predominantly contribute for this reaction.In this paper, we studied the photoproduction reaction
$ \gamma n \to K^{\ast 0} \Lambda $ based on the same reaction mechanism as that of$ \gamma p \to K^{\ast +} \Lambda $ in our previous study [5]. The interaction current and t-channel$ K^\ast $ exchange vanish owing to the neutral charges of$ K^{\ast 0} $ and n. The hadronic coupling constants, form factor cutoffs, and resonance masses and widths for$ \gamma n \to K^{\ast 0} \Lambda $ are the same as those of$ \gamma p \to K^{\ast +} \Lambda $ . The only adjustable parameters in the calculation of the amplitudes for$ \gamma n \to K^{\ast 0} \Lambda $ are the products of the resonance hadronic and electromagnetic coupling constants,$ g_{RN \gamma}^{(1)} g_{R\Lambda K^\ast}^{(1)} $ and$ g_{RN \gamma}^{(2)} g_{R\Lambda K^\ast}^{(1)} $ , which are determined using a fit to the available differential cross-section data for$ \gamma n \to K^{\ast 0} \Lambda $ . The fitted values for the$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ resonances are listed in Table 1. The corresponding results of the differential cross sections for$ \gamma n \to K^{\ast 0} \Lambda $ are plotted in Fig. 2.$N(2000)5/2^+$ 

$N(2060)5/2^-$ 

$g_{RN \gamma}^{(1)} g_{R\Lambda K^\ast}^{(1)}$ 

$-54.26\pm0.74$ 

$-8.13\pm0.51$ 

$g_{RN \gamma}^{(2)} g_{R\Lambda K^\ast}^{(1)}$ 

$-27.98\pm0.72$ 

$8.46\pm0.53$ 

Table 1. Fitted values of adjustable parameters in the
$\gamma n \to K^{\ast 0} \Lambda$ reaction.
Figure 2. (color online) Differential cross sections for
$ \gamma n \to K^{\ast 0} \Lambda $ as a function of$ \cos\theta $ with$ \theta $ being the scattering angle in center-of-mass frame. The black solid lines represent the results obtained from the full calculation. The red dotted, green dash-dotted, and blue dashed lines represent the individual contributions from the t-channel K exchange, s-channel$ N(2060)5/2^- $ exchange, and s-channel$ N(2000)5/2^+ $ exchange, respectively. The data are taken from the CLAS Collaboration [18].In Fig. 2, the black solid lines represent the results obtained from the full calculation. The red dotted, green dash-dotted, and blue dashed lines represent the individual contributions from the t-channel K exchange, s-channel
$ N(2060)5/2^- $ exchange, and s-channel$ N(2000)5/2^+ $ exchange, respectively. The contributions from the remaining individual terms are too small to be clearly observed with the scale used; hence, they are not plotted in the figure. Fig. 2 shows that our calculated differential cross sections for$ \gamma n \to K^{\ast 0} \Lambda $ agree quite well with the experimental data. The t-channel K exchange dominates the angular distributions in all the three energy points that were considered. Particularly, it is responsible for the peaks of the differential cross sections at the forward angles. The s-channel$ N(2060)5/2^- $ exchange provides significant contributions; considerable contributions from the s-channel$ N(2000)5/2^+ $ exchange are also observed.In Ref. [19], the differential cross sections of
$ \gamma n \to K^{\ast 0} \Lambda $ are almost fully described by the t-channel K exchange. In this study, we observed much smaller contributions from the t-channel K exchange. The difference arises from the t-channel form factors. In Ref. [19], a monopole form factor is used, and the cutoff parameter is fixed by the$ \gamma n \to K^{\ast 0} \Lambda $ differential cross section data, which results in$ \Lambda_K = 1050 $ MeV. In this study, a dipole form factor with the cutoff parameter$ \Lambda_K = 1009 $ MeV is employed, which has been determined by the high-precision differential cross-section data and the data on spin density matrix elements for$ \gamma p \to K^{\ast +} \Lambda $ in our previous study [5].In Ref. [20], the differential cross sections for
$ \gamma n \to K^{\ast 0} \Lambda $ are approximately described by the t-channel K-trajectory exchange. However, the angular distributions for the$ \gamma p \to K^{\ast +} \Lambda $ reaction are only qualitatively described owing to the lack of s-channel resonance exchanges. Particularly, the shapes of the angular distributions near the$ K^{\ast +}\Lambda $ threshold exhibited by the CLAS high-precision data, which are suggested to be dominated by the contributions from the$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ resonance exchanges [1, 4, 5], are missing.In this study, the contributions from the t-channel K exchange are not flexible. Instead, they are fully determined in our previous study of the
$ \gamma p \to K^{\ast +} \Lambda $ reaction [5], for which considerable data are available for the differential cross sections and spin density matrix elements.Fig. 3 shows the total cross sections of
$ \gamma n \to K^{\ast 0} \Lambda $ predicted in this study. For comparison, the total cross sections of$ \gamma p \to K^{\ast +} \Lambda $ reported in Ref. [5] are also presented. The dominant individual contributions arise from the t-channel K exchange, s-channel$ N(2060)5/2^- $ exchange, and s-channel$ N(2000)5/2^+ $ exchange in both the reactions, which are plotted with red dotted, green dash-dotted, and blue dashed lines, respectively. The individual contributions from other terms are too small to be clearly observed with the scale used; hence, they are not plotted in Fig. 3. The contributions from the t-channel K exchange dominate the total cross sections of$ \gamma n \to K^{\ast 0} \Lambda $ . Further, these contributions are much stronger than those observed in$ \gamma p \to K^{\ast +} \Lambda $ because the coupling constant$ g_{\gamma K^0 K^{\ast 0}} = -0.631 $ has a much larger magnitude than that of$ g_{\gamma K^+ K^{\ast +}} = 0.413 $ as determined by the radiative decays of$ K^{\ast 0} \to K^0 \gamma $ and$ K^{\ast +} \to K^+ \gamma $ . In both the reactions, the contributions from the t-channel K exchange are similar to those observed from the Born term, indicating negligible contributions from other nonresonant terms. For$ \gamma p \to K^{\ast +} \Lambda $ , the$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ exchanges significantly contribute to the cross sections, and the coherent sum of them dominates the total cross sections of this reaction. For$ \gamma n \to K^{\ast 0} \Lambda $ , the resonance contributions are much weaker but evident. Particularly, the s-channel$ N(2060)5/2^- $ exchange provides slightly weaker contributions in$ \gamma n \to K^{\ast 0} \Lambda $ than in$ \gamma p \to K^{\ast +} \Lambda $ , and the s-channel$ N(2000)5/2^+ $ exchange provides much smaller contributions in$ \gamma n \to K^{\ast 0} \Lambda $ than in$ \gamma p \to K^{\ast +} \Lambda $ .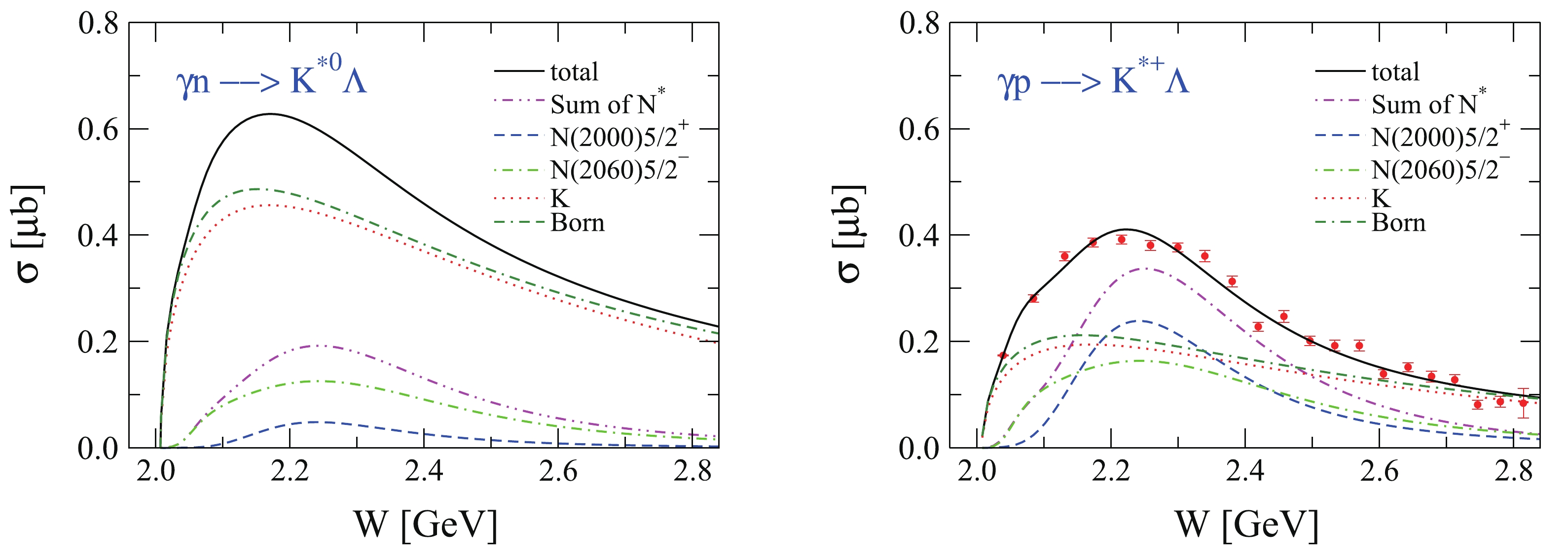
Figure 3. (color online) Predicted total cross sections with dominant individual contributions for
$ \gamma n \to K^{\ast 0} \Lambda $ (left) and$ \gamma p \to K^{\ast +} \Lambda $ (right). Data for$ \gamma p \to K^{\ast +} \Lambda $ are taken from the CLAS Collaboration [16] but not included in the fit.Fig. 3 shows that our predicated total cross sections of
$ \gamma n \to K^{\ast 0} \Lambda $ are approximately$ 1.5 $ times larger than those of$ \gamma p \to K^{\ast +} \Lambda $ . In Ref. [19], the maximum of the total cross sections was predicated to be approximately$ 0.4 $ μb, which is approximately equal to that of$ \gamma p \to K^{\ast +} \Lambda $ . In Ref. [20], the predicated total cross sections of$ \gamma n \to K^{\ast 0} \Lambda $ are approximately$ 1.1 $ times larger than those of$ \gamma p \to K^{\ast +} \Lambda $ . Experimental data on the total cross sections of$ \gamma n \to K^{\ast 0} \Lambda $ are called for distinguish these theoretical models. -
In this study, we investigated the photoproduction reaction
$ \gamma n \to K^{\ast 0} \Lambda $ based on the same reaction mechanism as that in our previous study of the$ \gamma p \to K^{\ast +} \Lambda $ reaction. Our aim was to obtain a unified description of the available differential cross-section data for the$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ reactions and the data on spin density matrix elements for the$ \gamma p \to K^{\ast +} \Lambda $ reaction within the same effective Lagrangian model. A combined analysis of all the available data for both these two reactions may incorporate more constraints on the theoretical model and result in more reliable understanding of the reaction mechanisms of the$ \gamma p \to K^{\ast +} \Lambda $ and$ \gamma n \to K^{\ast 0} \Lambda $ reactions.The interaction current and t-channel
$ K^\ast $ exchange vanish for$ \gamma n \to K^{\ast 0} \Lambda $ owing to the neutral charges of$ K^{\ast 0} $ and n. Furthermore, the t-channel K and κ exchanges, u-channel Λ, Σ, and$ \Sigma^\ast $ exchanges, and s-channel N,$ N(2060)5/2^- $ , and$ N(2000)5/2^+ $ exchanges are considered in calculating the reaction amplitudes. The hadronic coupling constants, propagators, and the resonance masses and widths were taken from our previous work of Ref. [5] for the study of$ \gamma p \to K^{\ast +} \Lambda $ . The adjustable parameters in this study are the products of the resonance hadronic and electromagnetic coupling constants,$ g_{RN \gamma}^{(1)} g_{R\Lambda K^\ast}^{(1)} $ and$ g_{RN \gamma}^{(2)} g_{R\Lambda K^\ast}^{(1)} $ , which are determined using a fit to the available differential cross-section data for$ \gamma n \to K^{\ast 0} \Lambda $ .The available differential cross-section data for
$ \gamma n \to K^{\ast 0} \Lambda $ have been reproduced quite well. The numerical results show that the contributions from the t-channel K exchange dominate the cross sections of the$ \gamma n \to K^{\ast 0} \Lambda $ reaction. Unlike Refs. [19, 20], where the cross sections for$ \gamma n \to K^{\ast 0} \Lambda $ are almost fully described by the t-channel K exchange and all other contributions are negligible, in this study, the contributions from the$ N(2060)5/2^- $ and$ N(2000)5/2^+ $ exchanges were observed to be considerable. The total cross sections of$ \gamma n \to K^{\ast 0} \Lambda $ were predicated to be$ 1.5 $ times larger than those of$ \gamma p \to K^{\ast +} \Lambda $ . More experimental data on this reaction are required to incorporate further constraints on the theoretical models. -
Author Y.M.Z. is grateful to Yu Zhang and Ai-Chao Wang for the useful and constructive discussions.
Photoproduction reaction γn → K*0Λ in an effective Lagrangian approach
- Received Date: 2021-10-14
- Available Online: 2022-02-15
Abstract: In our previous work [Phys. Rev. C 101, 014003 (2020)], the photoproduction reaction





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: