-
Recently, owing to the development of both experimental facilities and computation capabilities, the study on the shell evolution in neutron-rich nuclei has become an important and challenging subject. It provides a ground for understanding the composition of the nuclear force and how the elements in the universe are formed. The shell structures of atomic nuclei are firstly explained by the independent particle model (IPM). The nuclear mean field potential plus the spin-orbit (SO) coupling correctly produces magic numbers such as 8, 20, 28, 50, 82, and 126 in stable nuclei [1, 2]. Inside a nucleus, the short-range nucleon-nucleon (NN) repulsion combined with the Pauli exclusion principle make the independent particle motion reasonable in the first approximation. However, as more nucleons are added into the valence orbits outside the closed shell, the residual interaction between the valence nucleons must be taken into account. The extended version of the IPM, namely the interacting shell model, is then proposed to tackle this complicated many-body problem [3, 4]. Meanwhile, the (effective) single-particle energy changes accordingly, leading that a magic number may emerge or disappear, namely, the evolution of the shell closure. At present, it is believed that the monopole part of the NN interactions (especially the tensor force effect) and three-body interactions determine the shell evolution within the shell model context [5-7]. In this sense, new magic numbers such as
$ N = 32 $ and$ N = 34 $ may emerge in calcium isotopes and$ ^{14,16,22,24} $ O are expected to be four possible doubly-magic nuclei [7, 8], which are also experimentally confirmed to some extent [9].Under the above mentioned framework, the shell evolution is interpreted and understood in view of the effective single particle energy (ESPE), which is composed of the naive single particle energy (SPE) and the shift generated by the residual interactions between the valence nucleons. The latter one is actually being taken as the key physical quantity to detect the mechanics behind the shell evolution phenomenon. The former SPE comes from the calculated single-particle spectrum based on the mean-field potential experienced by an individual nucleon. As compared to the monopole part of the NN interactions or three-body interactions, the attention focused on the SPE seems to be quite limited when considering the shell structural evolution. This is partly owing to the fact that the contribution of the SPE to the final ESPE is relatively small, and the SPE usually varies smoothly, like for one isotopic chain [4]. Consequently, if one focuses on the change in the shell structure, the SPE can be only a basis and do not affect the variation in the ESPE, namely, the shell evolution. In contrast, the conventional magic numbers regulated by the gaps of the SPE spectrum have been very well known, whereas the deviation from this achievement is more appealing in terms of the structural evolution. However, the isospin dependence has been commonly absorbed into the single particle potential [10, 11], resulting in the single particle spectrum serving as the starting point in all practical many-body methods. With regard to the neutron-rich side of the Segrè chart, the large neutron-proton asymmetry would enhance the isospin effect in the nuclear mean field. The SPE can be then not as previously expected, which may bring a different mean field picture for the shell evolution in neutron rich nuclei.
The present study aims at clarifying the the isospin dependence of the SO potential regarding the evolution of shell closure, in particular for nuclei with extreme neutron-proton ratios. Recently, the shell structures of neutron rich nuclei have been analyzed to some extent by focusing on the isospin dependence of the SO splitting from the above phenomenological single-particle point of view [12]. Here, we are interested in conducting a systematical analysis on the shell evolution through concentrating on the isospin-related term of not only the mean-field Woods-Saxon (WS) potential but also the SO coupling, with the help of the available experimental spectra of single particle or hole states. One can then answer the question: How does the weakening or enhancement in the SO splitting affect the shell evolution in neutron rich nuclei from a single particle perspective? We hope that the present SPE results can provide a more reasonable baseline for probing into the shell evolution in exotic nuclei close to the neutron dripline. The remainder of this paper is organized as follows. The construction of the effective WS single particle potential and the isospin dependent term is introduced in Sec. II, and Sec. III presents detailed discussions on the evolution of various shells for some typical or reported isotopes. A summary is given in the last section.
-
Within the IPM, the key point is that a single nucleon motion is governed by the average field produced by all other nucleons. As is well known, the harmonic oscillator (HO) mean field combined with the SO coupling term was the first successful mean field treatment, predicting the correct sequence of energy levels and magic numbers [12]. However, currently, the subjects of nuclear physics have expanded far beyond the valley of stability into the broader region of nuclide chart, such as neutron rich exotic nuclei. At this time, the continuum spectrum of the mean field potential appears to be indispensable, whereas the outer part of the HO potential cannot take this responsibility. Moreover, in reality, one may expect the SO coupling to be reduced for neutron dripline nuclei with a diffusive nuclear surface because the SO interaction peaks at the surface of nuclei. This cannot be achieved by the gradient of the HO potential involved in the coefficient of the SO term either. Hence, the more realistic WS potential, a common choice in modern nuclear theoretical techniques [10, 13, 14], is taken to describe the single particle shell structure. As additional information, statistical correlation analysis was performed very recently to refine the parameterization of the mean-field Hamiltonian of WS type, serving the nuclear shape description [15].
After the subtle modifications via considering the reduced mass and the isospin symmetry [10], the total effective single-nucleon Hamiltonian reads as
$ H = \frac{p^2}{2\mu}+V(r)+V_{c}(r)+\frac{\hbar^2}{2\mu c^2r}\left(\frac{\partial}{\partial r}\widetilde V(r)\right) \boldsymbol{L}\cdot\boldsymbol{S}. $

(1) The first term is the single-nucleon kinetic energy, and
$ \mu $ is the reduced mass of the nucleon-core system. Based on the lowest order isospin invariant, the effective nuclear potential,$ V(r) $ , related with the scalar product of the isospin of the nucleon, t, and the core, T', is taken as [16]$ V(r) = -Vf(r,R,a),\quad V = V_0\left(1-\frac{4\kappa}{A}\langle\boldsymbol{t}\cdot\boldsymbol{T}^{'}\rangle\right), $

(2) where
$ V_0 $ is the strength parameter of the nuclear potential. The coefficient$ \kappa $ regulates the isospin dependent term of the nuclear potential, tuning the depth of the nuclear potential as well. As mentioned in Ref. [10], the value of$ \kappa $ is positive after the "minus" sign choice in the above formula, which is consistent with conventions [10, 12, 17, 18]. By combining the relationship, t + T′ = T, and the assumption that the isospin number is$ T = |T_z| = |N-Z|/2 $ for the ground state of one nucleus, the behavior of −4〈t·T′〉 is then determined as$-4\left\langle \boldsymbol{t}\cdot \boldsymbol{T}' \right\rangle =\left\{ \begin{matrix} \begin{align} & 3, \\ & \pm (N-Z+1)+2, \\ & \pm (N-Z-1)+2, \\ \end{align} & \begin{matrix} N=Z, \\ N\geqslant Z, \\ N\leqslant Z. \\ \end{matrix} \\ \end{matrix} \right. $

(3) Here, the upper and lower signs denote a proton and a neutron, respectively. Such a modified isospin dependence, introduced in the nuclear mean-field potential, can lead to interestingly different spectra for light nuclei around
$ N = Z $ [10]. The Coulomb potential,$ V_c(r) $ , corresponding to a nucleon electromagnetically interacting with a uniformly charged sphere of radius$ R_c $ , is given by$ V_c(r) = \frac{Z^{'}e^2}{4\pi\varepsilon_0}\left\{ \begin{aligned}\dfrac{3}{2R_c},\quad& r \leqslant R_c, \\ \dfrac{1}{r}, \quad\quad& r \geqslant R_c, \end{aligned} \right. $

(4) where
$ Z^{'} $ is the proton number of the core nucleus. As for the last SO coupling term, the potential,$ \widetilde V(r) $ , is supposed to be not equal to the original potential,$ V(r) $ , along with a different form factor [10]. Consequently, the form of$ \widetilde V(r) $ is constructed as$ \widetilde{V}(r) = -\widetilde{V}f(r,R_{\rm so},a_{\rm so}), \quad \widetilde{V} = \lambda V_0\left(1-\frac{4\kappa_{\rm so}}{A}\langle\boldsymbol{t}\cdot\boldsymbol{T}^{'}\rangle\right), $

(5) The characteristic function,
$ f(r,R,a) $ , as suggested by Woods and Saxon [13], has the Fermi form,$ f(r,R,a) = \left[1+\exp\left(\frac{r-R}{a}\right)\right]^{-1}, $

(6) where the size parameter,
$ R $ , and the surface diffuseness,$ a $ , are to be determined. Following the conventional choice of the WS potential parameterization, the size and diffuseness parameters are regulated by$ R = R_c = R_0A^{1/3} $ ,$ R_{\rm so} = R_{0, {\rm so}}A^{1/3} $ , and$ a = a_{\rm so} $ . As mentioned before, the isospin dependence in the mean-field NN potential appears to be increasingly important toward unstable nuclei with extreme neutron-proton ratios. More specifically, the strength of the single-particle SO potential may be enhanced in neutron-rich nuclei [12], whereas the reduced SO splitting, sometimes regarded as "shell quenching," is expected to be due to the damping of the radial nucleon density [7]. In this sense, to somewhat explore this debate and probe into the evolution of a single particle shell, one should pay special attention to the key isospin-related parameters,$ \kappa $ and$ \kappa_{\rm so} $ , in the strength of the central and SO interactions, respectively. In order to systematically investigate the isospin effect in the SPE evolution, three kinds of calculations with$ \kappa_{\rm so} = \pm\kappa, 0 $ are performed here with the GAMOW code [19], corresponding to the strengthened, weakened, and unchanged SO channel of the single-particle potential. It is worth noting that the unconventional negative$ \kappa_{\rm so} $ was discussed by Isakov et al. [20] in terms of the nature of two-body SO forces via the isovector dominance (see also supplemental materials in Ref. [7]). Similar to the global optimization procedure in Ref. [21], all above parameters in the single particle Hamiltonian are adjusted to single particle and single hole states in the vicinity of doubly magic nuclei$ ^{16}_{8} $ O,$ ^{40}_{20} $ Ca,$ ^{48}_{20} $ Ca,$ ^{100}_{50} $ Sn,$ ^{132}_{50} $ Sn, and$ ^{208}_{82} $ Pb, as listed in Refs. [10, 20]. In Table 1, the parameter set obtained in this study is presented and compared with other theoretical results for different cases of$ \kappa $ and$ \kappa_{\rm so} $ . One worthwhile point is that there are slight discrepancies between the present parameters and other reported values despite the same treatment of$ \kappa $ and$ \kappa_{\rm so} $ . This is actually common in the model fitting process, which is tackled in the model uncertainty evaluations via statistical methods [15].V0/MeV ro/fm r0,so/fm a = aso/fm λ κ Present 51.47 1.278 1.165 0.654 23.165 0.644 $\kappa_{\rm so} = \kappa$ 

Ref. [17] 51 1.27 1.27 0.67 32.13 0.647 $\kappa_{\rm so} = \kappa$ 

Ref. [18] 49.6 1.374(n)/1.275(p) 1.31(n)/1.32(p) 0.7 35(n)/36(p) 0.86 $\kappa_{\rm so} = \kappa$ 

Present 51.25 1.283 1.076 0.637 20.716 0.640 $\kappa_{\rm so} = -\kappa$ 

Ref. [12] 50.92 1.285 1.146 0.691 24.07 0.644 $\kappa_{\rm so} = -\kappa$ 

Present 51.40 1.279 1.129 0.647 22.112 0.643 $\kappa_{\rm so} = 0$ 

Ref. [10] 52.06 1.26 1.16 0.662 24.1 0.639 $\kappa_{\rm so} = 0$ 

Table 1. WS potential parameters obtained by fitting to the available single-particle and single-hole states around doubly-magic nuclei with restriction
$\kappa_{\rm so} = \pm\kappa,0$ and comparison with existing parameterizations.Before proceeding with the detailed results, it is necessary to point out the novelties of the present study compared with previous ones [10, 12]. The main objective of Ref. [10] was a systematical investigation on the WS-type single particle potential serving a many-body microscopic calculation, whereas the shell evolution behavior was pursued in Ref. [12] and this study. Moreover, the total energy surface of specific nuclei and the related shape coexistence were carefully examined in Ref. [12]. However, the detailed analysis on the evolution of shell structure is relatively-lacking despite the indication of the emergence and absence of magic numbers. In the present study, we focus on a comparative analysis between the SPE evolutions in this IPM picture and those from the interacting shell model (dominance of the tensor force) [8, 10] in detail, through a comprehensive choice of the isospin-related parameters, namely,
$ \kappa $ and$ \kappa_{\rm so} $ . This is significantly different from the content of Ref. [12], and should be useful for the refinement of the monopole channel of the NN interactions in the modern shell model. The purpose here is, as mentioned above, to reexamine and understand the role of the mean-field potential in the shell evolution phenomenon, especially toward the dripline region. In contrast, the specific results of the SPE scheme are improved or modified, such as the$ N = 14 $ and$ N = 16 $ shell gaps in the WS potential (rather than those in the schematic HO potential of Ref. [12]). Moreover, the additional figure of isotones around$ N = 32 $ and$ N = 34 $ is valuable for explore these new magic numbers. Furthermore, the$ \kappa_{\rm so} = 0 $ case is added here to be a benchmark. These components could also lead to different knowledge of shell evolution from the viewpoint of the IPM to some extent. -
The shell evolution in exotic nuclei has received special attention for decades [7, 22-26], such as the emergence of new magic numbers
$ N = 14 $ , 16, 32, and 34 and the disappearance of traditional magic number$ N = 20 $ [22-25]. Such exotic phenomena are supposed to be attributed to the monopole part of the NN interactions, especially the tensor force [27, 28], within the interacting shell model. In the present study, we attempt to systematically analyze these expected or reported evolutions of shell structure from the independent particle viewpoint. This procedure can not only directly check the isospin effect on the SPE evolution but also provide a more comprehensive benchmark for further microscopic studies on shell evolution in view of the ESPE variation. The emergence of new magic numbers and the evolution of the traditional shell closure are specifically discussed in the following subsections. -
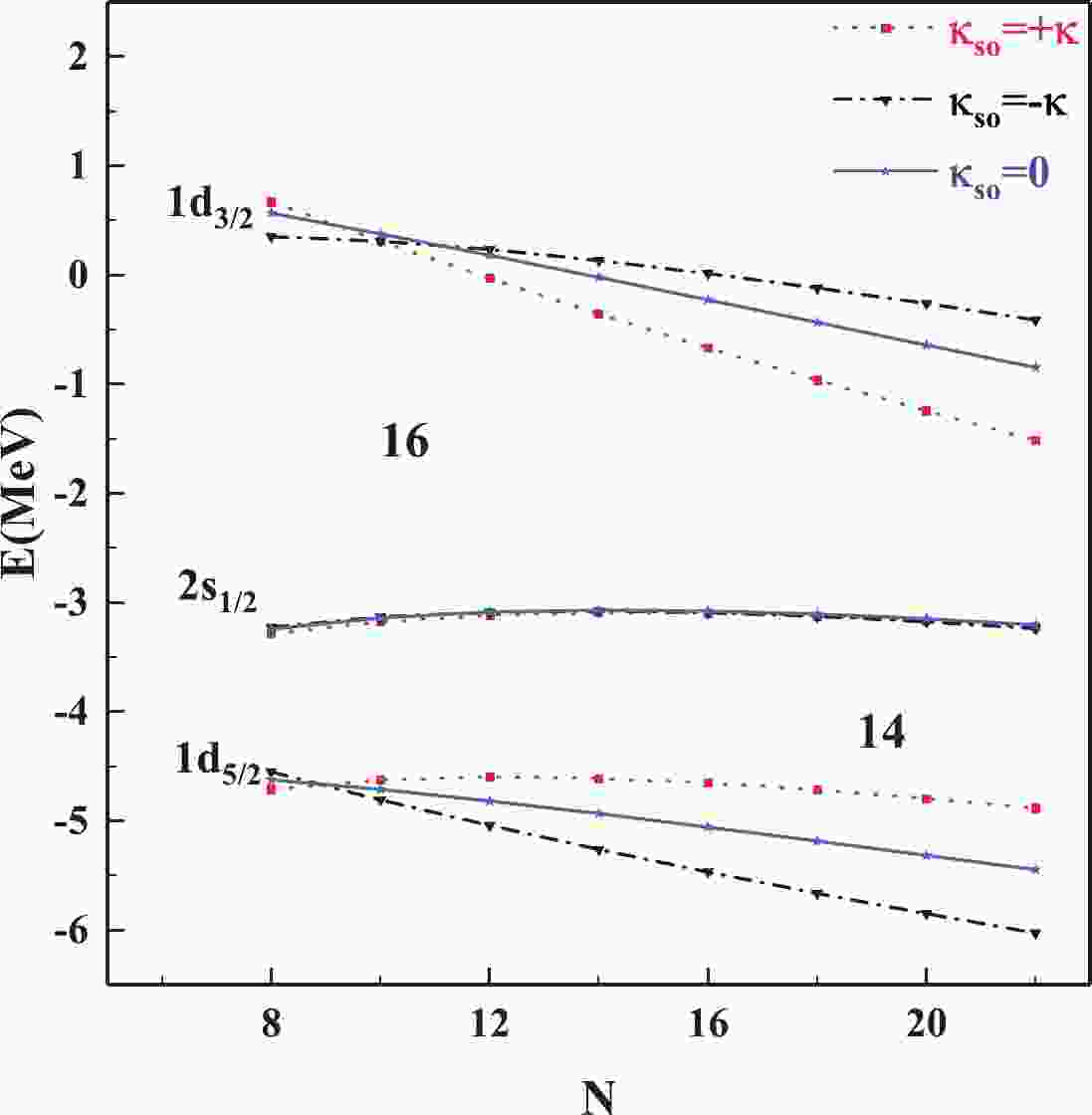
The
$ N = $ 14 shell gap is formed between the$ 1d_{5/2} $ and$ 2s_{1/2} $ orbits, whereas the$ N = $ 16 shell gap is located between the$ 2s_{1/2} $ and$ 1d_{3/2} $ orbits. The evolution of the ESPE of the$ 1d_{5/2} $ ,$ 2s_{1/2} $ , and$ 1d_{3/2} $ neutron orbits caused by the monopole interactions between the valence nucleons indicated that$ ^{22,24} $ O are quasi-doubly magic nuclei in the oxygen isotopic chain [8]. To be specific, the$ N = 14 $ gap is created by the filling of six neutrons in the$ 1d_{5/2} $ orbit. As the monopole interactions between the neutrons in the$ 1d_{5/2} $ orbit are globally attractive, the SPE of the$ 1d_{5/2} $ orbit gains an extra binding energy. Meanwhile, the SPE of the$ 2s_{1/2} $ orbit moves upward owing to the monopole interactions between the neutrons in the$ 1d_{5/2} $ and$ 2s_{1/2} $ orbits being slightly repulsive. As the neutrons start to fill the$ 2s_{1/2} $ orbit, a large$ N = 16 $ shell gap emerges owing to the presence of monopole interactions between the neutrons in the$ 2s_{1/2} $ orbit. In this study, the SPEs of the$ 1d_{5/2} $ ,$ 2s_{1/2} $ , and$ 1d_{3/2} $ neutron orbits are calculated from the single-particle viewpoint for the oxygen isotopic chain. To obtain a qualitative idea of the role played by the isospin term of single-particle SO potential in the shell evolution in neutron-rich nuclei, calculations with$ \kappa_{\rm so} = \pm\kappa $ and$ \kappa_{\rm so} = 0 $ are performed, respectively. In each calculation, the corresponding WS parameter set in Table 1 is used.Looking at the calculated SPEs in Fig. 1, one can notice that if one takes
$ \kappa_{\rm so} = +\kappa $ (red dotted line) weakening the strength of the SO potential in the neutron-rich nuclei, the SPEs of the$ 1d_{5/2} $ and$ 2s_{1/2} $ orbits stay roughly constant as the neutron number increases. The gap between them is about 1.7 MeV. Meanwhile, the SPE of$ 1d_{3/2} $ decreases rapidly. In fact, as more and more neutrons fill into the$ 1d_{5/2} $ orbit, this orbit should lose its energy rapidly owing to the attractive monopole interaction, whereas the$ 2s_{1/2} $ orbit should move upward owing to the slightly repulsive monopole interaction. These cases can be better explained if one takes$ \kappa_{\rm so} = -\kappa $ (black dotted line); then, the gap between the$ 1d_{5/2} $ and$ 2s_{1/2} $ orbits increases significantly in the neutron-rich nuclei. It changes from 1.6 MeV in$ ^{16} $ O to 2.9 MeV in$ ^{30} $ O, as companied by an obvious slope of the SPE curve of the$ 1d_{5/2} $ orbit. This slope is almost a constant, as shown in the figure, whereas it is expected to be smaller as the neutrons start to fill the$ 2s_{1/2} $ orbit (above$ N = 14 $ ) according to the result of the interacting shell model [7]. Besides, the$ 2s_{1/2} $ orbit is independent of the SO splitting from the single particle model perspective. Meanwhile, the$ 1d_{3/2} $ orbit gradually loses its energy in the neutron-rich nuclei, implying a less bound state. These present results, with$ \kappa_{\rm so} = -\kappa $ , are highly consistent with the results of the interacting shell model. The reason may be that the effect of the monopole interactions is accidentally partly replaced by the enhancement in the SO splitting. This point will be further discussed in the following cases. The energy difference between the$ 2s_{1/2} $ and$ 1d_{3/2} $ orbits, governing the$ N = 16 $ shell gap, is experimentally determined as$ 4.86 \pm 0.13 $ MeV [29], which is comparable to the present evaluation (approximately 4.0 MeV) for the oxygen isotopic chain with$ \kappa_{\rm so} = -\kappa $ . In a related manner, the situation with$ \kappa_{\rm so} = 0 $ (blue solid line), as expected, is somewhere in the middle of these two extreme cases of$ \kappa_{\rm so}\pm \kappa $ . This is actually similar to the following discussions. Hence, the case of$ \kappa_{\rm so} = 0 $ is not displayed to avoid visual disturbance without hampering the results and analysis. It must be mentioned that the results obtained in this study only show that$ N = 14 $ may be a new magic number because the gap in the neutron-rich nuclei is not large enough. Besides, the gap between the$ 1d_{3/2} $ and$ 2s_{1/2} $ orbits decreases with the increase in the neutron number,$ N $ , no matter which form of$ \kappa_{\rm so} $ is concerned. The present results, therefore, do not support the emergence of the$ N = 16 $ magic number to a large extent in the neutron-rich nuclei. However, if one takes$ \kappa_{\rm so} = -\kappa $ , the support could be relatively more positive. The above discussions are based on the systematics of one isotopic chain, and the conjecture can be more complete by comparing with the results of isotones, as shown in the next part. -
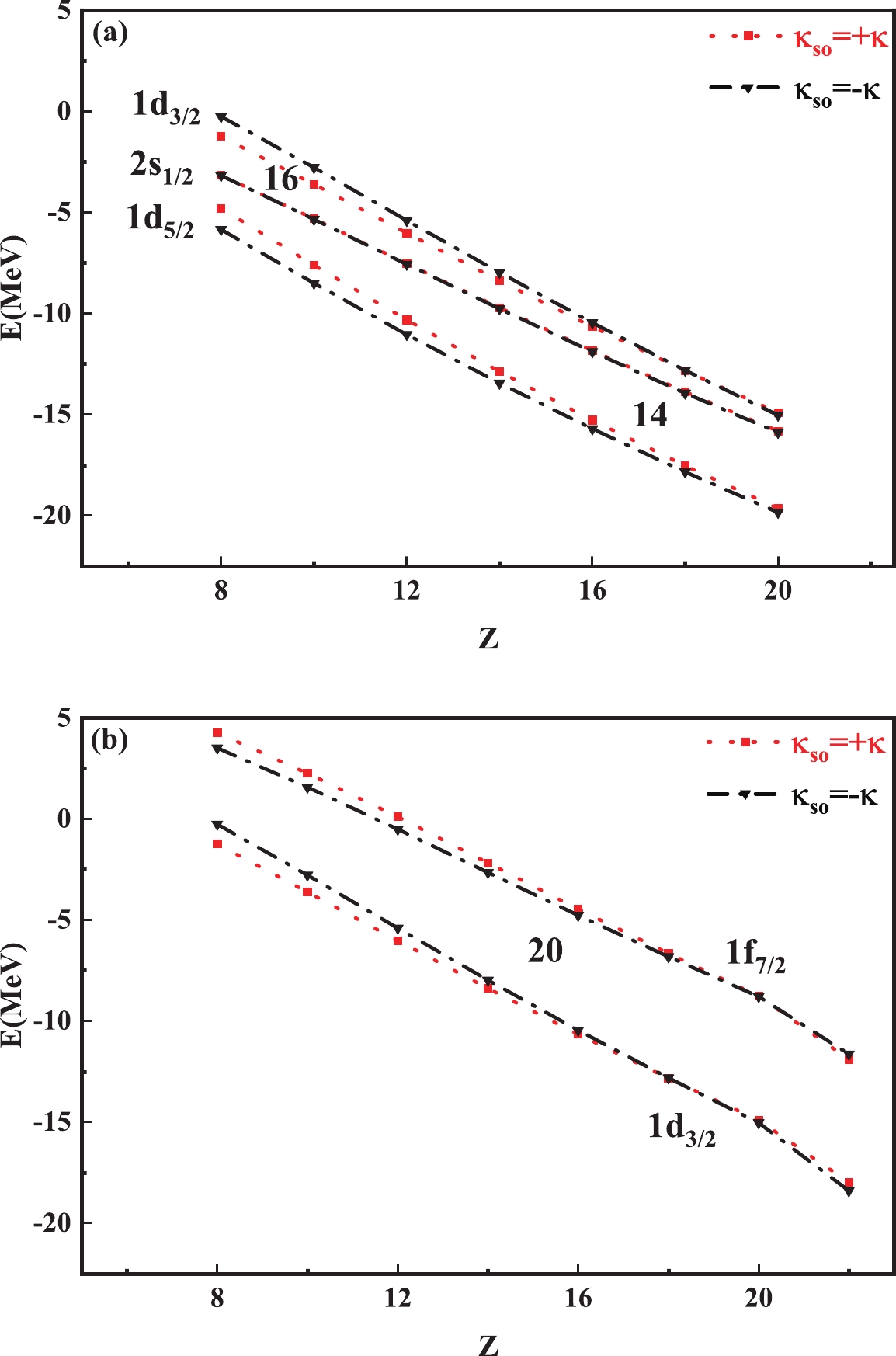
As compared with the monopole part of the neutron-neutron interaction mentioned in subsection A, the monopole part of the neutron-proton interactions, especially the tensor force, plays a major role in the appearance of the
$ N = 16 $ magic number and the disappearance of the$ N = 20 $ shell closure [7, 24, 27, 29]. The major$ N = 20 $ shell comes from the large gap between the$ 1d_{3/2} $ and$ 1f_{7/2} $ orbits, and the gap between the$ 2s_{1/2} $ and$ 1d_{3/2} $ orbits is supposed to produce one possible closed shell$ N = 16 $ . The magic number,$ N = $ 20, can arise naturally from the single particle point of view, whereas the new shell structure can be formed owing to the sizable spin-isospin coupling (tensor force) in exotic nuclei. In the framework of the interacting shell model, as the protons occupy the$ 1d_{5/2} $ orbit, the monopole interactions between the protons of the$ 1d_{5/2} $ orbit and the neutrons of the$ 1d_{3/2} $ orbit can lower the neutron$ 1d_{3/2} $ orbit with respect to the$ 2s_{1/2} $ orbit. In other words, the$ 1d_{3/2} $ neutron orbit moves upward relative to the$ 2s_{1/2} $ orbit when protons are taken out from the$ 1d_{5/2} $ orbit. Therefore, the$ N = 16 $ shell gap increases, whereas the$ N = 20 $ shell gap decreases owing to the fact that the effect of the interactions between the protons of the$ 1d_{5/2} $ orbit and the neutron the in$ 1_{7/2} $ orbit is relatively weaker.At present, the neutron number of the target nuclei is fixed at
$ N = 20 $ , and we perform a systematical calculation of the SPEs of the involved orbits in the evolution of the$ N = 16,\ 20 $ shells with the filling of the valence protons. Firstly, we concentrate on the evolution of the$ N = 20 $ shell gap, as shown in Fig. 2(b). The gap between the$ 1d_{3/2} $ and$ 1f_{7/2} $ orbits remains constant in the whole picture if one takes$ \kappa_{\rm so} = +\kappa $ (red dotted line). In fact, however, it should decrease as the proton number decreases when the number of protons is less than 16 due to a stronger force caused by the protons of$ 1d_{5/2} $ orbit acting on the neutrons of the$ 1d_{3/2} $ orbit than on those of the$ 1f_{7/2} $ orbit according to the interacting shell model analysis [7]. This point could be different if one takes$ \kappa_{\rm so} = -\kappa $ (black dotted line). In detail, by looking at the variation in the calculated SPEs in Fig. 2(b), one can see that the$ N = 20 $ gap indeed decreases when the proton number is less than 16, despite its slow speed. For illustration, the$ N = 20 $ gap is 4.2 MeV for$ ^{28} $ O (corresponding to the beginning of Fig. 2), and appears to be quite sizable compared to other theoretical results [10, 12]. Next, let us focus our attention to the evolution of the$ N = 16 $ gap, as shown in Fig. 2(a). The gap slowly increases as the proton number decreases, even though one takes$ \kappa_{\rm so} = +\kappa $ (red dotted line). It goes from 0.9 MeV in$ ^{40} $ Ca to 2.0 MeV in$ ^{28} $ O. This can gap increase to 3.0 MeV in$ ^{28} $ O if one takes$ \kappa_{\rm so} = -\kappa $ (black dotted line). Particularly, the slope of the SPE curve of$ 1d_{3/2} $ is larger when$ Z<16 $ . This is consistent with the conclusion that there are strong attractive monopole interactions between the nucleons of the$ l+1/2 $ and$ l-1/2 $ orbits [7, 24]. As the protons are taken out of the$ 1d_{5/2} $ orbit, the$ 1d_{3/2} $ neutron orbit moves upward. This indicates that a new magic number,$ N = 16 $ , may appear, whereas the disappearance of magic number$ N = 20 $ is not obvious. -
Other reported regions of the shell evolution are
$ N = 32 $ and 34, based on the unexpected behaviors of the excitation energies of first 2$ ^+ $ states and the large charge radii of Ca isotopes and their neighbors [9, 30, 31]. The$ N = 32 $ and$ N = 34 $ shell gaps are formed between the$ 2p_{3/2} $ and$ 2p_{1/2} $ orbits and between the$ 2p_{1/2} $ and$ 1f_{5/2} $ orbits, respectively. The strong attractive interaction between the proton in the$ 1f_{7/2} $ orbit and the neutron in the$ 1f_{5/2} $ orbit is expected to play a crucial role in this case, which is analogous to the mechanism leading to the production of the$ N = 16 $ new magic number [7]. As the eight protons in$ ^{56} $ Ni are taken away from the$ 1f_{7/2} $ orbit, new magic numbers$ N = 32 $ and 34 appear in the calcium isotopes. In this study, these two new magic numbers are investigated by calculating the SPEs of the related orbits from the independent particle viewpoint. In the left panel of Fig. 3, the varying SPE patterns of the$ 2p_{3/2} $ ,$ 2p_{1/2} $ , and$ 1f_{5/2} $ orbits are presented as the proton number decreases from 28 to 20 with fixed$ N = 28 $ . One can find that all orbits, in Fig. 3(a), move upward rapidly with the decrease in the proton number, and the$ N = 34 $ shell gap increases regardless of the choice of$ \kappa $ or$ \kappa_{\rm so} $ . Additionally, this gap increases a little faster if one takes$ \kappa_{\rm so} = -\kappa $ (black dotted line). As a typical point, the$ N = 34 $ shell gap is about 1.6 MeV in$ ^{48} $ Ca when$ \kappa_{\rm so} = -\kappa $ . Meanwhile, the gap between the$ 2p_{3/2} $ and$ 2p_{1/2} $ orbits roughly remains constant (about 1.4 MeV) in all cases. These are consistent with the determination of the shift of the$ 1f_{5/2} $ ,$ 2p_{1/2} $ , and$ 2p_{3/2} $ orbits due to the tensor- and central- force monopole contributions [7]. Particularly, the$ 1f_{5/2} $ orbit gradually elevates above the$ 2p_{1/2} $ orbit, leading to the final emergence of the new magic number,$ N = 32 $ , which takes place when the two protons are moved away from the$ 1f_{7/2} $ orbit, as shown in part (a) of Fig. 3.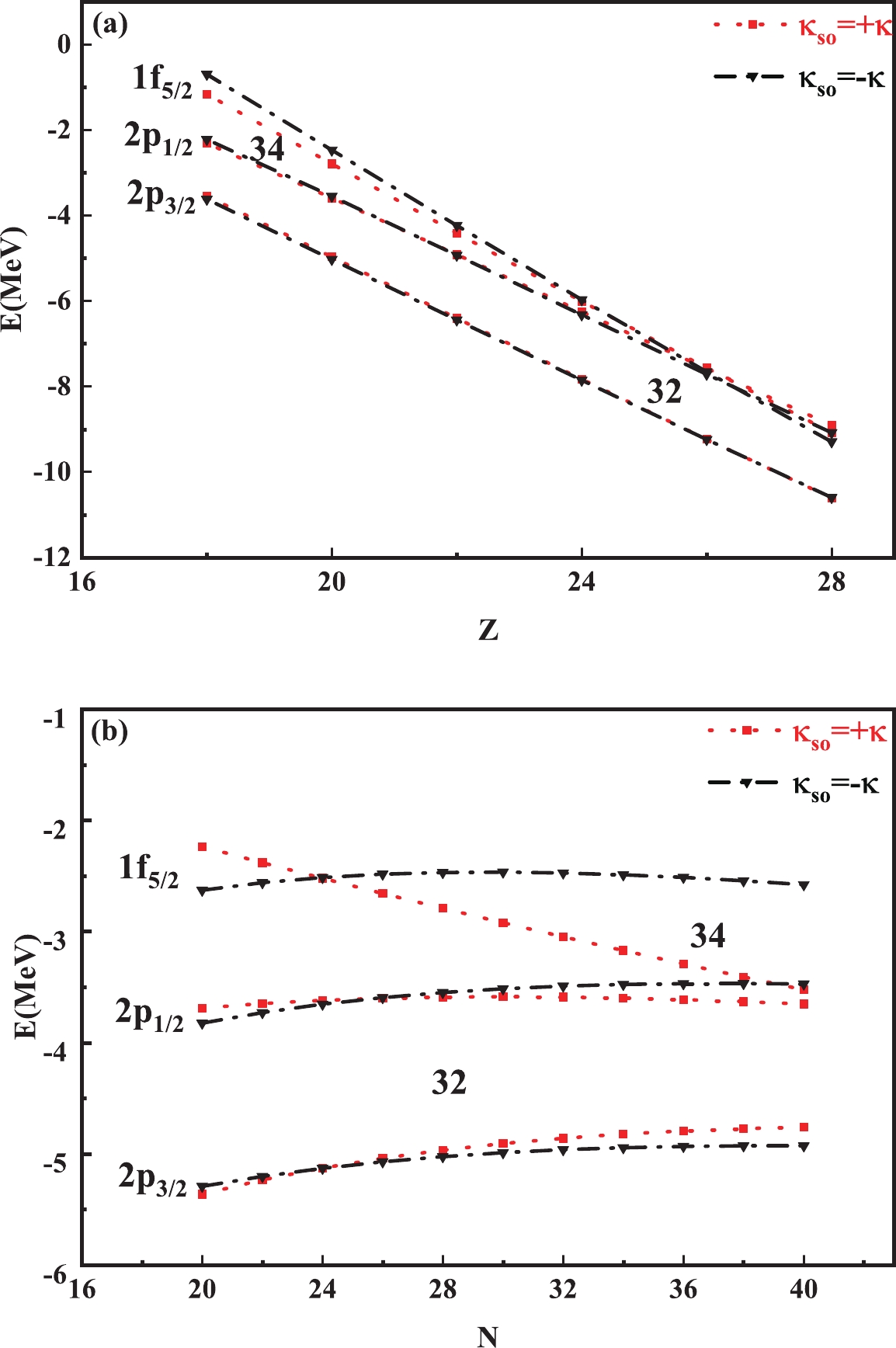
Figure 3. (color online) Calculated SPEs of the 2p3/2, 2p1/2, and 1f5/2 neutron orbits as functions of (a) the proton (N = 28 isotones) and (b) neutron (calcium isotopes) numbers with different choices of isospin-related parameters
$\kappa_{\rm so} = \pm \kappa$ and 0.Through the above systematical discussion on isotones with
$ N $ , one may conclude that the effect of the monopole part of the neutron-proton interactions on the evolution of the$ N = 32 $ and 34 shells is manifested to some extent by enhancing the strength of the SO splitting via the choice of$ \kappa_{\rm so} = -\kappa $ . Furthermore, one may expect to see what will happen when the$ 2p_{1/2} $ ,$ 2p_{3/2} $ , and$ 1f_{5/2} $ orbits start to be filled by the valence neutrons. The interacting shell model studies show that the monopole part of the neutron-neutron interactions can be repulsive, and its effect on the$ N = 32 $ and 34 shell evolution is limited by comparing the ESPEs of the involved orbits in$ ^{48} $ Ca and those in$ ^{54} $ Ca. Here, a similar conclusion can be obtained from the single particle viewpoint, as shown in part (b) of Fig. 3. By choosing$ \kappa_{\rm so} = \kappa $ and$ \kappa_{\rm so} = -\kappa $ , respectively, the calculated SPEs of the$ 2p_{3/2} $ ,$ 2p_{1/2} $ , and$ 1f_{5/2} $ orbits are presented versus the neutron number of the calcium isotopes, where one can find an evident distinction at the$ N = 34 $ subshell gap for both choices of$ \kappa $ and$ \kappa_{\rm so} $ . The near degeneracy between the$ 1f_{5/2} $ and$ 2p_{1/2} $ orbits in the neutron-rich nuclei is eliminated if one takes$ \kappa_{\rm so} = -\kappa $ for the SO potential. Moreover, under such a mean-field potential, the energy gap between these single orbits changes quite gently with increasing neutron number, which is consistent with the aforementioned comment about the limited influence of the neutron-neutron monopole interaction on the formation of the$ N = 32 $ and 34 subshell gaps. For instance, the$ N = 32 $ gaps of$ ^{48,54} $ Ca are both 1.5 MeV. Based on the above analysis, new magic numbers$ N = 32 $ and 34 can emerge by strengthening the single particle SO potential via the choice of$ \kappa_{\rm so} = -\kappa $ . Of course, one can notice that the present mechanism in the IPM does not always produce a shell evolution similar to that by the tensor force in the interacting shell model. As shown in Fig. 2 and Fig. 3(a), when the protons are removed from stable nuclei, the SO splitting of the neutron orbitals remains enlarged by the present SO potential. However, if the protons are removed from a$ j_{<} $ ($ j = l-1/2 $ ) orbital, the neutron SO splitting is reduced based on the tensor force. In this sense, one can imagine that a comprehensive knowledge of the competition between the mean-field and the residual NN interaction is indispensable to completely understand and predict the evolution of shell closure. -
Last but not least, we also study the evolution of the traditional neutron magic numbers,
$ N = 28 $ , 50, and 82, in neutron-rich nuclei. The investigation on these shell evolution is significant for realizing the fundamental properties of nuclei, such as the nuclear force and the nuclear shape coexistence [32-34]. However, the problem is made much more complex owing to the large number of involved nucleons, requiring more factors to be taken into account, like the nuclear deformation [35-38]. Although some experimental and theoretical results have been obtained, more details are still lacking. In the present study, we attempt to provide valuable information on this topic from the single particle perspective. Fig. 4 presents the varying SPEs of the related orbits with the proton number for the$ N = 28 $ ,$ N = 50 $ , and$ N = 82 $ isotones, respectively. It is found that the conventional magic number,$ N = 28 $ , is destroyed toward the neutron-rich region (see the left part (a) of Fig. 4), regardless of the choice of the single particle SO splitting.
Figure 4. (color online) Same as previous figures but for the evolution of the N = 28, 50, and 82 gaps as function of the proton number Z.
In comparison, with regard to the neutron-dripline, there is still an energy gap between the
$ 1g_{9/2} $ and$ 1d_{5/2} $ orbits, as shown in Fig. 4(b), corresponding to the$ N = 50 $ shell closure. However, the gap would be quite small in contrast with that in the neutron-deficient side of nuclide chart. For example, the energy gaps between the$ 1g_{9/2} $ and$ 1d_{5/2} $ orbits, of the extreme neutron-rich nucleus$ ^{70} $ Ca, are 0.7 MeV and 2.1 MeV, respectively, for cases$ \kappa_{\rm so} = \kappa $ and$ \kappa_{\rm so} = -\kappa $ . A similar situation occurs at the$ N = 82 $ shell gap; however, the gap is slightly larger for the extreme neutron-rich nuclei, implying the possible persistence of the magic number,$ N = 82 $ . A noteworthy fact is that in the three parts of Fig. 4, when all protons in the proton shell closure are taken out, the energy gap between the neutron orbits begins to decrease more drastically. As seen from the figure, the$ N = 28 $ shell gap decreases faster when$ Z<20 $ . Besides, the$ N = 50 $ and 82 shell gaps also drop quickly when$ Z<28 $ and$ Z<50 $ , respectively. These may indicate that the interactions between the protons and neutrons across the major shell closure may have an important impact on the shell evolution phenomenon. -
Within the WS mean-field potential combined with the SO coupling, we systematically study the robustness of the traditional magic numbers and the possible emergence of new shell closure in neutron-rich nuclei from a single particle perspective. By refining the isospin related term in the SO coupling potential, it is found that the well-known magic number
$ N = 28 $ disappears toward an extreme neutron-proton ratio, such as light nuclei with$ Z<12 $ . In comparison, the$ N = 20 $ neutron shell closure tends to be destroyed very gradually or may survive when it comes to the neutron-rich side of the nuclear chart. Moreover, the shell gaps at$ N = 50 $ and$ N = 82 $ are supposed to gradually decrease with decreasing proton-to-neutron ratio. These gaps are still sizable for these extreme neutron-rich light nuclei when the SO potential is enhanced owing to the high isospin asymmetry, i.e.,$ \kappa_{\rm so} = -\kappa $ . Recently reported magic numbers, like$ N = 14 $ , 16, 32, and 34, are understood in terms of the monopole NN interaction within the interacting shell model. Interestingly, one can also find positive signals for the emergence of these new magic numbers from the present single particle model, which implies that the aforementioned monopole interaction can be absorbed in the good mean-field treatment at least to a certain extent. The single-particle spectra, under such a simple scheme, may not only provide a reasonable starting point for the ensemble of shell model calculations in the continuum but also serve for exploring pairing correlation and nuclear deformation.
Shell evolution in neutron-rich nuclei: the single particle perspective
- Received Date: 2021-09-13
- Available Online: 2022-01-15
Abstract: The isospin dependence of spin-orbit (SO) splitting becomes increasingly important as N/Z increases in neutron-rich nuclei. Following the initial independent-particle strategy toward explaining the occurrence of magic numbers, we systematically investigated the isospin effect on the shell evolution in neutron-rich nuclei within the Woods-Saxon mean-field potential and the SO term. It is found that new magic numbers N = 14 and N =16 may emerge in neutron-rich nuclei if one changes the sign of the isospin-dependent term in the SO coupling, whereas the traditional magic number, N = 20, may disappear. The magic number N = 28 is expected to be destroyed despite the sign choice of the isospin part in the SO splitting, corresponding to the strength of the SO coupling term. Meanwhile, the N = 50 and 82 shells may persist within the single particle scheme, although there is a decreasing trend of their gaps toward extreme proton-deficient nuclei. Besides, an appreciable energy gap appears at N = 32 and 34 in neutron-rich Ca isotopes. All these results are more consistent with those of the interacting shell model when enhancing the strength of the SO potential in the independent particle model. The present study may provide a more reasonable starting point than the existing one for not only the interacting shell model but also other nuclear many-body calculations toward the neutron-dripline of the Segrè chart.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: