-
Supersymmetry (SUSY) [1-7] predicts new particles, each with a spin that differs by half a unit from their corresponding standard model (SM) particles. In SUSY models with conserved R-parity [8], SUSY particles are always produced in pairs, and the lightest supersymmetric particle (LSP) is stable and can be considered a potential dark matter candidate [9, 10].
Charginos
$ \tilde{\chi}^{\pm}_i $ $ (i = 1,2) $ and neutralinos$ \tilde{\chi}^0_j $ $ (j = 1,2,3,4) $ are referred to as electroweakinos. They are the mass eigenstates formed from linear superpositions of the Bino, Wino, and Higgsino particles, the superpartners of the charged and neutral Higgs bosons, and electroweak gauge bosons. The subscripts i and j indicate states of increasing mass. In the Minimal Supersymmetric Standard Model (MSSM), the magnitude of the Bino, Wino, and Higgsino mass parameters are referred to as$ M_1 $ ,$ M_2 $ , and μ respectively. The mass splitting between the electroweakinos mainly depends on the absolute values of$ M_1 $ ,$ M_2 $ , and μ. Two SUSY scenarios are considered in this paper. In the first scenario, the absolute values of the$ M_1 $ and$ M_2 $ parameters are considered to be near the weak scale and similar in magnitude, while the magnitude of μ is significantly larger such that$ |M_1|<|M_2|\ll |\mu| $ . In this case, the LSP$ \tilde{\chi}^0_1 $ is a Bino-like$ \tilde{\chi}^0_1 $ and the next to lightest supersymmetric particle (NLSP) is part of a Wino-like doublet that forms$ \tilde{\chi}^0_2 $ and$ \tilde{\chi}^{\pm}_1 $ . The second scenario considers the absolute value of μ to be near the weak scale, while the magnitudes of$ M_1 $ and$ M_2 $ are significantly larger, i.e.,$ |\mu|\ll |M_1|,|M_2| $ ; hence,$ \tilde{\chi}^0_1 $ ,$ \tilde{\chi}^{\pm}_1 $ , and$ \tilde{\chi}^0_2 $ are Higgsino-like and almost mass degenerate. The first scenario is favored for dark matter arguments, and the second one is motivated by naturalness considerations [11-13]; however, the latter scenario is a challenging experimental signature to search for due to the small mass splittings between the NLSP and LSP.Direct searches for chargino pair production with Bino-like or Higgsino-like LSPs were previously performed at the Large Electron-Positron Collider (LEP) and the Large Hadron Collider (LHC). This process was excluded by the LEP for
$ \tilde{\chi}^{\pm}_1 $ masses below 92.4 (91.9) GeV independent of the$ \tilde{\chi}^0_1 $ mass for the Higgsino (Bino) LSP case [14-19]. At ATLAS (CMS), chargino pair production that assumed a Bino-like LSP was excluded for$ \tilde{\chi}^{\pm}_1 $ masses up to 420 (200) GeV assuming a W-boson-mediated chargino decay [20, 21]. For the scenario assuming a Higgsino-like LSP,$ \tilde{\chi}^{\pm}_1 $ masses below 193 GeV were excluded for mass splittings down to 4.6 GeV, and mass splittings from 1.2 GeV to 30 GeV were excluded at the LEP bounds on the$ \tilde{\chi}^{\pm}_1 $ mass by ATLAS [22]. Light higgsinos with mass splittings below 1 GeV, which are preferred by naturalness conditions from low-energy fine-tuning measures, are still not excluded by the LHC and will also be highly challenging for the HL-LHC.For the Bino-like (Higgsino-like) LSP case, the increased center-of-mass energy of the CEPC will extend the search sensitivity for the
$ \tilde{\chi}^{\pm}_1 $ ($ \tilde{\chi}^{\pm}_1 $ and$ \tilde{\chi}^0_1 $ ) masses by more than 100 GeV compared to the LEP experiment. With a cleaner collision environment and better reconstruction and identification efficiency for low-energy particles [23], the CEPC will have an excellent sensitivity to highly compressed electroweakinos and sleptons (superpartners of leptons), which are very difficult to search for at the LHC and even the HL-LHC.The FCC-ee and ILC are proposed electron-positron colliders [24, 25]. The CEPC and FCC-ee are both circular colliders designed to be built and operated in several stages with center-of-mass energies from 90 to 350 GeV. The ILC is a linear collider with designed center-of-mass energies from 250 to 1 TeV. These colliders will primarily operate with center-of-mass energies at the ZH production threshold; hence, an energy of 240 GeV is assumed for these studies. A conservative systematic uncertainty of 5% is assumed in this study, which is consistent with the LEP results [16, 26, 27]. The results presented in this paper are expected to be largely independent of the specific detector, trigger, and data acquisition choices and can be easily considered as a reference for studies at the other two facilities with proper luminosity scaling.
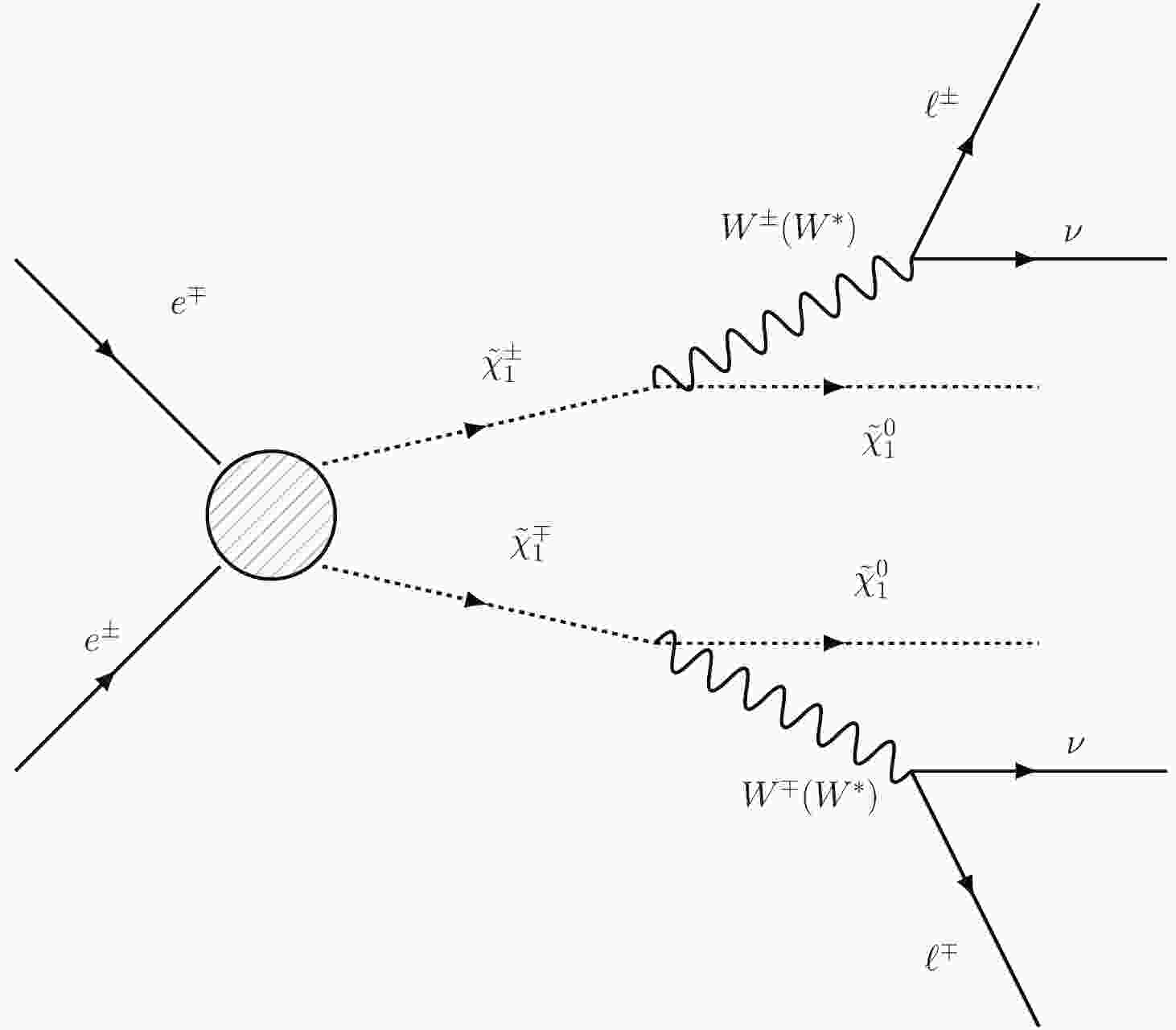
This paper presents studies on sensitivity to chargino pair production, followed by the chargino decay to a W boson and a Bino-like or Higgsino-like neutralino LSP, as illustrated in Fig. 1. To simplify the analysis, only leptonic W decays are considered. Events with two opposite-sign (OS) muons and significant recoil mass (
$ M_{\rm recoil} $ , the invariant mass of the recoil system against the two muons) are selected for all scenarios. -
The CEPC Conceptual Design Report (CDR) supplies detailed information on detectors and software [28]. Two types of CEPC detector concepts are proposed. The baseline concept is a particle-flow oriented detector equipped with an ultra-high granularity calorimeter, a low-material tracker, and a 3 Tesla solenoid. The alternative concept uses a dual readout calorimeter and a 2 Tesla solenoid. In this analysis, the CEPC baseline concept is used as the detector model.
The following software was used for the study: Whizard 1.95 [29] was used to generate the official SM MC simulated event samples. MadGraph 2.7.3 [30] and Pythia 8.244 [31] were used for the generation of SUSY MC simulated event samples. MokkaC 0.1.0 [32] was used to simulate the interactions between particles and the detector. Clupatra 00-10 [33] was used to reconstruct tracks from hits in the detector. The particle flow algorithm Arbor 3.4.2 [23] was used to reconstruct physics objects. LICH v4 [34] based on Multivariate Data Analysis (TMVA) [35] was used for lepton identification.
The
$ \tilde{\chi}^{\pm}_1 $ are pair produced from electron-positron collisions, and each$ \tilde{\chi}^{\pm}_1 $ decays into a W boson and a$ \tilde{\chi}^0_1 $ with a 100% branching ratio. No other sparticle is considered in the production or decay. The signal samples of chargino pair production in the Bino-like LSP case are parametrized as a function of the mass of the LSP and$ \tilde{\chi}^{\pm}_1 $ ; the lower bound on the chargino mass is set by the LEP limit, while the LSP mass is bound by the mass difference between the chargino and the W boson. Therefore, the$ \tilde{\chi}^{\pm}_1 $ mass varies in the range 90 - 119 GeV. The signal samples of chargino pair production in the Higgsino-like LSP case are parametrized as a function of two SUSY parameters μ and tanβ. μ varies in the range 90 - 118 GeV, while tanβ varies in the range 10 - 60. Samples containing$ 5\times 10^5 $ ($ 1\times 10^5 $ ) events are simulated for each signal point with the Bino-like (Higgsino-like) LSP.In this paper, reference points with
$ \tilde{\chi}^{\pm}_1 $ masses of 110 GeV and$ \tilde{\chi}^0_1 $ masses of 1, 10, or 25 GeV are used for the Bino-like LSP scenario to illustrate the typical features of the SUSY models to which this analysis is sensitive. The corresponding leading order (LO) cross section is 2789 fb, as computed by MadGraph. For the Higgsino-like LSP scenario, three reference points with tanβ of 30 and μ of 90, 106, or 118 GeV are used with theoretical LO cross sections of 1966, 1522.9, and 681.2 fb, respectively, as computed by MadGraph.This analysis only considers the dominant SM background processes of final states with two leptons (electrons, muons, or taus) and a significant recoil mass. The backgrounds are categorized into three types: Higgs processes, two fermion backgrounds, and four fermion backgrounds. The Higgs processes considered are
$ \nu\nu H, H\to\tau\tau $ , the two fermion backgrounds considered are the$ \mu\mu $ and$ \tau\tau $ processes, and the four fermion backgrounds include the ZZ, WW, single Z, single W, and Z or W mixing processes. The samples are normalised to a luminosity of 5.05 ab−1. The cross sections of the dominant background processes are shown in Table 1.Processes Cross sections (fb) $ \tau\tau $ 

4374.94 $ \nu\nu H, H\to\tau\tau $ 

3.07 $ ZZ $ or

$ WW \to \tau\tau\nu\nu $ 

205.84 $ ZZ \to \tau\tau\nu\nu $ 

9.2 $ \nu Z , Z \to \tau\tau $ 

14.57 $ ZZ $ or

$ WW \to \mu\mu\nu\nu $ 

214.81 $ ZZ \to \mu\mu\nu\nu $ 

18.17 $ WW \to \ell\ell $ 

392.96 $ \nu Z , Z \to \mu\mu $ 

43.33 $ \mu\mu $ 

4967.58 $ e\nu W , W \to \mu\nu $ 

429.2 $ e\nu W , W \to \tau\nu $ 

429.42 $ ee Z , Z \to \nu\nu $ 

29.62 $ ee Z , Z \to \nu\nu $ or

$ e\nu W , W \to e\nu $ 

249.34 Table 1. Cross-sections of the dominant background processes in the CEPC.
-
The event reconstruction consists of track, particle flow, and compound physics object reconstruction. Tracks are reconstructed from hits in the detector by Clupatra [33]. Particle flow reconstruction uses the tracks and the calorimeter hits to reconstruct single particle physics objects. The output of particle flow reconstruction can be used to reconstruct compound physics objects such as converted photons, taus, and jets. The identification efficiency of muons is 99.9% for energies above 2 GeV [34]. For muons with energies below 1.3 GeV at the edge of the barrel region or the overlap region of the barrel and endcap, the identification efficiency is lower than 90%. The recoil system consists of all the particles except the two OS charged muons. Without considering the beam energy spread, the resolution of the reconstructed recoil mass is between 300 and 400 MeV [28].
The following variables are efficient in discriminating the signal events from SM backgrounds:
●
$ \Delta R(\mu^{+},\mu^{-}) $ , the angular distance between two muons.●
$ \Delta R({\mu ^ \pm },{\rm recoil}) $ , the angular distance between the muons and the recoil system.●
$ |\Delta \phi(\mu^{\pm},{\rm recoil})| $ , the azimuthal distance between the muons and the recoil system.●
$ |\Delta \phi(\mu^{+},\mu^{-})| $ , the azimuthal distance between two muons.●
$ E_{\mu^{\pm}} $ , the energy of the muons.●
$ P_T^{\mu^{\pm}} $ , the transverse momentum of the muons.●
$ M_{\rm recoil} $ , the invariant mass of the two neutrinos and two LSPs.The signal regions were optimized and defined based on the above kinematic variables. Zn [36] was used as a sensitivity reference in the signal region optimization, the definition of which is shown in formula (1). A statistical uncertainty and a 5% global systematic uncertainty were taken into account in the Zn calculation.
$ Zn = \left[2\left((s+b)\ln\left[\frac{(s+b)(b+\sigma_b^2)}{b^2+(s+b)\sigma_b^2}\right]-\frac{b^2}{\sigma_b^2}\ln\left[1+\frac{\sigma_b^2s}{b(b+\sigma_b^2)}\right]\right)\right]^{1/2}. $

(1) Several kinematic distributions after the two OS muon selection with
$ E_{\mu} $ larger than 10 GeV (1 GeV) are shown in Fig. 2 (a), (b) (Fig. 2 (c), (d)), which indicate the good discrimination power between the signal and SM processes.
Figure 2. (color online) The kinematic distributions for (top) Bino-like and (bottom) Higgsino-like LSP cases. The stacked histograms show the expected SM backgrounds. The hatched bands represent the sum in quadrature of the statistical uncertainties of the total SM background. To illustrate, the distributions of three SUSY reference points (defined in Sec. II) are also shown as dashed lines. The first bin clearly includes the underflow events, and the last bin includes the overflow events.
-
For the Bino-like LSP scenario, events containing exactly two OS charged muons with energies larger than 10 GeV are selected. A selection of
$ \Delta R(\mu^{+},\mu^{-}) $ is used to reject background events from the$ \tau\tau $ and$ \mu\mu $ processes. Events are required to have$ P_T^{\mu^{\pm}} > $ 30 GeV to suppress the WW and Z$ \nu $ processes. The majority of the signal events have large recoil masses according to the signal topology, as shown in Fig. 2 (a); therefore,$ M_{\rm recoil} > $ 130 GeV is applied to reject the$ \mu\mu $ and ZZ background events and increase the signal sensitivity. The signal region definition is summarized in Table 2.Signal regions == 2 muons (OS) $ E_{\mu^{\pm}}> 10 $ GeV

$ 0.4< \Delta R(\mu^{+},\mu^{-})< 1.6 $ 

$ P_T^{\mu^{\pm}}> $ 30 GeV

$M_{\rm recoil} >$ 130 GeV

Table 2. Summary of the signal region selection requirements for chargino pair production with a Bino LSP.
The kinematic distributions of
$ M_{\rm recoil} $ and$ P_{T}^{\mu^{-}} $ , after applying all signal region requirements except on the shown variable, are given in Fig. 3. The "Others" component includes the$ \nu\nu H $ ,$ H\to\tau\tau $ ,$ ZZ $ or$ WW \to \tau\tau\nu\nu $ ,$ ZZ \to \tau\tau\nu\nu $ ,$ \nu Z , Z \to \tau\tau $ ,$ e\nu W , W \to \mu\nu $ ,$ e\nu W , W \to \tau\nu $ ,$ ee Z , Z \to \nu\nu $ ,$ ee Z , Z \to \nu\nu $ , and$ e\nu W , W \to e\nu $ processes. The black arrow indicates the signal region selection of this kinematic variable. The sensitivities shown in the lower pad of the figures are obtained from the cumulative signal and background events calculated in the direction of the cut arrow. The event yields from the background processes and signal reference points after signal region requirements are shown in Table 3. The dominant background contributions are from the$ ZZ $ or$ WW \to \mu\mu\nu\nu $ ,$ \mu\mu $ , and$ WW\to\ell\ell $ processes. The expected sensitivities as a function of the$ \tilde{\chi}^{\pm}_1 $ and$ \tilde{\chi}^0_1 $ masses with systematic uncertainties of 0% or 5% for the Bino-like LSP case are shown in Fig. 4. The discovery potential can reach the kinematic limit of$ \sqrt{s}/2 $ and is not sensitive to systematic uncertainties.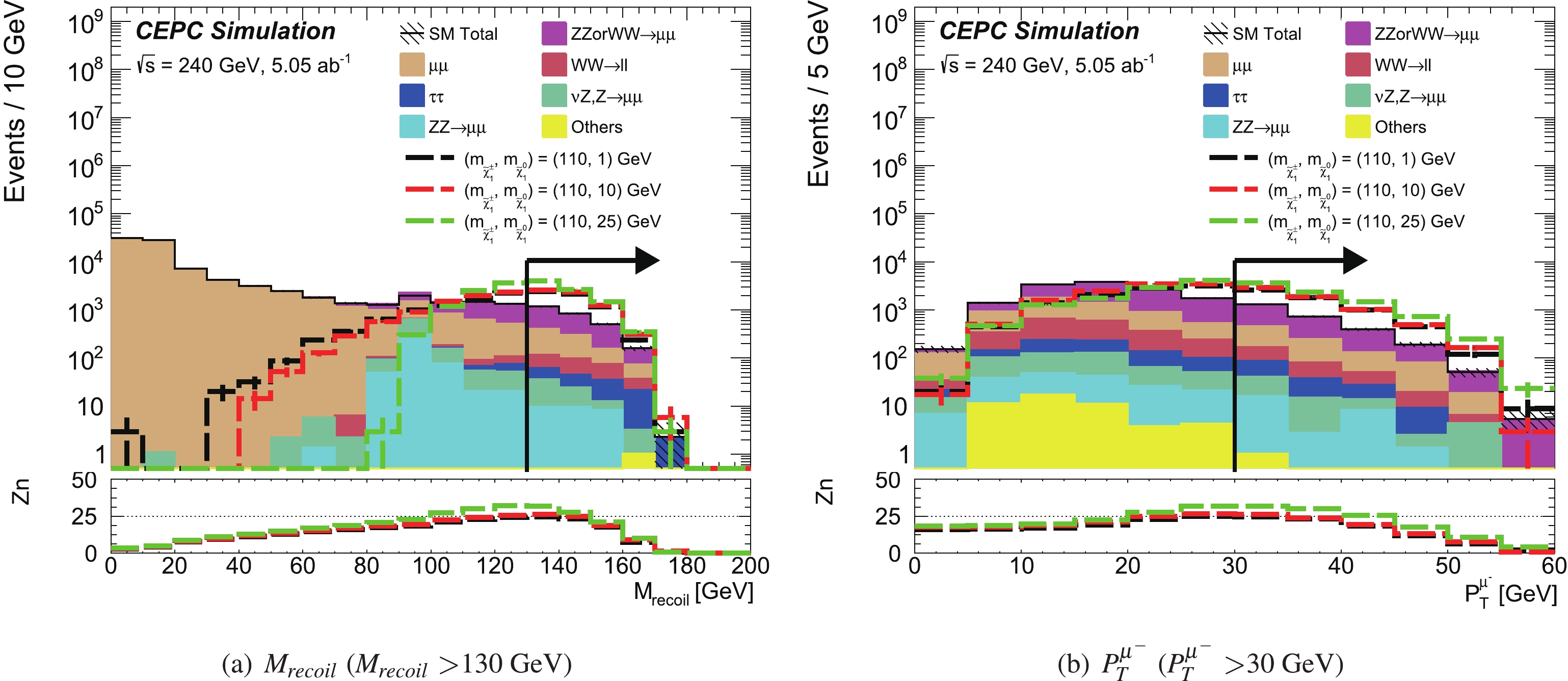
Figure 3. (color online) “N-1” distributions after signal region requirements for the Bino-like LSP case. All signal region requirements are applied except on the variable shown. The stacked histograms show the expected SM backgrounds. The hatched bands represent the sum in quadrature of the statistical uncertainties of the total SM background. To illustrate, the distributions from the SUSY reference points (defined in Sec. II) are also shown as dashed lines. The lower pad is the sensitivity Zn calculated with a statistical uncertainty and a 5% flat systematic uncertainty. The first bin clearly includes the underflow events, and the last bin includes the overflow events.
Processes Yields $ZZ\;{\rm or}\;WW\to\mu\mu\nu\nu$ 

1632±42 $ \mu\mu $ 

609±61 $ WW\to\ell\ell $ 

163±13 $ \tau\tau $ 

88±14 $ \nu Z,Z\to\mu\mu $ 

47.9±7.3 $ ZZ\to\mu\mu\nu\nu $ 

27.7±6.2 Others 0.74±0.74 Total background 2568±77 m ( $ \tilde{\chi}^{\pm}_1 $ ,

$ \tilde{\chi}^0_1 $ ) = (110, 1) GeV

5940±130 m ( $ \tilde{\chi}^{\pm}_1 $ ,

$ \tilde{\chi}^0_1 $ ) = (110, 10) GeV

6470±140 m ( $ \tilde{\chi}^{\pm}_1 $ ,

$ \tilde{\chi}^0_1 $ ) = (110, 25) GeV

8470±160 Table 3. The number of events with statistical uncertainties in the signal region of signals and SM backgrounds for chargino pair production in the Bino LSP case.
-
For the Higgsino-like LSP scenario, events containing exactly two OS muons with energies above 1.0 GeV are selected. The cuts on
$ E_{\mu^{\pm}} $ and$ \Delta R(\mu^{\pm},{\rm recoil}) $ are used to reject background events from the$ \tau\tau $ processes and Z or W mixing processes. A requirement of$ |\Delta \phi(\mu^{\pm},{\rm recoil})| < 2.9 $ is used to suppress the$ \mu\mu $ process, and$ |\Delta \phi(\mu^{+},\mu^{-})| <1.4 $ is used to suppress the background events with two back-to-back muons, such as from the$ \gamma\gamma\to\mu\mu $ process, where the photons are produced from the incoming electrons and positrons. Most of the signal events have large recoil masses according to the signal topology, as shown in Fig. 2 (c); therefore,$ M_{\rm recoil} > 237.5 $ GeV has been applied to reject the$ \mu\mu $ , Z or W mixing, and WW background events and increase signal sensitivity. The signal region definition for the Higgsino-like LSP case is summarized in Table 4.Signal regions == 2 muons (OS) $ E_{\mu^{\pm}}> 1.0 $ GeV

3.2 $< \Delta R(\mu^{\pm},{\rm recoil})< $ 4.6

$ |\Delta \phi(\mu^{\pm},{\rm recoil})|< 2.9 $ 

$ |\Delta \phi(\mu^{+},\mu^{-})|< 1.4 $ 

$ M_{\rm recoil}> 237.5 $ GeV

Table 4. Summary of signal region selection requirements for chargino pair production with a Higgsino LSP.
The kinematic distributions of
$ E_{\mu^{-}} $ and$ M_{\rm recoil} $ , after applying all signal region requirements except on the shown variable, are given in Fig. 5. The event yields from the background processes and signal reference points after signal region selections are presented in Table 5. The dominant background contributions are from the$ \nu Z , Z \to \mu\mu $ and$ \tau\tau $ processes. The expected sensitivities as a function of the$ \tilde{\chi}^{\pm}_1 $ mass and$ \tilde{\chi}^0_1 $ mass with systematic uncertainty assumptions of 0% or 5% for the Higgsino-like LSP case are shown in Fig. 6. The discovery sensitivity can again reach the kinematic limit of$ \sqrt{s}/2 $ and is not sensitive to systematic uncertainties and mass splitting between the NLSP and LSP. Sensitivity is also expected at lower mass splittings not explored in this study.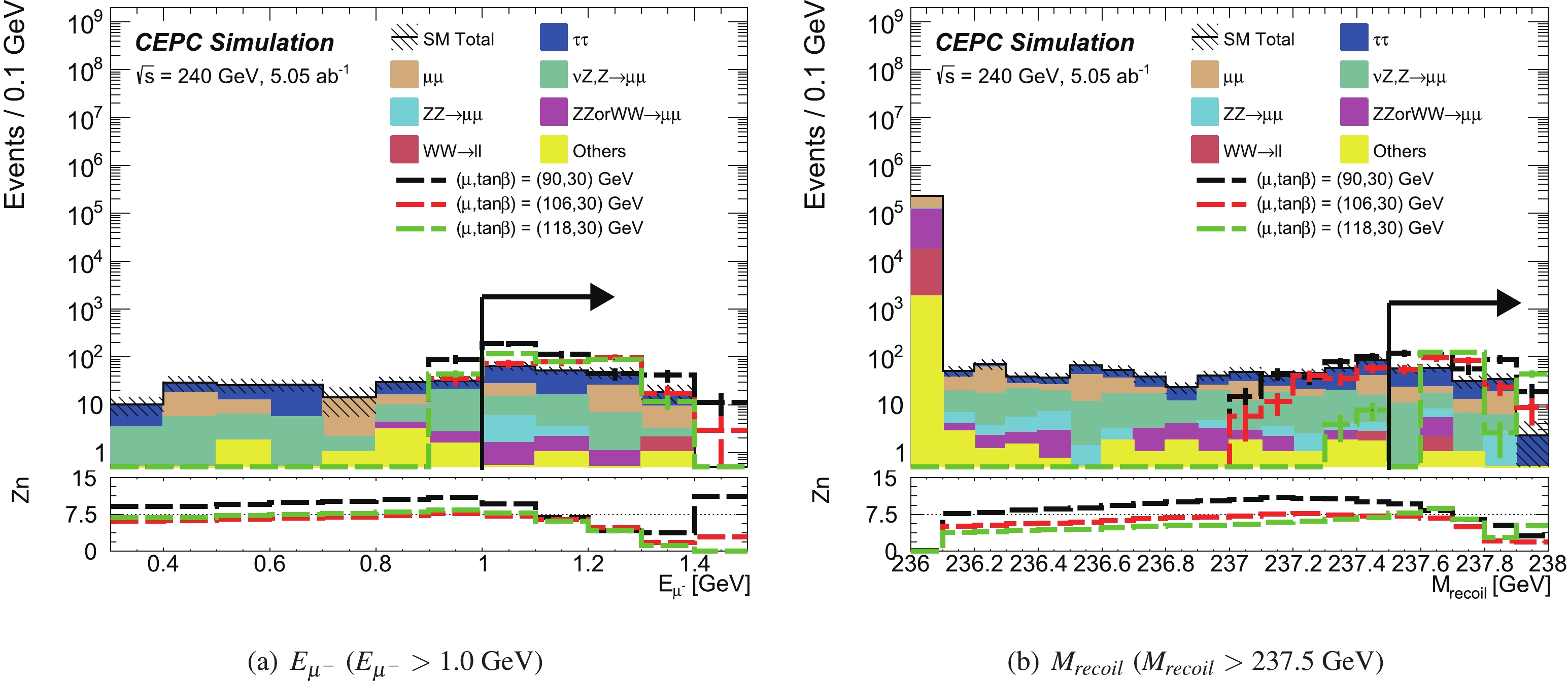
Figure 5. (color online) “N-1” distributions of the used variables after signal region requirements for the Higgsino-like LSP case. All signal region requirements are applied except on the variable shown. The stacked histograms show the expected SM backgrounds. The hatched bands represent the sum in quadrature of the statistical uncertainties of the total SM background. To illustrate, the distributions from the SUSY reference points (defined in Sec. II) are also shown as dashed lines. The lower pad indicates the Zn calculated with a statistical uncertainty and a 5% flat systematic uncertainty. The first bin clearly includes the underflow events, and the last bin includes the overflow events.
Processes Yields $ \tau\tau $ 

107 $ \pm $ 16

$ \mu\mu $ 

37 $ \pm $ 15

$ \nu Z,Z\to\mu\mu $ 

27.8 $ \pm $ 5.6

$ ZZ\to\mu\mu\nu\nu $ 

5.5 $ \pm $ 2.8

$ ZZ $ or

$ WW\to\mu\mu\nu\nu $ 

3.2 $ \pm $ 1.8

$ WW\to\ell\ell $ 

1.0 $ \pm $ 1.0

Others 2.6 $ \pm $ 1.6

Total background 183 $ \pm $ 23

(μ, tanβ) = (90 GeV, 30) 396 $ \pm $ 39

(μ, tanβ) = (106 GeV, 30) 267 $ \pm $ 28

(μ, tanβ) = (118 GeV, 30) 296 $ \pm $ 20

Table 5. The number of expected events and statistical uncertainties in the signal region of signals and SM backgrounds for chargino pair production in the Higgsino-like LSP case.
-
The studies presented in this paper demonstrate that the discovery sensitivity for electroweakinos with both a Bino-like LSP and a Higgsino-like LSP can reach up to a mass of
$ \sqrt{s}/2 $ at the CEPC. The sensitivity can be further improved if additional final states (i.e., electron and tau) are considered, alternate signal scenarios such as disappearing tracks or chargino pair production with photon initial-state radiation (ISR) are used, or more complicated analytical techniques (e.g., machine learning) are implemented.The prospective limits from the CEPC compared with the LEP and LHC results are shown in Fig. 7. In general, the sensitivity at the CEPC is mainly constrained by the center-of-mass energy and is not strongly dependent on the mass splitting between the NLSP and LSP; this allows the CEPC to cover highly compressed electroweakinos that are very difficult to search for at the LHC owing to the reduced acceptance and reconstruction efficiency of soft leptons.
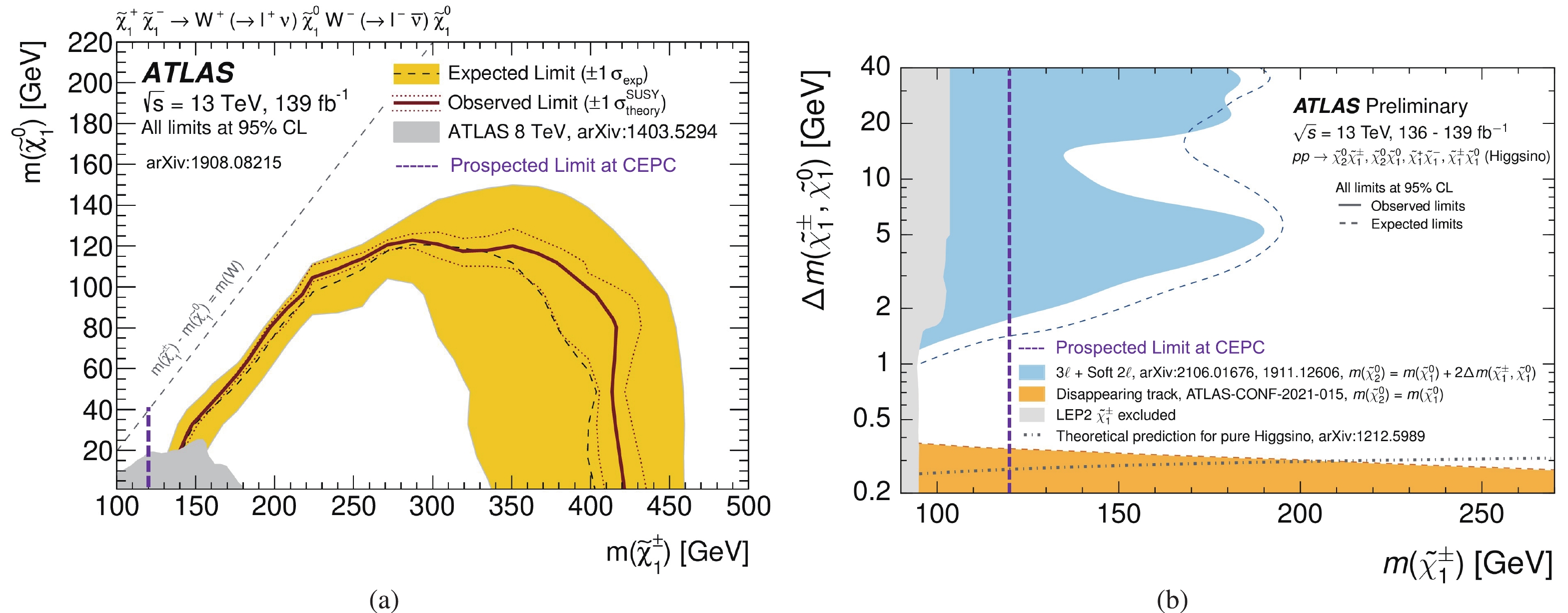
Figure 7. (color online) Observed and expected exclusion limits on SUSY simplified models for chargino-pair production with a (a) Bino-like LSP and (b) Higgsino-like LSP obtained using ATLAS. The observed limits obtained by the LEP are also shown for the Higgsino LSP case in Fig. 7 (b); however, this is not shown in Fig. 7 (a) because the limit of chargino mass is below 100 GeV. The prospective limits at the CEPC are also indicated by the dotted purple line for a rough comparison.
-
Prospective searches for chargino pair production via W boson decay in scenarios with a Bino-like LSP or Higgsino-like LSP are performed at the CEPC using simulated samples. With the assumption of a 5% systematic uncertainty, the discovery sensitivity of electroweakinos can reach
$ \sqrt{s}/2 $ . The choice of systematic uncertainty has no significant impact on the discovery sensitivity. The sensitivity can be further improved by considering more final states, additional signal scenarios, or more complex analytical techniques. Therefore, the CEPC can extend the sensitivity to new Supersymmetry particles and possible dark matter candiates with masses up to 120 GeV [14-19]. For the Higgsino-like LSP scenario, the CEPC has a high sensitivity to the compressed regions with a small mass splitting between$ \tilde{\chi}^{\pm}_1 $ and$ \tilde{\chi}^0_1 $ , which is very difficult to achieve in ATLAS and CMS experiments [22]. The results of this research are based on the CEPC expectations; however, they can also be considered as a reference for other lepton collider experiments at a center-of-mass energy close to 240 GeV, such as the ILC [24] and FCC-ee [25]. -
The authors thank Cheng-dong Fu, Gang Li, and Xiang-hu Zhao for the simulation code they provided.
Prospects for chargino pair production at the CEPC
- Received Date: 2021-05-14
- Available Online: 2022-01-15
Abstract: The proposed Circular Electron Positron Collider (CEPC) with a center-of-mass energy






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: