-
Photonuclear reactions are accompanied by the emission of a nucleon or a group of nucleons from a compound nucleus. This leads to an excited state of the final nucleus, with discharge of excitation energy in a time period of
$ 10^{-12} $ –$ 10^{-17} $ s. However, in some cases, at a low energy of the excitation level and a high degree of forbidden transition, long-lived excited states of the atomic nuclei occur. Such states are called isomeric or metastable states, and their half-lives can vary from nanoseconds to many years [1].Nuclei with isomeric (m) and unstable ground (g) states are of particular interest, as they allow the study of the metastable state population of this nucleus relative to its ground state, i.e., the isomeric ratio (
$ d(E) $ or$ d(E_{\rm{\gamma max}}) $ ) of the reaction products can be obtained. This characteristic is defined as the ratio of the cross-sections for the formation of the reaction product in the metastable$ \sigma_{{\rm{m}}}(E) $ and ground$ \sigma_{{\rm{g}}}(E) $ states:$ d(E) = \sigma_{{\rm{m}}}(E)/\sigma_{{\rm{g}}}(E) $ . The$ d(E) $ values in the literature are given by the ratio of the cross-sections for the formation of a product nucleus in the high-spin state (as a rule, this is a metastable state)$ \sigma_{\rm{H}}(E) $ to the cross-section for the low-spin state$ \sigma_{\rm{L}}(E) $ :$ d(E) = \sigma_{\rm{H}}(E)/\sigma_{\rm{L}}(E) $ [2-4]. In the case of research with the use of bremsstrahlung flux, this ratio$ d(E) $ is expressed through the bremsstrahlung flux-averaged cross-sections or yields of the reactions under study [4-6].Data on the isomeric ratios of the reaction products facilitate investigation of the issues related to the nuclear reactions and nuclear structure, such as the spin dependence of the nuclear level density, angular momentum transfer, nucleon pairing, and shell effects, and help refine the theory of gamma transitions, and test theoretical models of the nucleus [7-11]. The study of isomeric ratios using photonuclear reactions is advantageous because the γ-quantum introduces a small angular momentum and does not change the nucleon composition of the compound nucleus.
Studies in the energy range above the giant dipole resonance (GDR) and below the pion production threshold (30–145 MeV) are of interest, as the mechanism of the nuclear reaction changes here: from dominance of the GDR to dominance of the quasideuteron mechanism [12]. However, in this energy range, there remains a lack of experimental data on the cross-sections of multiparticle photonuclear reactions and isomeric ratios of the products of a nuclear reaction [13, 14]. This complicates the analysis of the mechanism of the nuclear reaction, as well as the systematization and analysis of the dependences of these quantities on various characteristics of the nucleus.
Experiments on the photodisintegration of the 181Ta nucleus in the GDR region have been performed in many works [15-22] using beams of quasi-monochromatic and bremsstrahlung photons. The partial cross-sections of photoneutron reactions at 181Ta were obtained using the method of direct registration of neutrons in the GDR region for
$(\gamma,{n})$ and$(\gamma,2{{n}})$ in [16]. In [17], studies of the partial cross-sections for the reactions$(\gamma,{{n}})$ ,$(\gamma,2{{n}})$ , and$(\gamma,3{{n}})$ , as well as for the reaction$(\gamma,4{{n}})$ up to an energy of 36 MeV were conducted. New data for these reactions were presented in [23]. Regarding the study of the photodisintegration of tantalum at higher energies of the bremsstrahlung γ-quanta, the results for$ E_{\rm{\gamma max}} $ = 55 MeV in the form of weighted average yields and at$ E_{\rm{\gamma max}} $ = 67.7 MeV in the form of a relative yield were presented in [24] and [12], respectively. In [25], experimental values of the total bremsstrahlung flux-averaged cross-sections$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ were obtained for the photoneutron reactions at 181Ta with emission of up to 8 neutrons at$ E_{\rm{\gamma max}} $ = 80–95 MeV and comparisons were made with the calculations using the Talys1.9 code with default parameters.Although numerous experiments on the photodisintegration of 181Ta [23] have been performed, the issue of the isomeric ratio for the products of the reaction 181Ta
$(\gamma,3{n})$ has not been sufficiently studied. Thus, the experimental values$ d(E_{\rm{\gamma max}}) $ for the product nuclei$ ^{178{\rm{m,g}}} $ Ta were presented in [24, 27, 28]. From the data reported in [12] at$ E_{\rm{\gamma max}} $ = 67.7 MeV, it is possible to obtain an estimated value of$ d(E_{\rm{\gamma max}}) $ equal to 0.28$ \pm $ 0.08. In [25], the experimental values of the isomeric ratio were found to be in the energy range$ E_{\rm{\gamma max}} $ = 80–95 MeV and the calculation was performed using the Talys1.9 code with default parameters. The comparison showed that the calculated values were two times greater than the experimental values. The data presented in [24, 28], measured at the same γ-quanta energy, differ significantly. The results reported in [27] and [25] in the energy ranges of 22-32 and 80-95 MeV, respectively, show close values of the isomeric ratio.In this work, we measured the bremsstrahlung flux-averaged cross-sections for the ground
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ and isomeric$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ states from the$^{181}{\rm{Ta}}(\gamma,3{n})^{178{\rm{m,g}}}{\rm{Ta}}$ reaction at the boundary energies of the bremsstrahlung spectra$ E_{\rm{\gamma max}} $ = 35–80 MeV. Based on these data, the values of the total average cross-sections$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ and the isomeric ratio$ d(E_{\rm{\gamma max}}) $ of the reaction products were obtained. To calculate the theoretical values of the average cross-sections and$ d(E_{\rm{\gamma max}}) $ , we used the partial cross-sections from the Talys1.95 code [26] for different models of the level density$ LD $ 1–6. The obtained experimental data were compared both with these calculations and the data reported in the literature. -
The experiments were performed by measuring the residual γ-activity of the irradiated sample, which enables simultaneous acquisition of data on different channels of the photonuclear reactions. This method is well known and has been described in several studies on multiparticle photonuclear reactions, for example, on the 93Nb nucleus [29, 30].
The block diagram of the experiment is shown in Fig. 1, similar to that in [29]. Electrons from the NSC KIPT electron linear accelerator LUE-40 [31, 32] with an initial energy
$ E_{\rm{e}} $ are incident on the target-convertor made of natural tantalum with cross dimensions of 20 mm × 20 mm and a thickness of 1.05 mm. To clean the flux of bremsstrahlung photons from the electrons, a cylindrical Al absorber with a diameter of 100 mm and length of 150 mm was used. The bremsstrahlung γ-flux were calculated using the open certified code GEANT4.9.2 [33] with due regard to the real geometry of the experiment, where the spatial and energy distributions of the electron beam were taken into account.
Figure 1. Schematic block diagram of the experiment. The upper part shows the measuring room and the room for accelerator performance control. The lower part shows (from right to left) two sections of the accelerator LUE-40, Ta converter, Al absorber, and bombardment chamber.
The targets made of natural tantalum and molybdenum with a diameter of 8 mm were placed in an aluminum capsule and, using a pneumatic transport system, were transported to the irradiation site and back to the detector. At the end of irradiation, the capsule with the targets was delivered to the measurement room and within 150–200 s, the sample under study was removed from the capsule and placed to measure the induced γ-activity. This made it possible to experimentally obtain data on the yield of the reaction
$^{181}{\rm{Ta}}(\gamma,3{n})^{178{\rm{g}}}{\rm{Ta}}$ , which has a relatively short half-life$ T_{1/2} = 9.31\pm0.03 $ min [1].In the experiments, ten pairs of natural Ta/Mo samples were exposed to radiation at different end-point bremsstrahlung energies
$ E_{\rm{\gamma max}} $ in the range of 35 to 80 MeV. The masses of the Ta and Mo targets were, ~43 mg and ~60 mg, respectively. The time of irradiation$ t_{\rm{irr}} $ and the time of residual activity spectrum measurement$ t_{\rm{meas}} $ were both 30 min. To exemplify, Fig. 2 shows two fragments of the γ-radiation spectrum from the tantalum target in the energy ranges$ 300 \leqslant E_{\gamma} \leqslant 600 $ keV and$ 1200 \leqslant E_{\gamma} \leqslant 1500 $ keV in which the used γ-lines of the 178Ta nucleus are located.
Figure 2. (color online) Fragment of the γ-radiation spectrum in the energy ranges of
$300 \leqslant E_{\gamma} \leqslant 600$ keV and$1200 \leqslant E_{\gamma} \leqslant 1500$ keV from the tantalum target of mass 42.928 mg after exposure to the bremsstrahlung γ-flux at$E_{\rm{\gamma max}}$ = 80.7 MeV, with$t_{\rm{irr}}$ = 30 min.For γ-radiation registration, a semiconductor HPGe detector (Canberra GC-2018) was used with resolutions of 1.8 keV and 0.8 keV (FWHM) for the energies
$ E_{\gamma} $ = 1332 keV and 122 keV, respectively. The absolute registration efficiency of the detector was calibrated with a standard set of γ-ray sources 22Na, 60Co, 133Ba, 137Cs, 152Eu, and$ ^{241}{\rm{Am}} $ .To investigate the reactions of interest, the residual activity γ-spectrum of the irradiated target was analyzed, and
$ \triangle A $ – the number of counts of γ-quanta in the full absorption peak were determined for the γ-lines corresponding to the nuclei-products$ ^{178{\rm{g}}} $ Ta and$ ^{178{\rm{m}}} $ Ta. Referring to the data from Ref. [1], Table 1 lists the parameters of both the reactions under study and the monitoring reaction, viz., the energy$ E_{\gamma} $ and intensity$ I_{\gamma} $ of the γ-lines in use.Nuclear reaction $E_{\rm{th}}$ /MeV a)

$J^\pi$ of nucleus-product

$T_{1/2}$ 

$E_{\gamma}$ /keV

$I_{\gamma}$ (%)

$^{181}{\rm{Ta} }(\gamma,3{n})^{178{\rm{g} } }{\rm{Ta} }$ 

22.05 $1^+$ 

9.31 (3) min 1350.68 (3) 1.18 (3) $^{181}{\rm{Ta} }(\gamma,{3n })^{ {\rm{178m} } }{\rm{Ta} }$ 

22.35 $(7)^-$ 

2.36 (8) h 426.383 (6) 97.0 (13) $^{100}{\rm{Mo} }(\gamma,{n})^{99}{\rm{Mo} }$ 

8.29 $1/2^+$ 

65.94 (1) h 739.50 (2) 12.13 (12) a) The values of the reaction thresholds $E_{\rm{th}}$ are obtained from the TALYS1.95 code.

Table 1. Spectroscopic data [1] on the nuclei-products from the reactions
$^{181}{\rm{Ta}}(\gamma,3{n})^{178\rm{m,g}}{\rm{Ta}}$ and the monitoring reaction$^{100}{\rm{Mo}}(\gamma,{n})^{99}{\rm{Mo}}$ .During the experiment, as the real conditions may deviate from the conditions used in the calculations, it can lead to an unexpected deviation of the bremsstrahlung flux on the target. To take this deviation into account, bremsstrahlung γ-flux monitoring by the
$^{100}{{\rm{Mo}}}(\gamma,{n})^{99}{{\rm{Mo}}}$ reaction yield was performed by comparing the experimentally obtained average cross-section values$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{exp}} $ with the computation data$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{th}} $ . The normalization coefficients$k = $ $ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{th}}$ /$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{exp}} $ were obtained and varied in a rather narrow range of 1.08 ÷ 1.15. To determine the experimental$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{exp}} $ values, the yield for the γ-line of energy$ E_{\gamma} $ = 739.50 keV and intensity$ I_{\gamma} $ = 12.13% (see Table 1). The average cross-section$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{th}} $ values were computed with the cross-sections$ \sigma(E) $ from the TALYS1.95 code. Details of the monitoring procedure can be found in [29, 34].The Ta converter and Al absorber used in the experiment generate neutrons that can cause the reaction
$^{100}{{\rm{Mo}}}({n},{2n})^{99}{{\rm{Mo}}}$ . The energy neutrons spectrum was calculated along with the fraction of neutrons with energies above the threshold of this reaction, similar to that in [35, 36]. The contribution of the$^{100}{{\rm{Mo}}}(n,2n)^{99}{{\rm{Mo}}}$ reaction to the value of the induced activity of the$ ^{99}{{\rm{Mo}}} $ nucleus has been estimated and it has been shown that this contribution is negligible compared to the contribution of$^{100}{{\rm{Mo}}}(\gamma,{n})^{99}{{\rm{Mo}}}$ .When calculating the values of the average reaction cross-sections, it was assumed that all radioactive isotopes were formed only as a result of the photonuclear reactions at 181Ta, as the concentration of the
$ ^{180{\rm{m}}} $ Ta isomer in a natural mixture of tantalum is negligible (0.012%). The self-absorption of γ-radiation from the reaction products in the target was calculated using the GEANT4.9.2 code, which was accounted for in the calculations.The uncertainty of the measurements of the average cross-sections
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ,$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ , and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ was determined as a squared sum of the statistical and systematic errors. The statistical error in the observed γ-activity is mainly associated with the statistics calculation for the total absorption peak of the corresponding γ-line and is estimated to be in the range of 2%–10% for$ E_{\gamma} $ = 1350.68 keV and up to 2% for$ E_{\gamma} $ = 426.383 keV. The systematic errors stem from the uncertainties in the 1) irradiation time – 0.25%–0.5%; 2) electron current – 0.5%; 3) γ-radiation detection efficiency – ~2%–2.5%, mainly due to the measuring error of the γ-radiation sources; 4) half-life period$ T_{1/2} $ of the reaction products and the intensity of the analyzed γ-quanta$ I_{\gamma} $ (see Table 1); 5) normalization of the experimental data to the yield of the monitoring reaction$^{100}{{\rm{Mo}}}(\gamma,{n})^{99}{{\rm{Mo}}}$ – 2.5%; and 6) the GEANT4.9.2 computational error for the bremsstrahlung γ-flux – ~1.5%.It should be noted that the systematic error in the
$^{100}{{\rm{Mo}}}(\gamma,{n})^{99}{{\rm{Mo}}}$ reaction yield is associated with three fundamentally unremovable errors, each of which is ~1%: unidentified isotopic composition of natural molybdenum, uncertainty in the intensity of the used γ-line$ I_{\gamma} $ [1], and the statistical error in determining the area under the peak of the normalizing γ-line. In the calculations, we used the value of the isotopic abundance of the$ ^{100}{{\rm{Mo}}} $ nucleus reported in [33], which is 9.63%.Thus, the experimental error of the obtained average cross-sections is within 6%–11%.
-
The theoretical values of the total
$ \sigma(E) $ and partial cross-sections of the$^{181}{\rm{Ta}}(\gamma,3{n})^{178}{\rm{Ta}}$ reaction for monochromatic photons were obtained from the TALYS1.95 code [26], which is installed on Linux Ubuntu-20.04. The calculations were performed for different level density ($ LD $ ) models. There are three phenomenological level density models and three options for the microscopic level densities:$ LD 1 $ : Constant temperature + Fermi gas model. In this model introduced by Gilbert and Cameron [37], the excitation energy range is divided into a low-energy part from$ E_0 $ up to a matching energy$ E_{\rm{M}} $ , where the so-called constant temperature law applies, and a high-energy part above, where the Fermi gas model applies.$ LD 2 $ : Back-shifted Fermi gas model. In the back-shifted Fermi gas model [38], the pairing energy is treated as an adjustable parameter and the Fermi gas expression is used down to$ E_0 $ .$ LD 3 $ : Generalized superfluid model (GSM). This model takes superconductive pairing correlations into account according to the Bardeen-Cooper-Schrieffer theory. The phenomenological version of the model [39, 40] is characterized by a phase transition from a superfluid behavior at low energy, where pairing correlations strongly influence the level density, to a high energy region, which is described by the Fermi gas model. The GSM thus resembles the constant temperature model to the extent that it distinguishes between low energy and a high energy region, although for the GSM, this distinction follows naturally from the theory and does not depend on the specific discrete levels that determine the matching energy. Instead, the model automatically provides a constant temperature-like behavior at low energies.$ LD 4 $ : Microscopic level densities (Skyrme force) from Goriely's tables. Using this model allows reading tables of microscopic level densities from the RIPL database. These tables were computed by S. Gorielyon based on the Hartree-Fock calculations for excitation energies up to 150 MeV and spin values up to I = 30.$ LD 5 $ : Microscopic level densities (Skyrme force) from Hilaire's combinatorial tables. The combinatorial model includes a detailed microscopic calculation of the intrinsic state density and collective enhancement. The only phenomenological aspect of the model is a simple damping function for the transition from spherical to deformed.$ LD 6 $ : Microscopic level densities (temperature-dependent HFB, Gogny force) from Hilaire’s combinatorial tables.The calculations of the total and partial cross-sections in the TALYS1.95 code for the
$^{181}{\rm{Ta}}(\gamma,{3n})^{178}{\rm{Ta}}$ reaction for different level density models are shown in Figs. 3(a), (b), and (c). It can be seen from the figures that the behavior of the cross-sections with energy for the$ LD $ 5 and$ LD $ 6 models is somewhat different from the others: the positions of the cross-section maxima are shifted toward higher energies. In addition, the height of the maxima of these curves in the case of the calculations for the formation of a nucleus in the isomeric state is significantly lower (by 1.5 times) compared with the other$ LD $ models. This leads to a decrease in the values of the total cross-section for the formation of the 178Ta nucleus calculated in the$ LD $ 5 and$ LD $ 6 models.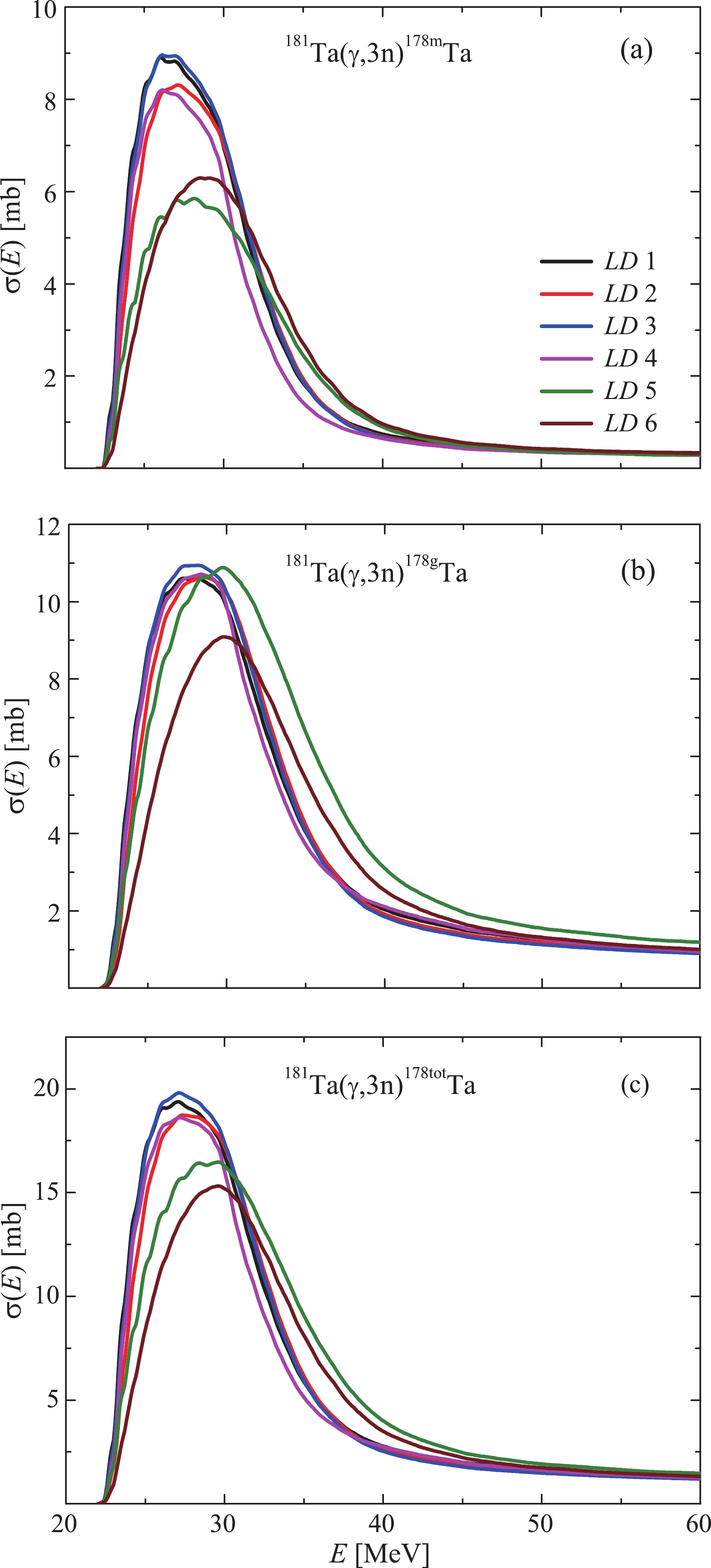
Figure 3. (color online) Partial and total cross-sections
$\sigma(E)$ for the reaction$^{181}{\rm{Ta}}(\gamma,{3n})^{178}{\rm{Ta}}$ from the TALYS1.95 code for different models of level density$LD$ 1-6. a) – cross-section of nucleus formation in the isomeric state, b) – in the ground state, c) – total cross-section. -
The values of the cross-sections
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ , averaged over the bremsstrahlung flux of the γ-quanta$ W(E,E_{\rm{\gamma max}}) $ from the threshold$ E_{\rm{th}} $ of the reaction under consideration to the boundary energy of the spectrum$ E_{\rm{\gamma max}} $ , were calculated using the cross-sections$ \sigma(E) $ from the TALYS1.95 code [26]. The bremsstrahlung flux-averaged cross-section$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ was calculated according to the formula:$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle = \frac {\displaystyle\int_{E_{\rm{th}}}^{E_{\rm{\gamma max}}}\sigma(E)\cdot W(E,E_{\rm{\gamma max}}){\rm d}E} {\displaystyle\int_{E_{\rm{th}}}^{E_{\rm{\gamma max}}}W(E,E_{\rm{\gamma max}}){\rm d}E}. $

(1) These calculated values of the average cross-sections were compared with the experimental values obtained in the work, which were calculated using the formula:
$ \begin{aligned}[b]& \langle{\sigma(E_{\rm{\gamma max}})}\rangle = \\& \frac{\lambda \triangle A}{N_x I_{\gamma} \ \varepsilon \Phi(E_{\rm{\gamma max}}) (1-\exp(-\lambda t_{\rm{irr}}))\exp(-\lambda t_{\rm{cool}})(1-\exp(-\lambda t_{\rm{meas}}))}, \end{aligned} $

(2) λ is the decay constant (
$ {\rm{ln}}2/T_{1/2} $ ), where$ \triangle A $ is the number of counts of γ-quanta in the full absorption peak (for the γ-line of the investigated reaction),$ N_x $ is the number of target atoms,$ I_{\gamma} $ is the intensity of the analyzed γ-quanta,$ \varepsilon $ is the absolute detection efficiency for the analyzed γ-quanta energy,${\rm{\Phi}}(E_{\rm{\gamma max}}) = {\int_{E_{\rm{th}}}^{E_{\rm{\gamma max}}}W(E,E_{\rm{\gamma max}}){\rm d}E}$ is the sum of the bremsstrahlung quanta in the energy range from the reaction threshold$ E_{\rm{th}} $ up to$ E_{\rm{\gamma max}} $ , and$ t_{\rm{irr}} $ ,$ t_{\rm{cool}} $ , and$ t_{\rm{meas}} $ are the irradiation time, cooling time, and measurement time, respectively. For further details, all the calculation procedures required to determine$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ are described in [25, 29, 34].If the product nucleus has an isomeric state, the value of the total averaged cross-section
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{\rm{tot}} $ (hereinafter$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ) of the reaction under study is calculated as the sum of$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ , respectively, of the average cross-sections for the population of the isomeric and ground states, each with its reaction threshold$ E_{\rm{th}} $ (see Table 1).The isomeric ratio of the reaction products is defined as the ratio of the cross-section
$ \sigma_{{\rm{m}}}(E) $ of the formation of the nucleus in the metastable (usually high-spin) state to the cross-section$ \sigma_{{\rm{g}}}(E) $ of the nucleus in the ground state. This definition enables estimation of the degree of the population of the metastable state concerning the ground state of the product nucleus.In the case of experiments on the bremsstrahlung beam of γ-quanta, the isomeric ratio is defined as the ratio of the yields or as the ratio of the average cross-sections for the formation of reaction products in the metastable and ground states. The expression for
$ d(E_{\rm{\gamma max}}) $ in terms of the average cross-sections can be written as:$ d(E_{\rm{\gamma max}}) = {\langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}}} / {\langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}}}. $

(3) -
The obtained experimental data on the bremsstrahlung flux-averaged cross-sections
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ,$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ , and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ for the$^{181}{\rm{Ta}}(\gamma,{3n})^{178}{\rm{Ta}}$ reactions in the end-point energy range of the bremsstrahlung γ-quanta$ E_{\rm{\gamma max}} $ = 35–80 MeV are presented in Figs. 4(a), (b), and (c). These figures also show the earlier results of our study [25] for the considered reaction (at$ E_{\rm{\gamma max}} $ = 80–95 MeV). Within the limits of experimental errors, the data presented in this work and that reported in [25] are in good agreement.
Figure 4. (color online) The bremsstrahlung flux-averaged cross-sections (partial and total) for the reaction
$^{181}{\rm{Ta}}(\gamma,{3n})^{178}{\rm{Ta}}$ : a) – the cross-section for the formation of a nucleus in the isomeric state, b) – in the ground state, c) – the total cross-section of the reaction. Points – experimental results of this work (filled) and [25] (empty), curves – calculated using the TALYS1.95 code for different models of the$LD$ 1-6 level density.The theoretical values of the average cross-sections were obtained from Eq. (1) using the bremsstrahlung fluxes corresponding to the real experimental conditions and are shown in Fig. 4. It can be seen from Fig. 4(a) that the experimental cross-sections for the formation of a nucleus in the isomeric state
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ are located below all the theoretical curves, but are closest to the calculations by models$ LD $ 5 and 6. In the case of the cross-section$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ , the experimental values are higher than all the calculations in the 35–60 MeV range, but at 65–95 MeV, there is good agreement with the calculation for the$ LD $ 5 model.As shown in Fig. 4(c), the theoretical values of the total averaged cross-section according to the
$ LD $ 1, 3 and$ LD $ 6 models differ by 20%–30%, forming a corridor in which all the experimental data$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ and calculations for$ LD $ 2, 4, and 5 are located. The insignificant difference between the theoretical values$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ for$ LD $ 2, 4, and 5 (up to 5% in the energy range of 45–95 MeV) does not allow any of them to be distinguished using the experimental results.In general, the analysis of the experimental values of
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ,$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ , and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ shows that the best agreement with the theoretical calculations using the TALYS1.95 code was achieved for the$ LD $ 5 model: Microscopic level densities (Skyrme force) from Hilaire's combinatorial tables. -
Figure 5 presents the experimental and theoretical values of the isomeric ratio
$ d(E_{\rm{\gamma max}}) $ of the reaction products$^{181}{\rm{Ta}}(\gamma,{3n})^{178{\rm{m,g}}}{\rm{Ta}}$ , calculated by Eq. (3) using the obtained$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ .
Figure 5. (color online) Isomeric ratios
$d(E_{\rm{\gamma max}})$ of the$^{181}{\rm{Ta}}(\gamma,{3n})^{178{\rm{m,g}}}{\rm{Ta}}$ reaction products. Experimental data: rhombuses – the results of this work (filled) and from [25] (empty), star – [24], circle – [12], square – [27], triangle – [28]. Solid lines – calculations of$d(E_{\rm{\gamma max}})$ using TALYS1.95 for the models$LD$ 1-6 (the lines are marked as in Fig. 4), dash-dotted line – approximation of all the experimental data by the horizontal line (0.335$\pm$ 0.008).The experimental values
$ d(E_{\rm{\gamma max}}) $ determined in this work coincide within the error with the results in the range$ E_{\rm{\gamma max}} $ = 80–95 MeV [25]. The analysis of the entire set of our experimental values shows that$ d(E_{\rm{\gamma max}}) $ are grouped around a constant value 0.343$ \pm $ 0.007. This result refines the previously obtained value of$ d(E_{\rm{\gamma max}}) $ , equal to 0.37$ \pm $ 0.02 [25]. We would like to draw attention to the tendency for an insignificant decrease in the isomeric ratio with decreasing energy$ E_{\rm{\gamma max}} $ .The value of the isomeric ratio
$ d(E_{\rm{\gamma max}}) $ enables estimation of the degree of the population of the metastable state concerning the ground state of the reaction product nucleus. The determined value of the isomeric ratio shows that the probability of the formation of a nucleus in the ground state of$ ^{178{\rm{g}}} $ Ta ($ J^{\pi} = 1^+ $ ) exceeds the probability of the formation of the isomeric state of$ ^{178{\rm{m}}} $ Ta ($ J^{\pi} = (7)^- $ ) by approximately three times.The experimental values of the isomeric ratio
$ d(E_{\rm{\gamma max}}) $ of the reaction products$ ^{181}{\rm{Ta}}(\gamma,{\rm{3n}})^{178{\rm{m,g}}}{\rm{Ta}} $ reported in the literature [12, 24, 27, 28] make it possible to expand the energy range to 24–95 MeV. In [27], the values of$ d(E_{\rm{\gamma max}}) $ were obtained for energies in the range of 24–32 MeV, and the constancy of the isomer ratio equal to 0.33$ \pm $ 0.07 was shown (in Fig. 5, they are shown only for 32 MeV). A joint analysis of the values from [12, 24, 25, 27] and this work shows that the experimental values of$ d(E_{\rm{\gamma max}}) $ are grouped near a constant value equal to 0.335$ \pm $ 0.008. As the value of$ d(E_{\rm{\gamma max}}) $ from [28] is significantly higher than all the experimental results, it was not used in the analysis.In [41], the isomeric ratios of the reaction products
$^{181}{\rm{Ta}}({p},{p3n})^{178{\rm{m,g}}}{\rm{Ta}}$ were obtained at proton energies of 100, 145, 200, 350, and 500 MeV using offline γ-spectroscopy. It was shown that the obtained isomeric ratios are constant and close to$ d(E) \sim $ 0.37–0.38 at 100–500 MeV. This value is consistent with the results of this work and coincides with an energy of 95–100 MeV. We would like to emphasize the experimental fact that, despite the different excitation mechanisms of the 181Ta nucleus, the isomeric ratio of the reaction products$ ^{178{\rm{m,g}}} $ Ta is the same.In Fig. 5, the theoretical values of the isomeric ratio
$ d(E_{\rm{\gamma max}}) $ calculated for the fluxes of bremsstrahlung γ-quanta for real experimental conditions are shown. All the calculated curves for$ d(E_{\rm{\gamma max}}) $ ($ LD $ 1-6) have the same dependence on the energy$ E_{\rm{\gamma max}} $ : the isomeric ratio slightly increases with decreasing energy. The main difference between the calculated curves lies in the absolute value of the isomeric ratio. The calculation for the$ LD $ 5 model lies below all the other models.The comparison shows that the default calculation (
$ LD $ 1) gives a value of$ d(E_{\rm{\gamma max}}) $ almost two times higher than the experimental value, and the best agreement with the experiment was achieved for the case of the$ LD $ 5 model.Note the different behavior of the calculated and experimental energy dependence of the isomeric ratios. The calculated value of
$ d(E_{\rm{\gamma max}}) $ increases with decreasing energy$ E_{\rm{\gamma max}} $ and the available experimental data tend to insignificantly (within the limits of the experimental errors) decrease. -
The present work was concerned with the investigation of the photoneutron reaction
$^{181}{\rm{Ta}}(\gamma,{3n})^{178{\rm{m,g}}}{\rm{Ta}}$ at the boundary energies of the bremsstrahlung spectra$ E_{\rm{\gamma max}} $ = 35–80 MeV using the residual γ-activity method. As a result, the flux-averaged cross-sections$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ,$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ , and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ of the photoneutron reactions$^{181}{\rm{Ta}}(\gamma,{3n})^{178{\rm{m,g}}}{\rm{Ta}}$ were obtained.The theoretical values
$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle $ ,$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{m}}} $ , and$ \langle{\sigma(E_{\rm{\gamma max}})}\rangle_{{\rm{g}}} $ were calculated using$ \sigma(E) $ from the TALYS1.95 code for different models of the$ LD $ 1-6 level density. A comparison of the experimental averaged cross-sections with the calculations showed that the best agreement was achieved for the$ LD $ 5 model: Microscopic level densities (Skyrme force) from Hilaire's combinatorial tables.The experimental values of the isomeric ratios
$ d(E_{\rm{\gamma max}}) $ of the reaction products were obtained in the energy range$ E_{\rm{\gamma max}} $ = 35–80 MeV. The determined$ d(E_{\rm{\gamma max}}) $ indicate a significant suppression of the population of the isomeric state of the$ ^{178{\rm{m}}} $ Ta nucleus concerning the ground state of$ ^{178{\rm{g}}} $ Ta (by approximately a factor of 3). The obtained$ d(E_{\rm{\gamma max}}) $ values show good agreement with the data reported in the literature. All the available experimental$ d(E_{\rm{\gamma max}}) $ [12, 24, 25, 27, 28] in the range$ E_{\rm{\gamma max}} $ = 24-95 MeV are grouped near a constant value of 0.335$ \pm $ 0.008.It was shown that the default calculation (
$ LD $ 1) gives a value of$ d(E_{\rm{\gamma max}}) $ that is almost two times higher than the experimental value. The closest agreement with the experiment was achieved for the$ LD $ 5 model.The different behavior of the energy dependence of the calculated and experimental isomeric ratios was observed. The calculated value of
$ d(E_{\rm{\gamma max}}) $ increases with decreasing energy$ E_{\rm{\gamma max}} $ and the available experimental data tend to slightly (within the experimental errors) decrease with decreasing energy$ E_{\rm{\gamma max}} $ . -
The authors would like to thank the staff of the linear electron accelerator LUE-40 NSC KIPT, Kharkiv, Ukraine, for their cooperation in the realization of the experiment.
Isomeric ratio of the 181Ta(γ, 3n)178m,gTa reaction products at energy Eγmax up to 95 MeV
- Received Date: 2027-07-14
- Available Online: 2022-01-15
Abstract: The photoneutron reaction





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: