-
Magnetic moment, as one fundamental property of the atomic nucleus, provides rich information and invaluable insights for a deeper understanding of nuclear structure problems, such as shell structure and tensor force. However, understanding the theoretical description of nuclear magnetic moments is one of the most frequently stated challenges for many nuclear physicists. Although extensive research has been carried out on nuclear structures in the past decades [1-7], none of the models have been able to address nuclear magnetic moments. Owing to its high sensitivity to nuclear wavefunctions, the nuclear magnetic moment serves as a useful tool for the stringent testing of nuclear models and has quickly attracted the attention of nuclear physicists, particularly regarding the magnetic moments of odd mass nuclei.
Early investigations involved the application of the well-known Landé g-factor to the available data of odd-A nuclei with different proton and neutron magnetic moments in the 1930s [8, 9]. Since the establishment of the independent particle shell model in 1949 by Mayer and Jensen, which explains the magic numbers
$ Z = 2, 8, $ $ 20, 28, 50, $ and 82 as well as$ N = 2, 8, 20, 28, 50, 82 $ , and 126, the magnetic moment of an odd-A nucleus has been interpreted as the contribution of the unpaired valence nucleon. This leads to the well-known Schmidt values,$ \begin{array}{ll} {{\mu_s}} \hspace*{-2mm} & = \; \langle (nl)\,jm|g_l\hat{l}_z+g_s\hat{s}_z|(nl)\,jm\rangle_{m = j} \\ & = \; \left\{ \begin{array}{ll} g_ll+\dfrac{1}{2}g_s, \qquad &\qquad j = l+1/2 \nonumber \\ \nonumber \\ \dfrac{j}{j+1}\left[g_l(l+1)-\dfrac{1}{2}g_s\right], &\qquad j = l-1/2, \nonumber\\ \end{array} \right. \end{array} $

where l is the orbital angular momentum of the valence nucleon, and j is the total angular momentum.
$ g_{l} = 1(0) $ and$ g_{s} = 5.586(-3.826) $ are the orbital and spin g-factors of the proton (or neutron), respectively. The magnetic moment in the above equation as a function of spin j results in the Schmidt lines.In the early 1950s [10, 11], it was observed that almost all nuclear magnetic moments are sandwiched between two Schmidt lines. Thereafter, significant efforts have been made to explain the deviation of nuclear magnetic moments from the Schmidt values, beyond investigations of single particle properties such as the Arima-Horie effect [12, 13]. Eventually, it was found that the deviation is contributed by the effects of a two-body meson exchange current (MEC, i.e., the exchange of the charged mesons) and configuration mixing (CM, or core polarization, i.e., the correlations beyond the mean field approximation) [7, 14, 15]. With these two corrections, the magnetic moments of odd-even nuclei around doubly magic nuclei can be reproduced well in both non-relativistic and relativistic frameworks [7, 16-24]. For odd A nuclei far from the magic nuclei, the effective spin and orbital g factor are usually adopted in different promising theoretical models [25], and are even applied for certain specific nuclei. However, there is still a lack of a unified model or theory to give precise predictions for a wide range of odd mass nuclei. Therefore, predictions of the magnetic moments of odd-A nuclei are highly anticipated.
Machine learning is a popular technique for dealing with complex systems owing to its powerful and convenient inference abilities. In the past decade, the prodigious development of machine learning applications has impacted many fields such as image recognition [26, 27] and language translation [28, 29]. It is also a powerful method to extract underlying features from big data generated by experiments. Parallel to the rise of machine learning techniques in daily and industrial applications, scientists have become increasingly interested in its potential for fundamental research, and physics is not an exception. Machine learning has been applied to diverse fields in physics over the past few years, such as particle physics [30-32], condensed matter physics [33, 34], and statistical physics [35].
In nuclear physics, machine learning has been used to learn enormous amounts of data and make predictions, for example, machine leaning with radial basis functions [36, 37] and neural networks. Compared with traditional neural networks [38, 39], Bayesian neural networks (BNN) can automatically solve the overfitting problem by introducing the prior distribution of parameters, and it can also avoid ill-inversed regression problems with uncertainty quantifications [40] since all parameters have probability distributions. Many successful applications of BNN have been performed in nuclear physics, for example, predictions of the nuclear mass [41-43], charge radius [44],
$ \beta $ -decay half-lives [45], and fission product yields [46]. In this respect, the BNN approach would be ideal to improve the magnetic moment descriptions of odd-A nuclei with the extreme single-particle shell model. In this study, the basic formulas of the BNN approach are given in Sec. II, the results of magnetic moments are discussed in Sec. III, and the summary and perspectives are presented in Sec. IV. -
In the Bayesian approach, the model parameters
$ \boldsymbol{\omega} $ are described probabilistically [42, 45]. The prior distribution$ p(\boldsymbol{\omega}) $ is a probability distribution over all possible values of$ \boldsymbol{\omega} $ . When a set of data$D = \left\{\left(\boldsymbol{x}_{1}, $ $ t_{1}\right), $ $ \left(\boldsymbol{x}_{2}, t_{2}\right), \ldots,\left(\boldsymbol{x}_{N}, t_{N}\right)\right\}$ is given, this distribution will be updated according to Bayes' theorem:$ p(\boldsymbol{\omega}\mid D) = \frac{p(D\mid\boldsymbol{\omega}) p(\boldsymbol{\omega})}{\displaystyle\int p(D \mid \boldsymbol{\omega}) p(\boldsymbol{\omega}) {\rm d} \boldsymbol{\omega}}, $

(1) where
$ \boldsymbol{x_{n}} $ and$ t_{n}(n = 1,2, \ldots, N) $ represent inputs and outputs, respectively, N is the number of data,$ p(D |\boldsymbol{\omega}) $ contains the information about parameters$ \boldsymbol{\omega} $ derived from observations,$ p(\boldsymbol{\omega}\midD) $ denotes the posterior distribution, and$\int p(D\mid\boldsymbol{\omega}) p(\boldsymbol{\omega}) {\rm d} \boldsymbol{\omega}$ is a normalization constant to ensure the integral of the posterior distribution is 1.For the likelihood function
$ p(D| \boldsymbol{\omega}) $ , a Gaussian distribution,$ p(D \mid \boldsymbol{\omega}) = \exp \left(-\chi^{2} / 2\right), $ is employed, where the objective function$ \chi^{2} $ is given by$ \chi^{2} = \sum\limits_{n = 1}^{N}\left(\frac{t_{n}-f(\boldsymbol{x};\boldsymbol{\omega})}{\Delta t_{n}}\right)^{2}, $

(2) where the standard deviation parameter
$ \Delta t_{n} $ is the associated noise scale [40-42]. The net function$ f(\boldsymbol{x} ; \boldsymbol{\omega}) $ is defined as$ f(\boldsymbol{x} ;\boldsymbol{\omega}) = a+\sum\limits_{j = 1}^{H} b_{j} \tanh \left(c_{j}+\sum_{i = 1}^{I} d_{j i} x_{i}\right), $

(3) where
$ \boldsymbol{x} = \left\{x_{i}\right\} $ and$ \boldsymbol{\omega} = \left\{a, b_{j}, c_{j}, d_{j i}\right\}, $ and H and I are the number of hidden layers and the number of input variables, respectively.The prior distributions
$ p(\boldsymbol{\omega}) $ of the model parameters are usually adopted as Gaussian distributions with zero means. The precisions (inverse of variances) of these Gaussian distributions are set as gamma distributions as in Refs. [42, 45], so that the precisions can change over a wide range. Therefore, it enables the BNN approach to automatically search the optimal values of precisions in the sampling process.After specifying the likelihood function
$ p(D\mid\boldsymbol{\omega}) $ and the prior distribution$ p(\boldsymbol{\omega}), $ the posterior distribution$ p(\boldsymbol{\omega} \midD) $ of the model parameters is obtained according to Eq. (2). The averaged nuclear magnetic moment prediction of BNN relates to a high-dimensional integral in the whole parameter space and can be obtained by a hybrid Markov chain Monte Carlo algorithm [47]:$ \langle f\rangle = \int f(\boldsymbol{x} ; \boldsymbol{\omega}) p(\boldsymbol{\omega} \mid D) {\rm d} \boldsymbol{\omega}. $

(4) An estimate of uncertainty in theoretical predictions can be obtained naturally at the same time, which is a criterion for evaluating the reliability of predicted results, using the following:
$ \Delta f = \sqrt{\left\langle f^{2}\right\rangle-\langle f\rangle^{2}}. $

(5) In this study, the BNN approach is used to reconstruct nuclear magnetic moment residuals between experimental data
$ \mu^{\mathrm{exp}} $ and the Schmidt values$ \mu^{\text {th }} $ , i.e.,$ t_{n} = \mu^{\exp }(\boldsymbol{x})-\mu^{\mathrm{th}}(\boldsymbol{x}). $

(6) Since the magnetic moments of odd-A nuclei have strong relations with the spin and Schmidt values, the nuclear spin I and the corresponding Schmidt magnetic moment value
$ \mu_{s} $ have inputs apart from Z and N to ascertain the effect of these two additional inputs. For simplicity, we use BNN-I2 and BNN-I4 to represent the BNN approaches with$ \boldsymbol{x} = (Z, N) $ and$ \boldsymbol{x} = (Z, N,I,\mu_{s}) $ , respectively. To ensure the number of parameters in the neural network are the same, the number of neurons in BNN-I2 and BNN-I4 are set as 45 and 30, respectively.The experimental data of nuclear magnetic moments are taken from the IAEA online database and table of recommended nuclear magnetic dipole moments [48, 49]. Only the nuclei whose spin and parity are determined and can be roughly explained by the extreme single-particle shell model remain. For example, for the ground state spin and parity of
$ ^{17} $ O is${{5}/{2}}^+$ , the odd neutron occupies the$ \nu1d_{\frac{5}{2}} $ orbital [50] in the extreme spherical single particle shell model. Conversely, for$ ^{89} $ Kr, the ground state spin and parity${{3}/{2}}^+$ [51] can not be explained by the odd neutron orbital neighbouring$ N = 53 $ in the extreme single-particle shell model, and therefore it will not be considered in the entire set. There are 227 odd-proton nuclei and 221 odd-neutron nuclei left and their experimental magnetic moments are taken as the training data. Since the contributions of the unpaired valence neutron and valence proton to the magnetic moment are different, the odd-neutron and odd-proton nuclei are studied by the BNN approach separately. -
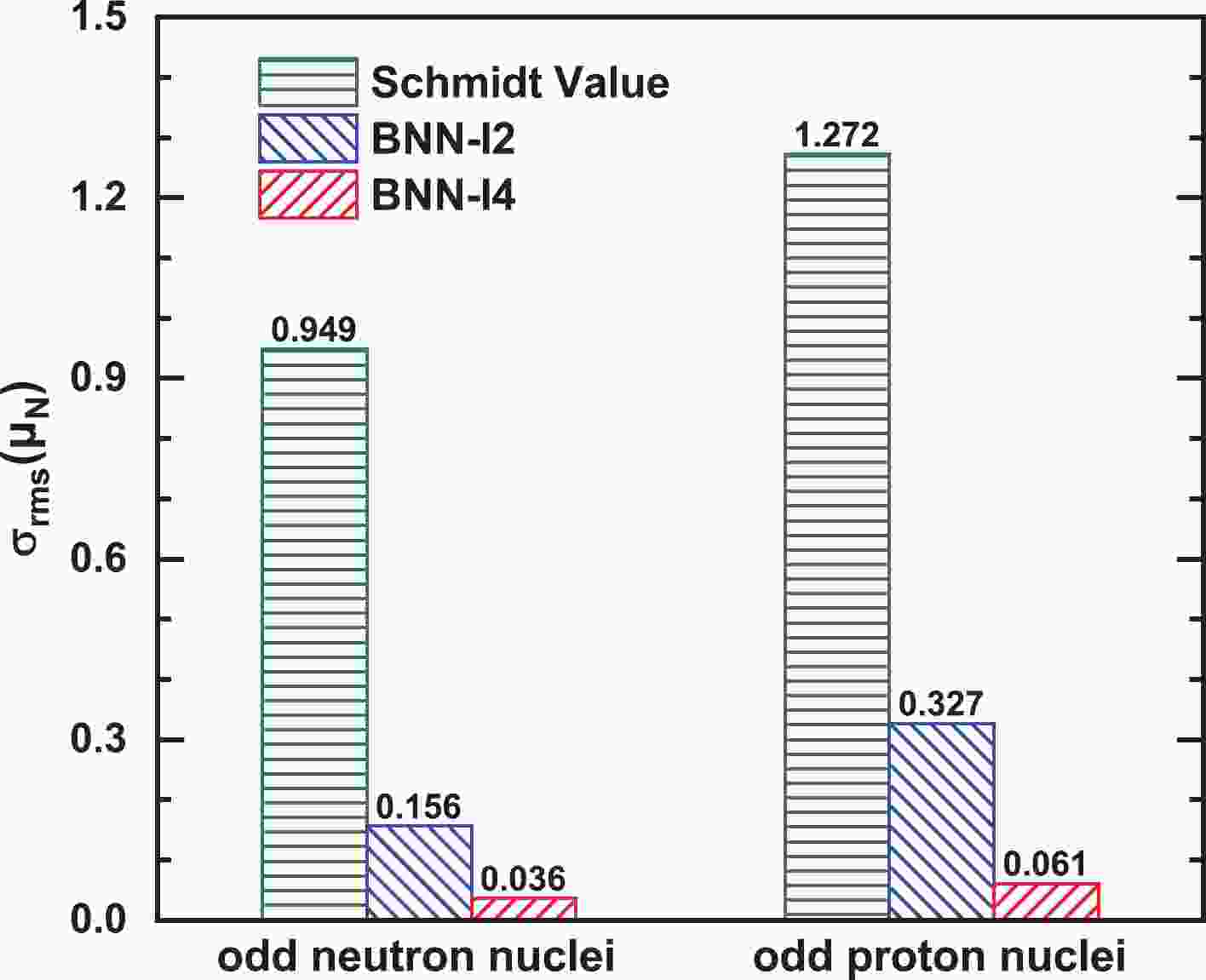
Figure 1 shows the nuclear magnetic moment predictions of the BNN-I2 and BNN-I4 approaches for odd-neutron nuclei and odd-proton nuclei, in comparison with the Schmidt values given by Eq. (1). It is clearly seen that the root-mean-square (rms) deviations of the Schmidt values are very large (0.949
$ \mu_\mathrm{N} $ and 1.272$ \mu_\mathrm{N} $ for odd-neutron nuclei and odd-proton nuclei, respectively). After the BNN approach is included, the corresponding rms deviations are significantly reduced. Compared with BNN-I2, the rms deviations of BNN-I4 are further reduced from 0.156$ \mu_\mathrm{N} $ to 0.036$ \mu_\mathrm{N} $ for odd-neutron nuclei and from 0.327$ \mu_\mathrm{N} $ to 0.061$ \mu_\mathrm{N} $ for odd-proton nuclei, respectively, which is very precise for the predictions of magnetic moments. In fact, the nuclear spin is closely related to the magnetic moment, and the extreme single particle shell model together with the corresponding Schmidt value is a useful approximation for odd A nuclei. Therefore, the above results indicate that the BNN approach is a reliable way to improve the accuracy of nuclear magnetic moment predictions based on a theoretical model by including known physics effects in the input layer. It should be noted that different combinations of physical quantities are tried as inputs, and it is found that the accuracy of the network is significantly correlated with spin, while the correlation with parity is relatively weak. Since the predictions from BNN-I4 are much better than those from BNN-I2, we are only showing the results based on the BNN-I4 approach.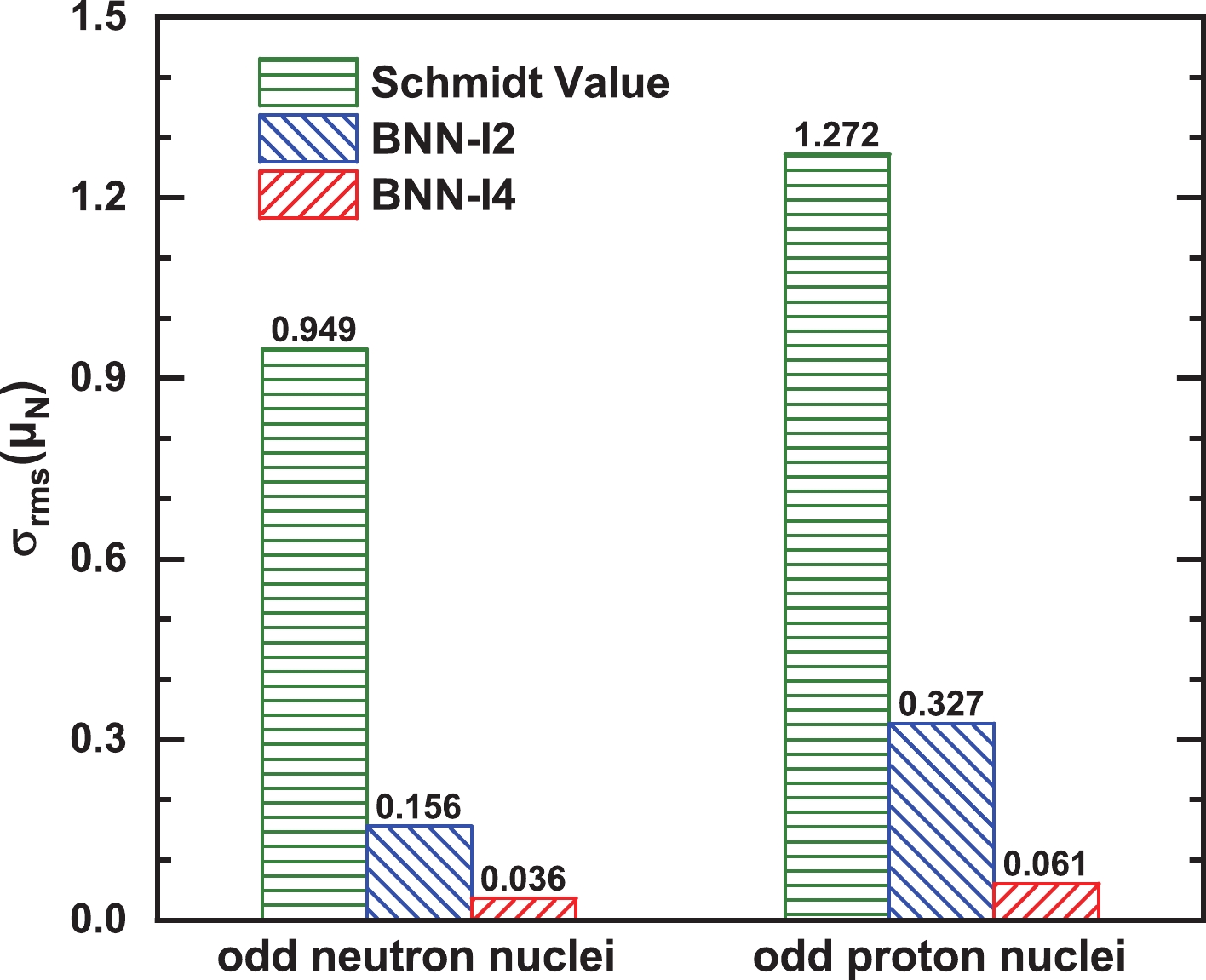
Figure 1. (color online) Root-mean-square deviations of nuclear magnetic moments for odd-neutron nuclei (left) and odd-proton nuclei (right) with respect to the experimental data from the Schmidt magnetic moment and those improved by the BNN approaches.
To further evaluate the prediction ability of the BNN approach, the entire data set of both odd-proton nuclei and odd-neutron nuclei are divided into two parts: the learning set and the validation set. The two learning sets are obtained by randomly selecting 190 nuclei from each entire set and the two corresponding validation sets are built with the remaining nuclei of each entire set (37 odd-proton nuclei and 31 odd-neutron nuclei). In Figs. 2 and 3, the magnetic moments of odd-neutron and odd-proton nuclei, obtained from the BNN-I4 approach, are compared with the experimental values in the learning set (a) and with the Schmidt values and the experimental values in the validation set (b).
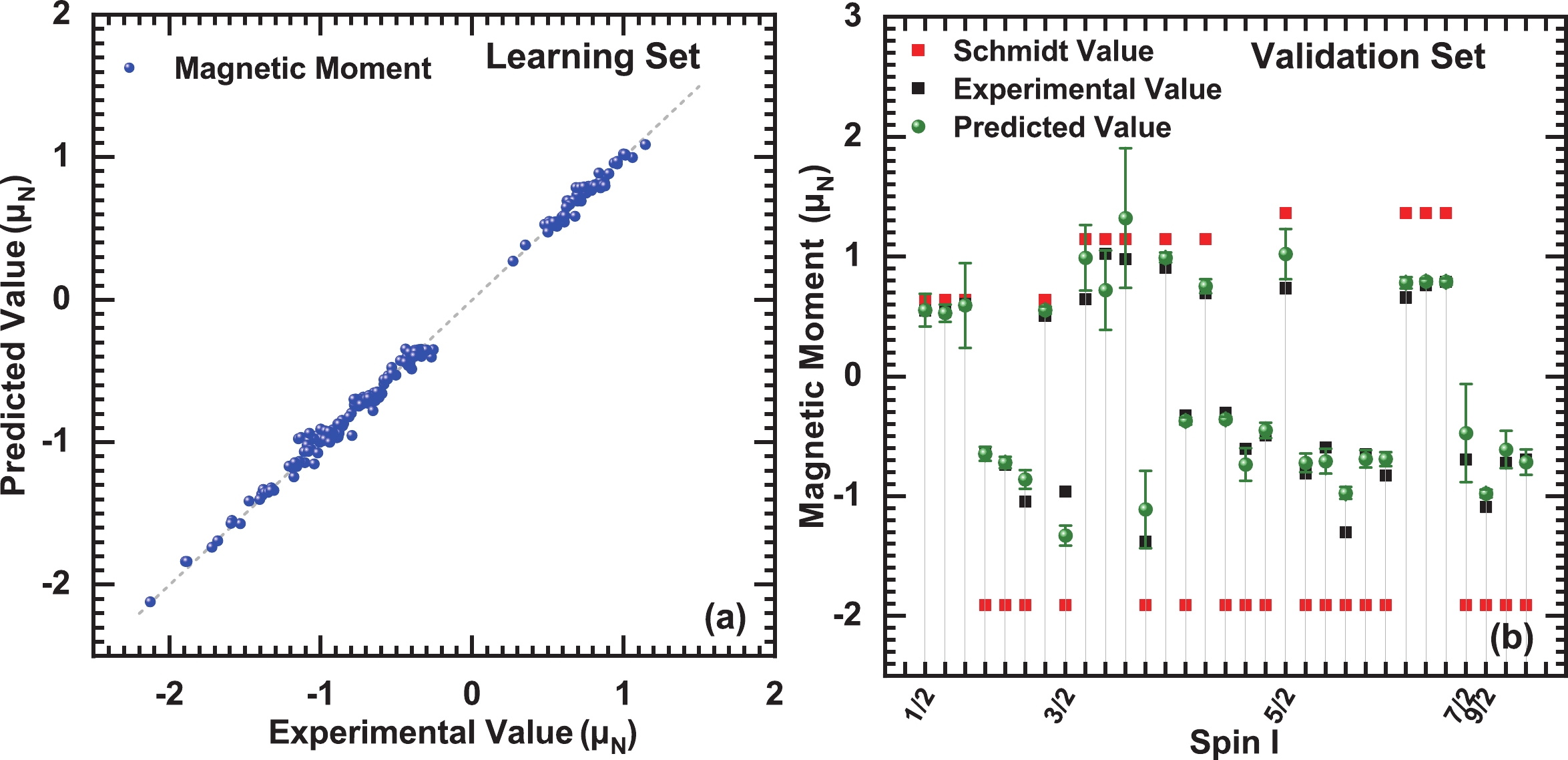
Figure 2. (color online) The magnetic moments of odd-neutron nuclei obtained from the BNN-I4 approach, in comparison with the experimental values in the learning set (a) and with Schmidt values and the experimental values in the validation set (b). Nuclei in panel (b) are arranged from small to large spin (I), and the repeated spin (I) values are omitted.

Figure 3. (color online) Same as Fig. 2, but for odd-proton nuclei.
From Figs. 2(a) and 3(a), it is found that almost all points are on the line
$ y = x $ , which means that the BNN-I4 predictions are very close to the experimental values. According to Figs. 2(b) and 3(b), the BNN predictions are also satisfactory for the nuclear magnetic moments in the validation set, although they are not used as the learning data. It is shown that the experimental data are sandwiched between the two Schmidt lines, and the Schmidt values clearly show large discrepancies from the data. The BNN-I4 approach remarkably improves the precision of predictions in the validation set; the deviations for most validated nuclei are less than 0.1$ \mu_\mathrm{N} $ . Although several nuclei exhibit relatively large deviations, their experimental values are still contained in the range of predictions and their uncertainties, which demonstrates that the BNN-I4 approach is a reliable method. Therefore, the interpolation ability of the BNN-I4 approach is also promising.Since the interpolation ability of BNN-I4 has been verified in Figs. 2 and 3, the entire sets are adopted as learning sets to assess the predictive power of the neural network for odd-neutron nuclei and odd-proton nuclei, respectively, and the differences in magnetic moments of odd mass nuclei between the experimental values and the predictions obtained from the BNN-I4 approach are shown in Fig. 4. It is clearly seen that BNN-I4 performed well in almost the entire range of both odd-neutron nuclei and odd-proton nuclei. More specifically, the deviations of 153 nuclei out of 227 (181 nuclei out of 221 nuclei) in odd-proton nuclei (odd-neutron nuclei) are within the range of 0.05
$ \mu_\mathrm{N} $ . The better predictive performance for odd-neutron nuclei is not a surprise because the Schmidt values of the extreme single-particle model give a better description of odd-neutron nuclei than those of odd-proton nuclei.
Figure 4. (color online) Differences in magnetic moments of odd-neutron nuclei (a) and odd-proton nuclei (b) between the experimental values and the predictions obtained from the BNN-I4 approach.
It is also interesting to examine the predictive power of the BNN approach along isotope chains. Taking Cd and Cs isotopes included in the 227 odd-proton nuclei as examples, the magnetic moment predictions obtained from the BNN-I4 approach are given in Fig. 5, in comparison with Schmidt values and the experimental values. It is clearly seen that for both chains, containing 14 isotopes, the magnetic moment predictions have been greatly improved by the BNN approach, and the total rms deviations of the Cd and Cs predictions are only 0.043
$ \mu_\mathrm{N} $ and 0.07$ \mu_\mathrm{N} $ , respectively. Specifically, the BNN-I4 approach can learn the evolution tendency for changes in magnetic moments as the neutron number increases, including the staggering at$ N = 61 $ and the sudden jump at$ N = 73 $ for Cd isotopes. It should be noted that the ground state spin and parity of Cd isotopes are${5}/{2}^+$ for$ 55\leqslant N\leqslant 63 $ and${1}/{2}^+$ for$ 65\leqslant N\leqslant 71 $ , with corresponding odd-neutron orbitals of$ \nu d_{5/2} $ and$ \nu s_{1/2} $ , respectively, and the same Schmidt value of$ -1.91\mu_\mathrm{N} $ . Therefore, the relatively small variations in the experimental magnetic moments between$ 55\leqslant N\leqslant 71 $ show that they have the same intrinsic structure, and the extreme single particle shell model is valid. As the neutron number increases to$ N = 73 $ , the corresponding ground-state spin becomes${3}/{2}^+$ and the odd-neutron occupies the$ \nu2d_{3/2} $ orbital. For Cs isotopes, the complicated evolution tendency has also been reproduced by considering the BNN approach, such as the$ N = 66 $ , 76 and 88 isotopes, which further indicates its powerful prediction ability.
Figure 5. (color online) Magnetic moment predictions obtained from the BNN-I4 approach, in comparison with Schmidt values and the experimental values for the Cd (a) and Cs (b) isotopes. The shadow region shows the uncertainties of BNN-I4.
Among all odd-mass nuclei, the doubly closed-shell
$ \pm1 $ nuclei have been paid special attention. In Fig. 6, the magnetic moments of$ jj $ shell$ \pm1 $ nuclei, that is,$ ^{207} $ Tl,$ ^{209} $ Bi,$ ^{207} $ Pb, and$ ^{209} $ Pb included in the 227 odd-proton nuclei and 221 odd-neutron nuclei obtained from the BNN-I4 approach, are given and compared with the corresponding Schmidt values, the previous relativistic calculations [22], the non-relativistic calculations [15], and the experimental values. The corresponding uncertainties are shown in the gray area. Both relativistic and non-relativistic calculations include the configuration mixing and meson exchange current corrections. It is obvious that the BNN-I4 approach reproduces the experimental magnetic moments very well. The overall rms deviations of the four nuclei with the BNN-I4 approach is 0.095$ \mu_\mathrm{N} $ , which is slightly less than 0.119$ \mu_\mathrm{N} $ (relativistic) and 0.124$ \mu_\mathrm{N} $ (non-relativistic). Compared with the relativistic and non-relativistic calculations that consider the meson exchange flow and configuration mixing effects, the predictions of BNN-I4 are still competitive.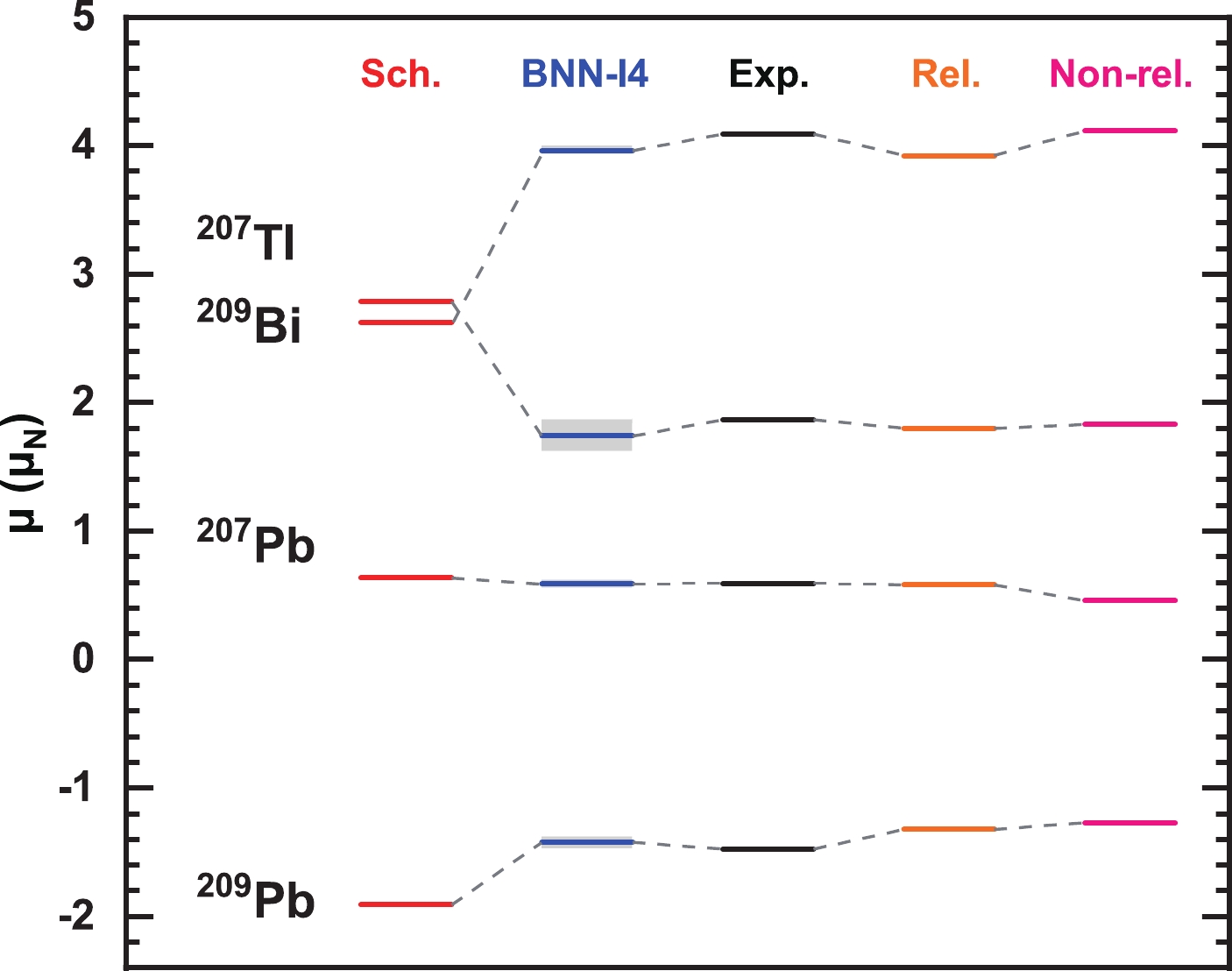
Figure 6. (color online) The magnetic moments of
$ ^{207} $ Tl,$ ^{209} $ Bi,$ ^{207} $ Pb, and$ ^{209} $ Pb obtained from the BNN-I4 approach with uncertainties shown in the gray area, in comparison with Schmidt values, the relativistic mean field (RMF) calculation results from Ref. [22], the nonrelativistic mean field calculation results from Ref. [22], and the experimental values.Furthermore, for
$ LS $ closed-shell nuclei$ \pm1 $ nucleon that are also included in the entire sets, the isoscalar and isovector magnetic moments using the BNN-I4 approach are shown in Figs. 7 (a) and (b), respectively, in comparison with the relativistic results [7], non-relativistic results [15], Schmidt values, and corresponding experimental data. It is seen that the BNN approach improves the predictions for all isoscalar magnetic moments, especially for isovector magnetic moments. Numerically, the rms deviations of the Schmidt values from the experimental data are 0.042 and 0.198$ \mu_\mathrm{N} $ for isoscalar and isovector magnetic moments, respectively, and the corresponding rms deviations with the BNN approach are decreased to 0.034 and 0.047$ \mu_\mathrm{N} $ , respectively. Moreover, the present BNN results are better than both the relativistic (0.081 and 0.134$ \mu_\mathrm{N} $ , respectively, for isoscalar and isovector magnetic moment) and non-relativistic results (0.008 and 0.156$ \mu_\mathrm{N} $ , respectively). It is worth mentioning that the BNN approach can effectively reproduce the isovector magnetic moments of$ A = 41 $ , while there are still relatively large deviations for both the relativistic and non-relativistic calculations. Overall, for the nuclei with doubly closed shells plus or minus one nucleon, BNN-I4 can effectively learn the isospin effect in nuclear magnetic moments and provide reasonable predictions.
Figure 7. (color online) Isoscalar magnetic moments obtained from the BNN-I4 approach with uncertainties shown in the gray area, in comparison with Schmidt values, the RMF calculation results, the nonrelativistic results, and the experimental values in (a). Similar to (a), but for the isovector magnetic moments in (b).
As the BNN approach can be applied to a wide range of nuclei and can provide accurate predictions, it is reasonable to make predictions for the magnetic moments of odd-A nuclei without available experimental data. As it is extrapolated too far away from the known region, there might be some new physics effects, which are hidden in the known region and hence cannot be discovered by training the neural network using the known data. Therefore, only the nuclei neighbouring the 227 odd-proton nuclei and 221 odd-neutron nuclei are considered, whose magnetic moments, with uncertainties less than
$ 0.5\mu_\mathrm{N} $ predicted by the BNN approach, are given in Table 1.Nuclei Orbital $ I^\pi $ 

$ \mu_{s} $ 

$\mu_{\rm Ext.}}$ 

$ ^{23} $ F

$ \pi 1d_{\frac{5}{2}} $ 

$ \dfrac{5}{2}^+ $ 

4.79 4.1(3) $ ^{23} $ Si

$ \nu 1d_{\frac{5}{2}} $ 

$\left(\dfrac{5}{2}\right)^+ $ 

−1.91 −0.9(3) $ ^{37} $ S

$ \nu 1f_{\frac{7}{2}} $ 

$\dfrac{7}{2}^-$ 

−1.91 −1.4(3) $ ^{39} $ Sc

$ \pi 1f_{\frac{7}{2}} $ 

$\left(\dfrac{7}{2}^-\right)$ 

5.79 5.6(4) $ ^{53} $ K

$ \pi 1d_{\frac{3}{2}} $ 

$\left(\dfrac{3}{2}^+\right)$ 

0.13 0.9(3) $ ^{41} $ Ti

$ \nu 1d_{\frac{3}{2}} $ 

$\dfrac{3}{2}^+$ 

1.15 1.1(5) $ ^{53} $ Co

$ \pi 1f_{\frac{7}{2}} $ 

$\left(\dfrac{7}{2}^-\right)$ 

5.79 5.0(4) $ ^{61} $ Co

$ \pi 1f_{\frac{7}{2}} $ 

$\dfrac{7}{2}^-$ 

5.79 4.8(1) $ ^{79} $ Cu

$ \pi 1f_{\frac{5}{2}} $ 

$\left(\dfrac{5}{2}^-\right)$ 

0.86 1.7(1) $ ^{59} $ Zn

$ \nu 2p_{\frac{3}{2}} $ 

$\dfrac{3}{2}^-$ 

−1.91 −0.5(3) $ ^{81} $ Ge

$ \nu 1g_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}^+\right)$ 

−1.91 −1.0(2) $ ^{93} $ Mo

$ \nu 2d_{\frac{5}{2}} $ 

$\dfrac{5}{2}^+$ 

−1.91 −1.0(1) $ ^{93} $ Ru

$ \nu 1g_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}\right)^+$ 

−1.91 −0.9(2) $ ^{97} $ Pd

$ \nu 2d_{\frac{5}{2}} $ 

$\left(\dfrac{5}{2}^+\right)$ 

−1.91 −0.8(1) $ ^{99} $ In

$ \pi 1g_{\frac{9}{2}} $ a

$\dfrac{9}{2}^+$ b

6.79 6.5(4) $ ^{103} $ In

$ \pi 1g_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}\right)^+$ 

6.79 6.0(5) $ ^{129} $ In

$ \pi 1g_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}^+\right)$ 

6.79 5.9(5) $ ^{101} $ Sn

$ \nu 2d_{\frac{5}{2}} $ 

$\left(\dfrac{5}{2}^+\right)$ 

−1.91 −1.0(3) $ ^{113} $ Sb

$ \pi 2d_{\frac{5}{2}} $ 

$\dfrac{5}{2}^+$ 

4.79 3.7(1) $ ^{135} $ Sb

$ \pi 1g_{\frac{7}{2}} $ 

$\left(\dfrac{7}{2}^+\right)$ 

1.72 3.1(2) $ ^{181} $ Tl

$ \pi 3s_{\frac{1}{2}} $ 

$\left(\dfrac{1}{2}^+\right)$ 

2.79 1.8(3) $ ^{197} $ Bi

$ \pi 1h_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}^-\right)$ 

2.63 4.7(2) $ ^{215} $ Bi

$ \pi 1h_{\frac{9}{2}} $ 

$\left(\dfrac{9}{2}^-\right)$ 

2.63 4.1(4) a Suggested odd proton orbital of ground state.
b Suggested ground state spin and parity.Table 1. Extrapolated magnetic moments (
$\mu_{\rm {Ext}.}$ ) of 23 odd-A nuclei with estimated uncertainties obtained from the BNN-I4 approach. The odd nucleon orbital and the Schmidt values ($ \mu_{s} $ ) are given as well. The brackets for$ I^\pi $ mean that the spin and parity have not yet been confirmed.Taking
$ ^{23} $ F as an example, the ground-state spin and parity are${5}/{2}^+$ , and the odd-proton occupies the$ \pi 1d_{\frac{5}{2}} $ orbital. BNN predicts a magnetic moment of 4.1$ \mu_\mathrm{N} $ with uncertainty 0.3$ \mu_\mathrm{N} $ , which is close to 3.9194(12)$ \mu_\mathrm{N} $ , the magnetic moment of a neighbouring nucleus$ ^{21} $ F with the same spin and parity of${5}/{2}^+$ . For$ ^{93} $ Mo, its ground state is${5}/{2}^+$ , and the corresponding experimental magnetic moment has not yet been determined; the present predicted value is$ -1.0(1) \;\; \mu_\mathrm{N} $ . In comparison, the magnetic moments of the excited state${21}/{2}^+$ and ground state of a neighbouring odd mass nuclei$ ^{91,93} $ Mo have been confirmed.It is also interesting to investigate the improvement by employing effective g factors. As the effective g factor 0.7
$ g_s $ is widely used in different theoretical models to better describe nuclear magnetic moments and magnetic dipole transitions, an effective Schmidt value ($\mu_{\rm eff}$ ) is adopted by replacing$ g_s $ in the Schmidt formula Eq. (1) with 0.7$ g_s $ . The rms deviation of the effective Schmidt value from experimental data is easily obtained as 0.51$ \mu_{\rm N} $ (0.71$ \mu_{\rm N} $ ) for the present 221 odd neutron nuclei (227 odd proton nuclei), which is much smaller than that of the Schmidt value 0.949$ \mu_{\rm N} $ (1.272$ \mu_{\rm N} $ ) for odd-neutron nuclei (odd-proton nuclei). When the Schmidt values are replaced with$\mu_{\rm eff}$ in the neural network using the same parameters, the rms deviations improved by the BNN are 0.038$ \mu_{\rm N} $ and 0.076$ \mu_{\rm N} $ for odd-neutron nuclei and odd-proton nuclei, respectively. These do not show significant improvements compared with the results from the Schmidt values (0.036$ \mu_{\rm N} $ for odd-neutron nuclei and 0.061$ \mu_{\rm N} $ for odd-proton nuclei) as well as the interpolation ability for the validation set. This means that the extreme single particle shell model with free g factors is a good and useful theoretical model for describing the magnetic moments of odd nuclei. -
In summary, we have employed the Bayesian neural network approach to improve nuclear magnetic moment predictions of the extreme single-particle shell model. Nuclear magnetic dipole moments of 227 odd-proton nuclei and 221 odd-neutron nuclei, taken from the IAEA online database, have been studied. The Schmidt magnetic moment obtained from the extreme single-particle shell model makes large rms deviations from data (0.949
$ \mu_\mathrm{N} $ and 1.272$ \mu_\mathrm{N} $ for odd-neutron nuclei and odd-proton nuclei, respectively). This further indicates that only valence nucleon approximation cannot effectively explain the experimental magnetic moments of odd-A nuclei. By including the nuclear spin and Schmidt magnetic moment in the input layer, the machine-learning approach can precisely describe the magnetic moments of odd-A nuclei (0.036$ \mu_\mathrm{N} $ for odd-neutron nuclei and 0.061$ \mu_\mathrm{N} $ for odd-proton nuclei). The extrapolation ability of the BNN has been verified by satisfactory predictions of nuclear magnetic moments in the validation set. The evolution of magnetic moments along isotopic chains, including the staggering and sudden jump trend which are difficult to describe using nuclear models, have been well reproduced by the BNN approach. The magnetic moments of doubly closed-shell$ \pm1 $ nuclei, including isoscalar and isovector magnetic moments have been well studied, and corresponding comparisons with non-relativistic and relativistic calculations have been performed. Finally, magnetic moments of 20 odd-A nuclei from light to heavy mass regions without any available experimental magnetic moments, were extrapolated by the BNN approach.The theoretical description of nuclear magnetic moments is one of the longest-standing subjects. It's difficult to effectively describe nuclear magnetic moments in the nuclide chart, especially with high precision. However, machine learning provides a good opportunity. In the future, more attention should be paid to the optimization of the neural network and improving the Schmidt magnetic moment formula to obtain a better description and a more reasonable extrapolation. The uniform description of quantities such as magnetic moment and mass are also highly expected with the same neural network.
Magnetic moment predictions of odd-A nuclei with the Bayesian neural network approach
- Received Date: 2021-07-28
- Available Online: 2021-12-15
Abstract: The Bayesian neural network approach has been employed to improve the nuclear magnetic moment predictions of odd-A nuclei. The Schmidt magnetic moment obtained from the extreme single-particle shell model makes large root-mean-square (rms) deviations from data, i.e., 0.949





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: