-
To date, transuranium nuclides with Z
$ \leqslant $ 118 have been synthesized and studied experimentally and theoretically [1-5]. One of the most dominant decays for these radioactive nuclei is α-decay, which is a powerful and precise tool to probe the nuclear structure, including half-life, α-clustering, the shell effect, and deformation [6-12].From a theoretical perspective, the α-decay half-life primarily depends on the penetration probability and preformation factor. The former has been calculated within the framework of the Wentzel-Kramers-Brillouin (WKB) approximation, which is mainly sensitive to the interaction potential between α-daughter particles and also α-particle energy. Concerning the quantum tunneling concept [13, 14], a confined α-particle, which carries kinetic energy in the parent nucleus potential with a non-zero penetration probability, has to escape from the potential barrier. Thereby, the choice of potential affects the half-life values. Hence, different theoretical methods have been suggested and developed such as the generalized liquid drop model (GLDM) [15-17], the density-dependent M3Y interaction and the mean-field potential [18, 19], and empirical formulas [20-23].
For the latter, the preformation factor (
$ P_{\alpha} $ ) refers to the probability of finding an α-cluster inside the parent nucleus; by determining this factor, more information on nuclear structure can be made available. Its probability magnitude should be less than or equal to one [24]. This quantity can be obtained from the ratios of the calculated to the experimental α-decay half-lives [25-28]; therefore, a theoretical model that can produce different penetration probabilities has a crucial role in computing$ P_{\alpha} $ . Moreover, the$ P_{\alpha} $ values can be obtained from the overlap between the wave function of the parent nucleus and the coupled-wave function of the α-daughter nucleus after the decay process [29, 30].Recently, the cluster formation model (CFM) [31-35] was proposed to extract the α-preformation factor in terms of the α-cluster formation energy, which is based on the differences in binding energy of the participating nuclide. This is in good agreement with different microscopical approaches. Deng et al. [36] studied the α-decay half-lives of nuclei around the Z = 82, N = 126 closed shells using the proximity potential 1977 formalism; they confirmed that the effective and microscopic
$ P_{\alpha} $ within the CFM reduce the discrepancy between theoretical and experimental data in the mentioned region.The proximity model is used to calculate the nuclear interaction energy between two nuclei by assuming the surface energy. It is satisfactorily used in producing the nuclear potential between two nuclei while they are considered spherical [37-40]. A more complex method of deriving this theory is used for the nuclear interaction between deformed–deformed pairs of nuclei [41-43]; one of the interacting nuclei may also be spherical. Due to this theorem, different physical quantities and phenomena have been studied [44-47].
Nuclei have many excited states in which α-decay can occur, from the ground state or isomeric state of the parent nucleus to the ground state or isomeric state of the daughter nucleus; Here, we consider those which decay from the ground state to the ground state or isomeric state with the same spin and parity, and whose minimum angular momentum transition is equal to zero, called favored α-decays [48, 49]. The main objective of this study is to take the deformation of daughter nuclei in the favored α-decay process under consideration. This article is organized as follows: The theoretical framework is summarized in Section II, the calculations and results are discussed in Section III, and the conclusion is revealed in Section IV.
-
The α-decay half-life of a parent nucleus can be determined using
$ T_{1/2} = \ln2/P_{\alpha}\nu_{0} P $ . Here,$ P_{\alpha} $ is the preformation probability, which will be discussed by the next section, and the assault frequency$ \nu_0 $ is related to the oscillation frequency ω [50]$ {\nu_{0}} = {\frac{\omega}{2\pi}} = {\frac{\left(2n_{r}+l+\dfrac{3}{2}\right)\hbar}{\left(2\pi\mu R_{n}^2\right)}} = {\frac{\left(G+\dfrac{3}{2}\right)\hbar}{\left(1.2\pi\mu R_{0}^2 \right)}}, $

(1) where
$ R_{n}^2 = \dfrac{3}{5} R_{0}^2 $ [51] and, due to the topic under study in this paper, the global quantum number G is equal to 22 [52].The α-decay penetration probability in a different orientation, using the WKB semi-classical approximation, is defined as
$ P = {\rm exp} \left( {{-\frac{2}{\hbar}} \int^{r_{b}}_{r_{a}} \sqrt{2\mu(V_{T}-Q_{\alpha})}}{\rm d}r \right), $

(2) where
$ {\mu} = m(A_{\alpha}+A_{d})/A_{\alpha} A_{d} $ is the reduced mass in which$ A_{\alpha} = 4 $ and$ A_{d} $ is the daughter nucleus. The$ r_{a} $ and$ r_{b} $ are the turning points, which are obtained from$ V_{\rm T}(r_{a} ) = Q_{\alpha} = V_{\rm T} (r_{b}) $ . The total interaction potential$ V_{\rm T} = V_{N}+V_{\rm C}+V_{l} $ between the α-particle and daughter nucleus is defined as the sum of the nuclear, Coulomb, and centrifugal potential, which has a deformation and orientation dependence.The nuclear term is introduced in detail in Ref. [37], which includes different modifications of
$ Prox.77 $ that are indicated in Table 1 and other versions of proximity potentials. For details of the deformation effect [42, 43], the mean curvature radius$ \overline{R} $ with azimuthal angle ϕ between the principal planes of curvature of two deformed nuclei is given byProximity version $\gamma_0$ 

$\kappa_s$ 

Proximity version $\gamma_0$ 

$\kappa_s$ 

$Prox.66 $ 

1.01734 1.79 $Prox.81-III $ 

1.2502 2.4 $Prox.76 $ 

1.460734 4 $Prox.88 $ 

1.2496 2.3 $Prox.79 $ 

1.2402 3 $Prox.95 $ 

1.25284 2.345 $Prox.81-I $ 

1.1756 2.2 $Prox.03-I $ 

1.08948 1.983 $Prox.81-II $ 

1.27326 2.5 $ModProx.88 $ 

1.65 2.3 Table 1. Prox.77 and its different modifications corresponding to Table 1 of Ref. [37].
$ \begin{aligned}[b] \frac{1}{\overline{R^{2}}} =& \frac{1}{R_{11}R_{12}} + \frac{1}{R_{21}R_{22}} + \left[\frac{1}{R_{11}R_{21}} + \frac{1}{R_{12}R_{22}}\right]{\rm sin}^{2}\phi \\& + \left[\frac{1}{R_{11}R_{22}} + \frac{1}{R_{21}R_{12}}\right]{\rm cos}^{2}\phi, \end{aligned} $

(3) where ϕ is equal to zero, as nuclei are considered to be in the same plane in this study.
$ R_{i1}(\alpha_{i}) $ and$ R_{i2}(\alpha_{i}) $ $ (i = 1,2) $ are the radii of curvature in the principal planes of each of the two nuclei$ R_{i1}(\alpha_{i}) = \left|\frac{[R^{2}_{i}(\alpha_{i})+ R^{'2}_{i}(\alpha_{i})]^{3/2}}{R^{2}_{i}(\alpha_{i})+ 2R^{'2}_{i}(\alpha_{i})-R_{i}(\alpha_{i}) R^{''}_{i}(\alpha_{i})}\right|, $

(4) $ R_{i2}(\alpha_{i}) = \left| \frac{R_{i}(\alpha_{i})\sin(\alpha_{i})+ [R^{2}_{i}(\alpha_{i})+R^{'2}_{i}(\alpha_{i})]^{3/2}} {R^{'}_{i}(\alpha_{i})\cos(\alpha_{i})+R^{'}_{i}(\alpha_{i})\sin(\alpha_{i})} \right|, $

(5) with a separation distance, R, between their centers, their minimum distance is defined as
$ s = \left| R-R_{1}(\alpha_{1})-R_{2}(\alpha_{2}) \right| , $

(6) with
$ {r_i (\alpha_i)} = {r_{0i} \left[1 + \sum\limits_{\lambda} \beta_{\lambda i} Y_{\lambda}^{(0)} (\alpha_i) \right] }, $

(7) where
$ r_{0i} = 1.28 A_{i}^{1/3}-0.76+0.8 A_{i}^{-1/3} $ . Here,$ \alpha_i $ is the angle between the radius vector and the symmetry axis of the$ i^{\rm th} $ nuclei. In this study we consider one of two nuclei to be spherical, Therefore, it has no deformation parameters.The rotational effect of two nucleus systems can be calculated using the l-dependent centrifugal potential, which is equal to
$ \hbar^{2} l(l+1)/2\mu r^{2} $ . l is the orbital angular momentum carried by the α-particle. The values that are used to calculate this potential are determined by utilizing the permitted transitions between the parent nucleus and the daughter nucleus.The Coulomb potential between spherical-deformed and oriented, taken from Ref. [53], is given as follows:
$ {V_C}(r,{\beta _\lambda },\theta ) = \left\{ {\begin{array}{*{20}{l}} {{Z_\alpha }{Z_d}{e^2}\left\{ {\dfrac{1}{r} + \dfrac{3}{{2\lambda + 1}}\dfrac{{r_T^\lambda }}{{{r^{\lambda + 1}}}}{\beta _\lambda }{Y_{\lambda ,0}}(\theta )} \right\}}&{{\rm{for}}\;r \geqslant {r_{01}}},\\ {{Z_\alpha }{Z_d}{e^2}\left\{ {\dfrac{1}{{2{r_T}}}\left[ {3 - {{\left(\dfrac{r}{{{r_T}}}\right)}^2}} \right] + \dfrac{3}{{2\lambda + 1}}\dfrac{{{r^\lambda }}}{{r_T^{\lambda + 1}}}{\beta _\lambda }{Y_{\lambda ,0}}(\theta )} \right\}}&{{\rm{for}}\;r \leqslant {r_{01}}}. \end{array}} \right. $ 
(8) This potential has high accuracy and provides time-saving during calculation. Because the deformation parameters from Möller
$ et \;al $ . [54] agree well with the existing magnitude of experimental deformation [55],$ \beta_{\lambda} $ values are taken from [54] for all calculations of the α-decay half-lives of deformed nuclei in this study. -
We have systematically studied a wide atomic range of 108 transuranium nuclei, from
$ Z = 93 $ onward, using 23 versions of spherical-deformed potentials for both the short-range attractive term and the Coulomb repulsive term of the potential barrier, in which the α-particle and the residual nuclei are considered spherical and deformed, respectively. It is interesting to see how the deformation affects the proximity potentials and the corresponding penetration probability in the α-decay process. Forinstance, the penetration probability for 253Fm → 249Cf+α (with$ \beta_{2} = 0.250 $ and$ \beta_{4} = 0.039 $ ) is plotted in each direction in Fig. 1 for seven selected versions. As shown, the nuclear potential for decay through$ \theta = 0^{\circ} $ is deeper than$ \theta = 90^{\circ} $ . Due to the proximity theory (The force between two gently curved surfaces as a function of the separation degree of freedoms is proportional to the interaction potential per unit area), we realize that a nucleus contains a thicker surface at$ \theta = 0^{\circ} $ and the stronger interaction in this area is due to the overlap of the nucleons. Although properties such as the Pauli exclusion principle, spin and parity, and isospin asymmetry play a role in the formation of a particle before emission, we can implicitly expect the probability of α-particle formation in this area to be more likely than others. Also, from this figure, we can see that the$ Q_{\alpha} $ line does not cross the total potential curve in some direction, such as prox. 66; as long as it appears in all directions, we are not able to calculate the penetration probability integral.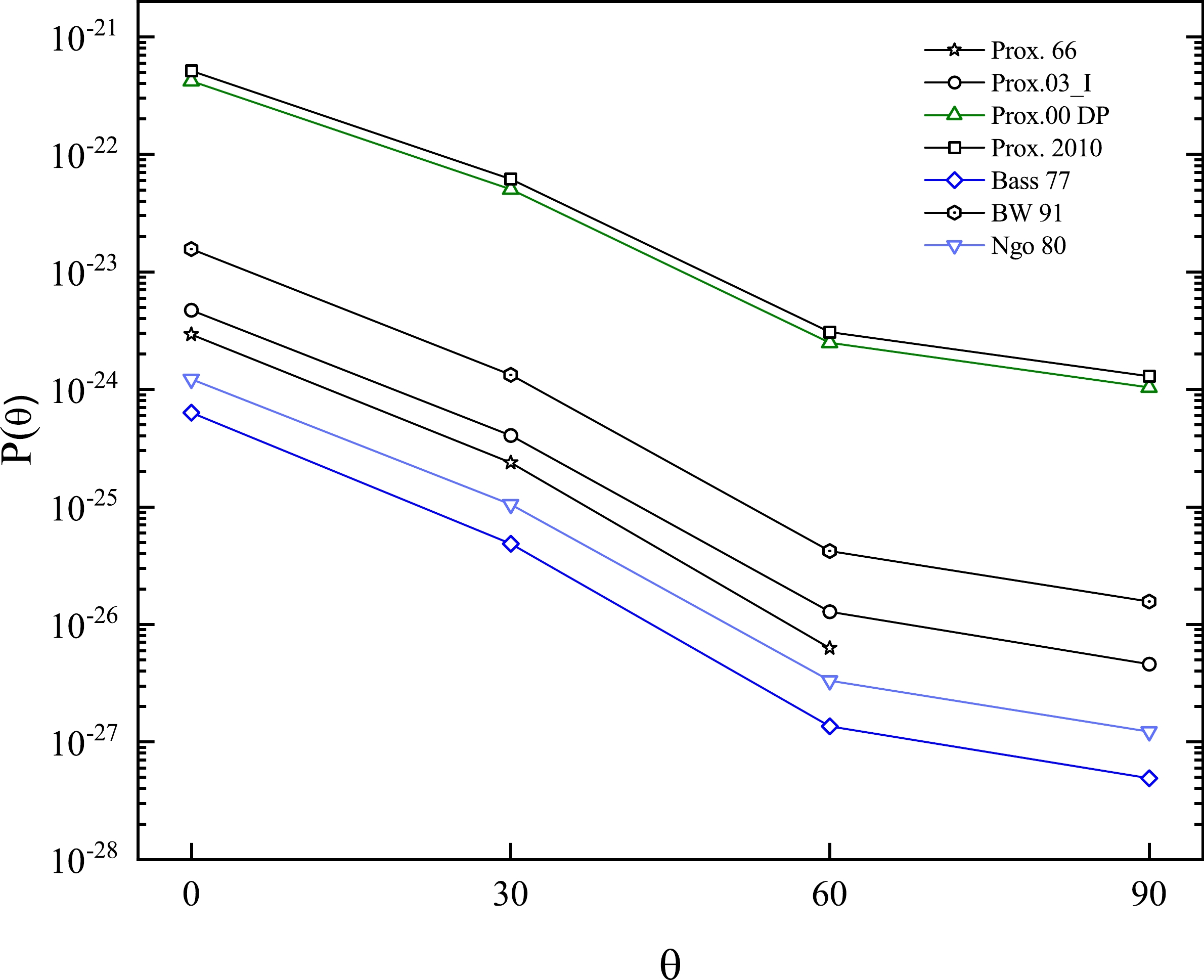
Figure 1. (color online) The penetration probability of the eight selected versions of proximity potentials with respect to the angles of the emitted α-particle.
The height and position of the barrier potential of the α-particle in a deformed nucleus depend on the angle at which the α-particle is emitted. The average penetrability is obtained using
$ P(\theta) = {\frac{1}{2} \int_{0}^{\pi} P \sin(\theta){\rm d}\theta }. $

(9) For the probability of the α-particle formation before penetration, the cluster-formation model is a proposed energy-dependent theory used to calculate the α preformation factor. The basic assumption in the CFM formalism is that the nucleons around the surface contribute to the preformation of the α-particle. In this model, the α-preformation factor is defined as
$ P_{\alpha} = {E_{f\alpha} / E} $ , where$ E_{f\alpha} $ is the formation energy of the α-cluster and E is the total energy of a considered system [31-35]. In order to obtain an accurate mass excess, which is vitally important to obtain the precise binding energies, data are provided by [56].We computed α-decay half-lives and evaluated a quantitative analysis using the root-mean-square deviation
$RMSD = \sqrt{1/N \sum_{i = 1}^N \Big[{\rm log}_{10}(T_{1/2,i}^{\rm Exp.})-{\rm log}_{10}(T_{1/2,i}^{\rm Theo.})\Big]^2},$

where N is the number of contributed nuclei, and experimental values of half-lives are given by [57], taking into account their branching ratios.
Since the parent nucleus can decay from the ground state (gs) to different possible states that satisfy the spin-parity rule
$ {|I_{i}-I_{j}| \leqslant l \leqslant I_{i}+I_{j}},\; \; \; \; \; \; \; \; \; {\pi_{i}\pi_{j} = (-1)^{l}}. $

(10) According to this equation, different values of l can transfer from the initial state to the final states; however, it is the minimum possible value of angular momentum that is of interest. Due to this value, the favored transition will occur provided
$ l = 0 $ . If not, transition to the daughter nucleus is hindered. All considered nuclei in this study are favored, and 22 nuclei involve decays to more than one level with the same spin and parity. The total 141 favored α-decays contain 54 even-even (e-e), 81 odd A, and 6 odd-odd (o-o) nuclei. The experimental data and the details of their isomeric states and energy levels are taken from [57]. The RMSDs of these groups are shown in columns two to four of Table 2, and each of their corresponding values after taking the preformation factor under consideration is presented in columns five to seven. Comparing the RMSDs of different proximity versions for e-e nuclei shows that$ Bass 77 $ and$ Ngo 80 $ have the least values. When Pα is taken under consideration,$ Ngo 80 $ obtains better results than$ Bass 77 $ . The deviation between the calculated and experimental values for e-e elements are shown in Fig. 2(a). We can see that these versions reproduce the experimental values very well.Proximity Potentials $P_{\alpha}^{1}$ 

$P_{\alpha}^{\rm CFM}$ 

e-e odd A o-o e-e odd A o-o $Prox. 66$ 

1.3660 2.6930 2.7633 0.7961 2.0759 2.0655 $Prox.76 $ 

2.0879 3.3049 3.4166 1.3441 2.5680 2.6440 $Prox.79 $ 

1.8156 3.0700 3.1693 1.0950 2.3686 2.4177 $Prox81-I $ 

1.7723 3.0382 3.1384 1.0559 2.3430 2.3899 $Prox81-II $ 

1.9395 3.1830 3.2929 1.2057 2.4640 2.5300 $Prox81-III $ 

1.9064 3.1546 3.2624 1.1756 2.4401 2.5022 $Prox.88 $ 

1.9165 3.1641 3.2737 1.1846 2.4482 2.5124 $Prox.95 $ 

1.9177 3.1650 3.2741 1.1857 2.4488 2.5129 $Prox03_I $ 

1.5815 2.8749 2.9624 0.8957 2.2122 2.2341 $ModProx88 $ 

2.4822 3.6703 3.8121 1.7189 2.8951 3.0165 $Prox.00 $ 

1.8242 3.0916 3.1951 1.1032 2.3868 2.4410 $Prox.00DP $ 

3.5506 4.6520 4.8360 2.7690 3.8184 4.0094 $Prox.2010 $ 

3.6436 4.7335 4.9148 2.8613 3.8966 4.0867 $Bass1977 $ 

0.8281 2.2505 2.2620 0.6547 1.8153 1.6867 $Bass1980 $ 

2.0303 3.2768 3.4024 1.2881 2.5461 2.6317 $CW1976 $ 

2.8746 4.0475 4.2094 2.1009 3.2450 3.3981 $BW1991 $ 

2.0596 3.3127 3.4370 1.3153 2.5778 2.6639 $Ngo1980 $ 

1.0474 2.4430 2.4907 0.5963 1.9144 1.8443 $Denisov $ 

4.3656 5.4038 5.6299 3.5799 4.5480 4.7921 $Denisov DP$ 

5.4896 6.4895 6.7427 4.7003 5.6155 5.8963 $AW95 $ 

1.8899 3.0318 3.1703 1.1799 2.3319 2.4164 $Dutt2011 $ 

1.9200 3.1811 3.2933 1.1870 2.4637 2.5308 $Guo2013 $ 

2.4293 3.6335 3.7766 1.6674 2.8625 2.9820 Table 2. RMSDs of
${\alpha}-$ decay half-lives of even-even, odd A, and odd-odd nuclei, when considering$P_{\alpha}.$ 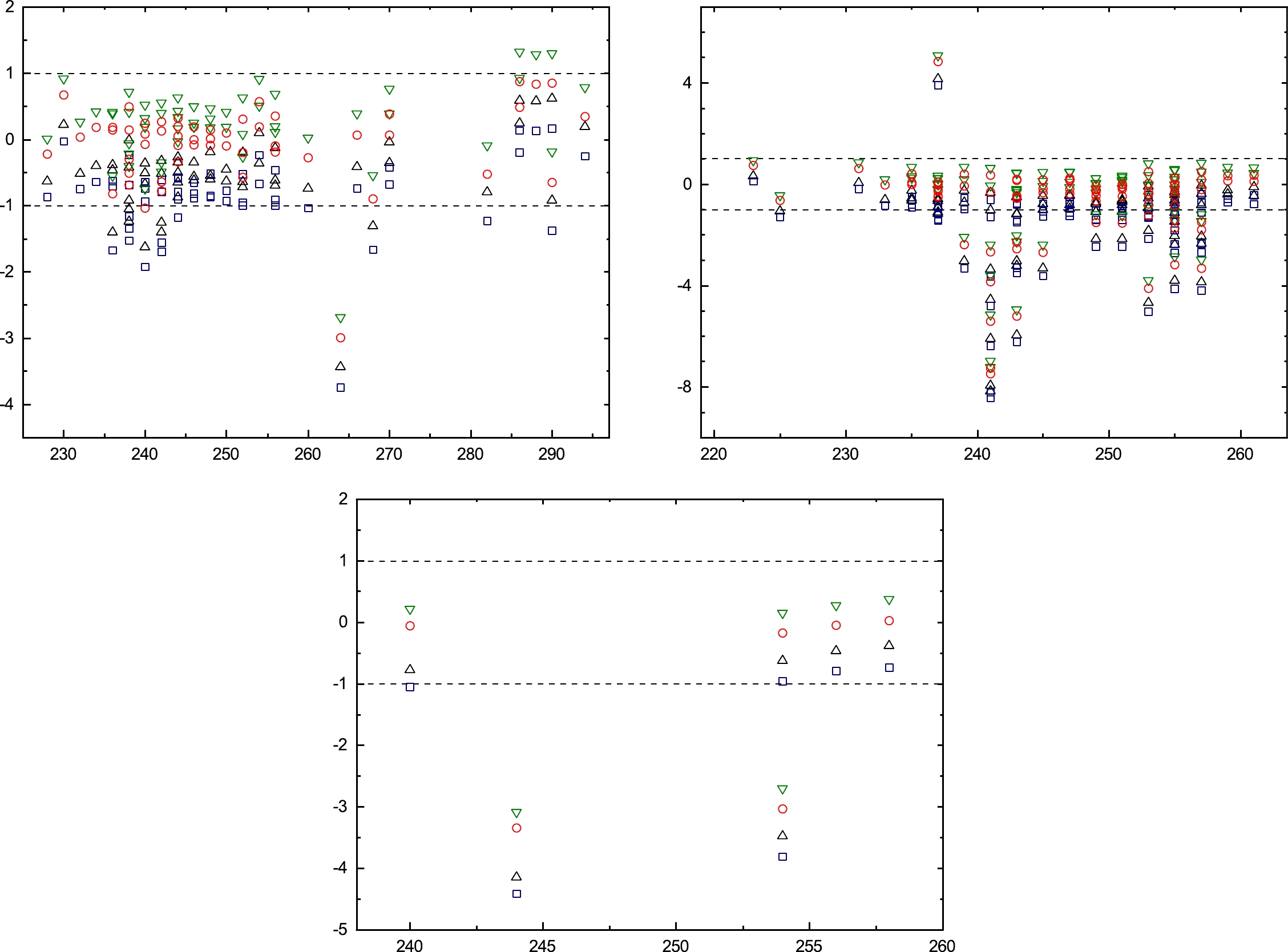
Figure 2. (color online) Deviation between the calculated and experimental α-decay half-lives for (a) even-even (b) odd A (c) odd-odd nuclei.
For the other two groups in Table 2,
$ Bass 77 $ and$ Ngo 80 $ are the most suitable versions; the deviation of the calculated values are represented in Fig. 2(b) and c for odd A and o-o nuclei, respectively.$ Prox.66 $ is not able to reproduce the half-life of just 290Fl. It is useful to notice that the experimental data can also impact the results. For instance, the 264Hs, which is recognizable in Fig. 2 a as the only A = 264, has an experimental α-decay half-life of 1 s, as reported in NUBASE2020 [57], while it is 1.08 ms in NUBASE2016 [58]; its α-decay half-life is$ 0.365 $ ms and$ 0.178 $ ms and after using Pα it becomes 2.07 ms and 1.01 ms for$ Bass 77 $ and$ Ngo 80 $ , respectively.To investigate the validity of the formalisms used in estimating the ground state (gs) to ground state or isomeric states (is), these 108 nuclei are grouped with respect to the energy level of the daughter nucleus that whether they are in their ground state or its isomeric states. Among the total 141 favored decays, 59 transitions are gs-gs and 82 transitions are gs-is, which their RMSD values are given in Table 3. Similar to Table 2, their corresponding values after preformation values are taken under consideration are shown. For gs-gs nuclei,
$ Bass 77 $ before and after using Pα are almost equal, whereas$ Ngo 80 $ with Pα is the outlying version. Figure 3 a shows the power of formalisms in producing experimental data of gs-gs nuclei. Furthermore, also$ Bass 77 $ and$ Ngo 80 $ can best satisfy the gs-is elements among all. Figure 3 b shows the deviation between these suitable versions and the experimental values.Proximity potentials $P_{\alpha}^{1}$ 

$P_{\alpha}^{\rm CFM}$ 

g.s.-g.s. g.s.-i.s. g.s.-g.s. g.s.-i.s. $Prox. 66$ 

1.3865 2.7512 0.9531 2.0824 $Prox.76 $ 

2.0324 3.3974 1.3535 2.6262 $Prox.79 $ 

1.7798 3.1522 1.1483 2.4105 $Prox81-I $ 

1.7383 3.1197 1.1165 2.3828 $Prox81-II $ 

1.8912 3.2718 1.2351 2.5151 $Prox81-III $ 

1.8608 3.2421 1.2107 2.4890 $Prox.88 $ 

1.8696 3.2522 1.2177 2.4979 $Prox.95 $ 

1.8708 3.2531 1.2185 2.4987 $Prox03_I $ 

1.5683 2.9469 1.0010 2.2375 $ModProx88 $ 

2.3980 3.7802 1.6789 2.9771 $Prox.00 $ 

1.7879 3.1749 1.1545 2.4302 $Prox.00DP $ 

3.4408 4.7824 2.6785 3.9327 $Prox.2010 $ 

3.5346 4.8635 2.7704 4.0112 $Bass1977 $ 

0.9399 2.2789 0.9338 1.7658 $Bass1980 $ 

1.9770 3.3699 1.3058 2.6031 $CW1976 $ 

2.7592 4.1765 2.0167 3.3506 $BW1991 $ 

1.9986 3.4094 1.3222 2.6390 $Ngo1980 $ 

1.1017 2.4897 0.8530 1.8920 $Denisov $ 

4.2357 5.5503 3.4625 4.6825 $Denisov DP $ 

5.3404 6.6522 4.5584 5.7699 $AW95 $ 

1.9032 3.0921 1.2804 2.3529 $Dutt2011 $ 

1.8701 3.2712 1.2166 2.5154 $Guo2013 $ 

2.3325 3.7493 1.6175 2.9484 Table 3. RMSDs of
${\alpha}-$ decay half-lives of ground state to ground state and isomeric states of nuclei, when considering$P_{\alpha}$ .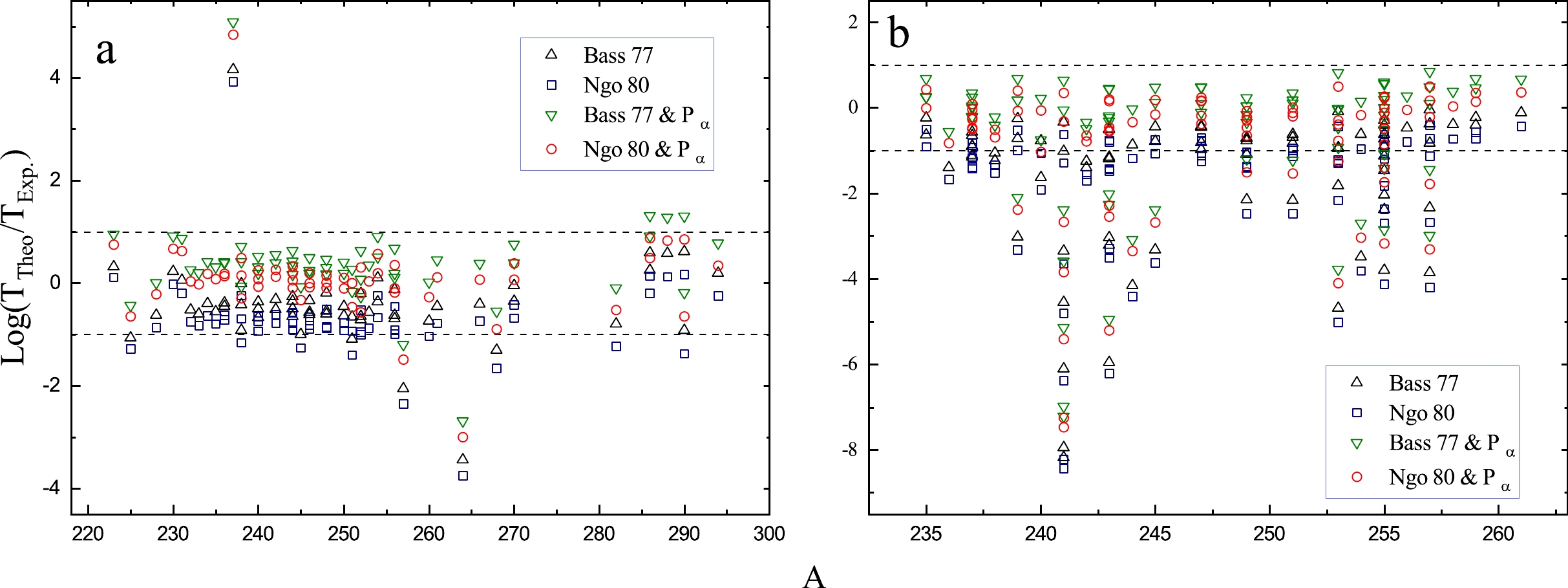
Figure 3. (color online) Deviation between calculated and experimental α-decay half-lives for
$ a) $ ground state to ground state and$ b) $ ground state to isomeric states.For the purpose of comparing our calculated half-lives with ones obtained from the analytical formula, a recent form of the universal decay law (UDL) [59] is used. The UDL for α and cluster decay modes is introduced as
$ {\rm{log}}_{10}(T_{1/2}) = aZ_{c} Z_{d} \sqrt{\frac{A}{Q_{c}}} +b \sqrt{AZ_{c} Z_{d} \left(A_{d}^{1/3} + A_{c}^{1/3}\right)}+c, $

(11) where
$ A = A_{c} A_{d}/(A_{c}+A_{d}) $ and the constant$ a = 0.4314 $ ,$ b = -0.4087 $ , and$ c = -25.7725 $ are determined by fitting to the experimental values of both α and cluster decays. The RMSD values from the UDL are equal to 0.6769, 1.8092, 1.7120, 0.9650, and 1.7550 for e-e, odd A, o-o, gs-gs, and gs-is nuclei, respectively.It is noticeable that the higher the probability of α-particle formation inside the parent nucleus, the more unstable the nucleus. Consequently, because the formation of α-particles is more difficult near magic numbers, they are more stable; this issue is implied in computation. Furthermore, as the preformation factor increases the half-life values, eventually, almost all versions considerably reduce the RMSDs. This is interpreted to reproduce the half-lives.
-
A wide range of favored α-decay nuclei in the atomic range 93
$ \leqslant $ Z$ \leqslant $ 118 has been studied to calculate their half-lives using various versions of proximity potentials within the WKB approximation formalism. In this study, to reproduce the nuclear and Coulomb barrier potential, we considered the shape of the α-particle and daughter nucleus to be spherical and deformed, respectively. It is indicated that the α-decay process is not an isotropic occurrence in space. Moreover, we employed the CFM theory to estimate the preformation factors. First, we analyzed these nuclei with respect to the number of protons and neutrons, and grouped them into even-even, odd A, and odd-odd nuclei. Second, considering the energy level of the daughter nucleus, the nuclei were categorized into two transitions: ground state to ground state and ground state to isomeric states. The obtained results indicated that$ Bass 77 $ and$ Ngo 80 $ are the most suitable versions for estimating the α-decay half-lives, and revealed that the α-preformation factor plays an invaluable role in half-life computation and decreases the RMSDs of all versions. These results may motivate developments and further research in the future.
Theoretical study on the favored alpha-decay half-lives of deformed nuclei
- Received Date: 2021-07-07
- Available Online: 2021-12-15
Abstract: A systematic study on the α-decay half-lives of nuclei in the range






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: