-
Measurements of photon induced reaction cross-sections of natural cadmium are connected with different fields of science, such as the production of medically useful radioisotopes and yield measurements of long-lived radioactive products for radioactive waste handling and dose estimations. Cadmium isotopes are also used in nuclear technology as an important material to make bearings and alloys as well as for electroplating. Therefore, its activation can be used to estimate the radiation dose deposited inside materials for industrial or even medical purposes. In natCd, there are eight different isotopes [1]: 116Cd (7.49%), 114Cd (28.73%), 113Cd (12.22%), 112Cd (24.13%), 111Cd (12.8%), 110Cd (12.49%), 108Cd (0.89%), and 106Cd (1.25%). The proton induced reactions of natCd are good sources for the production of medically important indium radioisotopes [2]. The radioisotopes 111mCd and 111In play a crucial role in time dependent perturbed angular correlation (TDPAC) studies for the investigation of material properties [3]. The radioisotope 109Cd is frequently used for detector calibration due to its long half-life and high γ-ray abundance [4]. Cadmium isotopes are also used to enhance the coherence length and output power of HeCd metallic lasers [5]. Important radioactive isotopes of Cd can be produced from the photon-induced reactions of natCd. Similarly, the photon-induced reactions of natCd produce different radioisotopes of Ag. Among them, 110mAg is frequently used as a γ-ray reference source. The radioisotopes 111gAg and 110mAg are also medically important radioisotopes for radiotherapy and imaging purposes [2, 6].
To maintain an optimal radioisotope production database, the addition of new, reliable experimental data is always important [7]. Previous studies were conducted in the giant dipole resonance (GDR) energy region for the production of 115mCd [8] and 111mCd [8, 9] using a γ-ray spectrometry technique; however, the [8, 9] results were higher than the estimated values. No further literature data have been found for any of the nuclides of interest, even in the GDR region. In a nuclear reaction, daughter products may have ground and meta-stable states with different nuclear spins. The ratio between the reaction cross sections of isomers with high spin
$ {(\sigma }_{\rm H} $ ) and low spin$ \left({\sigma }_{\rm L}\right) $ is known as the isomeric yield ratio$ \left({{\sigma }_{\rm H}}/{{\sigma }_{\rm L}}\right) $ [10]. There are few earlier experimental studies on the IR of 115m,gCd produced from the 116Cd(γ, n)115m,gCd reaction in the giant dipole resonance region [11-14], based on mono-energetic photon beams. However, the measured IR of g,m115Cd in the 116Cd(γ, n) reaction using bremsstrahlung endpoint energies of 50, 60, and 70 MeV is available in literature [15], and the IR at high neutron energies for the 116Cd(n, 2n)115m,gCd reactions [16] is also cited.Based on these data, in this study, well-established radiation activation and off-line γ-ray spectrometrywere employed to determine the nuclear reaction cross-sections and integral yields of the 115g,m,111m,109,107,105,104Cd and 113g,112,111g,110mAg radionuclides produced from natCd with the bremsstrahlung end-point energies of 50 and 60 MeV. The IR of 115m,gCd produced in the natCd(γ, n) reactions was also measured using the activation technique with these bremsstrahlung end-point energies. For comparison, the natCd(γ, xn)115g,m,111m,109,107,105,104Cd and natCd(γ, pxn)113g,112,111g,110mAg reaction cross sections were also theoretically calculated by employing the computer codes TALYS-1.95 [17] and EMPIRE-3.2 Malta [18]. The IR values from the present study with the bremsstrahlung end-point energies of 50 and 60 MeV are compared with the calculated values [17, 18] as well as with the available literature data [11-15].
-
Pulsed electron beams from the 100 MeV electron LINAC installed at the Pohang Accelerator Laboratory (PAL), Korea, were utilized for bremsstrahlung production. The 50 and 60 MeV electron beams were individually bombarded, one energy beam at a time, onto a tungsten converter foil with a thickness of 0.1 mm and a size of 10 cm × 10 cm, which was placed at a distance of 18 cm from its exit window. Details regarding the bremsstrahlung production using the linear accelerator are described elsewhere [19, 20]. The high-purity (99.99%) natural cadmium and 197Au metal foils were irradiated by bremsstrahlung radiation with end-point energies of 50 and 60 MeV. Two sets of 0.1 mm thick natCd foils with weights of 0.1782 and 0.1231 g and two sets of 0.1 mm thick 197Au foils with weights of 0.2478 and 0.2668 g were placed in air at a distance of 12 cm from the W-target in a perpendicular direction to the electron beam. These targets were irradiated for 236 and 125 min with the bremsstrahlung radiation with end-point energies of 50 and 60 MeV, respectively. The average beam current during irradiation was 20-36 mA with a repetition rate of 15 Hz and a pulse width of 2 μs.
The samples irradiated by the bremsstrahlung radiation with end-point energies of 50 and 60 MeV were taken out after sufficient cooling time. The off-line γ-ray counting was performed using a pre-calibrated HPGe detector coupled with a PC-based 4K channel analyzer. The HPGe detector used for γ-ray counting is an Ortec detector from Canberra. The dead time of the detector during the γ-ray counting was kept below 2% by changing the distance between the detector and irradiated samples; this prevented pile up and coincidence-summing effects. The resolution of the HPGe detector was 1.8 keV at full-width at half width (FWHM) at the photopeak of 1332.5 keV γ-ray of 60Co. The total detector efficiency was 20% at the 1332.5 keV γ-ray peak relative to a 7.62 cm × 7.62 cm NaI(Tl) detector. Typical γ-ray spectra of the reaction products produced from the natCd and 197Au monitor samples irradiated with bremsstrahlung radiation with an end-point energy of 60 MeV are shown in Fig. 1(a-c). The produced radionuclides were identified based on the respective γ-ray energies and half-lives of the radioactive isotopes [21, 22], as presented in Table 1.
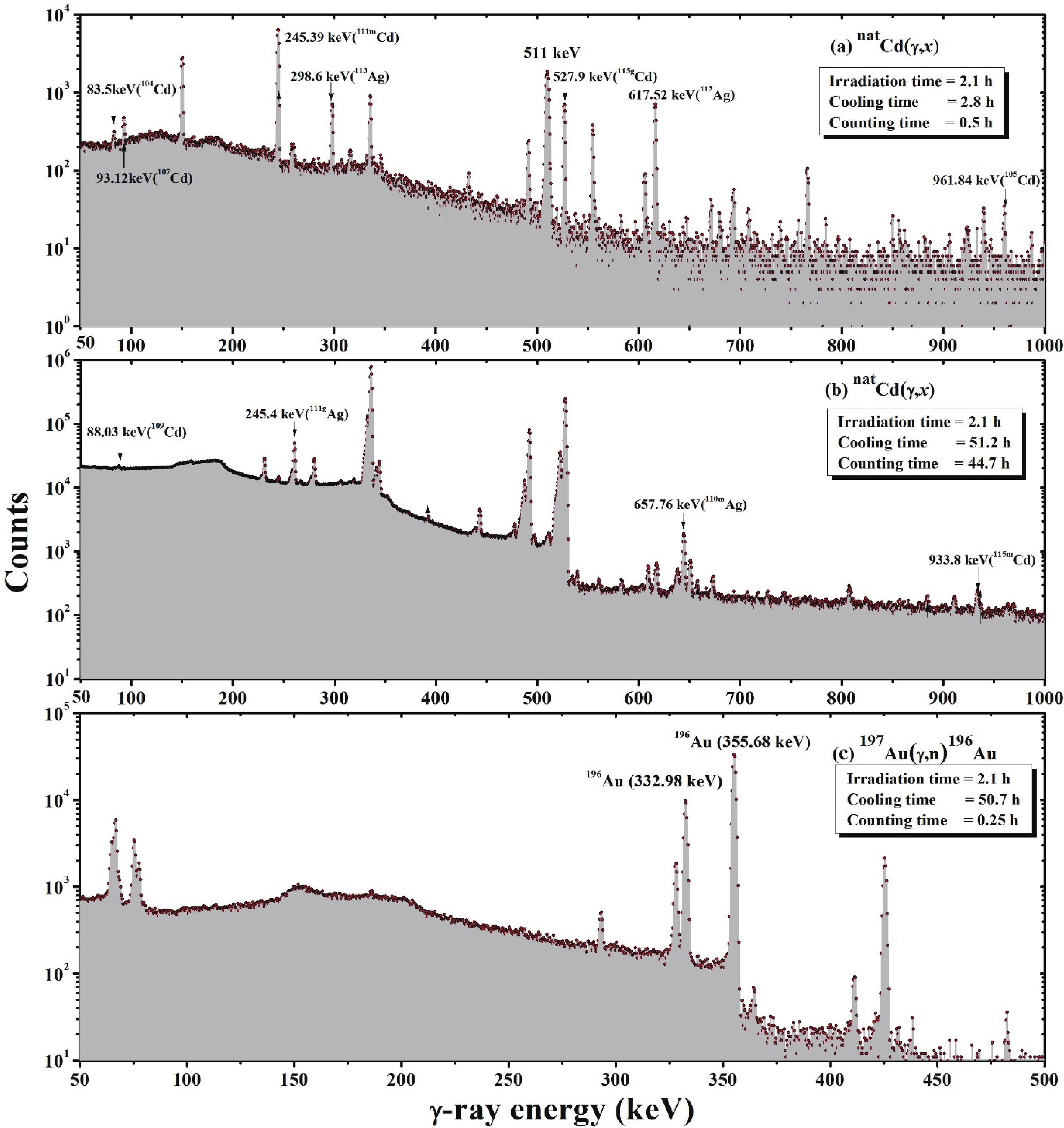
Figure 1. (color online) Typical γ-ray spectra of the products of the natCd(γ, x) reactions with cooling times of (a) 2.8 h and (b) 51.2 h, and (c) those of the 197Au(g, n) reaction with a cooling time of 50.7 h. The bremsstrahlung end-point energy used for the irradiation was 60 MeV.
Nuclides
(spin & parity)Half-life Decay mode
(%)g-ray energy
/keVγ-ray abundance
(%)Reactions Q-value
/MeVThreshold
/MeV115gCd (1/2)+ 53.46 h β- : 100.00 336.24 45.9 116Cd(γ, n) −8.699 8.700 Decay of 115mAg (T1/2 = 18 s) by β-(79%) 527.90 27.45 Decay of 115gAg (T1/2 = 20 m) by β-(100%) 115mCd (11/2)- 44.56 d β-: 100.00 158.03 0.02 116Cd(γ, n) −8.699 8.700 484.47 0.29 Decay of 115Ag (T1/2 = 20 m) by β-(100%) 933.80 2 111mCd (11/2)- 48.5 m IT : 100 150.82 29.1 111Cd(γ, g’) 0.0 0.0 112Cd(γ, n) −9.394 9.394 113Cd(γ, 2n) −15.934 15.935 245.39 94 114Cd(γ, 3n) −24.977 24.980 116Cd(γ, 5n) −39.817 39.824 109Cd (5/2)+ 461.9 d EC: 100 88.03 3.64 110Cd(γ, n) −9.915 9.915 111Cd(γ, 2n) −16.891 16.892 112Cd(γ, 3n) −26.285 26.288 113Cd(γ, 4n) −32.824 32.829 114Cd(γ, 5n) −41.867 41.875 116Cd(γ,7n) −56.707 56.722 107Cd (5/2)+ 6.5 h EC :100 93.12 4.7 108Cd(γ, n) −10.334 10.334 110Cd(γ, 3n) −27.572 27.575 111Cd(γ, 4n) −34.547 34.553 112Cd(γ, 5n) −43.941 43.950 828.93 0.163 113Cd(γ, 6n) −50.481 50.493 114Cd(γ, 7n) −59.524 59.541 116Cd(γ, 9n) −74.364 74.390 105Cd (5/2)+ 55.5 m EC :100 346.87 4.2 106Cd(γ, n) −10.870 10.870 108Cd(γ, 3n) −29.133 29.137 433.24 2.81 110Cd(γ, 5n) −46.371 46.381 111Cd(γ, 6n) −53.346 53.360 961.84 4.7 112Cd(γ, 7n) −62.740 62.759 113Cd(γ, 8n) −69.280 69.303 104Cd (0)+ 57.7 m EC :100 106Cd(γ, 2n) −19.306 19.308 66.6 2.4 108Cd(γ, 4n) −37.569 37.576 83.5 47 110Cd(γ, 6n) −54.808 54.822 709.3 19.5 111Cd(γ, 7n) −61.783 61.802 112Cd(γ, 8n) −71.177 71.201 113gAg (1/2)- 5.37 h β- : 100.00 258.72 1.64 114Cd(γ, p) −10.277 10.278 116Cd(γ, p2n) −25.117 25.120 298.6 10 Decay of 113mAg (T1/2 = 62 s, spin=7/2+) by IT(64%) Continued on next page Table 1. Nuclear spectroscopic data of the products of the natCd(γ, xn), natCd(γ, pxn), and 197Au(γ, n) reactions. The photo-peak activities of γ-ray energies marked with bold letters were used for calculations.
-
The photon fluxes (
${{\rm{\phi}} _{{E_{\rm e}}}}\left( {{E_\gamma }} \right)$ ) as a function of photon energy (Eγ) for the bremsstrahlung spectra with electron beam energies (Ee) of 50 and 60 MeV were simulated using the GEANT4 code [23] and are shown in Fig. 2. The integrated photon flux$\Phi \left( {{E_{\rm e}}} \right)\left( { = \int_{{E_{\rm th}}}^{{E_{\rm e}}} {{{\rm{\phi}} _{{E_{\rm e}}}}\left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } \right)$ from the threshold to the electron beam energy was measured using the photo-peak activity of a 355.68 keV (Iγ =87%) γ-line of 196gAu produced from the 197Au(γ, n)196gAu monitor reaction. The observed number of counts ($N_{\rm obs}^{{E_{\rm e}}}$ ) for the 355.68 keV γ-line of 196gAu was calculated by summing the counts under the full energy peak and subtracting the linear Compton back-ground, which is related to the integrated photon flux$\Phi \left( {{E_{\rm e}}} \right)$ as follows [24]:
Figure 2. (color online) Typical bremsstrahlung spectra for the end-point energies of 50 and 60 MeV simulated using the GEANT4 code.
$\Phi \left( {{E_{\rm e}}} \right) = \frac{{N_{\rm obs}^{{E_{\rm e}}}\left( {CL/LT} \right)\lambda }}{{n\left\langle {{{\rm{\sigma}} _R}\left( {{E_{\rm e}}} \right)} \right\rangle {I_\gamma }{{\rm{\varepsilon}} _\gamma }\left( {1 - {{\rm e}^{ - \lambda {T_{\rm irr}}}}} \right){{\rm e}^{ - \lambda {T_{\rm C}}}}\left( {1 - {{\rm e}^{ - \lambda CL}}} \right)}},$

(1) where n and λ are the number of atoms in the flux monitor (Au) sample and the decay constant for 196gAu, respectively. Iγ and εγ are the branching intensity and detection efficiency of the selected γ-line, respectively. Tirr and TC, are the irradiation and the cooling times, respectively. CL and LT are the clock and live counting times, respectively. The detection efficiencies were measured using the standard calibration sources of 152Eu and 133Ba.
$\left\langle {{{\rm{\sigma}} _R}\left( {{E_{\rm e}}} \right)} \right\rangle $ is the known average cross section of the 197Au(γ,n)196gAu monitor reaction taken from Ref. [24], which is 103.3±12.1 mb and 102.4±9.5 mb for the bremsstrahlung end-point energies of 50 and 60 MeV, respectively. Nuclear data, such as the half-lives, γ-ray abundances, reaction Q-values, and threshold energies of the products, are given in Table 1 [21, 22].Table 1-continued from previous Nuclides
(spin & parity)Half-life Decay mode
(%)g-ray energy
/keVγ-ray abundance
(%)Reactions Q-value
/MeVThreshold
/MeV112Ag (2)- 3.13 h β- : 100.00 606.82 3.1 113Cd(γ, p) −9.749 9.749 617.52 43 114Cd(γ, pn) −18.792 18.793 694.87 2.9 116Cd(γ, p3n) −33.632 33.637 111gAg (1/2)- 7.45 d β- : 100.00 245.40 1.24 112Cd(γ, p) −9.648 9.649 113Cd(γ, pn) −16.188 16.189 114Cd(γ, p2n) −25.231 25.234 342.13 7 116Cd(γ, p4n) −40.071 40.079 Decay of 111mAg (T1/2 = 1.08 m, spin=7/2+) by IT (99.3%) 110mAg (6)+ 249.83 d IT : 1.33 657.76 95.61 111Cd(γ, p) −9.084 9.084 112Cd(γ, pn) −18.478 18.479 113Cd(γ, p2n) −25.018 25.021 β- : 98.67 884.67 75 114Cd(γ, p3n) −34.061 34.066 116Cd(γ, p5n) −48.901 48.912 196gAu (2)- 6.18 d EC : 92.8
β- : 7.2355.68 87.0 197Au(γ, n) −8.072 8.073 -
Natural cadmium has eight stable isotopes with different isotopic abundances. The yield of the produced radionuclides is the sum of the isotope contributions based on their production threshold energies, as shown in Table 1. The eleven radio nuclides in Table 1 can be produced from natCd(γ, x)j reactions with different threshold values. The normalized yield contribution (
${Y_{i,j}}\left( {{E_{\rm e}}} \right)$ ) for each reaction of iCd(γ, x)j was obtained as follows [25]:${Y_{i,j}}\left( {{E_{\rm e}}} \right) = \frac{{\displaystyle\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{A_i}\;{{\rm{\sigma}} _{i,j}}\left( {{E_\gamma }} \right){\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} }}{{\displaystyle\sum\limits_{k = 1}^8 {\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{A_k}\;{{\rm{\sigma}} _{k,j}}\left( {{E_\gamma }} \right){\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } }},$

(2) where i and k are eight stable isotopes (i, k = 106, 108, 110, 111, 112, 113, 114, 116) in natCd, and j is eleven produced isotopes (115g,m,111m,109,107,105,104Cd and 113g,112,111g,110mAg).
${\rm{\phi}} \left( {{E_\gamma }} \right)$ is the photon flux calculated using the GEANT4 code [23], Ai(k) is the isotopic abundance, and${{\rm{\sigma}} _{i,j}}\left( {{E_\gamma }} \right)$ is the cross section for the iCd(γ, x)j reactions at the photon energy Eγ, which was calculated using the TALYS 1.95 code [17]. The normalized yield contributions for eleven radio isotopes j produced from various iCd(γ, x)j reactions are given in Table 2.Produced Nuclei Reaction Eth/MeV E e =50 MeV Ee =60 MeV ${Y_{i,j}}\left( {{E_{\rm e}}} \right)$ 

${F_{i,j}}\left( {{E_{\rm e}}} \right)$ 

${Y_{i,j}}\left( {{E_{\rm e}}} \right)$ 

${F_{i,j}}\left( {{E_{\rm e}}} \right)$ 

115gCd 116Cd(γ, n) 8.70 Y116,115= 100 F116,115= 0.934 Y116,115 = 100 F116,115= 0.940 115mCd 116Cd(γ, n) 8.70 Y116,115= 100 F116,115= 0.934 Y116,115 = 100 F116,115= 0.940 111mCd 111Cd(γ, g’) 0.0 Y111,111= 1.70 F111,111= 2.910 Y111,111 =1.40 F111,111= 2.710 112Cd(γ, n) 9.39 Y112,111= 64.9 F112,111= 0.890 Y112,111=62.6 F112,111= 0.901 113Cd(γ, 2n) 15.94 Y113,111= 18.5 F113,111= 0.554 Y113,111= 19.0 F113,111= 0.592 114Cd(γ, 3n) 24.96 Y114,111= 14.5 F114,111= 0.306 Y114,111= 16.0 F114,111= 0.359 116Cd(γ, 5n) 39.82 Y116,111= 0.40 F116,111= 0.080 Y116,111= 1.00 F116,111= 0.148 109Cd 110Cd(γ, n) 9.92 Y110,109= 75.7 F110,109= 0.848 Y110,109= 74.1 F110,109= 0.863 111Cd(γ, 2n) 16.89 Y111,109= 18.7 F111,109= 0.518 Y111,109= 18.7 F111,109= 0.560 112Cd(γ, 3n) 26.29 Y112,109= 4.60 F112,109= 0.278 Y112,109= 5.00 F112,109= 0.333 113Cd(γ, 4n) 32.83 Y113,109= 0.80 F113,109= 0.168 Y113,109= 1.10 F113,109= 0.231 114Cd(γ, 5n) 41.86 Y114,109= 0.20 F114,109= 0.059 Y114,109= 1.10 F114,109= 0.127 107Cd 108Cd(γ, n) 10.33 Y108,107= 67.5 F108,107= 0.823 Y108,107= 59.2 F108,107= 0.840 110Cd(γ, 3n) 27.58 Y110,107= 24.7 F110,107= 0.255 Y110,107= 24.5 F110,107= 0.316 111Cd(γ, 4n) 34.55 Y111,107= 7.30 F111,107= 0.145 Y111,107= 10.1 F111,107= 0.210 112Cd(γ, 5n) 43.95 Y112,107= 0.50 F112,107= 0.039 Y112,107= 5.80 F112,107= 0.108 113Cd(γ, 6n) 50.49 Y113,107= 0.00 F113,107= 0.00 Y113,107= 0.40 F113,107= 0.052 105Cd 106Cd(γ, n) 10.87 Y106,105= 98.6 F106,105= 0.786 Y106,105= 96.4 F106,105= 0.806 108Cd(γ, 3n) 29.14 Y108,105= 1.40 F108,105= 0.227 Y108,105= 1.60 F108,105= 0.286 110Cd(γ, 5n) 46.38 Y110,105= 0.00 F110,105= 0.020 Y110,105= 1.90 F110,105= 0.086 111Cd(γ, 6n) 53.36 Y111,105= 0.00 F111,105= 0.000 Y110,105= 0.10 F111,105= 0.033 104Cd 106Cd(γ, 2n) 19.31 Y106,104= 98.2 F106,104= 0.443 Y106,104= 96.2 F106,104= 0.488 108Cd(γ, 4n) 37.58 Y108,104= 1.80 F108,104= 0.107 Y108,104= 3.60 F108,104= 0.174 110Cd(γ, 6n) 54.82 Y110,104= 0.00 F110,104= 0.000 Y110,104= 0.20 F110,104= 0.016 113Ag 114Cd(γ, p) 10.28 Y114,113= 88.1 F114,113= 0.823 Y114,113= 92.9 F114,113= 0.840 116Cd(γ, p2n) 25.12 Y116,113= 11.9 F116,113= 0.302 Y116,113= 7.10 F116,113= 0.356 112Ag 113Cd(γ, p) 9.75 Y113,112= 27.0 F113,112= 0.862 Y113,112= 21.9 F113,112= 0.875 114Cd(γ, pn) 18.79 Y114,112= 71.8 F114,112= 0.460 Y114,112= 74.3 F114,112= 0.505 116Cd(γ, p3n) 33.64 Y116,112= 1.20 F116,112= 0.156 Y116,112= 3.80 F116,112= 0.234 111Ag 112Cd(γ, p) 9.65 Y112,111= 56.9 F112,111= 0.862 Y112,111= 49.9 F112,111= 0.875 113Cd(γ, pn) 16.19 Y113,111= 23.1 F113,111= 0.546 Y113,111= 23.0 F113,111= 0.585 114Cd(γ, p2n) 25.23 Y114,111= 19.9 F114,111= 0.297 Y114,111= 26.5 F114,111= 0.352 116Cd(γ, p4n) 40.08 Y116,111= 0.10 F116,111= 0.078 Y116,111= 0.60 F116,111= 0.146 110mAg 111Cd(γ, p) 9.08 Y111,110= 17.5 F111,110= 0.905 Y111,110= 10.7 F111,110= 0.914 112Cd(γ, pn) 18.48 Y112,110= 58.7 F112,110= 0.466 Y112,110= 49.2 F112,110= 0.511 113Cd(γ, p2n) 25.02 Y113,110= 16.4 F113,110= 0.301 Y113,110= 18.3 F113,110= 0.356 114Cd(γ, p3n) 34.06 Y114,110= 7.40 F114,110= 0.151 Y114,110= 21.6 F114,110= 0.215 116Cd(γ, p5n) 48.91 Y116,110= 0.00 F116,110= 0.004 Y116,110= 0.20 F116,110= 0.065 Table 2. Normalized yield (%) and photon flux correction factor (
${F_{i,j}}\left( {{E_{\rm e}}} \right)$ ) for the iCd(γ, xn)j reactions.The threshold value (Eth) of the monitor reaction 197Au(γ, n)196Au is 8.07 MeV, as seen in Table 1. However, the production thresholds for the elevenradionuclides (j =115g,m;111m;109m,107m;105m;104mCd and 113g;112;111g;110mAg) are different from the monitor reaction as listed in Table 1. Therefore, a flux correction factor is required to correct the measured photon flux from the iCd(γ, x)j reactions to that from the monitor reaction. The photon flux correction factors
${F_{i,j}}\left( {{E_{\rm e}}} \right)$ for iCd(γ, x)j were calculated as follows [25]:${F_{i,j}}\left( {{E_{\rm e}}} \right) = {{\int\limits_{E_{\rm th}^{i,j}}^{{E_{\rm e}}} {{\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} } \Big/ {\int\limits_{E_{\rm th}^{\rm Au}}^{{E_{\rm e}}} {{\rm{\phi}} \left( {{E_\gamma }} \right){\rm d}{E_\gamma }} }},$

(3) where i and j have the same definitions as in Eq. (2).
$E_{\rm th}^{i,j}$ and$E_{\rm th}^{\rm Au}$ are the threshold energies for the iCd(γ, x)j and 197Au(γ,n)196gAu reactions, respectively.${\rm{\phi}} \left( {{E_\gamma }} \right)$ is the photon flux as a function of photon energy Eγ, taken from Fig. 2, which was simulated using the GEANT4 code [23]. The obtained correction factors to correct the different reactions to the monitor reaction are given in Table 2.The yield-weighted flux correction factors
$C_j^T\left( {{E_{\rm e}}} \right)$ for the jCd(γ, x)j reactions were calculated using Eqs. (2) and (3) as follows:$C_j^T\left( {{E_{\rm e}}} \right) = {{\sum\limits_i {\left( {{Y_{i,j}}\left( {{E_{\rm e}}} \right) \times {F_{i,j}}\left( {{E_{\rm e}}} \right)} \right)} } \Big/ {\sum\limits_i {{Y_{i,j}}\left( {{E_{\rm e}}} \right)} }}.$

(4) The obtained yield-weighted flux correction factors
$C_j^T\left( {{E_{\rm e}}} \right)$ for the eleven produced isotopes (j) are listed in Table 3. The yield-weighted photon flux$\Phi _j^C\left( {{E_{\rm e}}} \right)$ with the yield-weighted flux correction factors for the natCd(γ, x)j reactions were obtained as follows:Nuclear reactions Total correction factors ( $C_j^T\left( { {E_{\rm e}} } \right)$ )

Bremsstrahlung end-point energy, Ee/MeV 50 60 natCd(γ, n)115gCd 0.934 0.941 natCd(γ, n)115mCd 0.934 0.941 natCd(γ, xn)111mCd 0.774 0.774 natCd(γ, xn)109Cd 0.753 0.765 natCd(γ, xn)107Cd 0.629 0.602 natCd(γ, xn)105Cd 0.778 0.783 natCd(γ, xn)104Cd 0.437 0.476 natCd(γ, pxn)113gAg 0.761 0.806 natCd(γ, pxn)112Ag 0.565 0.576 natCd(γ, pxn)111gAg 0.676 0.665 natCd(γ, pxn)110mAg 0.492 0.416 Table 3. Yield-weighted flux correction factor for the natCd(γ, x)j reactions.
$\Phi _j^C\left( {{E_{\rm e}}} \right) = C_j^T\left( {{E_{\rm e}}} \right) \times \Phi \left( {{E_{\rm e}}} \right).$

(5) -
We determined the flux-weighted average cross sections using the yield-weighted photon flux
$\Phi _j^C\left( {{E_{\rm e}}} \right)$ for the natCd(γ, x)j reactions (the produced nuclei j is given as 115gm,111m,109,107,105,104Cd and 113g,112,111g,110mAg). The nuclear spectroscopic data for the reaction products were taken from Refs. [21, 22] and given in Table 1. Once the observed number counts under the photo-peak ($N_{\rm obs}^{{E_\gamma }}$ ) was acquired for the characteristic γ-ray energy of the produced radionuclide j, the flux-weighted average cross sections of the natCd(γ, x)j reactions were obtained as follows [25]:$\left\langle {{\rm{\sigma}} _j^{\rm nat}\left( {{E_{\rm e}}} \right)} \right\rangle = \frac{{N_{\rm obs}^{{E_{\rm e}}}\left( {CL/LT} \right)\lambda }}{{n\Phi _j^C\left( {{E_{\rm e}}} \right){I_\gamma }{{\rm{\varepsilon}} _\gamma }\left( {1 - {{\rm e}^{ - \lambda {T_{\rm irr}}}}} \right){{\rm e}^{ - \lambda {T_C}}}\left( {1 - {{\rm e}^{ - \lambda CL}}} \right)}},$

(6) where all terms have the same meaning as in Eq. (1) and
$\Phi _j^C\left( {{E_{\rm e}}} \right)$ is the yield-weighted photon flux as given in Eq. (5). -
The flux-weighted average cross sections were also theoretically calculated for all the residual nuclides of interest based on the TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] nuclear codes and compared with the experimental data, which are presented in Table 4. The calculations based on TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] were performed with their default parameters. The photon-induced reaction cross sections (
${\rm{\sigma}} _R^x\left( {{E_i}} \right)$ ) for the natCd(γ, x) reactions were calculated based on mono-energetic photons using the TALYS 1.95 [17] and EMPIRE-3.2 Malta [18] codes. In the calculations, all possible exit channels of the nuclear reactions of the given projectile energy were considered. The flux-weighted average cross sections$\left( {\left\langle {{{\rm{\sigma}} _x}\left( E \right)} \right\rangle } \right)$ for the natCd(γ, x) reactions were calculated as follows:Reaction Bremsstrahlung end-point energy/MeV Flux-weighted average cross-section
$\left\langle {{\sigma _i}} \right\rangle $ /mb

Present work Theoretical calculations TALYS 1.95 [17] Empire 3.2 Malta [18] natCd(γ, xn)115gCd 50 2.432 ± 0.345 2.521 3.631 60 2.123 ± 0.261 2.330 3.544 natCd(γ, xn)115mCd 50 0.5 ± 0.071 0.534 0.778 60 0.446 ± 0.059 0.493 0.760 natCd(γ, xn)111mCd 50 1.461 ± 0.219 0.458 0.811 60 1.413 ± 0.212 0.449 0.785 natCd(γ, xn)109Cd 50 12.346 ± 1.786 9.082 8.381 60 10.210 ± 1.501 8.466 7.724 natCd(γ, xn)107Cd 50 0.733 ± 0.101 0.788 0.656 60 0.681 ± 0.094 0.834 0.711 natCd(γ, xn)105Cd 50 0.43 ± 0.065 0.669 0.702 60 0.385 ± 0.059 0.632 0.651 natCd(γ, xn)104Cd 50 0.105 ± 0.015 0.121 0.112 60 0.087 ± 0.011 0.112 0.086 natCd(γ, xn)113g+mAg 50 0.534 ± 0.075 0.057 0.108 60 0.501 ± 0.061 0.057 0.110 natCd(γ, xn)112Ag 50 0.318 ± 0.043 0.068 0.159 60 0.367 ± 0.046 0.081 0.172 natCd(γ, xn)111g+mAg 50 0.126 ± 0.019 0.0425 0.121 60 0.123 ± 0.018 0.045 0.119 natCd(γ, xn)110mAg 50 0.026 ± 0.005 0.017 0.032 60 0.027 ± 0.004 0.026 0.035 Table 4. Flux-weighted average cross sections for the natCd(γ, xn) and natCd(γ, pxn) reactions.
$\left\langle {{\sigma _x}\left( E \right)} \right\rangle = {{\int\limits_{{E_{\rm th}}}^{{E_{\gamma \max }}} {\sigma _R^x({E_i})\;\varphi ({E_i}){\rm d}E} }\Bigg/ {\int\limits_{{E_{\rm th}}}^{{E_{\gamma \max }}} {\varphi ({E_i}){\rm d}E} }},$

(7) where
$ \left({E}_{i}\right) $ is the bremsstrahlung photon flux as a function of energy (E) simulated by the GEANT 4 code [23], as shown in Fig. 2. -
The measured flux-weighted average cross sections are presented in different figures along with theoretical calculations and previously published data. The numerical values of all the cross sections and the uncertainties are given in Table 4. As previously stated, natural cadmium has eight stable isotopes (116,114,113,112,111,110,108,106Cd). Thus, during irradiation, the production of a specific radionuclide is prone to contribution from many reaction channels based on the projectile energy.
The overall uncertainties in the results were calculated by taking the square root of the quadratic sum of all independent statistical and systematic uncertainties [19]. The resulting statistical uncertainties were mainly contributed by the counting statistics from the observed number of counts under the photo-peak of each γ-line (1.5%~10.5%). This was estimated by accumulating the data for an optimum time that depends on the half-life of the produced nuclides. In contrast, the systematic uncertainties were calculated from the uncertainties of the flux estimation (~11.5%), the detector efficiency (~3%), the half-life of the reaction products (~2%), the distance between the sample and detector (~2%), the γ-ray abundance (~2%), the irradiation and cooling time (~2%), the current and electron beam energy (~1%), and the number of cadmium target nuclei (~0.3%). The total systematic uncertainty is approximately 12.58%. The overall uncertainty is found to be between ~12.67% and ~16.07%.
-
When natural cadmium is irradiated with bremsstrahlung radiation with end-point energies of 50 and 60 MeV, six cadmium isotopes are directly produced through natCd(γ, xn) reactions, except the 115g,mCd nuclides, which can be indirectly produced from the β- decay of 115g,mAg, as given in Table 1.
In this study, the flux-weighted average cross sections of the natCd(γ, xn)115g,m,111m,109,107,105,104Cd reactions at the bremsstrahlung end-point energies of 50 MeV and 60 MeV are determined for the first time and presented in Table 4. All measurements of the produced cross sections of the cadmium isotopes are exclusive, that is, there is no contribution from any other short-lived radionuclides in the measurements. Even the 109,107,105,104Cd radionuclides have no isomers; hence, their reaction cross sections are also independent. For comparison, the cross sections for the reactions as a function of the mono-energetic photons were calculated using the TALYS-1.95 and Empire 3.2 codes with default parameters; the flux-weighted average cross sections were then calculated using Eq. (7).
-
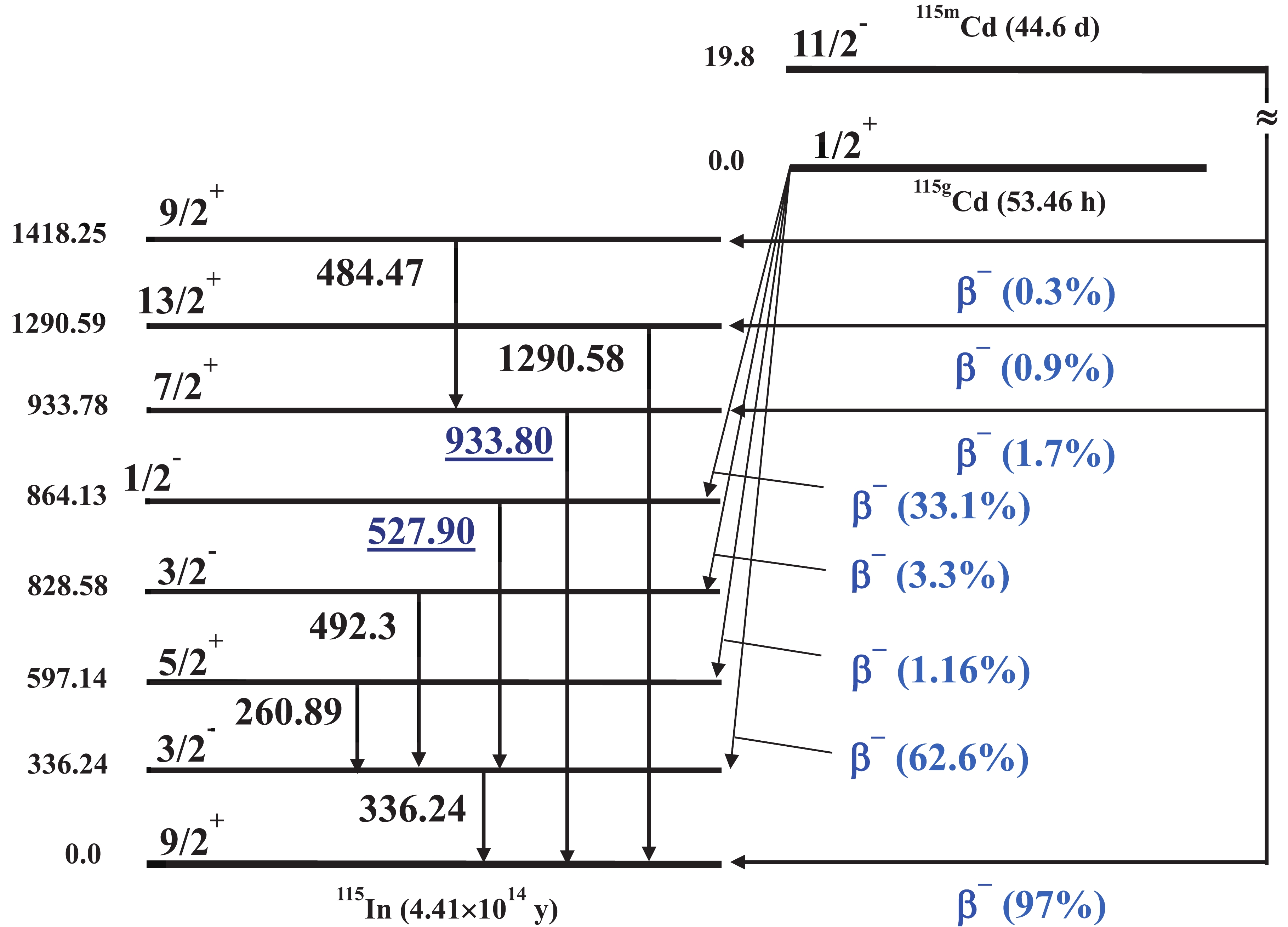
The radioisotope 115Cd is produced directly through the 116Cd(γ, n) reaction and indirectly through the β- decay of 115Ag. It has a short-lived ground state 115gCd (T1/2=53.46 h) and a long-lived meta-stable state 115mCd (T1/2=44.56 d). The simplified energy level and the decay scheme of 115m,gCd is shown in Fig. 3. The meta-stable state 115mCd with a half-life of 44.6 d decays directly to the ground state of 115In by the β- process with a branching ratio of 97%. Meanwhile, approximately 1.7% of the meta-stable state decays to the ground state of 115In (jπ=9/2+) through the excited state of 115In (jπ=7/2+) by emitting a 933.8 keV γ-ray. The unstable ground state 115gCd (jπ=1/2+) decays to the 336.24 keV state of 115In (Jπ = 1/2-) by a β- process with a branching ratio of 62.6%, which decays to the ground state of 115In (Jπ = 9/2+) via M4 transition by emitting a characteristic γ-ray of 336.2 keV. On the other hand, the unstable ground state 115gCd decays to the 864.1 keV state of 115In (J π = 1/2+) by a β- process with a branching ratio of 33.1%, which then decays to the 336.2 keV state of 115In (J π = 1/2-) by emitting a 527.9-keV γ-ray. In order to identify the 115m,gCd isomeric pairs, we used the 933.8 keV and 527.9 keV photo-peaks for the 115mCd and 115gCd nuclides, respectively. It is observed that both the metastable and ground states seem to be individual.
The measured results for the natCd(γ, xn)115g;115mCd reactions are compared with the theoretical values obtained with the TALYS-1.95 and Empire 3.2 codes, as shown in Fig. 4. There is no literature data for the natCd(γ, xn)115gCd reaction. It is clear that the theoretical values from both the TALYS-1.95 and Empire 3.2 codes are in agreement with the data from this study, as shown in Fig. 4. However, there is only one set of literature data regarding the low energy side of the GDR region for the natCd(γ, xn)115mCd reaction [8], which was obtained with mono-energetic photons. To compare those results with the results of this study, we calculated the flux-weighted average cross section for the literature value using Eq. (7), as shown in Fig. 4. The flux-weighted average cross sections for literature data in the low energy region were higher than the theoretical results. However, the present results are lower than the values obtained with the TALYS-1.95 and Empire 3.2 codes, as shown in Fig. 4.

Figure 4. (color online) The experimental flux-weighted average cross sections of natCd(γ, xn)115gCd and natCd(γ, xn)115mCd reactions as a function of bremsstrahlung end-point energy along with the theoretical calculations using the TALYS-1.95 and EMPIRE-3.2 codes.
Based on the measured experimental cross sections of the metastable and ground states from Table 4, we obtained the isomeric yield ratio (IR=σh/σl) of 115gCd (nuclear spin=1/2+) and 115mCd (nuclear spin=11/2-) in the natCd(γ, xn) reactions, which are given in Table 5 for various bremsstrahlung end-point energies. The photon-induced IR values from this study, the literature data in the GDR region [11-14], and our previous results [15] are listed in Table 5 and shown in Fig. 5. The IR values for neutron-induced 116Cd(n, 2n)115g,mCd reactions taken from previous data [16] and those theoretically calculated using TALYS-1.95, EMPIRE-3.2 Malta, and TENDL-2019 [26] are also presented in Table 5 and Fig. 5.
Reaction Projectile energy/MeV Excitation energy/MeV Isomeric ratio ( ${IR} = { { {\sigma _{\rm HighSpin} } }/{\sigma _{\rm LowSpin} } }$ )

Experimental work [Ref.] Theoretical calculations TALYS 1.95 [17] Empire 3.2 Malta [18] natCd(γ, xn)115g,mCd 50 13.922 0.206 ± 0.041 [A] 0.212 0.214 60 13.928 0.210 ± 0.038 [A] 0.212 0.214 116Cd(γ, n)115gmCd 9.43 9.072 0.180 ± 0.019 [12] 0.015 0.004 116Cd(γ, n)115g,mCd 20 13.803 0.117 ± 0.012 [14] 0.205 0.213 116Cd(γ, n)115g,mCd 20 13.803 0.148 ± 0.020 [11] 0.205 0.214 116Cd(γ, n)115g,mCd 22 13.841 0.120 ± 0.020 [13] 0.209 0.214 116Cd(γ, n)115g,mCd 23.5 13.857 0.158 ± 0.016 [14] 0.209 0.214 116Cd(γ, n)115g,mCd 50 13.922 0.186 ± 0.020 [15] 0.212 0.214 116Cd(γ, n)115g,mCd 60 13.928 0.202 ± 0.020 [15] 0.212 0.214 116Cd(γ, n)115g,mCd 70 13.933 0.209 ± 0.019 [15] 0.212 0.214 116Cd(n, 2n)115g,mCd 13.4 19.04 0.95 ± 0.13 [16] 1.321 1.189 116Cd(n, 2n)115g,mCd 14 19.64 0.98 ± 0.14 [16] 1.360 1.246 116Cd(n, 2n)115g,mCd 14.68 20.32 1.0 ± 0.14 [16] 1.398 1.295 116Cd(n, 2n)115g,mCd 14.81 20.45 1.05 ± 0.15 [16] 1.410 1.295 116Cd(n, 2n)115g,mCd 16.5 22.14 1.25 ± 0.18 [16] 1.510 1.364 116Cd(n, 2n)115g,mCd 17.95 23.59 1.36 ± 0.19 [16] 2.810 2.690 116Cd(n, 2n)115g,mCd 19.76 25.40 1.59 ± 0.22 [16] 3.461 3.101 [A] Present work. Table 5. Isomeric yield ratio of 115m,gCd from the 116Cd(γ, n) and 116Cd(n, 2n) reactions.
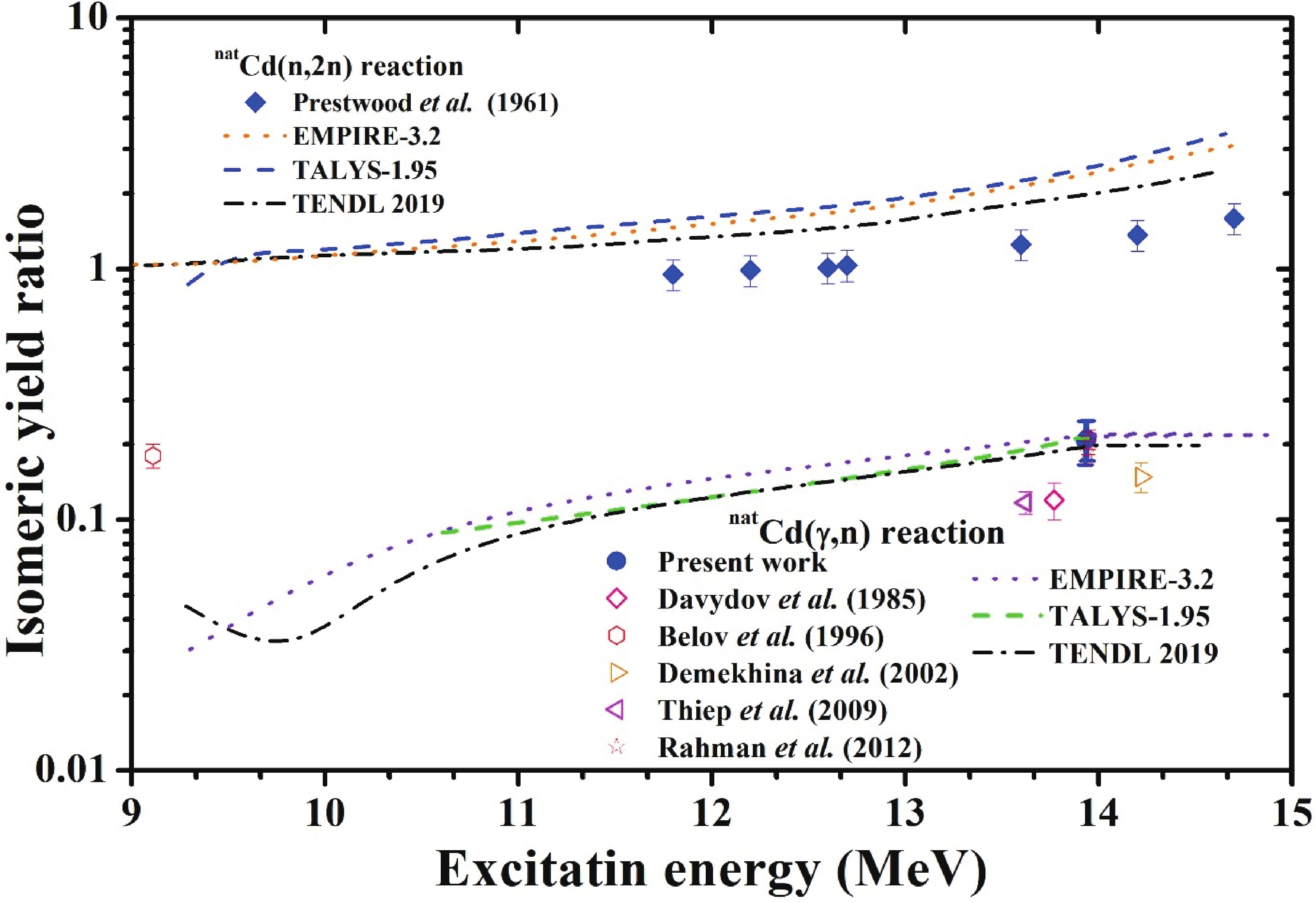
Figure 5. (color online) Isomeric cross section ratio (IR=σh/σl) of 115g,mCd in the (γ, n) and (n, 2n) reactions as a function of excitation energy of the compound nucleus.
In order to understand the effects of spin and input angular momentum, outgoing particles, and excitation energy, the IR values from the different reaction channels were compared. The average excitation energy
$ \left( {\left\langle {{E^*}\left( E \right)} \right\rangle } \right) $ of the compound nucleus from the threshold energy (Eth) to the bremsstrahlung end-point energy (Ee) was determined using the following expression [27, 28]:$\left\langle {{E^*}\left( {{E_{\rm e}}} \right)} \right\rangle = \frac{{\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{\rm{\phi}} \left( E \right){{\rm{\sigma}} _R}\left( E \right)E{\rm d}E} }}{{\int_{{E_{\rm th}}}^{{E_{\rm e}}} {{\rm{\phi}} \left( E \right)} {{\rm{\sigma}} _R}\left( E \right){\rm d}E}},$

(8) where
${\rm{\phi}} \left( E \right)$ represents the photon flux as a function of photon energy (E) for the bremsstrahlung spectra, which was calculated using the Geant4 code, as shown in the Fig. 2. The reaction cross section (${{\rm{\sigma}} _R}\left( E \right)$ ) was calculated using the default option in the TALYS-1.95 code. The calculated average excitation energies for the 116Cd(γ,n) reaction corresponding to different bremsstrahlung end-point energies are given in Table 5.The excitation energy (E*) of the compound nucleus in the neutron and charged particle induced reactions was calculated as follows:
${E^*} = {E_{\rm p}} + \left( {{\Delta _{\rm T}}\, + \,{\Delta _{\rm p}}} \right)\, - \,{\Delta _{\rm CN}},$

(9) where Ep is the projectile energy, and
${\Delta _{\rm CN}}$ ,${\Delta _{\rm T}}$ , and${\Delta _{\rm p}}$ are the mass excess values of the compound nucleus, target, and projectile, respectively. The mass excess values are taken from the Nuclear Wallet Cards [29].As seen in Fig. 5, the experimental IR values in the 116Cd(γ, n) reaction are in agreement with the theoretical values. However, in the 116Cd(n, 2n) reaction, the theoretical values from TALYS-1.95, EMPIRE-3.2, and TENDL-2019 are higher than the experimental values. Additionally, in the 116Cd(n, 2n) reaction, the theoretical values from TALYS-1.95 and EMPIRE-3.2 are slightly different. TENDL-2019 data are lower than the TALYS-1.95 data but are close to the experimental data. These differences are due to the use of default parameters in the current calculations with TALYS-1.95. Furthermore, the figure shows that the IR values of 115m,gCd increase with increasing excitation energy. However, at the same excitation energy, the IR values of 115m,gCd in the 116Cd(n, 2n) reaction are significantly higher than those in the 116Cd(γ, n) reaction. In the 116Cd(γ, n) reaction, the compound nucleus is 116Cd*, which has a 0+ spin. On the other hand, in the 116Cd(n, 2n) reaction, the compound nucleus is 117Cd*, which has a 11/2- spin in the excited state and ½+ spin in the ground state. At a high excitation energy, the compound nucleus of 117Cd* with a high spin value of 11/2- will be favorable in the 116Cd(n, 2n) reaction. Thus, the high spin isomeric product 115mCd with a spin state of 11/2- will preferably be populated in the 116Cd(n, 2n) reaction, which results in a high IR value. This observation indicates the role of the spin of a compound nucleus alongside excitation energy. A similar observation can be made from our previous studies on the isomer ratio of 106m,gAg and 104m,gAg from the natAg (γ, xn) [30] and natAg(n, xn) [28] reactions, which support our present observations.
-
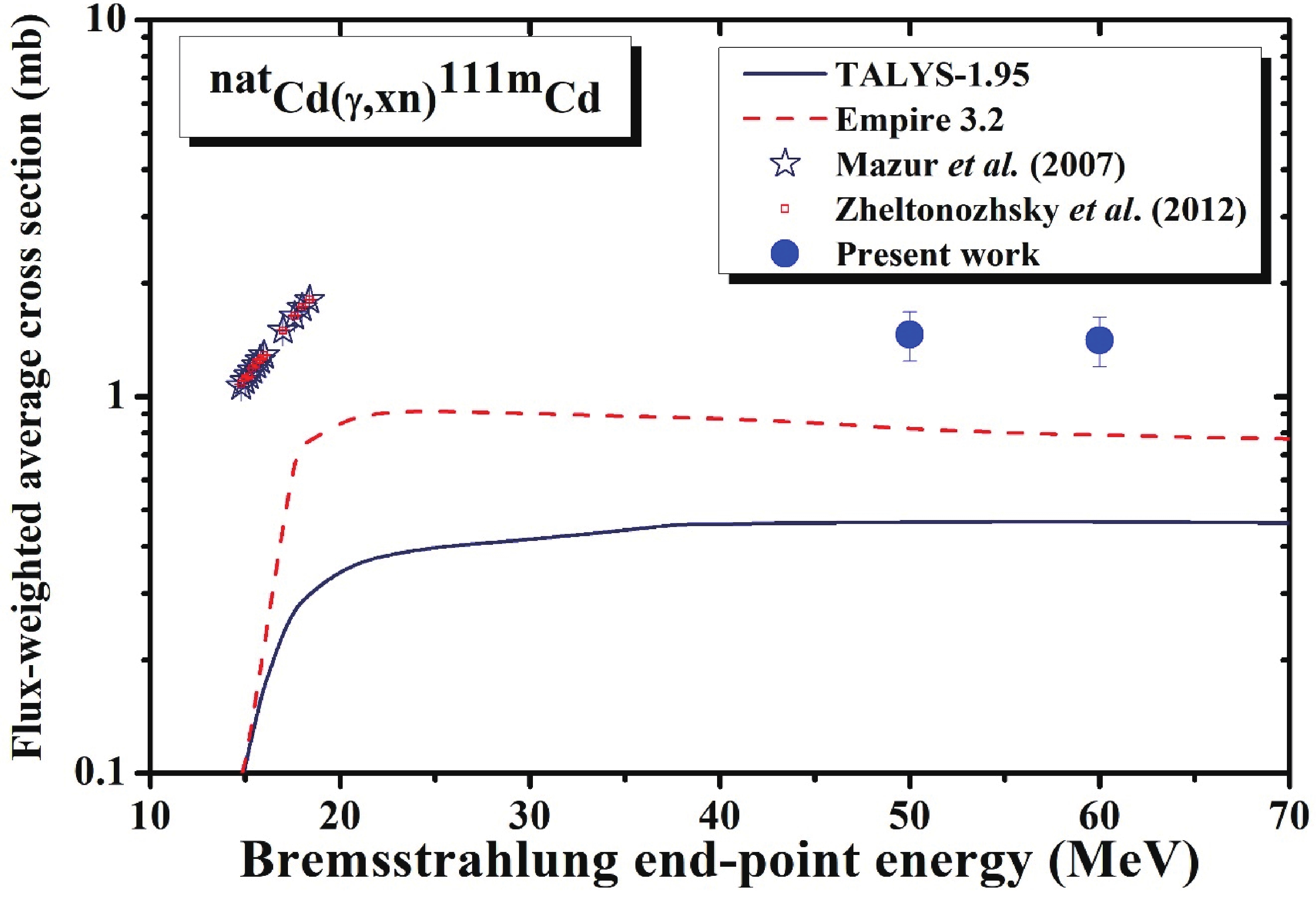
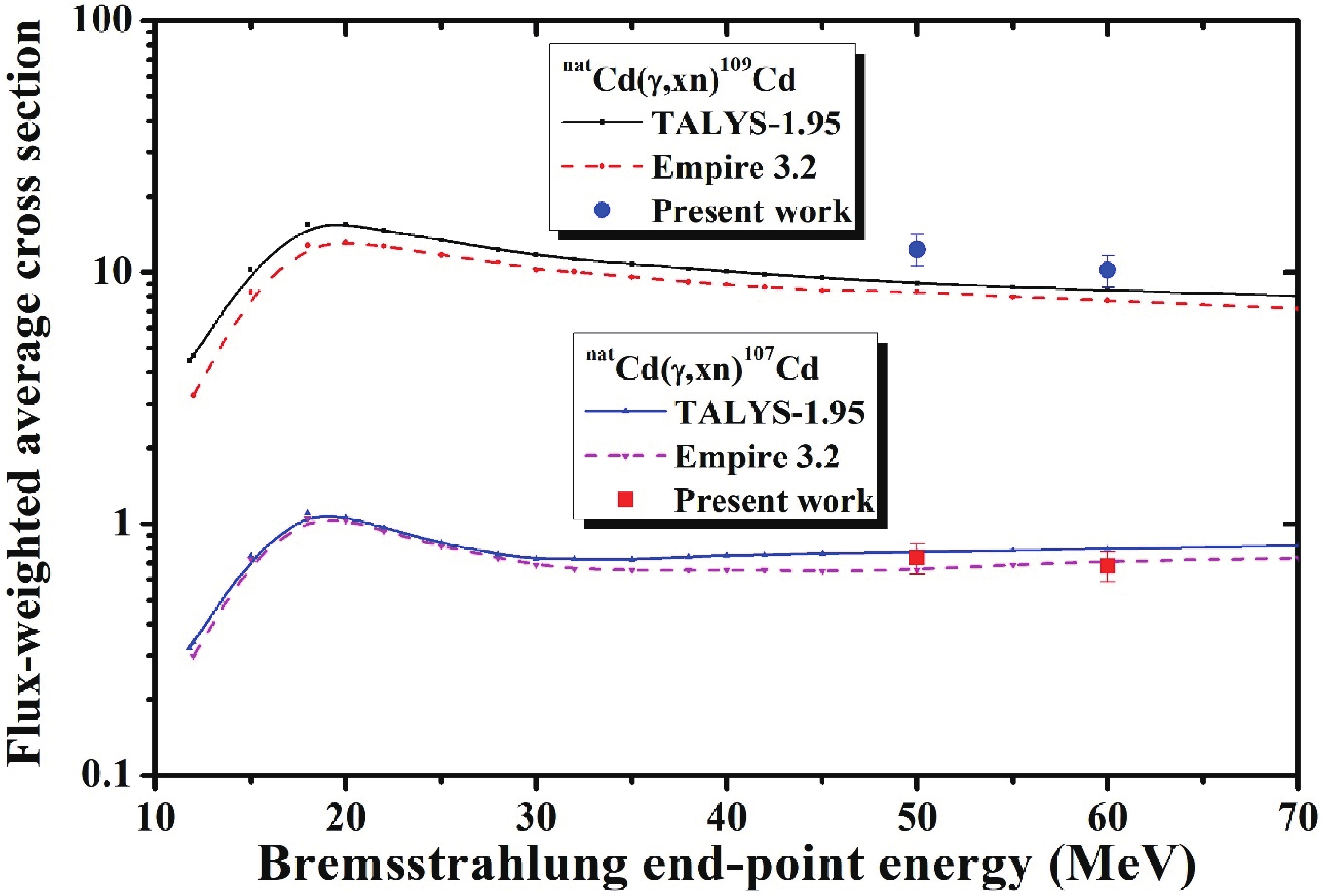
The isomeric state 111mCd (48.5 min, 11/2+) was identified by the pure and independent 245.39 keV γ-line. For the production of 111mCd from the 112Cd target, only two previous experimental data sets in the GDR energy region based on mono-energetic photons were available [8, 9]; these were found to be higher than the theoretical values obtained using the TALYS-1.95 and EMPIRE-3.2 Malta codes as shown in Fig. 6 and provided in Table 4. The figure and table also show that the current results follow the graphical shape but are higher than the theoretical values; they are the closest to the values calculated using the Empire-3.2 code.
-
The radionuclide 109Cd (461.9 d, 5/2+) was identified by the pure and independent 88.03 keV γ-line. The measured natCd(γ, xn)109Cd reaction cross-sections could onlybe compared with the theoretical calculations because no previous data has been found, as shown in Fig. 7 and tabulated in Table 4. In the figure, it is clear that the currently measured and theoretical values are in good agreement, in terms of not only shape but also magnitude.
-
The flux-weighted average formation cross sections of 107Cd (6.5 h, 5/2+) were measured based on the 93.12 keV γ line. The measurements for the natCd(γ, xn)107Cd reaction were performed for the first time and thus could only be compared with the theoretical values. Fig. 7 shows that the measurements are in good agreement with both of the calculations, but they are closer to the EMPIRE-3.2 Malta calculations.
-
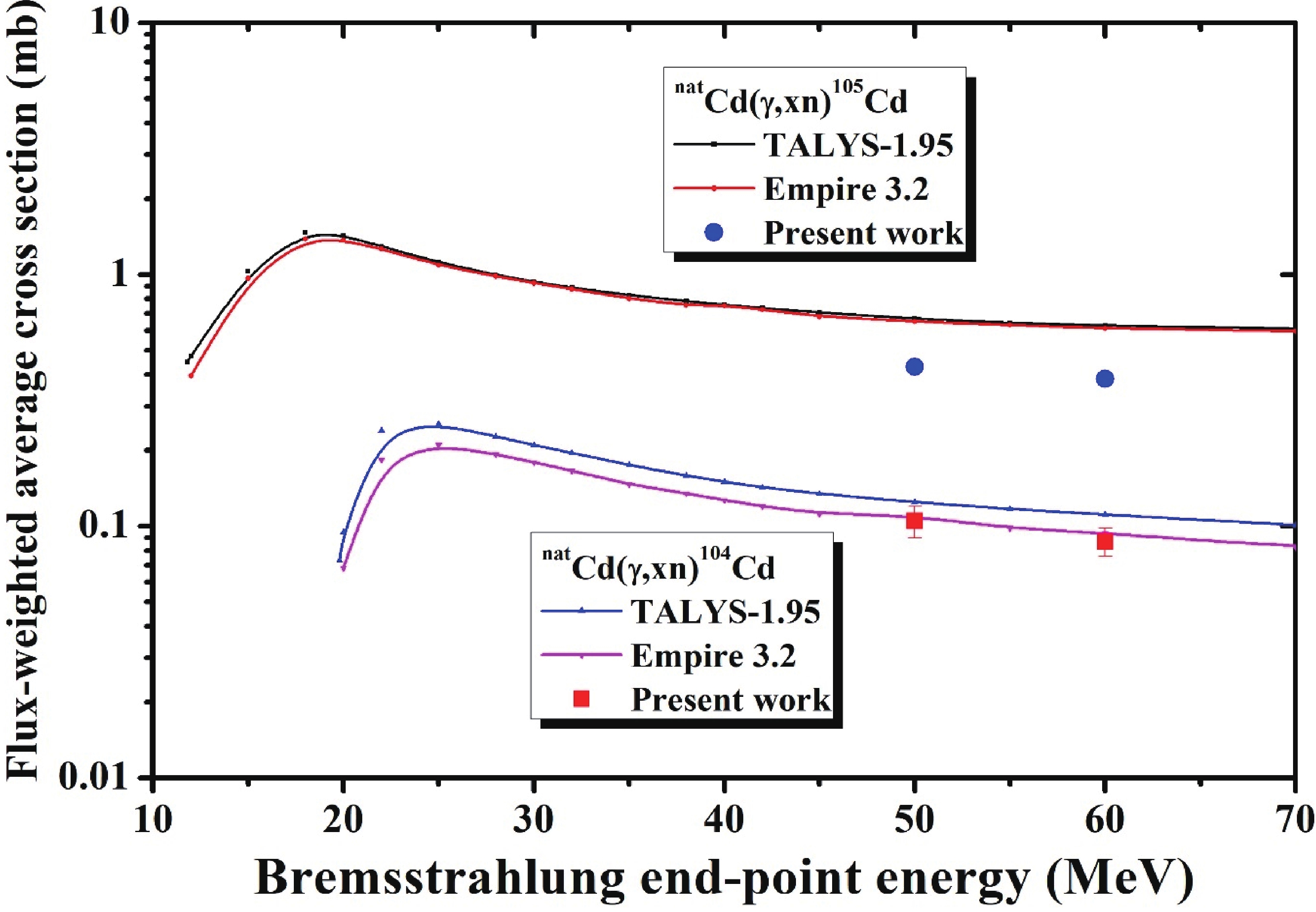
The flux-weighted average formation cross sections for 105Cd (55.5 min, 5/2+) were measured based on the independent 961.84 keV γ-line. The radioisotope (105Cd) is without an isomer. For this reaction, no literature data were available; hence, its measurements were also only compared with the theoretical calculations. In Fig. 8 and Table 4, it is clear that the flux-weighted average reaction cross sections calculated by the EMPIRE-3.2 Malta and TALYS-1.95 codes are almost the same, but they are higher than the currently presented results for the natCd(γ, xn)105Cd reaction.
-
The flux-weighted average formation cross section measurements of 104Cd (57.7 min, 0+) were also performed based onthe independent 83.5 keV γ-line. This reaction was studied for the first time and thus could only be compared with the theoretical values. In Table 4 and Fig. 8, the measured cross sections for the natCd(γ, xn)104Cd reaction are shown to be in good agreement with both calculations in terms of shape and magnitude, but they are more precisely matched with the EMPIRE-3.2 Malta calculations.
-
Radioisotopes of silver (113g,112,111g,110mAg) were formed directly through (γ, pxn) reactions. During theirdirect production, 113gAg and 111gAg were populated by their short-lived metastable states by isomeric transition (IT). Therefore, their reaction cross sections were considered as cumulative values. 112Ag has no isomer, while 110mAg has no contribution from any other radioisotope for its production; hence, their formation cross sections are exclusive and independent. Further details on silver residual nuclides are given below.
-
The deduced cumulative formation cross sections of 113gAg (5.37 h, 1/2-) include the direct production and the production through decay of the short-lived isomeric state 113mAg (62 s, 7/2+), as presented in Fig. 9 and listed in Table 4. Measurements of the natCd(γ, pxn)113gAg reaction cross sections were performed using the 298.6 keV γ-line. Moreover, it is important to note that the production probability of the meta-stable state is low due to its high spin state (7/2+); therefore, we may conclude that 113mAg has a low contribution to the cumulative formation cross section of 113gAg. The measurements from the reaction were only compared with the theoretical values due to unavailability of published data. In Fig. 9(a), it is shown that the measured values for the reaction are higher than the calculated values; however, they exhibit the same tendency as the incident photon energy increases.
-
The natCd(γ, pxn)112Ag reaction cross-sections were measured based on the 617.52 keV γ-line of 112Ag (3.13 h, 2-). This γ-line is also contributed to by 105Cd and 106mAg. However, after separating the contributions, it was found that their combined contribution to the 617.52 keV γ-line was only ~2%-3%, and thus, they were added to the photo peak area uncertainty. These measurements were only compared with the theoretical values due to unavailability of published data. In Fig. 9(b) and Table 4, the measured values are revealed to be higher than the calculated values; however, both follow a similar trend when the incident photon energy is increased. Moreover, the magnitude of the current measurements are shown to be closer to the EMPIRE-3.2 calculation than the TALYS calculation.
-
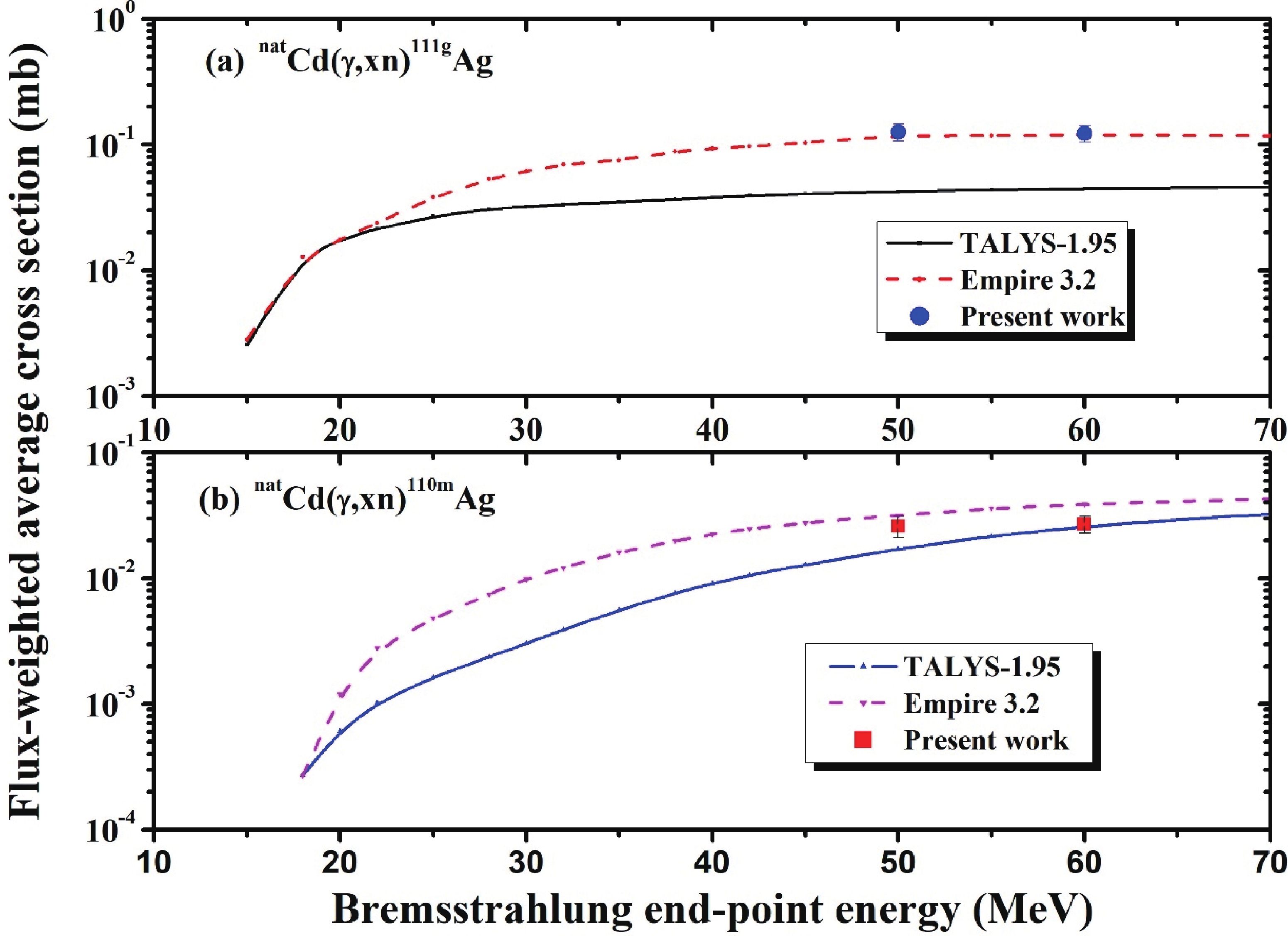
For measurements of the flux-weighted average production cross section of 111gAg (7.45 d, 1/2-), the situation is the same as in the previous case with (113gAg). It is formed directly via the (γ, pxn) reaction and through the IT (99.3%) decay of the simultaneously produced short-lived 111mAg (1.08 min, 7/2+). In this case,the nuclear spin of the metastable state is higher; hence, its production probability is lower than that of the ground state. Based on this, we may once again conclude that the cumulative cross section measurements of 111gAg have a low 111mAg decay contribution. A comparison of the present results with theoretical values is shown in Fig. 10(a) and Table 4.
-
Flux-weighted average production cross sections of 110mAg (249.83 d, 6+) were measured based on the 657.76 keV γ-line. The gamma-ray spectrum was taken after sufficient time had passed to ensure other short-lived nuclides such as 105Cd, which contaminate the 657.76 keV γ-line, had sufficiently decayed. The measured results, along with the calculated values, are shown in Fig. 10(b) and listed in Table 4. Both of the results are consistent and higher than the theoretical values but closer to the values calculated using the EMPIRE-3.2 code.
-
The production of cadmium and silver isotopes are important for medical and industrial applications and for a better understanding of their production in photon induced nuclear reactions. Therefore, the integrated yields (Bq/g.μAh) of cadmium and silver isotope productions from natCd(γ, x) reactions were measured in a procedure similar to that used for the integral yields of rhodium isotopes from the 103Rh(γ, x) reaction [19, 31]. The integral yields of cadmium and silver isotope productions from natCd(γ, x) reactions are given in Table 6.
Reaction Isotope Yields/(Bq/g·A·h) Bremsstrahlung end-point energy/MeV 50 60 natCd(γ, xn)115gCd 115gCd (8.83±0.57)×106 (8.52±0.60)×107 natCd(γ, xn)115mCd 115mCd (1.86±0.12)×106 (1.80±0.19)×107 natCd(γ, xn)111mCd 111mCd (4.48± 0.28)×106 (8.99±0.61)×107 natCd(γ, xn)109Cd 109Cd (3.62±0.26)×107 (2.49±0.21)×108 natCd(γ, xn)107Cd 107Cd (1.71±0.12)×106 (1.73± 0.12)×107 natCd(γ, xn)105Cd 105Cd (1.44±0.13)×106 (1.17±0.14)×107 natCd(γ, xn)104Cd 104Cd (1.8±0.12)×105 (1.73±0.15)×106 natCd(γ, pxn)113g+mAg 113m+gAg (1.58±0.11)×106 (1.67±0.11)×107 natCd(γ, pxn)112Ag 112Ag (7.0±0.41)×105 (8.74±0.53)×106 natCd(γ, pxn)111g+mAg 111gAg (3.3±0.24)×105 (3.55±0.32)×106 natCd(γ, pxn)110mAg 110mAg (6.0±0.65)×104 (5.6±0.40)×105 Table 6. Integral isotopic yield of different products from the natCd(γ, xn) and natCd(γ, pxn) reactions.
-
The flux-weighted average photon induced nuclear reaction cross-sections for the natCd(γ, xn; x=1-6)115g,m,111m,109,107,105,104Cd and natCd(γ, xnyp; y=1 x=1-5)113g,112,111g,110mAg reactions as well as the isomeric yield ratios of 115g,mCd in the 116Cd(γ, n) reaction were measured with the bremsstrahlung end-point energies of 50- and 60- MeV. Integral yield was also measured to assess the activities produced in the nuclear reactions. The photon induced formation reaction cross sections of natCd and the IR value of 115Cd were calculated using the TALYS-1.95 and EMPIRE-3.2 codes and the evaluated data taken from the TENDL-2019 library. In most of the cases, calculated values from the TALYS and EMPIRE codes matched each other and the experimental value. It was also found that the flux-weighted average cross sections increased sharply in the GDR region due to photo absorption and then decreased slightly in QDR region due to the opening of particle emission reaction channels. The isomeric yield ratio of 115g,mCd in the 116Cd(γ, n) reaction from this study and previously published data was compared with literature data for the 116Cd(n, 2n) reaction. It was found that the experimental IR values of 115g,mCd in the natCd(γ, xn) reaction agree with the calculations but were well below the IR values due to the 116Cd(n, 2n) reaction. The isomeric yield ratio previously measured in the 116Cd(n, 2n) reaction was lower than the calculated values for the same reaction; this is most likely due to the use of default parameters in the theoretical calculations. It was also observed that the theoretical and experimental values increased with excitation energy. However, at the same excitation energy, the IR values in the 116Cd(n, 2n) reaction were significantly higher than those in the 116Cd(γ, n) reaction due to the higher spin of the compound nucleus in the former. This indicates the role of compound nucleus spin alongside the effect of excitation energy.
-
The authors express their sincere thanks to the staff of the Pohang Accelerator Laboratory (PAL), Pohang, Korea, for the excellent operation and their support during the experiment.
Measurements of natCd(γ, x) reaction cross sections and isomer ratio of 115m,gCd with the bremsstrahlung end-point energies of 50 and 60 MeV
- Received Date: 2021-07-07
- Available Online: 2021-12-15
Abstract: The flux-weighted average cross sections of natCd(γ, xn)115g,m,111m,109,107,105,104Cd and natCd(γ, x)113g,112,111g,110mAg reactions were measured at the bremsstrahlung end-point energies of 50 and 60 MeV. The activation and off-line γ-ray spectrometric technique was carried out using the 100 MeV electron linear accelerator at the Pohang Accelerator Laboratory, Korea. The natCd(γ, xn) reaction cross sections as a function of photon energy were theoretically calculated using the TALYS-1.95 and the EMPIRE-3.2 Malta codes. Then, the flux-weighted average cross sections were obtained from the theoretical values of mono-energetic photons. These values were compared with the flux-weighted values from the present study and were found to be in general agreement. The measured experimental reaction cross-sections and integral yields were described for cadmium and silver isotopes in the natCd(γ, xn)115g,m,111m,109,107,105,104Cd and natCd(γ, x)113g,112,111g,110mAg reactions. The isomeric yield ratio (IR) of 115g,mCd in the natCd(γ, xn) reaction was determined for the two bremsstrahlung end-point energies. The measured isomeric yield ratios of 115g,mCd in the natCd(γ, xn) reaction were also compared with the theoretical values of the nuclear model codes and previously published literature data of the 116Cd(γ, n) and 116Cd(n, 2n) reactions. It was found that the IR value increases with increasing projectile energy, which demonstrates the characteristic of excitation energy. However, the higher IR value of 115g,mCd in the 116Cd(n, 2n) reaction compared to that in the 116Cd(γ, n) reaction indicates the role of compound nuclear spin alongside excitation energy.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: