-
Pseudospin symmetry (PSS), discovered in 1969, is an important phenomenon in nuclear physics, which is physically related to the shell model. In 1949, the spin-orbit potential was introduced by Mayer and Jensen [1, 2], respectively, which led to the correct reproduction of magic numbers and the establishment of the famous nuclear shell model. Twenty years later, quasi-degeneracy was observed in heavy nuclei between single-nucleon partners with quantum numbers
$ (n,l,j = l+1/2) $ and$ (n-1, l+2, j = l +3/2) $ , where$ n,l,j $ are the radial, orbital, and total angular momentum quantum numbers, respectively [3, 4]. The quasi-degenerate partners were suggested as the pseudospin partners$ (\tilde n = n,\tilde l = l+1,j = \tilde l\pm1/2) $ , which has been discussed in a number of phenomena in nuclear structure, including nuclear superdeformed configurations [5], identical bands [6], quantized alignment [7], pseudospin partner bands [8], magnetic moments and transitions [9], and γ-vibrational states in nuclei [10], as well as nucleon-nucleus and nucleon-nucleon scatterings [11]. Moreover, the role of PSS in the structure of halo nuclei [12] and superheavy nuclei [13] was studied in detail.Although the discovery of PSS has attracted the attention of physicists, its origin and destroying mechanism have not yet been clarified. Based on the shell model of harmonic oscillator potential, Bahri et al. [14] pointed out that the special ratio between the intensity of the spin-orbit interaction and the intensity of the orbit-orbit interaction is the reason for PSS, and this ratio can be explained by the relativistic mean field (RMF) theory [15]. Blokhin et al. [16] showed that the normal state can be transformed into the pseudospin state (
$ \tilde l $ ,$ \tilde s $ ) by a spiral unitary transformation. Using the RMF theory, in 1997, Ginocchio [17] presented PSS as a relativistic type of symmetry by solving the Dirac equation describing a spherical nucleus. Additionally, the conditions for strict PSS are that the sum of scalar potential S and vector potential V in the Dirac equation is zero, and pseudoorbital angular momentum$ \tilde l $ is the orbital angular momentum in the spin of the Dirac wave function. Subsequently, Meng et al. [18] proposed a more general strict symmetry condition, i.e.,$ \Sigma = S + V = constant $ , and indicated that the PSS in a real nucleus is related to the pseudocentrifugal barrier (PCB) and pseudospin-orbital coupling potential (PSOP). Since then, some progress has been made on PSS in various systems, including extensions of the PSS study from stable to exotic nuclei [19], from bound to resonant states [20], from nucleon to anti-nucleon spectra [21], from nucleon to hyperon spectra [22], and from spherical to deformed nuclei [23, 24]. More detailed progress on PSS can be found in literature reviews [25, 26].In recent years, there has been an increasing interest in the exploration of continuum and resonant states, especially in studies of exotic nuclei with unusual N/Z ratios. Considering that exotic nuclei are weakly bound and their Fermi surfaces are very close to the continuum threshold, the continuum, especially the resonances in the continuum, play a key role in the formation of these exotic phenomena [27, 28]. For this reason, many methods were developed for nuclear single-particle resonances; these include the scattering phase shift method [29], Jost function method [30, 31], Green's function method [32-35], analytic continuation in the coupling constant (ACCC) method [36-38], real stabilization method [39, 40], and complex scaling method [41, 42].
Based on these methods, the PSS in single-particle resonant states have been studied. In Ref. [20], the PSS for the resonant states in
$ ^{208} $ Pb is investigated by solving the Dirac equation with Woods-Saxon vector and scalar potentials in combination with the ACCC method. In Ref. [43], the RMF theory is combined with the ACCC method to determine the energies and widths of single-particle resonant states in the Sn isotopes, and an isospin dependence of PSS is clearly shown in the resonant states. In Ref. [44], the PSS in the single-proton resonant states in$ ^{120} $ Sn is discussed by examining the energies, widths, and wavefunctions. In 2012, Lu et al. gave a rigorous verification of PSS in single-particle resonant states [30]. In 2013, we applied the complex scaling method to study the resonances and PSS in the Dirac-Morse potential [45]. In 2019, Sun et al. investigated the spin and pseudospin symmetry in single-particle resonant states by solving the Dirac equation containing a Woods-Saxon potential with Green's function method [46].Based on these theories, numerous excellent studies have been conducted. The complex momentum representation (CMR) is also an effective method to study the PSS in resonant states. Considering that the RMF is one of the most successful microscopic theoretical models, which has been widely used to study weakly bound nuclei [15, 26, 27, 47-49], we proposed a new scheme in 2016 [50] to explore the resonances in the RMF framework, where the Dirac equation is directly solved in the complex momentum representation and the bound and resonant states are dealt with equally. By using the newly developed method, we obtained, not only narrow resonance, but also wide resonance that was difficult to obtain before, and the physical mechanism of halo structure in some exotic nuclei [51-54] was proposed. Recently, based on the RMF-CMR method, we investigated PSS in single-particle resonant states and its isospin dependence [55].
In 2010, within the framework of the RMF theory [56], we obtained detailed knowledge on the contribution of different fields of mesons to pseudospin energy splitting in the single-particle bound state. However, for resonant states, the influence of different fields of mesons on PSS has not been examined in detail for real nuclei. By using the RMF-CMR method [50], we can extract the splitting of the energies, widths, and wavefunctions between the single-neutron resonant pseudospin partners and check the contribution of the different fields of mesons to pseudospin splitting, which is our original purpose for writing this article. We will show the theoretical framework in Sec. II, the detailed calculation results and data analysis in Sec. III, and, finally, a summary in Sec. IV.
-
In order to study the resonant partners in
$ ^{208} $ Pb, the formalism of RMF-CMR is introduced. The basic assumption of the RMF theory is that the Lagrangian density of this system is obtained through the exchange and interaction of various mesons and photons.$ \begin{aligned}[b] \mathcal{L} =& \bar{\psi}\left({\rm i} \gamma_{\mu} \partial^{\mu}-M\right) \psi+\frac{1}{2} \partial_{\mu} \sigma \partial^{\mu} \sigma-U(\sigma)-\frac{1}{4} \Omega_{\mu \nu} \Omega^{\mu v} \\& +\frac{1}{2} m_{\omega}^{2} \omega_{\mu} \omega^{\mu}-\frac{1}{4} \vec{R}_{\mu v} \vec{R}^{\mu v}+\frac{1}{2} m_{\rho}^{2} \vec{\rho}_{\mu} \vec{\rho}^{\mu}-\frac{1}{4} F_{\mu v} F^{\mu v} \\ &-\bar{\psi}\left(g_{\sigma} \sigma+g_{\omega} \gamma_{\mu} \omega^{\mu}+g_{\rho} \gamma_{\mu} \vec{\tau} \vec{\rho}^{\mu}+e \gamma_{\mu} A^{\mu}\right) \psi, \end{aligned} $

(1) where M is the nuclear mass,
$ {m_\sigma }({g_\sigma }),{m_\omega }({g_\omega }),{m_\rho }({g_\rho }) $ are the mass and coupling constants of different mesons, respectively, and the non-linear couplings of$ \sigma $ read as$ U(\sigma ) = \dfrac{1}{2}m_\sigma ^2{\sigma ^2} + \dfrac{1}{3}{g_2}{\sigma ^3} + \dfrac{1}{4}{g_3}{\sigma ^4} $ . Based on the Lagrangian density, the Dirac equation can be obtained as follows:$ [\vec{\alpha} \cdot \vec{p}+\beta(M+S)+V] \psi_{i} = \varepsilon_{i} \psi_{i}, $

(2) where S is the scalar potential and V is the vector potential. The expression is as follows:
$ \left\{ \begin{array}{l} S(\vec{r}) = g_{\sigma} \sigma(\vec{r}) ,\\ V(\vec{r}) = g_{\omega} \omega^{0}(\vec{r})+g_{\rho} \tau_{3} \rho^{0}(\vec{r})+e A^{0}(\vec{r}). \end{array} \right. $

(3) For convenience, here we express
$ {g_\sigma }\sigma (\vec r) $ ,$ {g_\omega }{\omega ^0}(\vec r) $ , and$ {g_\rho }{\tau _3}{\rho ^0}(\vec r) $ as$ {V_\sigma }(\vec r) $ ,$ {V_\omega }(\vec r) $ , and$ {V_\rho }(\vec r) $ .In order to obtain the resonant states, we rewrote Eq. (2) into an equation representing momentum space, and we can obtain the bound states, resonant states, and continuous spectrum simultaneously
$ \int {\rm d} \vec k'\langle \vec k|H|\vec k'\rangle \psi (\vec k') = E\psi (\vec k), $

(4) where
$ H = \vec{\alpha} \cdot \vec{p}+\beta(M+S(\vec{r}))+V(\vec{r}) $ . In the case of spherical nuclei, the momentum wave function can be expressed by upper and lower components$ \psi(\vec{k}) = \left(\begin{array}{l} f(k) \phi_{l j m_{j}}\left(\Omega_{k}\right) \\ g(k) \phi_{\tilde{l} j m_{j}}\left(\Omega_{k}\right) \end{array}\right). $

(5) By separating the angular part and bringing the radial part into Eq. (2), the Dirac equation can be expressed as
$ \left\{ \begin{array}{l} M f(k)-k g(k)+\int k^{\prime 2} {\rm d} k^{\prime} V_+\left(k, k^{\prime}\right) f\left(k^{\prime}\right) = \varepsilon f(k) ,\\ -k f(k)-M g(k)+\int k^{\prime 2} {\rm d} k^{\prime} V_-\left(k, k^{\prime}\right) g\left(k^{\prime}\right) = \varepsilon g(k) ,\end{array} \right.$

(6) with
$ V_+\left(k, k^{\prime}\right) = \frac{2}{\pi} \int r^{2} {\rm d} r \Sigma(r) j_{l}\left(k^{\prime} r\right) j_{l}(k r), $

(7) $ V_-\left(k, k^{\prime}\right) = \frac{2}{\pi} \int r^{2} {\rm d} r \Delta(r) j_{\tilde l}\left(k^{\prime} r\right) j_{\tilde l}(k r), $

(8) where
$ {\Sigma}(r) = V(r)+S(r) $ ,$ {\Delta} (r) = V(r)-S(r) $ .The bound and resonant states can be obtained by solving the above equations.
$ \left\{ \begin{array}{l} f(r) = i^{l} \sqrt{\dfrac{2}{\pi}} \int k^{2} {\rm d} k j_{l}(k r) f(k) ,\\ g(r) = i^{\tilde l} \sqrt{\dfrac{2}{\pi}} \int k^{2} {\rm d} k j_{\tilde l}(k r) g(k). \end{array} \right. $

(9) Finally, according to the Eq. (9), the upper and lower component wave functions can be transformed into coordinate space for processing, and the details of the solution process can be seen in Ref. [50].
-
Based on the formalism presented earlier, we explored the single-neutron resonant states and their pseudospin for
$ ^{208} $ Pb. The interactions were adopted as the NL3 parameters [57]. In the calculations, the single-neutron energies and wavefunctions for bound states and resonances can be obtained, and, for resonances, we can calculate their widths simultaneously. The single neutron spectrum in$ ^{208} $ Pb in the form of pseudospin partners according to pseudoangular momentum$ {\tilde l} $ are displayed in Fig. 1 with the corresponding$ \Sigma(r) $ potential. In the single-neutron resonant states, three pairs of pseudospin partners were found as$ 2{\tilde g} $ ,$ 1{\tilde i} $ , and$ 1{\tilde j} $ , respectively. Fig. 1, it can be seen that for the the pseudospin partners with pseudoangular momentum$ {\tilde l}>0 $ , there is always a state without a pseudospin partner called intruder states. The appearance of intruder states can be explained by examining the zeros in Jost functions [31]. In addition, these intruder states can also be explained by the method of supersymmetric quantum mechanics [58-61]. We also notice that pseudospin partners have a clear threshold effect; for example, pseudospin partners$ 3{\tilde p} $ ,$ 2{\tilde f} $ ,$ 2{\tilde g} $ ,$ 1{\tilde h} $ , and$ 1{\tilde i} $ are very close to the continuum threshold and the energy splitting between them are less than 1 MeV. The pseudospin partners near the zero potential energy surface tend to show better symmetry, and hence, the study of symmetry in this area becomes more interesting.
Figure 1. (color online) Pseudospin partners of the single-neutron spectra in
$ ^{208} $ Pb with the RMF-CMR method. The line is the mean-field potential$ \Sigma(r) $ for neutrons.When
$ {\rm d}{\Sigma}/{\rm d}r = 0 $ , the system presents exact pseudospin symmetry [18]. Unfortunately, the condition is not satisfied in a realistic system. For the$ ^{208} $ Pb examined in this study, we have seen that exact pseudospin symmetry cannot be achieved, as discussed using Fig. 1. Pseudospin splitting is either large or small, but it can not be zero; hence, exploring the pseudospin splittiing will help to understand the character of this system. In order to check the pseudospin splitting induced by the different fields of mesons, we set$ {V_X}(\vec r) \to {\lambda _X}V(\vec r) $ to investigate the dependencies of the energy, width, and wavefunction splitting of resonant pseudospin partners on the coupling constant$ \lambda _X $ , where X denotes$ \sigma $ ,$ \omega $ , and$ \rho $ , respectively. We performed the RMF-CMR calculations to obtain the variation of$ \Sigma(r) $ potential under different meson fields, which is displayed in Fig. 2. It is revealed that the$ \Sigma(r) $ potential of subfigures (a) and (b) clearly changes, while the$ \Sigma(r) $ potential of subfigures (c) and (d) has a small range of variation with coefficient. In Fig. 2(a), with the increase in$ \lambda _{\sigma} $ from 0.96 to 1.04, the depth of the potential decreases monotonically and the surface of the potential moves outwards. From Fig. 2(b), we can see that the variation of$ \Sigma(r) $ potential with$ \lambda _{\omega} $ is completely opposite to that in Fig. 2(a), that is, with an increase in$ \lambda _{\omega} $ , the depth of the potential increases monotonically and the surface of the potential moves inwards. To further explore the competitive relationship between the$ {\sigma} $ -field and the$ {\omega} $ -field, we fixed the coefficient of the$ {\rho} $ -field, and uniformly changed the strength of the$ {\sigma} $ and$ {\omega} $ fields. We can clearly see that the change in$ \Sigma(r) $ potential is very small in Fig. 2(c), which confirms that the effect of the$ {\sigma} $ -field and$ {\omega} $ -field on potential is opposite, and the degree is almost identical. Considering that the$ \Sigma(r) $ potential does not clearly change with$ \lambda _{\rho} $ , we extended the range of$ \lambda _{\rho} $ from 0.6 to 1.4. Even so, we can see from Fig. 2(d) that the change in$ \Sigma(r) $ is not obvious, and the$ \Sigma(r) $ gradually becomes slightly shallow and the surface of the potential moves a little inwards, which indicates that the$ {\rho} $ -meson field has little influence on$ \Sigma(r) $ potential.
Figure 2. (color online) The change of neutron
$ \Sigma(r) $ potential when the intensity of the meson field is changed under different meson fields.To demonstrate the evolution of PSS in resonant states, we analyzed the dependence of pseudospin splittings on the meson field strengths. Keeping
$ \lambda _{\omega} $ and$ \lambda _{\rho} $ fixed at 1.0, we varied$ \lambda _{\sigma} $ in order to see how the energies and widths of the pseudospin partners were sensitive to the strength of the$ {\sigma} $ -field. This dependence is shown in Fig. 3, where the open and filled marks represent the resonant and bound partners, respectively. With an increase in$ \lambda _{\sigma} $ , the$ {\Sigma} $ potential well becomes deeper, and some single-neutron resonant states evolve into bound states. Since the relationship between the pseudospin energy splitting of the bound partners and the strength of the meson field has been discussed in detail in Ref. [56], the variation trend of the resonant pseudospin splitting with the strength of the meson field is the focus of this paper. It can be seen from Fig. 3 that, for a given$ \lambda _{\sigma} $ , the energy and width splitting between the different pseudospin partners is different for different pseudospin partners, with no exceptions. It shows that PSS is correlated with the quantum numbers of single-neutron states and preserves a dynamic character as reported in Refs. [20, 43, 62, 63] for bound states and resonances. From Fig. 3(a), for all the pseudospin partners$ (2g_{9/2},1i_{11/2}) $ ,$ (2h_{11/2},1j_{13/2}) $ ,$ (2i_{13/2},1k_{15/2}) $ ,$ (3d_{5/2},2g_{7/2}) $ , and$ (3f_{7/2},2h_{9/2}) $ , the pseudospin energy splittings' tendency to change with$ \lambda _{\sigma} $ is in agreement with the case of bound states [56]. As$ \lambda _{\sigma} $ increases, the energy splittings of all the resonant pseudospin partners decrease monotonously. The same trend is found in Fig. 3(b) for width variation with increasing$ \lambda _{\sigma} $ . For example, the energy splitting of$ (2g_{9/2},1i_{11/2}) $ at$ {\lambda _\sigma } = 0.9 $ is 6 times that of$ {\lambda _\sigma } = 0.98 $ , and the width splitting of$ (2g_{9/2},1i_{11/2}) $ at$ {\lambda _\sigma } = 0.9 $ is 10 times that of$ {\lambda _\sigma } = 0.96 $ .
Figure 3. (color online) The variation of energy splitting and width splitting of pseudospin partners with
$ {\sigma} $ meson field intensity in$ ^{208} $ Pb. The open and filled marks represent the resonant and bound partners, respectively.In addition, the evolution of splitting is almost identical for the different resonant pesudospin partners, and does not present a connection with the quantum numbers of partners, which is different from that of the bound pesudospin partners [56]. By comparing the variation of splitting with
$ {\lambda _\sigma } $ for the partners with fixed$ {\tilde n} $ , the sensitivity of energy and width splitting to$ {\lambda _\sigma } $ can be disclosed. For example, the energy and width splittings between the$ (2h_{11/2},1j_{13/2}) $ partner was almost the same as that between the partner$ (2i_{13/2},1k_{15/2}) $ with the coupling constant$ {\lambda _\sigma } $ increasing from 0.98 to 1.02. In Ref. [56], the dependence of level inversion on$ {\lambda _\sigma } $ is seen for several bound partners, but such a situation does not happen in the resonant partners. The occurrence of this phenomenon is related to pseudocentrifugal barrier and the pseudospinorbital potential [18]. The pseudospin partners in a resonance state near the Fermi surface, which have better symmetry. The splitting between different pseudospin partners becomes smaller and, with increasing$ {\lambda _\sigma } $ , for all the resonant partners,$ \Delta E = {E_{n,l,j = l + 1/2}} - $ $ {E_{n - 1,l + 2,j = l + 3/2}} $ is always less than 0 and$ \Delta \Gamma = {\Gamma _{n,l,j = l + 1/2}}- $ $ {\Gamma _{n - 1,l + 2,j = l + 3/2}} $ remains positive over the range of$ {\lambda_\sigma} $ considered here. All these indicate that the$ {\sigma} $ meson field plays an important role in influencing the PSS of resonant partners. As far as this conclusion is concerned, it is similar to that in bound partners.A similar trend was observed when we varied
$ {\lambda _\omega } $ and fixing all other coupling constants. The results are shown in Fig. 4. From Fig. 4(a), the pseudospin splittings' tendency to change with$ {\lambda _\omega } $ is consistent with the case of bound states [56]. When$ {\lambda _\omega } $ increases, the energy splitting dramatically increases for all the resonant partners . The same trend is found in Fig. 4(b) for width variation except for$ (2h_{11/2},1j_{13/2}) $ with$ {\lambda _\sigma } $ increasing from 1.08 to 1.1. It can be found that the energy splitting of$ (2h_{11/2},1j_{13/2}) $ at$ {\lambda _\omega } = 1.1 $ is 31 times that of$ {\lambda _\omega } = 0.96 $ , and the width splitting of the$ (2h_{11/2},1j_{13/2}) $ partners at$ {\lambda _\omega } = 1.1 $ is 31 times that of$ {\lambda _\omega } = 0.96 $ . Compared with the$ {\sigma} $ -field, the splitting develops toward the opposite direction, but the sensitivity of the splitting to the coupling constant is similar, which shows that the$ {\sigma} $ and$ \omega $ fields have an opposite contribution to the PSS. These differences can be understood by the shape of the$ \Sigma(r) $ potential given in Figs. 1(a) and 1(b). Further, the inversion of energy splitting can be seen for the partner$ (2i_{13/2},1k_{15/2}) $ . With increasing$ {\lambda _\omega } $ , the pseudospin energy splitting varies from$ {E_{n,l,j = l + 1/2}} > {E_{n - 1,l + 2,j = l + 3/2}} $ to$ {E_{n,l,j = l + 1/2}} < $ $ {E_{n - 1,l + 2,j = l + 3/2}} $ , which is similar to Ref. [64]. All of these indicate that the$ {\omega} $ -field also plays a significant role in influencing the PSS for resonant partners.
Figure 4. (color online) The variation of energy splitting and width splitting of pseudospin partners with
$ {\omega} $ meson field intensity in$ ^{208} $ Pb. The open and filled marks represent the resonant and bound partners, respectively.In reality, from Fig. 3 and Fig. 4, we found that
$ {\lambda _\sigma } $ and$ {\lambda _\omega } $ are not completely independent parameters. When equally varying the strength of the$ {\sigma} $ and$ {\omega} $ fields, the variations of pseudospin energy and width splitting are very small, as shown in Fig. 5. The results show that the$ {\sigma} $ -field contribution to the pseudospin energy and width splitting has nearly the same magnitude as the one obtained by the$ {\omega} $ -field, but is opposite in sign. This can be clarified from the change in shape of the$ \Sigma(r) $ potential given in Fig. 1(c).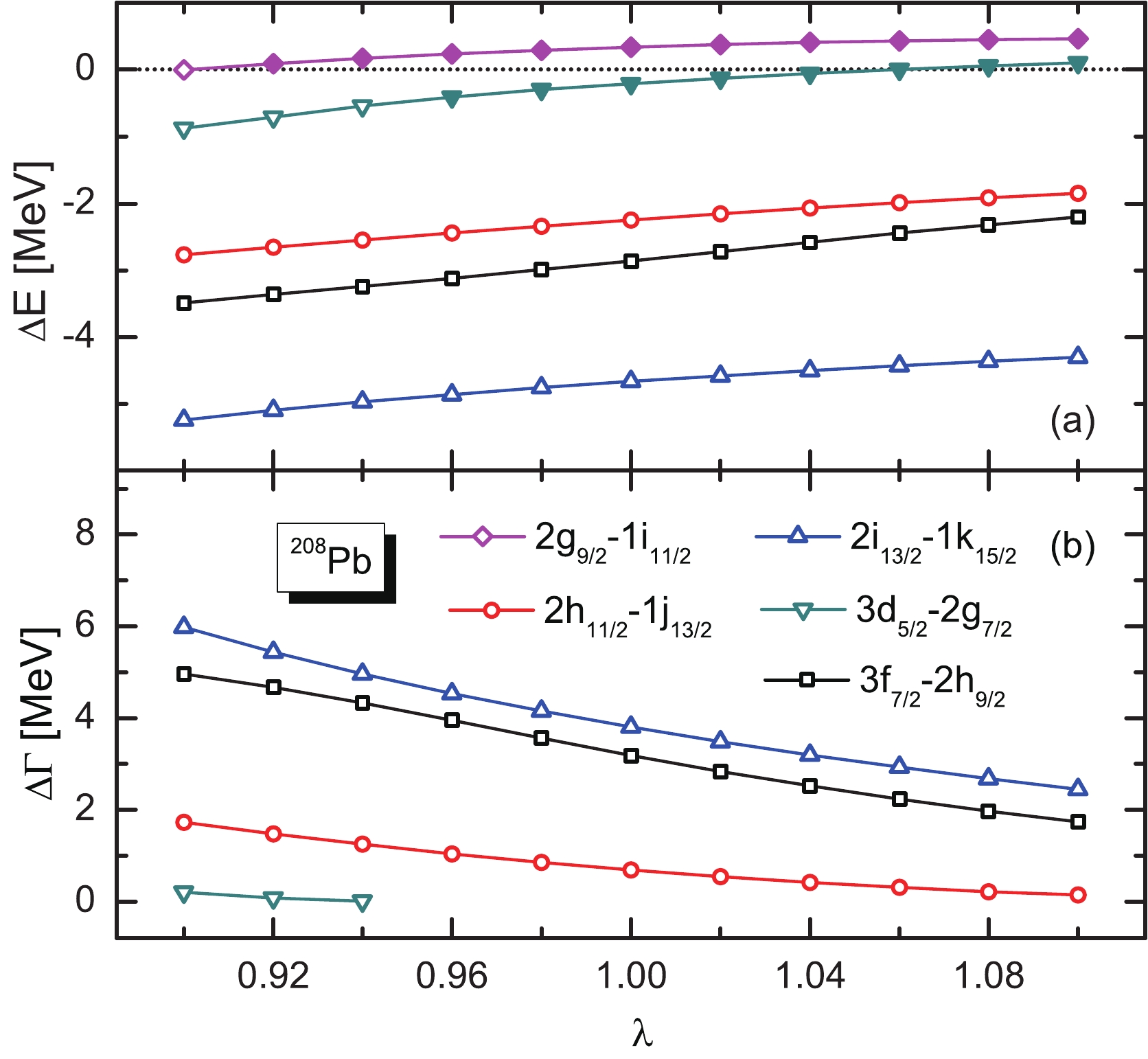
Figure 5. (color online) The variation of energy splitting and width splitting of pseudospin partners with
${\sigma}$ meson field intensity in$^{208}$ Pb. The open and filled marks represent the resonant and bound partners, respectively.Finally, we kept
$ {\lambda _\sigma } $ and$ {\lambda _\omega } $ fixed at 1 but varied$ \lambda_\rho $ in order to study the sensitivity of the resonant pseudospin partners to the strength of the$ \rho $ -field. The results are presented in Fig. 6 and the following behavior is observed: as$ \lambda_\rho $ increases, the energy and width splitting slowly increases. Such characteristics are consistent with the case of bound states [56], which can be explained by Fig. 2(d). It is noted that the the coupling constant$ {\lambda _\rho} $ in Fig. 6 varies from 0.0 to 2.0, that is, compared with$ {\lambda _\sigma } $ and$ {\lambda _\omega } $ , the value range of$ {\lambda _\rho} $ has been expanded. In contrast with the$ {\sigma} $ and$ {\omega} $ fields, the energy splitting is less sensitive to the$ \rho $ -field. For example, from Fig. 6(a), the energy splitting of the$ (3f_{7/2}, 2h_{9/2}) $ partner is only reduced by 1.8 MeV from$ {\lambda _\rho } = 0.0 $ to$ {\lambda _\rho } = 2.0 $ . In Fig. 6 (b), with an increasing$ \lambda_\rho $ , the width splitting also increases slowly and its variation range is small, which is similar to the evolution of energy splitting. The increase in width splittings in the$ (2h_{11/2},1j_{13/2}) $ partner and$ (3d_{5/2},2g_{7/2}) $ partner is less than 1 MeV with$ \lambda _\rho $ changing from 0 to 2.0. For the resonant partners$ (3f_{7/2},2h_{9/2}) $ and$ (2i_{13/2},1k_{15/2}) $ , the width splitting increases slightly, but the increasing scope is far smaller than that by the$ {\sigma} $ and$ \omega $ fields. These result indicate that the$ \rho $ -field only provides a minor contribution to PSS, and the PSS comes mainly from the cancellation of the$ {\sigma} $ and$ {\omega} $ fields.
Figure 6. (color online) The variation of energy splitting and width splitting of pseudospin partners with
$ {\rho} $ meson field intensity in$ ^{208} $ Pb. The open and filled marks represent the resonant and bound partners, respectively.So far, the effect has not been examined on the wavefunction. As PSS is a relativistic type of symmetry, the wave functions of pseudospin partners satisfy certain relations. According to the PSS limit [17], the lower component wave functions of pseudospin partners are completely consistent. In real nuclei, the lower component wave functions of pseudospin partners are very similar, which have been tested for the bound partners in both spherical and deformed nuclei [23, 65-68]. There have been discussions on the pseudospin symmetry of wave function for resonant partners [44, 46, 55], but these discussions on PSS were only based on intuitive judgments of wave function similarity in the coordinate space in a finite range. They cannot provide quantitative results on the degree of wave function similarity since the resonant states are non-local and their wave functions are divergent in the coordinate space. Hence, it is difficult to compare the similarity of wave functions in the coordinate space. Just like the real parts of the wave functions for
$ (2h_{11/2}, 1j_{13/2}) $ in Fig. 7. With the increase in radius, the resonant wave functions are diffused. Whether the wave functions for resonant partners will have similar features at large radii becomes unclear.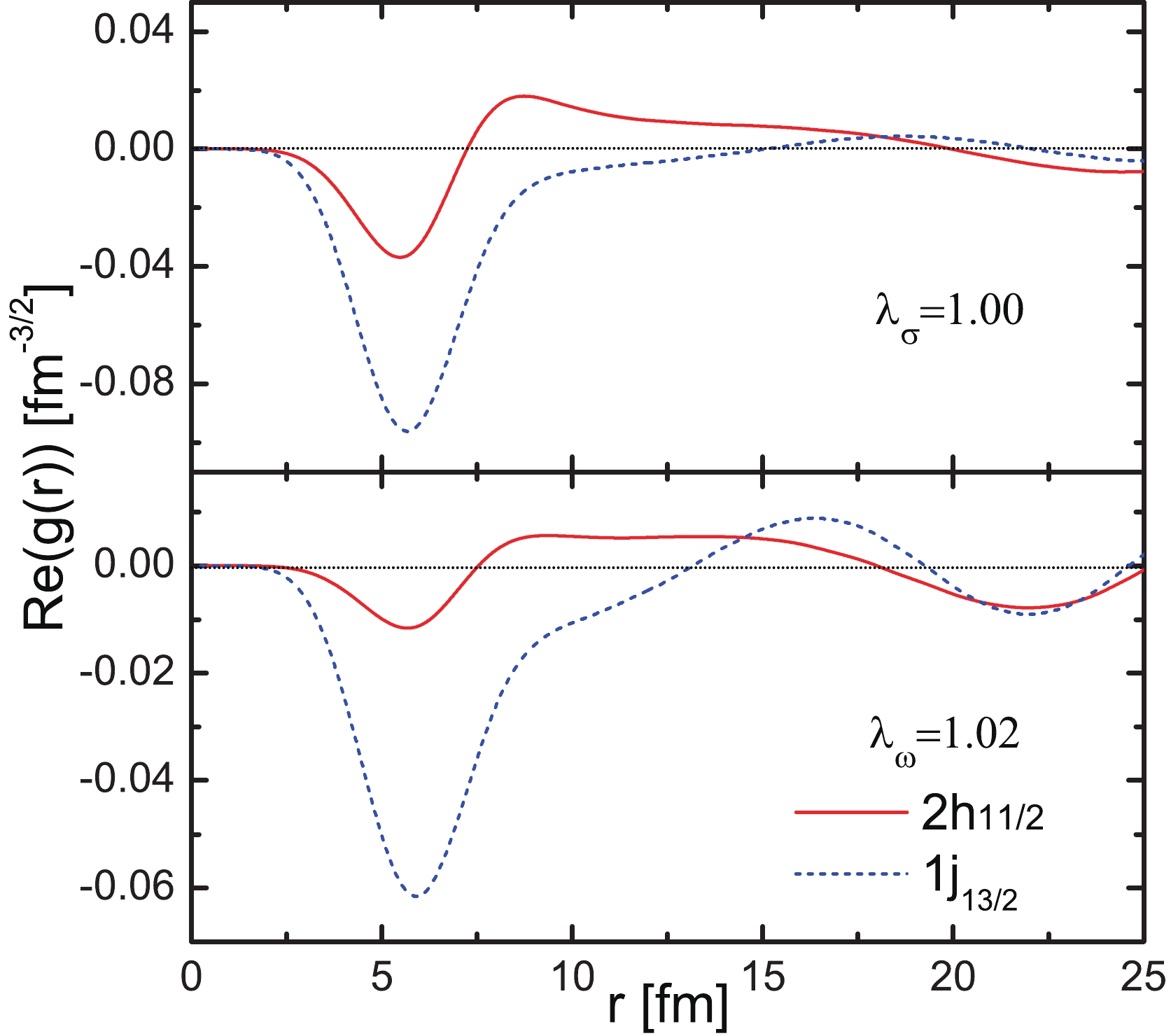
Figure 7. (color online) Real parts of the lower components of Dirac spinors for the pseudospin partner
$(2h_{11/2}, 1j_{13/2})$ in the coordinate space.However, for a better understanding of the conditions of PSS, we checked the influences from different fields of mesons. According to Heisenberg's uncertainty relation, the wave functions of resonant states in the momentum space are local and square integrable. It was appropriate to compare the pseudospin similarity of wave functions in the momentum representation and it was especially convenient to quantitatively obtain the pseudospin splittings of wave functions in the momentum space. The real parts of the lower components of wave functions for the resonant pseudospin partners
$ (2h_{11/2}, 1j_{13/2}) $ with the different fields of mesons are displayed in Figs. 8-11. The splitting of wave functions between the partners is defined as
Figure 8. (color online) Real parts of the lower components of Dirac spinors for the pseudospin partner
$ (2h_{11/2}, 1j_{13/2}) $ in the momentum space with several different parameters of the$ {\sigma} $ meson field.
Figure 9. (color online) The same as Fig. 8, but for the
${\omega}$ meson field.
Figure 10. (color online) The same as Fig. 8, but with uniform strength of the
${\sigma}$ meson field and the${\omega}$ meson field.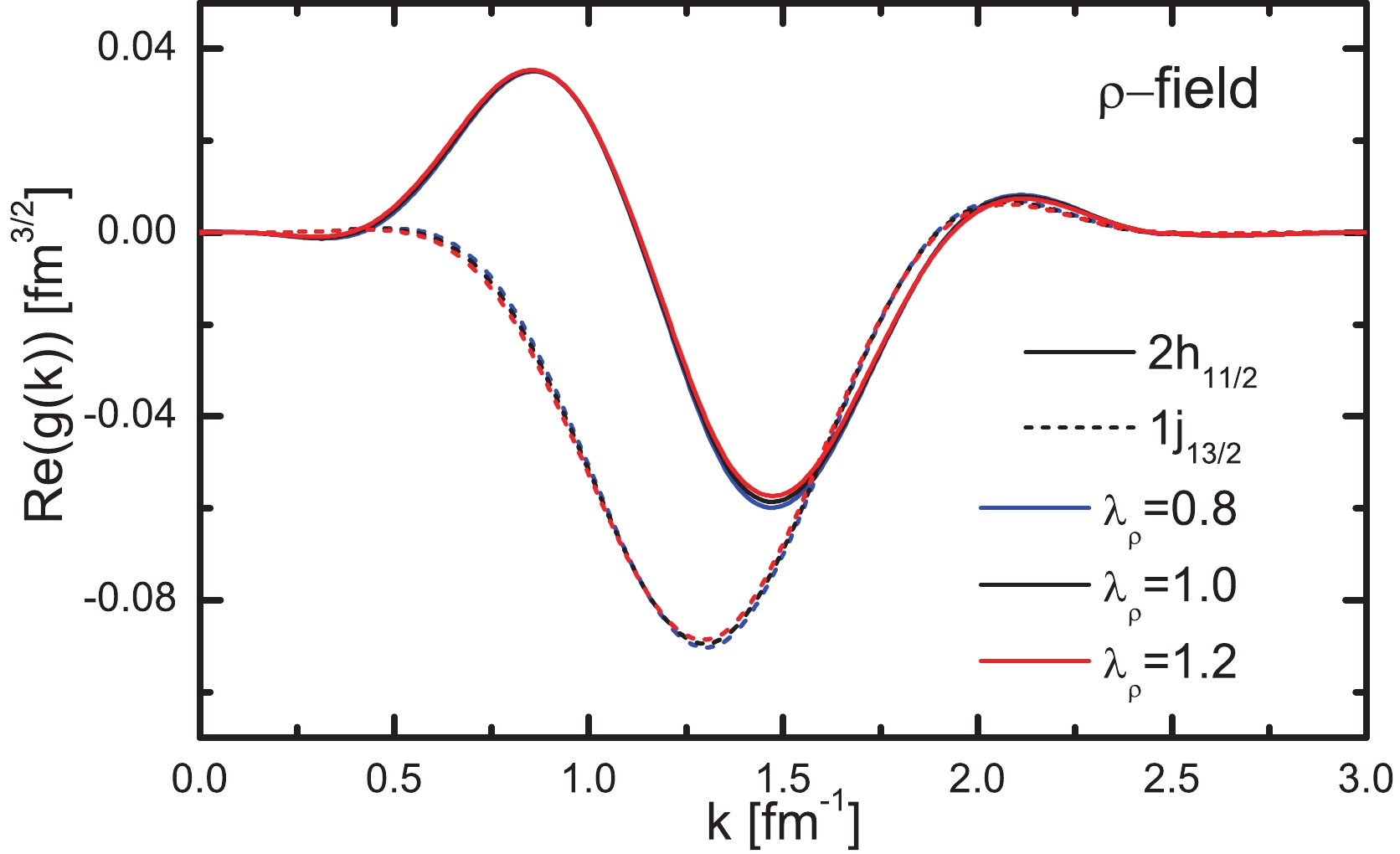
Figure 11. (color online) The same as Fig. 8, but for the
$ {\rho} $ meson field.$ \Delta G = \int_{0}^{\infty}\left|k^{2}\left[g_{a}(k)-g_{b}(k)\right]^{2}\right| {\rm d}k, $

(10) where
$ g_{a}(k) $ and$ g_{b}(k) $ are the lower components of Dirac spinors in the momentum space.Real parts of the lower components of Dirac spinors for the resonant pseudospin partner
$ (2h_{11/2}, 1j_{13/2}) $ with several different values of$ {\lambda _\sigma } $ are plotted in Fig. 8. Similar to the wave functions in coordinate space, the wave function of$ 1j_{13/2} $ is below the$ 2h_{11/2} $ in the momentum space. Moreover, with the increase of k, the wave function gradually moves away from the origin. When k increases to$ 2.5\;{\rm fm}^{-1} $ , all the wave functions return to the horizontal axis, indicating that those are convergent. From Fig. 8, the calculated ratios of the wave function splitting corresponding to different values of$ {\lambda _\sigma } $ (from 0.98 to 1.02) are 3.68: 3.46: 3.31; that is to say, the wave function splitting decreases with the increase in$ {\lambda _\sigma } $ . This is consistent with the trend of energy and width splittings.The pseudospin wave function splitting with variable
$ {\lambda _\omega } $ is shown in Fig. 9. For the resonant partner$ (2h_{11/2}, 1j_{13/2}) $ , the ratio of the wavefunction splitting with the increase in$ {\lambda _\omega } $ is 3.32: 3.46: 3.64, which is also consistent with that of energy and width splittings. In addition, the change trend of wave function splitting caused by the$ {\omega} $ meson field is opposite to that by the$ {\sigma} $ meson field.When
$ {\lambda _\sigma } = {\lambda _\omega } $ is set, the wave functions for the resonant partner is shown in Fig. 10. It is difficult to distinguish the wave functions with different strengths of fields. When$ {\lambda _\sigma } = {\lambda _\omega } $ increases from 0.98 to 1.02, the calculated ratio of wave function splitting is 3.47: 3.46: 3.44, which shows that the variations of wavefunction splitting here are very small.From Fig. 11, the same situation occurs in the
$ {\rho} $ meson field; even if the parameter changes from 0.8 to 1.2, the change in wave function splitting is not obvious. Corresponding to$ {\lambda _\rho } = 0.8, 1.0, 1.2 $ , the calculated ratio for wavefunction splitting in the resonant partner$ (2h_{11/2}, 1j_{13/2}) $ is 3.39: 3.46: 3.54, which agrees with that of the energy and width splitting with$ \lambda _\rho $ . This indicates that, as far as the wavefunction is concerned, the$ {\rho} $ meson field has little influence on PSS. -
The RMF-CMR theory, a combination of the relativistic mean field (RMF) theory and the complex momentum representation (CMR), was adopted to check the pseudospin symmetry in the single-neutron resonant states in
$ ^{208} $ Pb. Influences from different fields of mesons on the pseudospin symmetry were investigated, and the splitting of the energies, widths, and wavefunctions between the resonant pseudospin partners were extracted. It is shown that the energy and width splittings between the resonant pseudospin partners decrease with increasing$ \sigma $ -field strength, and increase with increasing$ \omega $ -field strength. In comparison with the$ \sigma $ and$ \omega $ fields, the$ \rho $ -field produces a more minor influence on energy and width splitting for the resonant pseudospin partners, which indicates that$ \sigma $ and$ \omega $ fields are dominant in influencing the pseudospin symmetry, and the pseudospin splitting comes from the competition between the$ \sigma $ and$ \omega $ fields. Note that the trend for the change in energy splitting in the resonant partners with the strength of the meson field is in agreement with the case for the bound partners. At the same time, some differences were observed between the influence of various meson fields on the PSS in the bound and resonant states; these have been discussed in detail.Moreover, considering that only the wavefunctions of resonant states in the momentum space converge, the pseudospin wavefunction splitting for resonant partners in momentum space and its dependence on the strength of the meson field were calculated and analyzed. The trend of wave function splitting with
$ {\lambda _\sigma } $ ,$ {\lambda _\omega } $ , and$ \lambda_\rho $ is consistent with that of the energy and width splittings in resonant partners. -
Helpful discussions with Prof. Jian-You Guo are acknowledged.
Influence of different fields of mesons on the pseudospin symmetry in single-neutron resonant states
- Received Date: 2021-07-06
- Available Online: 2021-12-15
Abstract: In the framework of the relativistic mean field theory combined with the complex momentum representation method, we elucidate the pseudospin symmetry in the single-neutron resonant states and its dependence on the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: