Evaluation of pre-neutron-emission mass distributions of neutron-induced typical actinide fission using scission point model

Fission is one of the most complex processes in nuclear physics, involving a strong interplay between the nuclear structure and dynamics. In neutron-induced actinide nuclei fission, the parent nucleus transforms into a variety of daughter pairs characterized by different charge and mass yields and kinetic energies. The highly excited primary fission fragments are deexcited by the emissions of prompt neutrons and prompt γ-rays to form the primary fission products. The primary fission products are usually highly neutron rich and unstable and gradually evolve to secondary fission products through β-decay. Each primary fission fragment retains its individuality. Calculating fission fragment mass yields has a wide range of applications in various fields, ranging from understanding of the cosmos in astrophysical explosions to reactor operations [1-9].

It was interpreted in analogy by the fission of a charged liquid drop shortly after the discovery of nuclear fission. Fission occurs as a result of competition between the disrupting effect of Coulomb repulsion and the stabilizing effect of surface tension [10-12]. In recent years, many theoretical methods have been developed to calculate and reproduce the fission fragment mass distribution, which is one of the most important tests in the theoretical model describing the nuclear fission process. Macroscopic models [13-20] are used to explain the mechanism of nuclear fission by a numerical solution of the Langevin equations [21-23] or quantum-mechanical tools [24-25]. Microscopic models [26-31] describe the nuclear fission based upon the consideration of an effective energy density functional theory [32-33] and the time-dependent Hartree-Fock method [34-37], which is minimized in a chosen trial subspace of the full many-body Fock space while subject to external constraints on the density distribution. The macroscopic-microscopic approaches [38-42] are developed to calculate the nuclear potential-energy surface by uniting a macroscopic liquid-drop like energy functional and a microscopic contribution expressing the shell and pairing corrections, which can calculate the potential energy of any nuclear system with Z protons and N neutrons as a function of the nuclear shape. Macroscopic models, microscopic models, and macroscopic-microscopic approaches have been widely used in calculating potential energy surface distributions and nuclear masses at the ground state. Moreover, the developed statistical approaches [43-48] and phenomenological approaches [49-57] can calculate and predict the manifold fission observables with reasonable accuracy, which provide reliable fission yields required for applications in nuclear technology.

The scission point model, as a typical statistical approach, can calculate and reproduce yield distributions where the nuclear structure of the fragments is considered. With high excitation energy, the shape of the fissioning nucleus tends to be spherical. At the scission-point, both daughter nuclei are gradually deformed owing to the nuclear and Coulomb interactions (polarization effect). The potential energy surfaces are determined by all possible configurations at the scission-point. [43] This is well described in Refs. [43-48] from symmetric to asymmetric charge distributions for neutron-induced actinide nuclei fission with increasing incident neutron energy.

The problem of the dependence of the fission fragment mass distributions on the excitation energy is highly relevant at the present time. The symmetric components of the mass and charge yields are enhanced with increasing excitation energy. In this work, the scission point model is improved by considering the excitation-dependent liquid drop energy model to calculate and evaluate the mass distributions of neutron-induced typical actinide fission, including ^235,238U, ²³⁷Np, ²³⁹Pu, and ²³²Th. The improved scission point model can calculate the pre-neutron-emission mass distributions for incident-neutron-energies up to 99.5 MeV with reasonable accuracy.

At the scission point, it is assumed that the parent fissioning nucleus separates into a pair of daughter nuclei when the deformation is large enough, $ (A,Z) \to ({A_L},{Z_H}) + $$ ({A_L},{Z_H}) $. As shown in the dinuclear system (DNS) model, the scission configurations can be described using two nearly touching fragments with $ ({A_L},{Z_L}) $ and $ ({A_H},{Z_H}) $. The deformation parameter is $ {\beta _i} $, where $ i = L,H $ denotes the light and heavy fragments of the DNS, respectively [58].

The statistical scission-point model relies on the assumption that statistical equilibrium is established at the scission point. The fission fragment distribution is determined by the probability of given fragmentation combinations. The potential energy surface $ U $ in Eq. (1) of the DNS system at the scission-point as a function of the deformations and the internuclear distance $ R $ between fragments is described as

where $ {B_i} $ in Eq. (2) is the binding energy, $ {V_C} $ is the Coulomb potential, and $ {V_N} $ is the nuclear potential. The binding energies $ {B_i}({A_i},{Z_i},{\beta _i},E_i^ * ) $ ($ i = L,H $) as a function of the quadrupole deformations $ {\beta _i} $ are calculated using the macroscopic microscopic method [59]. The values of $ {\beta _i} $ change from 0.0 to 0.6 with a step of 0.05, which represents the quadrupole of two fragments. The scission configuration is imagined as two axially deformed and uniformly charged ellipsoids.

The binding energy of each fragment is composed of the excitation-dependent liquid drop energy $U_i^{\rm LD}$ and the shell correction energy $\delta U_i^{\rm shell}$ [59-60]. The shell correction is obtained by the traditional Strutinsky procedure, which is the sum of the shell energies of protons and neutrons. The binding energy can be expressed as

It is assumed that the fissioning nucleus is in thermal equilibrium at the scission point. $ E_i^ * $ is the excitation energy of the fission fragment.

The influence of excitation energy on mass distributions results from the tricky competition between the macroscopic liquid-drop energies and the microscopic shell corrections at scission. Particularly, it is necessary to consider the influence of the excitation energy effects on the deformations of light and heavy fragments in the scission point model, considering the excitation-dependent liquid drop energy model.

The liquid-drop surface energy $ U_i^s $ in Eq. (3) is highly sensitive and increases with increasing excitation energy to nuclear excitation energy; it is calculated as

The Coulomb energy $U_i^{\rm C}$ in Eq. (4) is reduced with increasing excitation energy and is described as

The volume energy $ U_i^v $ in Eq. (5) per particle E/A decreases with excitation energy, and is expressed as

The symmetry energy $U_i^{\rm sym}$ in Eq. (6) is nearly independent of excitation energy, calculated as

with isospin asymmetry $ I{\text{ = (}}{N_i} - {Z_i}{\text{)/}}{A_i} $. $ {a_s} $, $ {a_v} $, $ {a_c} $, and ${a_{\rm sym}}$ are taken from Ref. [60].

The shell damping correction with excitation energy $ E_i^* $ in Eq. (7) is introduced as

where $ {E_D} = 18.5\;{\rm{MeV}} $ is the damping constant, meaning the speed of washing out the shell correction against the excitation energy.

The interaction potential consists of the Coulomb interaction potential $ {V_C}({A_i},{Z_i},{\beta _i},R) $ of the two uniformly charged ellipsoids and nuclear interaction potential $ {V_N}({A_i},{Z_i},{\beta _i},R) $ in Eq. (8). The Coulomb interaction can be calculated by using Wong’s formula [61]. For the nuclear potential, Skyrme-type interaction without considering the momentum and spin dependence is adopted [62].

with $ {F_{in,ex}} = {f_{in,ex}}{\text{ + }}{f'_{in,ex}}\dfrac{{{N_L} - {Z_L}}}{{{A_L}}}\dfrac{{{N_H} - {Z_H}}}{{{A_H}}} $.

The $ {N_L}({N_H}) $ is the neutron number of the light (heavy) nucleus of the DNS system. Currently, some parameters are defined as ${C_{\text{0}}}{\text{ = 300}}\;{\rm{MeV}} \cdot \rm f{m^3}$, $ {f_{in}} = 0.09 $, $ {f_{ex}} = - 2.59 $, $ {f'_{in}} = 0.42 $, $ {f'_{ex}} = 0.54 $. The nuclear density distribution functions, $ {\rho _{\text{1}}} $ and $ {\rho _{\text{2}}} $, are of two-parameter Woods-Saxon form with a nuclear radius parameter of $ {r_0} = 1.02 - 1.16\;{\rm{fm}} $ and a diffuseness parameter of $ a = 0.51 - 0.56\;{\rm{fm}} $, depending on the charge and mass numbers of the nucleus [62]. R corresponds to $ {R_m}({A_i},{Z_i},{\beta _i}) $, at which point the potential pocket takes the minimum value of interaction potential.

The relative formation probability w in Eq. (9) of the DNS with fragments of certain charge numbers, mass numbers, and deformations can be described as

$ T $ is the temperature, which is calculated by $T = \sqrt {{E^ * }/a}$, where $a = A/12\;\rm Me{V^{ - 1}}$ is the level density parameter in the Fermi-gas model. The quasifission barrier $ {B_{qf}} $ denotes the depth of the potential pocket, which is calculated as the difference of the potential energy at the bottom of the potential pocket ($R = {R_m} = {R_1}[1 + \sqrt {5/(4\pi )} {\beta _1}] + $$ {R_2}[1 + \sqrt {5/(4\pi )} {\beta _2}] + 0.5\;{\rm{fm}}$) and at the top of the outer barrier ($R = {R_{\text{b}}} = {R_1}[1 + \sqrt {5/(4\pi )} {\beta _1}] + {R_2}[1 + \sqrt {5/(4\pi )} {\beta _2}] + $$ 1.5\;{\rm{fm}}$) with $ {R_i} = {r_0}A_i^{1/3} $. Notably, the dynamical process is not explicitly performed in this work, with the influence of dynamical effects on the charge distribution being restricted by the minimum value of the quasifission barrier $ {B_{qf}} $ [62]. $ {B_{qf}} $ must be larger than 0.9 MeV to perform the dynamical process.

$ {\beta _L} $ and $ {\beta _H} $ should be integrated over to acquire the mass-charge distribution of the fission fragments Y in Eq. (10).

Eventually, the total mass distributions of the fission fragments should be normalized to 200% by definition. The normalization constant $ {N_0} $ is calculated with the following equation: $ {N_0} = {{200\% } / {\sum\nolimits_{{Z_i},{A_i}} {Y({A_i},{Z_i},{E^ * })} }} $. In the scission-point model, the pre-neutron-emission mass distributions Y in Eq. (11) can be expressed as

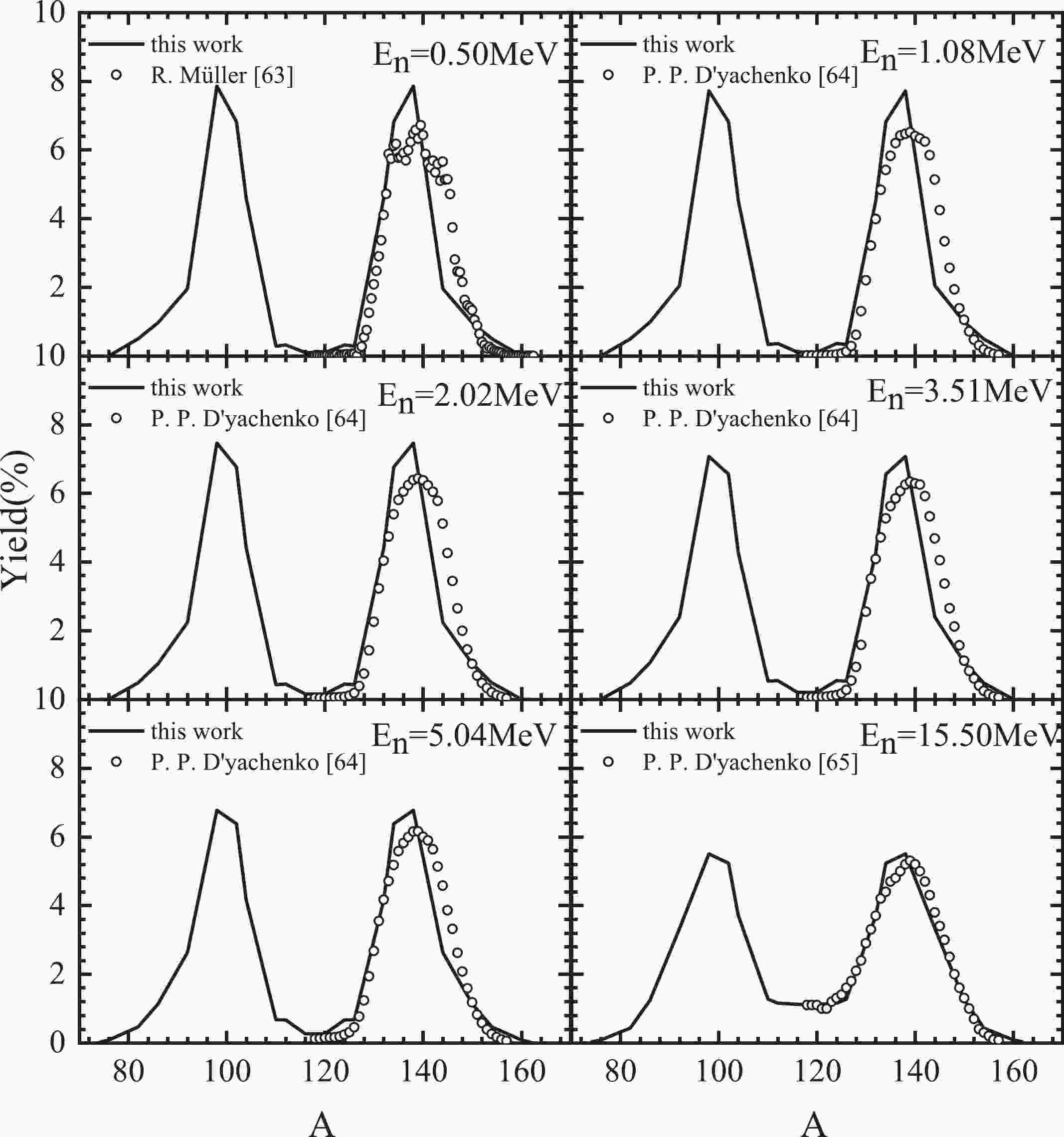
To verify the applicability of the improved scission point model, we calculate the pre-neutron-emission mass distributions for neutron-induced ²³⁵U, ²³⁸U, ²³⁷Np, ²³⁹Pu and ²³²Th fission. Figure 1 shows the calculated results of pre-neutron-emission mass distributions of ²³⁵U(n,f), which are compared with experimental data [63-65]. One can see that the calculated results are in good agreement with experimental data at the neutron energy range from 0.50 MeV to 15.50 MeV; the peak-to-valley ratio decreases with increasing energy. In a word, the improved scission point model can calculate the pre-neutron-emission mass distributions of the ²³⁵U(n,f) reaction with reasonable accuracy.

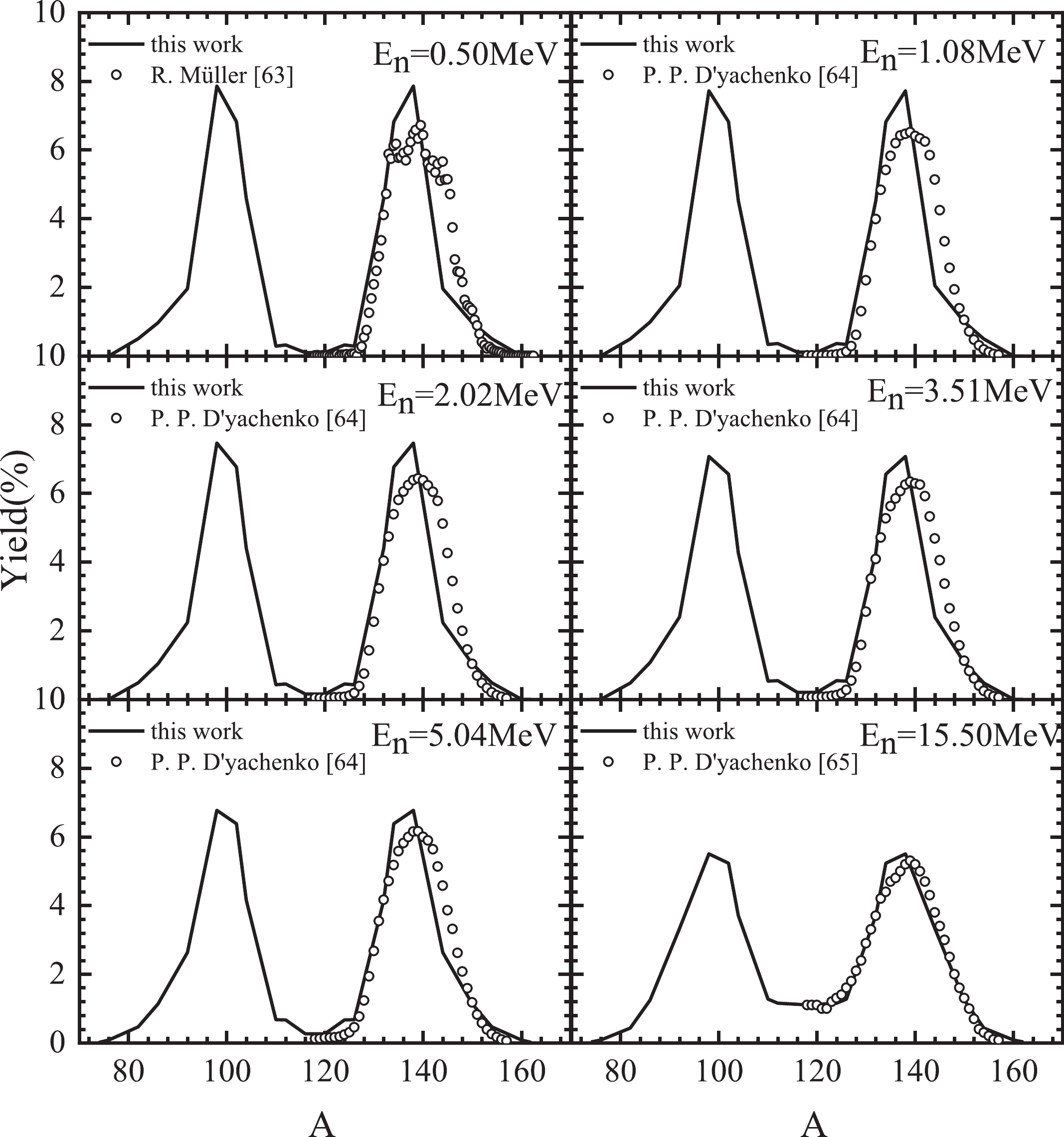
Figure 1.  Comparison between the calculated pre-neutron-emission mass distributions (solid lines) and experimental data (symbols) for neutron-induced ²³⁵U with incident-neutron-energies of 0.50, 1.08, 2.02, 3.51, 5.04, and 15.50 MeV.

The calculated pre-neutron-emission mass distributions for neutron-induced ²³⁸U fission are shown in Figs. 2-3, which agree quite well with the experimental data [66-68] with incident-neutron-energy up to 99.5 MeV. In Fig. 2, the incident-neutron-energies range from 1.6 MeV to 5.8 MeV, and the improved scission point model can precisely calculate the pre-neutron-emission mass distributions of the ²³⁸U(n,f) reaction. As shown in Fig. 3, the peak-to-valley ratio decreases with increasing energy. With increasing neutron energy, the mass yields clearly show an increase in the symmetric region and a decrease in the asymmetric region. The mass distributions of the fission fragments of ²³⁸U nuclei still have a pronounced asymmetric shape even at a high excitation energy of 99.5 MeV. The shell correction energy is decreased with increasing excitation energy. We consider the excitation-dependent liquid drop energy model so that the peak-to-valley ratio increases with the neutron energy up to 99.5 MeV with reasonable accuracy. The effect of excitation energy on the peak-valley ratio of the mass yield is well described by our model.

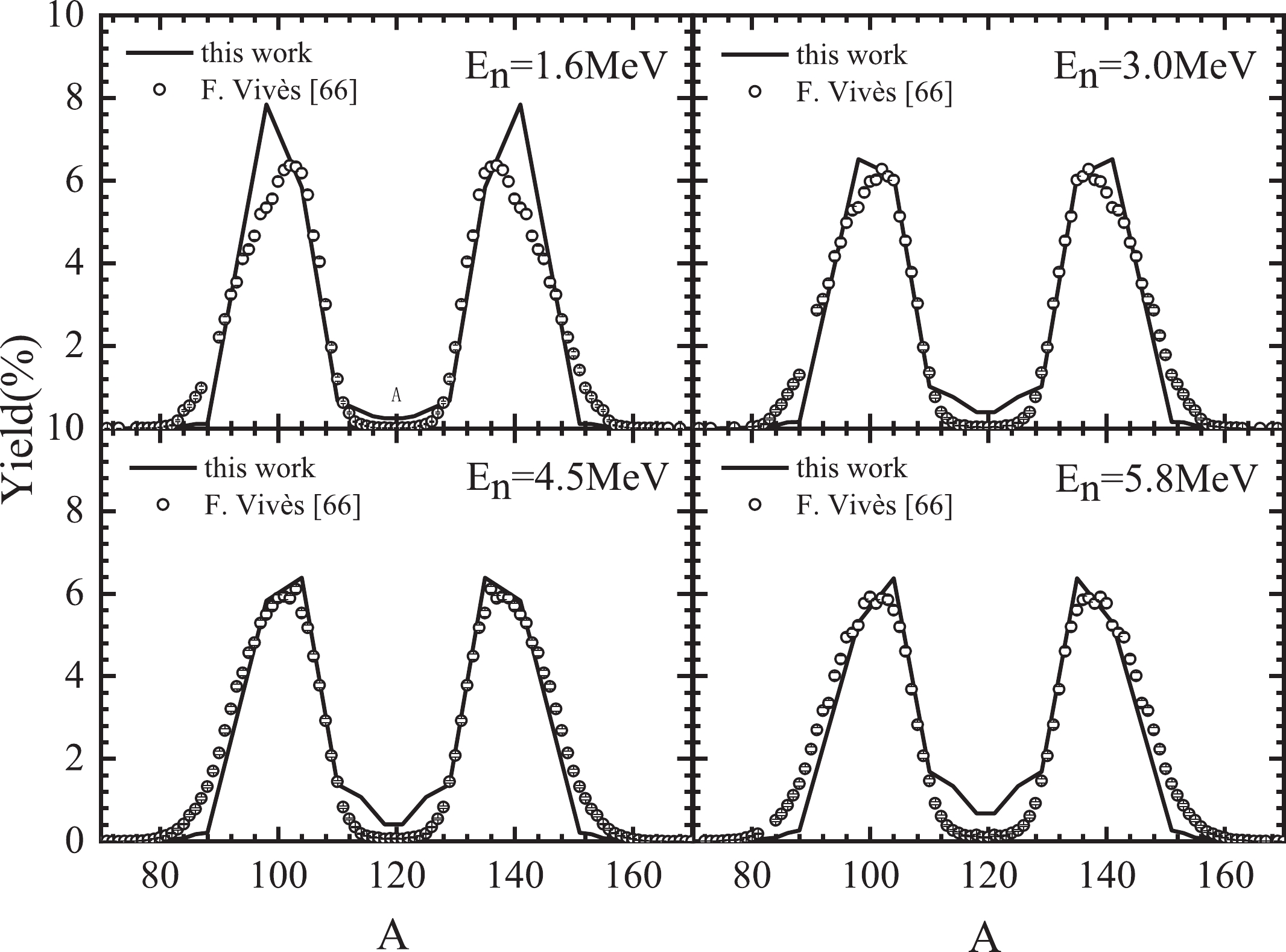
Figure 2.  Calculated and experimental results of pre-neutron-emission mass distributions for the ²³⁸U(n,f) reaction.

Figure 3.  Comparison between the calculated pre-neutron-emission mass distributions (solid lines) and experimental data (symbols) for neutron-induced ²³⁸U with incident-neutron-energies of 10.0,16.5, 22.5, 32.8, 59.9, and 99.5 MeV.

To study the influence of excitation energy on the shape of the mass distribution, we calculate ²³⁸U(n,f) at incident-neutron-energies of 10.0, 32.8, 59.9, and 99.5 MeV as shown in Fig. 4. With increasing incident-neutron-energy, there are obvious changes such as the increase in valley height as well as the decrease in peak height (including A_L = 96-106 and A_H = 133-143) in the pre-neutron-emission mass distributions [69]. At large excitation energies, the mass distribution is mainly explained by the liquid-drop model with the disappearance of the shell-correction energy. The improved scission point model also accurately describes these behaviors.

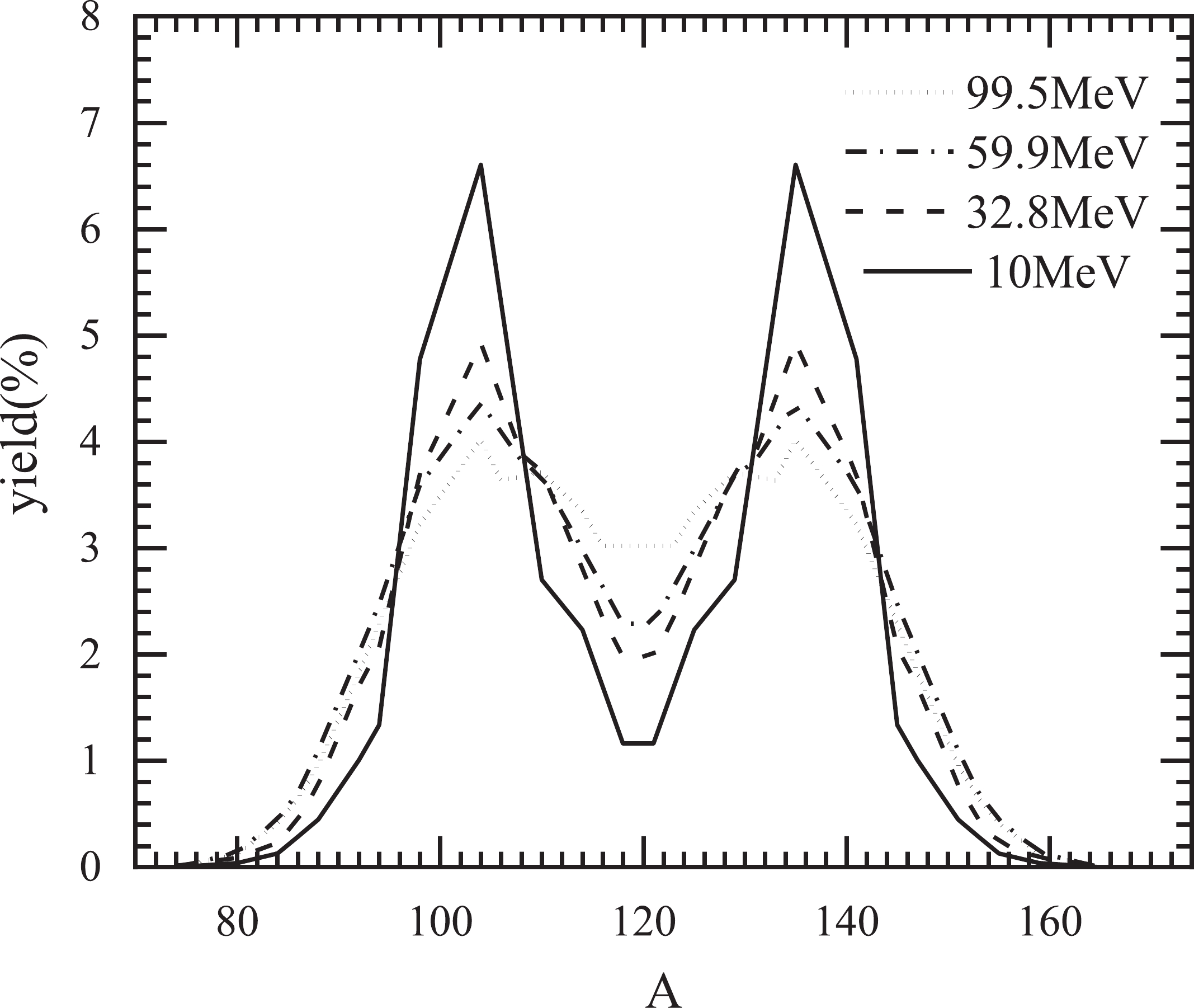
Figure 4.  Calculated pre-neutron-emission mass distributions for the ²³⁸U(n,f) reaction at different incident-neutron-energies.

Figure 5 and 6 show the calculated pre-neutron-emission mass distributions for ²³⁷Np(n,f) and ²³⁹Pu(n,f) reactions at different incident energies, respectively, which are compared with experimental data [70-71]. The comparisons show an overall good consistency. The calculated results show a good agreement with the experimental data, which indicates that the improved scission point model can reproduce the experimental results reasonably well for neutron-induced ²³⁷Np and ²³⁹Pu fission.

Figure 5.  Comparison between the calculated pre-neutron-emission mass distributions (solid lines) and experimental data (symbols) for the ²³⁷Np(n,f) reaction with incident-neutron-energies of 1.0, 3.0, 4.0, and 5.5 MeV.

Figure 6.  Comparison between the calculated pre-neutron-emission mass distributions (solid lines) and experimental data (symbols) for the ²³⁹Pu(n,f) reaction with incident-neutron-energies of 0.72, 1.72, 2.72, and 4.48 MeV.

Figure 7 shows the calculated pre-neutron-emission mass distributions for neutron-induced ²³²Th fission, which are compared with experimental data [67] with incident energies from 22.5 to 59.9 MeV. With increasing incident-neutron-energy, the double-humped mass distributions gradually change to a triple-humped shape, and the third-peak height even catches up with the peak of the asymmetric fission component for experimental data on pre-neutron-emission mass distributions. The results calculated by the improved scission point model agree with the experimental data on the asymmetric fission components. However, the calculated pre-neutron-emission mass distributions are opposite to the experimental data in the symmetric fission component. Particularly, the level density parameter $ a $ and damping constant $ {E_D} $ should be further adjusted to be suitable for calculating the triple-humped shape of the pre-neutron-emission mass distribution for the ²³²Th(n,f) reaction.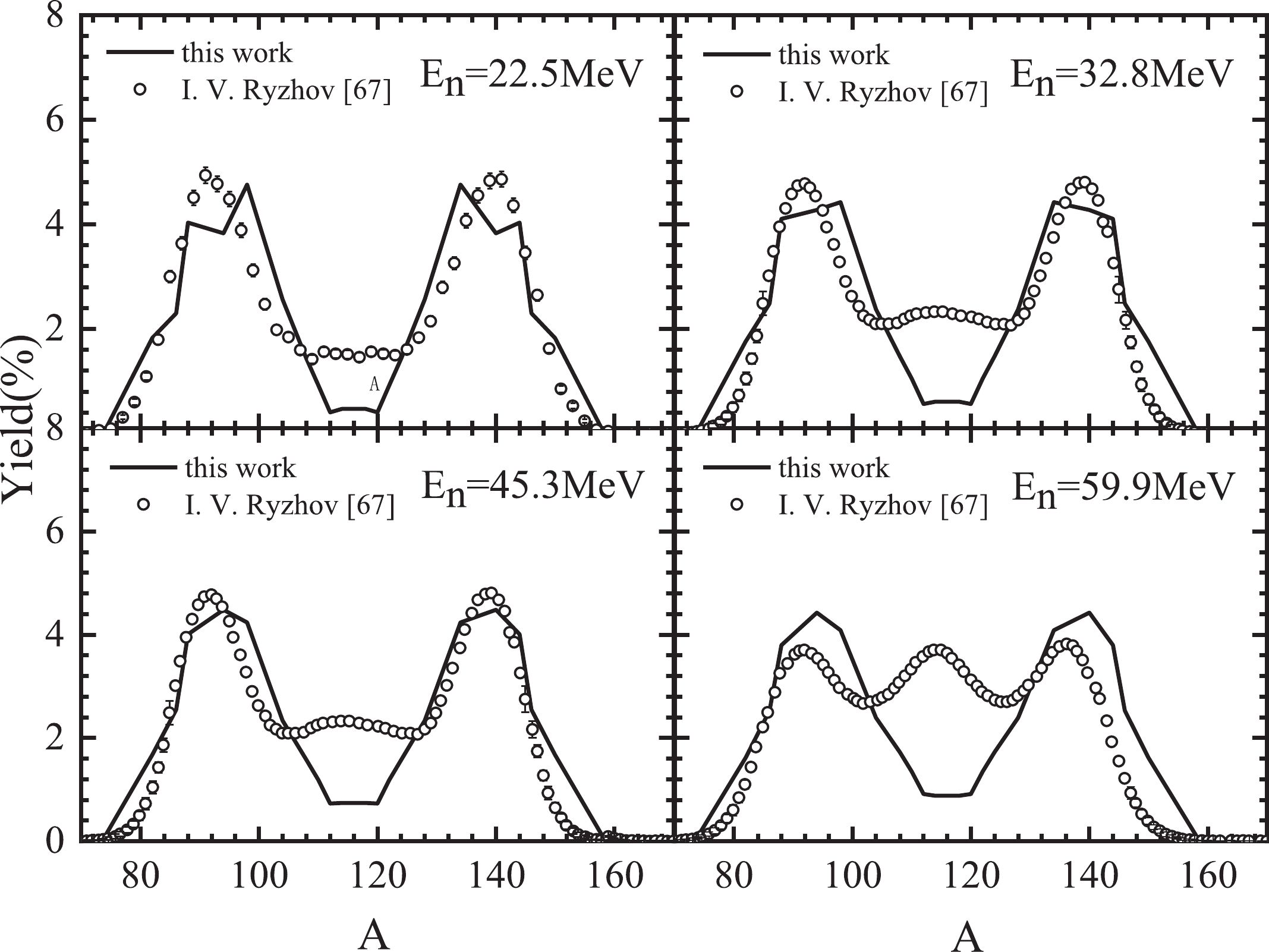

Figure 7.  Calculated and experimental results of pre-neutron-emission mass distributions for the ²³²Th$ (n,x\tilde nf) $ reaction with incident-neutron-energies of 22.5, 32.8, 45.3, and 59.9 MeV.

The improved scission point model can precisely calculate pre-neutron-emission mass distributions for neutron-induced actinide nuclei fission with incident-neutron-energies up to 99.5 MeV. Particularly, considering the excitation-dependent liquid drop energy, all calculated results are in good agreement with the experimental data, and the improved scission point model best describes the experimental results, especially in the yields and distribution tendency. The improved scission point model shows a significant advance with regard to accuracy.

In this work, based upon the consideration of the excitation-dependent liquid drop energy model and two discrete variables for deformations, the scission point model is improved to evaluate the pre-neutron-emission mass distributions of neutron-induced typical actinide fission with incident-neutron-energies up to 99.5 MeV. Given the good agreement with existing experimental data, the improved scission point model shows a significant advance with regard to accuracy for calculating pre-neutron-emission mass distributions of neutron-induced typical actinide fission.

As for low energy neutron-induced fission (lower than 5.5 MeV), the calculated pre-neutron-emission mass distributions are in good agreement with experimental data for the ²³⁵U, ²³⁸U, ²³⁷Np, and ²³⁹Pu(n,f) reactions. With increasing incident-neutron-energy, the improved scission point model performs very well for reproduction of pre-neutron-emission mass distributions for neutron-induced actinide nuclei fission for ²³⁸U with incident-neutron-energies up to 99.5 MeV, owing to the consideration of the excitation-dependent liquid drop energy model. Particularly, the effect of excitation energy on the peak-valley ratio of the mass yield is well described by the improved scission point model; the mass yields show an increase in the symmetric region and a decrease in the asymmetric region with increasing neutron energy.

The theoretical frame ensures that the improved scission point model is able to provide quantitative calculations of the pre-neutron-emission mass distributions with reasonable accuracy for a wide range of fissioning systems, which can be used to evaluate the fission fragment mass distributions for understanding the cosmos in astrophysical explosions and designing novel nuclear reactors and nuclear transmutation systems.