-
The Cabibbo-Kobayashi-Maskawa (CKM) matrix elements are important parameters of the standard model and can be extracted from pure- and semi-leptonic heavy meson decay processes. Of these, semi-leptonic processes have more accurate experimental data since they are not subject to helicity suppression. Recent measurements [1-3] of the semi-leptonic decays
$ D\to K\,e\,\nu_e $ ,$ D\to K\,\mu\,\nu_{\mu} $ , and$ D\to \pi\,e\,\nu_e $ yielded updated branching fractions, so that the products of form factors and the CKM matrix$ f_{D\to P}(0)|V_{cq}| $ can be extracted directly. Therefore, the precision prediction of the$ D\to P $ form factors is essential for determining the CKM matrix elements from semi-leptonic decay processes.Theoretically, the heavy-to-light form factors could be calculated using nonperturbative methods, such as the lattice QCD [4], QCD sum rules [5], light-cone sum rules [6-8], and quark models [9-12]. The lattice QCD approach is a QCD-based non-perturbative numerical method that is more suitable for studying small energy-release processes. Thus, phenomenological models are required to extrapolate the lattice results to the whole kinematic region. Lattice simulations have been applied to the
$ D\to P $ transition form factors in [13-17]. The approach that uses the QCD sum rules is based on the local operator product expansion (OPE) and quark hadron duality ansatz, and has been widely used in hadron physics. To evaluate the heavy-to-light form factors, the 3-point QCD sum rules must be employed [18-22]. In the large recoil region, the light-cone sum rules (LCSR) approach is more appropriate. The nonperturbative input in the LCSR reresents the light-cone distribution amplitudes (LCDAs) of hadrons, and the LCDAs of both the initial and final state hadrons can be employed. The$ D\to P $ form factors have been studied with light meson LCSR in [23-25]. The latest predictions of the CKM matrix elements$ |V_{cd}| = 0.225\pm 0.005\pm $ $ 0.003_{-0.012}^{+0.016} $ and$ |V_{cd}|/|V_{cs}| = 0.236\pm0.006\pm0.003\pm0.013 $ [25] are in agreement with the CLEO data$ |V_{cd}| = $ $ 0.234\pm0.007\pm0.002\pm0.025 $ and$ |V_{cs}| = 0.985\pm0.009\pm $ $ 0.003\pm0.103 $ [26], indicating that the leading order predictions are reliable. In this work, we apply the D-meson LCSR for evaluating the$ D\to P $ form factors. The advantage of our method is that LCDAs that are used in the calculation for different final states are universal.The idea of the D-meson LCSR is borrowed from the B-meson LCSR [27, 28], which has been widely used in heavy flavor physics for investigating the
$ B\to V $ ,$ B\to P $ , and$ \Lambda_b $ decay processes such as in [29-32], where QCD corrections and power suppressed contributions have been investigated. When this approach is applied to the D-meson decay, one may worry about the reliability of the light-cone OPE since the energy release is much smaller. In actuality, the light-cone OPE is completely feasible, since the momentum of the interpolation current of the final state is space-like. The D-meson LCDA is the nonperturbative input in the D-meson LCSR; therefore, the predicted form factors can be employed for determining the D-meson LCDA. The heavy meson LCDA is defined in the framework of the heavy quark effective theory (HQET), where the heavy quark expansion is used. Since the charm quark mass is not sufficiently large, the leading power predictions are less accurate. To overcome these shortcomings, we include the power suppressed contributions. In the present paper, we consider the contribution from the higher-twist D-meson LCDAs, including the two-particle and three-particle cases. Although the precision of our predictions is limited, the reliability of our predictions will be improved owing to the inclusion of power suppressed contributions. Of course, the power suppressed contributions considered in this work are not complete; yet, they provide at least some instructive results. With the predicted form factors at hand, we can constrain the CKM matrix elements$ |V_ {cq}| $ .This paper is structured as follows. In Sect. II, we present the formalism of the QCD sum rules and provide the leading-twist contributions to the LCSRs for
$ D \to \pi, K $ form factors at$ \mathcal{O}(\alpha_s) $ . In Sect. III, the higher-twist contributions from two- and three-particle D-meson LCDAs are studied. In Sect. IV, we present the numerical analysis with the predicted form factors from two different D-meson LCDA models. In Sect. V, we present our conclusions. -
We start with the vacuum-to-D-meson correlation function, defined with the matrix element of the time-ordered product of a pseudoscalar meson interpolating current and a weak current, as follows:
$\begin{aligned}[b] \Pi_{\mu}(n \cdot p,\bar n \cdot p) =& \int {\rm d}^4x \; {\rm e}^{{\rm i} p\cdot x} \langle 0 |T\left\{\bar{d}(x) \not n \, \gamma_5 \, q(x), \,\, \bar{q}(0) \, \Gamma_\mu \, c(0) \right\}|\bar D(p+q) \rangle \\ = & \left\{ \begin{array}{l} \Pi(n \cdot p,\bar n \cdot p) \, n_\mu +\widetilde{\Pi}(n \cdot p,\bar n \cdot p) \, \bar n_\mu \,, \qquad \Gamma_{\mu} = \gamma_{\mu} \\ \Pi_T(n \cdot p,\bar n \cdot p) \, \left [n_{\mu} - \dfrac{n \cdot q} {m_D} \, \bar n_{\mu} \right ] \,. \qquad \quad\quad \Gamma_{\mu} = \sigma_{\mu \nu} \, q^{\mu} \end{array} \quad \right. \, \end{aligned} $ 
(1) In the above equation,
$ p+q\equiv m_Dv $ is the four-momentum of the D-meson, and p is the momentum of the light pseudoscalar meson. We introduce two light-cone vectors$ \bar{n}_{\mu} $ and$ n_{\mu} $ that satisfy$ n^2 = \bar{n}^2 = 0 $ and$ n\cdot \bar{n} = 2 $ , and employ the power counting scheme of light pseudoscalar meson four-momentum, which is valid in the heavy quark limit$ n\cdot p\sim{\cal O}(m_D),\,\,\,\bar{n}\cdot p\sim m_s\sim{\cal O}(\Lambda),$

(2) where
$ \Lambda $ refers to the QCD energy scale. To guarantee the QCD factorization of the correlation function, we consider the heavy quark limit when calculating the leading power contribution. Then, the charm quark mass is regarded as a hard scale, and p is hard-collinear, which is similar to$ B\to P,V $ transitions. The leading power factorization formulae for the correlation function in$ \Lambda/m_c $ are given by$ \begin{aligned}[b] \Pi =& \tilde{f}_D(\mu) \, m_D \sum \limits_{k = \pm} \, C^{(k)}(n \cdot p, \mu) \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; J^{(k)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^{k}(\omega,\mu) \,, \\ \widetilde{\Pi} = & \tilde{f}_D(\mu) \, m_D \sum \limits_{k = \pm} \, \widetilde{C}^{(k)}(n \cdot p, \mu) \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; \widetilde{J}^{(k)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^{k}(\omega,\mu) \,, \\ \Pi_T =& - {{\rm i} \over 2} \, \tilde{f}_D(\mu) \, m_D^2 \, \sum \limits_{k = \pm} \, C^{(k)}_T(n \cdot p, \mu, \nu) \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; J^{(k)}_T \left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^{k}(\omega,\mu) \,,\end{aligned} $ 
(3) where functions
$ C^{(k)} $ and$ J^{(k)} $ are the hard and jet functions, respectively. The D-meson LCDAs are defined by the following renormalized matrix element [20]$ \langle 0 | \left ( \bar{u}\, Y_s^{\dagger} \right )_{\alpha}(\tau \, \bar{n}) \,\left ( Y_s^{\dagger}\,h_v \right)_{\beta} (0) | D(v)\rangle = - \frac{{\rm i} \tilde f_D(\mu) \, m_D}{4} \bigg \{ \frac{1+ \not v}{2} \, \left [ 2 \, \tilde{\phi}_{D}^+(\tau, \mu) + \left ( \tilde{\phi}_{D}^-(\tau, \mu) -\tilde{\phi}_{D}^+(\tau, \mu) \right ) \not n \right ] \, \gamma_5 \bigg \}_{\alpha \beta}\,. $

(4) In the above equation,
$ Y_s(\tau \bar{n}) $ is the soft Wilson line, ensuring the gauge invariance$ Y_s(\tau \, \bar n) = {\rm P} \, \left \{ {\rm Exp} \left [ {\rm i} \, g_s \, \int_{- \infty}^{\tau} \, {\rm d}x \, \bar n \cdot A_{s}(x \, \bar n) \right ] \right \} \,, $

(5) and
$ \tilde f_D(\mu) $ is the renormalization-scale dependent HQET decay constant$ \tilde{f}_D(\mu) = \left \{ 1 - {\alpha_s(\mu) \, C_F \over 4 \, \pi} \, \left [3\, \ln{\mu \over m_c} + 2 \right ] \right \}^{-1} \, f_D \,. $

(6) For one-loop accuracy, the hard and jet functions are given by [33]
$ \begin{aligned}[b] C^{(+)} = & \widetilde{C}^{(+)} = C_T^{(+)} = 1 \,, \qquad C^{(-)} = {\alpha_s \, C_F \over 4 \pi} \, {1 \over \bar r} \, \left [ 1 + { r \over \bar r} \, \ln r \right ] \,, \\ \widetilde{C}^{(-)} = & 1- {\alpha_s \, C_F \over 4 \pi} \, \left [ 2 \, \ln^2 {\mu \over n \cdot p} + 5 \, \ln {\mu \over m_b} - \ln^2 r - 2 \, {\rm Li}_2 \left (- { \bar r \over r } \right )+ { 2 - r \over r-1} \, \ln r + {\pi^2 \over 12} + 5 \right ] \,, \\ C_T^{(-)} = & 1 + {\alpha_s \, C_F \over 4 \pi} \, \left [ -2 \, \ln {\nu \over m_b} - 2 \, \ln^2 {\mu \over n \cdot p} - 5 \, \ln {\mu \over n \cdot p}- 2 \, {\rm Li}_2 (1-r) - {3 - r \over 1 -r} \, \ln r - {\pi^2 \over 12} - 6 \right ] \,, \\ J^{(+)} = & {\alpha_s \, C_F \over 4 \pi} \, \left (1 - {\bar n \cdot p \over \omega} \right ) \, \ln \left (1- {\omega \over \bar n \cdot p} \right ) \,, \\ \widetilde{J}^{(+)} = & {\alpha_s \, C_F \over 4 \pi} \, \left [ r \, \left (1 - {\bar n \cdot p \over \omega} \right ) + {m_q \over \omega} \right ] \, \ln \left (1- {\omega \over \bar n \cdot p} \right ) \,, \\ J_T^{(+)} =& {\alpha_s \, C_F \over 4 \pi} \, \left [ - \, \left (1 - {\bar n \cdot p \over \omega} \right ) + {m_q \over \omega} \right ] \, \ln \left (1- {\omega \over \bar n \cdot p} \right ) \,, \\ J^{(-)} = & 1 \,, \\ \widetilde{J}^{(-)} = & J_T^{(-)} = 1 + \frac{\alpha_s \, C_F}{4 \, \pi} \, \Bigg [ \ln^2 { \mu^2 \over n \cdot p (\omega- \bar n \cdot p) } - 2 \ln {\bar n \cdot p -\omega \over \bar n \cdot p } \, \ln { \mu^2 \over n \cdot p (\omega- \bar n \cdot p) } \, \\ & - \ln^2 {\bar n \cdot p -\omega \over \bar n \cdot p } - \left ( 1 + {2 \bar n \cdot p \over \omega} \right ) \ln {\bar n \cdot p -\omega \over \bar n \cdot p } -{\pi^2 \over 6} -1 \Bigg ] \,, \end{aligned} $ 
(7) where
$ \nu $ is the renormalization scale of the tensor current. Conventions of r and$ \bar{r} $ are$ r = n\cdot p/m_c $ and$ \bar{r} = 1-r $ , respectively.To obtain the next-to-leading-logarithmic (NLL) accuracy factorization formulae, we employ the renormalization group equation in the momentum space, and consider the factorization scale
$ \mu $ as a hard-collinear scale$\mu_{hc}\sim \sqrt{\Lambda_{\rm QCD}\,m_c}$ . By solving the evolution equations, we obtain the NLL resummation improved expressions for the hard function and the HQET decay constant$ \begin{aligned}[b] \widetilde{C}^{(-)}(n \cdot p, \mu) = & U_1(n \cdot p, \mu_{h1}, \mu) \,\, \widetilde{C}^{(-)}(n \cdot p, \mu_{h1})\,, \\ C^{(-)}_{T}(n \cdot p, \mu, \nu) = & U_1(n \cdot p, \mu_{h1}, \mu) \,\, U_3(\nu_{h}, \nu) \,\, C^{(-)}_{T}(n \cdot p, \mu_{h1}, \nu_{h}) \,, \\ \tilde{f}_D(\mu) =& \, U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \,\,, \end{aligned} $

(8) where the expressions for the evolution functions
$ U_1 $ ,$ U_2 $ , and$ U_3 $ are presented in the appendix. Then, the factorization formulae for the correlation functions at the NLL accuracy read$ \begin{aligned}[b] \Pi =& \left [ U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \right ]\, m_D \, \, \bigg \{ \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; J^{(+)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^+(\omega,\mu) \\ & + \, C^{(-)}(n \cdot p, \mu) \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; \, \phi_D^-(\omega,\mu) \, \bigg \}\,, \\ \widetilde{\Pi} =& \left [ U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \right ]\, m_D \, \, \bigg \{ \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; \widetilde{J}^{(+)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^+(\omega,\mu) \end{aligned}$ 
$ \begin{aligned}[b] & + \,\left [ U_1(n \cdot p, \mu_{h1}, \mu) \,\, \widetilde{C}^{(-)}(n \cdot p, \mu_{h1}) \right ] \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; \widetilde{J}^{(-)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^-(\omega,\mu) \, \bigg \}\,, \\ \Pi_T = & - {{\rm i} \over 2} \, \left [ U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \right ]\, m_D^2 \, \, \bigg \{ \int_0^{\infty} {{\rm d}\omega \over \omega- \bar n \cdot p}\; J_T^{(+)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^+(\omega,\mu) \\ & + \,\left [ U_1(n \cdot p, \mu_{h1}, \mu) \,\, U_3(\nu_{h}, \nu) \,\, C^{(-)}_{T}(n \cdot p, \mu_{h1}, \nu_{h}) \right ] \, \\ & \times \, \int_0^{\infty} {{\rm d} \omega \over \omega- \bar n \cdot p}\; J_T^{(-)}\left({\mu^2 \over n \cdot p \, \omega},{\omega \over \bar n \cdot p}\right) \, \phi_D^-(\omega,\mu) \, \bigg \} \,. \end{aligned}$

(9) The definitions of the
$ D\to P $ form factors and the decay constant of the pseudoscalar meson are given by$ \begin{aligned}[b] \langle P(p)| \bar q \, \gamma_{\mu} \, c| \bar D (p+q)\rangle = & f_{D \to P}^+(q^2) \, \left [ 2 p + q -\frac{m_D^2-m_{P}^2}{q^2} q \right ]_{\mu} + f_{D \to P}^{0}(q^2) \, \frac{m_D^2-m_{P}^2}{q^2} q_{\mu} \,, \\ \langle P(p)| \bar q \, \sigma_{\mu \nu} \, q^{\nu}\, c| \bar D (p+q)\rangle =& {\rm i} \, {f_{D \to P}^{T}(q^2) \over m_D + m_P}\, \left [ q^2 \,\, (2 p + q)_{\mu} \, -(m_D^2-m_{P}^2) \, q_{\mu} \right ] \,, \\ \langle 0 |\bar d \not n \, \gamma_5 \, q | P(p) \rangle =& {\rm i} \, n \cdot p \, f_{P} \,, \end{aligned} $

(10) where
$ f_{D \to P}^{+}(q^2) $ and$ f_{D \to P}^{T}(q^2) $ are the vector and tensor$ D\to P $ form factors, respectively. By inserting the above equations into the hadronic-level vacuum-to-D-meson correlation function$ \Pi_{\mu}(n \cdot p,\bar n \cdot p) = \frac{\langle 0|\bar{d}\not n \,\gamma_5\,q|P(p)\rangle\langle P(p)|\bar{q}\,\Gamma_{\mu}\,c|\bar{D}(p+q)\rangle}{m_P^2-p^2}+{\rm continuum\; states}, $

(11) we readily obtain the hadronic representations of the correlation function for the vector and tensor Dirac structures
$ \begin{aligned}[b] \Pi_{\mu, V}(n \cdot p,\bar n \cdot p) =& \frac{f_{P} \, m_D}{2 \, (m_{P}^2/ n \cdot p - \bar n \cdot p)} \bigg \{ \bar n_{\mu} \, \left [ \frac{n \cdot p}{m_D} \, f_{D \to P}^+ (q^2) + f_{D \to P}^{0} (q^2) \right ] + \, n_{\mu} \, \frac{m_D}{n \cdot p-m_D} \, \, \left [ \frac{n \cdot p}{m_D} \, f_{D \to P}^+ (q^2) - f_{D \to P}^{0} (q^2) \right ] \bigg \} \, \\& + \int_{\omega_s}^{+\infty} \, \frac{{\rm d} \omega^{\prime} }{\omega^{\prime} - \bar n \cdot p - {\rm i} 0} \, \left [ \rho_{V, 1}^{h}(\omega^{\prime}, n \cdot p) \, n_{\mu} \, +\rho_{V, 2}^{h}(\omega^{\prime}, n \cdot p) \, \bar{n}_{\mu} \right ] \,, \\ \Pi_{\mu, T}(n \cdot p,\bar n \cdot p) =& - {\rm i} \, \frac{f_{P} \, n \cdot p }{2 \, (m_{P}^2/ n \cdot p - \bar n \cdot p)} \, {m_D^2 \over m_D+m_P} \, \left [ n_{\mu} - {n \cdot q \over m_D} \, \bar n_{\mu} \right ] \, f_{D \to P}^{T} (q^2) \\ & + \int_{\omega_s}^{+\infty} \, \frac{{\rm d} \omega^{\prime} }{\omega^{\prime} - \bar n \cdot p - {\rm i} 0} \, \, \left [ n_{\mu} - {n \cdot q \over m_D} \, \bar n_{\mu} \right ] \, \rho_{T}^{h}(\omega^{\prime}, n \cdot p) \,. \end{aligned}$

(12) To obtain the NLL LCSR for the
$ D \to P $ form factors for the leading power in the heavy quark expansion, one can match the HQET representation and the hadronic representation based on the parton-hadron duality ansatz. Implementing the Borel transformation, one obtains$ \begin{aligned}[b] f_{P} \,\, {\rm exp} \left [- {m_{P}^2 \over n \cdot p \,\, \omega_M} \right ] \,\, \left \{ \frac{n \cdot p} {m_D} \, f_{D \to P}^{+, \, \rm 2PNLL}(q^2) \,, \,\,\, f_{D \to P}^{0, \, \rm 2PNLL}(q^2) \right \} \, =& \left [ U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \right ] \,\, \int_0^{\omega_s} \,\, {\rm d} \omega^{\prime} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, \\ & \times \bigg \{\widetilde{\phi}_{D, \, {\rm eff}}^+ (\omega^{\prime}, \mu) + \, \left [ U_1(n \cdot p, \mu_{h1}, \mu) \,\, \widetilde{C}^{(-)}(n \cdot p, \mu_{h1}) \right ]\, \widetilde{ \phi}_{D, \, {\rm eff}}^- (\omega^{\prime}, \mu) \\ &\pm \, { n \cdot p - m_D \over m_D} \, \left [\phi_{D, \, \rm {eff}}^+ (\omega^{\prime}, \mu) + C^{(-)}(n \cdot p, \mu_{h1}) \, \phi_{D, \, \rm {eff}}^- (\omega^{\prime}, \mu) \right ] \bigg \} \,, \\ f_{P} \,\, {\rm exp} \left [- {m_{P}^2 \over n \cdot p \,\, \omega_M} \right ] \,\, \frac{n \cdot p} {m_D+m_P} \, f_{D \to P}^{T, \, \rm 2PNLL}(q^2) \, =& \left [ U_2(\mu_{h2}, \mu) \, \tilde{f}_D(\mu_{h2}) \right ] \,\, \int_0^{\omega_s} \,\, {\rm d} \omega^{\prime} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, \bigg \{ \widehat{\phi}_{D, \, \rm {eff}}^+ (\omega^{\prime}, \mu) \\&+ \,\left [ U_1(n \cdot p, \mu_{h1}, \mu) \,\, U_3(\nu_{h}, \nu) \,\, C^{(-)}_{T}(n \cdot p, \mu_{h1}, \nu_{h}) \right ] \, \widetilde{ \phi}_{D, \, \rm {eff}}^- (\omega^{\prime}, \mu) \bigg \} \,. \end{aligned} $

(13) The effective D-meson DAs are defined as [33]
$ \begin{aligned}[b]\widetilde{\phi}_{D, \, \rm {eff}}^+ (\omega^{\prime}, \mu) = & {\alpha_s \, C_F \over 4 \, \pi} \, \left [ r \, \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, {\phi_D^+(\omega, \mu) \over \omega} - m_q \, \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, \ln \left ( {\omega - \omega^{\prime} \over \omega^{\prime}} \right ) \,\, {{\rm d} \over {\rm d} \omega} \, {\phi_D^+(\omega, \mu) \over \omega} \right ] \,, \\ \widetilde{\phi}_{D, \, \rm {eff}}^- (\omega^{\prime}, \mu) =& \phi_{D}^-(\omega^{\prime}, \mu) + \frac{\alpha_s \, C_F}{4 \, \pi} \,\, \Bigg \{ \int_0^{\omega^{\prime}} \,\, {\rm d} \omega \,\,\, \left [ {2 \over \omega - \omega^{\prime}} \,\,\, \left (\ln {\mu^2 \over n \cdot p \, \omega^{\prime}} - 2 \, \ln {\omega^{\prime} - \omega \over \omega^{\prime}} \right )\right ]_{\oplus} \, \phi_{D}^-(\omega, \mu) \\ &- \int_{\omega^{\prime}}^{\infty} \,\, {\rm d} \omega \,\,\, \bigg [ \ln^2 {\mu^2 \over n \cdot p \, \omega^{\prime}} - \left ( 2 \, \ln {\mu^2 \over n \cdot p \, \omega^{\prime}} + 3 \right ) \,\, \ln {\omega - \omega^{\prime} \over \omega^{\prime}} + \, 2 \,\, \ln {\omega \over \omega^{\prime}} + {\pi^2 \over 6} - 1 \bigg ] \, {{\rm d} \phi_{D}^-(\omega, \mu) \over {\rm d} \omega} \Bigg \} \,, \\ \phi_{D, \, \rm {eff}}^+ (\omega^{\prime}, \mu) =& {\alpha_s \, C_F \over 4 \, \pi} \, \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, {\phi_D^+(\omega, \mu) \over \omega} \,, \qquad \phi_{D, \, \rm {eff}}^- (\omega^{\prime}, \mu) = \phi_D^-(\omega^{\prime}, \mu) \,, \\ \widehat{\phi}_{D, \, \rm {eff}}^+ (\omega^{\prime}, \mu) = & {\alpha_s \, C_F \over 4 \, \pi} \, \left [ - \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, {\phi_D^+(\omega, \mu) \over \omega} - m_q \, \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, \ln \left ( {\omega - \omega^{\prime} \over \omega^{\prime}} \right ) \,\, {{\rm d} \over {\rm d} \omega} \, {\phi_D^+(\omega, \mu) \over \omega} \right ] \,, \end{aligned}$

(14) where the strange quark mass effect at
$ \alpha_{s} $ could be observed in the above equation. The plus function entering (14) is defined as$ \int_0^{\infty} \, {\rm d} \omega \, \left [ f(\omega, \omega^{\prime}) \right ]_{\oplus} \, g(\omega) = \int_0^{\infty} \, {\rm d} \omega \, f(\omega, \omega^{\prime}) \left [ g(\omega) - g(\omega^{\prime}) \right ] \,. $

(15) -
In this section, we will evaluate the higher-twist contributions from two-particle and three-particle D-meson LCDAs. To compute the three-particle higher-twist contributions of the
$ D\to\pi\,,K $ form factors, we apply the light-cone expansion of the quark propagator in the background gluon field [34]$ \langle 0 | {\rm T} \, \{\bar q (x), q(0) \} | 0\rangle \supset {\rm i} \, g_s \, \int_0^{\infty} \,\, {{\rm d}^4 k \over (2 \pi)^4} \, {\rm e}^{-{\rm i} \, k \cdot x} \, \int_0^1 \, {\rm d} u \, \left [ {u \, x_{\mu} \, \gamma_{\nu} \over k^2 - m_q^2} - \frac{(\not k + m_q) \, \sigma_{\mu \nu}}{2 \, (k^2 - m_q^2)^2} \right ] \, G^{\mu \nu}(u \, x) \,, $ 
(16) where only the one-gluon part is considered. The D-meson three-particle LCDAs are defined as [33, 35]
$ \begin{aligned}[b] \langle 0| \bar q(nz_1) g_s\,G_{\mu\nu}(nz_2)\Gamma h_v(0) |\bar D(v)\rangle = & \frac14 F_D(\mu) {\rm{Tr}}\biggl\{\gamma_5 \Gamma (1 + \not v) \biggl[ (v_\mu\gamma_\nu-v_\nu\gamma_\mu) \big[{\Psi}_A-{\Psi}_V \big]-{\rm i}\sigma_{\mu\nu}{\Psi}_V - (n_\mu v_\nu-n_\nu v_\mu){X}_A \\&+ (n_\mu \gamma_\nu-n_\nu \gamma_\mu)\big[W+{Y}_A\big] - {\rm i} \epsilon_{\mu\nu\alpha\beta} n^\alpha v^\beta \gamma_5 \widetilde{X}_A + {\rm i} \epsilon_{\mu\nu\alpha\beta} n^\alpha \gamma^\beta\gamma_5 \widetilde{Y}_A \\&- (n_\mu v_\nu-n_\nu v_\mu)\not n\,{W} + (n_\mu \gamma_\nu-n_\nu \gamma_\mu)\notn\,{Z} ]\}(z_1,z_2;\mu)\,, \end{aligned} $

(17) where the convention is
$ \epsilon_{0123} = -1 $ . Then, one obtains three-particle higher-twist contributions to the correlation function of the vacuum-to-D-meson at the tree-level [33]$ \begin{aligned}[b]\Pi_{\mu, V}^{(3P)}(n \cdot p,\bar n \cdot p) = & -{\tilde{f}_D(\mu) \, m_D \over n \cdot p } \, \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \, \int_0^1 {\rm d} u \, {1 \over \left [\bar n \cdot p - \omega_1 - u \, \omega_2 \right ]^2} \\ & \times \, \bigg \{ \bar n_{\mu} \, \left [ \rho_{\bar n, \rm{LP}}^{(3P)}(u, \omega_1, \omega_2, \mu) + {m_q \over n \cdot p} \, \rho_{\bar n, \rm{NLP}}^{(3P)}(u, \omega_1, \omega_2, \mu) \right ] \\ & +\, n_{\mu} \, \left [ \rho_{n, \rm{LP}}^{(3P)}(u, \omega_1, \omega_2, \mu) + {m_q \over n \cdot p} \, \rho_{n, \rm{NLP}}^{(3P)}(u, \omega_1, \omega_2, \mu) \right ] \bigg \} \,, \\ \Pi_{\mu, T}^{(3P)}(n \cdot p,\bar n \cdot p) =& {{\rm i} \over 2} \, {\tilde{f}_D(\mu) \, m_D^2 \over n \cdot p } \, \, \left [ n_{\mu} - {n \cdot q \over m_D} \, \bar n_{\mu} \right ] \, \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \, \int_0^1 {\rm d} u \, {1 \over \left [\bar n \cdot p - \omega_1 - u \, \omega_2 \right ]^2} \\ &\times \bigg \{ \rho_{T, \rm{LP}}^{(3P)}(u, \omega_1, \omega_2, \mu) + {m_q \over n \cdot p} \, \rho_{T, \rm{NLP}}^{(3P)}(u, \omega_1, \omega_2, \mu) \bigg \} \,, \end{aligned} $

(18) where the
$ m_q $ terms lead to the SU(3) flavor symmetry breaking effect, and the expressions for$ \rho_{i, \rm{LP}}^{(3P)} $ and$ \rho_{i, \rm{NLP}}^{(3P)} $ ($ i = n\,, \bar n \,, T $ ) are presented in the appendix.The two-particle higher-twist D-meson LCDAs are defined as [35]
$ \begin{aligned}[b]\langle 0 | \left (\bar d \, Y_s \right)_{\beta} (x) \, \left (Y_s^{\dagger} \, h_v \right )_{\alpha}(0)| \bar D(v)\rangle =& - \frac{{\rm i} \tilde f_D(\mu) \, m_D}{4} \, \int_0^{\infty} \, {\rm d} \omega \, {\rm e}^{-{\rm i} \, \omega \, v \cdot x} \, \bigg \{ \frac{1+ \not v}{2} \, \, \bigg [ 2 \, \left ( \phi_{D}^+(\omega, \mu) + x^2 \, g_D^+(\omega, \mu) \right ) \\& - {1 \over v \cdot x} \, \left [ \left ( \phi_{D}^+(\omega, \mu) - \phi_{D}^-(\omega, \mu) \right ) + x^2 \, \left ( g_{D}^+(\omega, \mu) - g_{D}^-(\omega, \mu) \right ) \right ] \, \not x \bigg ] \, \gamma_5 \bigg \}_{\alpha \beta}\,, \end{aligned} $

(19) where
$ g_D^+ $ and$ g_D^- $ are of twist-four and twist-five nature, respectively. One could expand$ g_D^+ $ and$ g_D^- $ in terms of three-particle LCDAs with the operator identities [35, 36]$\begin{aligned}[b] \frac{\partial}{\partial x^\mu} \bar q(x)\gamma^\mu \Gamma [x,0] h_v(0) =& - {\rm i}\int_0^1 u {\rm d} u\, \bar q(x)[x,ux] x^\rho gG_{\rho\mu}(ux)[ux,0] \gamma^\mu \Gamma h_v(0)\,, \\ v^\mu \frac{\partial}{\partial x^\mu} \bar q(x) \Gamma [x,0] h_v(0) =& \phantom- {\rm i}\int_0^1 \bar u {\rm d} u\, \bar q(x)[x,ux] x^\rho gG_{\rho\mu}(ux)[ux,0] v^\mu \Gamma h_v(0) + (v\cdot\partial) \bar q(x) \Gamma [x,0] h_v(0)\,. \end{aligned} $

(20) Applying the relations between the two forms of the D-meson LCDAs [33]
$ \begin{aligned}[b] \Phi_3(\omega_1, \omega_2, \mu) = & \Psi_A(\omega_1, \omega_2, \mu) - \Psi_V(\omega_1, \omega_2, \mu) \,, \\ \Phi_4(\omega_1, \omega_2, \mu) = & \Psi_A(\omega_1, \omega_2, \mu) + \Psi_V(\omega_1, \omega_2, \mu) \,, \\ \Psi_4(\omega_1, \omega_2, \mu) =& \Psi_A(\omega_1, \omega_2, \mu) + X_A(\omega_1, \omega_2, \mu) \,, \\ \tilde{\Psi}_4(\omega_1, \omega_2, \mu) =& \Psi_V(\omega_1, \omega_2, \mu) - \tilde{X}_A(\omega_1, \omega_2, \mu) \,, \\ \Phi_5(\omega_1, \omega_2, \mu) =& \Psi_A(\omega_1, \omega_2, \mu) + \Psi_V(\omega_1, \omega_2, \mu) + 2 \, \left [ Y_A - \tilde{Y}_A + W \right ] (\omega_1, \omega_2, \mu)\,, \\ \Psi_5(\omega_1, \omega_2, \mu) =& - \Psi_A(\omega_1, \omega_2, \mu) + X_A(\omega_1, \omega_2, \mu) - 2 \, Y_A(\omega_1, \omega_2, \mu) \,, \\ \tilde{\Psi}_5(\omega_1, \omega_2, \mu) = & - \Psi_V(\omega_1, \omega_2, \mu) - \tilde{X}_A(\omega_1, \omega_2, \mu) + 2 \, \tilde{Y}_A(\omega_1, \omega_2, \mu) \,, \\ \Phi_6(\omega_1, \omega_2, \mu) = & \Psi_A(\omega_1, \omega_2, \mu) - \Psi_V(\omega_1, \omega_2, \mu) + 2 \, \left [ Y_A + \tilde{Y}_A + W - 2 \, Z \right ] (\omega_1, \omega_2, \mu) \,, \end{aligned}$

(21) the nontrivial relations for the D-meson LCDAs in the momentum space could be obtained
$\begin{aligned}[b] - \omega \, {{\rm d} \over {\rm d} \omega} \, \phi_D^-(\omega, \mu) =& \phi_D^+(\omega, \mu) - 2 \, \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2^2} \, \Phi_3(\omega, \omega_2, \mu) + 2 \, \int_0^{\omega} \, \, {{\rm d} \omega_2 \over \omega_2^2} \, \Phi_3(\omega-\omega_2, \omega_2, \mu) \\& + \, 2 \, \int_0^{\omega} \, \, {{\rm d} \omega_2 \over \omega_2} \, {{\rm d} \over {\rm d} \omega} \, \Phi_3(\omega-\omega_2, \omega_2, \mu) \,, \end{aligned} $

(22) $ \begin{aligned}[b] -2 \, {{\rm d}^2 \over {\rm d} \omega^2} \, g_D^+(\omega, \mu) = & \left [ {3 \over 2} + (\omega - \bar \Lambda) \, {{\rm d} \over {\rm d} \omega} \right ] \, \phi_D^+(\omega, \mu) - {1 \over 2} \, \phi_D^-(\omega, \mu) + \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2 } \, {{\rm d} \over {\rm d} \omega} \, \Psi_4(\omega, \omega_2, \mu) \\ & - \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2^2 } \, \Psi_4(\omega, \omega_2, \mu) + \int_0^{\omega} \, {{\rm d} \omega_2 \over \omega_2^2 } \, \Psi_4(\omega-\omega_2, \omega_2, \mu) \,, \end{aligned}$

(23) $ \begin{aligned}[b] -2 \, {{\rm d}^2 \over {\rm d} \omega^2} \, g_D^-(\omega, \mu) = & \left [ {3 \over 2} + (\omega - \bar \Lambda) \, {{\rm d} \over {\rm d} \omega} \right ] \, \phi_D^-(\omega, \mu) - {1 \over 2} \, \phi_D^+(\omega, \mu) + \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2 } \, {{\rm d} \over {\rm d} \omega} \, \Psi_5(\omega, \omega_2, \mu) \\& - \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2^2 } \, \Psi_5(\omega, \omega_2, \mu) + \int_0^{\omega} \, {{\rm d} \omega_2 \over \omega_2^2 } \, \Psi_5(\omega-\omega_2, \omega_2, \mu) \,, \end{aligned} $

(24) $ \begin{aligned}[b] \phi_D^-(\omega, \mu) =& \left (2 \, \bar \Lambda - \omega \right ) \, {{\rm d} \phi_D^+(\omega, \mu) \over {\rm d} \omega} - 2 \, \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2^2 } \, \Phi_4(\omega, \omega_2, \mu) + \, 2 \, \int_0^{\omega} \, {{\rm d} \omega_2 \over \omega_2} \, \left ( {{\rm d} \over {\rm d} \, \omega_2} + {{\rm d} \over {\rm d} \, \omega} \right ) \, \Phi_4(\omega-\omega_2, \omega_2, \mu) \\ &+ \, 2 \, \int_0^{\omega} \, {{\rm d} \omega_2 \over \omega_2} \, {{\rm d} \over {\rm d} \omega} \, \, \Psi_4(\omega-\omega_2, \omega_2, \mu) - \, 2 \, \int_0^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {{\rm d} \over {\rm d} \omega} \, \, \Psi_4(\omega, \omega_2, \mu) \,, \end{aligned} $

(25) which is consistent with Fourier transformed results from [35] (see appendix for details). By inserting two-particle D-meson LCDAs into the correlation function, one could obtain two-particle higher-twist corrections to the vacuum-to-D-meson correlation function at the tree-level
$ \begin{aligned}[b] \Pi_{\mu, \, V}^{\rm 2PHT} =& - 4 \, {\tilde{f}_D(\mu) \, m_D \over n \cdot p } \, \bar n_{\mu} \, \bigg \{ - {1 \over 2} \, \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \, \int_0^1 {\rm d} u \, {\bar u \, \Psi_5(\omega_1, \omega_2, \mu) \over (\bar n \cdot p - \omega_1 - u \, \omega_2)^2} + \int_0^{\infty} \, {{\rm d} \omega \over (\bar n \cdot p -\omega)^2} \, \hat{g}_D^-(\omega, \mu) \bigg \} \,, \\ \Pi_{\mu, \, T}^{\rm 2PHT} =& 2 \, {\rm i} \, {\tilde{f}_D(\mu) \, m_D^2 \over n \cdot p } \, \, \left [ n_{\mu} - {n \cdot q \over m_D} \, \bar n_{\mu} \right ] \, \bigg \{ - {1 \over 2} \, \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \, \int_0^1 {\rm d} u \, {\bar u \, \Psi_5(\omega_1, \omega_2, \mu) \over (\bar n \cdot p - \omega_1 - u \, \omega_2)^2} \, + \int_0^{\infty} \, {{\rm d} \omega \over (\bar n \cdot p -\omega)^2} \, \hat{g}_D^-(\omega, \mu) \bigg \} \,, \end{aligned} $

(26) where
$ \hat{g}_D^{-}(\omega, \mu) $ is given by$ \hat{g}_D^-(\omega, \mu) = {1 \over 4} \, \int_{\omega}^{\infty} \, {\rm d} \rho \, \bigg \{ (\rho - \omega) \, \left [ \phi_D^+(\rho) - \phi_D^-(\rho) \right ] - 2 \, (\bar \Lambda - \rho) \, \phi_D^-(\rho) \bigg \} \,. $

(27) Collecting the two-particle and three-particle contributions at the tree-level, and matching the hadronic- and partonic-level predictions with the aid of the dispersion relation, the following expressions are obtained after the Borel transformation:
$ \begin{aligned}[b] & {f_{P} \, n \cdot p \over 2} \,\, {\rm exp} \left [- {m_{P}^2 \over n \cdot p \,\, \omega_M} \right ] \,\, \left [ f_{D \to P}^{+, \, \rm HT}(q^2) + \frac{m_D} {n \cdot p} \, f_{D \to P}^{0, \, \rm HT}(q^2) \right ] \,\\ =& - {\tilde{f}_D(\mu) \, m_D \over n \cdot p} \, \Bigg \{ {\rm e}^{-\omega_s/\omega_M} \, H_{\bar n, \rm LP}^{\rm 2PHT}(\omega_s, \mu) + \int_0^{\omega_s} \, {\rm d} \omega^{\prime} \, {1 \over \omega_M} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, H_{\bar n, \rm LP}^{\rm 2PHT}(\omega^{\prime}, \mu) \\ & + \int_0^{\omega_s} \, {\rm d} \omega_1 \, \int_{\omega_s - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {\rm e}^{-\omega_s/\omega_M} \, \Bigg [ H_{\bar n, \rm LP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) + {m_q \over n \cdot p} \, H_{\bar n, \rm NLP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] \\ & + \int_0^{\omega_s} \, {\rm d} \omega^{\prime} \, \int_0^{\omega^{\prime}} \, {\rm d} \omega_1 \, \int_{\omega^{\prime} - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {1 \over \omega_M} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, \Bigg [ H_{\bar n, \rm LP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) + {m_q \over n \cdot p} \,H_{\bar n, \rm NLP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] \Bigg \} \,, \end{aligned} $

(28) $ \begin{aligned}[b] &{f_{P} \, n \cdot p \over 2} \,\, {\rm exp} \left [- {m_{P}^2 \over n \cdot p \,\, \omega_M} \right ] \, {m_D \over n \cdot p -m_D} \, \left [ f_{D \to P}^{+, \, \rm HT}(q^2) - \frac{m_D} {n \cdot p} \, f_{D \to P}^{0, \, \rm HT}(q^2) \right ] \, \\ =& - {\tilde{f}_D(\mu) \, m_D \over n \cdot p} \, \Bigg \{ \int_0^{\omega_s} \, {\rm d} \omega_1 \, \int_{\omega_s - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {\rm e}^{-\omega_s/\omega_M} \, \Bigg [ H_{n, \rm LP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \\ & + {m_q \over n \cdot p} \, H_{n, \rm NLP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] + \int_0^{\omega_s} \, {\rm d} \omega^{\prime} \, \int_0^{\omega^{\prime}} \, {\rm d} \omega_1 \, \int_{\omega^{\prime} - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {1 \over \omega_M} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, \Bigg [ H_{n, \rm LP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \\ & + {m_q \over n \cdot p} \,H_{n, \rm NLP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] \Bigg \} \,, \end{aligned} $

(29) $ \begin{aligned}[b]f_{P} \, n \cdot p \, {\rm exp} \left [- {m_{P}^2 \over n \cdot p \,\, \omega_M} \right ] \,\, f_{D \to P}^{T, \, \rm HT}(q^2) \, =& - {\tilde{f}_D(\mu) \, (m_D +m_P) \over n \cdot p} \, \Bigg \{ {\rm e}^{-\omega_s/\omega_M} \, H_{T, \rm LP}^{\rm 2PHT}(\omega_s, \mu) + \int_0^{\omega_s} \, {\rm d} \omega^{\prime} \, {1 \over \omega_M} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, H_{T, \rm LP}^{\rm 2PHT}(\omega^{\prime}, \mu) \\ & + \int_0^{\omega_s} \, {\rm d} \omega_1 \, \int_{\omega_s - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {\rm e}^{-\omega_s/\omega_M} \, \Bigg [ H_{T, \rm LP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \end{aligned} $

$ \begin{aligned}[b]& + {m_q \over n \cdot p} \, H_{T, \rm NLP}^{\rm 3PHT} \left ({\omega_s - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] + \int_0^{\omega_s} \, {\rm d} \omega^{\prime} \, \int_0^{\omega^{\prime}} \, {\rm d} \omega_1 \, \int_{\omega^{\prime} - \omega_1}^{\infty} \, {{\rm d} \omega_2 \over \omega_2} \, {1 \over \omega_M} \, {\rm e}^{-\omega^{\prime}/\omega_M} \, \Bigg [ H_{T, \rm LP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \\& + {m_q \over n \cdot p} \,H_{T, \rm NLP}^{\rm 3PHT} \left ({\omega^{\prime} - \omega_1 \over \omega_2}, \omega_1, \omega_2, \mu \right ) \Bigg ] \Bigg \} \,, \end{aligned} $

(30) where
$ H_{i, \rm LP}^{\rm 2PHT} $ and$ H_{i, \rm (N)LP}^{\rm 3PHT} $ ($ i = n, \, \bar n, \, T $ ) are given by$ \begin{aligned}[b] H_{\bar n, \rm LP}^{\rm 2PHT}(\omega, \mu) =& H_{T, \rm LP}^{\rm 2PHT}(\omega, \mu) = 4 \, \hat{g}_D^-(\omega, \mu) \,, \\ H_{n, \rm LP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) =& 2 \, (u-1) \, \Phi_4(\omega_1, \omega_2, \mu) \,, \\ H_{n, \rm NLP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) =& \tilde{\Psi}_5(\omega_1, \omega_2, \mu) - \Psi_5(\omega_1, \omega_2, \mu) \,, \\ H_{\bar n, \rm LP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) =& \tilde{\Psi}_5(\omega_1, \omega_2, \mu) - \Psi_5(\omega_1, \omega_2, \mu) \,, \\ H_{\bar n, \rm NLP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) =& 2 \,\Phi_6(\omega_1, \omega_2, \mu) \,, \\ H_{T, \rm LP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) = & 2\, (1-u) \,\Phi_4(\omega_1, \omega_2, \mu) - \Psi_5(\omega_1, \omega_2, \mu) + \tilde{\Psi}_5(\omega_1, \omega_2, \mu) \,, \\ H_{T, \rm NLP}^{\rm 3PHT} (u, \omega_1, \omega_2, \mu) =& \Psi_5(\omega_1, \omega_2, \mu) - \tilde{\Psi}_5(\omega_1, \omega_2, \mu) + 2 \, \Phi_6(\omega_1, \omega_2, \mu) \,. \end{aligned} $

(31) One can observe from equations (28)-(30) that the large recoil symmetry is broken by three-particle higher-twist contributions. Finally, we obtain the sum rules for the
$ D\to P $ form factors, as follows:$ \begin{aligned}[b] f_{D \to P}^+(q^2) = & f_{D \to P}^{+, \rm 2PNLL}(q^2) + f_{D \to P}^{+, \, \rm 2PHT}(q^2) + f_{D \to P}^{+, \, \rm 3PHT}(q^2) \,, \\ f_{D \to P}^{0}(q^2) =& f_{D \to P}^{0, \rm 2PNLL}(q^2) + f_{D \to P}^{0, \, \rm 2PHT}(q^2) + f_{D \to P}^{0, \, \rm 3PHT}(q^2) \,, \\ f_{D \to P}^{T}(q^2) = & f_{D \to P}^{T, \rm 2PNLL}(q^2) + f_{D \to P}^{T, \, \rm 2PHT}(q^2) + f_{D \to P}^{T, \, \rm 3PHT}(q^2) \, \end{aligned} $

(32) where all the three form factors are
$ \mathcal{ O}(\Lambda/m_c)^{5/2} $ . -
D-meson LCDAs are the fundamental nonperturbative inputs in the D-meson LCSR. The model of the higher-twist D-meson LCDAs can be expressed with the matrix elements of local operators [20],
$ \begin{aligned}[b]\\[-8pt] \langle 0 | \bar q \, g_s \, G_{\mu \nu} \, \Gamma \, h_v | \bar D(v) \rangle = - {\tilde{f}_D(\mu) \, m_D \over 6} \, \Bigg \{ {\rm i} \, \lambda_H^2 {\rm Tr} \left [ \gamma_5 \, \Gamma \, {1 + \not v \over 2} \, \sigma_{\mu \nu} \right ] + \, (\lambda_H^2 - \lambda_E^2) \,{\rm Tr} \left [ \gamma_5 \, \Gamma \, {1 + \not v \over 2} \, (v_{\mu} \, \gamma_{\nu} - v_{\nu} \, \gamma_{\mu} ) \right ] \Bigg \} \,. \end{aligned} $ 
(33) Implementing the standard strategy of the LCSR, one obtains the three-particle higher-twist D-meson LCDA sum rules, as follows [33]
$ \begin{aligned}[b]\\[-6pt] [\tilde{f}_D(\mu)]^2 \, m_D \, (\lambda_H^2 + \lambda_E^2) \, \Phi_5(\omega_1, \omega_2, \mu) \, =& - {g_s^2 \, C_F \, N_c \over 96 \, \pi^4} \, \int_{\omega_1 + \omega_2 \over 2}^{\omega_0} \, {\rm d}s \, {\rm exp} \left [{\bar \Lambda - s \over \omega_M} \right ] \, \omega_1 \, (\omega_1 + \omega_2 - 2 \, s)^3 \, \theta(2 \, s - \omega_1 - \omega_2) \,, \\ [\tilde{f}_D(\mu)]^2 \, m_D \, (\lambda_H^2 + \lambda_E^2) \, \Psi_5(\omega_1, \omega_2, \mu) \, =& {g_s^2 \, C_F \, N_c \over 192 \, \pi^4} \, \int_{\omega_1 + \omega_2 \over 2}^{\omega_0} \, {\rm d}s \, {\rm exp} \left [{\bar \Lambda - s \over \omega_M} \right ] \, \omega_2 \, (\omega_1 + \omega_2 - 2 \, s)^3 \, \theta(2 \, s - \omega_1 - \omega_2) \,, \\[\tilde{f}_D(\mu)]^2 \, m_D \, (\lambda_H^2 + \lambda_E^2) \, \tilde{\Psi}_5(\omega_1, \omega_2, \mu) \, = &{g_s^2 \, C_F \, N_c \over 192 \, \pi^4} \, \int_{\omega_1 + \omega_2 \over 2}^{\omega_0} \, {\rm d}s \, {\rm exp} \left [{\bar \Lambda - s \over \omega_M} \right ] \, \omega_2 \, (\omega_1 + \omega_2 - 2 \, s)^3 \, \theta(2 \, s - \omega_1 - \omega_2) \,, \\ [\tilde{f}_D(\mu)]^2 \, m_D \, (\lambda_E^2 - \lambda_H^2) \, \Phi_6(\omega_1, \omega_2, \mu) \, =& {g_s^2 \, C_F \, N_c \over 128 \, \pi^4} \, \int_{\omega_1 + \omega_2 \over 2}^{\omega_0} \, {\rm d}s \, {\rm exp} \left [{\bar \Lambda - s \over \omega_M} \right ] \, (\omega_1 + \omega_2 - 2 \, s)^4 \, \theta(2 \, s - \omega_1 - \omega_2) \,,\end{aligned} $

(34) We first introduce the local duality model by taking the limit
$ \omega_M\to\infty $ of the sum rules (34). Using the normalization conditions [33]$ \begin{aligned}[b] \Phi_5(z_1 = z_2 = 0, \mu) =& \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \,\, \Phi_5(\omega_1, \omega_2, \mu) = {\lambda_E^2 + \lambda_H^2 \over 3} \,, \\ \Psi_5(z_1 = z_2 = 0, \mu) =& \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \,\, \Psi_5(\omega_1, \omega_2, \mu) = - {\lambda_E^2 \over 3} \,, \\ \tilde{\Psi}_5(z_1 = z_2 = 0, \mu) =& \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \,\, \tilde{\Psi}_5(\omega_1, \omega_2, \mu) = - {\lambda_H^2 \over 3} \,, \\ \Phi_6(z_1 = z_2 = 0, \mu) =& \int_0^{\infty} \, {\rm d} \omega_1 \, \int_0^{\infty} \, {\rm d} \omega_2 \,\, \Phi_6(\omega_1, \omega_2, \mu) = {\lambda_E^2 - \lambda_H^2 \over 3} \,, \end{aligned} $

(35) we obtain the local duality models for the twist-five and twist-six D-meson LCDAs,
$ \begin{aligned}[b] \Phi_5^{\rm LD}(\omega_1, \omega_2, \mu) =& {35 \over 64} \, (\lambda_E^2 + \lambda_H^2) \, {\omega_1 \over \omega_0^7} \, (2 \, \omega_0 - \omega_1-\omega_2)^4 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \Psi_5^{\rm LD}(\omega_1, \omega_2, \mu) =& - {35 \over 64} \, \lambda_E^2 \, {\omega_2 \over \omega_0^7} \, (2 \, \omega_0 - \omega_1-\omega_2)^4 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \tilde{\Psi}_5^{\rm LD}(\omega_1, \omega_2, \mu) =& - {35 \over 64} \, \lambda_H^2 \, {\omega_2 \over \omega_0^7} \, (2 \, \omega_0 - \omega_1-\omega_2)^4 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \Phi_6^{\rm LD}(\omega_1, \omega_2, \mu) = & {7 \over 64} \, (\lambda_E^2 - \lambda_H^2) \, {1 \over \omega_0^7} \, (2 \, \omega_0 - \omega_1-\omega_2)^5 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,,\end{aligned} $

(36) and they satisfy the following asymptotic behaviors [33]
$ \Phi_5(\omega_1, \omega_2, \mu) \sim \omega_1 \,, \qquad \Psi_5(\omega_1, \omega_2, \mu) \sim \tilde{\Psi}_5(\omega_1, \omega_2, \mu) \sim \omega_2 \,, \qquad \Phi_6(\omega_1, \omega_2, \mu) \sim 1 \,. $

(37) The remaining models for the two-particle and three-particle D-meson LCDAs are given by [35]
$ \begin{aligned}[b] \phi_D^{+, \rm LD}(\omega, \mu) =& {5 \over 8 \, \omega_0^5} \, \omega(2 \, \omega_0 - \omega)^3 \, \theta(2 \, \omega_0 - \omega)\,, \\ \phi_D^{-, \rm LD}(\omega, \mu) = & {5 (2 \, \omega_0 - \omega)^2 \over 192\, \omega_0^5} \, \bigg \{6 \, (2 \, \omega_0 - \omega)^2 - {7 \, (\lambda_E^2 - \lambda_H^2) \over \omega_0^2} \, (15 \, \omega^2 - 20 \, \omega \, \omega_0 + 4 \, \omega_0^2) \bigg \} \, \theta(2 \, \omega_0 - \omega)\,, \\ \Phi_3^{\rm LD}(\omega_1, \omega_2, \mu) = & {105 \, (\lambda_E^2 - \lambda_H^2) \over 8 \, \omega_0^7} \, \omega_1 \, \omega_2^2 \, \left (\omega_0 - {\omega_1 + \omega_2 \over 2} \right )^2 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \Phi_4^{\rm LD}(\omega_1, \omega_2, \mu) =& {35 \, (\lambda_E^2 + \lambda_H^2) \over 4 \, \omega_0^7} \, \omega_2^2 \, \left (\omega_0 - {\omega_1 + \omega_2 \over 2} \right )^3 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \Psi_4^{\rm LD}(\omega_1, \omega_2, \mu) =& {35 \, \lambda_E^2 \over 2 \, \omega_0^7} \, \omega_1 \, \omega_2 \, \left (\omega_0 - {\omega_1 + \omega_2 \over 2} \right )^3 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,, \\ \tilde{\Psi}_4^{\rm LD}(\omega_1, \omega_2, \mu) = & {35 \, \lambda_H^2 \over 2 \, \omega_0^7} \, \omega_1 \, \omega_2 \, \left (\omega_0 - {\omega_1 + \omega_2 \over 2} \right )^3 \, \theta(2 \, \omega_0 - \omega_1 - \omega_2) \,. \end{aligned}$

(38) The effective LCDA defined in (27) can be obtained using the above formulae, as follows:
$ \begin{aligned} \hat{g}_D^{-, \rm LD}(\omega, \mu) = {\omega \, (2 \, \omega_0 - \omega)^3 \over \omega_0^5} \, \left \{ {5 \over 256} \, (2 \, \omega_0 - \omega)^2 - {35 \, (\lambda_E^2 - \lambda_H^2) \over 1536} \, \left [ 4 - 12 \, \left ( {\omega \over \omega_0} \right ) + 11 \, \left ( {\omega \over \omega_0} \right )^2 \right ]\right \} \, \theta(2 \, \omega_0 - \omega) \,,\end{aligned}$

(39) with the following equation of motion (EOM) constraint [35]
$ \omega_0 = {5 \over 2} \, \lambda_D = 2 \, \bar \Lambda\,, \qquad 3 \, \omega_0^2 = 14 \, (2 \, \lambda_E^2 + \lambda_H^2)\,. $

(40) Combined with the asymptotic behaviors (37), the exponential model for the twist-five and twist-six D-meson LCDAs can be obtained by implementing an exponential falloff at large momenta, as follows:
$ \begin{aligned}[b]\Phi_5^{\rm exp}(\omega_1, \omega_2, \mu) =& {\lambda_E^2 + \lambda_H^2 \over 3 \, \omega_0^3} \, \omega_1 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \Psi_5^{\rm exp}(\omega_1, \omega_2, \mu) = & - {\lambda_E^2 \over 3 \, \omega_0^3} \, \omega_2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \tilde{\Psi}_5^{\rm exp}(\omega_1, \omega_2, \mu) =& - {\lambda_H^2 \over 3 \, \omega_0^3} \, \omega_2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \Phi_6^{\rm exp}(\omega_1, \omega_2, \mu) = & {\lambda_E^2 - \lambda_H^2 \over 3 \, \omega_0^2} \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,. \end{aligned} $

(41) Exponential models for the remaining D-meson LCDAs have been evaluated in [35], and their corresponding expressions are given by
$ \begin{aligned}[b] \phi_D^{+, \, \rm exp}(\omega, \mu) =& {\omega \over \omega_0^2} \, {\rm e}^{-\omega/\omega_0} \,, \\ \phi_D^{-, \, \rm exp}(\omega, \mu) =& {1 \over \omega_0} \, {\rm e}^{-\omega/\omega_0} - {\lambda_E^2 - \lambda_H^2 \over 9 \, \omega_0^3} \,\\&\times \left [ 1 - 2 \, \left ( {\omega \over \omega_0} \right ) + {1 \over 2} \, \left ( {\omega \over \omega_0} \right )^2 \right ] \, {\rm e}^{-\omega/\omega_0} \,, \\ \Phi_3^{\rm exp}(\omega_1, \omega_2, \mu) =& {\lambda_E^2 - \lambda_H^2 \over 6 \, \omega_0^5} \, \omega_1 \, \omega_2^2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \Phi_4^{\rm exp}(\omega_1, \omega_2, \mu) =& {\lambda_E^2 + \lambda_H^2 \over 6 \, \omega_0^4} \, \omega_2^2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \Psi_4^{\rm exp}(\omega_1, \omega_2, \mu) =& {\lambda_E^2 \over 3 \, \omega_0^4} \, \omega_1 \, \omega_2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \,, \\ \tilde{\Psi}_4^{\rm exp}(\omega_1, \omega_2, \mu) =& {\lambda_H^2 \over 3 \, \omega_0^4} \, \omega_1 \, \omega_2 \, {\rm e}^{-(\omega_1 + \omega_2)/\omega_0} \, \end{aligned} $

(42) and the expression for the two-particle twist-five LCDA reads
$\hat{g}_D^{-, \, \rm exp}(\omega, \mu) = \omega \, \left \{ {3 \over 4} - {\lambda_E^2 - \lambda_H^2 \over 12 \, \omega_0^2} \, \left [ 1 - \left ( {\omega \over \omega_0} \right ) + {1 \over 3} \, \left ( {\omega \over \omega_0} \right )^2 \right ] \right \} \, {\rm e}^{-\omega/\omega_0} \, $

(43) with the EOM constraints [35]
$\omega_0 = \lambda_D = {2 \over 3} \, \bar \Lambda\,, \qquad 2 \, \bar \Lambda^2 = 2 \, \lambda_E^2 + \lambda_H^2 \,. $

(44) Two different D-meson LCDA models, the exponential model and the local duality model, were adopted in this work. Because the three HQET parameters
$ \lambda_D(\mu) $ ,$ \lambda_E(\mu) $ , and$ \lambda_H(\mu) $ are constrained by the EOM, and the ratio$ R(\mu) $ ($ R(\mu) = \lambda_E^2(\mu)/\lambda_H^2(\mu) $ ) is insensitive to perturbative and nonperturbative QCD corrections, we will consider$ R(\mu) $ and$ \lambda_D(\mu) $ as the input in our numerical analysis. The renormalization scale dependence of the inverse moment is evaluated from the one loop equation of$ \phi_D(\omega,\mu) $ [37, 38]$\frac{\lambda_D(\mu_0)}{\lambda_D(\mu)} = 1 + {\alpha_s(\mu_0) \, C_F \over 4 \, \pi} \, \ln {\mu \over \mu_0} \, \left [2 - 2\, \ln {\mu \over \mu_0} - 4 \, \sigma_{1}(\mu_0) \right ] + {\cal O}(\alpha_s^2)\,, $

(45) and the definition of the inverse-logarithmic moment
$ \sigma_{i}(\mu_0) $ is [39]$ \sigma_n(\mu) = \lambda_D(\mu)\int_{0}^{\infty}\frac{{\rm d}\omega}{\omega}{\rm ln}^n\frac{\mu_0}{\omega}\phi_{D}^+(\omega,\mu). $

(46) We obtain the values of
$ \lambda_D(\mu_0) $ by matching our predicted zero momentum transfer$ D\to\pi $ vector form factor with the results from pion LCDAs$ f_{D\to\pi}^+(0) = 0.67_{-0.07}^{+0.10} $ [25]$ \lambda_D(\mu_0) = \left\{ \begin{array}{l} 260^{+24}_{-34} \,\, {\rm MeV} \,, \quad (\rm Exponential \,\, Model) \\ 295^{+25}_{-33} \,\, {\rm MeV} \,. \quad (\rm Local \,\, Duality \,\, Model) \end{array} \right. \, $

(47) -
Except for the D-meson LCDAs, we present various values of input parameters in Table 1. The masses and lifetimes of hadrons, and quark masses in the
$ \overline{\rm{MS}} $ scheme were taken from the Particle Data Group (PDG) [40]. The factorization scale interval$ \mu\in[1,1.4]\,\rm GeV $ with the central value$1.2\;\rm GeV$ was the same as in [41], where the maximum of the factorization scale was consistent with [25]. In the sum rules, we used the same internal sum rule parameters as in [42]Parameter DATA Parameter DATA $ m_D $ 

$ 1.86965\pm0.05\, \rm GeV $ 

$ \mu_{h1} $ 

$ 1.288\pm0.020\, \rm GeV $ 

$ \tau_D $ 

$ (1.040\pm0.007)\times10^{-12}\,s $ 

$ \mu_{h2} $ 

$ 1.288\pm0.020\, \rm GeV $ 

$ m_c $ 

$ 1.288\pm0.020\, \rm GeV $ 

$ \mu_0 $ 

$ 1\, \rm GeV $ 

$ m_d $ 

$ 4.71\pm0.09\, \rm MeV $ 

$ f_D $ 

$ 212.0\pm0.7\, \rm MeV $ 

$ \lambda_E^2/\lambda_H^2 $ 

$ 0.5\pm0.1\,\rm GeV^2 $ 

$ \sigma_1(\mu_0) $ 

$ 1.5\pm1 $ 

$ 2\lambda_E^2+\lambda_H^2 $ 

$ 0.25\pm0.15\,\rm GeV^2 $ 

$ \sigma_2(\mu_0) $ 

$ 3\pm2 $ 

$ \bar{\Lambda} $ 

$ 0.58\, \rm GeV $ 

$ \begin{aligned}[b]M^2 =& (1.25 \pm 0.25) \, {\rm GeV^2},\,\\ s_0^{\pi} =& (0.70 \pm 0.05) \, {\rm GeV^2},\\\, s_0^{K} =& (1.05 \pm 0.05) \, {\rm GeV^2}.\end{aligned} $

(48) In the following discussion, we will take the exponential model as the default model of D-meson LCDAs. We firstly focus on the breakdown of different contributions to the
$ D\to\pi $ vector form factors. As shown in Fig. 2, for the leading power contribution, the NLL resummation will lead to a (5%–17%) reduction of the leading logarithmic (LL) result. As for the power suppressed contributions, the two-particle twist-five contribution is the dominant contribution, which leads to the$ {\mathcal O} $ (27%–36%) correction to the leading power form factor$ f_{D\to\pi}^+(q^2) $ of$ D\to\pi $ . However, the three-particle higher-twist contribution is tiny, which reduces the form factor$ f_{D\to\pi}^{+,\rm 2\,PNLL} $ by$ {\cal O}$ (1%). The SU(3) flavor symmetry breaking effects between different final states of pion and kaon are defined as
Figure 2. (color online) The momentum-transfer dependence of the vector
$ D\to\pi $ form factors, different form factors from the leading power LL contribution, the leading power NLL contribution, the two-particle higher-twist contribution and the three-particle higher-twist contribution are listed.$ R_{ SU(3)}^{i} (q^2) = \frac{f_{D \to K}^{i}(q^2)}{f_{D \to \pi}^{i}(q^2)} \,, \qquad ({\rm with} \,\, i = +, \, 0, \, T) \, $

(49) and the results are presented in Fig. 3. The SU(3) flavor symmetry breaking effects of the scalar and vector form factors
$R_{SU(3)}^{0,+} (0)$ were adjusted to reproduce the results from pion LCDA [25], and the tensor result$R_{SU(3)}^{T} (0)$ = 1.39 agreed with the result from Lattice QCD [17],$R_{SU(3)}^{T} (0)$ = 1.36. As we neglected the masses of the up and down quarks, the SU(3) flavor symmetry breaking effects originated from the strange quark mass, the difference between the pion and kaon threshold parameters, and the discrepancy between the decay constants$ f_{\pi} $ and$ f_{K} $ . Different from the B-meson decays, the strange quark appeared in the charged current of D decays. The dependencies of the leading power form factor at NLL$ f_{D\to\pi}^{+,\rm NLL} $ and total form factor$ f_{D\to\pi}^{+,\rm tot} $ of$ D\to\pi $ at$ q^2 = 0 $ on the Borel parameter$ M^2 $ , the effective threshold parameter$ s_0 $ , and the factorization scale$ \mu $ are shown in Fig. 1. Observing the left two panels, we find that the uncertainties owing to$ M^2 $ and$ s_0 $ are both$ {\cal O} $ (10%), and the higher-twist contributions to the leading power form factor are insensitive to the HQET parameters. As shown in the right panel of Fig. 1, the uncertainty owing to the factorization scale is small in the interval of$ \mu\in[1,1.4]\,\rm GeV $ .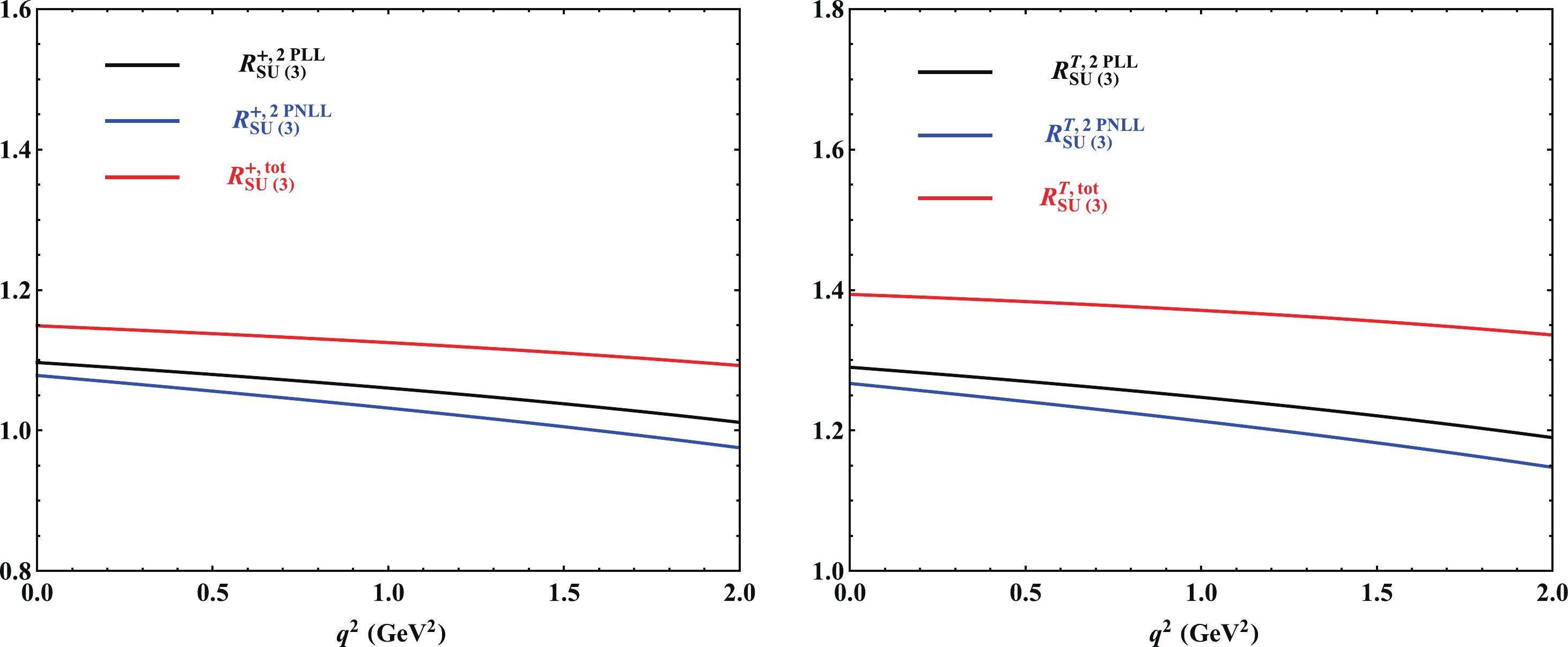
Figure 3. (color online) The SU(3)-flavor symmetry breaking effects between the
$ D\to\pi $ and$ D\to K $ form factors from the vector and tensor$ c\to q $ weak current.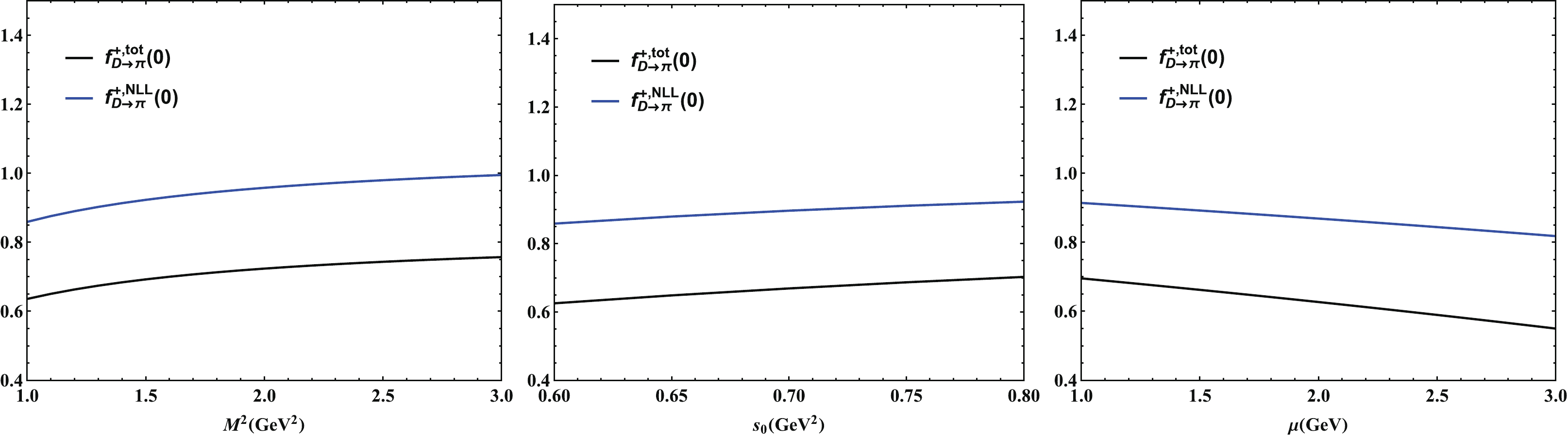
Figure 1. (color online) Dependencies of the vector
$ D\to\pi $ form factors on the Borel parameter$ M^2 $ , the effective threshold$ s_0 $ , and the factorization scale$ \mu $ .To guarantee the reliability of the LCSR, we directly calculated the form factors in the space-like region
$ q^2\in[-2,\,0]\,\rm GeV^2 $ . The results could be analytically continued to the positive kinematic region by applying the following conformal transformation:$z(q^2, t_0) = \frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}} {\sqrt{t_+-q^2}+\sqrt{t_+-t_0}} \,, $

(50) then, the branching cut region of
$ q^2 $ was mapped onto a disk$ |z(q^2, \, t_0)|\leqslant 1 $ . In the above equation,$ t_{+} $ and$ t_0 $ are given by$ t_+ = (m_D + m_{P})^2 $

(51) $ t_0 = (m_D + m_P) \, (\sqrt{m_D} + \sqrt{m_P})^2 \,. $

(52) The series expansion for the
$ D\to P $ form factors is similar to that for the B-meson decay [43], owing to the heavy quark symmetry$ \begin{aligned}[b] f_{D \to P}^{+, T}(q^2) =& {f_{D \to P}^{+, T}(0) \over 1 - q^2/m_{D_{(s)}^{\ast}}^2} \, \bigg \{ 1 + \, \sum_{k = 1}^{N-1} \, b_{k, P}^{+, T} \, \bigg ( z(q^2, \, t_0)^k - z(0, \, t_0)^k \\ &- \, (-1)^{N-k} \, {k \over N} \, \left [ z(q^2, \, t_0)^N - z(0, \, t_0)^N \right ] \bigg ) \bigg \} \,, \\ f_{D \to P}^{0}(q^2) =& f_{D \to P}^{0}(0) \, \left \{ 1 + \, \sum_{k = 1}^{N} \, b_{k, P}^{0} \, \left ( z(q^2, \, t_0)^k - z(0, \, t_0)^k \right ) \right \} \,, \end{aligned} $

(53) where we set N= 2 for vector and tensor form factors and N= 1 for scalar form factors.
In [44], certain symmetries of the soft contributions with large final state light meson momentum have been studied, which could be broken by perturbative QCD corrections and higher-twist contributions. These large recoil symmetry relations for the form factors are as follows [45]:
$ f_+(q^2) = \frac{m_D}{n\cdot p} \, f_0(q^2) = \frac{m_D}{m_D+m_P} \, f_T(q^2). $

(54) Within the framework of QCD factorization (QCDF), we could obtain the factorization formulae for the heavy-to-light D-meson form factors at one loop from [45], by changing the bottom quark to a charm quark
$ \begin{aligned}[b]f_{D \to P}^{0}(q^2) =& {n \cdot p \over m_D} \, f_{D \to P}^+(q^2) \,\left [ 1 + {\alpha_s \, C_F \over 2 \, \pi} \, \left (1 - { n \cdot p \over n \cdot p - m_D} \, \ln {n \cdot p \over m_D} \right ) \right ] \, \\&+ \, {m_D - n \cdot p \over n \cdot p } \, {\alpha_s \, C_F \over 4 \, \pi} \, {8\, \pi^2 \, f_D \, f_P \over N_c \, m_D} \, \int_0^1 \, {\rm d} u \, { \phi_P(u, \mu) \over \bar u} \,\int_0^{\infty} \, {\rm d} \omega \, {\phi_D^+(\omega, \mu) \over \omega} \,, \end{aligned} $ 
(55) $ \begin{aligned}[b] f_{D \to P}^{T}(q^2) =& {m_D + m_P \over m_D} \, f_{D \to P}^+(q^2) \, \left [ 1 + {\alpha_s \, C_F \over 4 \, \pi} \, \left ( \ln {m_c^2 \over \mu^2} + 2\, { n \cdot p \over n \cdot p - m_D} \, \ln {n \cdot p \over m_D} \right ) \right ] \, \\& - \, {m_D + m_P \over n \cdot p } \, {\alpha_s \, C_F \over 4 \, \pi} \, {8\, \pi^2 \, f_D \, f_P \over N_c \, m_D} \, \int_0^1 \, {\rm d} u \, { \phi_P(u, \mu) \over \bar u} \, \int_0^{\infty} \, {\rm d} \omega \, {\phi_D^+(\omega, \mu) \over \omega} \,, \end{aligned}$

(56) where
$ \phi_P(u, \mu) $ denotes the twist-two pseudoscalar meson LCDA. The form factor ratios for the semi-leptonic D-meson decay could be obtained from (54)$ \begin{aligned}[b]& R_{D \to \pi}^{0 \, +}(q^2) = {m_D \over n \cdot p} \, {f_{D \to \pi}^{0}(q^2) \over f_{D \to \pi}^+(q^2)} \,, \\& R_{D \to \pi}^{T \, +}(q^2) = {m_D \over m_D + m_{\pi}} \, {f_{D \to \pi}^{T}(q^2) \over f_{D \to \pi}^+(q^2)} \,, \end{aligned}$

(57) and the predictions of QCDF and LCSR are shown in Fig. 4. We find that the predictions of
$ R_{D \to \pi}^{0 \, +}(q^2) $ are consistent with each other while the prediction of$ R_{D \to \pi}^{T \, +}(q^2) $ is different. Compared with the lattice prediction$ R_{D \to \pi}^{T \, +}(0) = 0.827 $ [17], our result is more preferable, while the QCDF calculation is less reliable for D decays.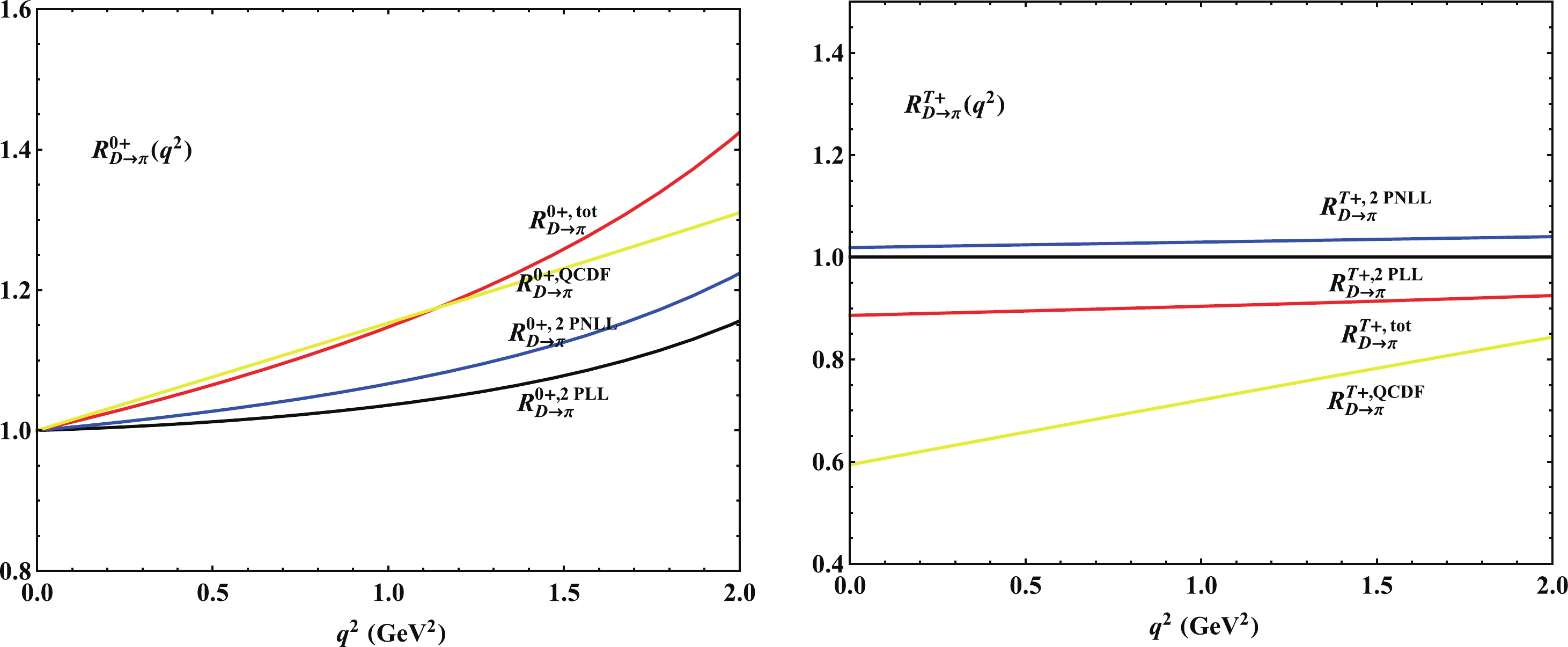
Figure 4. (color online) The large-recoil symmetry breaking effects of the
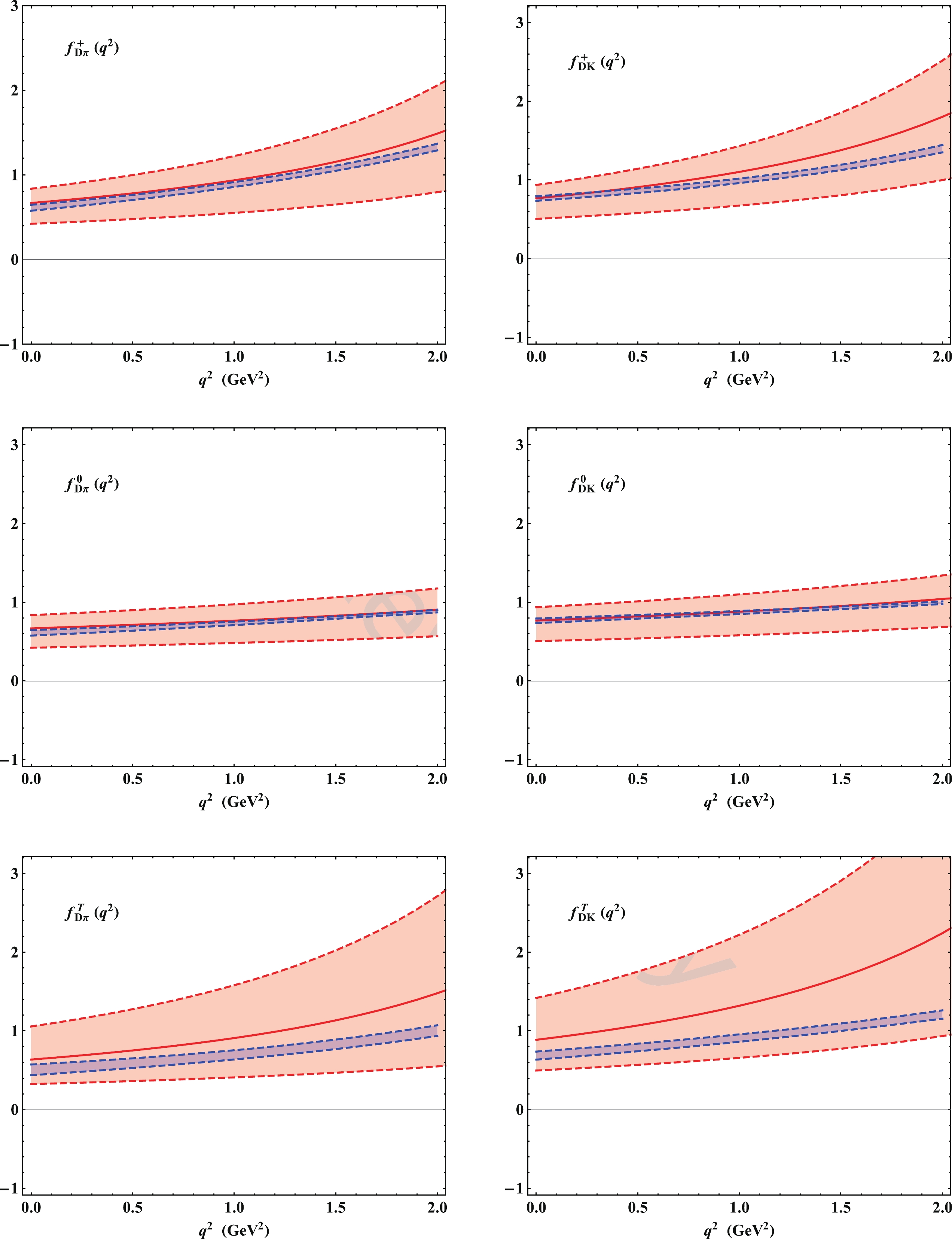
$ D\to\pi $ form factors, computed using the LCSR approach (the LL, NLL accuracy results and the overall result) and using the QCD factorization approach.Predictions for different models are shown in Fig. 5, where the vector
$ D\to\pi $ form factor prediction at$ q^2 = 0 $ for the exponential model was obtained by fitting the results of [25]. Although the values at$ q^2 = 0 $ are almost the same, the predictions of the local duality model are more sensitive to the transfer momentum. The dependence of the form factors on the momentum transfer with uncertainties associated with various parameters is shown in Fig. 6. Comparing our predictions with the results obtained using the Lattice QCD, we find that the uncertainties of our predictions are larger and the uncertainties of the tensor form factors are more significant. Although the uncertainties in this work are significant, the shapes of the$ D\to P $ form factors obtained using the two methods coincide. Based on the dominant uncertainties for different parameters in Table 2, the uncertainties of the NLP corrections are dominated by the inverse moment. However, the significant errors of the shape parameters$ b_{1,P}^i\, (i = 0,T) $ are from the model dependence of the D-meson LCDAs. For the tensor form factors, variation of the renormalization scale$ \nu $ also leads to large errors.
Figure 5. (color online) Dependence of the
$ D\to\pi\,,K $ form factors on the nonperturbative models of the D-meson LCDAs.Parameters Central value $ \lambda_D $ 

$ \sigma_1 $ 

$ M^2 $ 

$ s_0 $ 

$ \mu $ 

$ \phi_D^{\pm}(\omega) $ 

$ \nu $ 

$ f_{D \to \pi}^{+, 0}(0) $ 

0.668 +0.103 +0.026 +0.024 +0.018 +0.003 − − −0.067 −0.028 −0.033 −0.020 −0.018 − − $ b_{1, \pi}^{+} $ 

−0.69 +0.136 +0.049 +0.014 +0.041 0 0 − −0.107 −0.038 −0.020 −0.044 −0.164 −0.874 − $ b_{1, \pi}^{0} $ 

−2.10 +0.158 +0.036 +0.031 +0.077 0 0 − −0.073 −0.033 −0.046 −0.083 −0.372 −0.553 − $ f_{D \to \pi}^{T}(0) $ 

0.637 +0.126 +0.032 +0.024 +0.021 +0.003 − +0.379 −0.083 −0.034 −0.034 −0.023 −0.031 − −0.108 $ b_{1, \pi}^{T} $ 

−0.96 +0.185 +0.065 +0.004 +0.021 0 0 +0.227 −0.141 −0.050 −0.005 −0.022 −0.463 −0.911 −0.431 $ f_{D \to K}^{+, 0}(0) $ 

0.768 +0.091 +0.024 +0.010 +0.007 +0.002 − − −0.061 −0.025 −0.013 −0.008 −0.23 − − $ b_{1, K}^{+} $ 

−1.025 +0.102 +0.035 +0.044 +0.034 0 0 − −0.058 −0.025 −0.064 −0.037 −0.135 −1.076 − $ b_{1, K}^{0} $ 

−2.103 +0.250 +0.060 +0.078 +0.060 0 0 − −0.140 −0.060 −0.113 −0.064 −0.362 −0.706 − $ f_{D \to K}^{T}(0) $ 

0.888 +0.135 +0.035 +0.016 +0.011 +0.002 − +0.485 −0.091 −0.037 −0.021 −0.012 −0.045 − −0.138 $ b_{1, K}^{T} $ 

−0.960 +0.185 +0.065 +0.004 +0.021 0 0 +0.227 −0.141 −0.050 −0.005 −0.022 −0.463 −0.911 −0.431 Table 2. Theoretical predictions of model
$ \phi_{D,\rm I}^+(\omega,\mu_0) $ for the shape parameters and the normalizations of the$ D \to \pi, K $ form factors at$ q^2 = 0 $ entering the z expansion with the dominant uncertainties from variations of different input parameters.To extract the CKM matrix elements
$ |V_{cq}| $ , we follow the strategy presented in [46], where the following integral was used:$ \Delta \zeta_{\ell}(q_1^2, q_2^2) = {1 \over |V_{cq}|^2} \, \int_{q_1^2}^{q_2^2} \, {\rm d} q^2 \, {{\rm d} \, \Gamma (D \to \pi \ell \nu) \over {\rm d} q^2} \, \,. $

(58) The differential decay rate for
$ D\to P\,\ell\,\nu $ is given by$ \begin{aligned}[b] {{\rm d} \, \Gamma (D \to P \ell \nu)\over {\rm d} q^2} = & {G_F^2 \, |V_{cq}|^2 \over 192 \, \pi^3 \, m_D^3} \, \lambda^{3/2}(m_D^2, m_{\pi}^2, q^2) \, \left ( 1 -{m_l^2 \over q^2} \right )^2 \,\\&\times \left ( 1 + {m_l^2 \over 2 \, q^2} \right ) \, \Bigg [ |f_{D \to \pi}^+ (q^2)|^2 \\&+ \, {3 \, m_l^2 \, (m_D^2 - m_{\pi}^2)^2 \over \lambda(m_D^2, m_{\pi}^2, q^2) \, (m_l^2 + 2\, q^2) } \, |f_{D \to \pi}^{0} (q^2)|^2 \Bigg ] \,,\end{aligned} $

(59) where
$ \lambda(a, b, c) = a^2 + b^2 + c^2- 2 \, ab -2 \, ac - 2 \, bc $ . Employing the predictions of the$ D\to\pi $ form factors in this work, we obtain the following result for the$ \zeta $ function, after the integration of$ q^2 $ from 0 to 2.9$ \rm GeV^2 $ $ \begin{aligned}[b] &\Delta \zeta_{\mu}(0, 2.9 \, {\rm GeV^2}) \\ = & \left ( 0.152\,{}^{+0.054}_{-0.032} \, \big|_{\lambda_D}\,{}^{+0.002}_{-0.005} \, \big|_{\sigma_1} \,{}^{+0.0}_{-0.033} \, \big|_{M^2} \,{}^{+0.011}_{-0.014} \, \big|_{s_0} \,{}^{+0.023}_{-0.00} \, \big|_{\phi_D^{\pm}} \right ) \,\,\, {\rm ps}^{-1} \\ =& 0.152^{+0.102}_{-0.107} \,\,\, {\rm ps}^{-1} \,, \end{aligned} $

(60) where the second line is the result including the uncertainties associated with various parameters. Adopting the experimental measurement
$ \mathcal{B}(D^+\to\pi^0e^+\nu_e) = (3.63\pm $ $ 0.08\pm0.05)\times 10^{-3} $ from the BES-III collaboration [3], we extract the CKM matrix elements$ |V_{cd}| $ $ |V_{cd}| = 0.151\,{}^{+0.091}_{-0.043} \big |_{\rm th.}\,{}^{+0.017}_{-0.02} \big |_{\rm exp.} . $

(61) By changing the down quark to the strange quark, and repeating the above calculation with the
$ q^2 $ interval (0~1.8)$ \rm GeV^2 $ , we obtain$ \begin{aligned}[b]&\Delta \zeta_{\mu}(0, 1.8 \, {\rm GeV^2}) \\=& \left ( 0.104\,{}^{+0.027}_{-0.017} \, \big|_{\lambda_D}\,{}^{+0.001}_{-0.005} \, \big|_{\sigma_1} \,{}^{+0.0}_{-0.023} \, \big|_{M^2} \,{}^{+0.002}_{-0.003} \, \big|_{s_0} \,{}^{+0.022}_{-0.00} \, \big|_{\phi_D^{\pm}} \right ) \,\,\, {\rm ps}^{-1} \\ = & 0.104^{+0.06}_{-0.07} \,\,\, {\rm ps}^{-1} \,, \end{aligned} $

(62) and the CKM matrix elements can be extracted by adopting the experimental result of the
$ D\to K \, e\,\nu_e $ branching ratio$ \mathcal{B}(D^+\to\bar{K}^0e^+\nu_e) = (8.6\pm0.06\pm0.15)\times 10^{-2} $ [3]$ |V_{cs}| = 0.89\,{}^{+0.467}_{-0.234} \big |_{\rm th.}\,{}^{+0.008}_{-0.008} \big |_{\rm exp.} . $

(63) Compared with the latest results from Lattice QCD and experiments (Table 3), our prediction of
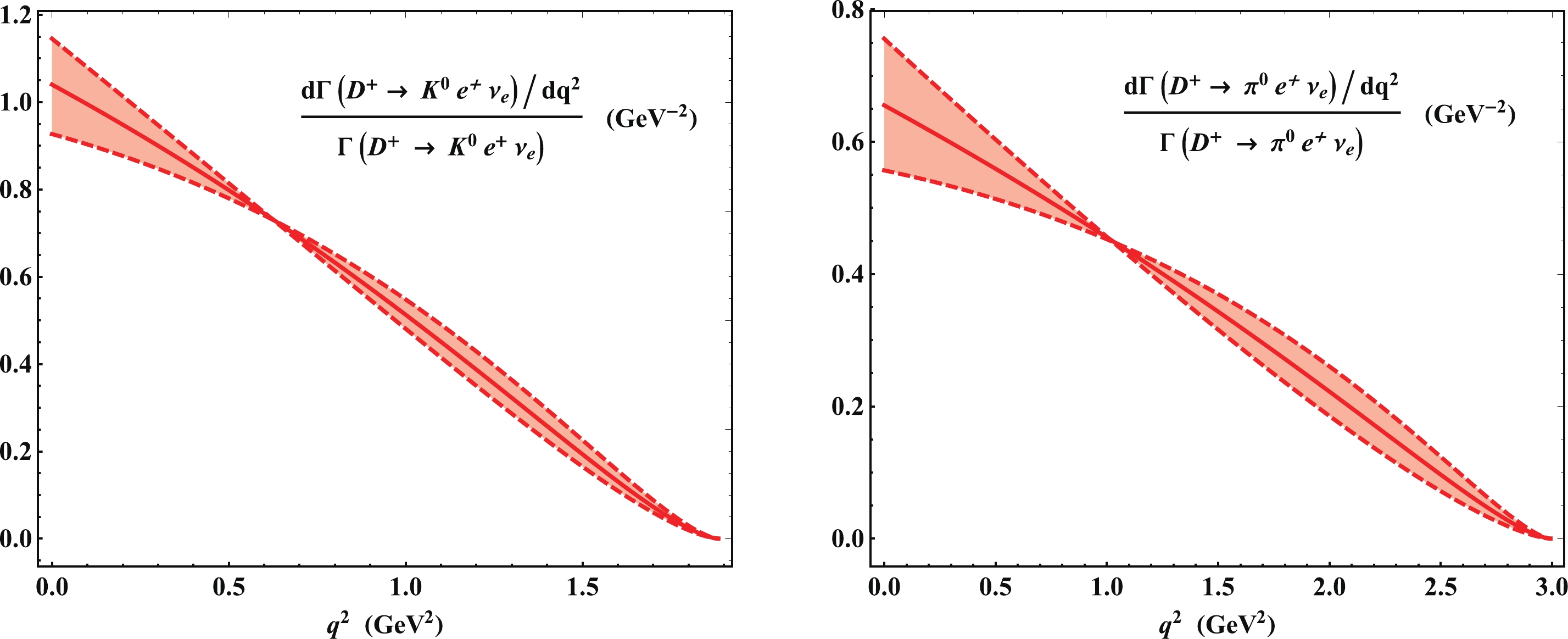
$ |V_{cd}| $ is much lower than others, which indicates that the predicted form factors are too large. This result may be owing to the fact that many important power suppressed contributions, such as the power suppressed term in the heavy-to-light current, were not taken into account. A more careful study of the power suppressed contribution is needed. In Fig. 7, we present the normalized differential$ q^2 $ distributions of$ D\to\pi,\,K $ . Considering that no experimental data are available, we hope that relevant experiments could be conducted in the future.Table 3. Predicted CKM matrix element values from ETM and BES-III collaborations.
-
The
$ D\to P $ transition form factors are the fundamental nonperturbative parameters in the semi-leptonic and non-leptonic D decays; thus, they are of great importance for determining the CKM matrix elements$ V_{cq} $ . Employing the LCSR method, we calculated the$ D \to \pi, \,K $ form factors, including the NLL resummation of the leading order contribution and the higher-twist contributions from the two-particle and three-particle D-meson LCDAs at the tree level. The numerical results indicate that the corrections from the two-particle higher-twist contributions are$ \mathcal{O} $ (27%–36%), while corrections from three-particle higher-twist contributions are negligible. The SU(3) flavor symmetry breaking and the large recoil symmetry breaking effects were also studied in this work. Especially, the predicted SU(3) flavor symmetry breaking effect of vector (scalar) and tensor were$R_{SU(3)}^{+}$ ($R_{SU(3)}^{0}$ ) = 1.12 and$R_{SU(3)}^T$ = 1.39, and our predicted$R_{SU(3)}^T$ result was consistent with the lattice result, 1.36 [17]. The large recoil symmetry, which holds for soft form factors, can be broken by three-particle higher-twist corrections. When comparing the predictions of the QCDF and LCSR for the large recoil symmetry breaking effect, we found that the QCDF prediction of$ R_{D\to\pi}^{T+} $ is less preferable and our result is closer to the lattice data.As some parameters (such as the inverse moment and the shape of the D-meson LCDA) are not well determined, the uncertainties of our predictions of form factors are large. To study the uncertainties associated with different variables, we adjusted the inverse moment to reproduce the vector
$ D\to\pi $ form factor result from the pion LCSR. The predicted form factors were further applied to extract the CKM matrix elements. By utilizing the measured branching ratios and by integrating the$ \zeta $ function, we obtained the predicted$ |V_{cd}| = 0.151\,{}^{+0.091}_{-0.043} \big |_{\rm th.}\,{}^{+0.017}_{-0.02} \big |_{\rm exp.} $ and$ |V_{cs}| = 0.89\,{}^{+0.467}_{-0.234} \big |_{\rm th.}\,{}^{+0.008}_{-0.008} \big |_{\rm exp.} $ . Comparing our results with the experimental and the lattice results, we found that the prediction of$ |V_{cs}| $ is close to the former. Although$ |V_{cd}| $ in this work was lower than the results reported by the BES-III and the ETM collaborations, this result is still reasonable within the uncertainties of the predicted CKM matrix elements, and a more careful study with profound investigations of the power corrections is needed to reduce the uncertainties. We can further investigate the subleading power contributions not considered in this paper, such as the subleading power correction from heavy quark expansion in HQET, the subleading power corrections from the quark propagator expansion at the tree level, and the four-particle D-meson LCDA corrections. -
The author would like to thank Yu-Ming Wang for illuminating discussions.
-
We borrowed the evolution functions
$ U_1(E_\gamma,\mu_h,\mu) $ and$ U_2(E_\gamma,\mu_h,\mu) $ from [39], and$ U_2(E_\gamma,\mu_h,\mu) $ was obtained by setting the cusp anomalous dimension to zero. Details can be found in this reference.$\tag{A1} \begin{aligned}[b]\\[-6pt] U_1(E_\gamma,\mu_h,\mu) = & \exp\left(\,\int_{\alpha_s(\mu_h)}^{\alpha_s(\mu)} {\rm d}\alpha_s\, \left[ \frac{\gamma(\alpha_s)}{\beta(\alpha_s)} + \frac{\Gamma_{\rm cusp}(\alpha_s)}{\beta(\alpha_s)} \left( \ln\frac{2 E_\gamma}{\mu_h} - \int_{\alpha_s(\mu_h)}^{\alpha_s} \frac{d\alpha_s^\prime}{\beta(\alpha_s^\prime)} \right) \right]\right) \\ =& \,\exp\left(\, -\frac{\Gamma_0}{4\beta_0^2} \left( \frac{4\pi}{\alpha_s(\mu_h)}\left[\ln r-1+\frac{1}{r}\right] -\frac{\beta_1}{2 \beta_0} \,\ln^2 r +\left(\frac{\Gamma_1}{\Gamma_0}-\frac{\beta_1}{\beta_0}\right) \left[r-1-\ln r\right]\right) \right) \\& \times\,\left(\frac{2 E_\gamma}{\mu_h}\right)^ {-\frac{\Gamma_0}{2\beta_0} \ln r} r^{-\frac{\gamma_0}{2\beta_0}} \times \Bigg[1 - \frac{\alpha_s(\mu_h)}{4\pi}\,\frac{\Gamma_0}{4\beta_0^2} \,\bigg(\frac{\Gamma_2}{2\Gamma_0} \left[1-r\right]^2 +\frac{\beta_2}{2\beta_0} \left[1-r^2+2 \ln r\right] \\& -\,\frac{\Gamma_1\beta_1}{2\Gamma_0\beta_0} \left[3-4 r+r^2+2 r \ln r\right] +\frac{\beta_1^2}{2\beta_0^2} \left[1-r\right]\left[1-r-2\ln r\right] \bigg) \\&+\,\frac{\alpha_s(\mu_h)}{4\pi}\left( \ln\frac{2E_\gamma}{\mu_h} \left(\frac{\Gamma_1}{2\beta_0}-\frac{\Gamma_0\beta_1}{2\beta_0^2}\right) +\frac{\gamma_1}{2\beta_0}-\frac{\gamma_0\beta_1}{2\beta_0^2}\right) \left[1-r\right] + {\cal O}(\alpha_s^2)\Bigg]. \end{aligned} $ 
The QCD evolution factor
$ U_3(\nu_{h}, \nu) $ is given in [33]$\tag{A2} \begin{aligned}[b] U_3(\nu_{h}, \nu) =& {\rm Exp} \bigg [ \int_{\alpha_s(\nu_{h})}^{\alpha_s(\nu)} \, {\rm d} \alpha_s \, \frac{\gamma_T(\alpha_s)}{\beta(\alpha_s)} \bigg ] \, \\ =& z^{- \frac{\gamma_T^{(0)}}{2 \,\beta_0}} \bigg [1+ \frac{\alpha_s(\nu_{h})}{4 \pi} \, \left ( {\gamma_T^{(1)} \over 2 \, \beta_0} - {\gamma_T^{(0)} \, \beta_1 \over 2 \, \beta_0^2 } \right ) (1-z) +{\cal O}(\alpha_s^2) \bigg ]\,, \end{aligned} $

with
$ z = \alpha_s(\nu)/\alpha_s(\nu_h) $ . The anomalous dimension$ \gamma_T(\alpha_s) $ for the tensor current at the two-loop accuracy is [47]$\tag{A3} \begin{aligned}[b] \\[-8pt]\gamma_T(\alpha_s) =& \sum_{n = 0}^{\infty} \, \left ( {\alpha_s(\mu) \over 4 \, \pi} \right )^{n+1} \, \gamma_T^{(n)} \,,\\ \gamma_T^{(0)} =& - 2\, C_F \,, \\ \gamma_T^{(1)} = & C_F \, \left [ 19 \, C_F \, -{257 \over 9} \, C_A + {52 \over 9} \, n_f \, T_F \right ]\,. \end{aligned} $

-
The expressions for
$ \rho_{i, \rm{LP}}^{(3P)} $ and$ \rho_{i, \rm{NLP}}^{(3P)} $ ($ i = n\,, \bar n \,, T $ ) were evaluated in [33], and they are given by$\tag{B1} \begin{aligned}[b] \rho_{\bar n, \rm{LP}}^{(3P)} = & (1-2 \, u) \, \left [ X_A - \Psi_A- 2 \, Y_A\right ] -\tilde{X}_A - \Psi_V + 2\, \tilde{Y}_A \,, \\ \rho_{\bar n, \rm{NLP}}^{(3P)} =& 2 \, \left [ \Psi_A - \Psi_V \right ] + 4 \, \left [ W + Y_A + \tilde{Y}_A - 2 \, Z \right ] \,, \\ \rho_{n, \rm{LP}}^{(3P)} = & 2\, (u-1) \, \left ( \Psi_A + \Psi_V \right ) \,, \\ \rho_{n, \rm{NLP}}^{(3P)} =& \left ( \Psi_A - \Psi_V \right ) - \, \left [ X_A + \tilde{X}_A - 2 \, Y_A - 2\, \tilde{Y}_A \right ] \,, \\ \rho_{T, \rm{LP}}^{(3P)} =& (1-2 \,u) \, \left ( \Psi_V + X_A - 2 \, Y_A \right ) + \Psi_A - \tilde{X}_A + 2\, \tilde{Y}_A \,, \\ \rho_{T, \rm{NLP}}^{(3P)} =& \left ( \Psi_A - \Psi_V + X_A + \tilde{X}_A \right ) + 2 \, \left [ 2\, W + Y_A + \, \tilde{Y}_A - 4 \, Z \right ] \,, \end{aligned}$

-
One could obtain the D-meson LCDAs by changing the bottom quark to the charm quark, owing to the heavy quark symmetry. Following [35, 36], we could express the twist 4 DA
$ g_D^+ $ and twist 5 DA$ g_D^- $ in terms of three particle DAs. Applying the operator identities (20), we obtain$\tag{C1a} \Bigg[z\frac{{\rm d}}{{\rm d}z}+1\Bigg]\Phi_-(z) = \Phi_+(z) + 2 z^2 \int_0^1 u {\rm d} u\,\Phi_3(z,uz)\,, $

$ \tag{C1b} \begin{aligned}[b]2 z^2 \mathrm{G}_+(z) =& - \Bigg[ z \frac{{\rm d}}{{\rm d}z} - \frac12 + {\rm i} z \bar \Lambda \Bigg] \Phi_+(z)\\& - \frac{1}{2}\Phi_-(z) - z^2 \int_0^1 \bar u {\rm d} u\,{\Psi}_4(z,uz)\,,\end{aligned} $

$ \tag{C1c} \begin{aligned}[b]2 z^2 \mathrm{G}_-(z) =& - \Bigg[ z \frac{{\rm d}}{{\rm d}z} - \frac12 + {\rm i} z \bar \Lambda \Bigg] \Phi_-(z) \\&- \frac12 \Phi_+(z) - z^2 \int_0^1 \bar u {\rm d} u\,{\Psi}_5(z,uz)\,, \end{aligned} $

$\tag{C1d}\begin{aligned}[b] \Phi_-(z) =& \left(z \frac{{\rm d}}{{\rm d}z}+1 + 2{\rm i} z \bar \Lambda \right) \Phi_+(z) \\&+ 2 z^2 \int_0^1 {\rm d}u\, \Big[ u \Phi_4(z,uz) + {\Psi}_4(z,uz)\Big],\end{aligned}$

where
$ \tag{C2} \mathrm{G}_\pm(z,\mu) = \int\limits_0^\infty {\rm d}\omega \, {\rm e}^{-{\rm i}\omega z}g_\pm(\omega,\mu) $

and
$ \tag{C3}\bar\Lambda = m_D -m_c\,.$

Implementing the definition of the momentum space distributions
$\tag{C4} \Psi_A(z_1,z_2) = \int_{0}^{\infty}{\rm d}\omega_1\int_{0}^{\rm infty}{\rm d}\omega_2 {\rm e}^{-{\rm i}\omega_1z_1-{\rm i}\omega_2z_2}\psi_A(\omega_1,\omega_2)\,, $

and performing the Fourier transformation, we obtain (22), (23), (24) and (25).
Higher-twist corrections to the ${\boldsymbol{D\to\pi,K}}$ form factors from light-cone sum rules
- Received Date: 2021-07-10
- Available Online: 2021-11-15
Abstract: We calculate the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






























 DownLoad:
DownLoad: