-
Recently, reactions involving carbon isotopes have attracted increasingly intense experimental and theoretical attention. Some quasielastic-scattering data for the proton-rich unstable nuclei
$ ^{9,10,11} {\rm{C}}$ and neutron-rich unstable nuclei$ ^{13,14} {\rm{C}}$ have also been reported in the literature. In the process of describing the elastic scattering, the optical model potential (OMP) plays a key role in those reactions involved with$ ^{9,10,11,13,14} {\rm{C}}$ . Also, it is known that the global phenomenological OMP is constructed by fitting a great amount of experimental data in a certain range of energy and mass. Thus, the basic elastic scattering observables can be reliably predicted using the OMP in the region where no experimental measurement data exist [1]. However, to date, only a few experiments have been performed on the reactions of$ ^{9,10,11,13,14} {\rm{C}}$ projectiles because of experimental difficulties. Because of the large data uncertainties as well as the lack of sufficient data points, it is difficult to obtain reliable global OMPs on the basis of the existing experimental data.In addition, the description of elastic scattering data for the reactions induced by the unstable nuclei
$ ^{9,10,11,13,14} {\rm{C}}$ would be associated with the nuclear structure properties of these carbon isotopes. These unstable nuclei exhibit different nuclear structure properties. For example, the valence protons are charged and in p-shell orbit for the proton-rich carbon isotopes$ ^{9,10,11} {\rm{C}}$ , while for the neutron-rich carbon isotopes$ ^{13,14} {\rm{C}}$ , there are extra valence neutrons.Previously, the global OMP of carbon isotope
$ ^{12} {\rm{C}}$ projectiles has been constructed using the energy dependent optical model parameters and identical Woods–Saxon shapes for the real and imaginary parts. The obtained global OMP gave a satisfactory description of$ ^{12} {\rm{C}}$ elastic scattering [2]. Also, the global OMP of$ ^{9} {\rm{Be}}$ projectiles has also been achieved [3] and can describe the elastic scattering of isotopic chain Be and B projectiles well [4, 5]. Therefore, it would be interesting to investigate if the systematic phenomenological OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ , which are stable nuclei, can describe the elastic scattering of the unstable nuclei$ ^{9,10,11,13,14} {\rm{C}}$ . In this work, we will apply the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs to describe the elastic scattering of the isotopes$ ^{9,10,11,13,14} {\rm{C}}$ . Some properties of the nuclear reaction and nuclear structure will be further analyzed by comparing between the predictions and the available experimental data.The organization of the paper is as follows. In Sec. II, the phenomenological OMP formula and methods are described for the elastic scattering of
$ ^{9,10,11,13,14} {\rm{C}}$ projectiles. In Sec. III, the elastic scattering observables are predicted using the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ , which are further compared with the existing experimental data. Finally, the main conclusions of this work are summarized in Sec. IV. -
Details regarding the theoretical formula of
$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs can be found in Refs. [2, 3]. Thus, we present only a brief description here. The OMPs of Woods-Saxon type$ \begin{aligned}[b] V(r,E) =& V_{R}(E)f(r,R_{R},a_{R})+{\rm i}W_{V}(E)f(r,R_{V},a_{V})\ \\ & +{\rm i}(-4W_{S}(E)a_{S})\frac{\rm d}{{\rm d}r}f(r,R_{S},a_{S})+V_{C}, \end{aligned} $

(1) were used in the optical model calculations.
$ V_{R}(E) $ ,$ W_{S}(E) $ , and$ W_{V}(E) $ are the energy-dependent potential depths and expressed as$ V_{R}(E) = V_{0}+V_{1}E+V_{2}E^{2}, $

(2) $ W_{S}(E) = \max\{0,W_{0}+W_{1}E\}, $

(3) $ W_{V}(E) = \max\{0,U_{0}+U_{1}E\}. $

(4) The Coulomb potential
$ V_{C} $ is taken as a uniform charged sphere with radius$ R_{C} $ .The radial functions are given by
$ f(r,R_{i},a_{i}) = (1+\exp[(r-R_{i})/a_{i}])^{-1}, $

(5) $ R_{i} = r_{i}A^{\frac{1}{3}}, \; \; \; \; \; \; i = R, S, V, C, $

(6) where A is the target mass number.
$ r_{R} $ ,$ r_{S} $ ,$ r_{V} $ , and$ r_{C} $ are respectively the radius parameters of the real, surface, and volume imaginary potentials, as well as the Coulomb potential.$ a_{R} $ ,$ a_{S} $ , and$ a_{V} $ are the corresponding diffuseness parameters. In particular, the radius parameter of the real potential is expressed as$ r_{R} = r_{R_{0}}+r_{R_{1}}A^{\frac{1}{3}}. $

(7) The
$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs have been constructed on the basis of the experimental data of elastic-scattering angular distributions and total reaction cross sections for targets from$ ^{24} {\rm{Mg}}$ to$ ^{209} {\rm{Bi}}$ below 200 MeV [3, 3]. In the following, we apply the obtained$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs to predict the elastic scattering observables for$ ^{9,10,11,13,14} {\rm{C}}$ projectiles and compare them with the available experimental data. -
The elastic-scattering angular distributions were predicted using the global OMPs of
$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ for the reactions of the proton-rich nuclei$ ^{9,10,11} {\rm{C}}$ induced on different targets. The comparisons of elastic-scattering angular distributions with the experimental data [6, 7] were performed for$ ^{9,11} {\rm{C}}$ +$ ^{208} {\rm{Pb}}$ at 227.0, 222.0, and 226.0 MeV, which is well above the Coulomb barrier. The global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ give a similar and satisfactory reproduction of the corresponding experimental data. The results of the$ ^{12} {\rm{C}}$ global OMP are shown in Fig. 1.
Figure 1. Comparisons of the
$^{9,11}{\rm{C}}$ elastic-scattering angular distributions calculated using the$^{12}{\rm{C}}$ global OMP with the corresponding experimental data for$^{208}{\rm{Pb}}$ .For
$ ^{10} {\rm{C}}$ projectiles, the elastic-scattering angular distributions for$ ^{27} {\rm{Al}}$ and$ ^{58} {\rm{Ni}}$ targets were predicted using the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs, respectively. The calculated results were compared with the experimental data at two times the barrier 29.0 MeV and near the barrier 35.3 MeV [8, 9]. The results are shown in Fig. 2. It is clear that the calculation with the$ ^{9} {\rm{Be}}$ global OMP gave a better description of the experimental data, although the cross sections are underestimated at backward angles at 35.3 MeV. The ground state of the proton-rich nucleus$ ^{10} {\rm{C}}$ has$ J_{\pi} $ =$ 0^{+} $ and is the only nucleus thought to have a Brunnian (super-Borromean) structure. The coupling effect is important, especially for backward angles in the vicinity of the Coulomb barrier [8]. Thus, the elastic-scattering angular distributions may arise from the coupled-channel contribution of the$ 2^{+} $ excited state. In addition, the elastic-scattering angular distributions for$ ^{10} {\rm{C}}$ +$ ^{208} {\rm{Pb}}$ predicted and compared with the experimental data [7, 10] at 66.0, 226.0, and 256.0 MeV are also shown in Fig. 2. The theoretical results agree with the data at 226.0 and 256.0 MeV. For 66.0 MeV, the results correspond to an energy close to the Coulomb barrier. There is some divergence between the theoretical results and the experimental data.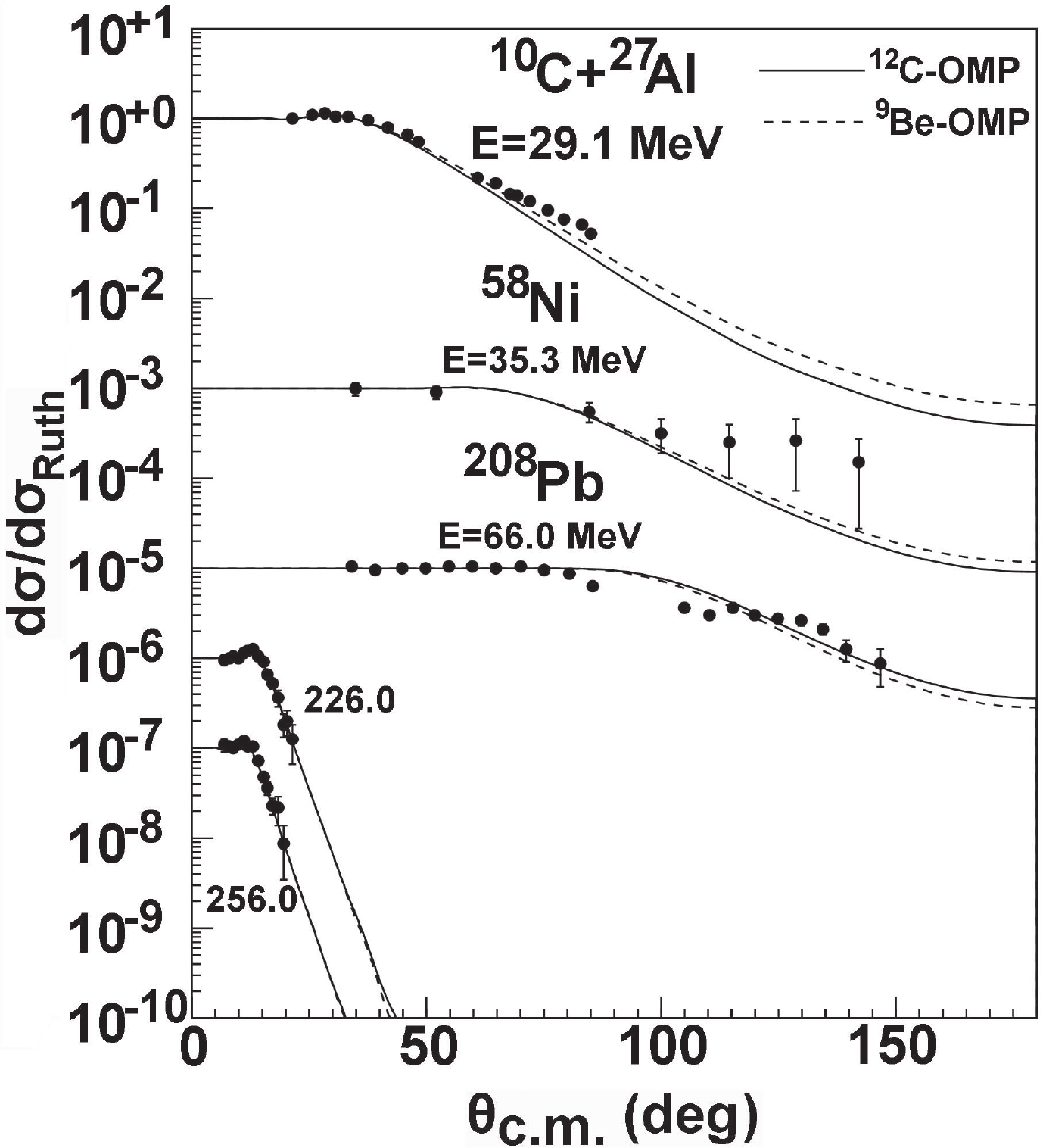
Figure 2. Comparisons of the
$^{10}{\rm{C}}$ elastic-scattering angular distributions predicted using the$^{12}{\rm{C}}$ and$^{9}{\rm{Be}}$ global OMPs with the corresponding experimental data for$^{27}{\rm{Al}}$ ,$^{58}{\rm{Ni}}$ , and$^{208}{\rm{Pb}}$ .For the total reaction cross sections of
$ ^{9,10,11} {\rm{C}}$ , there are experimental data only for$ ^{\rm nat.} {\rm{Si}}$ and$^{\rm nat.} {\rm{Pb}}$ . We also performed a comparison of the predicted results of the total reaction cross sections to the corresponding experimental data. The total reaction cross sections for the reaction of$ ^{9} {\rm{C}}$ induced on$ ^{28} {\rm{Si}}$ were predicted using the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ . Compared with the existing experimental data from$^{\rm nat.} {\rm{Si}}$ [11, 12], the theoretical results are both in good agreement with the data from Ref. [12] and smaller than the data from Ref. [11]. The results are presented in Fig. 3.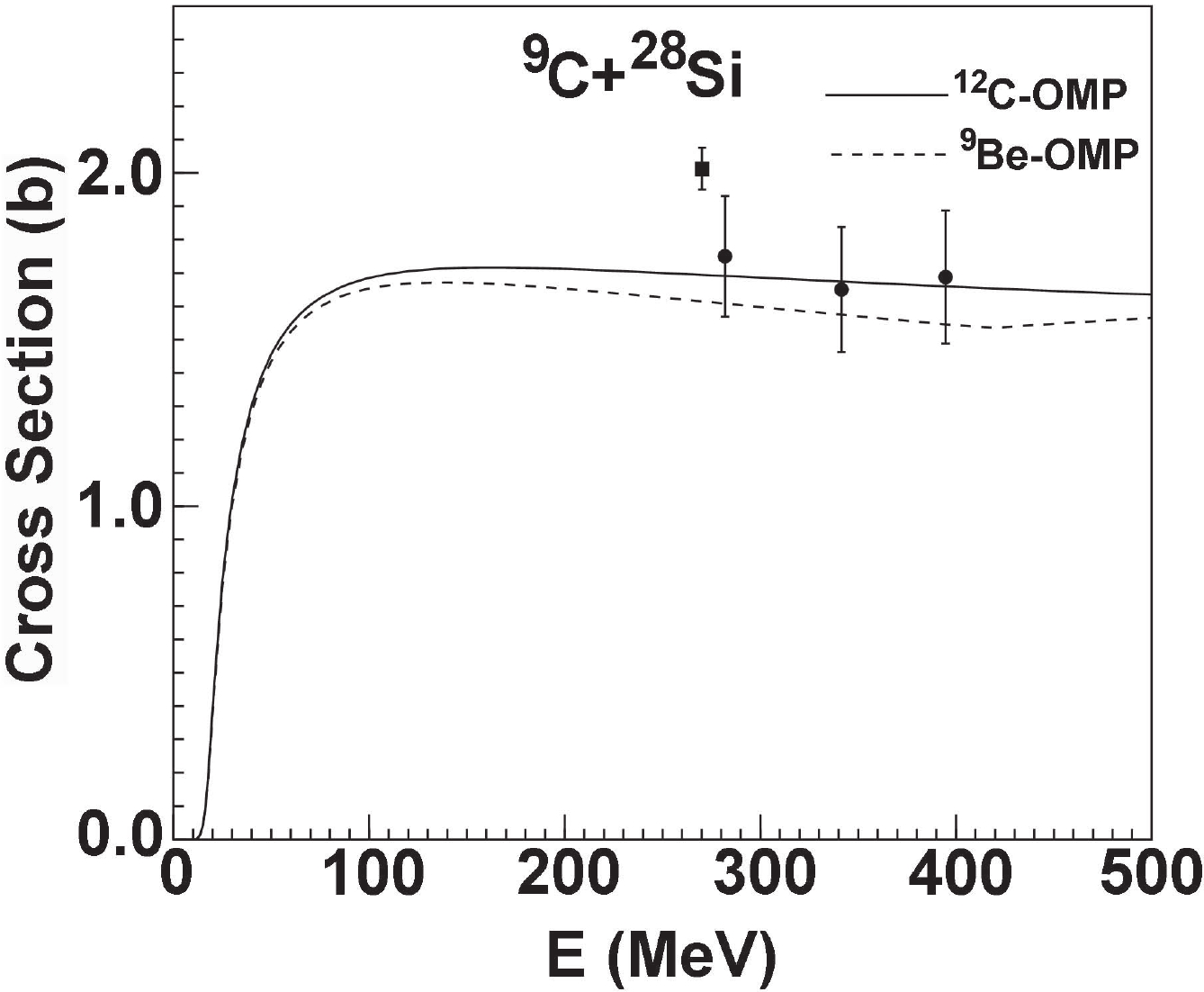
Figure 3. Comparisons of the total reaction cross sections predicted using the
$^{12}{\rm{C}}$ and$^{9}{\rm{Be}}$ global OMPs with the corresponding experimental data for the reaction of$^{9}{\rm{C}}$ +$^{28}{\rm{Si}}$ .Figures 4 and 5 show predictions of the total reaction cross sections for the reactions of
$ ^{10} {\rm{C}}$ induced on$ ^{28} {\rm{Si}}$ and$ ^{208} {\rm{Pb}}$ . From these figures, it is clear that the predictions using the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ are in good agreement with the data derived from the measurements of elastic-scattering angular distribution [7, 10] for the reaction of$ ^{10} {\rm{C}}$ induced on$ ^{208} {\rm{Pb}}$ , while the theoretical results with the global OMP of$ ^{9} {\rm{Be}}$ give a better description of elastic scattering for the reaction of$ ^{10} {\rm{C}}$ induced on$ ^{28} {\rm{Si}}$ in comparison with the existing experimental data [12]. For the reactions of$ ^{11} {\rm{C}}$ induced on$ ^{28} {\rm{Si}}$ and$ ^{208} {\rm{Pb}}$ , the predictions are similar to those of$ ^{10} {\rm{C}}$ . The results are shown in Figs. 6 and 7.
Figure 4. Same as Fig. 3, but for
$^{10}{\rm{C}}$ +$^{28}{\rm{Si}}$ .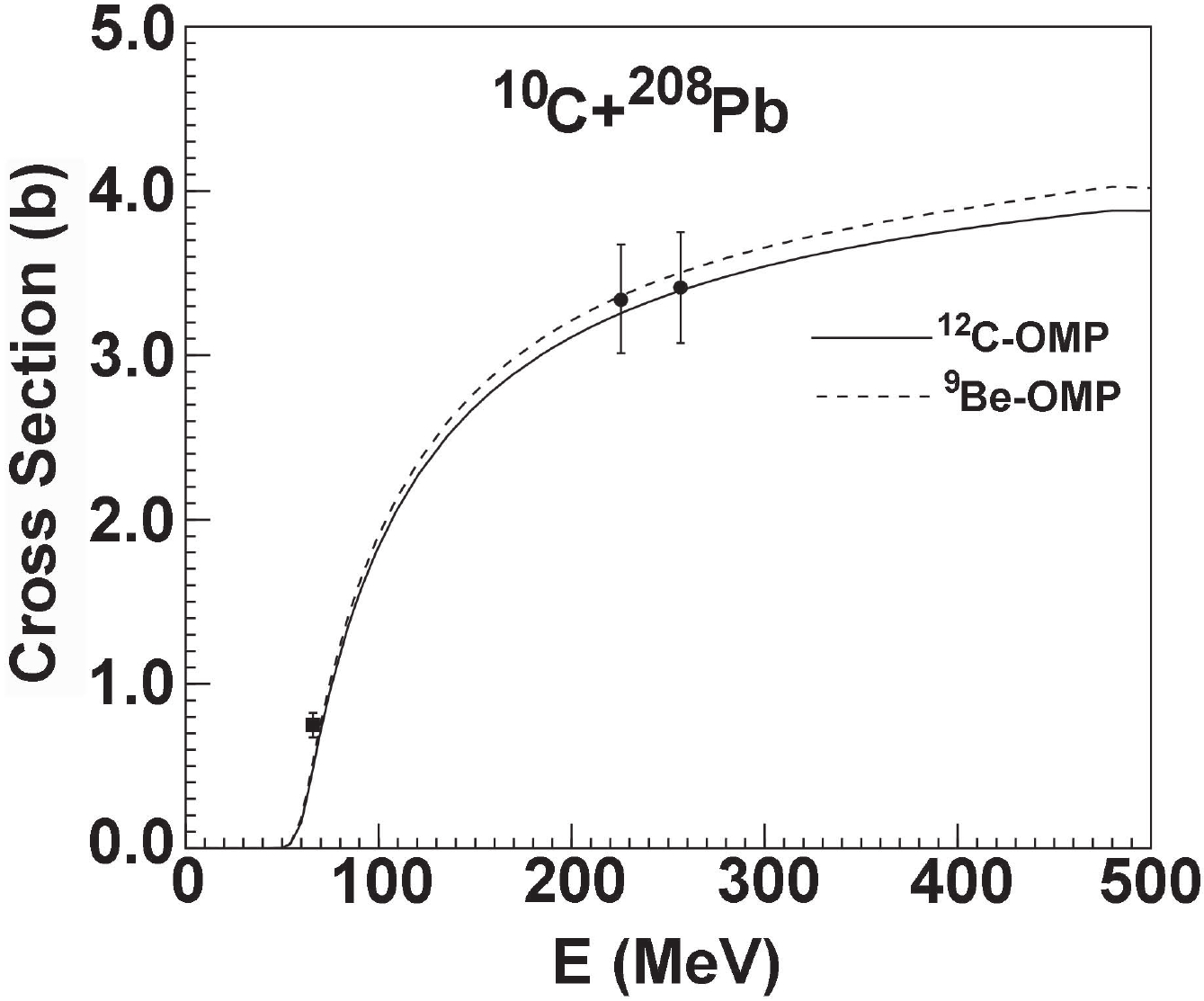
Figure 5. Same as Fig. 3, but for
$^{10}{\rm{C}}$ +$^{208}{\rm{Pb}}$ .
Figure 6. Same as Fig. 3, but for
$^{11}{\rm{C}}$ +$^{28}{\rm{Si}}$ .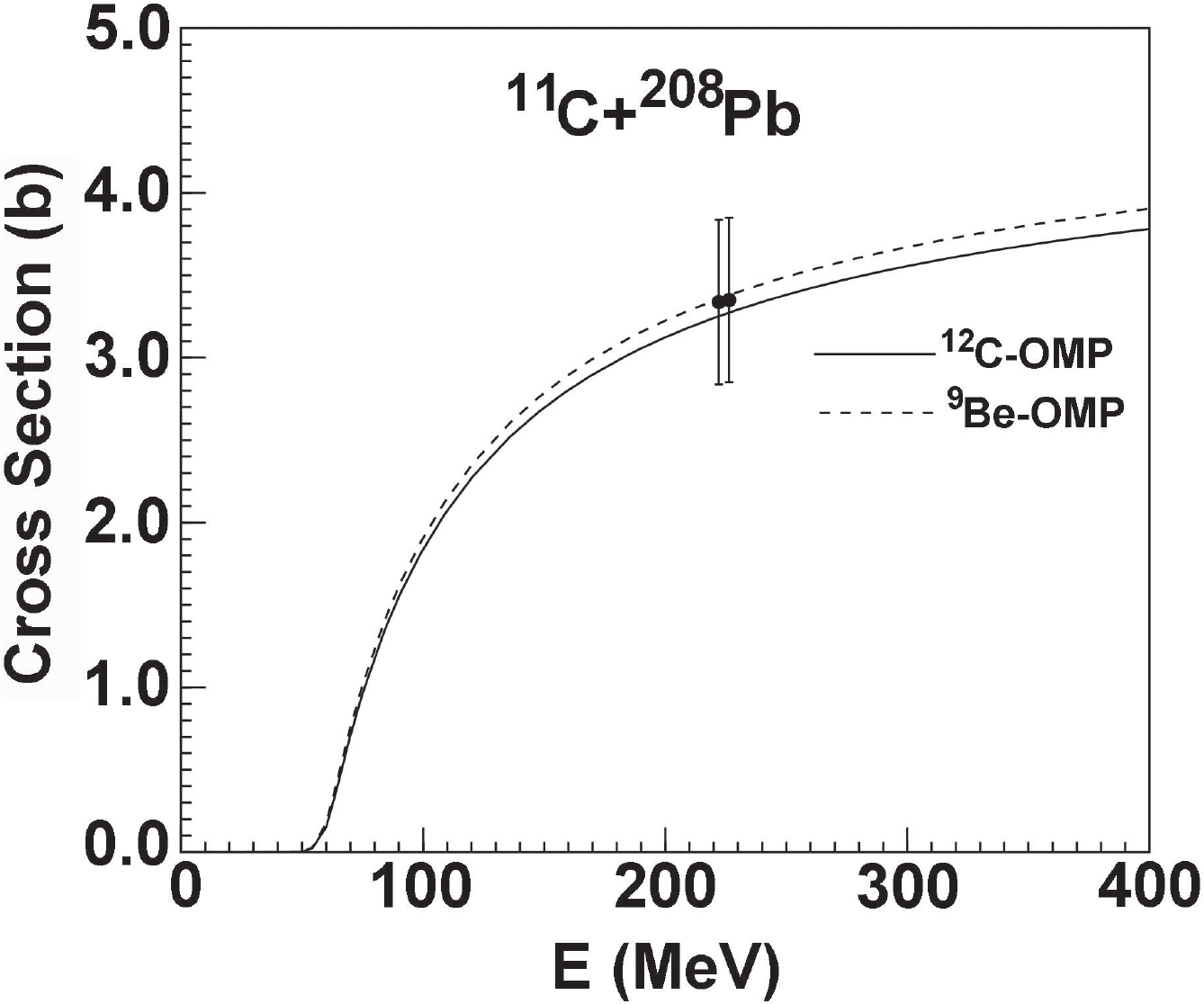
Figure 7. Same as Fig. 3, but for
$^{11}{\rm{C}}$ +$^{208}{\rm{Pb}}$ . -
The elastic-scattering angular distributions and total reaction cross sections for the neutron-rich nuclei
$ ^{13,14} {\rm{C}}$ projectiles were also predicted using the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ . The elastic-scattering angular distributions for the$ ^{13} {\rm{C}}$ +$ ^{28} {\rm{Si}}$ reaction were measured at 25.0, 30.0, 34.0, and 60.0 MeV [13, 14]. The neutron-rich nucleus$ ^{13} {\rm{C}}$ is always treated as a single valence neutron bound to a$ ^{12} {\rm{C}}$ nuclear core [13]. Therefore, the results were predicted using the$ ^{12} {\rm{C}}$ global OMP. Compared with the existing experimental data, the results agree well with the data at these energies. The results are shown in Fig. 8.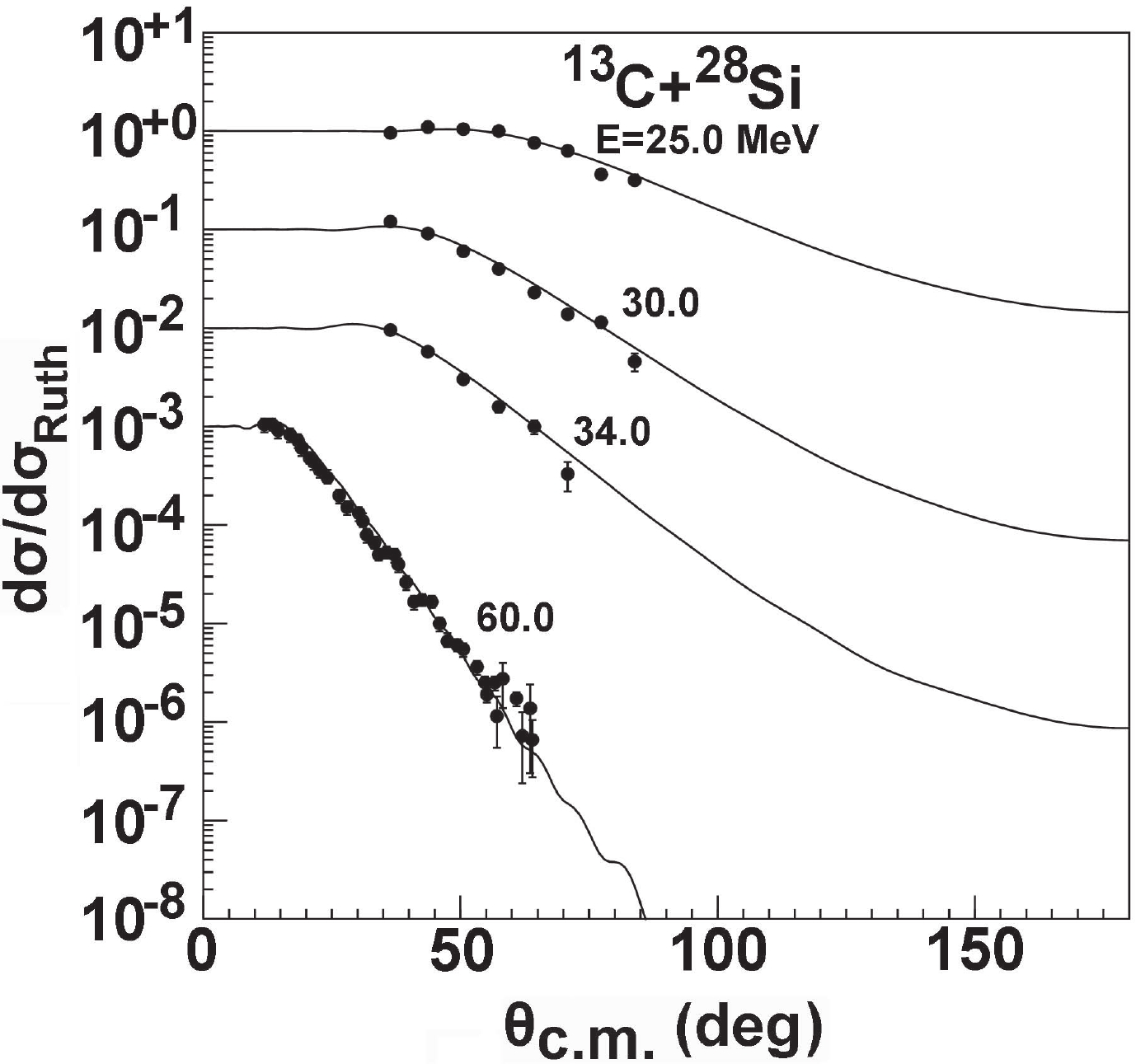
Figure 8. Comparisons of the
$^{13}{\rm{C}}$ elastic-scattering angular distributions calculated using the$^{12}{\rm{C}}$ global OMP with the corresponding experimental data for$^{28}{\rm{Si}}$ .In addition, the elastic-scattering angular distributions are reported for the reactions of
$ ^{14} {\rm{C}}$ induced on different targets. The elastic-scattering angular distributions of some targets were also predicted using the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs for$ ^{14} {\rm{C}}$ projectiles. A comparison with the experimental data [15, 16] shows that the shape of the theoretical curve is reasonable. However, the global OMP cannot give a satisfactory description, and there is some divergence between results in the backward-angle area. To improve the conformity, the radius parameter of the real part potential$ r_{R_{1}} $ was changed from 0.0273 to 0.0573 while keeping all the other parameters unchanged. The elastic-scattering angular distributions were calculated and compared with the experimental data [15, 16] at 51.0 and 71.0 MeV, respectively. These results are shown in Figs. 9 and 10. From these figures, it can be observed that good agreement is obtained between calculated and experimental results.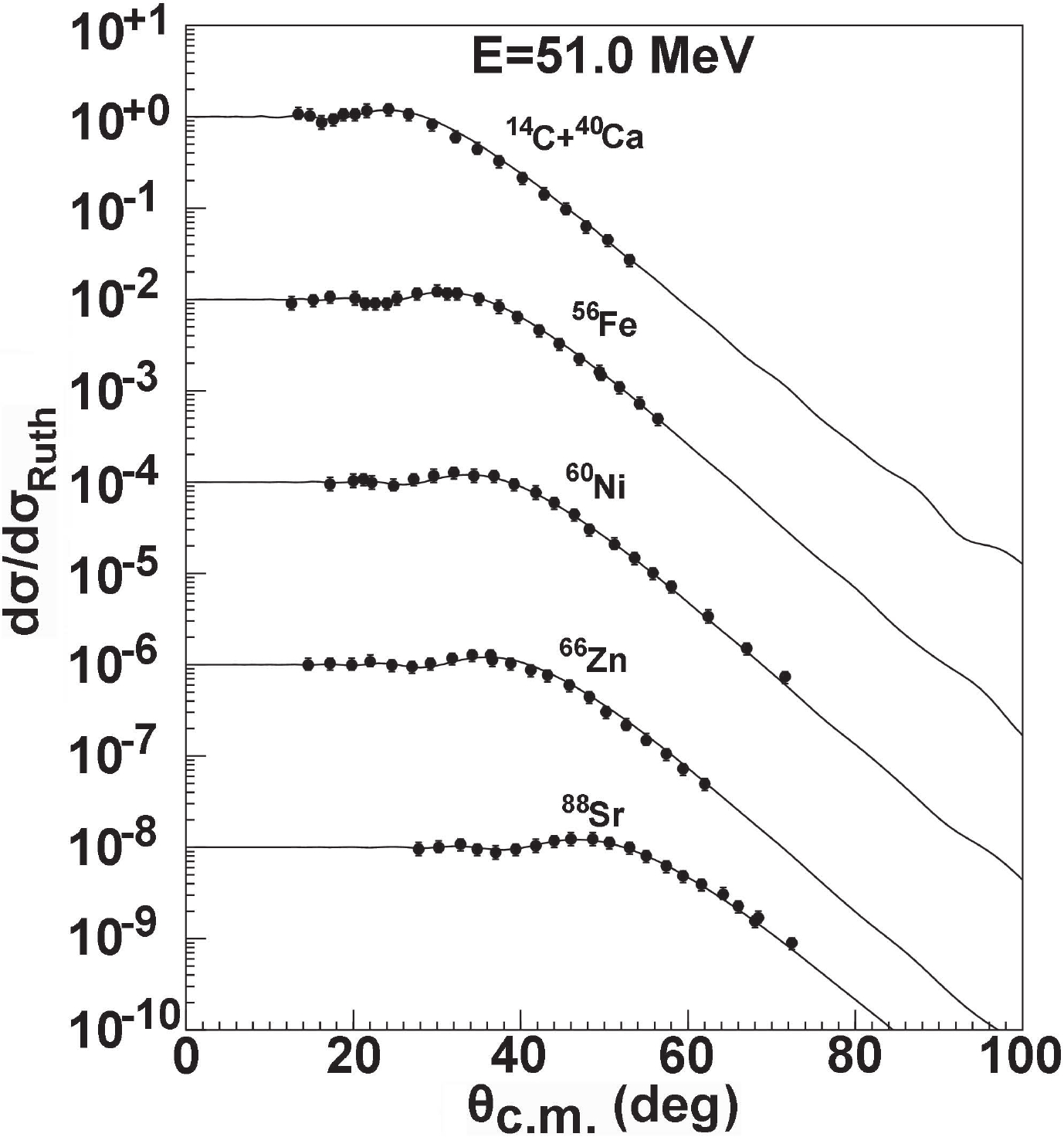
Figure 9. Comparisons of the
$^{14}{\rm{C}}$ elastic-scattering angular distributions calculated using the improved global OMP with the corresponding experimental data at 51.0 MeV.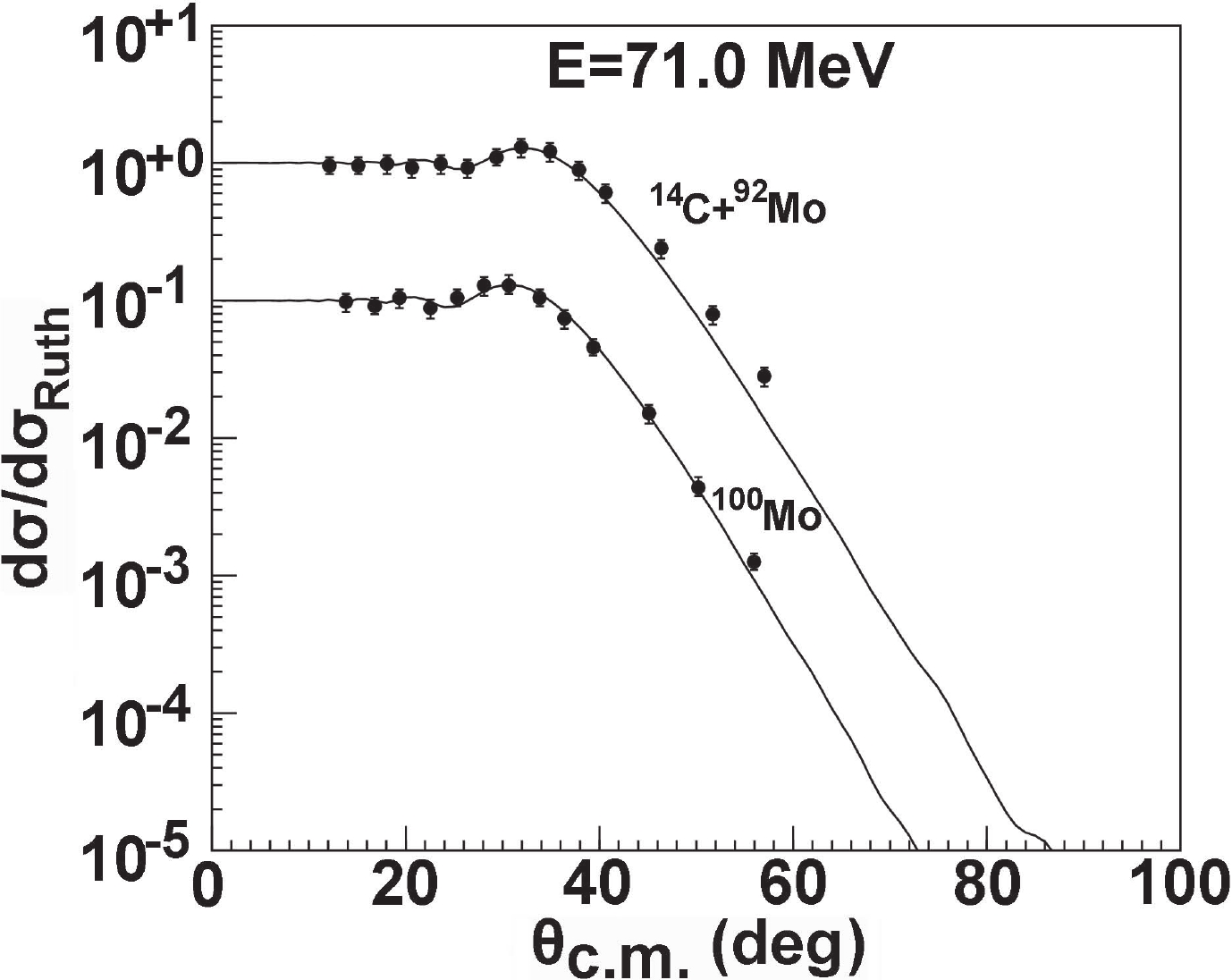
Figure 10. Same as Fig. 9, but for 71.0 MeV.
The total reaction cross sections for the reactions of
$ ^{13} {\rm{C}}$ and$ ^{14} {\rm{C}}$ induced on different targets were further predicted and compared with the existing experimental data. Good agreement is also found between them. Figure 11 shows a comparison of the total reaction cross sections of$ ^{13} {\rm{C}}$ and$ ^{14} {\rm{C}}$ impinging on a$ ^{28} {\rm{Si}}$ target with the experimental data [11].
Figure 11. Comparisons of the
$^{13,14}{\rm{C}}$ total reaction cross sections calculated using the$^{12}{\rm{C}}$ global OMP with the corresponding experimental data for$^{28}{\rm{Si}}$ .One question that arises is how can the global OMPs of the stable nuclei
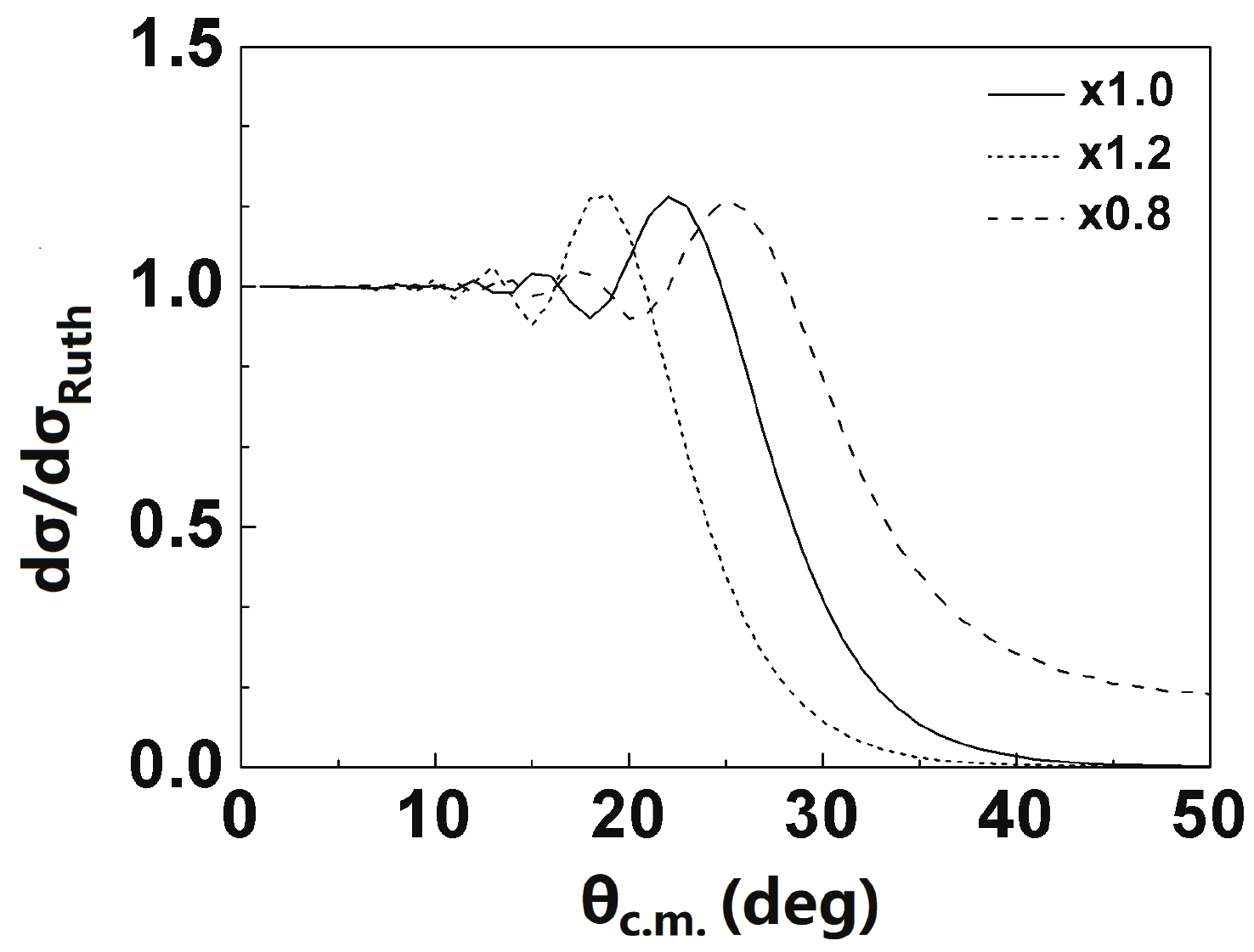
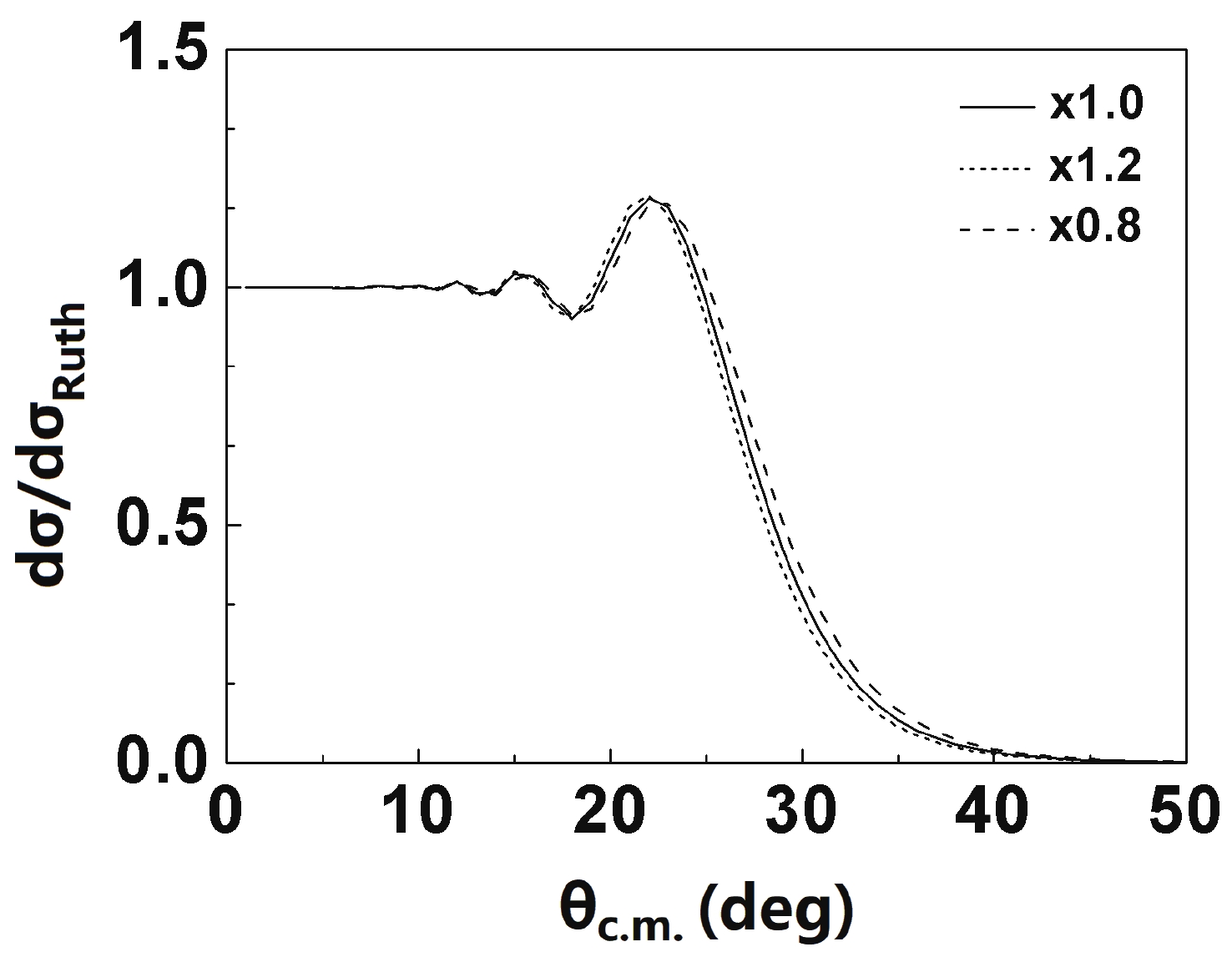
$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ give a good description of the elastic-scattering angular distributions and total reaction cross sections for the other carbon isotopes? To answer this question, the sensitivity of potential parameters is further investigated by calculating the elastic-scattering angular distributions when the radius parameters and potential depth of the$ ^{12} {\rm{C}}$ global OMP are changed within 20% while keeping all other parameters unchanged. The results for$ ^{11} {\rm{C}}$ +$ ^{208} {\rm{Pb}}$ at 150 MeV are shown in Figs. 12 and 13. From these figures, it is clear that the elastic-scattering angular distribution is sensitive to changes in the radius parameters of the real and imaginary potentials, while not sensitive to the changes in potential depth for the heavy-ion reaction. The global OMP of$ ^{9} {\rm{Be}}$ gives a similar result with respect to the impact on elastic scattering data. It is now clear that the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs can better describe the elastic-scattering angular distributions and the total reaction cross sections of some unstable isotopes, primarily because of the universality of given radius parameters. Similar to the stable nuclei$ ^{6,7} {\rm{Li}}$ potentials based on the single-folding model [17] and global phenomenological optical model [18, 19], they can also give a good description of the elastic scattering for those reactions induced by some stable and unstable nuclei. In particular, for the proton-rich nuclei$ ^{9,10,11} {\rm{C}}$ , the valence protons are charged and in p-shell orbit. They are simultaneously bounded by the Coulomb barrier and centrifugal barrier, and the breakup effect is not obvious. Therefore, the elastic scattering for the reactions induced by the unstable nuclei$ ^{9,10,11} {\rm{C}}$ are similar to those of the stable nuclei, and they can be described using the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ . For the neutron-rich nucleus$ ^{13} {\rm{C}}$ , the elastic scattering can be well described using the$ ^{12} {\rm{C}}$ global OMP. It is possible that the presence of the extra neutron in$ ^{13} {\rm{C}}$ does not influence the reaction mechanism, which is governed by the collective excitation of the$ ^{12} {\rm{C}}$ core [20]. However, the valence nucleon of the neutron-rich nucleus$ ^{14} {\rm{C}}$ is a neutron, which leads to Coulomb barrier reduction. Then, the breakup-coupling effects will be enhanced for the breakup channel. In this case, the global OMPs constructed on the basis of the stable nuclei are not applicable to it. -
The elastic scattering observables of the isotopic chain
$ ^{9,10,11,13,14} {\rm{C}}$ described with the existing$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs is an efficient method for investigation of the global OMPs' universality and understanding the$ ^{9,10,11,13,14} {\rm{C}}$ nuclei structure. In the present work, the elastic scattering observables involving the carbon isotopes$ ^{9,10,11,13,14} {\rm{C}}$ are predicted with the obtained global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ . The global OMPs of$ ^{9} {\rm{Be}}$ and$ ^{12} {\rm{C}}$ give a satisfactory description of the elastic scattering for the reactions of$ ^{9,10,11,13} {\rm{C}}$ induced on different targets. For the neutron-rich carbon isotope$ ^{14} {\rm{C}}$ , the results predicted using the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs are not in good agreement with the experimental data in the backward-angle area. By changing the real part radius parameter of the$ ^{12} {\rm{C}}$ global OMP, the predictions can give a satisfactory description of the$ ^{14} {\rm{C}}$ elastic scattering. Furthermore, the sensitivity of potential parameters is further investigated by calculating the elastic-scattering angular distributions when the potential radius parameters and potential depth are changed within 20%. It is shown that the elastic scattering data are sensitive to the radius parameters, while they are not sensitive to the potential depth for the heavy-ion reaction. The results suggest that the radius parameters given in the global OMPs of$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ have a certain universality. Further analysis including more experimental data for heavier projectiles will be conducted using the$ ^{12} {\rm{C}}$ and$ ^{9} {\rm{Be}}$ global OMPs. Theoretical efforts should also be made to understand the relations between the radius and energy dependence for these heavy-ion global OMPs.
Description of elastic scattering induced by the unstable nuclei 9,10,11,13,14C
- Received Date: 2021-05-12
- Available Online: 2021-11-15
Abstract: The elastic-scattering angular distributions and total reaction cross sections of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: