-
Recently, experiments of
$ pp $ and$ p $ Pb collisions at energies available at the CERN Large Hadron Collider (LHC) revealed a series of interesting properties of hadron production, such as ridge and collectivity [1-4] as well as enhancement of strangeness and baryon to meson ratios [5-8]. These striking observations are possibly related to a prominent topic in strong interactions, i.e., the formation of a small droplet of Quark-Gluon Plasma (QGP) in$ pp $ and$ p $ Pb collisions. Theoretical studies along this direction have been extensively conducted in the last few years, addressing different aspects. The key point is how to understand and simulate the small final-state parton system created in the$ pp $ and$ p $ Pb collisions at LHC energies. These studies usually focus on the application of hydrodynamics to simulations of mini-QGP evolution [9-16], the search for new features in string formation just before hadronization by various mechanisms such as color re-connection [17-21], the search for new features in string(cluster) fragmentation or parton(quark) coalescence mechanism at hadronization [22-27], etc.In our recent studies on the
$ pp $ collisions at two collision energies$ \sqrt{s} = 7,13 $ TeV [27-29] and on the$ p $ Pb collisions at$ \sqrt{s_{NN}} = 5.02 $ TeV [25, 30], we found that an equal-velocity combination mechanism of constituent quarks and antiquarks at hadronization can systematically describe the experimental data for the$ p_{T} $ spectra of light-flavor hadrons and single-charmed hadrons in the low and intermediate$ p_{T} $ range in these collision systems. The constituent quark degrees of freedom just before hadronization play an important role in hadron production in these collisions, which may be related to possible formation of QGP droplets in$ pp $ and$ p $ Pb collisions at LHC energies. Compared with the traditional fragmentation mechanism usually applied in small collision systems, this quark-combination "new'' feature of hadronization should be studied further, assisted by the available experimental data on the$ pp $ and$ p $ Pb collisions at other collision energies at LHC.In this paper, we use an equal-velocity quark combination model to study the production of light-flavor hadrons and single-charmed hadrons in the
$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. Firstly, we use the model to describe the experimental data of light-flavor hadrons [31-33]. We pay particular attention to how to systematically relate the observed properties of hadrons to the quark$ p_T $ spectra at hadronization. For example, we correlate the$ p_{T} $ spectrum of$ \Omega $ and that of$ \phi $ using a scaling method, to directly relate to the$ p_{T} $ distribution of strange quarks at hadronization. Another example is that we can relate the non-monotonic$ p_{T} $ dependence of the$ \Omega/\phi $ ratio to the shape of the logarithm of the strange quark distribution. Second, using the$ p_{T} $ spectra of light-flavor quarks obtained from the study of light-flavor hadrons and a charm quark distribution which is consistent with perturbative QCD calculations, we further study the equal-velocity combination of light-flavor and charm (anti-)quarks, to explain the production properties of single-charmed hadrons. We compare model results with experimental data for differential cross-sections of$ D^{0,+} $ ,$ D_{s}^{+} $ and$ \Lambda_{c}^{+} $ [34, 35]. We predict the differential cross-sections of$ \Xi_{c}^{0,+} $ and$ \Omega_{c}^{0} $ and several baryon to meson ratios, such as$ \Xi_{c}^{0,+}/D^{0} $ and$ \Omega_{c}^{0}/D^{0} $ , for future tests.The paper is organized as follows. In Sec. II, we briefly introduce a particular quark combination model under the equal-velocity combination approximation. In Sec. III, we show the results for the
$ p_{T} $ spectra of light-flavor hadrons in the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. In Sec. IV, we show the results for the$ p_{T} $ spectra and spectrum ratios of single-charmed hadrons. In Sec. V, we give the summary of our work. -
In this section, we briefly introduce a particular quark combination model that was proposed in a recent work [25]. This model applies a simplified combination criterion, i.e., the equal-velocity combination (EVC), to determine how constituent quarks and antiquarks at hadronization form hadrons. This EVC model was inspired by the quark number scaling property observed in the
$ p_{T} $ spectra of strange hadrons [25, 29]. The model has successfully described the$ p_{T} $ spectra of light-flavor hadrons and single-charmed hadrons in the ground state, for the$ pp $ collisions at$ \sqrt{s} = 7,13 $ TeV and$ p $ Pb collisions at$ \sqrt{s_{NN}} = 5.02 $ TeV. Our latest studies on the elliptic flow and$ p_{T} $ spectra of hadrons in relativistic heavy-ion collisions [36-39] also support the EVC model.Assuming a stochastic combination of quarks and antiquarks in hadronization, the momentum distribution of the formed hadron
$f_{h}\left(p\right)\equiv {\rm d}N_{h}/{\rm d}p$ in the laboratory frame can be constructed using those of quarks and antiquarks,$\begin{aligned}[b] f_{B_{j}}(p_{B}) = & \int\mathrm{d}p_{1}\mathrm{d}p_{2}\mathrm{d}p_{3}{\cal R}_{B_{j}}(p_{1},p_{2},p_{3};p_{B})\\&\times f_{q_{1}q_{2}q_{3}}(p_{1},p_{2},p_{3}), \end{aligned}$

(1) $ f_{M_{j}}(p_{M}) = \int\mathrm{d}p_{1}\mathrm{d}p_{2}{\cal R}_{M_{j}}(p_{1},p_{2};p_{M})f_{q_{1}\bar{q}_{2}}(p_{1},p_{2}),$

(2) where
$ f_{q_{1}q_{2}q_{3}}(p_{1},p_{2},p_{3}) $ and$ f_{q_{1}\bar{q}_{2}}(p_{1},p_{2}) $ are the joint momentum distributions for$ q_{1}q_{2}q_{3} $ and$ q_{1}\bar{q}_{2} $ in the laboratory frame, respectively.$ {\cal R}_{B_{j}}(p_{1},p_{2},p_{3};p_{B}) $ is the combination probability function for the three quarks$ q_{1}q_{2}q_{3} $ with the momenta$ p_{1} $ ,$ p_{2} $ , and$ p_{3} $ forming a baryon$ B_{j} $ with the quark composition$ q_{1}q_{2}q_{3} $ and momentum$ p_{B} $ .$ {\cal R}_{M_{j}}(p_{1},p_{2};p_{M}) $ is interpreted in a similar manner.In the EVC approximation, a hadron is formed by the combination of constituent quarks and/or antiquarks with the same velocities. Because the momentum has the property
$ p_{i} = \gamma m_{i}v\propto m_{i} $ at a given velocity, the momentum of the participant (anti-)quark$ p_{i} $ is a particular fraction$ x_{i} = p_{i}/p\propto m_{i} $ of the momentum of hadron$ p $ , where$ m_{i} $ is the constituent mass of the quark$ i $ . Considering the momentum conservation$ \sum_{i}p_{i} = p $ , we obtain$ \begin{array}{l} x_{i} = \begin{cases} \dfrac{m_{i}}{m_{1}+m_{2}+m_{3}} & i = 1,2,3\ \ {\rm{for}}\ B(q_{1}q_{2}q_{3})\\ \dfrac{m_{i}}{m_{1}+m_{2}} & i = 1,2\ \ {\rm{for}}\ M(q_{1}\bar{q}_{2}) \end{cases}. \end{array} $

(3) The constituent masses of the quarks are
$ m_{u} = m_{d} = 0.3 $ GeV,$ m_{s} = 0.5 $ GeV, and$ m_{c} = 1.5 $ GeV. The combination function therefore has the following simple form:$ {\cal R}_{B_{j}}(p_{1},p_{2},p_{3};p_{B}) = \kappa_{B_{j}}\prod\limits_{i = 1}^{3}\delta(p_{i}-x_{i}p_{B}),$

(4) $ {\cal R}_{M_{j}}(p_{1},p_{2};p_{M}) = \kappa_{M_{j}}\prod\limits_{i = 1}^{2}\delta(p_{i}-x_{i}p_{M}). $

(5) $ \kappa_{B_{j}} $ and$ \kappa_{M_{j}} $ are independent of the momentum but can depend on the number of (anti-) quarks in hadronization, as well as on the properties of the formed hadron such as the spin.Substituting the combination functions in Eqs. (4) and (5) into Eqs. (1) and (2), we obtain
$ f_{B_{j}}\left(p_{B}\right) = \kappa_{B_{j}}\,f_{q_{1}q_{2}q_{3}}\left(x_{1}p_{B},x_{2}p_{B},x_{3}p_{B}\right), $

(6) $ f_{M_{j}}\left(p_{M}\right) = \kappa_{M_{j}}f_{q_{1}\bar{q}_{2}}\left(x_{1}p_{M},x_{2}p_{M}\right). $

(7) Integrating the above equations over the momentum, we obtain the number of the formed hadrons
$ N_{B_{j}} = \kappa_{B_{j}}\int{\rm d}p_{B}f_{q_{1}q_{2}q_{3}}\left(x_{1}p_{B},x_{2}p_{B},x_{3}p_{B}\right), $

(8) $ N_{M_{j}} = \kappa_{M_{j}}\int{\rm d}p_{M}f_{q_{1}\bar{q}_{2}}\left(x_{1}p_{M},x_{2}p_{M}\right). $

(9) The integral of the joint momentum distribution of (anti-) quarks can be rewritten as
$ \int{\rm d}p_{B}f_{q_{1}q_{2}q_{3}}\left(x_{1}p_{B},x_{2}p_{B},x_{3}p_{B}\right) = \frac{N_{q_{1}q_{2}q_{3}}}{A_{B_{j}}}, $

(10) $ \int{\rm \mathrm{d}}p_{M}f_{q_{1}\bar{q}_{2}}\left(x_{1}p_{M},x_{2}p_{M}\right) = \frac{N_{q_{1}\bar{q}_{2}}}{A_{M_{j}}} $

(11) with
$ N_{q_{1}q_{2}q_{3}} = \iiint\mathrm{d}p_{1}\mathrm{d}p_{2}\mathrm{d}p_{3}f_{q_{1}q_{2}q_{3}}\left(p_{1,}p_{2},p_{3}\right),$

(12) $ N_{q_{1}\bar{q}_{2}} = \iint\mathrm{d}p_{1}\mathrm{d}p_{2}f_{q_{1}\bar{q}_{2}}\left(p_{1},p_{2}\right). $

(13) Here,
$ N_{q_{1}\bar{q}_{2}} $ is the number of all$ q_{1}\bar{q}_{2} $ pairs at hadronization. In general, we have$ N_{q_{1}\bar{q}_{2}} = N_{q_{1}}N_{\bar{q}_{2}} $ where$ N_{q_{1}} $ is the number of$ q_{1} $ in system and$ N_{\bar{q}_{2}} $ is that of$ \bar{q}_{2} $ .$ N_{q_{1}q_{2}q_{3}} $ is the number of all possible$ q_{1}q_{2}q_{3} $ combinations. In general,$ N_{q_{1}q_{2}q_{3}} $ equals to$ N_{q_{1}}N_{q_{2}}N_{q_{3}} $ for different quark flavors,$ N_{q_{1}}(N_{q_{1}}-1)N_{q_{2}} $ for two identical quark flavors and$ N_{q_{1}}(N_{q_{1}}-1)(N_{q_{1}}-2) $ for three identical quark flavors. The coefficients$ A_{B_{j}} $ and$ A_{M_{j}} $ are introduced to characterize the effect of the joint momentum distribution of (anti-) quarks with correlated momenta on the number of the formed hadrons.Substituting Eqs. (10) and (11) into Eqs. (8) and (9), we obtain
$ N_{B_{j}} = N_{q_{1}q_{2}q_{3}}\frac{\kappa_{B_{j}}}{A_{B_{j}}} = N_{q_{1}q_{2}q_{3}}P_{q_{1}q_{2}q_{3}\rightarrow B_{j}}, $

(14) $ N_{M_{j}} = N_{q_{1}\bar{q}_{2}}\frac{\kappa_{M_{j}}}{A_{M_{j}}} = N_{q_{1}\bar{q}_{2}}P_{q_{1}\bar{q}_{2}\rightarrow M_{j}}. $

(15) The coefficient ratio
$ \kappa_{B_{i}}/A_{B_{i}} $ thus has an intuitive physical meaning; that is, it is the momentum-integrated probability of$ q_{1}q_{2}q_{3} $ forming$ B_{j} $ . Therefore, we denote it as$ P_{q_{1}q_{2}q_{3}\rightarrow B_{j}} $ in the second equality.$ \kappa_{M_{j}}/A_{M_{j}} $ denotes the momentum-integrated probability of the$ q_{1}\bar{q}_{2} $ pair forming$ M_{j} $ , and we denote it as$ P_{q_{1}\bar{q}_{2}\rightarrow M_{j}} $ .Because of the non-perturbative nature of
$ P_{q_{1}q_{2}q_{3}\rightarrow B_{i}} $ and$ P_{q_{1}\bar{q}_{2}\rightarrow M_{i}} $ , we will parameterize them in the following text. Here, we consider the formation of hadrons in two sectors. One is light-flavor hadrons, which are exclusively composed of light-flavor (anti-)quarks. Another is single-charmed hadrons, which are composed of a charm (anti-)quark and light-flavor (anti-)quark(s). For convenience, light-flavor quarks are denoted as$ l_{i} $ ($ l_{i} = d,u,s $ ) and$ N_{l_{i}} $ are their numbers. The number of all light-flavor quarks is$ N_{l} = \sum_{l_{i}}N_{l_{i}} $ , and a similar notation is used for anti-quarks. Charm quarks are denoted as$ c $ , and$ N_{c} $ is their number.Considering the stochastic feature of the quark combination and flavor independence of strong interactions, the combination probability of light-flavor (anti-)quarks can be parameterized by
$ P_{l_{1}l_{2}l_{3}\rightarrow B_{j}} = C_{B_{j}}N_{\rm iter}\frac{\overline{N}_{B}}{N_{lll}},$

(16) $ P_{l_{1}\bar{l}_{2}\rightarrow M_{j}} = C_{M_{j}}\frac{\overline{N}_{M}}{N_{l\bar{l}}}, $

(17) where we use
$ \overline{N}_{B}/N_{lll} $ to denote the average probability of three light-flavor quarks combining into a baryon and$ \overline{N}_{M}/N_{l\bar{l}} $ to denote the average probability of a light-flavor quark and antiquark pair combining into a meson. Here,$ \overline{N}_{B} $ and$ \overline{N}_{M} $ are the average number of all light-flavor baryons and that of all mesons.$ N_{lll} = N_{l}(N_{l}-1)(N_{l}-2) $ is the number of all possible three quark combinations and$ N_{l\bar{l}} = N_{l}N_{\bar{l}} $ is the number of all possible light-flavor quark antiquark pairs.$N_{\rm iter}$ is the number of permutations for$ l_{1}l_{2}l_{3} $ ; it is set to 6 for three different flavors, 3 for two identical flavors, and 1 for three identical flavors.$ C_{B_{j}} $ and$ C_{M_{j}} $ are introduced to tune the production weight of hadrons with the same quark content but different spins. In this paper, we only consider the ground state$ J^{P} = 0^{-},\,1^{-} $ mesons and$ J^{P} = (1/2)^{+},\,(3/2)^{+} $ baryons in the flavor SU(3) group. We introduce the parameter$ R_{V/P} $ to denote the relative production weight of the vector mesons to the pseudoscalar mesons with the same flavor composition. Then, we get$ C_{M_{j}} = 1/(1+R_{V/P}) $ for$ J^{P} = 0^{-} $ mesons and$C_{M_{j}} = R_{V/P}/(1+R_{V/P})$ for$ J^{P} = 1^{-} $ mesons. Similarly, we introduce the parameter$ R_{D/O} $ to denote the relative production weight of the decuplet baryons to the octet baryons with the same flavor composition. Then, we have$ C_{B_{j}} = 1/(1+R_{D/O}) $ for$ J^{P} = (1/2)^{+} $ baryons and$C_{B_{j}} = $ $ R_{D/O}/(1+R_{D/O})$ for$ J^{P} = (3/2)^{+} $ baryons, except$C_{\Lambda} \,=\, $ $ C_{\Sigma^{0}} \,=\, 1/(2+R_{D/O}),~ \; C_{\Sigma^{*0}} \,=\, R_{D/O}/(2+R_{D/O}),~\; C_{\Delta^{++}} \,=\, C_{\Delta^{-}} =$ $C_{\Omega^{-}} = 1 $ . Here,$ R_{V/P} $ and$ R_{O/D} $ are set to 0.45 and 0.5, respectively, according to our recent work on the$ pp $ collisions at$ \sqrt{s} = $ 13 TeV [29].Similar to Eqs. (16) and (17), the combination probability of a charm quark and light-flavor (anti-)quark(s) can be parameterized by
$ P_{cl_{1}l_{2}\rightarrow B_{j}} = C_{B_{j}}N_{\rm iter}\frac{\overline{N}_{B_{c}}}{N_{cll}}, $

(18) $ P_{c\bar{l}_{1}\rightarrow M_{j}} = C_{M_{j}}\frac{\overline{N}_{M_{c}}}{N_{c\bar{l}}}, $

(19) where
$ N_{cll} = N_{c}N_{l}(N_{l}-1) $ ,$ N_{c\bar{l}} = N_{c}N_{\bar{l}} $ and$N_{\rm iter}$ equals to 1 as$ l_{1} = l_{2} $ or 2 as$ l_{1}\neq l_{2} $ . In this paper, we consider the ground state$ J^{P} = 0^{-},\,1^{-} $ single-charmed mesons,$ J^{P} = \left(1/2\right)^{+} $ triplet and sextet single-charmed baryons, and$ J^{P} = \left(3/2\right)^{+} $ sextet single-charmed baryons. Similar to light-flavor mesons, we introduce the parameter$ R'_{V/P} $ to denote the relative production weight of the vector mesons to the pseudoscalar mesons. Different from light-flavor baryons, we introduce two parameters for single-charmed baryons. We use the parameter$ R_{S1/T} $ to denote the relative production weight of$ J^{P} = \left(1/2\right)^{+} $ sextet baryons to$ J^{P} = \left(1/2\right)^{+} $ triplet baryons with the same flavor composition, and another parameter$ R_{S3/S1} $ to denote that of$ J^{P} = \left(3/2\right)^{+} $ sextet baryons to$ J^{P} = \left(1/2\right)^{+} $ sextet baryons. We take$ R'_{V/P} = 1.5 $ ,$ R_{S1/T} = 0.5 $ and$ R_{S3/S1} = 1.4 $ according to our previous work on single-charmed hadrons [30]. We emphasize that yields and momentum spectra of final state charmed baryons$ \Lambda_{c}^{+} $ ,$ \Xi_{c}^{0,+} $ and$ \Omega_{c}^{0} $ after taking strong and electromagnetic decays into account are actually insensitive to the parameters$ R_{S1/T} $ and$ R_{S3/S1} $ .The unitarity of the hadronization process constrains the number of the formed hadrons
$ \overline{N}_{M}+3\overline{N}_{B}+\overline{N}_{M_{\bar{c}}}+2\overline{N}_{B_{c}} = N_{l}, $

(20) $ \overline{N}_{M}+3\overline{N}_{\bar{B}}+\overline{N}_{M_{c}}+2\overline{N}_{\bar{B}_{\bar{c}}} = N_{\bar{l}}, $

(21) $ \overline{N}_{M_{c}}+\overline{N}_{B_{c}} = N_{c}, $

(22) $ \overline{N}_{M_{\bar{c}}}+\overline{N}_{\bar{B}_{\bar{c}}} = N_{\bar{c}}, $

(23) where we neglect the contribution of multi-charmed hadrons. Because of the small contribution of the relative production ratio
$ N_{c}/N_{l}\sim\mathcal{O} $ (1%) in high energy$ pp $ ,$ p $ A, and AA collisions, we can neglect the contribution of charmed hadrons in Eqs. (20) and (21) and then obtain the separate constraints for$ N_{l} $ and$ N_{c} $ , respectively.For collisions at LHC energies, the approximation of the charge conjugation symmetry
$ N_{q_{i}} = N_{\bar{q}_{i}} $ and$ N_{h} = N_{\bar{h}} $ is usually satisfied. Therefore, the above unitarity constraints are reduced to$ \overline{N}_{M}+3\overline{N}_{B}\approx N_{l} $ and$ \overline{N}_{M_{c}}+\overline{N}_{B_{c}} = N_{c} $ . We can define the competition factor$ R_{B/M} = \overline{N}_{B}/\overline{N}_{M} $ to quantify the production weight of baryons in the light-flavor sector and consider it as a model parameter. Then, we can calculate$ \overline{N}_{B} = \frac{R_{B/M}}{1+3R_{B/M}}N_{l}, $

(24) $ \overline{N}_{M} = \frac{1}{1+3R_{B/M}}N_{l}. $

(25) We found that
$ R_{B/M} = 0.087\pm0.04 $ can well explain data of yield densities of light-flavor hadrons in relativistic heavy-ion collisions at RHIC and LHC energies and those in the$ pp $ and$ p $ Pb collisions at LHC energies [38, 40, 41]. We also define the competition factor$ R_{B/M}^{\left(c\right)} $ for single-charmed hadrons and obtain$ \overline{N}_{B_{c}} = \frac{R_{B/M}^{(c)}}{1+R_{B/M}^{(c)}}N_{c}, $

(26) $ \overline{N}_{M_{c}} = \frac{1}{1+R_{B/M}^{(c)}}N_{c}. $

(27) We found that
$ R_{B/M}^{\left(c\right)} $ is approximately$ 0.425\pm0.025 $ in our recent works [27, 30] by fitting the midrapidity data of$ \Lambda_{c}^{+} $ for the$ pp $ collisions at$ \sqrt{s} = 7 $ TeV and those for the$ p $ Pb collisions at$ \sqrt{s_{NN}} = 5.02 $ TeV measured by ALICE collaboration [42].Quark momentum distributions
$ f_{q_{1}q_{2}q_{3}}(p_{1},p_{2},p_{3}) $ and$ f_{q_{1}\bar{q}_{2}}(p_{1},p_{2}) $ are the inputs to the model. When they are given, we can obtain$ N_{q_1 q_2 q_3} $ ,$ N_{q_1 \bar{q}_2} $ ,$ N_{q_i} $ , and$ N_{\bar{q}_i} $ after integrating over momenta. Then, substituting Eqs. (24)-(25) into Eqs. (16)-(17) and subsequently substituting the latter into Eqs. (14)-(15), we obtain the yields for light-flavor hadrons. Using Eqs. (14)-(15) and Eqs. (10)-(11), we calculate coefficients$ \kappa_{B_j} $ and$ \kappa_{M_j} $ . Substituting them into Eqs. (6)-(7), we obtain the momentum distributions for light-flavor hadrons. Calculations for single-charmed hadrons are similar.We also consider the physical situation in which the numbers of quarks are not fixed values but fluctuate event by event in high energy collisions. As we did in Ref. [41], we consider the Poisson distribution as the base line to simulate the numbers of quarks of different kinds of flavors produced in the midrapidity range in each event. Then, we take the event average of the numbers of hadrons, to obtain their yield densities. We note that the effect of the quark number fluctuations only weakly affects the production of mesons and baryons containing up and down quarks but strongly affects multi-strange baryons such as
$ \Omega^- $ [41]. The fluctuations of the momentum distributions of quarks are not considered at the moment.We finally consider the decay effects of short-life hadrons on the production of stable hadrons
$ \begin{array}{l} f_{h_{j}}^{\rm (final)}(p) = f_{h_{j}}(p)+\sum\limits_{i\neq j}\int {\rm d}p'f_{h_{i}}(p')D_{ij}(p',p), \end{array} $

(28) where the decay function
$ D_{ij}(p',p) $ is calculated by decay kinetics and decay branch ratios reported by Particle Data Group [43].As a short summary of this section, we emphasize that the EVC model is essentially a statistical model based on the constituent quark degrees of freedom at hadronization. The model is described in the momentum representation, and the space-time information about hadronization is not incorporated at present. In deriving the momentum spectra and yields of hadrons, a stochastic feature of quark combination and flavor-independence of strong interactions are mainly used. The effect of the broken flavor symmetry is taken into account, on the one hand, by the difference in the momentum distributions (and also numbers) of quarks with different flavors, which will be discussed in the following text. On the other hand, it is accounted for by flavor-dependent parameters, such as the difference between
$ R_{B/M} $ of light-flavors and$ R_{B/M}^{(c)} $ of charms. In addition, non-perturbative dynamics in the combination process, which are difficult to calculate using first principles, are parameterized in the model. We expect that the values of these parameters, such as$ R_{V/P} $ and$ R_{B/M} $ , will be stable in different high energy collisions, as indicated by our available studies up to now. Finally, the momentum distribution${\rm d}N_{h,q}/{\rm d}p$ is a general denotation. In this paper, we focus on the transverse production of hadrons at midrapidity; then, the momentum distribution${\rm d}N_{h,q}/{\rm d}p$ refers to${\rm d}N_{h,q}/{\rm d}p_{T}{\rm d}y$ at midrapidity. -
In our model, momentum distributions of light-flavor constituent quarks at hadronization are inputs. Because they are difficult to calculate from first principles in the low
$ p_T $ range, we determine them by fitting the experimental data for identified hadrons in our model. Considering that the available experimental measurements are mainly inclusive distributions, here we assume the factorization approximation for the joint momentum distribution of (anti-) quarks, i.e.,$f_{q_{1}q_{2}q_{3}}\left(p_{T_{1}},p_{T_{2}},p_{T_{3}}\right) = f_{q_{1}}\left(p_{T_{1}}\right)\times $ $ f_{q_{2}}\left(p_{T_{2}}\right)f_{q_{3}}\left(p_{T_{3}}\right)$ and$ f_{q_{1}\bar{q}_{2}}\left(p_{T_{1}},p_{T_{2}}\right) = f_{q_{1}}\left(p_{T_{1}}\right)f_{\bar{q}_{2}}\left(p_{T_{2}}\right) $ . In addition, we assume the isospin symmetry$f_{u}\left(p_{T}\right) = $ $ f_{d}\left(p_{T}\right)$ and the charge-conjugation symmetry$f_{q_{i}}\left(p_{T}\right) = $ $ f_{\bar{q}_{i}}\left(p_{T}\right)$ for the$ p_{T} $ spectra of (anti-)quarks at midrapidity at LHC energies. Finally, we have only two inputs$ f_u(p_T) $ and$ f_s(p_T) $ in the light-flavor sector, which can be conveniently determined by the experimental data for only a few hadrons.In this section, we study the production of light-flavor hadrons in the low and intermediate
$ p_T $ range at midrapidity, for the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. In particular, we discuss a quark number scaling property for the$ p_{T} $ spectra of$ \Omega^- $ and$ \phi $ and study the$ p_{T} $ dependence of the$ \Omega/\phi $ ratio. We also study the property of the extracted$ p_{T} $ spectra of up quarks and strange quarks. -
In this subsection, we discuss an interesting correlation between the
$ p_{T} $ spectrum of$ \Omega^- $ and that of$ \phi $ , which gives the first insight into the hadron production mechanism at hadronization.$ \Omega $ and$ \phi $ consist of strange quarks/antiquarks, exclusively. In the EVC model, the$ p_{T} $ spectra of$ \Omega^- $ and$ \phi $ have simple expressions$ f_{\Omega}\left(3p_{T}\right) = \kappa_{\Omega}\left[f_{s}\left(p_{T}\right)\right]^{3},$

(29) $ f_{\phi}\left(2p_{T}\right) = \kappa_{\phi}f_{s}\left(p_{T}\right)f_{\bar{s}}\left(p_{T}\right) = \kappa_{\phi}\left[f_{s}\left(p_{T}\right)\right]^{2},$

(30) where we used
$ f_{s}\left(p_{T}\right) = f_{\bar{s}}\left(p_{T}\right) $ for midrapidity at the LHC energy. We then obtain the following correlation$ \begin{array}{l} f_{\phi}^{1/2}\left(2p_{T}\right) = \kappa_{\phi,\Omega}f_{\Omega}^{1/3}\left(3p_{T}\right), \end{array} $

(31) where the coefficient
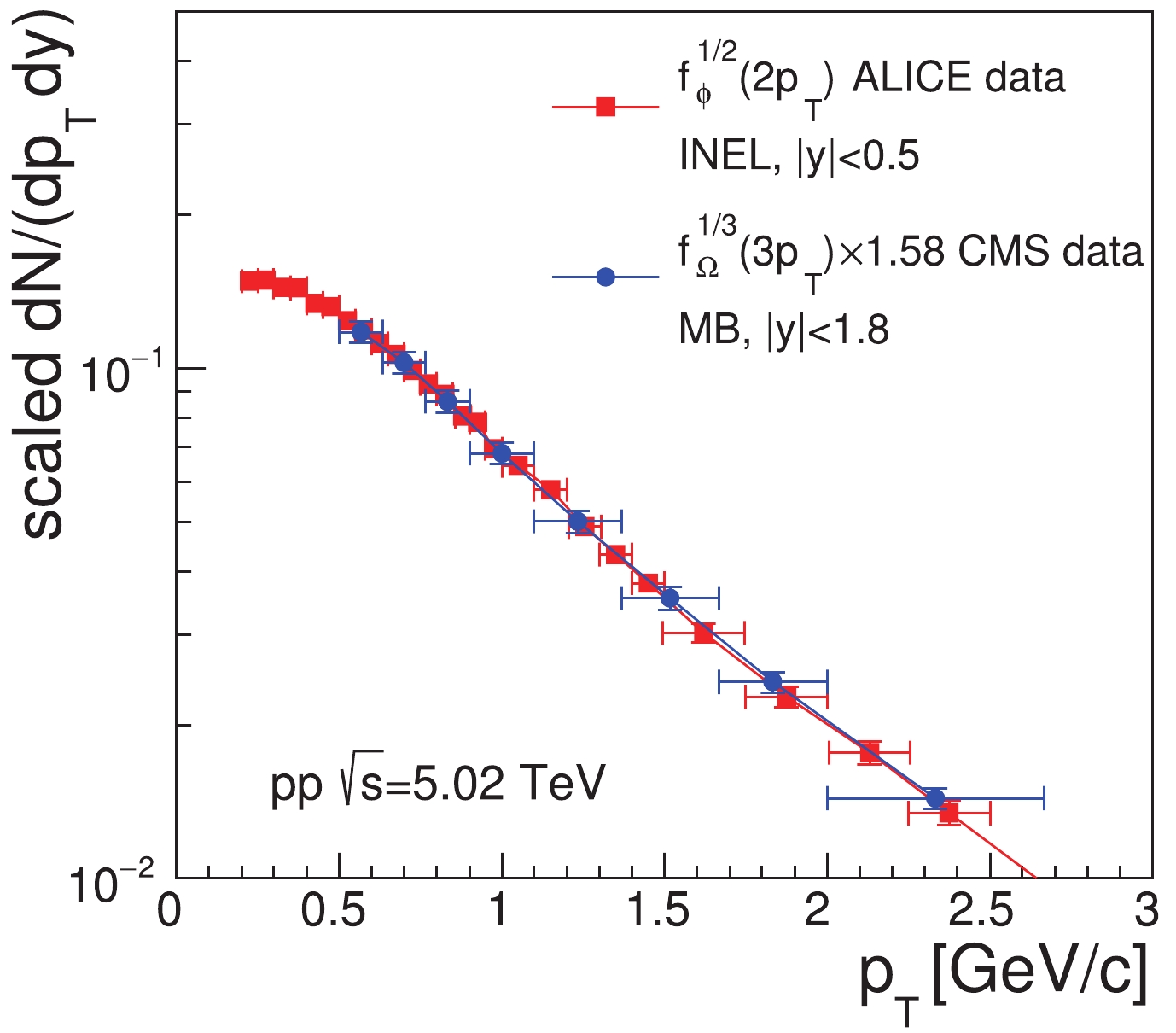
$ \kappa_{\phi,\Omega} = \kappa_{\phi}^{1/2}/\kappa_{\Omega}^{1/3} $ is independent of$ p_{T} $ . Eq. (31) means that, in the stochastic combination scenario of quarks and antiquarks at hadronization, the$ p_{T} $ spectra of$ \Omega^- $ and$ \phi $ have a strong correlation, based on the number of strange (anti-)quarks they contain. Therefore, we call Eq. (31) the quark number scaling property.In Fig. 1, we test Eq. (31) using the preliminary data of the
$ p_{T} $ spectrum of$ \phi $ in the rapidity interval$ |y|<0.5 $ for inelastic events in the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV, as measured by the ALICE collaboration [31], and using the data of$ \Omega $ (i.e.,$ \Omega^{-}+\bar{\Omega}^{+} $ ) in the rapidity interval$ |y|<1.8 $ for minimum-bias events, as measured by the CMS collaboration [33]. By examining the available experimental data for$ p_{T} $ spectra of hyperons in$ pp $ collisions at$ \sqrt{s} = 7 $ TeV measured by ALICE collaboration and those by CMS collaboration [44-46], we notice that the average transverse momentum$ \langle p_{T}\rangle $ and the shape of$ p_{T} $ distributions measured by two collaborations are quite consistent, although the center values of$ {\rm d}N/{\rm d}y $ measured by two collaborations have a certain difference. Therefore, in this paper, we put two data sets in$ pp $ collisions at$ \sqrt{s} = $ 5.02 TeV into together to test our model. To compare the scaled data from the two different collaborations, the coefficient$ \kappa_{\phi,\Omega} $ was set to 1.58 but not the direct calculation of our model. The scaled data for$ \Omega $ are in a good agreement with those for$ \phi $ . Furthermore, we know from Eqs. (29) and (30) that Eq. (31) equals to$ f_{s}\left(p_{T}\right) $ multiplied by the$ p_{T} $ -independent coefficient$ \sqrt{\kappa_{\phi}} $ . Therefore, Fig. 1 also gives us direct information about the$ p_{T} $ spectrum of strange quarks at hadronization in the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. -
We parameterize the
$ p_{T} $ spectrum of quarks by a Lévy-Tsallis functional form [47]. According to Eq. (30), we can use our model to fit the scaled data for$ \phi $ in Fig. 1, to obtain the$ p_{T} $ spectrum of strange quarks$ f_{s}\left(p_{T}\right) $ at hadronization. We further use the model to fit the experimental data of the$ p_{T} $ spectrum of the proton [32], to obtain the$ p_{T} $ spectrum of up/down quarks$ f_{u}\left(p_{T}\right) $ at hadronization. The properties of$ f_s(p_T) $ and$ f_u(p_T) $ will be discussed in Sec. III.D.After obtaining
$ f_u(p_T) $ and$ f_s(p_T) $ , we can calculate the$ p_{T} $ spectra of various light-flavor hadrons. In Fig. 2(a), we firstly show the fit results for the proton data, which were used for obtaining$ f_u(p_T) $ . In Fig. 2(b), we show the result for the$ p_T $ spectrum of$ \left(K^{*0}+\bar{K}^{*0}\right)/2 $ and compare it with the experimental data [48]; a good agreement is observed. Note that the data for$ \phi $ , proton, and$ K^{*} $ are all the ALICE data for inelastic events and for the rapidity interval$ |y|<0.5 $ . In Fig. 2(c) and (d), we present the results for$ \Lambda+\bar{\Lambda} $ and$ \Xi^{-}+\bar{\Xi}^{+} $ and compare them with the experimental data from the CMS collaboration [33]. Because CMS experiments select the minimum-bias events and rapidity interval$ |y|<1.8 $ , which are different from those for the ALICE experiments, we multiplied our results for$ \Lambda $ and$ \Xi $ by 0.85, to test the shape of the$ p_{T} $ distributions of hyperons predicted by our model. We observe a good agreement between the shapes of the$ p_{T} $ spectra of two hyperons. -
In Fig. 3(a), we show the fit results for the
$ p_{T} $ spectrum of$ \phi $ and the calculated result for the$ p_{T} $ spectrum of$ \Omega $ (i.e.,$ \Omega^{-}+\bar{\Omega}^{+} $ ), for the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. Similar to the case of$ \Lambda $ and$ \Xi $ in Fig. 2, here we also multiplied our result for$ \Omega $ by 0.85, to compare with the shape of the experimental data for the$ p_{T} $ spectrum of$ \Omega $ , as measured by the CMS collaboration [33]. As indicated by the quark number scaling property in Fig. 1, we see that the$ p_{T} $ spectra of$ \phi $ and$ \Omega $ can be simultaneously described by our model.In Fig. 3(b), we show the result for the
$ \Omega/\phi $ ratio as a function of$ p_{T} $ and compare with experimental data. Here, the experimental data for the$ \Omega/\phi $ ratio were calculated by the data of their inclusive$ p_{T} $ spectra in Fig. 3 (a), with the propagation of statistical uncertainties [31, 33]. We see that the ratio$ \Omega/\phi $ firstly increases with$ p_{T} $ in the low$ p_{T} $ range ($ p_{T}\lesssim2.5 $ GeV/c) and then decreases with$ p_{T} $ at larger$ p_{T} $ . Our model result, indicated by the solid line, well explains the experimental data.This non-monotonic
$ p_{T} $ dependence of the ratio of baryon to meson and, in particular, the enhancement in the low$ p_{T} $ range have been observed many times in relativistic heavy-ion collisions [49-53] and in the$ pp $ and$ p $ Pb collisions at LHC energies [8, 44, 54]. This typical behavior of the baryon to meson ratio is usually regarded as the consequence of the quark combination mechanism at hadronization [55-59]. In this paper, taking the$ \Omega/\phi $ ratio as an example, we perform a simple derivation to further clarify the underlying physics of such$ p_{T} $ dependence of the baryon to meson ratio in the low and intermediate$ p_{T} $ ranges.To understand the
$ p_{T} $ dependence of the$ \Omega/\phi $ ratio, we calculate the slope of the ratio$ \begin{aligned}[b] \left[\frac{f_{\Omega}\left(p_{T}\right)}{f_{\phi}\left(p_{T}\right)}\right]^{'} =& \frac{f_{\Omega}\left(p_{T}\right)}{f_{\phi}\left(p_{T}\right)}\left[\frac{f_{\Omega}^{'}\left(p_{T}\right)}{f_{\Omega}\left(p_{T}\right)}-\frac{f_{\phi}^{'}\left(p_{T}\right)}{f_{\phi}\left(p_{T}\right)}\right] \\ =& \frac{f_{\Omega}\left(p_{T}\right)}{f_{\phi}\left(p_{T}\right)}\left[\frac{\partial\ln\left(f_{s}\left(p_{T}/3\right)\right)}{\partial\left(p_{T}/3\right)}-\frac{\partial\ln\left(f_{s}\left(p_{T}/2\right)\right)}{\partial\left(p_{T}/2\right)}\right]. \end{aligned} $

(32) Using the mean-value theorem, the bracketed term on the last line becomes
$ \frac{\partial\ln\left(f_{s}\left(p_{T}/3\right)\right)}{\partial\left(p_{T}/3\right)}-\frac{\partial\ln\left(f_{s}\left(p_{T}/2\right)\right)}{\partial\left(p_{T}/2\right)} = -\frac{1}{6}p_{T}\left[\ln f_{s}\left(\xi\right)\right]^{''} $

(33) with
$ p_{T}/3<\xi<p_{T}/2 $ . Finally, we have$ \left[\ln\frac{f_{\Omega}\left(p_{T}\right)}{f_{\phi}\left(p_{T}\right)}\right]^{'} = -\frac{1}{6}p_{T}\left[\ln f_{s}\left(\xi\right)\right]^{''}, $

(34) which means that the slope of the
$ \Omega/\phi $ ratio is affected by the second derivative of the logarithm of the strange quark distribution.The second derivative of a distribution signals that the distribution is convex or concave in its shape. This can be conveniently inferred from Fig. 1 or Fig. 4. We see that
$ \left[\ln f_{s}(p_{T,s})\right]^{''}<0 $ as$ p_{T,s}\lesssim0.9 $ GeV/c and$ \left[\ln f_{s}(p_{T,s})\right]^{''}>0 $ as$ 1.0\lesssim p_{T,s}\lesssim2.5 $ GeV/c. Therefore, the$ \Omega/\phi $ ratio increases with$ p_{T} $ in the range$ p_{T}\lesssim2-3 $ GeV/c and decreases with$ p_{T} $ at larger$ p_{T} $ .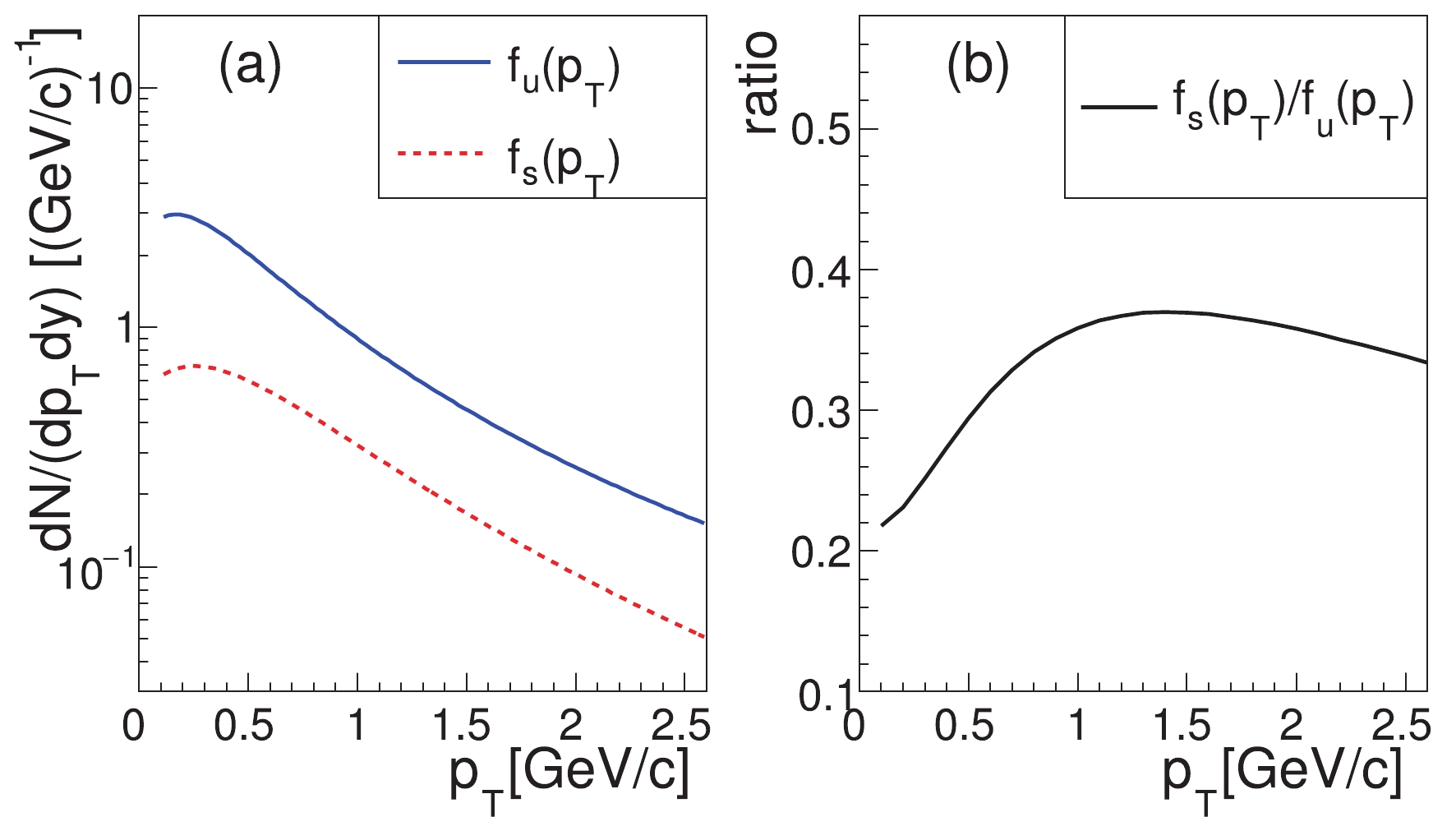
Figure 4. (color online) (a)
$p_{T}$ spectra of up and strange quarks at hadronization, for the inelastic$pp$ collisions at$\sqrt{s} = 5.02$ TeV. (b) The ratio$f_{s}\left(p_{T}\right)/f_{u}\left(p_{T}\right)$ .As is known, quarks of small
$ p_T $ mainly come from soft QCD processes, and the$ p_T $ distributions of these quarks are usually described by a thermal-like function$ \exp[-\sqrt{p_{T}^{2}+m^{2}}/T] $ , which has the property$ \left[\ln f_{s}\left(p_{T,s})\right)\right]^{''} $ $ < 0 $ , leading to an increase in the$ \Omega/\phi $ ratio. Quarks with large$ p_T $ mainly come from hard QCD processes, and the$ p_T $ distributions of these quarks are usually described by a jet-like function$ (1+p_{T}/p_{0})^{-n} $ with$ p_{0}>0 $ and$ n>0 $ , which has the property$ \left[\ln f_{s}\left(p_{T,s}\right)\right]^{''}>0 $ , leading to a reduction in the$ \Omega/\phi $ ratio. Therefore, we emphasize that the observed non-monotonic$ p_{T} $ dependence of the$ \Omega/\phi $ ratio depends not only on the quark combination mechanism but also on the property of the momentum distribution of strange quarks at hadronization. -
In Fig. 4(a), we show the
$ p_{T} $ spectra of up and strange quarks at hadronization, extracted from data for$ \phi $ and proton, for the inelastic$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. The ratio of the$ p_{T} $ -integrated yield density between strange quarks and up quarks, i.e., the strangeness suppression factor$ \lambda_{s} = \frac{{\rm d}N_{s}/{\rm d}y}{{\rm d}N_{u}/{\rm d}y} $

(35) is approximately 0.3. In panel (b), we show the strange quark to up quark spectrum ratio. We see that the ratio increases with
$ p_{T} $ as$ p_{T}\lesssim1 $ GeV/c and then weakly decreases at higher$ p_{T} $ . We note that this was also observed in the$ pp $ collisions at other collision energies, as well as in relativistic heavy-ion collisions [25, 29, 38].The difference between the
$ p_{T} $ spectra of up quarks and strange quarks affects the$ p_{T} $ spectra of the formed hadrons with different strange quark contents. In Fig. 5, we show the ratios$ \left(\Lambda+\bar{\Lambda}\right)/ \left(p+\bar{p}\right) $ ,$ \left(\Xi^{-}+\bar{\Xi}^{+}\right)/\left(\Lambda+\bar{\Lambda}\right) $ , and$ \left(\Omega^{-}+\bar{\Omega}^{+}\right)/\left(\Xi^{-}+\bar{\Xi}^{+}\right) $ as functions of$ p_{T} $ . Symbols indicate experimental data, while different lines correspond to the model results. The experimental data for the three ratios were calculated by the data of their inclusive$ p_{T} $ spectra with propagation of statistical uncertainties [32, 33]. We see that the data for the three ratios in the low$ p_{T} $ range ($ p_{T}\lesssim4 $ GeV/c) all increase with$ p_{T} $ . In our model, this is owing to the quark level property shown in Fig. 4(b) as$ p_{T,q}\lesssim1.3 $ GeV/c. The hierarchy in the magnitudes for the data of the three ratios can be understood in our model in terms of the ratios of yield densities,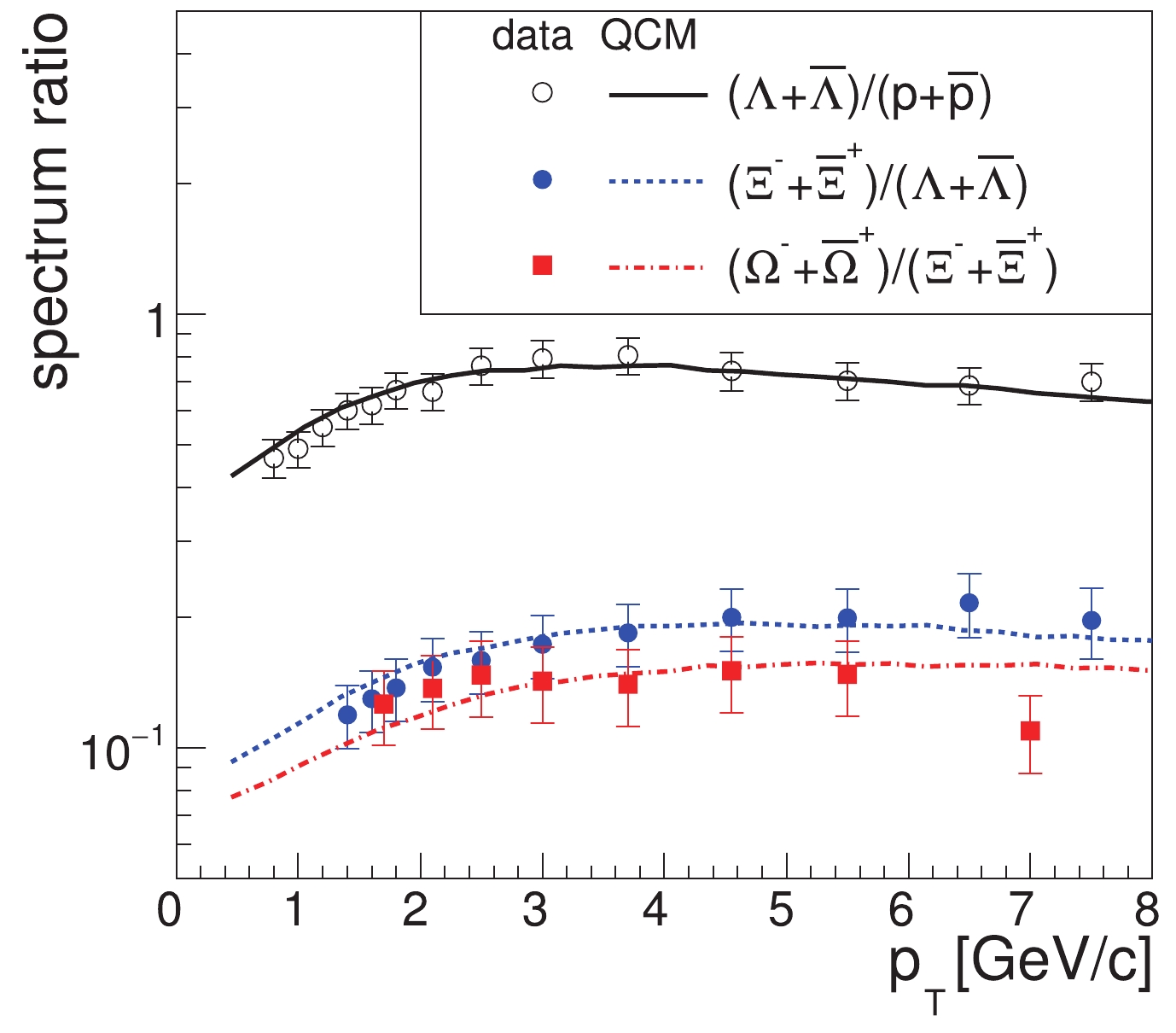
Figure 5. (color online) Spectral ratios
$\left(\Lambda+\bar{\Lambda}\right)/\left(p+\bar{p}\right)$ ,$(\Xi^{-}+\bar{\Xi}^{+})/ $ $ \left(\Lambda+\bar{\Lambda}\right)$ , and$\left(\Omega^{-}+\bar{\Omega}^{+}\right)/\left(\Xi^{-}+\bar{\Xi}^{+}\right)$ as functions of$p_{T}$ . Experimental data are from [32, 33].$ \frac{{\rm d}N_{\Lambda}/{\rm d}y}{{\rm d}N_{p}/{\rm d}y} \approx\frac{7.7}{4}\lambda_{s}, $

(36) $ \frac{{\rm d}N_{\Xi}/{\rm d}y}{{\rm d}N_{\Lambda}/{\rm d}y} \approx\frac{3}{7.7}\lambda_{s}, $

(37) $ \frac{{\rm d}N_{\Omega}/{\rm d}y}{{\rm d}N_{\Xi}/{\rm d}y} \approx\frac{1}{3}\lambda_{s}, $

(38) where the coefficients before
$ \lambda_{s} $ are owing to the iteration factor$N_{\rm iter}$ in Eq. (16) and strong/electromagnetic decay contribution of decuplet baryons (see [29, 60] for the detailed analytical expressions of their yields). -
In this section, we study the production of single-charmed hadrons in the
$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. We firstly extract the$ p_{T} $ spectrum of charm quarks and compare it with the calculation result of the perturbative QCD method. Then, we present the results for$ D $ mesons and$ \Lambda_{c}^{+} $ baryon, and we compare them with experimental data. We also predict the$ p_{T} $ -differential cross-sections of$ \Xi_{c}^{0,+} $ and$ \Omega_{c}^{0} $ and their ratios with respect to$ D $ mesons, as a function of$ p_{T} $ . -
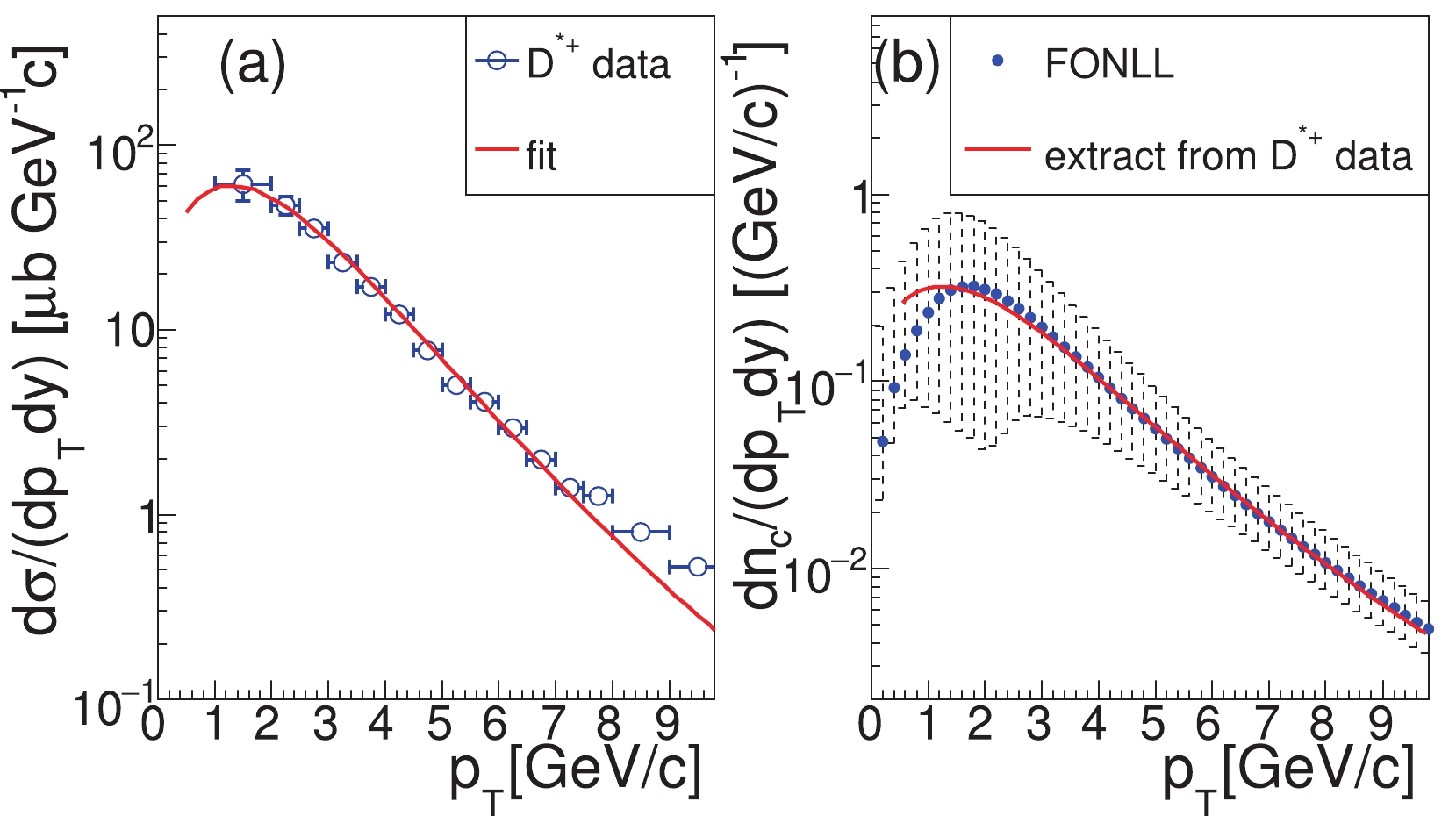
In Fig. 6(a), we apply the EVC model to fit the experimental data for differential cross-sections of
$ D^{*+} $ for the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. For this fit, we have used the$ p_{T} $ spectrum of$ u $ quarks obtained in the previous section and then obtained the$ p_{T} $ distribution for charm quarks at hadronization. In panel (b), we show the normalized charm quark distribution and compare it with the perturbative QCD calculation results obtained using the Fixed-Order Next-to-Leading-Logarithmic (FONLL) scheme [61, 62]. We observed a good consistency in the studied$ p_{T} $ range, within theoretical uncertainties. By fitting the$ D^{*+} $ data, we obtained the$ p_{T} $ integrated cross-section for charm quarks as${\rm d}\sigma_{c}/{\rm d}y = 1.0$ mb. This value is higher than the center value for the default FONLL calculation$ 0.461_{-0.31}^{+0.58} $ mb [61, 62] but is still within the theoretical uncertainty. -
Using the
$ p_{T} $ spectrum of charm quarks from the above subsection and those of light-flavor quarks from Sec. III.D, we calculated the$ p_{T} $ spectra of other single-charmed hadrons. In Table 1, we firstly present the$ p_{T} $ -integrated cross-section${\rm d}\sigma/{\rm d}y$ of$ D^{0,+} $ ,$ D_{s}^{+} $ ,$ \Lambda_{c}^{+} $ ,$ \Xi_{c}^{0,+} $ , and$ \Omega_{c}^{0} $ , for the inelastic$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. We firstly list analytical expressions and then numerical results as${\rm d}\sigma_{c}/{\rm d}y = 1.0\,{\rm mb}$ and compare the latter with available experimental data [34, 35].$\dfrac{{\rm d}\sigma}{{\rm d}y}$ 

analytical numerical/ $\mu{\rm b}$ 

data/ $\mu{\rm b}$ 

$D^{0}$ 

$\dfrac{1+1.677R'_{V/P} }{1+R'_{V/P} }\dfrac{1}{2+\lambda_{s} }\dfrac{1}{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

429 $447\pm20$ 

$D^{+}$ 

$\dfrac{1+0.323R'_{V/P} }{1+R'_{V/P} }\dfrac{1}{2+\lambda_{s} }\dfrac{1}{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

181 $184\pm13$ 

$D_{s}^{+}$ 

$\dfrac{\lambda_{s} }{2+\lambda_{s} }\dfrac{1}{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

91.5 $95\pm9$ 

$\Lambda_{c}^{+}$ 

$\dfrac{4}{\left(2+\lambda_{s}\right)^{2} }\dfrac{R_{B/M}^{(c)} }{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

225 $230\pm16$ 

$\Xi_{c}^{0}$ 

$2\dfrac{\lambda_{s} }{\left(2+\lambda_{s}\right)^{2} }\dfrac{R_{B/M}^{(c)} }{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

33.8 $\Xi_{c}^{+}$ 

$2\dfrac{\lambda_{s} }{\left(2+\lambda_{s}\right)^{2} }\dfrac{R_{B/M}^{(c)} }{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

33.8 $\Omega_{c}^{0}$ 

$\dfrac{\lambda_{s}^{2} }{\left(2+\lambda_{s}\right)^{2} }\dfrac{R_{B/M}^{(c)} }{1+R_{B/M}^{(c)} }\dfrac{{\rm d}\sigma_{c} }{{\rm d}y}$ 

5.07 In Fig. 7, we present the results for the
$ p_{T} $ spectra of$ D^{0,+} $ ,$ D_{s}^{+} $ , and$ \Lambda_{c}^{+} $ , for the inelastic$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV and compare them with the experimental data reported by the ALICE collaboration [34, 35]. We find a good agreement for these four hadrons in the low$ p_{T} $ range ($ p_{T}\lesssim7 $ GeV/c). At higher transverse momenta,$ p_{T}\gtrsim8 $ GeV/c, the results for$ D^{0,+} $ obtained using our model are lower than the corresponding experimental data, to a certain extent. This under-estimation maybe indicate the increased importance of the fragmentation mechanism for charm quark hadronization at large$ p_T $ .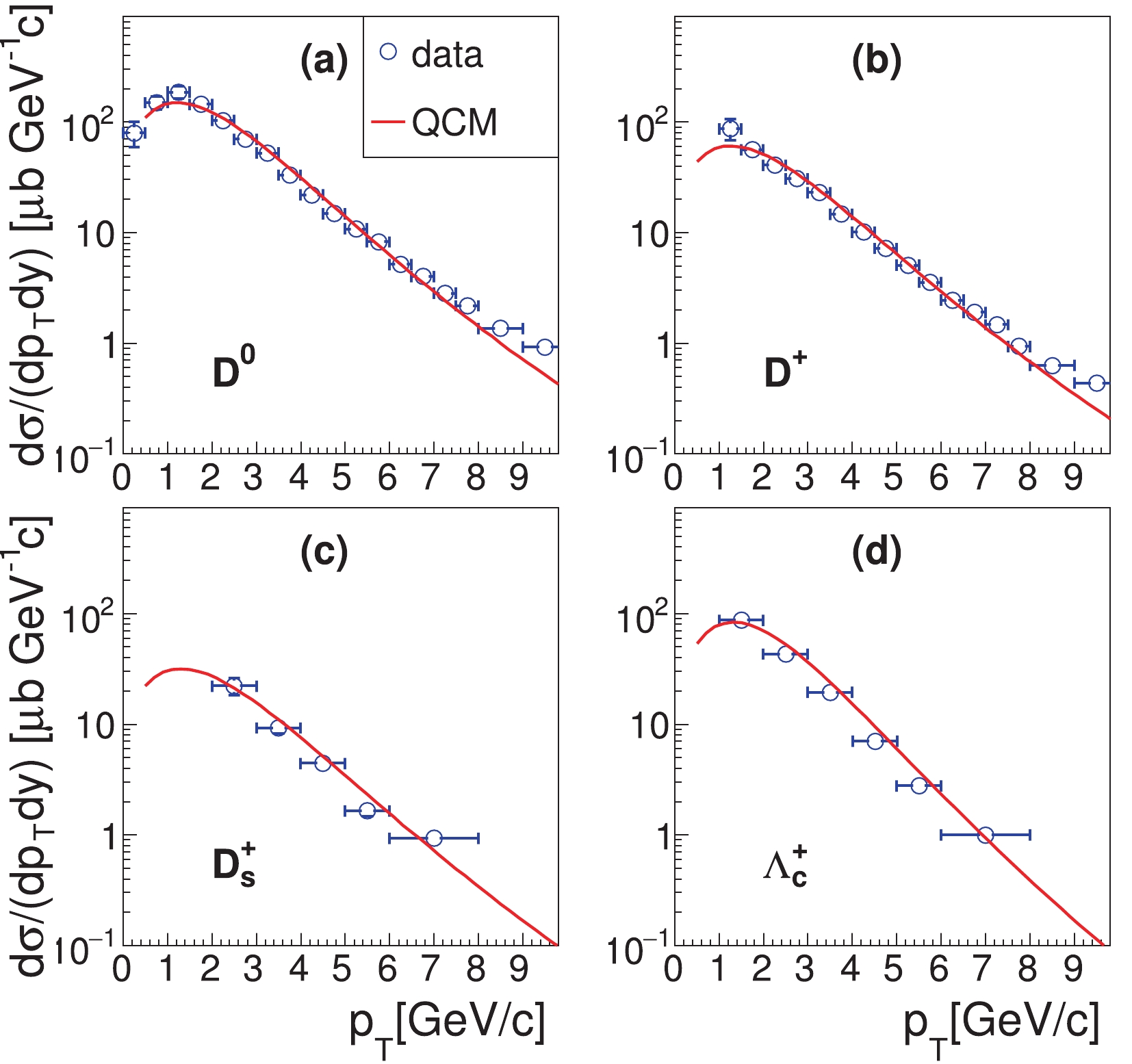
Figure 7. (color online)
$p_{T}$ spectra of$D^{0,+}$ ,$D_{s}^{+}$ and$\Lambda_{c}^{+}$ at midrapidity, for the inelastic$pp$ collisions at$\sqrt{s} = 5.02$ TeV. The lines that are labeled "QCM" indicate the results obtained using our model, while symbols correspond to the experimental data [34, 35].In Fig. 8(a), we show the predicted
$ p_{T} $ spectra of$ \Xi_{c}^{0} $ and$ \Omega_{c}^{0} $ , for the inelastic$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. Compared with the production of$ \Lambda_{c}^{+} $ , the production of$ \Xi_{c}^{0} $ and that of$ \Omega_{c}^{0} $ are suppressed, owing to the cascade strangeness. As shown by their$ p_{T} $ -integrated cross-sections in Table 1, we have
Figure 8. (color online) (a)
$p_{T}$ spectra of$\Xi_{c}^{0}$ and$\Omega_{c}^{0}$ at midrapidity, for the inelastic$pp$ collisions at$\sqrt{s} = 5.02$ TeV. (b) Ratios between charmed baryons as a function of$p_{T}$ .$ \Lambda_{c}^+:\Xi_{c}^{0}:\Omega_{c}^{0} = 1:\frac{1}{2}\lambda_{s}:\frac{1}{4}\lambda_{s}^{2}, $

(39) Because
$ \lambda_s\approx0.3 $ for the inelastic$ pp $ collisions, we see in Fig. 8(b) that the ratio$ \Xi_{c}^{0}/\Lambda_{c}^{+} $ is approximately 0.1-0.2, while the ratio$ \Omega_{c}^{0}/\Lambda_{c}^{+} $ is approximately 0.02-0.03 in the low and intermediate$ p_T $ range. The ratio$ \Omega_{c}^{0}/\Xi_{c}^{0} $ is also on the order of$ \lambda_{s}/2 $ and therefore is close to$ \Xi_{c}^{0}/\Lambda_{c}^{+} $ . In addition, we see that the three ratios increase with$ p_T $ in the low$ p_T $ range, which is owing to the difference between$ f_s(p_T) $ and$ f_u(p_T) $ , as shown in Fig. 4.The baryon to meson ratio, when plotted as a function of
$ p_{T} $ , is sensitive to the production mechanism of hadrons during hadronization. In Fig. 9, we show the results for the ratios of charmed baryons to charmed mesons, as a function of$ p_{T} $ , for the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. In Fig. 9 (a), we firstly show the result for$ \Lambda_{c}^{+}/D^{0} $ as the solid line. Compared with the experimental data for$ \Lambda_{c}^{+}/D^{0} $ [34], our model explains well the downward trend in the experimental data at$ p_{T}\gtrsim2 $ GeV/c. In the low$ p_{T} $ range ($ p_{T}\lesssim2 $ GeV/c), the ratio obtained using our model increases with increasing$ p_{T} $ . This behavior can be tested in the future as more precise experimental data for this$ p_{T} $ range become available. We note that the experimental data for the$ p $ Pb and Pb-Pb collisions at small$ p_{T} $ have indicated this property [34].
Figure 9. (color online) Ratios of charmed baryons to charmed mesons as a function of
$p_{T}$ , at midrapidity, for inelastic$pp$ collisions at$\sqrt{s} = 5.02$ TeV.We further present the result for
$ \left(\Xi_{c}^{0}+\Xi_{c}^{+}\right)/D^{0} $ in Fig. 9(a) and that for$ \Omega_{c}^{0}/D^{0} $ in Fig. 9(b). We see that the magnitude of$ \left(\Xi_{c}^{0}+\Xi_{c}^{+}\right)/D^{0} $ at$ p_{T}\approx 3 $ GeV/c is approximately 0.16, while that of$ \Omega_{c}^{0}/D^{0} $ is only approximately 0.015. This hierarchical property is owing to the cascade strangeness suppression, as shown in Eq. (39).In order to reduce the effect of the strangeness suppression and the dependence of the model parameters on these baryon to meson ratios, we propose two new ratios
$ \Lambda_{c}^{+}/\left(D^{0}+D^{+}\right) $ and$ \Xi_{c}^{0}/D_{s}^{+} $ . From Table 1, the two ratios in the$ p_{T} $ -integrated cross-sections have the same magnitude$ \frac{{\rm d}\sigma_{\Lambda_{c}^+}/{\rm d}y}{{\rm d}\sigma_{D^{0}+D^+}/{\rm d}y} = \frac{{\rm d}\sigma_{\Xi_{c}^{0}}/{\rm d}y}{{\rm d}\sigma_{D_{s}^+}/{\rm d}y} = \frac{2}{2+\lambda_{s}}R_{B/M}^{(c)}. $

(40) They are independent of the model parameter
$ R'_{V/P} $ , which is different from the$ \Lambda_{c}^{+}/D^{0} $ ratio. They are also insensitive to$ \lambda_{s} $ , since a change in$ \lambda_{s} $ (e.g., 0.3-0.33) only weakly (1%) affects the two ratios. Finally, the two ratios are directly related to the production competition of baryon to meson in the charm sector, which is characterized by the parameter$ R_{B/M}^{(c)} $ in our model. Therefore, we propose these two ratios as direct observables of the baryon production weight in the charm sector. The two ratios as functions of$ p_{T} $ are shown in Fig. 9(c); evidently, they are close to each other.In Fig. 9(d), we show the result for
$ \Omega_{c}^{0}/D_{s}^{+} $ as a function of$ p_{T} $ . As indicated by their ratio in the$ p_{T} $ -integrated cross-section$ \frac{{\rm d}\sigma_{\Omega_{c}^{0}}/{\rm d}y}{{\rm d}\sigma_{D_{s}^+}/{\rm d}y} = \frac{\lambda_{s}}{2+\lambda_{s}}R_{B/M}^{(c)}, $

(41) this ratio is smaller than
$ \Xi_{c}^{0}/D_{s}^{+} $ by a factor$ \lambda_{s}/2 $ . In addition, we see that the peak position of the ratio$ \Omega_{c}^{0}/D_{s}^{+} $ is located at approximately$ p_{T}\approx $ 3-4 GeV/c, which is larger than the peak position of the ratios$ \Lambda_{c}^{+}/D^{0} $ and$ \Lambda_{c}^{+}/\left(D^{0}+D^{+}\right) $ by about 1 GeV/c. This is the kinetic effect caused by the difference between the up quark distribution and strange quark distribution, as shown in Fig. 4. -
In this paper, we have used a quark combination model with equal-velocity combination approximation to study the production of light-flavor hadrons and single-charmed hadrons in the
$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. The systematic comparison of our model results with available experimental data indicates the effectiveness of the model, which is consistent with our previous studies on the$ pp $ collisions at$ \sqrt{s} = $ 7 and 13 TeV [27-30].By examining the preliminary data for the
$ p_{T} $ spectra of$ \Omega $ and$ \phi $ at midrapidity, we found that the two spectra exhibit a quark number scaling property, which gives a first signal for the quark combination mechanism in the$ pp $ collisions at$ \sqrt{s} = 5.02 $ TeV. This scaling property further enables us to conveniently extract the$ p_{T} $ spectra of strange quarks at hadronization. By fitting experimental data of hadrons containing up/down quarks such as the proton, we also obtained the$ p_{T} $ spectra of up/down quarks. Using the extracted spectra of up/down and strange quarks, we calculated the$ p_{T} $ spectra of$ K^{*0} $ ,$ \Lambda $ , and$ \Xi $ , which contain both up/down quarks and strange quarks, and we found a good agreement with the corresponding experimental data. We studied the$ p_{T} $ dependence of the$ \Omega/\phi $ ratio and found that the increasing/decreasing trend of the ratio with respect to$ p_{T} $ is closely related to the concave/convex shape of the logarithm of the strange quark distribution. We also studied the difference between the$ p_{T} $ spectra of up/down quarks and that of strange quarks and used it to explain the difference between the$ p_{T} $ spectra of different kinds of baryons.Using the EVC model, we obtained the differential cross-section of charm quarks as a function of
$ p_{T} $ , by fitting the experimental data for$ D^{*+} $ . We found that it is quite consistent in shape with the results obtained using the perturbative QCD method FONLL. Applying the equal-velocity combination of charm quarks and light-flavor quarks, we successfully explained the experimental data for differential cross-sections of$ D^{0,+} $ ,$ D_{s}^{+} $ , and$ \Lambda_{c}^{+} $ as functions of$ p_{T} $ . We predicted the differential cross-sections of$ \Xi_{c}^{0,+} $ and$ \Omega_{c}^{0} $ . Compared with that of$ \Lambda_{c}^{+} $ , the production of$ \Xi_{c}^{0,+} $ and$ \Omega_{c}^{0} $ is suppressed because the abundance of strange quarks at hadronization is suppressed compared with up/down quarks. We predicted that the ratio$ \Xi_{c}^{0,+}/D^{0} $ is approximately 0.16 and$ \Omega_{c}^{0}/D^{0} $ is approximately 0.015, owing to the cascaded suppression of strangeness. We also proposed several ratios, such as$ \Xi_{c}^{0}/D_{s}^{+} $ and$ \Omega_{c}^{0}/D_{s}^{+} $ , to further demonstrate the effect of cascaded suppression of strangeness caused by the number of strange quarks involving a combination with charm quarks. These predictions can be tested by analyzing future experimental data at the LHC.
Production of light-flavor and single-charmed hadrons in pp collisions at ${ \sqrt{\boldsymbol s} = {\bf 5.02 }}$ TeV in an equal-velocity quark combination model
- Received Date: 2021-07-07
- Available Online: 2021-11-15
Abstract: We apply an equal-velocity quark combination model to study the production of light-flavor hadrons and single-charmed hadrons at midrapidity in the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



































 DownLoad:
DownLoad: