-
The limit of nuclear existence has been a longstanding fundamental question in nuclear science. There are approximately 3200 isotopes that have been confirmed experimentally so far [1, 2]. Nuclear existence ends at the drip lines, where there is no enough binding energy to prevent the last nucleon(s) from escaping the nucleus. On the proton-rich side, since it is closer to the stable nuclides, the drip line is relatively easy to determine, and most recently, that of neptunium
$ (Z = 93) $ has been determined experimentally [3]. On the neutron-rich side, however, due to the long distance separating it from the valley of stability, the neutron drip line is established experimentally only for light nuclei, i.e., from hydrogen$ (Z = 1) $ to neon$ (Z = 10) $ [4]. For the heavier elements, the location of the neutron drip line is based on theoretical predictions and is thus uncertain.The location of the neutron drip line and the masses of the neutron-rich nuclei are essential to understand the structure of weakly bound nuclei, the astrophysical rapid neutron capture process, and the origin of elements in the universe. Exploration of highly neutron-rich nuclei is extremely challenging both for the nuclear theory and experiments. The production rates of the neutron-rich nuclei are very low in experiments. It is anticipated that the development of the next generation of radioactive ion-beam will open up a new window to nuclei that were heretofore inaccessible. Theoretically, the description of weakly bound exotic systems requires proper treatment of the pairing, deformation, continuum effects, and coupling among them [5-10].
Beyond the neutron drip line, the phenomenon of reentrant binding is predicted in microscopic calculations [11-20]. This phenomenon was indicated earlier in the calculations of light nuclei [11] and is now spread throughout the nuclear landscape on the neutron-rich side. Predicted by various density functional theories, nuclei around
$ Z = 60\sim100 $ are found likely to exist beyond the primary neutron drip lines [12-17]. Such behavior is due to the presence of neutron shell closure, and the local changes of the shell structure induced by deformation variations also play an important role.To study the loosely bound system around the neutron drip line, the nuclear theory should be able to treat the asymptotic behavior of the nuclear many-body wavefunctions properly [5-10, 21]. In the deformed relativistic Hartree-Bogoliubov theory in continuum [9, 22], the deformed relativistic Hartree-Bogoliubov formalism is solved in the Dirac Woods-Saxon basis, in which the radial wave functions have a proper asymptotic behavior at a large distance from the nuclear center [23]. A new nuclear mass table is being prepared using the DRHBc theory [24], which has been previously applied successfully to describe various nuclear properties [8, 10, 21, 25-31].
The limits of nuclear charge and mass are marked by the superheavy nuclei. It is encouraging to explore the neutron drip line and the properties of the neutron-rich nuclei in the superheavy nuclear mass region. To date, the heaviest nucleus observed in experiments is the nucleus with
$ Z = 118 $ and$ A = 294 $ [32, 33]. The production cross-section of superheavy nuclei is extremely low, and their structural information is rarely revealed in experiments. An indirect method is to study lighter nuclei in the transfermium mass region with$ Z>100 $ , which are the heaviest systems accessible in present in-beam experiments [34-36]. It is expected that the ground-state properties and the nuclear structure studies of the transfermium nuclei will lead to a more reliable prediction of the location of the spherical island of stability [34, 37].In the present work, nuclear masses near the neutron drip line from No
$ (Z = 102) $ to Ds$ (Z = 110) $ are calculated using the deformed relativistic Hartree-Bogoliubov theory in continuum with density functional PC-PK1 [38]. The previously predicted neutron shell closure at$ N = 258 $ [15, 27] is confirmed, and the possible existence of the bound nuclei beyond the neutron drip line is predicted in$ Z = 106,108 $ , and$ 110 $ isotopes by the DRHBc theory. The microscopic mechanism resulting in such a phenomenon is analyzed. This paper is organized as follows. The DRHBc formalism and the numerical details of the calculations are briefly introduced in Sec. II. The prediction of the possible nuclear existence beyond the neutron drip lines is presented in Sec. III, and the microscopic mechanism leading to this phenomenon as well as the influence of higher orders of deformation are analyzed in Sec. IV. Finally, a brief summary is provided in Sec. V. -
The details of the DRHBc theory can be found in Refs. [9, 22, 39, 40]. The DRHBc theory with a point-coupling density functional has been presented in Ref. [24]. For simplicity, we only briefly describe the main formalism here. The relativistic Hartree-Bogoliubov (RHB) equation is
$ \begin{pmatrix} h_{D}-\lambda_{\tau} & \Delta \\ -\Delta^{\ast} & -h_{D}^{\ast}+\lambda_{\tau} \end{pmatrix} \begin{pmatrix} U_{k} \\ V_{k} \end{pmatrix} = E_{k}\begin{pmatrix} U_{k} \\ V_{k} \end{pmatrix},$

(1) which is solved in a Dirac Woods-Saxon basis [23].
$ E_{k} $ is the quasiparticle energy, and$ (U_{k} ,V_{k})^{\mathrm{T}} $ is the quasiparticle wave function.$ \lambda_{\tau} $ ($ \tau = n\ \mathrm{or}\ p $ ) is the Fermi energy. The pairing potential$ \Delta $ is$ \Delta(\boldsymbol{r}_{1},\boldsymbol{r}_{2}) = V^{pp}(\boldsymbol{r}_{1},\boldsymbol{r}_{2})\kappa(\boldsymbol{r}_{1},\boldsymbol{r}_{2}), $

(2) where
$ \kappa(\boldsymbol{r}_{1},\boldsymbol{r}_{2}) $ is the pairing tensor, and$ V^{pp}(\boldsymbol{r}_{1},\boldsymbol{r}_{2}) $ is a density dependent force of zero-range$ V^{pp}(\boldsymbol{r}_{1},\boldsymbol{r}_{2}) = V_{0}\frac{1}{2}(1-P^{\sigma})\delta(\boldsymbol{r}_{1}-\boldsymbol{r}_{2})\left[1-\frac{\rho(\boldsymbol{r}_{1})}{\rho_{\mathrm{sat}}}\right]. $

(3) $ V_0 $ is the pairing strength,$ \rho_{\mathrm{sat}} $ is the saturation density of nuclear matter and$ \dfrac{1}{2}(1-P^{\sigma}) $ is the projector for the spin$ S = 0 $ component. The Dirac Hamiltonian$ h_{D} $ is expressed as$ h_{D} = \boldsymbol{\alpha}\cdot\boldsymbol{p}+V(\boldsymbol{r})+\beta[M+S(\boldsymbol{r})] $

(4) with
$ S(\boldsymbol{r}) $ and$ V(\boldsymbol{r}) $ being the scalar and vector potentials, respectively. For an axially deformed nuclei with the reflection symmetric shape, the potential can be expanded in terms of Legendre polynomials,$ f(\boldsymbol{r}) = \sum\limits_{\lambda}f_{\lambda}(r)P_{\lambda}(\cos\theta),\ \lambda = 0,2,4,6\cdots $

(5) with
$ f_{\lambda}(r) = \frac{2\lambda+1}{4\pi}\int {\rm d}\Omega f(\boldsymbol{r})P_{\lambda}(\cos\theta). $

(6) The relativistic Hartree-Bogoliubov equations are solved in a spherical Dirac Woods-Saxon basis to obtain the wave functions. The total energy of a nucleus can be obtained as [7]
$ \begin{aligned}[b] E_{\mathrm{RHB}} =& \sum\limits_{k>0}(\lambda_{\tau}-E_{k})v^2_k\\& -\int {\rm d}\boldsymbol{r} \Bigg\{\frac{1}{2}\alpha_{S}\rho^2_S+\frac{1}{2}\alpha_{V}\rho^2_V+\frac{1}{2}\alpha_{TV}\rho^2_3\\& +\frac{2}{3}\beta_{S}\rho^3_S+\frac{3}{4}\gamma_{S}\rho^4_S+\frac{3}{4}\gamma_{V}\rho^4_V+\frac{1}{2}\delta_{S}\rho_S \Delta\rho_S\\ & +\frac{1}{2}\delta_{V}\rho_V \Delta\rho_V+\frac{1}{2}\delta_{TV}\rho_3 \Delta\rho_3+\frac{1}{2}eA_{0}\rho_p\Bigg \}\\ &-E_{\mathrm{pair}}+E_{\mathrm{c.m.}}. \end{aligned}$

(7) where
$v^2_k = \displaystyle\int {\rm d}\boldsymbol{r}V^{\dagger}_k(\boldsymbol{r})V_k(\boldsymbol{r})$ , and the densities are$ \begin{aligned}[b] \rho_S(\boldsymbol{r}) =& \sum\limits_{k>0}V^{\dagger}_k(\boldsymbol{r})\gamma_0 V_k(\boldsymbol{r}),\\ \rho_V(\boldsymbol{r}) =& \sum\limits_{k>0}V^{\dagger}_k(\boldsymbol{r})V_k(\boldsymbol{r}),\\ \rho_3(\boldsymbol{r}) =& \sum\limits_{k>0}V^{\dagger}_k(\boldsymbol{r})\tau_3 V_k(\boldsymbol{r}). \end{aligned}$

(8) The pairing energy is calculated as
$ E_{\mathrm{pair}} = -\frac{1}{2}\int {\rm d}\boldsymbol{r} k(\boldsymbol{r})\Delta(\boldsymbol{r}). $

(9) The center-of-mass (c.m.) correction energy is given by
$ E_{\mathrm{c. m.}} = -\frac{1}{2mA} \langle\hat{\boldsymbol P}^2\rangle $

(10) with A the mass number and
$ \hat{\boldsymbol P} $ the total momentum for nucleus in the c.m. frame.The present calculations are carried out with the density functional PC-PK1. The numerical details are the same as those used in Ref. [24]. The Dirac Woods-Saxon basis is chosen with the box size
$ R_{ \rm{box}} = 20 $ fm and the mesh size$ \Delta r = 0.1 $ fm. The numbers of states in the Dirac sea and Fermi sea are set to be the same. The energy cutoff for the Woods-Saxon basis is taken as$ E^{+}_{ \rm{cut}} = 300 $ MeV, and the angular momentum cutoff is$ J_{ \rm{max}} = 23/2\hbar $ . The density-dependent zero-range pairing force is adopted, and the pairing strength is determined by the experimental odd-even differences in binding energies. For the particle-particle channel, with a pairing window of$ 100 $ MeV, the saturation density$ \rho_{ \rm{sat}} = 0.152 $ fm$ ^{-3} $ , and pairing strength$ V_0 = -325.0 $ MeV fm$ ^3 $ . The convergence check of the Legendre expansion has been performed [41], and$ \lambda_{ \rm{max}} = 10 $ is used in the present work. -
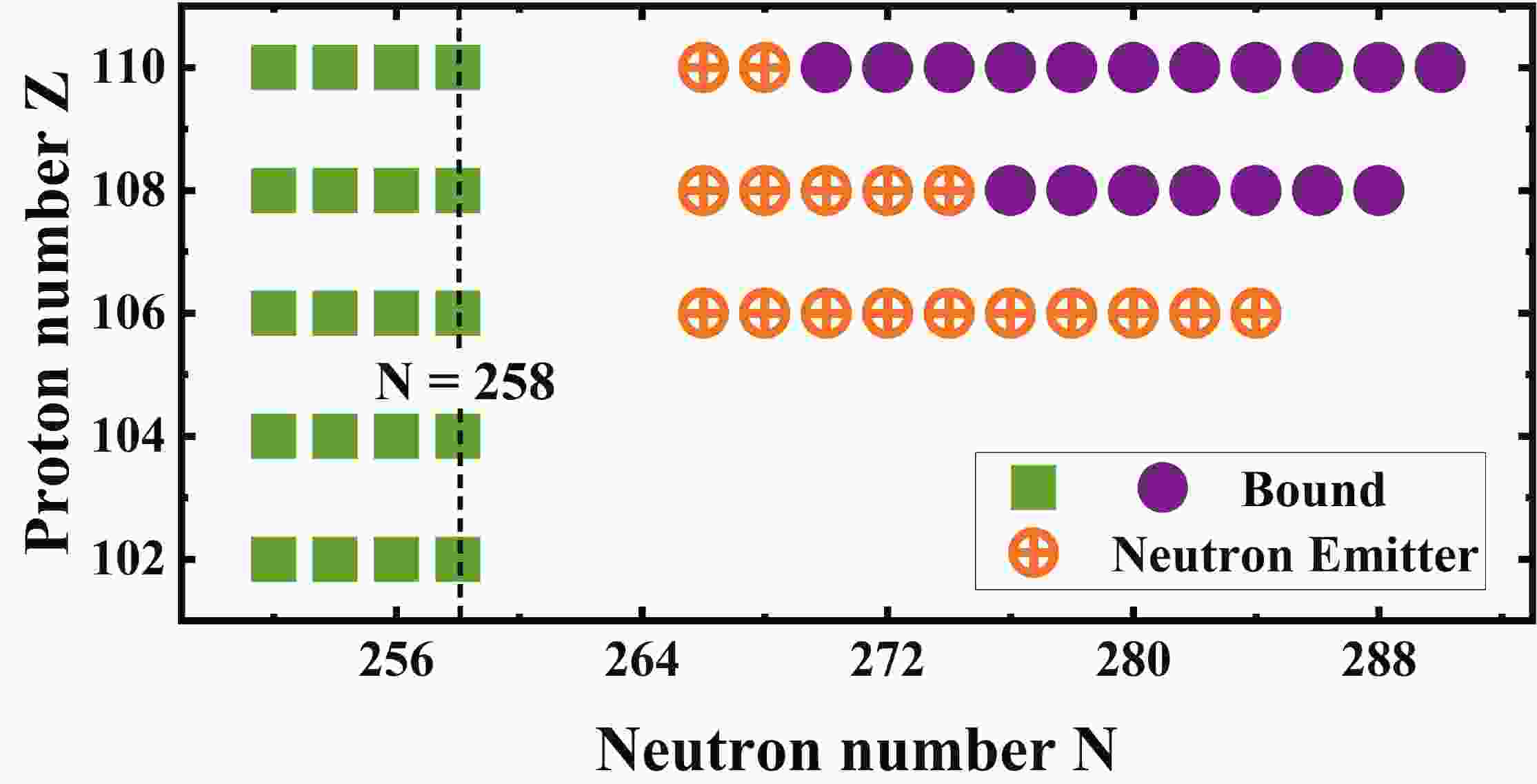
Figure 1 illustrates the section of the nuclear chart that shows the possible existence of nuclei beyond the neutron drip lines from No to Ds obtained in the DRHBc calculations. The drip line of an isotopic chain is defined by its proton/neutron separation energies. Since the present calculations are performed only for even-even nuclei, and also due to the pairing correlations, the two-neutron separation energies
$ S_{2n}(Z,N) = B(Z,N-2)- $ $ B(Z,N) $ are used to specify the neutron drip line, where$ B(Z,N) $ is the binding energy of a nucleus with proton number Z and neutron number N. A nucleus being bound against two-neutron emission necessitates its two-neutron separation energy$ S_{2n} $ to be positive, and the nucleus is unbound against two-neutron emission when its$ S_{2n} $ is negative.
Figure 1. (color online) Section of the nuclear chart showing the possible nuclear existence beyond the neutron drip line from No
$ (Z = 102) $ to Ds$ (Z = 110) $ in the DRHBc calculations, which includes only the even-even nuclei. The predicted spherical neutron shell closure at$ N = 258 $ is denoted by dashed line. The bound nuclei within and beyond the neutron drip lines are denoted by the solid squares and circles, respectively. The nuclei bound against two-neutron emission while unbound against multi-neutron emission are denoted by the crossed circles.As shown in Fig. 1, the spherical neutron closure is predicted at
$ N = 258 $ , which is consistent with the calculations by other density functional theories [15, 16, 42]. The neutron drip line from No to Ds is located at$ N = 258 $ , and the nuclear binding ends at$ N = 258 $ for No and Rf$ (Z = 104) $ . It is very interesting that the phenomenon of reentrant binding beyond the neutron drip lines occurs for Sg$ (Z = 106) $ , Hs$ (Z = 108) $ , and Ds. For Sg, nuclei with$ 266\leqslant N\leqslant284 $ are bound against two-neutron emission, i.e., they have positive two-neutron separation energies, while they are unbound against multi-neutron emission, i.e., the multi-neutron separation energies$ B(Z,N)-B(Z = 106, $ $ N = 258) $ are negative. For Hs, nuclei with$ 266\leqslant N\leqslant288 $ are bound against two-neutron emission, and among these, nuclei with$ 266 \leqslant N \leqslant 274 $ are unbound against multi-neutron emission. For Ds, the situation is similar to that of Hs isotopes, i.e., nuclei with$ 266\leqslant N\leqslant290 $ are bound against two-neutron emission and unbound against multi-neutron emission for$ N = 266,268 $ . An enhanced stability trend is demonstrated from No to Ds. It is necessary to investigate the heavier elements along this line [43]. -
We take Ds isotopes near the neutron drip line as an example to reveal the microscopic mechanism of reentrant binding beyond the drip line. Table 1 shows the detailed results from
$ ^{362} {\rm{Ds}}$ to$ ^{404} {\rm{Ds}}$ . The single neutron energy levels of the nuclei around$ ^{368} {\rm{Ds}}$ are shown in Fig. 2. One can see that for the spherical nuclei$ ^{368} {\rm{Ds}}$ ,$ ^{370} {\rm{Ds}}$ , and$ ^{372} {\rm{Ds}}$ , a large shell gap appears for these three nuclei at$ N = 258 $ , which indicates the nature of spherical shell closure. According to the two-neutron separation energies,$ ^{368} {\rm{Ds}}$ is a bound nucleus, whereas$ ^{370} {\rm{Ds}}$ and$ ^{372} {\rm{Ds}}$ are not. This is because the neutron Fermi surface of$ ^{368} {\rm{Ds}}$ is just at the$ N = 258 $ spherical shell. For the ground state, all the 258 neutrons occupy the single-particle levels below the continuum threshold (shown by the dot-dashed line in Fig. 2). For$ ^{370} {\rm{Ds}}$ ($ ^{372} {\rm{Ds}}$ ), there are two (four) neutrons mainly occupying the$ 1k_{15/2} $ orbital, which are just above the continuum threshold. Therefore, the Fermi energies of$ ^{370,372} {\rm{Ds}}$ are positive, and their two-neutron separation energies are negative, and thus,$ ^{370,372} {\rm{Ds}}$ are unbound against two-neutron emission. For$ ^{374} {\rm{Ds}}$ , six more neutrons, in comparison with$ ^{368} {\rm{Ds}}$ , lead to deformation of$ \beta_{2} = 0.064 $ . Three deformed single-particle levels stemming from the spherical orbitals$ 2i_{13/2} $ and$ 1k_{15/2} $ drop, and their energies become negative. The increased deformation leads to a much smaller$ N = 258 $ shell gap as the neutron number N increases. For the ground state, the six neutrons mainly occupy the three levels just below the continuum threshold, and the Fermi energy becomes negative with a very small absolute value. However,$ ^{374} {\rm{Ds}}$ is still unbound against two-neutron emission due to the negative two-neutron separation energy, which can be explained by a loss of pairing energy. For$ ^{376} {\rm{Ds}}$ , the deformation increases, five deformed single-particle levels drop below the continuum threshold, and there is no energy gap around the Fermi surface. The two-neutron separation energy is positive, and the Fermi energy is negative.$ ^{376} {\rm{Ds}}$ is bound against two-neutron emission but unbound against multi-neutron emission.$ ^{378} {\rm{Ds}}$ is very similar to$ ^{376} {\rm{Ds}}$ . For the heavier isotopes up to$ ^{400} {\rm{Ds}}$ , the deformation$ \beta_{2} $ keeps increasing, and more deformed single-particle levels stemming from the$ 2i_{13/2} $ and$ 1k_{15/2} $ orbitals drop below the continuum threshold.$ ^{380-400} {\rm{Ds}}$ are all bound nuclei. Therefore, we see that the nuclear deformation can strongly influence the single-particle levels and the shell structures. It plays a vital role in reentrant binding beyond the drip lines in the presence of shell effects at neutron closure$ (N = 258) $ .A N B/MeV $ S_{2n} $ /MeV

$ \lambda_{n} $ /MeV

$ \beta_{2} $ 

$ Z=110 $ (Ds)

362 252 2284.175 3.311 −1.468 −0.084 364 254 2287.042 3.311 −1.570 −0.051 366 256 2290.220 3.178 −1.421 −0.034 368 258 2293.352 3.132 −0.834 0.000 370 260 2292.776 −0.576 0.255 0.000 372 262 2292.224 −0.552 0.237 0.000 374 264 2291.931 −0.293 −0.113 0.064 376 266 2292.448 0.517 −0.325 0.097 378 268 2293.115 0.667 −0.337 0.118 380 270 2293.724 0.609 −0.317 0.136 382 272 2294.359 0.635 −0.358 0.155 384 274 2295.126 0.767 −0.454 0.177 386 276 2296.139 1.013 −0.555 0.201 388 278 2297.258 1.119 −0.555 0.218 390 280 2298.299 1.041 −0.481 0.232 392 282 2299.146 0.847 −0.405 0.243 394 284 2299.886 0.741 −0.370 0.253 396 286 2300.566 0.679 −0.330 0.260 398 288 2301.156 0.590 −0.275 0.265 400 290 2301.593 0.437 −0.141 0.269 402 292 2301.674 0.081 0.008 0.273 404 294 2301.555 −0.119 0.071 0.277 Table 1. Ground-state properties of Ds isotopes with
$ 252\leqslant N\leqslant294 $ calculated using the DRHBc theory. The two-neutron unbound nuclei are underlined.
Figure 2. (color online) Single-neutron energy levels in the canonical basis near the Fermi surface of Ds isotopes with
$ 256\leqslant N\leqslant270 $ . The neutron Fermi energy$ \lambda_{n} $ of each isotope is denoted by hollow stars.As the existence of the bound nuclei beyond the drip line is affected strongly by the nuclear deformation, it is essential to investigate how strong the influence of the different orders of deformation is on this phenomenon. We perform the DRHBc constrained calculations at
$ \beta_{2} = 0 $ and unconstrained calculations with the Legendre expansion truncation$ \lambda_{\mathrm{max}} = 2 $ (only including quadrupole deformation$ \beta_{2} $ ),$ \lambda_{\mathrm{max}} = 4 $ (including quadrupole and hexadecapole deformations$ \beta_{2} $ and$ \beta_{4} $ ), and$ \lambda_{\mathrm{max}} = 6 $ (including$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ ), respectively. The calculated total energies relative to that of$ ^{368} {\rm{Ds}}$ $ (N = 258) $ as a function of the neutron number for$ ^{364-402} {\rm{Ds}}$ are presented in Fig. 3. One can see that for the calculations with$ \beta_{2} = 0 $ ,$ E-E_{N = 258} $ increases at$ N>258 $ . No bound nuclei would exist beyond the drip line. For the calculation of$ \lambda_{\mathrm{max}} = 2 $ , there are 4 unbound, 3 two-neutron emission bound while multi-neutron emission unbound, and 12 bound nuclei beyond the neutron drip line. Comparing with the result of$ \lambda_{\mathrm{max}} = 10 $ , there is 1 additional two-neutron emission bound but multi-neutron emission unbound nucleus beyond the drip line. For the calculation of$ \lambda_{\mathrm{max}} = 4 $ , except for the quantitive differences, the obtained bound nuclei are the same as those of the$ \lambda_{\mathrm{max}} = 10 $ calculation. For the calculations of$ \lambda_{\mathrm{max}} = 6 $ , the results are very similar to those of$ \lambda_{\mathrm{max}} = 10 $ , except that there is 1 additional bound nucleus obtained in the calculations with$ \lambda_{\mathrm{max}} = 6 $ . It demonstrates clearly that the nuclear deformation is vital to the existence of the bound nuclei beyond the drip lines.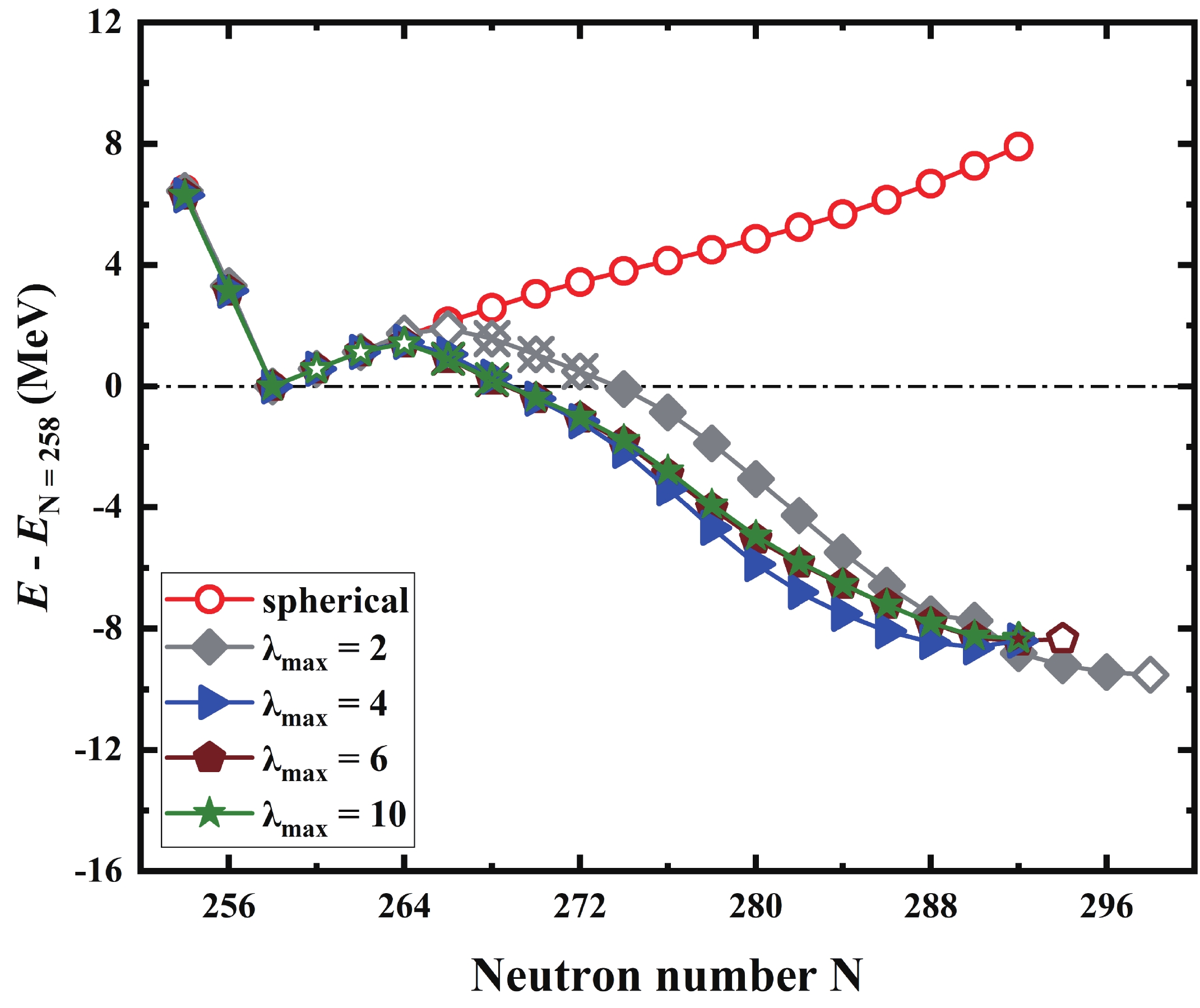
Figure 3. (color online) DRHBc calculated total energies relative to that of
$ ^{358} {\rm{Ds}}$ (N = 258) under different expansion orders of deformation. The bound and unbound nuclei are denoted by the solid and open symbols, respectively. The nuclei that are bound against two-neutron emission while unbound against multi-neutron emission are denoted by the crossed open symbols. -
The deformed relativistic Hartree-Bogoliubov theory in continuum is used to calculate the nuclear masses in the transfermium region from No to Ds. The calculations lead to the prediction of the possible existence of the bound nuclei beyond the neutron drip lines in
$ Z = 106,108 $ , and$ 110 $ isotopes. We take the Ds isotopes as an example to analyze the microscopic mechanism of the phenomenon of reentrant binding. Detailed investigations are performed based on the single-particle level structure and the occupation of the valence neutrons in the single-particle orbitals near the Fermi surface. It is found that, by locally changing the single-particle structures in the presence of shell effects at neutron closure at$ N = 258 $ , the nuclear deformation plays a vital role in the existence of the bound nuclei beyond the neutron drip lines. Further investigation shows that not only the quadrupole deformation$ \beta_{2} $ but also the hexadecapole deformation$ \beta_{4} $ and high-order deformation$ \beta_{6} $ are indispensable in reentrant binding beyond the drip line. In the present investigation, only the effect of axial symmetry deformations are discussed. Exploration of this phenomenon by extending the present DRHBc theory to include the triaxial deformation is expected in the future. -
We thank the members of DRHBc Mass Table Collaboration for helpful discussions.
Possible existence of bound nuclei beyond neutron drip lines driven by deformation
- Received Date: 2021-06-10
- Available Online: 2021-10-15
Abstract: Based on the relativistic calculations of the nuclear masses in the transfermium region from No





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: