-
It is believed that the heavy ion collisions at the Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) have produced a new state of matter, called strongly coupled quark gluon plasma (QGP) [1-3]. One of the signatures of QGP formation is the dissociation of heavy quarkonium [4]. Previous research has indicated that the immediate cause of this dissociation is Debye screening. However, a puzzle was revealed in the recent experiment of charmonium(
$ c\bar{c} $ ): the$ c\bar{c} $ suppression at the RHIC (lower energy density) was stronger than that at the LHC (larger energy density) [5, 6]. Obviously, this finding is in conflict with the Debye screening and the thermal activation [7, 8]. To explain this, D. E Kharzeev argued [9] that an anomalously strong suppression of$ c\bar{c} $ near the deconfinement transition could be a consequence of the nature of deconfinement. This inference was based on the lattice QCD results [10-13], which indicated a large amount of entropy S associated with the heavy quarkonium (or$ q\bar{q} $ ) in QGP, and this entropy was found to grow as a function of the distance between$ q\bar{q} $ . In the proposal of [9], the entropy gives rise to the entropic force$ {\cal{F}} = T\frac{\partial S}{\partial L}, $

(1) where T is the temperature of the plasma, and L is the inter-quark distance of
$ q\bar{q} $ . It has been conjectured [9] that the entropic force plays the leading role in the deconfinement transition itself and indicates a possible relation of the observed peak in the entropy near the deconfinement transition to the long string condensation [14-22].AdS/CFT correspondence [23-25], which maps a d dimensional quantum field theory to its dual gravitational theory, living in
$ d+1 $ dimensional, has yielded many important insights for studying different aspects of QGP [26]. Using AdS/CFT, D. Kharzeev first calculated the entropic force for$ {\cal{N}} = 4 $ super Yang-Mills (SYM) plasma [27]. Therein, it was found that the narrow and strong peak in the entropy near the transition temperature is related to the deconfinement of quarkonium. Soon after, this idea was extended to various cases, e.g., the entropic force of moving quarkonium was investigated in [28]. The chemical potential effect on the entropic force was studied in [29]. Moreover, this quantity has been addressed from AdS/QCD [30]. Other related results can be found in [31-33].In this study, we are interested in investigating the entropic force in strongly coupled theories with an anisotropic scaling symmetry in time and a spatial direction. In particular, we will consider hyperscaling violation theories [34-38], which are covariant under a generalized Lifshitz scaling symmetry with the dynamical exponent z and hyperscaling violation exponent
$ \theta $ and apply their gravity duals. Because of different scaling of time and space, these theories are intrinsically non-relativistic. In contrast, the metrics of these theories are scale invariant but not conformally invariant. From a QCD point of view, such theories could be used as a basis for new AdS/QCD constructions. Recently, the hyperscaling violation theories have been used to describe the string theory [39-43] and holographic superconductors [44-47]. Moreover, some QCD observables or quantities, e.g., Schwinger effect [48] and the heavy quark potential [49, 50], have been addressed in such theories. Motivated by this, in this study, we investigate the entropy force in hyperscaling violation theories. Specifically, we want to understand how the non-relativistic parameters z and$ \theta $ modify the entropy force as well as the quarkonium dissociation.The paper is organized as follows. In the next section, we introduce the hyperscaling violation theories given in [43]. In section III, we study the behavior of the entropic force with respect to a heavy quarkonium in these theories and analyze the effects of z and
$ \theta $ on it. In section IV, we summarize the results and present some discussions. -
Let us start with a brief review of the backgrounds with hyperscaling violation [43]. The corresponding metric takes the form [39, 51]
$ {\rm d}s^2 = u^{\theta}\left[-\frac{{\rm d}t^2}{u^{2z}}+\frac{b_0{\rm d}u^2+{\rm d}x^i{\rm d}x^j}{u^2}\right], $

(2) and is invariant under a generalized Lifshitz scaling
$t\to \Lambda^zt,\;u\to\Lambda u,\;x^i\to\Lambda x^i,\;{\rm d}s^2\to \Lambda^{-\theta }{\rm d}s^2$ , where$ b_0 = \ell^2 $ with$ \ell $ the IR scale. z is the dynamical Lifshitz parameter (also called the dynamical critical exponent), which characterizes the behavior of system near the phase transition.$ \theta $ denotes the hyperscaling violation exponent that is responsible for the nonstand scaling of physical quantities and controls the transformation of the metric.The scalar curvature is
$ {\cal{R}} = -\frac{3\theta^2-4(z+3)\theta+2(z^2+3z+6)}{b_0}u^{-\theta}. $

(3) Note that the geometry is flat for
$ \theta = 2 $ ,$ z = 0,1 $ . It is Ricci flat for$ \theta = 4 $ ,$ z = 3 $ , and in Ridler coordinates for$ \theta = 0 $ ,$ z = 1 $ .Using a radical redefinition
$ u = (2-z)r^{1/(2-z)}, $

(4) and rescaling
$ x^i $ and t, one gets$ {\rm d}s^2\sim r^{\frac{\theta-2}{2-z}}\left[-f(r){{\rm d}t^2}+\frac{{\rm d}r^2}{f(r)}+{\rm d}x^i{\rm d}x^i\right] ,\quad\;\; f(r) = f_0\left(\frac{r}{\ell}\right)^{\frac{2(1-z)}{2-z}}, $

(5) with
$ f_0 = (2-z)^{2(1-z)} $ . The boundary is at$ r = \infty $ when$ \dfrac{\theta-2}{2-z}<0 $ and at$ r = 0 $ when$ \dfrac{\theta-2}{2-z}>0 $ .The energy scale reads
$ E\simeq u^{(\theta -2z)/2}\simeq r^{(\theta -2z)/2(2-z)}. $

(6) As discussed in [43], the metrics (5) satisfy the Gubser conditions (in the context of holography, many non-trivial flows become singular upon dimensional reduction, leading to the Gubser criterion for the acceptability of a naked singularity [52]), given by
$ \frac{2z+3(2-\theta)}{2(z-1)-\theta}>0,\quad \frac{z-1}{2(z-1)-\theta}>0,\quad \frac{2(z-1)+3(2-\theta)}{2(z-1)-\theta}>0, $

(7) and the thermodynamic stability condition
$ \frac{z}{2(z-1)-\theta}>0. $

(8) The generalizations of (5) to include finite temperature are
$ {\rm d}s^2\sim\left(\frac{r}{\ell}\right)^{-\alpha}\left[-f(r){{\rm d}t^2}+\frac{{\rm d}r^2}{f(r)}+{\rm d}x^i{\rm d}x^i\right], $

(9) with
$ f(r) = f_0\left(\frac{r}{\ell}\right)^{2\beta}\left[1-\left(\frac{r}{r_h}\right)^\gamma\right], $

(10) where
$ \alpha = \frac{\theta-2}{z-2}, \qquad \beta = \frac{z-1}{z-2}, \qquad \gamma = \frac{2z+3(2-\theta)}{2(2-z)}. $

(11) The Hawking temperature reads
$ T = \frac{f_0}{8\pi\ell}\left(\frac{r_h}{\ell}\right)^{\frac{z}{z-2}}\left|\frac{2z-3\theta+6}{z-2}\right|. $

(12) For further details on the hyperscaling violation backgrounds, we refer to [43].
-
We now proceed to holographically compute the entropic force for the background metric (9) following [27]. The Nambu-Goto action is
$ S_{\rm NG} = T_{\rm F}\int {\rm d}\tau {\rm d}\sigma{\cal{L}} = -\frac{1}{2\pi\alpha^\prime}\int {\rm d}\tau {\rm d}\sigma\sqrt{-{\rm det} g_{\alpha \beta}}, \qquad $

(13) where
$ T_{\rm F} = \dfrac{1}{2\pi\alpha^\prime} $ is the fundamental string tension and$ \alpha^{\prime} $ is related to the 't Hooft coupling$ \lambda $ by$ \dfrac{R^2}{\alpha^\prime} = \sqrt{\lambda} $ (hereafter, we set$ R = 1 $ ). g represents the determinant of the induced metric with$ g_{\alpha\beta} = g_{\mu\nu}\frac{\partial X^\mu}{\partial\sigma^\alpha} \frac{\partial X^\nu}{\partial\sigma^\beta}, $

(14) where
$ X^\mu $ and$ g_{\mu\nu} $ are the target space coordinates and metric, respectively.For our purpose, we take the static gauge
$ t = \tau, \qquad x = \sigma, \qquad y = 0,\qquad z = 0, $

(15) and assume r depends only on
$ \sigma $ $ r = r(\sigma), $

(16) thus, the induced metric becomes
$ g_{00} = -b(r)f(r), \quad g_{01} = g_{10} = 0, \quad g_{11} = b(r)\left[1+\frac{\dot {r}}{f(r)})\right], $

(17) with
$ b(r) = (r/\ell)^{-\alpha} $ and$ \dot r = {\rm d}r/{\rm d}\sigma $ ; then, the Lagrangian density reads$ {\cal{L}} = \sqrt{b^2(r)[f(r)+\dot r^2]}. $

(18) Since
$ {\cal{L}} $ does not depend on$ \sigma $ explicitly, the corresponding Hamiltonian is a constant, that is$ {\cal{H}} = \frac{\partial{\cal{L}}}{\partial \dot{r}}\dot{r}-{\cal{L}} = {\rm Constant}. $

(19) Imposing the boundary condition at the tip of the U-shaped string
$ \dot r = 0,\qquad r = r_c\qquad (r_h>r_c) , $

(20) one gets
$ \dot{r} = \sqrt{\frac{f^2(r)b^2(r)-f(r)f(r_c)b^2(r_c)}{f(r_c)b^2(r_c)}} , $

(21) with
$ f(r_c) = f_0\left(\frac{r_c}{\ell}\right)^{2\beta} \left[1-\left(\frac{r_c}{r_h}\right)^\gamma\right],\qquad b(r_c) = \left(\frac{r_c}{\ell}\right)^{-\alpha}. $

(22) The inter-distance of
$ q\bar{q} $ can be calculated by integrating (21)$ L = 2\int_0^{r_c}{\rm d}r\sqrt{\frac{A(r_c)B(r)}{A^2(r)-A(r)A(r_c)}} . $

(23) with
$ A(r) = b^2(r)f(r),\quad B(r) = b^2(r),\quad A(r_c) = b^2(r_c)f(r_c), $

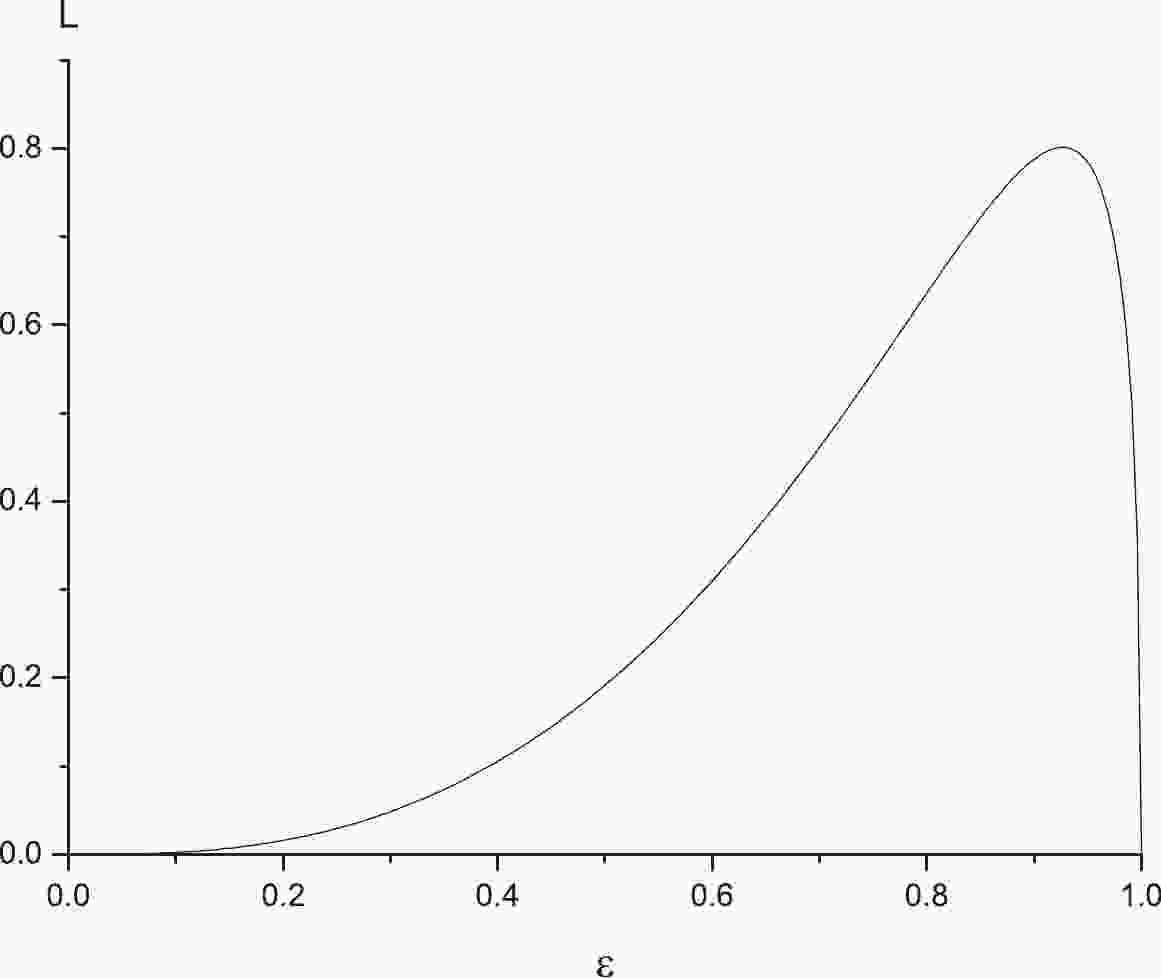
(24) the plot of L against
$ \varepsilon $ with$ \varepsilon = r_c/r_h $ is shown in Fig. 1. Here, we take$ z = 1.6,\;\theta = 1 $ (other values of z and$ \theta $ lead to a similar trend).The next task is to calculate entropy, given by
$ S = -\frac{\partial F}{\partial T}, $

(25) where F is the free energy of
$ q\bar{q} $ , which is related to the on-shell action of the fundamental string in the dual geometry. Note that this quantity has been holographically studied at zero temperature [53] and finite temperature [54, 55]. Broadly speaking, there are two cases for F.1. If
$ L > \dfrac{c}{T}$ (c denotes the maximum value of$ LT $ ), some new configurations should be considered [56], and then, there are a few possible choices of F [57], e.g., one may choose a configuration of two disconnected trailing drag strings [58, 59]. Under such conditions, the free energy is$ F^{(1)} = \frac{1}{\pi \alpha^{\prime}}\int_0^{r_c}{\rm d}r, $

(26) leading to
$ S^{(1)} = \sqrt{\lambda}\theta\left(L-\frac{c}{T}\right), $

(27) where
$\theta \left(L-\dfrac{c}{T}\right)$ is the Heaviside step function.2. If
$ L < \dfrac{c}{T} $ , the fundamental string is connected; then, the free energy of$ q\bar{q} $ can be obtained by plugging (21) into (18), that is$ F^{(2)} = \frac{1}{\pi\alpha^{\prime}}\int_0^{r_c}\sqrt{\frac{A(r)B(r)}{A(r)-A(r_c)}} , $

(28) then, from (12), (25), and (28), one gets
$ S^{(2)} = -\frac{\partial F^{(2)}}{\partial T} = -\frac{\partial F^{(2)}}{\partial r_h}\Bigg/\frac{\partial T}{\partial r_h}, $

(29) where
$ \begin{aligned}[b]&\frac{\partial F^{(2)}}{\partial r_h} = \frac{1}{2\pi\alpha^{\prime}}\\ \times &\int_0^{r_c}\frac{A^\prime(r)B(r)[A(r)-A(r_c)]-A(r)B(r)[A^{\prime}(r)-A^{\prime}(r_c)]}{\sqrt{A(r)B(r)[A(r)-A(r_c)]^3}}, \end{aligned} $

(30) $ \frac{\partial T}{\partial r_h} = \frac{f_0}{8\pi\ell}\left|\frac{2z-3\theta+6}{z-2}\right|\ell^{\frac{z-2}{z}}\frac{z}{z-2}r_h^{\frac{2}{z-2}}, $

(31) with
$A^{\prime}(r) = b^2(r)f_0\left(\frac{r}{\ell}\right)^{2\beta}\gamma r^\gamma r_h^{-\gamma-1}, $

(32) $ A^{\prime}(r_c) = A^{\prime}(r)|_{r = r_c}, $

(33) note that by plugging
$ z = 1 $ and$ \theta = 0 $ in (29), the entropic force for$ {\cal{N}} = 4 $ SYM [27] can be reproduced, as expected.Next, we calculate the entropy force. Before we get to that, we determine the value range of z and
$ \theta $ . According to the Gubser condition of (7) and the thermodynamic stability of (8), one has$ 1<z<2, \qquad \theta<2, \qquad \theta<z. $

(34) Taken together, one can numerically calculate the entropic force from (29). In Fig. 2, we plot
$ {S^{(2)}}/\sqrt \lambda$ versus$ LT $ for different values of z and$ \theta $ ; here, we have used the relation$ \dfrac{1}{\alpha^\prime} = \sqrt{\lambda} $ . From the left panel, one can see that, with fixed z, increasing$ \theta $ leads to larger entropy at small distances, whereas from the right panel, one finds that, with fixed$ \theta $ , increasing z leads to smaller entropy at small distances. As stated earlier, the entropic force is found to grow as a function of the distance (see (1)) and is responsible for the quarkonium dissociation. Thus, one concludes that increases$ \theta $ increases the entropic force, thus enhancing the quarkonium dissociation, while z has the opposite effect.
Figure 2. (color online)
$ S^{(2)}/\sqrt{\lambda} $ versus$ LT $ for different$ \theta $ and z. Left:$ z = 1.5 $ , and from left to right,$ \theta = 1,0,-1 $ . Right:$ \theta = 1 $ , and from left to right,$ z = 1.6,1.7,1.75 $ .To analyze how the temperature influences the entropic force in the hyperscaling violation backgrounds, we plot
$ S^{(2)}/\sqrt{\lambda} $ versus L with fixed z and$ \theta $ in Fig. 3. One finds that increasing T leads to an increase in the entropic force, in accord with the finding in [33]. The physical meaning of our results will be discussed in the next section. -
In this paper, we studied the entropic destruction of heavy quarkonium in the non-relativistic backgrounds. We considered Lifshitz and hyperscaling violation theories, which are strongly coupled theories with an anisotropic scaling symmetry in time and a spatial direction. An understanding of how the entropic force changes according to these theories may be essential for theoretical predictions. We discussed how the entropic force depends on the non-relativistic parameters z and
$ \theta $ . It is shown that increasing z decreases the entropic force, thus reducing the quarkonium dissociation. Namely, the quarkonium melts harder in the presence of an anisotropic scaling symmetry in time and a spatial direction. In contrast, we find that an increase in$ \theta $ increases the entropic force, indicating that the inclusion of$ \theta $ (means hyperscaling violation in the dual field theory) enhances the quarkonium dissociation.We would like to point out that the heavy quarkonium discussed here mainly refers to charmonium, because most of the bottomonium (
$ b\bar{b} $ ) has smaller sizes and is thus much less affected by the entropic force [31]. In fact, the available data show that the$ b\bar{b} $ suppression is indeed stronger at the LHC [60, 61] than at the RHIC [62, 63].Finally, it is relevant to mention that the imaginary potential [64] has been proposed to be responsible for melting the heavy quarkonium recently. It would be interesting to investigate this quantity in hyperscaling violation theories as well. We leave this for further study.
Entropic destruction of heavy quarkonium with hyperscaling violation
- Received Date: 2021-06-11
- Available Online: 2021-10-15
Abstract: We study the entropic destruction of heavy quarkonium in strongly coupled theories with an anisotropic scaling symmetry in time and a spatial direction. We consider Lifshitz and hyperscaling violation theories, which are covariant under a generalized Lifshitz scaling symmetry with the dynamical exponent z and hyperscaling violation exponent






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: