-
After the discovery of the Higgs boson [1, 2], the Standard Model (SM) of particle physics has achieved great success in describing particles up to energies of approximately 1 TeV [3]. However, there are still many unanswered questions and many unexplained phenomena, such as the symmetry of matter and antimatter, the sources of CP violation, and the nature of dark matter (DM) particles. This suggests that the Standard Model is potentially a low energy approximation of a more fundamental theory. However, the Standard Model of Big Bang Cosmology, known as "
$ \Lambda $ CDM", is successful in describing the Universe's large scale structure formation and evolution, the state of the early Universe, and the abundance of the different forms of matter and energy [4-6]. This theory makes predictions that have been supported by new observations (e.g., lensing of the CMB [7, 8], B-mode polarisation [9], and the kinetic Sunyaev Zeldovich (SZ) effect). Observed astrophysical and cosmological evidence has confirmed the existence of DM and established its density in the universe [10]. However, the SM does not sufficiently explain DM. Currently, we have minimal information about the properties of dark matter particles. Among all DM candidates, Weakly Interacting Massive Particles (WIMPs) are a promising option as they offer a natural interpretation of the relic abundance of DM when the thermal history of the universe is rebuilt [11].Among the various scenarios beyond the SM, the Inert Doublet Model (IDM) is one of the simplest models that explains the WIMP dark matter candidate. In this model, an isospin doublet scalar field is added to the SM Higgs sector, which is assumed to be odd under a discrete
$ Z_2 $ symmetry. After electroweak symmetry breaking, four$ Z_2 $ odd scalar particles are generated, i.e., one CP-even H, one CP-odd A, and two charged$ H^\pm $ scalar bosons. Among them, the lightest scalar boson may serve as a dark matter candidate. The$ Z_2 $ symmetry ensures that these new scalar particles cannot decay into final states that only include SM particles. In addition, the additional isospin doublet scalar does not directly interact with the SM fermions at tree level. Their interactions with the Standard Model particles are achieved via gauge coupling and the quartic term with the SM Higgs in the scalar potential.The lightest scalar Higgs in the IDM, as a dark matter candidate, needs to be able to reconstruct the correct DM relic abundance. In Refs. [12, 13], they discovered that three allowed mass regimes for the lightest Higgs satisfy the relic abundance requirement. The scalar dark matter particle has also been explored by various direct and indirect experiments and high energy colliders. In recent direct detection experiments, the dark matter particle mass has been constrained to approximately one half of the SM-like Higgs boson mass (125 GeV) or above approximately 500 GeV [12, 14, 15]. In Ref. [16], the authors investigated the constraint for the IDM parameter space from dark matter annihilation induced gamma-rays in dwarf spheroidal galaxies. IDM phenomena at hadron colliders have been studied in the literature, such as
$ H^+H^- $ ,$ HH^{\pm} $ ,$ HA $ pair production, followed by the subsequent decay chains$ A \to ZH $ ,$ H^{\pm} \to W^{\pm}H $ [15, 17-24]. The prospects for discovering a scalar dark matter particle in the IDM at future lepton colliders have been discussed [25-30]. Additionally, the constraint for the IDM using vector boson fusion was also investigated in Ref. [31]. With the option of an$ e^+e^- $ collider, it can also be run in$ \gamma\gamma $ mode (at an energy scale similar to that of the primary electron-positron design). The charged Higgs pair can be produced directly in the IDM in$ \gamma\gamma $ collider mode, which provides additional opportunities for discovering the charged Higgs boson. In this study, we investigated the production of a charged Higgs pair in a$ \gamma\gamma $ collider.This paper is organized as follows. In section II, we briefly describe the framework of the inert doublet model. The relic abundance of dark matter is calculated in section III. In section IV, we summarize the theoretical and phenomenological constraints on the scalar potential of the IDM. In section V, we present the numerical results of the total and differential cross sections for charged Higgs pair production. In section VI, we analyze the charged Higgs pair signatures at the
$ \gamma\gamma $ collider with its subsequent decay$ H^{\pm} \to W^{\pm}H $ . Finally, a short summary is given in Section VII. -
The inert doublet model is one of the simplest extensions of the Standard Model (SM). It contains two SU(2) complex scalar fields
$ \Phi_{1} $ and$ \Phi_{2} $ , which are invariant in discrete$ Z_2 $ symmetry. The scalar field$ \Phi_{1} $ is almost the same as the SM Higgs field, which is$ Z_2 $ even with hypercharge$ Y = 1 $ . Under$ Z_2 $ symmetry,$ \Phi_{1} $ satisfies the transformation$ \Phi_{1} \rightarrow \Phi_{1} $ . The field$ \Phi_2^{} $ is odd under the$ Z_2^{} $ symmetry with hypercharge$ Y = 1/2 $ , which satisfies the transformation$ \Phi_{2} \rightarrow - \Phi_{2} $ under$ Z_2 $ . Under electroweak symmetry,$ SU(2)_{\rm L}\times U(1)_{\rm Y} $ , and the discrete$ Z_2 $ symmetry, the Higgs sector potential of the IDM is$ \begin{aligned}[b] V(\Phi_1,\Phi_2) = &\mu^2_1|\Phi_1|^2+\mu^2_2|\Phi_2|^2 +\frac{1}{2}\lambda_1|\Phi_1|^4+\frac{1}{2}\lambda_2|\Phi_2|^4 \\ &+\!\lambda_3|\Phi_1|^2|\Phi_2|^2 \!+\!\lambda_4|\Phi_1^\dagger\Phi_2|^2 \!+\!\frac{1}{2}\{ \lambda_5(\Phi_1^\dagger\Phi_2)^2\!+\!{\rm h.c.}\}. \end{aligned}$

(1) In the CP-conservation case, all parameters are real. The theoretical constraints for these coupling parameters from perturbative unitarity are provided in Refs. [32, 33]. In
$ Z_2 $ symmetry,$ \Phi_2 $ has a zero vacuum expectation value (VEV), and the SM like field,$ \Phi_1 $ , takes part in electroweak symmetry breaking (EWSB). After EWSB, the doublet scalar fields are expanded around a physical vacuum.$ \Phi_1^{} = \begin{pmatrix} G^+\\ \dfrac{1}{\sqrt{2}}(h+v+{\rm i} G^0) \end{pmatrix} ,\;\;\;\; \ \Phi_2^{} = \begin{pmatrix} H^+\\ \dfrac{1}{\sqrt{2}}(H+{\rm i}A) \end{pmatrix}, $

(2) where
$ G^+ $ and$ G^0 $ are the charged and neutral Goldstone bosons that manifest as the longitudinal components of the gauge bosons, and h is the SM-like Higgs boson with mass$ m_h = 125 $ GeV. The vacuum expectation value (VEV) of$ \Phi_1 $ is$ v = 246 $ GeV. The second doublet field$ \Phi_2 $ contains four$ Z_2^{} $ odd scalar bosons: a CP even neutral scalar boson H, a CP odd neutral scalar boson A, and two charged Higgs bosons$ H^\pm $ . The masses of these scalar bosons are given as$ m_h^2 = \lambda_1 v^2, $

(3) $ m^2_{H^+} = \mu_2^2+\frac{1}{2}\lambda_3 v^2, $

(4) $ m_H^2 = \mu_2^2+\frac{1}{2}(\lambda_3+\lambda_4+\lambda_5)v^2, $

(5) $ m_A^2 = \mu_2^2+\frac{1}{2}(\lambda_3+\lambda_4-\lambda_5)v^2. $

(6) Assuming
$ \lambda_5<0 $ , the lightest CP even neutral scalar boson H is stable and can be a dark matter candidate. The IDM scalar sector can be specified by six free parameters:$ \{ \lambda_1, \; \lambda_2, \; \lambda_3, \; \lambda_4, \; \lambda_5, \; \mu_2 \}. $

(7) By introducing the abbreviation
$ \lambda_L = \dfrac{1}{2}(\lambda_3+\lambda_4-|\lambda_5|) $ , the above six parameters can be modified into a set of more meaningful parameters,$ \{ m_{H^{\pm}}, m_A, m_H, m_h, \lambda_L, \lambda_2 \}, $

(8) where
$ m_{H^{\pm}},\; m_A, \;m_H $ are the four$ Z_2^{} $ odd scalar boson masses,$ \lambda_L $ corresponds to the coupling of the dark matter and SM-like Higgs boson, which is relevant for dark matter annihilation, and the quartic coupling$ \lambda_2 $ corresponds to the self-interaction in the dark sector. -
Dark matter relic abundance can be obtained by solving the non-equilibrium Boltzmann equation,
$ \frac { {\rm d}n_{\chi} } {{\rm d}t} + 3 {{H}} {{n}}_{\chi} = - \langle \sigma v \rangle \left( {{n}}_{ \chi }^{2} - \left({{n}}_{\chi}^{ {\rm{eq}} } \right)^{2} \right), $

(9) where
$ n_{\chi} $ is the number density of dark matter particles, H is the expansion rate of the universe, and$ \langle \sigma v \rangle $ is the thermally averaged annihilation cross section.Introducing the comoving number density
$ Y = n/s $ and substituting temperature for$ x = \dfrac{m_{\chi} }{T} $ , the non-equilibrium Boltzmann equation is modified to$ \frac { {\rm d} Y } { {\rm d} x } = - \frac {s} { {H} x^{ 2 } } \langle \sigma v \rangle \left( Y^{ 2 } - \left( Y^{\rm eq} \right)^{2} \right). $

(10) Solving this equation, we can obtain the number density as a function of the temperature. By integrating the function from
$ x = x_f $ to$ x \to \infty $ , we obtain the number density$ Y_{\infty } $ .Using the result
$ Y_{\infty } $ , we can acquire the final relic density$ \Omega h^{2} $ ,$ \Omega h^{2} \equiv \frac {\rho_{\chi} } {\rho_{\rm c} } h^{2} = \frac {m_{\chi} Y_{\infty} s_{\infty} } { 1.05 \times 10^{-5} \;\mathrm {GeV} \mathrm {cm}^{-3} }, $

(11) where
$ {\rho_{\rm c} } $ is the critical energy density of the universe,$ {\rho_{\chi} } $ is the energy density of dark matter, and$ s_{\infty} $ is the entropy density in the present universe.The software Micromegas [34] was employed to calculate the relic abundance of dark matter. The relevant SM input parameters are chosen as
$ \begin{aligned}[b] &m_{W} \!=\! 80.379 {\rm\ GeV},\; m_{Z} \!=\! 91.1876 {\rm\ GeV},\; m_{H} \!=\! 125.18 {\rm\ GeV}, \\ &G_F \!\!=\!\! 1.1663787\!\!\times\!\! 10^{-5}\;\! {\rm GeV}^{-\!2}, m_{b} \!\!=\! 4.18 {\rm\ GeV}, m_{t} \!\!=\!\! 173.0 {\rm\ GeV}, \\ &\alpha_s(m_Z) \!=\! 0.1181,\;\alpha \!=\! 7.297352\!\times\! 10^{-3} , \;m_{c} \!=\! 1.275 {\rm\ GeV}. \end{aligned} $

(12) As mentioned above, we chose
$ {m_{H},\; m_{A},\; m_{H^{\pm}},\; \lambda_{L},\; \lambda_{2}} $ as five independent input parameters of the IDM. The annihilation cross section is only calculated to the leading order (LO); thus, the relic density is not sensitive to the parameter$ \lambda_{2} $ . Assuming the mass hierarchy$ m_{H^{\pm} } \geqslant $ $ m_{A} > m_{H} $ for the inert scalar bosons, the lightest scalar H becomes the dark matter particle candidate. Typically, the roles of$ m_{H} $ and$ m_{A} $ are interchangeable. Generally, the masses can be divided into three regions: i. low mass (1-80 GeV), ii. intermediate mass (80-500 GeV), and iii. high mass (500-1000 GeV).As
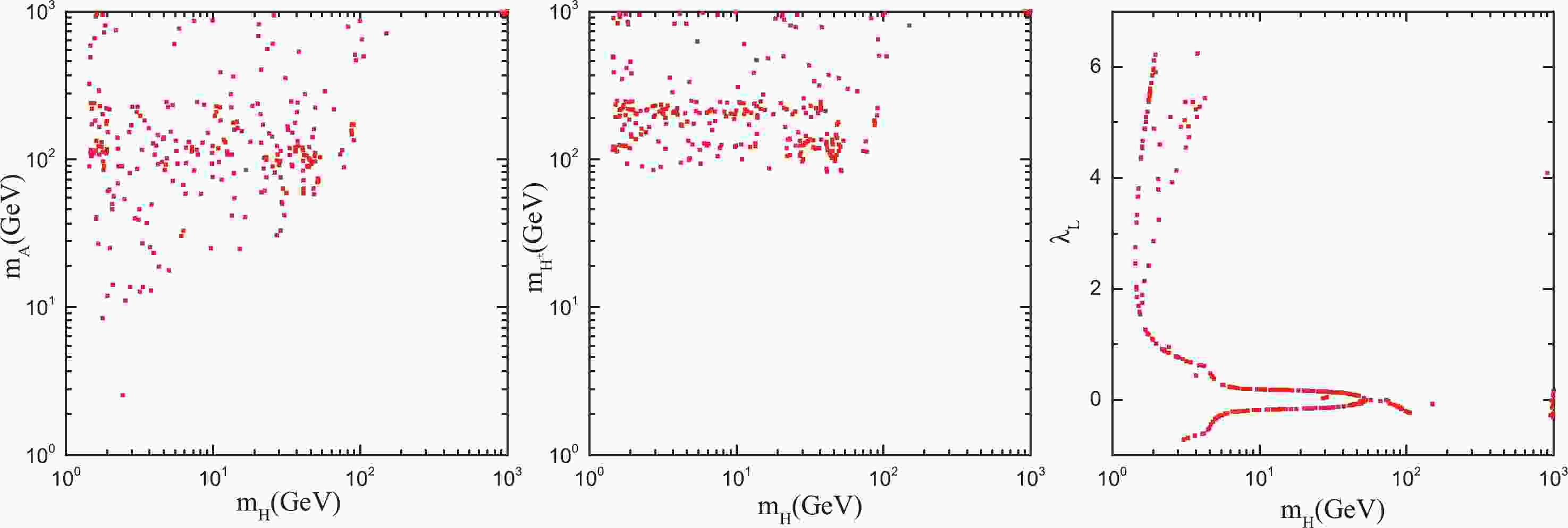
$ \lambda_2 $ is only related to the self-coupling of inert particles, its variation has little effect on the relic abundance of dark matter particles; thus, it was fixed as$ \lambda_2 = 8\pi/3 $ . The other three mass parameters$ m_{H},\; m_{A}, \;m_{H^{\pm}} $ were scanned from 1 to 1000 GeV and$ \lambda_L $ from –0.75 to 6.28. When the DM relic density was in agreement with the Planck measurements:$ 0.119 < \Omega_{\rm DM}h^2 < 0.121 $ ; these data points were saved.The reserved points were projected onto two dimension planes, presented in Fig. 1. The mass range of
$ m_H $ was concentrated in the low mass region, below 150 GeV, in all three graphs. The mass range of$ m_{H^\pm} $ was mainly above 80 GeV. When$ \lambda_L $ was close to zero, we easily found an appropriate point in the large$ m_H $ area corresponding to the correct relic abundance. When$ \lambda_L $ was larger than 1,$ m_H $ was only observed at 1-3 GeV.
Figure 1. (color online) Projections of the saved points in the
$ m_H-m_{A} $ (left),$ m_H-m_{H^\pm} $ (middle), and$ m_H-\lambda_L $ (right) planes.Six groups of parameters were selected as benchmark points, as follows:
BP1:
$ \lambda_L $ = −0.067137,$ m_H $ = 48.47607,$ m_{A} $ = 159.37519,$ m_{H^\pm} $ = 171.83007BP2:
$ \lambda_L $ = −0.061830,$ m_H $ = 49.07796,$ m_{A} $ = 104.58929,$ m_{H^\pm} $ = 177.79335BP3:
$ \lambda_L $ = 4.37294,$ m_H $ = 1.57134,$ m_{A} $ = 183.29679,$ m_{H^\pm} $ = 192.24964BP4:
$ \lambda_L $ = 0.13490,$ m_H $ = 32.23363,$ m_{A} $ = 158.16124,$ m_{H^\pm} $ = 194.83879BP5:
$ \lambda_L $ = −0.15581,$ m_H $ = 3.1979,$ m_{A} $ = 196.59793,$ m_{H^\pm} $ = 201.52571BP6:
$ \lambda_L $ = 5.83958,$ m_H $ = 1.87152,$ m_{A} $ = 173.96496,$ m_{H^\pm} $ = 186.41257In Fig. 2, we present the function of the relic abundance of dark matter with the parameters
$ m_H $ ,$ m_A $ ,$ m_{H^\pm} $ and$ \lambda_L $ . As the above six parameter sets have similar characteristics, we have used BP1 as an example. From Fig. 2 (left), we observed that when the parameter$ m_H $ or$ m_A $ was approximately half the Higgs mass, the relic density was greatly reduced. This is due to the particles easily merging into an on-shell Higgs and then decaying into SM particles, thus dramatically reducing the dark matter relic density. When$ m_A $ or$ m_{H^\pm} $ reached the high mass region, the relic density was unaffected. In Fig. 2 (right), the relic density$ \Omega h^{2} $ is displayed as a function of$ \lambda_L $ , with the other parameters fixed. The relic density parameter$ \Omega h^{2} $ first increased and then decreased rapidly over the whole range of$ \lambda_L $ , reaching its maximum value near zero. -
In this section, we summarize the theoretical and experimental limitations of the extended scalar sector potential of the IDM.
First, the perturbation of the theory requires that all scalar coupling constants cannot exceed
$ 4\pi $ [35].$ \begin{aligned}[b] &| \lambda_{1,2,3,4,5}| \leqslant 4\pi \,, \quad |\lambda_3+\lambda_4\pm\lambda_5| < 4\pi \,, \quad \\ &|\lambda_4\pm\lambda_5| < 8\pi \,, \quad \;\, |\lambda_3+\lambda_4| < 4\pi. \end{aligned} $

(13) In order to obtain a stable vacuum, the following parameters must be positive [36-38],
$ \begin{aligned}[b] &\lambda_1^{} > 0,\;\;\ \lambda_2^{} > 0,\;\; \sqrt{\lambda_1 \lambda_2^{}} + \lambda_3^{} > 0,\ \\ &\lambda_3^{}+\lambda_4^{} - |\lambda_5^{}| + \sqrt{\lambda_1 \lambda_2^{}}> 0. \end{aligned} $

(14) The unitary of the S-matrix for processes
$ 2 \to 2 $ scattering at the perturbative level requires all the couplings [39, 40],$ \begin{aligned}[b]& |\lambda_3 \pm \lambda_4 | \leqslant 8 \pi, \quad |\lambda_3 \pm \lambda_5 | \leqslant 8 \pi, \quad |\lambda_3+ 2 \lambda_4 \pm 3\lambda_5 | \leqslant 8 \pi, \\ &\big|-\lambda_1 - \lambda_2 \pm \sqrt{(\lambda_1 - \lambda_2)^2 + \lambda_4^2} \big| \leqslant 8 \pi, \\ &\big|-3\lambda_1 - 3\lambda_2 \pm \sqrt{9(\lambda_1 - \lambda_2)^2 + (2\lambda_3 + \lambda_4)^2} \big| \leqslant 8 \pi, \\ &\big|-\lambda_1 - \lambda_2 \pm \sqrt{(\lambda_1 - \lambda_2)^2 + \lambda_5^2} \big| \leqslant 8 \pi. \end{aligned} $

The Peskin-Takeuchi parameters
$ S,\;T,\;U $ are strictly limited by the electroweak precision observables. The deviations from the SM prediction$ \Delta S $ and$ \Delta T $ are experimentally provided as$ \Delta S = 0.03\pm0.09 $ and$ \Delta T = 0.07\pm $ $ 0.08 $ . The contribution from the IDM can be calculated as described in Ref. [41]. This typically prohibits large mass splittings amongst inert states, although for DM masses with$ M_{H^0}\gtrsim 500 $ GeV, relatively small splittings are required, especially when combined with the relic density constraint [42, 43].The experimental constraints for inert scalars mainly originate from the large electron-positron collider (LEP) and large hadron collider (LHC) at CERN.
First, the constraints on the new scalar particles at the LEP come from measurements of the
$ Z\rightarrow A H $ ,$ Z\rightarrow H^+ H^- $ ,$ W^\pm\rightarrow A H^\pm $ , and$ W^\pm\rightarrow H H^\pm $ decays, which imply that$ m_A + m_H \geqslant m_Z $ ,$ 2m_{H^\pm}\geqslant m_{Z} $ , and$ m_{H^\pm} + m_{H,A} \geqslant $ $ m_{W} $ . Second, SUSY searches at LEP II have lead to constraints on the charged Higgs mass,$ m_{H^\pm}\gtrsim 70 $ GeV [44]. The LEP II analysis excluded models satisfying$ m_{H}<80 $ GeV,$ m_{A} \leqslant 100 $ GeV, and$ |m_{A}-m_{H}| \geqslant 8 $ GeV [45].The constraints on the IDM at the LHC originate principally from the SM Higgs boson decay width. The new couplings from the IDM can either increase the invisible branching ratio or alter the strength of the Higgs boson and diphoton coupling [41, 46-48]. This strictly limits the mass of the inert lightest scalar particle to less than
$ m_h/2 $ and has little restriction on the masses above$ m_h/2 $ . Direct di-leptons plus missing energy searches have also been performed to restrict the inert scalar masses to the region of$ m_{H}\lesssim 60 $ GeV and$ m_A \lesssim 150 $ GeV [49].From these constraints, we found that the IDM is strongly restricted if the masses of the inert scalar particles are less than 100 GeV and have few constraints for masses above 500 GeV.
-
To maintain the symmetry of
$ Z_2 $ , the scalar particles in the IDM are always produced in pairs at the collider. The lightest scalar particle H in the IDM is stable and is the dark matter candidate, as other scalar particles will eventually decay into H associated SM particles, such as via$ A \to H Z $ ,$ H^{\pm} \to H W^{\pm} $ . These scalar particles only couple to the Higgs boson and electroweak gauge bosons of the Standard Model; thus, the production cross section for double scalar particles is typically small. However, the charged Higgs boson$ H^\pm $ can couple to photons through electromagnetic interactions. Predictably, the cross section of the double charged Higgs production in a$ \gamma\gamma $ collider is considerable. In this section, we consider the following process at a$ \gamma\gamma $ collider,$ \gamma \gamma \to H^+ H^-. $

(15) The tree-level Feynman diagrams are illustrated in Fig. 3. The cross section of this process is only related to the mass of
$ H^{\pm} $ and is independent of the other four parameters,$ \lambda_{L},\; \lambda_{2},\; m_{H},\; m_{A} $ , in the IDM.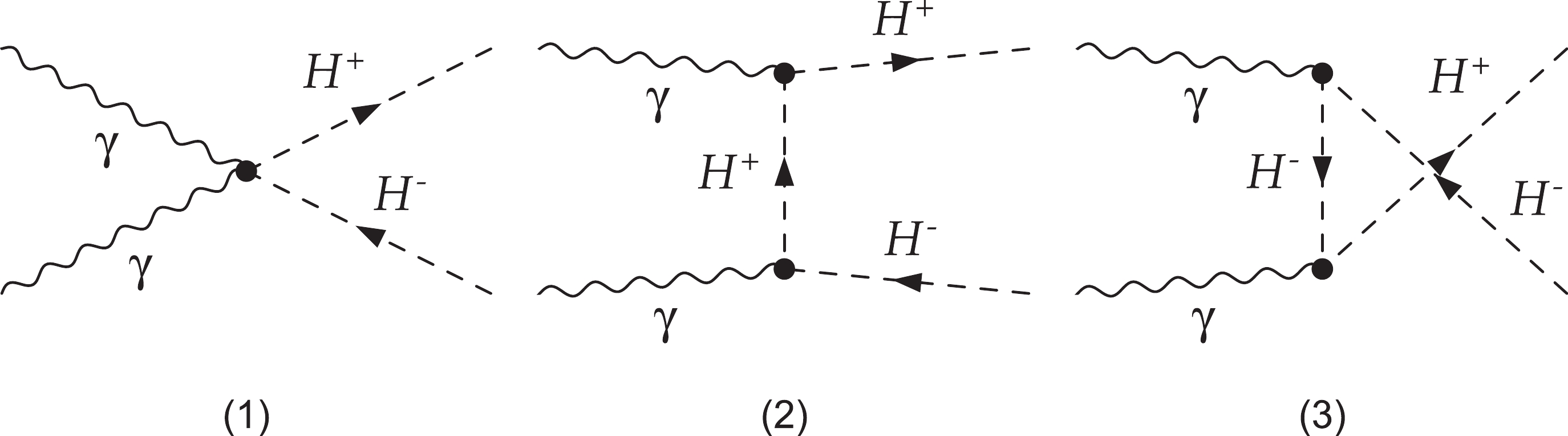
Figure 3. Feynman diagrams for the process
$ \gamma \gamma \to H^+ H^- $ in the IDM at the$ \gamma\gamma $ collider.The hard photon beam of the
$ \gamma\gamma $ collider can be obtained using the laser backscattering technique at the$ e^+e^- $ linear collider [50-53]. We denote$ \hat{s} $ and s as the center-of-mass energies of the$ \gamma\gamma $ and$ e^+e^- $ systems, respectively. After calculating the cross section$ \hat{\sigma}(\hat{s}) $ for the subprocess$ \gamma\gamma \to H^+ H^- $ in photon collision mode, the total cross section at an$ e^+e^- $ linear collider can be obtained by folding$ \hat{\sigma}(\hat{s}) $ with the photon distribution function that is given in Refs. [54-56]. The cross section for the$ e^+e^- \to $ $ \gamma\gamma \to H^+ H^- $ process is expressed as$ \sigma_{\rm tot}(e^+e^- \to \gamma\gamma \to H^+ H^- ,\; s) = \int^{x_{\rm max}}_{2m_H^{\pm}/\sqrt{s}} {\rm d}z\frac{{\rm d}{\cal L}_{\gamma\gamma}}{{\rm d}z} \hat{\sigma}(\hat{s} = z^2 s ). $

(16) The distribution function of photon luminosity is expressed as
$ \frac{{\rm d}{\cal L}_{\gamma\gamma}}{{\rm d}z} = 2z\int_{z^2/x_{\rm max}}^{x_{\rm max}} \frac{{\rm d}x}{x} f_{\gamma/e}(x)f_{\gamma/e}(z^2/x), $

(17) where
$ f_{\gamma/e} $ is the photon structure function, and x is the fraction of the energy of the incident electron carried by the back-scattered photon, which were interfaced by the CompAZ code [57]. In the low x region ($ x\leqslant 0.1 $ ), the photon spectrum is not properly described and is underestimated. Therefore, it is qualitatively better for larger values of x of the longitudinal momentum of the electron beam. However, for$ x > 2(1+\sqrt{2})\simeq 4.8 $ , the high energy photons can disappear through$ e^+e^- $ pair creation in the collision with a following laser photon.The Feynman Rules were extracted by the program FeynRules [58] from the Lagrangian of the IDM and then output to Universal FeynRules Output (UFO) files [59]. For the cross-section calculation and simulation for the signal and background, we utilized the Monte Carlo event generator MadGraph@NLO(MG5) [60]. PYTHIA6 [61] was utilized for parton shower and hadronization, with the options of ISR and RSR included. Delphes [62] was then employed to account for the detector simulations, and MadAnalysis5 was used for analysis, where the (mis-) tagging efficiencies and fake rates were assumed to be their default values in Delphes. The IDM mediator width was automatically computed using the MadWidth module for each parameter point.
In Fig. 4 (left), we present the cross sections as functions of the colliding energy
$ \sqrt{s} $ for the process$ e^+e^- \to \gamma \gamma \to H^+ H^- $ by setting$ m_H^{\pm} = 50,100, 150, 200, $ $ 250\; {\rm GeV} $ , separately. From this, we observed that with increasing colliding energy$ \sqrt{s} $ , the total cross section for the process$ e^+e^- \to \gamma \gamma \to H^+ H^- $ initially increased rapidly. When the colliding energy$ \sqrt{s} $ reached approximately 1 TeV, the total cross section only increased slightly. Thus, we can obtain larger cross sections for the process$ e^+e^- \to \gamma \gamma \to H^+ H^- $ by raising the colliding energy$ \sqrt{s} $ . In Fig. 4 (right), the total cross section is plotted for different masses of$ m_H^{\pm} $ at the$ e^+ e^- $ collider for$ \sqrt{s} $ = 500, 1000, 1500, and 3000 GeV. With increasing charge Higgs mass$ m_H^{\pm} $ , the total cross section decreased. When its mass was close to half of the center of mass energy, the cross section rapidly approached zero.
Figure 4. (color online) Cross sections of
$ e^+e^- \to \gamma \gamma \to H^+ H^- $ production as a function of the center-mass energy when the mass$ m_H^{\pm} $ is fixed (left) and the cross sections as functions of the mass$ m_H^{\pm} $ when the center-mass energy is fixed (right) in the IDM at the$ \gamma\gamma $ collider. -
Since the lightest scalar boson H is stable, the charged Higgs
$ H^{\pm} $ particles will eventually decay into H and SM particles. In this section, we present the Monte Carlo simulation and explore the sensitivity in the photon-photon collider through the following channel:$ \gamma \gamma \to H^+ H ^- \to W^+ W^- H H, $

(18) where H is assumed to be the lightest scalar particle in the IDM leaving missing energy in the detector and making it almost impossible to reconstruct events. The W boson decays to an electron or muon and its antineutrino. The Feynman diagrams for the process
$ \gamma \gamma \to H^{+} H ^{-} \to $ $ W^{+} W^{-} H H $ are presented in Fig. 5.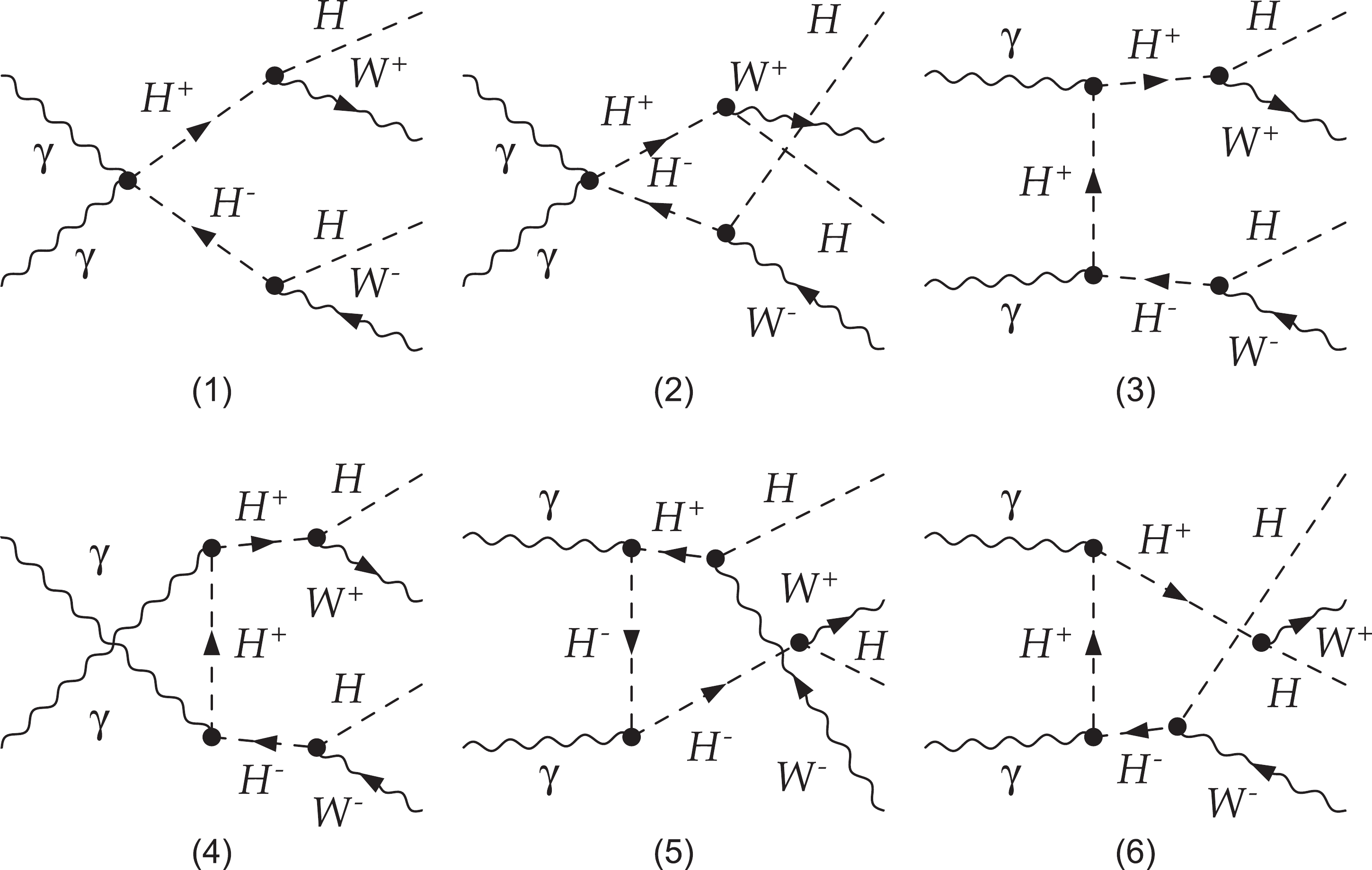
Figure 5. Feynman diagrams for the process
$ \gamma \gamma \to H^{+} H ^{-} \to W^{+} W^{-} H H $ in the IDM.The dominant signal for the pure leptonic channel in the IDM is
$\ell^{+} \ell^{-}+\not\!\! E_{T}$ , where$ \ell $ = e,$ \mu $ , which can be obtained from either the decay channel$ H^{\pm} \to W^{\pm} H $ , with$ W^{\pm} \to \ell^{\pm} \nu $ or the decay channel$ H^{\pm} \to W^{\pm} A $ , with$ W^{\pm} \to \ell^{\pm} \nu $ and$ A \to H Z^{\ast} \to H \nu \overline {\nu} $ , depending on the parameters. Although the decay mode$ H^{\pm} \to W^{\pm} A $ is kinematically forbidden for the benchmark points, there are some parameters that allow$ H^{\pm} \to W^{\pm} A $ to decay in phase space. The decay width of$ H^{\pm} \to W^{\pm} A $ is lower than$ H^{\pm} \to W^{\pm} H $ , and the ratio of the partial decay width of a Z boson decaying to invisible is approximately 20%. Thus, the contribution from the second decay chain can be neglected when comparing the first case for most allowed parameter points. Here, we will focus on the process$ \gamma \gamma \to H^{+} H ^{-} \to W^{+} W^{-} H H $ with the decay$ W^{\pm} \to \ell^{\pm} \nu $ . The cross sections for the process$ \gamma \gamma \to H^{+} H ^{-}\to $ $ W^{+} W^{-} H H $ in the IDM with$ \sqrt{s} = $ $ 500 $ GeV for the benchmark points are given in Table 1.BP1 BP2 BP3 BP4 BP5 BP6 $\sigma/fb$ 

1.362 1.014 4.318 3.296 3.683 5.168 Table 1. Cross sections for the process
$ e^+e^- \to \gamma \gamma \to $ $ H^{+} H^{-}\to W^{+} W^{-} H H $ in the IDM with$ \sqrt{s}=500 $ GeV.In the pure leptonic channel, the signal of this process is two leptons
$ l^+l^- $ plus missing$ E_{T} $ , with the backgrounds of the Standard Model mainly$ W^{+} W^{-} $ , Drell-Yan process, top-quark pair production ($ t\bar{t} $ ), and$ WZ $ and$ ZZ $ processes. For the Drell-Yan process, the two leptons are always back-to-back with very small$ E_{T} $ , which can be easily distinguished from the large missing$ E_{T} $ signal. The final state of top-quark pair production contains a large number of hadrons, which are also easily eliminated in the photon-photon collider. The$ WZ $ and$ ZZ $ processes can also be largely suppressed by the two lepton invariant mass cuts of the Z boson. These backgrounds can be neglected after suitable cuts. Therefore, they are not listed in the following analysis. Therefore, we analyze the main irreducible background$ W^{+} W^{-} $ production.In our simulation, we first applied some basic cuts for the selection of events:
$ p_T^\ell > 20 \; {\rm GeV}, \;\;\;\; |\eta_\ell| < 2.0, \;\;\;\; \Delta R_{\ell\ell} > 0.4, $

(19) where
$ p_T^{\ell} $ and$ \eta_{\ell} $ are the transverse momentum and the pseudorapidity of the leptons, respectively, and$ \Delta R = \sqrt{\Delta \phi^2 + \Delta\eta^2} $ is the particle separation among the leptons in the final state with$ \Delta \phi $ and$ \Delta\eta $ being the separation in the azimuth angle and rapidity. The$ \eta_{\ell} $ acceptance region avoids the gap between the barrel and endcap, where the misidentification probability is the greatest.According to the differential distribution between the signal and background, we can improve the ratio of signal to background by making suitable kinematical cuts. In Fig. 6, we display the distributions of some kinematical variables for the signal and background at 500 GeV. We first select
$ N(\ell) = 2 $ , for which the signal is almost entirely concentrated in the low$ p_{T}^{\ell} $ region; thus, we reject$ p_{T}^{\ell} > $ 70 GeV. Then, as the signal decreases faster than the background in the high invariant mass region,$ M(\ell^+,\ell^-) < 125 \; \rm {GeV} $ is also required. Finally, we require the transverse missing energy$\not\!\! E_{T} > 95$ GeV to further improve the discovery significance.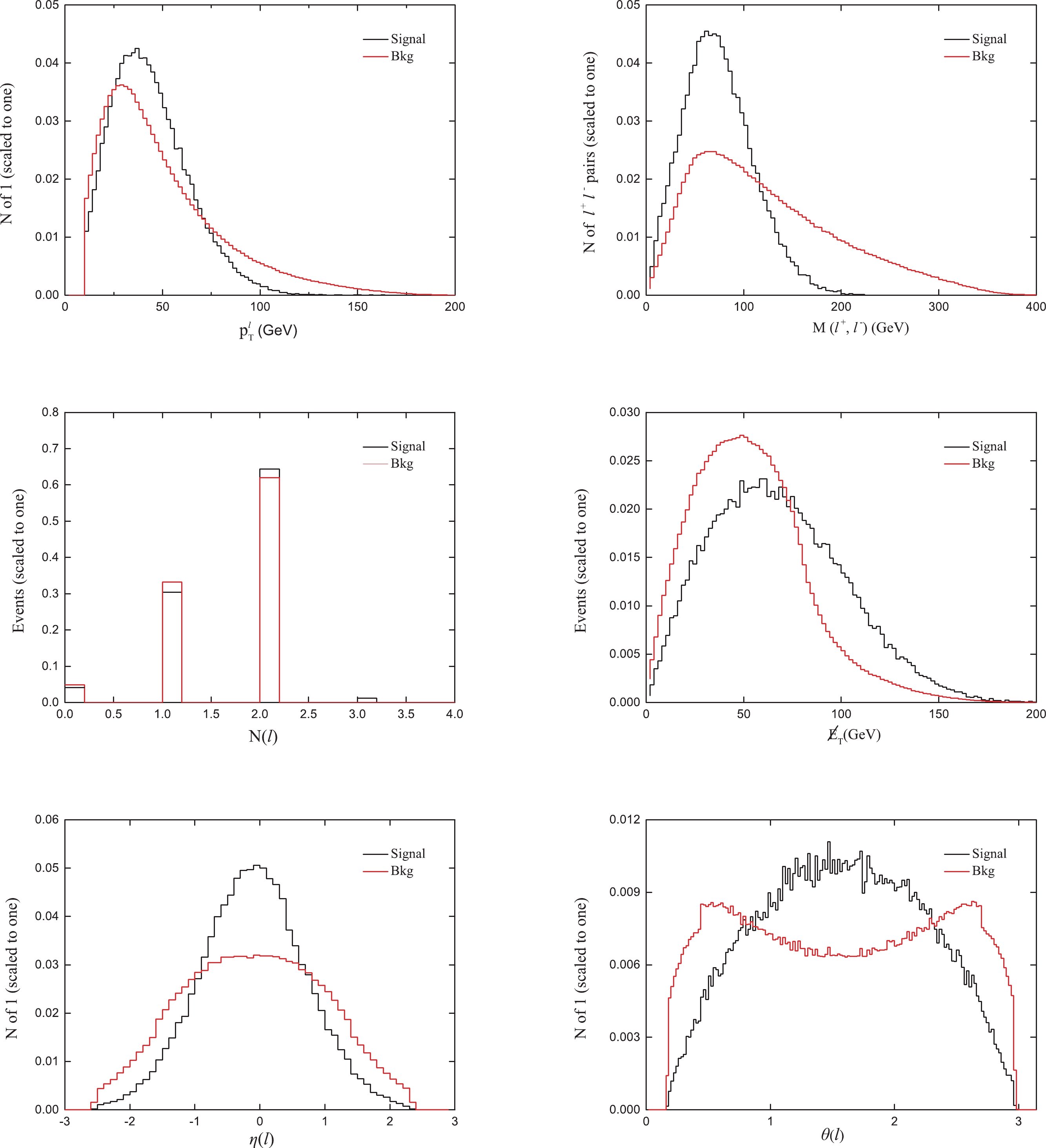
Figure 6. (color online) Normalized distributions of the leptonic transverse momentum
$ p_{T}^{\ell} $ , the invariant mass$ M(\ell^+,\ell^-) $ , numbers of leptons$ N(\ell) $ , the transverse missing energy$ \not\!\!E_{T} $ , angle$ \theta $ , and pseudorapidity$ \eta $ for the signal and background with$ \sqrt{s} $ = 500 GeV.For a short summary, the cut-based selections are listed here:
(1) Basic cut:
$ p_T^{\ell}>20 $ GeV,$ |\eta_{\ell}|<2.0 $ and$ \Delta R_{\ell\ell}> 0.4 $ ;(2) Cut 1 means the basic cuts require
$ N(\ell) = 2 $ ;(3) Cut 2 means Cut 1 plus the requirement of
$ p_T^{\ell} < 70\; \rm {GeV} $ ;(4) Cut 3 means Cut 2 plus the requirement of the invariant mass of two leptons
$ M(\ell^+, \ell^-) < 125\; \rm {GeV} $ ;(5) Cut 4 means Cut 3 plus the requirement of the transverse missing energy
$\not\!\! E_{T} > 95\; \rm{GeV}$ .The results for the signal for BP2 and backgrounds (with luminosity
$ = 3000\; {\rm fb}^{-1} $ ) are shown in Table 2 at each cut. The values of the discovery significance$ S/\sqrt{B+S} $ are also provided, where S and B are the numbers of signal and total background events, respectively. After applying several cuts, the background can be greatly reduced, and the discovery significance$ S/\sqrt{B+S} $ can reach up to$ 13.653\sigma $ . Thus, we can potentially observe the IDM effect through the charged Higgs$ H^{\pm} $ pair in some parameter space with large luminosity at the$ \gamma\gamma $ collider.Cuts Signal Background $ S/\sqrt{B+S} $ 

Basic cuts $ 3.039\times10^{3} $ 

$ 2.616\times10^{6} $ 

1.880 Cut 1 $ 1.956\times10^{3} $ 

$ 1.623\times10^{6} $ 

1.534 Cut 2 $ 1.592\times10^{3} $ 

$ 1.036\times10^{6} $ 

1.563 Cut 3 $ 1.528\times10^{3} $ 

$ 7.294\times10^{5} $ 

1.787 Cut 4 $ 3.438\times10^{2} $ 

$ 2.904\times10^{2} $ 

13.653 Table 2. Number of events for the signal (
$ W^{+} W^{-} H H $ ) for BP2 and the main backgrounds ($ W^{+} W^{-} $ ) after each cut at 500 GeV with integrated luminosity$ L = 3000\;{\rm fb}^{-1} $ . The discovery significance$ S/\sqrt{B+S} $ at each cut is also shown.In Fig. 7, we present the distribution of the parameter points for the discovery significance
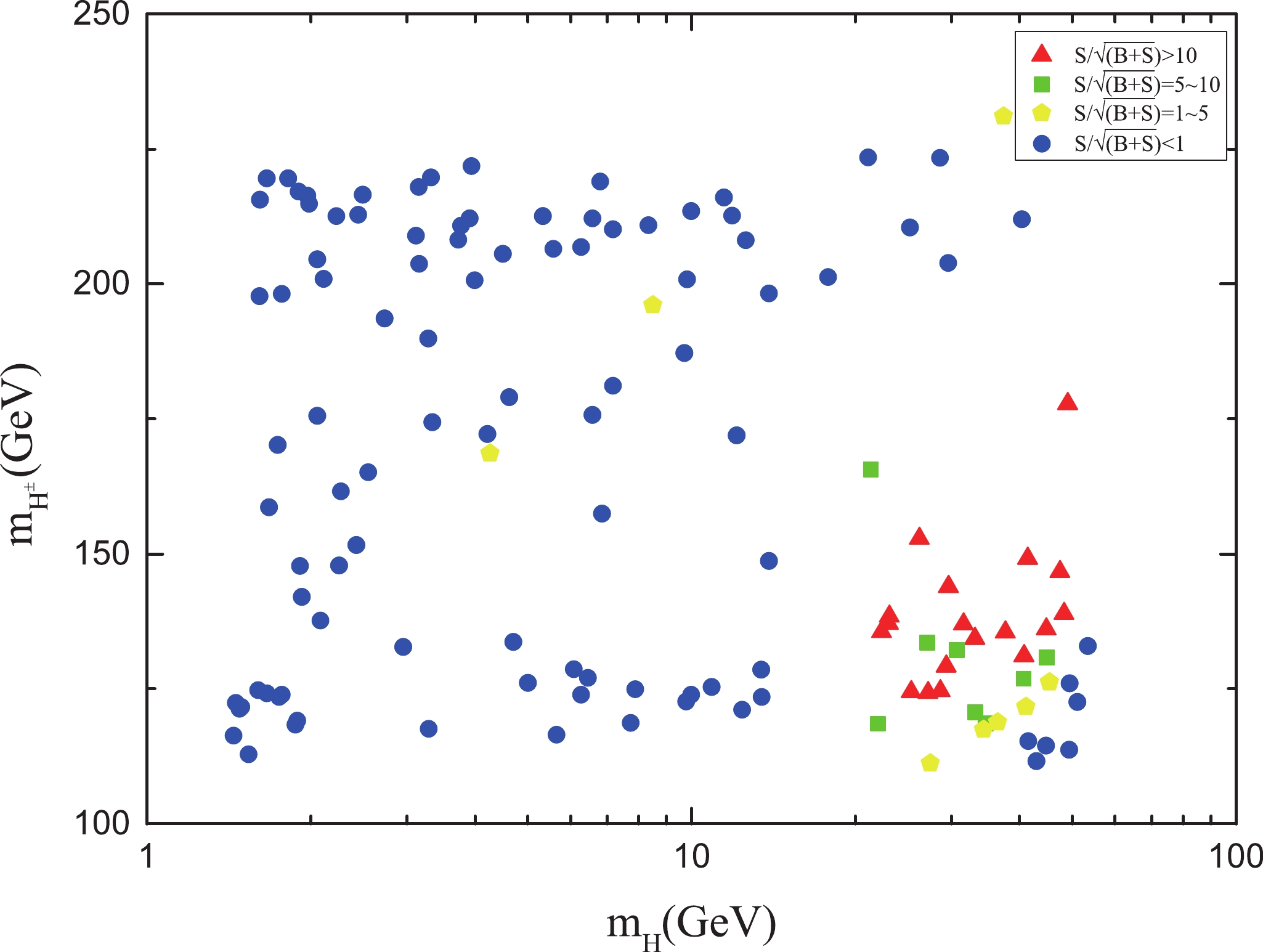
$ S/\sqrt{B+S} $ in the$ m_{H^{+}}-m_H $ plane with an integrated luminosity of$ 3000\;{\rm fb}^{-1} $ at$ \sqrt{s} $ = 500 GeV. The different colours represent value ranges of the significance. We investigated the effects of the coupling parameter$ \lambda_2 $ ,$ \lambda_L $ , and the scalar even particle mass$ m_A $ , finding that the cross section changes only minimally when varying these input parameters. From Fig. 7, we observed that the parameter points with high significance were mainly concentrated in the range of$ m_H $ from 10 to 50 GeV and$ m_{H^{+}} $ from 110 to 180 GeV. If the CEPC or ILC can be built, these parameter points in the IDM model have the potential to be detected or excluded. -
The Inert Doublet Model is one of the simplest extensions of the Standard Model, which provides a scalar DM particle candidate. In this study, we investigated double charged Higgs
$ H^{\pm} $ pair production in the IDM at a$ \gamma\gamma $ collider. Assuming that the lightest scalar Higgs is the dark matter particle, we calculated the corresponding relic abundance, scanned the IDM parameter space, and obtained the parameter points satisfying the relic abundance of dark matter in our universe. We also analyzed the pure lepton decay process of the double charged Higgs$ H^{\pm} $ and the backgrounds of the Standard Model and optimized the selection criteria, employing suitable cuts on the kinematic variables to maximize the signal significance. We found that with the high luminosity option of the$ \gamma\gamma $ collider, this decay channel has the potential to probe the IDM in the mass range of 1-250 GeV. In a scenario with light dark matter having a mass of approximately 10-50 GeV, a charged Higgs in the mass range of 110-180 GeV provides the highest probability of detection, with a signal significance of approximately$ 10 \sigma $ at an integrated luminosity of approximately 3000$ {\rm fb}^{-1} $ .
Searches for dark matter via charged Higgs pair production in the Inert Doublet Model at a γγ collider
- Received Date: 2021-05-25
- Available Online: 2021-10-15
Abstract: The Inert Doublet Model (IDM) is one of the simplest extensions beyond the Standard Model (SM) with an extended scalar sector, which provides a scalar dark matter particle candidate. In this study, we investigated the double charged Higgs production at a






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: