-
The ground-state properties of finite nuclei, throughout the periodic table, have been successfully described by self-consistent mean field methods (SCMF) and density functional theories (DFT) [1-5]. In such approaches, one starts, in general, from non-relativistic two-body effective nucleon-nucleon (NN) interactions or from relativistic Lagrangians, and the parameters of the effective interactions are fitted to the properties of nuclear matter and some selected data of finite nuclei. These methods have also been extended to describe the properties of various collective giant resonances in finite nuclei [6-16]. The study of giant resonances is known as one of the most important tools for probing the structural properties of finite nuclei and constraining the equation of state of nuclear matter [17-28].
The giant resonances have been experimentally found to be located in the energy region of 10 to 30 MeV. For some modes of giant resonances, the low-lying states, such as the Pygmy dipole resonances (PDR) in exotic nuclei, are found to be experimentally below 10 MeV. The PDR exhausts for approximately several percentages of the TRK sum rule [29-33], and plays a significant role in constraining the equation of state of nuclear matter. Another low-lying state, the first 2+ state in finite nuclei, is also very important in nuclear structure study because the shell structure can be evidenced by a relatively high-lying first excited 2+ state and a relatively small electric quadrupole transition probability to the ground state [34, 35].
It is well known that pairing correlations play a predominant role in most nuclear phenomena [36-47]. For the NN pairing interaction, the bare interaction in the
$ ^1S_0 $ or$ ^3SD_1 $ channel is usually adopted as the NN pairing interaction in the nuclear matter calculation as the first step. For the strongly correlated nuclear many-body systems, one has to consider the various medium effects on the NN pairing interaction, such as the self-energy, induced interaction, and vertex corrections [48-57]. However, it is rather complicated to calculate the pairing correlation in finite nuclei using the many-body method directly. The isospin and density dependent pairing interaction is usually obtained by fitting the neutron gaps from the microscopic calculations within local density approximation [58-61], indicating a correlation between the pairing interaction and microscopic many-body results; the interaction can be easily used in the calculations of finite nuclei. A satisfactory description of superfluidity in nuclear matter has not yet been achieved; much effort shall be made in the future. A recent attempt has been made at the construction of an energy-density functional for superfluid systems starting from a bare inter-particle interaction with the help of the functional renormalization group [62].On the other hand, an effective density-dependent zero range pairing interaction has been widely adopted in the mean field calculation. Many theoretical works have been devoted to clarifying the effect of the density-dependence of the zero-range pairing interaction on the ground state properties of finite nuclei [63-67], such as the odd-even mass staggering. To get a better description on the energies and transition probabilities of the first 2+ state in open shell nuclei, one has to include the contribution of the pairing correlation both in the ground and excited state calculations. As we know, only a few studies focused on the effect of the density-dependence of pairing on the properties of the low-lying 2+ state. In Ref. [68], the excitation energies and transition probabilities of the first 2+ state in Sn and Pb isotopes were studied within the self-consistent theory of finite Fermi systems based on the Fayans energy density functional [69]. The volume and surface pairing were adopted to analyze the effect of the density-dependence of the effective pairing interaction. The effect was found to be noticeable. In this work, we explored the effect of the density-dependence of zero-range pairing interaction on the excitation energies and transition probabilities of the first 2+ states in Sn isotopes. The calculations are done in the Hartree-Fock(HF)+BCS plus QRPA method within the Skyrme energy density functional. We examined the impact of surface, mixed, and volume pairings on the properties of the first 2+ state, and analyzed, in detail, the effect of the different pairings on the energies and transition probabilities.
The paper is organized as follows. In Sec. II, the theoretical methods are briefly introduced. In Sec. III, the results calculated in the three types of pairings are shown. Particularly, by comparing the data, the effect of the pairing correlations on the low-lying quadrupole state are discussed. Finally, Sec. IV presents the conclusion.
-
In this work, the HF+BCS plus QRPA approaches were employed in our calculations. The HF+BCS method can be easily found in Refs. [70, 71], thus, we will not repeat it in this work. The QRPA method is performed after the HF+BCS calculation; therefore, we briefly review the QRPA main equations as below. The QRPA matrix equations are given by
$ \left( {\begin{array}{*{20}{c}} A&B\\ { - {B^*}}&{ - {A^*}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{X^\nu }}\\ {{Y^\nu }} \end{array}} \right) = {E_\nu }\left( {\begin{array}{*{20}{c}} {{X^\nu }}\\ {{Y^\nu }} \end{array}} \right), $

(1) where
$ E_{\nu} $ is the eigenvalue of the ν-th QRPA state, Xν and Yν are the corresponding forward and backward two-quasiparticle amplitudes, respectively. The details on the matrix elements A and B can be found in Ref. [72].For a given excited state
$ E_{\nu} $ , the contribution of the proton and neutron quasiparticle configurations is determined by the QRPA amplitudes,$ A_{ab} = |X^{\nu}_{ab}|^{2}-|Y^{\nu}_{ab}|^{2}, $

(2) and the normalization equation is
$ \sum\limits_{a \geq b}A_{ab} = 1. $

(3) The reduced transition probability for any multipole operator
$ \hat{F}_{J} $ is written as$ \begin{aligned}[b] B(EJ,0\rightarrow\nu)& = \frac{1}{2J+1}\left|\sum\limits_{c \geqslant d}b_{cd}(EJ)\right|^{2}\\ & = \dfrac{1}{2J+1}\left|\sum\limits_{c \geqslant d}(X^{\nu}_{cd}+Y^{\nu}_{cd})(v_{c}u_{d}+u_{c}v_{d})\langle c\|\hat{F}_{J}\|d\rangle\right|^{2}, \end{aligned} $

(4) here, ν represents the ν-th QRPA excited state, and 0 represents the QRPA ground state.
The discrete spectra are averaged with the Lorentzian distribution
$ S(E) = \sum\limits_{\nu} B(EJ,0\rightarrow\nu)\frac{1}{\pi}\frac{\Gamma/2}{(E-E_\nu)^2+\Gamma^2/4}, $

(5) where Γ is the width of the Lorentz distribution and is taken to be 1 MeV in present calculations.
After solving the QRPA equation, various moments are defined as
$ m_k = \int E^kS(E){\rm d}E. $

(6) In the HF+BCS plus QRPA calculations, an effective density-dependent zero-range pairing interaction is used, it is
$ V_{\rm pair}({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2}) = V_{0}\left [1-\eta\left (\frac{\rho({\boldsymbol{r}})}{\rho_{0}}\right )\right ]\delta({\boldsymbol{r}}_{1}-{\boldsymbol{r}}_{2}), $

(7) where
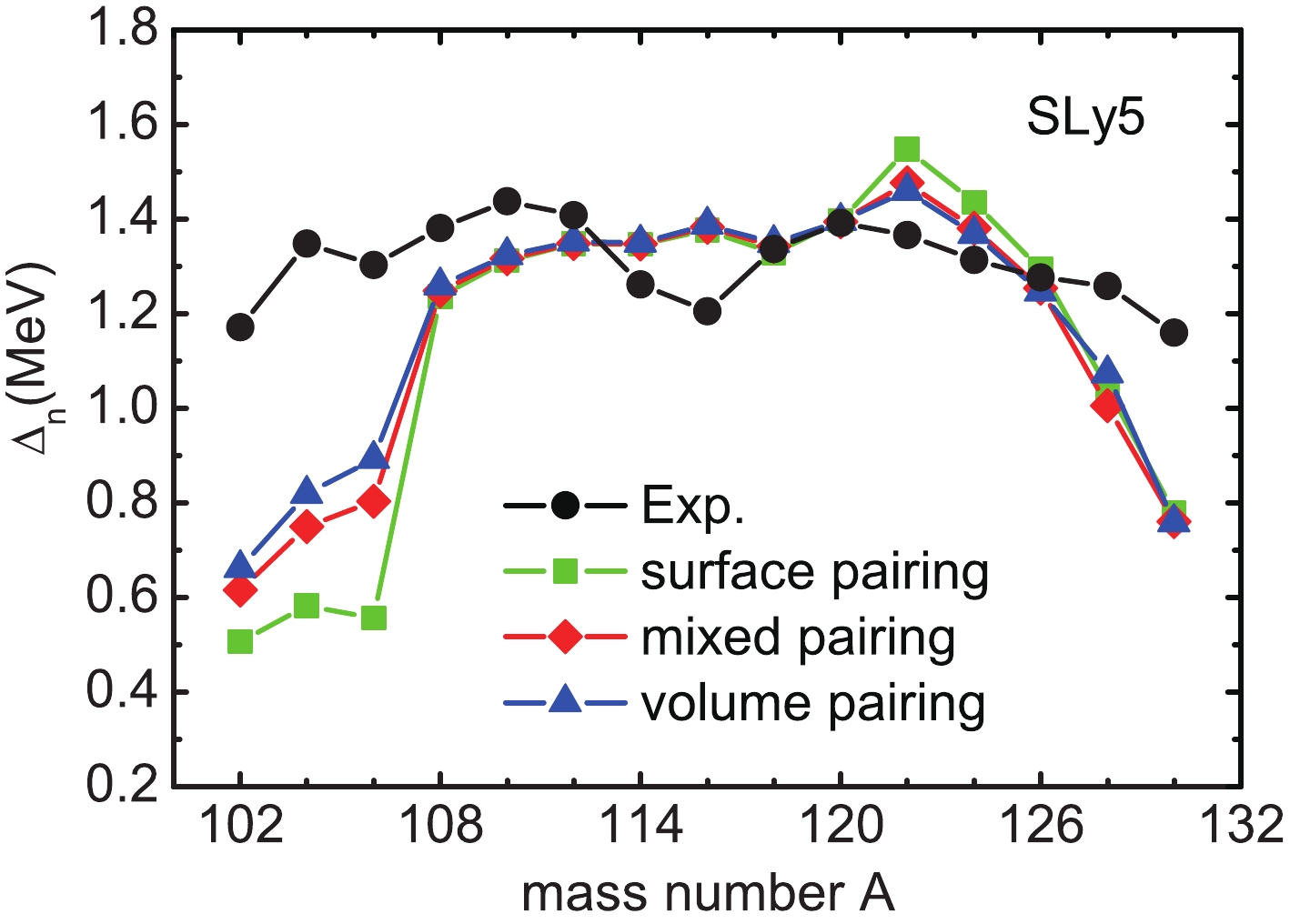
$ \rho_{0} $ is the density at nuclear saturation, and is set as 0.16 fm−3. η represents the pairing type; the surface, mixed, and volume pairing interactions are adopted when η is fixed as 1.0, 0.5, and 0.0, respectively.$ \rho({\boldsymbol{r}}) $ is the particle density. In the present study, the SLy5 Skyrme force [73] is adopted as the particle-hole interactions in the ground and excited state calculations. The neutron levels below the neutron Fermi surface and three levels above the neutron Fermi energy are chosen as the BCS pairing window in the present calculations. The pairing strength$ (V_{0}) $ is taken as −805.0, −408.0, and −272.0 MeV·fm3 for the surface, mixed, and volume pairing interactions, respectively. The values are adjusted to reproduce the empirical neutron gap in 120Sn ($ \Delta_n $ = 1.392 MeV). The same value is then extended to the calculations of other Sn isotopes. We show the calculated neutron pairing gaps$ \Delta_{n} $ in Fig. 1. The values are calculated using the HF+BCS approach within the SLy5 interaction together with the surface, mixed, and volume pairing interactions, respectively. Additionally, the empirical data are also shown in Fig. 1, which are obtained within the empirical five-point mass formula [74], and the binding energies are taken from Ref. [75]. Fig. 1 shows that the calculated neutron pairing gaps in the region of$ ^{102-106} {\rm{Sn}}$ and$ ^{128-130} {\rm{Sn}}$ underestimate the corresponding empirical data. This may be because we use the five-point formula to extract the empirical pairing gaps as done in our previous paper [18]. To reduce the difference of the nuclei with a neutron number close to the magic number, as proposed in [74], the simplest three-point formula$ \Delta^{(3)}_C(N) $ is used to provide a good measure of the neutron pairing gap in the even-N nuclei because it removes to a large extent the contribution from the nuclear mean field as well as the contributions from the shell structure details. For the other Sn isotopes, the calculated results given by the three types of pairing interactions are comparable to the empirical data. As a whole, our results are not the best fit for the data because the pairing strengths are fixed using the gap value of 120Sn only. -
For the Sn isotopes, a nearly spherical shape was predicted using various Skyrme forces in Ref. [76], thus, we adopt a spherical shape in our calculations. The quasiparticle states are obtained by solving HF+BCS in the coordinate space with a box boundary condition, where the size of the box is set as 24 fm. We have checked that the predicted ground state properties of the Sn isotopes, such as the binding energies and charge radii, agree well with the experimental data. After solving the HF+BCS equation in the coordinate space, we build up a model space of two-quasiparticle configurations for quadrupole excitation, and then solve the QRPA matrix equations in the model space. The eight nodes shell cut-off is adopted to build up the QRPA model space, which is large enough so that the calculated energy-weighted sum rule exhausts practically 99.9% of the double-commutator value.
The properties of first 2+ state in the Sn and Pb isotopes had been studied within the relativistic or non-relativistic approaches [77-80]. These works were devoted to studying the sensitivity of the first 2+ state to the neutron excess; only a few studies focused on the sensitivity of the first 2+ state to the density-dependence of the pairing interaction. Therefore, it would be interesting to examine the effect of different density-dependences of pairing interactions on the excitation energies and the transition probabilities of the first 2+ state in Sn isotopes. For this evaluation, we performed the fully self-consistent QRPA calculation with the Skyrme energy density functional with surface, mixed, and volume pairings. Fig. 2 shows the predicted excitation energies and reduced electric transition probabilities of the first 2+ state in the Sn isotopes. The green squares, red diamonds, and blue triangles represent the results given by surface, mixed, and volume pairing interactions. The corresponding experimental values are also plotted in the figure; the data are taken from Ref. [81].

Figure 2. (color online) Upper panel: Experimental and theoretical values of the first 2+ state excitation energies for the Sn isotopes using SLy5 Skyrme force with surface, mixed, and volume pairings. Lower panel: Corresponding reduced electric transition probabilities. The experimental data are taken from Ref. [81].
From Fig. 2, it can be observed the experimental excitation energies of the first 2+ state from
$ ^{102} {\rm{Sn}}$ to$ ^{130} {\rm{Sn}}$ are almost constant. This impression is because we use a large scale in the vertical axis to include the data of$ ^{132} {\rm{Sn}}$ . Actually, the energies are slightly fluctuated around 1.2 MeV. The experimental electric transition probabilities show a parabolic variation with a peak in$ ^{112} {\rm{Sn}}$ although the parabolic shape is not strongly shown in the figure because we use large scale in the vertical axis. The parabolic variation of the data is presented and discussed in Refs. [81, 82]. For nuclei$ ^{132} {\rm{Sn}}$ and$ ^{134} {\rm{Sn}}$ , the theoretical values for both the excitation energies and electric transition probabilities agree well with the experimental data. About the results for nuclei from$ ^{102} {\rm{Sn}}$ to$ ^{130} {\rm{Sn}}$ , as a whole, the trends of the experimental excitation energies and the reduced electric transition probabilities of the first 2+ state for those nuclei is well reproduced within our calculations. The theoretical excitation energies fluctuated around 1.2 MeV although the fluctuation is slightly larger compared to the case of experimental data. Our theoretical results overestimate the experimental excitation energies in the mass region of 120 to 130, whereas for the mass less than 120, the calculated values are lower than the experimental data. For the reduced electric transition probabilities, the theoretical results calculated with the surface, mixed and volume pairings also show a parabolic variation with a peak in$ ^{112} {\rm{Sn}}$ ; however, the difference between the theoretical results and experimental data in some mass region is large. The theoretical results in the mass 102 to 106 and 118 to 126 underestimate the data, whereas for nuclei with mass from 110 to 114, the predicted values are larger than the data, especially in the case of surface pairing. Of course, there is still room left to improve the calculations in the mean field level, for example, one may try to get better agreement for the pairing gaps in Sn isotopes, not just fit the gap in 120Sn and extend the value to other Sn isotopes. The difference could be further reduced if one considers the contribution from other many-body correlations. All of these mentioned above are not our purpose of this paper, we may take into account these effects in the future.It should be noted that the calculated results also depend on the used pairing interaction. The results given by volume pairing are much better than the other two both for the excitation energy and reduced electric transition probability. The surface pairing predicts very different results from the other two in our present calculations. In the mass 102 to 122, the calculated excitation energies are systematically lower than the data of the mixed and volume pairings. The calculated reduced electric transition probabilities of the surface pairing in the mass 102 to 106 and 118 to 124 are also lower than the data of the mixed and volume pairings; however, for the mass from 110 to 114, the results of the surface pairing are much larger than the data of the other two. The difference between the results of the mixed and volume pairings is small in the entire mass region.
In Fig. 3, we show the isoscalar quadrupole QRPA strength distributions of
$ ^{112} {\rm{Sn}}$ . The results are obtained using surface (green dashed line), mixed (red short-dotted line), and volume (blue solid line) pairings. The figure shows that the energies and strengths of the low-lying quadrupole states are more sensitive to the used pairing interaction. The centroid energies of the strength in the high energy region obtained using the three types of pairing are all approximately 15.0 MeV. Their strength distributions are also similar to each other, which means that the density-dependence of the pairing interaction has almost no influence on the properties of the high-lying quadrupole states. This feature of the high-lying quadrupole states is also true for the other Sn isotopes. In the figure, we also include the experimental mean value of the excitation energy of the high-lying quadrupole states for$ ^{112} {\rm{Sn}}$ . The data is approximately 13.4 MeV [83], which is lower than our prediction. The excitation energy of the high-lying quadrupole states is much sensitive to the effective mass of the applied effective interaction [84]. The effective mass of the SLy5 interaction is 0.70, which is lower than the empirical value. The agreement between the data and theoretical prediction could be improved if one uses an effective interaction with the effective mass close to the empirical value.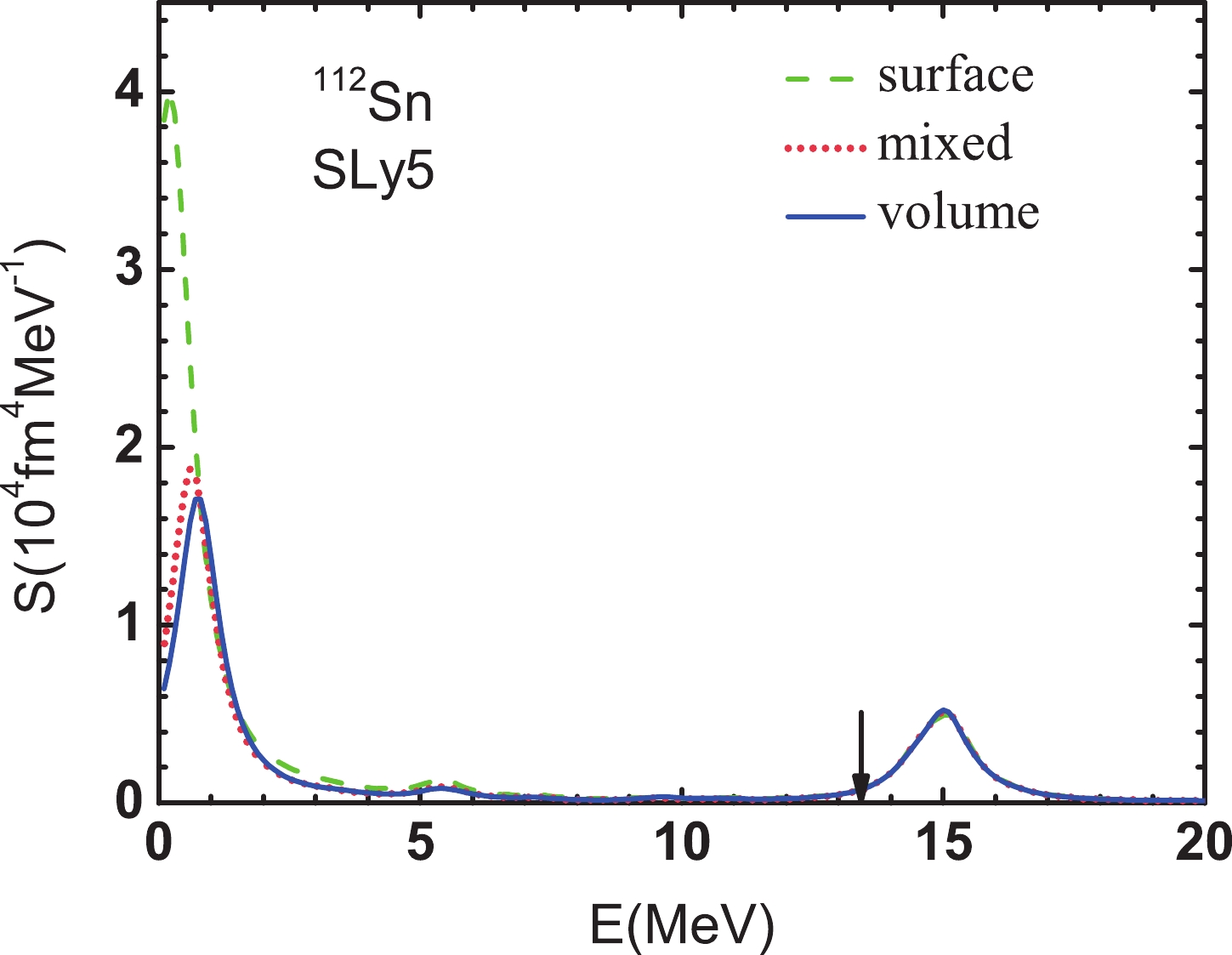
Figure 3. (color online) Isoscalar quadrupole QRPA strengths of
$ ^{112} {\rm{Sn}}$ . The lines are the results given by the SLy5 interaction with the surface, mixed, and volume pairings, respectively. The arrow indicates the experimental mean excitation energy of the giant quadrupole resonance.In the following paragraphs, we analyze the effect of the density-dependence of the pairing interaction on the properties of the first 2+ state in the Sn isotopes; we take the nucleus
$ ^{112} {\rm{Sn}}$ as an example. The low-lying states are mainly contributed due to the configurations formed from the states around the Fermi surface. Table 1 lists the quasipartilce energies$ {{E}}_{q.p.} $ , occupied probabilities$ v^{2} $ , and gaps of neutron states around the Fermi energy in$ ^{112} {\rm{Sn}}$ . The results are obtained using the SLy5 interaction with the surface, mixed, and volume pairings, separately. By analyzing the data in the table, we deduce that the quasiparticle energies (except for$ 1{h}_{11/2} $ ) given by the surface pairing are the lowest ones, the values using volume pairing are the largest ones, and the values given by the mixed pairing are in between. Similar conclusions are true for the occupied probabilities and gaps. The differences in the quasiparticle energies, occupied probabilities, and gaps may lead to the difference in the calculated first 2+ state.States Surface Mixed Volume ${{E}}_{q.p.}$ 

$v^{2}$ 

Gap ${{E}}_{q.p.}$ 

$v^{2}$ 

Gap ${{E}}_{q.p.}$ 

$v^{2}$ 

Gap $\nu1g_{9/2}$ 

7.88 0.99 1.40 7.95 0.99 1.47 7.97 0.99 1.49 $\nu2d_{5/2}$ 

2.01 0.91 1.14 2.12 0.91 1.24 2.16 0.90 1.29 $\nu1g_{7/2}$ 

1.33 0.55 1.32 1.44 0.56 1.43 1.48 0.56 1.46 $\nu3s_{1/2}$ 

1.12 0.29 1.02 1.28 0.33 1.21 1.36 0.34 1.29 $\nu2d_{3/2}$ 

1.48 0.19 1.16 1.50 0.21 1.22 1.52 0.21 1.25 $\nu1h_{11/2}$ 

3.07 0.07 1.59 2.93 0.06 1.42 2.87 0.06 1.36 Table 1. Quasipartilce energies
${{E}}_{q.p.}$ , occupied probabilities$v^{2}$ , and gaps of neutron states around the Fermi energy in 112Sn. The results are obtained using SLy5 interaction with surface, mixed, and volume pairings.It would be interesting to show the configurations of the first 2+ state. In Table 2, the QRPA amplitudes of the selected configurations larger than 0.01 are presented. The results are calculated using the surface, mixed, and volume pairings, separately. Most of these major configurations are neutron quasiparticle configurations, and only one is formed from the proton
$ 1{g}_{9/2} $ and$ 2{d}_{5/2} $ states. The calculated, reduced transition amplitudes$ b_{cd} $ are all positive, which shows the collectivity of the first 2+ state. The first four configurations (namely$ (2{d}_{3/2}1{g}^{-1}_{7/2})^\nu $ ,$ (1{g}_{7/2}1{g}^{-1}_{7/2})^\nu $ ,$ (3{s}_{1/2}2{d}^{-1}_{5/2})^\nu $ , and$ (2{d}_{3/2}3{s}^{-1}_{1/2})^\nu $ ) give the largest contributions to the first 2+ state because the occupied probabilities of states$ 1{g}_{7/2} $ ,$ 2{d}_{5/2} $ , and$ 3{s}_{1/2} $ are relatively large. Similar to the properties of the quasiparticle states, the table shows that the two-quasiparticle excitation energies given by the surface pairing are the lowest (expect for the neutron$ (1{h}_{11/2}1{h}^{-1}_{11/2})^\nu $ and proton$ (2{d}_{5/2}1{g}^{-1}_{9/2})^\pi $ configurations), whereas the volume pairing produces the largest two-quasiparticle excitation energies. This may cause the calculated first 2+ excitation energies produced by surface pairing to be the lowest among the three calculations. For each configuration, the changing of the QRPA amplitudes$ A_{ab} $ has no unified behaviour for the surface, mixed, and volume pairing. For the reduced transition amplitudes, it can be observed that the surface pairing gives the largest values, whereas the data produced by the volume pairing are the lowest ones. We also summed the reduced transition amplitudes$ b_{cd} $ in Table 2. The values are 125.54, 86.02, and 80.03 fm2 in the case of surface, mixed, and volume pairings, respectively. Consequently, the reduced transition strength calculated with surface pairing is the largest among the three pairing interactions, whereas the value from the volume pairing is the smallest.Configurations Surface Mixed Volume $E_{2q.p.}$ 

$A_{ab}$ 

$b_{cd}$ 

$E_{2q.p.}$ 

$A_{ab}$ 

$b_{cd}$ 

$E_{2q.p.}$ 

$A_{ab}$ 

$b_{cd}$ 

$(2d_{3/2}1g^{-1}_{7/2})^\nu$ 

2.80 0.24 21.07 2.94 0.22 14.60 2.99 0.22 14.01 $(1g_{7/2}1g^{-1}_{7/2})^\nu$ 

2.65 0.23 27.94 2.87 0.24 18.89 2.95 0.24 18.04 $(3s_{1/2}2d^{-1}_{5/2})^\nu$ 

3.13 0.14 18.38 3.39 0.14 12.16 3.52 0.13 11.44 $(2d_{3/2}3s^{-1}_{1/2})^\nu$ 

2.59 0.13 11.79 2.78 0.13 8.31 2.88 0.12 7.99 $(2d_{5/2}1g^{-1}_{9/2})^\pi$ 

5.65 0.05 22.83 5.63 0.08 15.83 5.63 0.08 15.23 $(2d_{3/2}2d^{-1}_{3/2})^\nu$ 

2.96 0.05 7.09 3.01 0.05 5.11 3.03 0.05 3.04 $(1h_{11/2}1h^{-1}_{11/2})^\nu$ 

6.14 0.03 7.47 5.85 0.03 4.49 5.75 0.03 4.09 $(2d_{3/2}2d^{-1}_{5/2})^\nu$ 

3.49 0.03 5.38 3.62 0.03 3.72 3.68 0.03 3.56 $(2d_{5/2}2d^{-1}_{5/2})^\nu$ 

4.02 0.02 3.59 4.23 0.02 2.91 4.33 0.02 2.93 Table 2. Quasiparticle configurations giving major contribution to the first 2+ states in 112Sn. The two-quasiparticle excitation energies (
$E_{2q.p.}$ in MeV), their QRPA amplitudes$A_{ab}$ and the corresponding reduced transition amplitudes$b_{cd}$ (fm2) of these configurations are calculated using SLy5 Skyrme interaction with surface, mixed, and volume pairings, respectively. Additionally, π (ν) represents the proton (neutron) state.There are two kinds of mechanisms in the pairing effect on the collective excitations. One is a static effect, which has been mainly discussed above. The other is the dynamical pairing effect, which is caused by the residual pairing interaction entering the QRPA calculations and has been discussed in Refs. [85-88]. To quantify the dynamical pairing effect in this study, we present in Table 3 the excitation energies and isoscalar transition probabilities of first 2+ state in
$ ^{112} {\rm{Sn}}$ calculated with the surface, mixed, and volume pairings in the three different cases: the pairings are dropped (included) in both the ground and excited state calculations (case 1(3)), and the pairings are included in the ground state calculations but excluded in the excited states calculations (case 2). Comparing the results in cases 1 and 2, it can be observed that the static pairing plays a role in the calculations and enhances both the excitation energies and isoscalar transition probabilities. The difference in the calculations of cases 2 and 3 is that dynamical pairing is included in case 3. Comparing the results in case 2 and 3, it is found that the dynamical pairing lowers the excitation energies in the calculations with the surface, mixed, and volume pairings; it also enhances the isoscalar transition probability for the surface pairing and reduces the values for the mixed and volume pairings.States Case 1 Case 2 Case 3 ${{E}}_{2^+_1}$ 

B(E2)IS ${{E}}_{2^+_1}$ 

B(E2)IS ${{{E}}}_{2^+_1}$ 

B(E2)IS Surface 0.48 0.373 0.50 4.952 0.21 6.302 Mixed 0.48 0.373 0.81 3.317 0.63 2.956 Volume 0.48 0.373 0.91 3.030 0.75 2.706 Table 3. Excitation energies and isoscalar transition probabilities (B(E2)IS) of the first 2+ state in 112Sn calculated with surface, mixed, and volume pairings in three different cases (for details please see the text). The units for the energy and transition probabilities are in MeV and 104fm4, respectively.
Finally, the proton (a, c) and neutron (b, d) transition densities of the first 2+ state (a, b) and high-lying quadrupole state (c,d) in
$ ^{112} {\rm{Sn}}$ are displayed in Fig. 4. The results presented by the dashed, short-dotted, and solid lines are obtained by the surface, mixed, and volume pairing, respectively. In figures (a) and (b), the proton (neutron) transition density given by the surface pairing is much stronger than the ones by the mixed and volume pairings, whereas the results are similar in the case of the mixed and volume pairings. For the high-lying quadrupole state, the difference of the proton (neutron) transition densities given by the three pairing interactions are small, which means the transition density in the high-lying quadrupole state is not sensitive to the density-dependence of the pairing. -
In conclusion, we examined the effect of the density-dependence of pairing interactions on the low-lying quadrupole state of Sn isotopes. The properties of the ground state were calculated within the HF+BCS approach, and the SLy5 Skyrme interaction with the surface, mixed, and volume pairings was employed, separately. The pairing strengths were fixed by reproducing the neutron pairing gap in 120Sn. The predicted ground state properties of the Sn isotopes agreed well with the experimental data. The fully self-consistent QRPA was used to calculate the isoscalar giant quadrupole resonance in the Sn isotopes. Correspondingly, the surface, mixed, and volume pairing interactions were adopted in the particle-particle channel when solving the QRPA equations. The first 2+ state excitation energies and the corresponding transition probabilities given by the three pairing interactions were presented. We also discussed the effect of the pairings on these quantities in detail.
We deduced that the surface, mixed, and volume pairings indeed affect the properties of the low-lying quadrupole state in Sn isotopes. Particularly, they have a strong impact on the excitation energies and the corresponding transition probabilities of the first 2+ state. In the mass region from 102 to 122, the surface pairing produced the lowest excitation energy, whereas the volume pairing produced the highest value for each Sn isotope. For the electric transition probabilities, the values given by the surface pairing in the two mass regions of 102 to 106 and 116 to 126 were slightly smaller than the data given by the other two pairings; however, the surface pairing strongly affected the transition probabilities in
$ ^{110-114} {\rm{Sn}}$ . Taking$ ^{112} {\rm{Sn}}$ as an example, we carefully analyzed the effect of the density-dependence of pairing on the properties of the quasiparticle state, two-quasiparticle excitation energy, reduced transition amplitude, and transition densities. We found that the two-quasiparticle excitation energies produced by the surface pairing were systematically smaller than those of the other two, whereas the reduced transition amplitudes were the largest ones. The feature causes different excitation energies and transition probabilities of the first 2+ state. In addition to the static effect, the dynamical effect of the pairing correlation is also discussed. It reduces the excitation energies for the three pairings, but has different effects on the isoscalar transition probabilities. We also verified the results by using other Skyrme interactions such as SGII. The conclusion remains.
Effect of pairing correlation on low-lying quadrupole states in Sn isotopes
- Received Date: 2021-02-24
- Available Online: 2021-09-15
Abstract: We examined the low-lying quadrupole states in Sn isotopes in the framework of fully self-consistent Hartree-Fock+BCS plus QRPA. We focus on the effect of the density-dependence of pairing interaction on the properties of the low-lying quadrupole state. The SLy5 Skyrme interaction with surface, mixed, and volume pairings is employed in the calculations, respectively. We find that the excitation energies and the corresponding reduced electric transition probabilities of the first 2+ state are different, given by the three pairing interactions. The properties of the quasiparticle state, two-quasiparticle excitation energy, reduced transition amplitude, and transition densities in 112Sn are analyzed in detail. Two different mechanisms, the static and dynamical effects, of the pairing correlation are also discussed. The results show that the surface, mixed, and volume pairings indeed affect the properties of the first 2+ state in the Sn isotopes.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: