-
Studies of neutron-rich nuclei are very important not only in nuclear physics (e.g., for testing nuclear models and studying the evolution of nuclear structures [1-4]) but also for the studies of stellar nucleosynthesis in nuclear astrophysics [5]. Many existing and planned radioactive beam facilities aim at producing and measuring neutron-rich nuclei, especially those close to the neutron drip-line. At these nuclear physics facilities, projectile fragmentation, spallation, and fission reactions involving energies on the order of hundreds of MeV/nucleon are the most widely used production mechanisms for exotic nuclei. For instance, many isotopes between neutron and proton drip-lines have been produced by intermediate-energy fragmentation, spallation, and fission reactions at the A1900 separator at MSU [1-3, 6], the Fragment Separator (FRS) at GSI [7-11], the BigRIPS separator at RIKEN [4, 12-15], and the RIBLL-CSR facility at IMP with a time-of-flight detector [16-18]. For designing nuclear physics experiments at these facilities, accurate cross sections of fragmentation, spallation, and in-flight fission reactions are essential. These cross sections are also critical for many other applications, such as simulations of the cosmic-ray nuclei propagation in the galaxy [19, 20], cancer therapy using heavy ions or protons [21], and design of accelerator-driven subcritical reactor systems [22].
A much higher production of even-Z fragments than the neighboring odd-Z ones, the so-called odd-even staggering (OES), has been observed in many cross sections measured in different fragmentation as well as spallation reactions. However, quantitative studies of this OES remained scarce until more isotopic cross sections with both A and Z identification were accurately measured; see, e.g., Refs. [17, 18, 23] and references therein. Recently, quantitative comparisons of this OES have been performed by using extensive accurate isotopic cross sections of some neutron- and proton-rich fragments, measured in various fragmentation and spallation reactions [17, 18, 24, 25]. These comparisons strongly support the notion that this OES is almost independent of projectile-target combinations as well as of the projectile energy; thus, this OES is universal across different fragmentation and spallation systems [24, 25]. This universal OES is thought to stem mainly from the OES of the particle-emission threshold energies in excited nuclei during the final evaporation phase [17, 18, 23, 26]. Owing to the lack of accurate experimental cross sections for exotic nuclei near the neutron drip-line, the quantitative OES studies for many of such exotic nuclei are missing; thus, the OES universality is still unclear for them.
Theoretically, different reaction models have been developed for calculating fragmentation or spallation cross sections. For instance, a simple empirical parametrization EPAX3 [27] without the OES and an improved parametrization FRACS [28] including the OES have been constructed for fast calculations of fragmentation cross sections. In addition, both Monte Carlo models (e.g., the abrasion-ablation model [26]) and
$ Q_{g} $ systematics [3] seem to be very sensitive to nuclear mass models used in their cross section calculations. Many studies have demonstrated that the above reaction models do not adequately reproduce the OES for experimental cross sections of fragments over a wide range of Z [17, 18, 23]. In particular, accurate calculations of these cross sections are extremely challenging for isotopes approaching the drip-lines. Finally, four OES relations based on the universal OES in various reaction systems have been proposed recently for very fast and accurate calculations of fragmentation and spallation cross sections [29]. These accurate OES relations, as well as other reaction models, should be benchmarked with more experimental data, especially for isotopes approaching the neutron drip-line.Considering that the universality of OES and OES relations proposed in our previous publications [24, 25, 29] is mostly based on accurate experimental data not far from stability, the present work is focused on validating the universality of the OES and OES relations by using the cross sections for many isotopes near the neutron drip-line, as measured for several fragmentation and in-flight fission reactions [1, 3, 14, 15]. Recently, production cross sections of many very neutron-rich nuclei close to the neutron drip-line have been measured for two fragmentation reactions, i.e., 132 MeV/nucleon
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3], by Tarasov et al.. Since these experimental cross sections have very large relative uncertainties (typically above 40%) with probable existence of spurious OES structures, OES magnitudes were not studied and used in our previous accurate OES evaluations in Refs. [24, 25]. In this work, the OES for these cross sections measured for the above two fragmentation reactions will be quantitatively calculated and carefully compared with those evaluated from many accurate experimental data. For some very neutron-rich nuclei, the OES in their measured cross sections will be applied for extending the OES magnitudes previously evaluated in Refs. [24, 25]. In addition, four OES relations proposed in Ref. [29] will be validated further with these experimental data approaching the neutron drip-line. Finally, the OES for some experimental cross sections of neutron-rich isotopes produced by in-flight fission 345 MeV/nucleon$ ^{238} $ U+$ ^{9} $ Be [14, 15] are also investigated in this work, and the OES relations are applied for calculations of projectile fission cross sections. -
Our previous studies in Refs. [17, 18, 24, 25, 28, 29] reveal that it is very suitable to calculate the OES in production cross sections of isotopes along a constant isospin
$ T_{z} = (N-Z)/2 $ chain. According to these studies, the OES magnitude for experimental cross sections of four neighboring nuclei along a constant isospin$ T_{z} $ chain can be well described using a third-order difference formula$ \begin{aligned}[b] D^{\text{exp}}_{\text{CS}}\left({Z,N}\right) =& \frac{1}{8}\left(-1\right)^{Z+1}\{\ln{Y\left(Z+3,N+3\right)}-\ln{Y\left(Z,N\right)}\\& -3\left[\ln{Y\left(Z+2,N+2\right)}-\ln{Y\left(Z+1,N+1\right)}\right]\}, \end{aligned} $

(1) which is also adopted in the present work. Here,
$ Y(Z,N) $ is the production cross section (or yield) of a particular nucleus with a proton number Z and a neutron number$ N = Z + 2T_{z} $ . The absolute value of$ D^{\text{exp}}_{\text{CS}} $ stands for the strength of the OES in experimental data. A positive (negative)$ D^{\text{exp}}_{\text{CS}} $ represents an enhanced production of even (odd) Z nuclei.Isotopic cross sections of some very neutron-rich nuclei produced by two fragmentation reactions, namely 132 MeV/nucleon
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3], have been measured, while their relative errors are typically above 40%. The OES magnitudes in these experimental data are calculated using Eq. (1) for many neutron-rich fragments with ($ N - Z $ ) from 2 to 21. Considering that the large errors in these experimental data may lead to spurious staggering structures [30], their OES magnitudes should be scrutinized by comparing with OES magnitudes in Refs. [24, 25] evaluated from extensive accurate experimental data (with small relative uncertainties, under 15%).For neutron-rich fragments with (
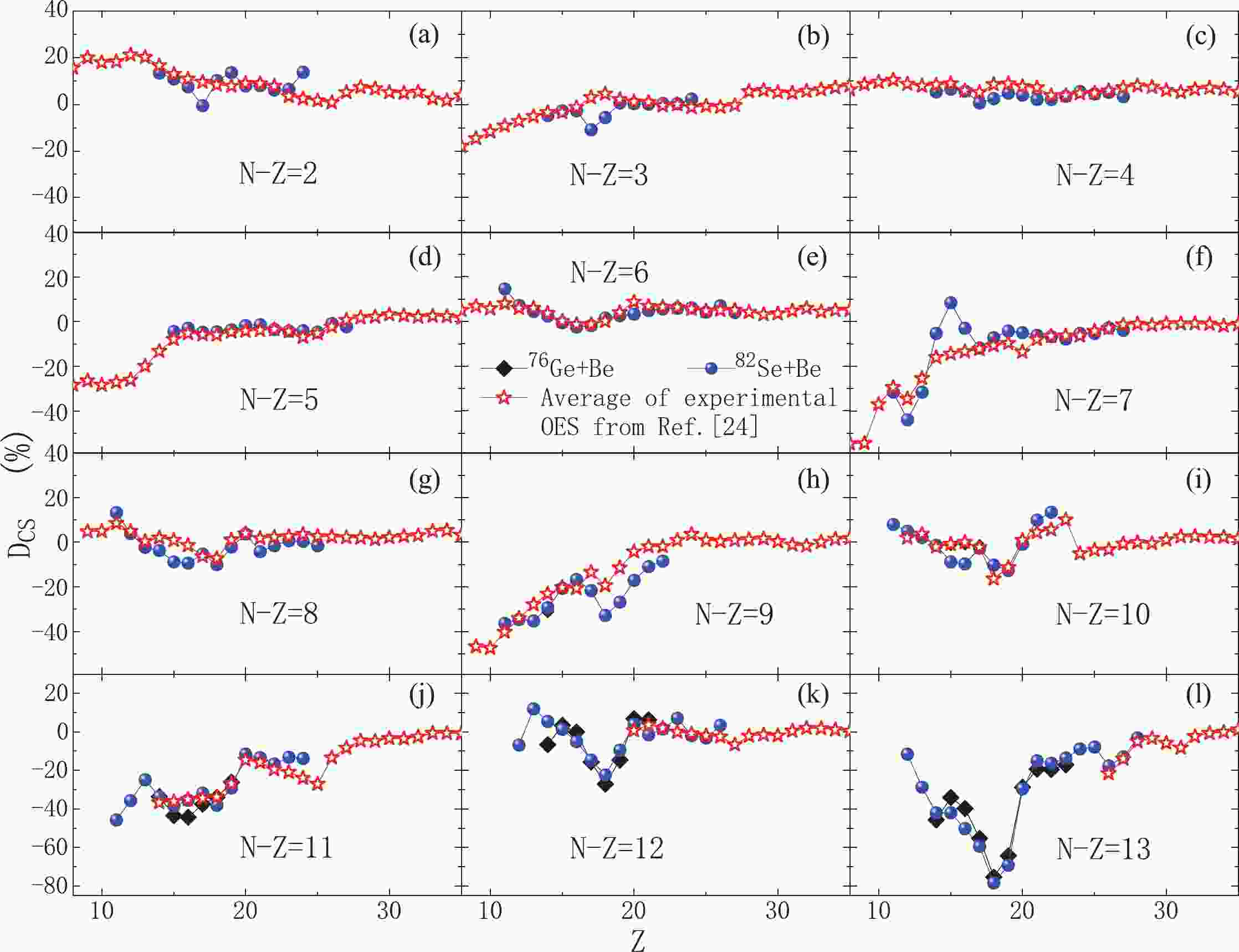
$ N - Z $ ) from 2 to 13, the OES magnitudes derived from their cross sections measured in 132 MeV/nucleon$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3] are compared with accurate OES magnitudes previously evaluated in Refs. [24, 25], and the results are shown in Fig. 1. According to these comparisons, most OES magnitudes from two experimental data sets are in a good agreement, and they also agree well with our previous accurate OES evaluations in Refs. [24, 25] (open stars in Fig. 1). Previous OES evaluations for a few isotopes (e.g.,$ N-Z = 12 $ ones with Z from 22 to 25) obtained from interpolating neighboring ones [24] are also consistent with these experimental data. Some local deviations between the OES magnitudes in$ ^{82} $ Se+$ ^{9} $ Be and previous evaluations are observed for some$ N-Z = 7 $ and$ N-Z = 9 $ fragments, with Z from 14 to 21, as displayed in panels (f) and (h) of Fig. 1. These evident deviations are not unexpected, considering large uncertainties (typically above 40%) of cross sections measured in$ ^{82} $ Se+$ ^{9} $ Be [3].
Figure 1. (color online) OES magnitudes calculated by Eq. (1) using isotopic cross sections measured in two fragmentation reactions, namely 132 MeV/nucleon
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3]. For clarity, experimental error bars, above 20% in most cases, are not shown. These OES magnitudes are compared with those evaluated in Ref. [24] from extensive accurate experimental data. The data are displayed for neutron-rich nuclei from (a)$ N-Z = 2 $ to (l)$ N-Z = 13 $ .For some (very neutron-rich) low-Z fragments with (
$ N - Z $ ) from 10 to 21, there are no accurate OES evaluations in Refs. [24, 25], and their OES magnitudes are first obtained from the above two experimental data sets. In such cases, previous OES evaluations in Refs. [24, 25] are extended and new OES evaluations are suggested for these very neutron-rich isotopes. As illustrated in Fig. 2, most OES magnitudes from two fragmentation experiments ($ ^{76} $ Ge+$ ^{9} $ Be [1] and$ ^{82} $ Se+$ ^{9} $ Be [3]) also agree with each other, although there are some large discrepancies in some cases. These large discrepancies shown in panels (e), (g), and (h) of Fig. 2 are caused by the large uncertainties of measured cross sections. As an example, for$ N-Z = 16 $ fragments around Z = 16 in panel (g), the relative uncertainties of their cross sections, where strong discrepancies exist, are above 70%. The average values of the OES magnitudes derived from two experimental data sets are adopted as new OES evaluations; see green open squares in Fig. 2. The evolution tendency of the new OES evaluations for low-Z fragments obtained in this work generally agrees well with that of previous evaluations for high-Z ones from Refs. [24, 25].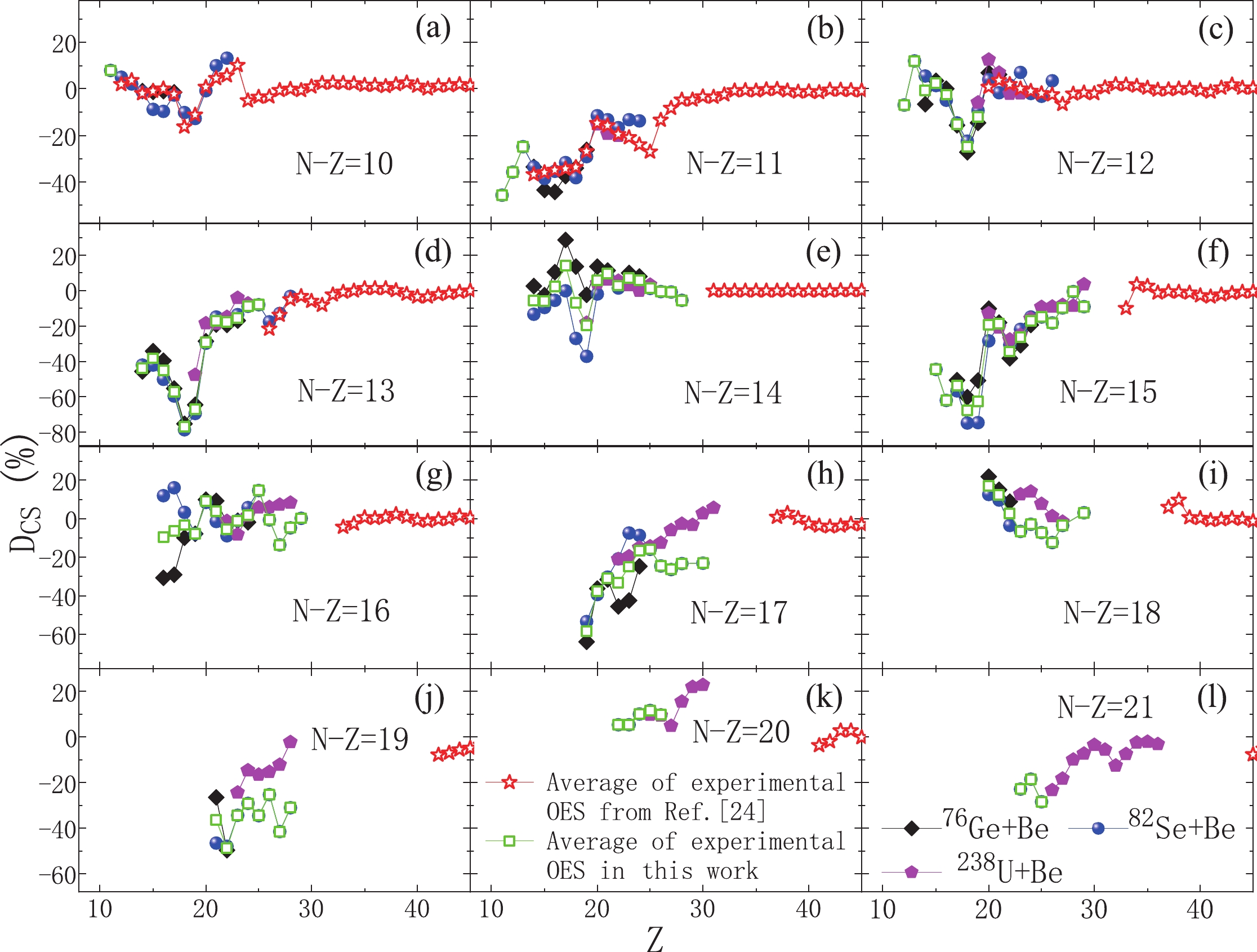
Figure 2. (color online) OES magnitudes, calculated by Eq. (1) using isotopic cross sections measured in 132 MeV/nucleon
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3], are applied to derive the OES magnitudes evaluated in this work (open squares) for fragments whose OES magnitudes are not evaluated in Ref. [24]. For comparison, the OES magnitudes evaluated in Ref. [24] and those derived from experimental data produced by 345 MeV/nucleon$ ^{238} $ U+$ ^{9} $ Be [14, 15] are also presented. Experimental error bars, typically above 20%, are not shown. The data are displayed for very neutron-rich nuclei from (a)$ N-Z = 10 $ to (l)$ N-Z = 21 $ . -
Considering that the above experimental cross sections of very neutron-rich isotopes generally have large uncertainties, careful comparisons between them and other experimental data are necessary. To validate the new OES magnitudes evaluated in this work, OES magnitudes in extra experimental cross sections produced by in-flight fission 345 MeV/nucleon
$ ^{238} $ U+$ ^{9} $ Be measured at RIKEN [14, 15] were also calculated using Eq. (1). The relative uncertainties of these experimental data measured at RIKEN [14, 15] were typically above 30%. In general, the above OES magnitudes evaluated from the cross sections measured in Refs. [1, 3] (open squares in Fig. 2) were consistent with those derived from Refs. [14, 15], as shown in Fig. 2. This good agreement gives us confidence in the OES magnitudes evaluated in this work. A few evident discrepancies between the two sets of results are observed in panels (i) and (j) of Fig. 2, which can be explained by very large relative uncertainties ($ > $ 40%) of these cross sections measured at RIKEN.In addition, some experimental data around
$ Z = 30 $ from Refs. [14, 15] in panels (h), (j), (k), and (l) of Fig. 2, where there are no experimental data from Refs. [1, 3], seem to be also consistent with OES magnitudes around$ Z = 40 $ (open stars) previously evaluated from accurate cross sections with small uncertainties [24], although there is still a gap between them. To fill this gap between$ Z = 30 $ and$ \sim $ 40, quantitative OES studies for more experimental cross sections will be performed and reported. -
In the following, cross sections of very neutron-rich isotopes (including dozens of new ones) produced by
$ ^{76} $ Ge+$ ^{9} $ Be [1],$ ^{82} $ Se+$ ^{9} $ Be [3], and$ ^{238} $ U+$ ^{9} $ Be [14, 15]) measured in the above mentioned experiments are used for validating the calculations by a set of OES relations recently proposed by Mei in Ref. [29]. On the basis of Eq. (1), four OES relations are constructed [29]:$ \begin{aligned}[b] Y\left(Z,N\right) =& \left(\frac{Y\left(Z+1,N+1\right)}{Y\left(Z+2,N+2\right)}\right)^{3}Y\left(Z+3,N+3\right)\\& \times\exp[8\left(-1\right)^{Z}D_{\text{CS}}\left({Z,N}\right)], \end{aligned} $

(2) $ \begin{aligned}[b] Y\left(Z+1,N+1\right) =& \left(\frac{Y\left(Z,N\right)}{Y\left(Z+3,N+3\right)}\right)^{1/3}Y\left(Z+2,N+2\right)\\& \times\exp[8\left(-1\right)^{Z+1}D_{\text{CS}}\left({Z,N}\right)/3], \end{aligned} $

(3) $ \begin{aligned}[b] Y\left(Z+2,N+2\right) =& \left(\frac{Y\left(Z+3,N+3\right)}{Y\left(Z,N\right)}\right)^{1/3}Y\left(Z+1,N+1\right)\\& \times\exp[8\left(-1\right)^{Z+2}D_{\text{CS}}\left({Z,N}\right)/3], \end{aligned} $

(4) $ \begin{aligned}[b] Y\left(Z+3,N+3\right) =& \left(\frac{Y\left(Z+2,N+2\right)}{Y\left(Z+1,N+1\right)}\right)^{3}Y\left(Z,N\right)\\& \times\exp[8\left(-1\right)^{Z+3}D_{\text{CS}}\left({Z,N}\right)], \end{aligned} $

(5) where the exponential factors are dominated by the OES magnitude
$ D_{\text{CS}}(Z,N) $ .$ D_{\text{CS}}(Z,N) $ values are generally obtained from OES evaluations in Ref. [24] and this work.Interpolation calculations by using two OES relations [Eqs. (3) and (4)] are compared with the cross sections of neutron-rich nuclei measured in two reactions, i.e., 132 MeV/nucleon
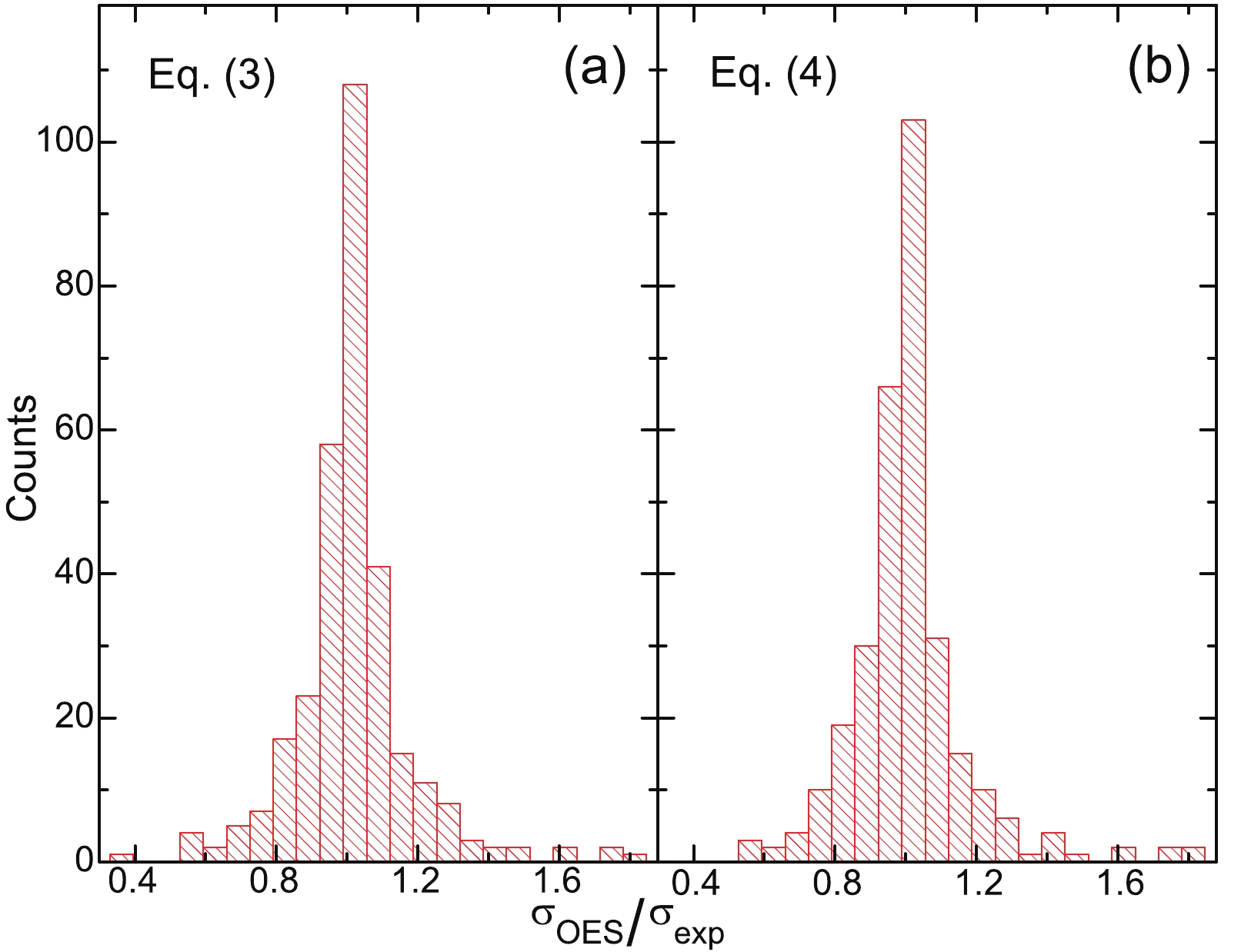
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3]; see their ratios in panels (a) and (b) of Fig. 3, respectively. In the calculations with these OES relations, the values of$ D_{\text{CS}} $ are from accurate evaluations in Ref. [24] when they are available. Otherwise, they are from the new OES magnitudes evaluated in this work, which are the average of OES from the two experimental data sets in Refs. [1, 3]. As illustrated in Fig. 3, most experimental cross sections can be excellently reproduced by Eqs. (3) and (4) within their uncertainties, considering that the relative uncertainties are typically above 40%. Compared with the results reported in Ref. [29], a relatively wider distribution is observed for the ratio values in Fig. 3, which is caused by significantly larger uncertainties of experimental data used in this work. Similar agreements (within a factor around 2) can be achieved between the extrapolation calculations by Eqs. (2) as well as (5) and most measured cross sections. The good agreement between the cross sections calculated by the above OES relations and the measured data supports the notion that these OES relations are also applicable for accurate calculations of the cross sections of isotopes approaching the neutron-drip line.Some typical examples are given in the following, in order to validate the above OES relations further by using more experimental data near the neutron drip-line. The OES relation calculated using Eqs. (2) and (3), as well as the OES magnitudes evaluated in this work, are checked by comparing with experimental cross sections of neutron-rich nuclei with
$ N-Z = 15 $ as well as$ N-Z = 17 $ produced by in-flight fission of$ ^{238} $ U in two experiments at RIKEN in 2008 [14] and 2010 [15]. As shown in panel (a) of Fig. 4, the results of the calculations using Eqs. (2) and (3) are in a good agreement with the experimental cross sections of$ N-Z = 15 $ nuclides reported in Ref. [14] and$ N-Z = 17 $ ones reported in Ref. [15]. The$ D_{\text{CS}} $ values used in these calculations are from the new OES magnitudes evaluated in this work.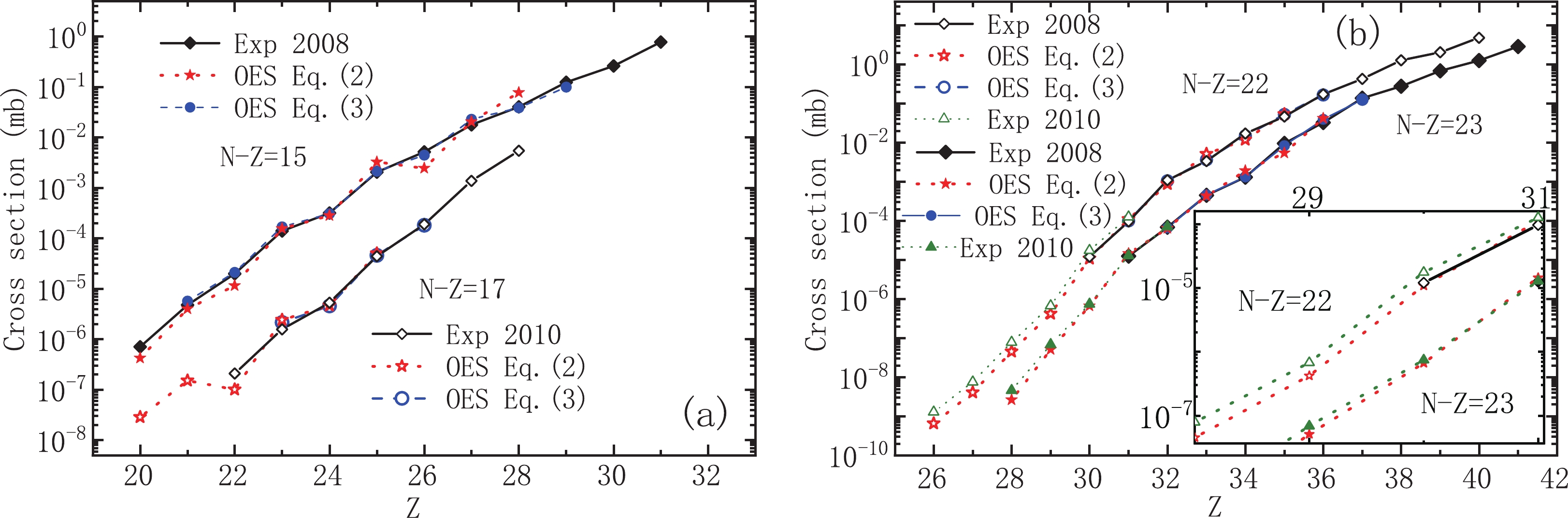
Figure 4. (color online) (a) Comparison between cross sections of neutron-rich nuclei with
$ N-Z = 15 $ and$ N-Z = 17 $ produced by$ ^{238} $ U in-flight fission measured in two experiments at RIKEN (in 2008 [14] and 2010 [15]) and predictions from two OES relations, i.e., Eqs. (2) and (3). (b) Comparison between cross sections of very neutron-rich nuclei with$ N-Z = 22 $ and$ N-Z = 23 $ approaching the neutron drip-line produced by 345 MeV/nucleon$ ^{238} $ U+$ ^{9} $ Be measured in two experiments at RIKEN (in 2008 [14] and 2010 [15]) and calculations by two OES relations, i.e., Eqs. (2) and (3). The inset shows an amplified view for light-mass nuclei.Finally, the calculations using the OES relations [Eqs. (2) and (3)] are compared with the cross sections of very neutron-rich nuclei with
$ N-Z = 22 $ and$ N-Z = 23 $ produced by$ ^{238} $ U+$ ^{9} $ Be at 345 MeV/nucleon measured in the above experiments at RIKEN (in 2008 [14] and 2010 [15]).$ D_{\text{CS}} $ values used in these calculations are derived from the experimental data that were acquired in 2010 [15]. For$ N-Z = 23 $ nuclei, the calculated cross sections generally agree with the actual data. But, for$ N-Z = 22 $ nuclei, systematic deviations between two experiments are observed in panel (b) of Fig. 4. It seems that the absolute cross sections of$ N-Z = 22 $ nuclei measured in 2010 [15] are approximately 1.3 times larger than those reported in 2008 [14] and OES relation calculations. These systematic deviations between two experiments may be caused by their inappropriate determinations of beam intensities or calculations of transmission efficiency. In a recent publication [31], similar systematic deviations between experimental cross sections from two$ ^{238} $ U+$ ^{9} $ Be experiments at RIKEN (reported in Refs. [15, 31]) have been pointed out.According to all of the above comparisons presented in Figs. 3 and 4 as well as our previous results, OES relations can be used for accurately calculating isotopic cross sections over a wide range of values, from several mb to 10
$ ^{-12} $ mb. Thus, they are likely to be very useful for reliable calculations of small cross sections of new isotopes close to their drip-lines. Further validation of these OES relations will be performed when more experimental data on cross sections (especially accurate ones) near drip-lines will become available. -
The OES magnitudes in production cross sections of exotic nuclei near the neutron drip-line, measured for two fragmentation reactions, i.e., 132 MeV/nucleon
$ ^{76} $ Ge+$ ^{9} $ Be [1] and 139 MeV/nucleon$ ^{82} $ Se+$ ^{9} $ Be [3], were calculated and compared with our previous OES evaluations. In general, the OES magnitudes in these experimental data were in a good agreement with our previous OES evaluations from accurate experimental data. New OES evaluations obtained in this work are recommended for some very exotic nuclei near the neutron drip-line, which were not studied in our previous studies. In addition, the OES relations proposed by us in Ref. [29] were validated by comparing with these experimental data. The comparison revealed that interpolation calculations using Eqs. (3) and (4) reproduced most of the experimental data within their uncertainties (typically above 40%), while extrapolation calculations using Eqs. (2) and (5) agreed with experimental data within a factor of 2. Finally, additional experimental cross sections from 345 MeV/nucleon$ ^{238} $ U+$ ^{9} $ Be [14, 15] were used for validating new OES evaluations and OES relations. All of the studies in this work indicate that new OES evaluations and OES relations can be employed for exotic isotopes near the neutron drip-line; thus, they are likely to be particularly useful for future experiments aimed at new isotopes.
Odd-even staggering for production cross sections ofnuclei near the neutron drip-line
- Received Date: 2021-04-13
- Available Online: 2021-08-15
Abstract: In our previous studies [Phys. Rev. C 97, 044619 (2018); Phys. Rev. C 103, 044610 (2021)], a universal odd-even staggering (OES) has been observed in extensive cross sections of isotopes not far from stability, measured for different fragmentation and spallation reactions. Four OES relations have been proposed on the basis of this OES universality. However, it is still unclear whether this OES universality and OES relations are applicable to many isotopes near the drip-lines. Here, the OES in recent experimental cross sections of very neutron-rich nuclei approaching the drip-line (from





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: