-
Based on the observation of 1.809 MeV γ-ray results from space detectors in the 1980s, a large amount (2–3
$ M_\odot $ ) of radionuclide 26Al has been proven to exist in the galaxy [1], which demonstrates that the nucleosynthesis processes of 26Al is currently active. Since 26Al has a half-life of$ 7.25 \times 10^5 $ yr, we can infer that it was produced in a relatively recent age. Since the thermonuclear reactions that generate 26Al require very high temperatures, the astrophysical sites that produced 26Al should be explosive or in the convective environment of Wolf-Rayet stars, which can eject the 26Al production into interstellar space. Today, the origin of 26Al in the galaxy has become a popular topic in nuclear astrophysics.Since the first observation of 1.809 MeV γ-rays by the HEAO-3 satellite in 1982 [2], many studies have achieved significant progress on this subject [3-11], and the results indicate that the main reaction to generate 26Al is 25Mg(
$ p,\gamma $ )26Al. The ground state of 26Al will decay to the excited state of 26Mg and the observed 1.809 MeV γ-ray results from the de-excitation process of the 26Mg excited state. A short-lived isomeric state with a half life of 6.35 s occurs at$ E_x $ = 228 keV in 26Al, which decays to the ground state of 26Mg without emitting 1.809 MeV γ-rays. Therefore, the ground state fraction$ f_0 $ of the 25Mg($ p,\gamma $ )26Al reaction must be considered in the study of interstellar 26Al.Interstellar 26Al is primarily generated from Mg-Al reaction cycles of hydrogen burning in massive stars. The proton capture reaction of Mg isotopes is crucial in the reaction cycle. The (
$ p,\gamma $ ) reaction on Mg is dominated by narrow resonances in the energy range from 50 to 350 keV. Their resonance strengths should be determined precisely in experiments to study their contribution to the interstellar 26Al production.In this article, we report the direct measurements of
$ ^{24,25,26} {\rm{Mg}}$ ($ p,\gamma $ ) reactions using the newly designed JUNA accelerator [12]. The resonance strengths and branching ratios of the E = 214 keV resonance in 24Mg($ p,\gamma $ )25Al, E = 304 keV resonance in 25Mg($ p,\gamma $ )26Al, and E = 326 keV resonance in 26Mg($ p,\gamma $ )27Al at the ground laboratory are measured. The experimental results provide references for Jinping deep underground experiments. -
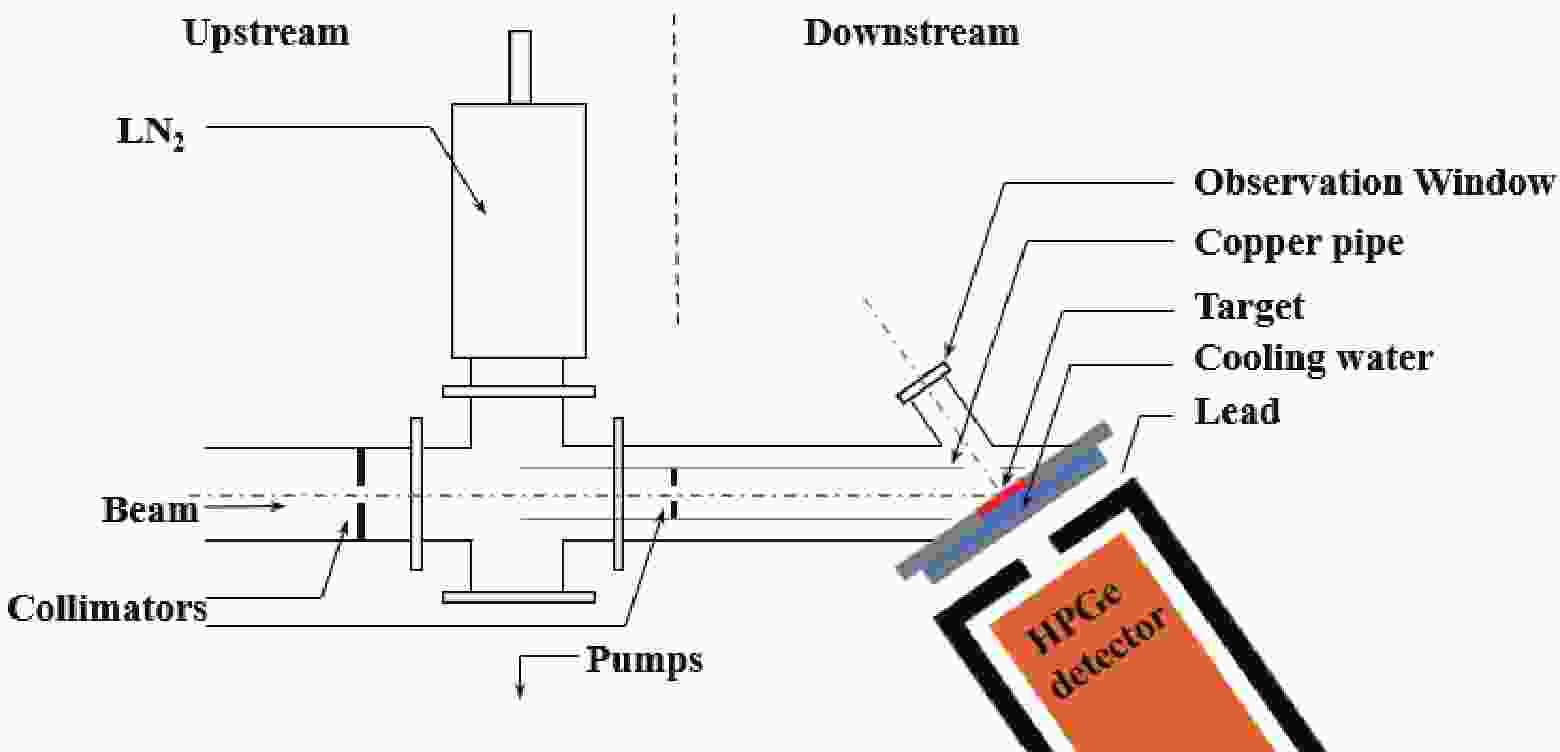
The experiment was conducted on the newly built high-current 400 kV accelerator [13] for the JUNA experiment, which was designed and manufactured at the China Institute of Atomic Energy in Beijing. The JUNA accelerator can supply high ion beams of H+ and He+ with a high current of 10 mA, or He2+ of 2 mA, for which the maximum energy is doubled to 800 keV. In this experiment, the proton capture reaction on magnesium isotopes was measured in the energy range of
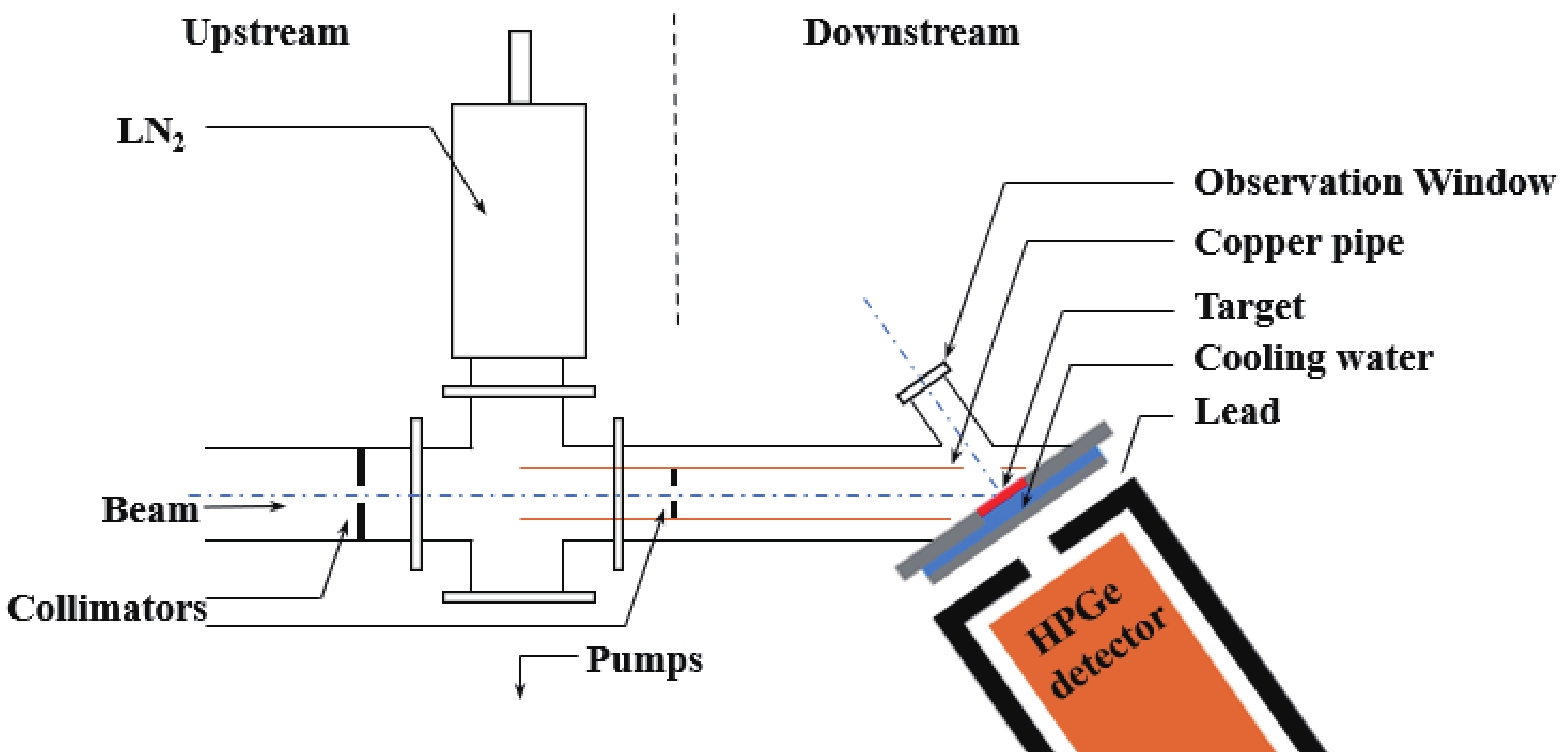
$ E_p $ = 220 - 400 keV. The experimental setup is shown in Fig. 1. The proton beam focused on the water-cooled target after passing through two collimators with diameters of 12 and 8 mm, respectively. A copper pipe was placed in front of the target and cooled using LN2 to minimize the carbon deposition on the target surface. A negative voltage of 300 V was applied to the copper pipe to gather the secondary electrons from the target. The voltage was optimized to obtain a maximum beam current.Compared with the traditional solid targets, the targets used in this experiment were improved by covering a Cr protective layer over the surface of the evaporated Mg targets. Cr is the hardest metal in nature. It oxidizes slowly and can protect a target when plated over its surface. Since the atomic number of Cr is significantly larger than that of Mg, the cross section of proton capture on Cr can be negligible compared with Mg. First, natural metal Mg was evaporated onto a 3 mm thick copper [14] to create an Mg target with a thickness of 40 μg/cm2. A Cr layer of 23 nm was then sputtered on the surface of the Mg target. This Cr-Mg-Cu structure target can effectively reduce the radiation damage, as indicated in Refs. [15, 16]. The radiation damage manifested as a change in the composition of the target and thus increased the uncertainty of the experimental results. For a narrow resonance reaction with consistent experimental conditions, the maximum yield is proportional to the effective stopping power; therefore, it is only related to the composition of the target. Figure 2 shows the yield plateau of the 25Mg(
$ p,\gamma $ )26Al reaction at the E = 304 keV resonance with and without a Cr protective layer. The composition of the target with a Cr layer remained basically unchanged under the radiation of 47.5 C proton beams, while the maximum yields of the target without a Cr layer decreased by approximately 10% under the radiation of 20.1 C proton beams. The protected target exhibited high durability against intense beams in the experiment to measure the low cross-section reaction.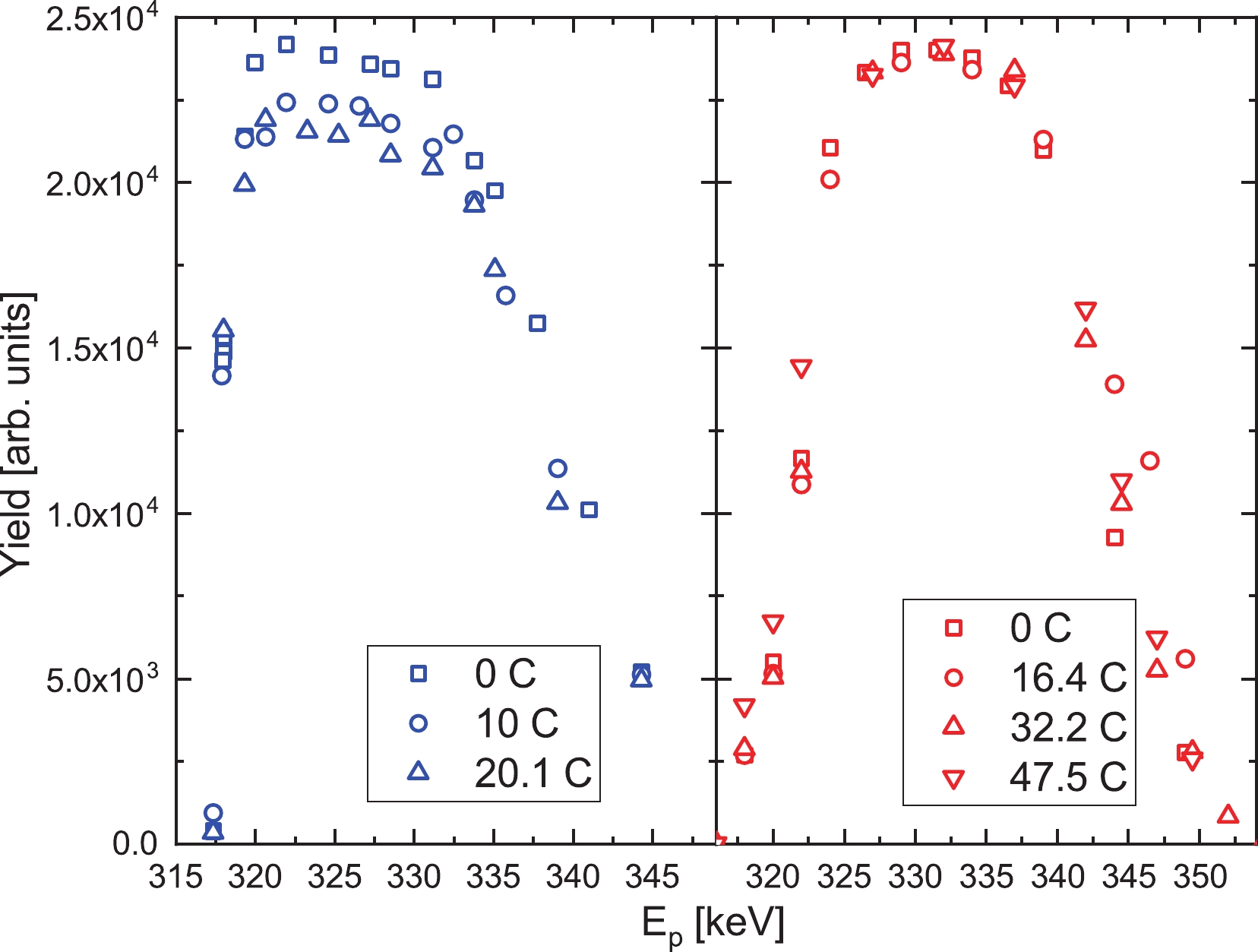
Figure 2. (color online) Yield curves obtained for the E = 304 keV resonance of 25Mg(
$ p,\gamma$ )26Al for the Mg target (left) and Cr-coated Mg target (right). The squares, circles, and triangles on the left represent the scan of the Mg target without a Cr layer after bombardment with 0, 10, and 20.1 C proton beams, and the squares, circles, positive triangles, and inverted triangles on the right represent the scan of the Cr-coated Mg target after bombardment with 0, 16.4, 32.2, and 47.5 C proton beams, respectively.The γ-ray spectra of this experiment were measured using an HPGe detector with a relative efficiency of 175% and a resolution of 2.1 keV at
$ E_\gamma $ = 1.3 MeV. The detector was placed at 55° with respect to the relative beam direction parallel to the target, the distance between the detector and the target was 25 cm, and the summing-effect was less than 1%. The detector was shielded with 5 cm thick lead planks, and the background could be reduced by almost an order of magnitude.The absolute efficiency of the HPGe detector was determined using a 56Co γ-ray source with an uncertainty of 1%. For high-energy γ-rays, the efficiency was calibrated using resonances of well-studied reactions, an E = 259 keV resonance of 14N(
$ p,\gamma $ )15O [17] and E = 315 keV resonance of 27Al($ p,\gamma $ )28Si [18]. The calibration encompassed an energy range from 0.8 to 10.1 MeV. The maximum γ-ray energy of the Mg isotope was 8.6 MeV, and all γ-rays from proton capture reactions on Mg isotopes were within the range of the energy calibration. In the calibration experiment, a TiN target and metal Al target produced through magnetron sputtering were bombarded with a proton beam of 300 μA. The efficiencies obtained by the reactions were determined from the known branching ratios and resonance strengths. Figure 3 shows the results of the absolute efficiencies of the HPGe detector. The uncertainties were primarily due to the uncertainty of the statistics, as well as the branching ratios and resonance strengths from 14N($ p,\gamma $ )15O [17] and 27Al($ p,\gamma $ )28Si [18] reactions. We also performed a Geant4 [19] simulation for the experimental setup, and the simulation results agreed closely with the experimental data within a 1% difference, and the total efficiency uncertainty was approximately 2%, deduced from the weighted average of all the experimental data. -
For a narrow resonance, the absolute resonance strength of the (
$ p,\gamma $ ) reaction is determined by the maximum thick-target yield$Y_{\rm max}$ , according to [20]$ Y_{\max} = \dfrac{\lambda^{2}}{2}b_{\gamma}\omega\gamma\dfrac{m_{\rm Mg}+m_{p}}{m_{\rm Mg}}\dfrac{1}{\varepsilon_{\rm eff}}\varepsilon(E_\gamma), $

(1) where λ,
$ b_{\gamma} $ ,$ \omega\gamma $ ,$m_{\rm Mg}$ ,$ m_{p} $ ,$\varepsilon_{\rm eff}$ , and$ \varepsilon(E_\gamma) $ represent the de Broglie wavelength at the resonance energy, branching ratio, resonance strength, masses of magnesium and proton, effective stopping power, and absolute efficiency at$ E_\gamma $ , respectively. Considering the main components of the target, the effective stopping power of Mg targets is expressed by$ \varepsilon_{\rm eff} = \dfrac{1}{X_{\rm Mg}} \left(\varepsilon_{\rm Mg} + \dfrac{N_{\rm O}}{N_{\rm Mg}}\varepsilon_O \right), $

(2) where
$X_{\rm Mg}$ is the relative isotopic abundance of stable magnesium isotope, and$N_{\rm O}$ and$N_{\rm Mg}$ are the number densities of oxygen and magnesium in the target, respectively. The values of$ {\varepsilon_{\rm{Mg}}} $ ,$ {\varepsilon_{\rm{O}}} $ , and$X_{\rm Mg}$ are provided in Refs. [21, 22].Evaporated Mg targets are expected to consist of a pure layer of magnesium; however, these targets are known to consist of the compound Mg5O owing to oxidization during target preparation [23]. In this study, the
$N_{\rm O}$ /$N_{\rm Mg}$ ratio was determined to be$ 21.3 \pm $ 2.0% by measuring the yield of the E = 189 keV resonance in the 25Mg($ p,\gamma $ )26Al reaction [16] and E = 143 keV resonance in the 18O($ p,\gamma $ )19F reaction [24] simultaneously using a$4 \pi $ BGO detector array and a 150 μg/cm2 25Mg target. The BGO detector was composed of eight identical BGO segments, each with a length of 25 cm and a radial thickness of 6.3 cm, covering a 45° azimuthal angle. The summing efficiency and energy resolution of the BGO array were 60% and 4% at 7 MeV under the temperature of −10 °C. As shown in Fig. 4, the summing energy spectrum of the 25Mg($ p,\gamma $ )26Al ($ E_{\gamma} $ = 6.5 MeV) and 18O($ p,\gamma $ )19F ($ E_{\gamma} $ = 8.1 MeV) reactions were reproduced using the Geant4 simulation. The uncertainties for the$N_{\rm O}$ /$N_{\rm Mg}$ ratio ($ \sim 10$ %) were due to the uncertainties of the resonance strengths of 18O($ p,\gamma $ )19F ($ \sim 6.5$ %) and 25Mg($ p,\gamma $ )26Al ($ \sim 6.7$ %), the geometric uncertainties of the BGO detector simulations ($ \sim 4$ %), and statistics ($ \sim 1$ %). The ratio supported the Mg5O structure of the target. Using the ratio and the abundance data, the effective stopping power values for proton in 24Mg, 25Mg, and 26Mg target at the resonance energies were deduced to be 22.3, 151.7, and 133.4 eV cm2 10-15 atoms, respectively. The uncertainties ($ \sim 3.7$ %) of these values resulted from the stopping power uncertainties ($ \sim 3.9$ %) [21] and the$N_{\rm O}$ /$N_{\rm Mg}$ ratio ($ \sim 10$ %).
Figure 4. (color online) γ-ray spectrum captured using a BGO detector at E = 189 keV resonance of 25Mg(
$ p,\gamma$ )26Al reaction ($ E_{\gamma}$ = 6.5 MeV) and E = 143 keV resonance of 18O($ p,\gamma$ )19F reaction ($ E_{\gamma}$ = 8.1 MeV). The blue dots and solid red line represent the measurement and Geant4 simulation, respectively.The 24Mg(
$ p,\gamma $ )25Al, 25Mg($ p,\gamma $ )26Al and 26Mg($ p,\gamma $ )27Al reactions were measured at$ E_p $ = 242, 330, and 354 keV, respectively, over an minimum charge integration of 10 C using a proton beam of approximately 2 mA. The γ-ray spectra of the measurements are shown in Figs. 5, 6, 7. The triple-line γ-ray sets in the figures denote the full-energy, single-escape, and double-escape peaks. Since the reaction yields measured in this experiment were relatively large, both resonance strength and branching ratio were accurately obtained even at a distance of 25 cm. Some natural and beam-induced γ-ray lines can be observed in the figures, such as 40K, 208Tl, and the reactions of 13C($ p,\gamma $ )14N and 19F($ p,\alpha\gamma $ )16O. They resulted from the adsorption of air by the target and reagent of the machining. These peaks had a slight effect in obtaining resonance strengths and branching ratios because of the high energy resolution of the HPGe detector. The dead time rate was less than 5%, which was corrected in the data analysis. In the measurement, the target composition was established with the yields of 24Mg($ p,\gamma $ )25Al at E = 214 keV before and after the measurement.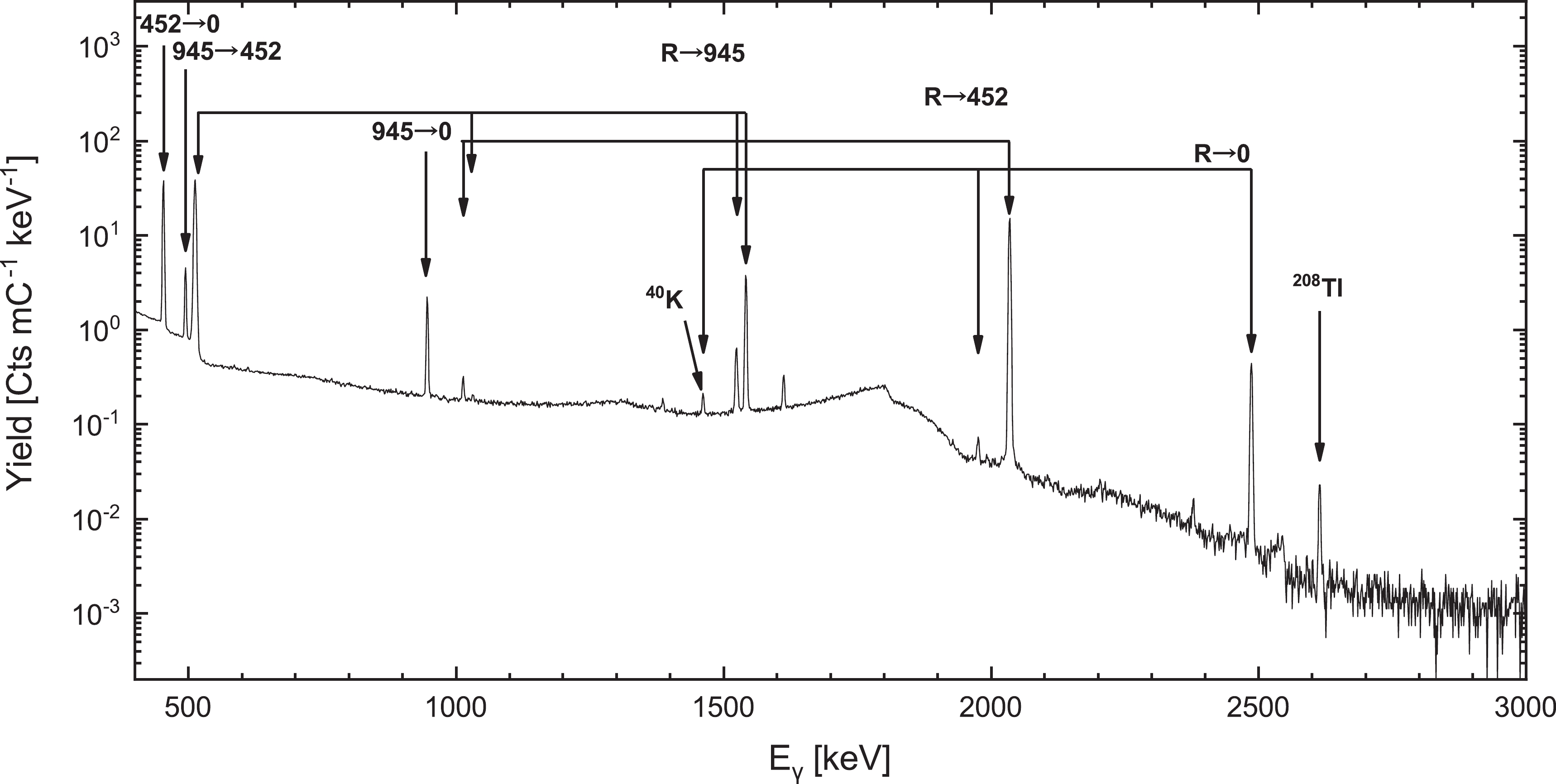
Figure 5. HPGe γ-ray spectra of 24Mg(
$ p,\gamma$ )25Al at E = 214 keV with accumulated proton beam of 12 C. All the primary transitions and secondary transitions are labeled.
Figure 6. HPGe γ-ray spectra of 25Mg(
$ p,\gamma$ )26Al captured at the E = 304 keV using an accumulated proton beam of 16 C. The primary transitions with a branching ratio greater than 2% and two important secondary transitions ($ 417 \rightarrow 0$ and$ 1057\rightarrow 228$ ) are labeled.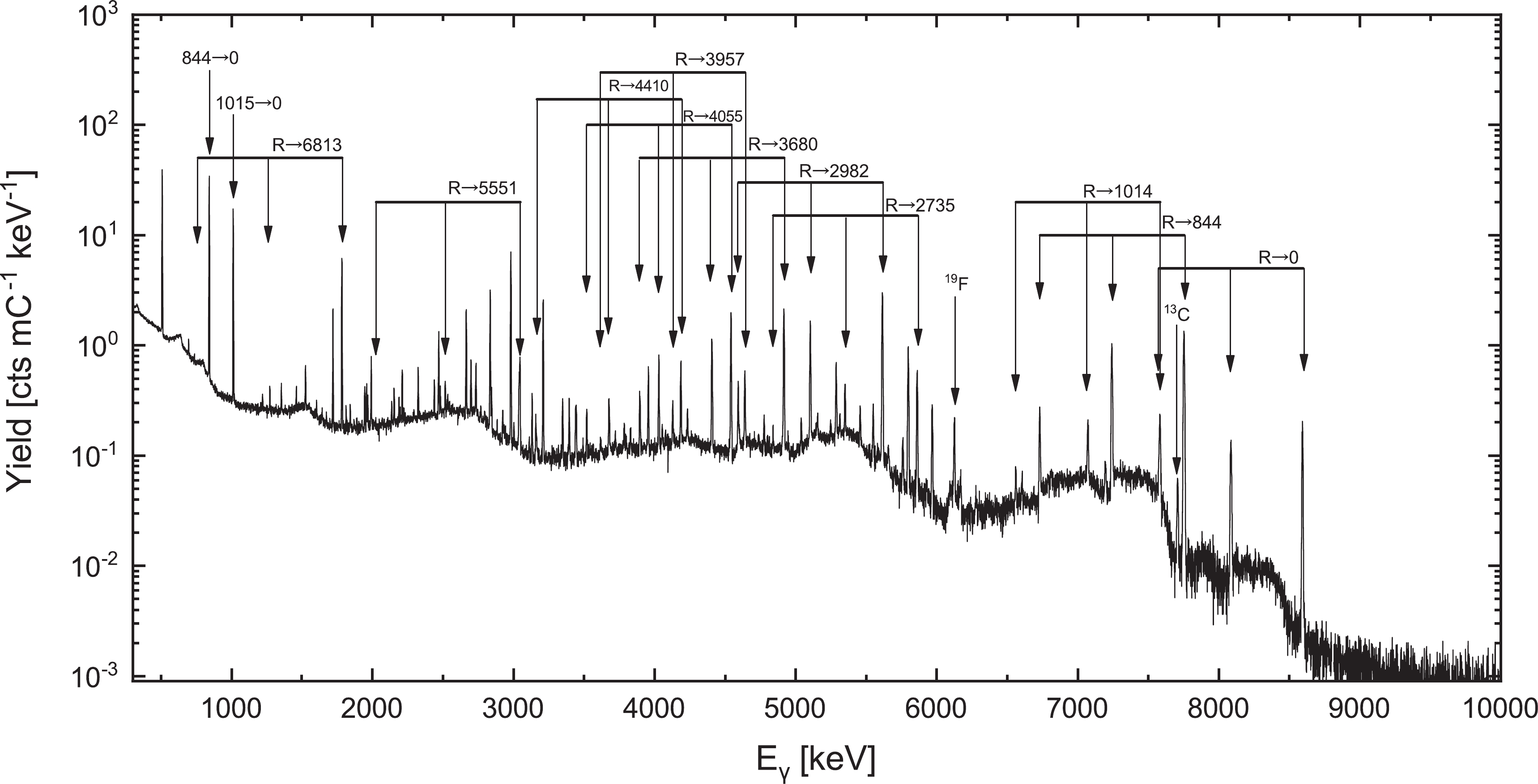
Figure 7. The HPGe γ-ray spectra of 26Mg(
$ p,\gamma$ )27Al at E = 326 keV using an accumulated proton beam of 10 C. The primary transitions with a branching ratio greater than 2% and an important secondary transition$ 844\rightarrow 0$ are labeled.The branching ratio of the primary γ-rays in the reactions can be calculated using
$ b_{\gamma}(i) = \dfrac{Y_{i}/\varepsilon(E_{\gamma_{i}})}{\displaystyle\sum_{i}^{} Y_{i}/\varepsilon(E_{\gamma_{i}})} , $

(3) where
$ Y_{i} $ is the yield for the ith γ-ray, and$ \varepsilon(E_{\gamma_{i}}) $ is the absolute efficiency of the corresponding primary γ-rays. The level energies for the compound nuclei were referenced from level diagrams of online nuclear data at the NNDC [25]. The peak area was extracted by fitting the spectra with a Gaussian distribution and linear background, and it was then used to determine the total yields with the Geant4 simulation. For the very weak and overlapped γ-ray lines, the simulation results were used to obtain the peak areas. By analyzing the energy spectra of three proton capture reactions on Mg target, the branching ratios for the 24Mg($ p,\gamma $ )25Al, 25Mg($ p,\gamma $ )26Al, and 26Mg($ p,\gamma $ )27Al reactions were extracted and listed as given in Tables 1, 2, and 3, together with other existing results. The results of this study were in agreement with the data from Refs. [15, 23, 26]. The ground state fraction$ f_{0} $ of the 25Mg($ p,\gamma $ )26Al reaction at 304 keV resonance was determined to be 85.9$ \pm 1.0$ % using our study's primary γ-ray branching ratio and the cascade branching ratio data from NNDC [25]. The value agreed with the value of Limata et al., (87.8$ \pm $ $ 1.2$ %) [15], and this indicated a more 26Al isomeric state production in the stellar Mg-Al reaction cycle.Table 1. Primary γ-ray branching ratios of the 24Mg(
$ p, $ $ \gamma$ )25Al E = 214 keV resonance from this and previous studies.$ E_{x}$ 

This study [15] [23] 5916 0.07 ± 0.02 0.09 ± 0.02 5726 0.09 ± 0.02 0.10 ± 0.01 0.12 ± 0.03 5457 0.15 ± 0.06 5396 0.24 ± 0.03 0.22 ± 0.02 0.35 ± 0.05 4940 0.12 ± 0.07 0.08 ± 0.01 4622 0.27 ± 0.11 0.28 ± 0.07 0.38 ± 0.06 4599 0.11 ± 0.03 0.12 ± 0.01 0.13 ± 0.04 4548 1.26 ± 0.08 1.30 ± 0.07 2.0 ± 0.1 4349 0.03 ± 0.01 4206 0.18 ± 0.04 0.25 ± 0.02 0.25 ± 0.05 4192 18.9 ± 0.3 19.1 ± 0.3 14.7 ± 0.8 3963 0.18 ± 0.03 0.17 ± 0.01 0.12 ± 0.05 3750 0.90 ± 0.05 0.92 ± 0.02 1.5 ± 0.1 3681 1.02 ± 0.05 1.09 ± 0.03 0.71 ± 0.08 3675 0.92 ± 0.13 0.86 ± 0.13 0.59 ± 0.06 3596 4.31 ± 0.20 4.29 ± 0.07 3.3 ± 0.2 3160 11.3 ± 0.05 11.4 ± 0.2 15.6 ± 0.9 3073 0.13 ± 0.05 0.11 ± 0.04 0.08 ± 0.05 2913 3.07 ± 0.14 3.04 ± 0.05 4.2 ± 0.3 2661 1.06 ± 0.06 1.00 ± 0.02 1.6 ± 0.1 2545 1.45 ± 0.03 1.46 ± 0.03 0.9 ± 0.1 2365 0.37 ± 0.05 0.47 ± 0.02 0.27 ± 0.07 2068.9 6.3 ± 0.1 6.0 ± 0.1 6.5 ± 0.4 1759 15.80 ± 0.3 16.1 ± 0.3 22.7 ± 1.3 417 31.71 ± 0.4 31.8 ± 0.5 24 ± 1.4 0 0.058 ± 0.004 Table 2. Primary γ-ray branching ratios of the 25Mg(
$p, $ $ \gamma$ )26Al E = 304 keV resonance from this and previous studies.$ E_{x}$ 

This study [15] [23] 7858 0.08 ± 0.03 0.09 ± 0.02 0.17 ± 0.03 7280 < 0.01 0.03 ± 0.01 7071 0.51 ± 0.04 0.30 ± 0.02 0.25 ± 0.02 6993 0.15 ± 0.02 0.17 ± 0.02 0.20 ± 0.02 6813 12.04 ± 0.13 12.1 ± 0.1 12.6 ± 0.7 6776 0.06 ± 0.02 0.06 ± 0.01 0.06 ± 0.02 6651 0.47 ± 0.02 0.45 ± 0.02 0.50 ± 0.04 6605 1.31 ± 0.03 1.26 ± 0.03 1.41 ± 0.09 6158 0.65 ± 0.03 0.71 ± 0.03 0.72 ± 0.05 6116 0.46 ± 0.02 0.44 ± 0.02 0.34 ± 0.04 6081 0.57 ± 0.03 0.59 ± 0.03 0.55 ± 0.05 5752 0.79 ± 0.05 0.80 ± 0.03 0.89 ± 0.06 5551 2.15 ± 0.05 2.07 ± 0.05 0.39 ± 0.03 5438 0.39 ± 0.04 0.22 ± 0.03 0.52 ± 0.04 5248 0.90 ± 0.04 0.94 ± 0.03 0.95 ± 0.06 5156 0.72 ± 0.03 0.71 ± 0.03 0.03 ± 0.02 4812 0.35 ± 0.02 0.54 ± 0.03 0.59 ± 0.05 4410 2.86 ± 0.09 2.96 ± 0.07 3.1 ± 0.2 4055 10.90 ± 0.1 10.9 ± 0.2 10.7 ± 0.6 3957 2.62 ± 0.07 2.64 ± 0.07 2.6 ± 0.2 3680 13.43 ± 0.2 14.5 ± 0.2 13.9 ± 0.8 2982 21.26 ± 0.2 19.7 ± 0.3 20.2 ± 0.1 2735 4.52 ± 0.1 4.43 ± 0.09 4.3 ± 0.3 1014 2.37 ± 0.1 2.04 ± 0.07 2.3 ± 0.2 844 18.28 ± 0.2 19.3 ± 0.3 20.2 ± 0.1 0 2.15 ± 0.04 2.06 ± 0.05 2.5 ± 0.2 Table 3. Primary γ-ray branching ratios of the 26Mg(
$p, $ $ \gamma$ )27Al E = 326 keV resonance from this and previous studies.Using the branching ratios determined in this study, the absolute resonance strengths ωγ could be obtained from the maximum thick-target yield using Eq. (1). The resonance strengths of E = 214 keV in 24Mg(
$ p,\gamma $ )25Al, E = 304 keV in 25Mg($ p,\gamma $ )26Al and E = 326 keV in 26Mg($ p,\gamma $ )27Al determined in this and other studies are listed in Table 4. The uncertainties of the our results were due to the uncertainties in the statistics ($ \sim 1$ %) in HPGe measurement, efficiency calibration ($ \sim 2$ %), effective stopping power ($ \sim 3.7$ %), and charge integration ($ \sim 2$ %).Table 4. Absolute resonances strengths of proton capture reaction in magnesium isotopes.
For the E = 214 keV resonance in the 24Mg(
$ p,\gamma $ )25Al reaction, the$ \omega\gamma $ = 11.5 ± 0.5 meV was determined in this study, and the value was in agreement with the data from the previous studies [15, 26-28]. We recommend a resonance strength of$ \omega\gamma $ = 11.3 ± 0.5 meV for the 24Mg($ p,\gamma $ )25Al 214 keV resonance using the method of weighted average [29]. The resonance strength of 25Mg($ p,\gamma $ )26Al at E = 304 keV was determined to be 31.2 ± 1.5 meV, which closely agreed with the NACRE value [28] and the results reported in Refs. [15, 23, 30, 31] but with a small uncertainty. Based on the results, we recommended a value of$ \omega\gamma $ = 31.0 ± 1.0 meV for the resonance strength. For the resonance strength of E = 326 keV in 26Mg($ p,\gamma $ )27Al, this study indicated a resonance strength of$ \omega\gamma $ = 279 ± 13 meV, which was consistent with the value reported in Refs. [15, 32] within error bars but much smaller than the earlier NACRE compilation value [28] from the very earlier studies [23, 33-37]. Therefore, after discarding the questionable threefold higher values [34-37], we recommend a resonance strength of$ \omega\gamma $ = 274 ± 8 meV for the 26Mg($ p,\gamma $ )27Al 326 keV resonance. -
In this study, we precisely measured the resonance strengths and branching ratios for the reactions 24Mg(
$ p,\gamma $ )25Al, 25Mg($ p,\gamma $ )26Al, and 26Mg($ p,\gamma $ )27Al at 214, 304, and 326 keV, respectively, using the newly built JUNA accelerator at the ground laboratory. Through the protection of a Cr layer sputtered on the surface of Mg target, the radiation protection capability of the target was significantly improved. This avoided the change in target composition caused by radiation and reduced the experimental uncertainties. Compared with previous experiments, we increased the precision of the resonance strengths.The success of this experiment has provided an overall systematic calibration for the planned underground JUNA experiment. We also present the recommended resonance strengths of 11.3 ± 0.5 meV for the 24Mg(
$ p,\gamma $ )25Al reaction at E = 214 keV, 31.0 ± 1.0 meV for the 25Mg($ p,\gamma $ )26Al reaction at E = 304 keV, and 274 ± 8 meV for the 26Mg($ p,\gamma $ )27Al reaction at 326 keV based on the results of this and other recent studies. The results provide more accurate inputs for the Mg-Al cycle network calculations. In the near future, the direct measurement of resonance strength of 92 and 189 keV in the 25Mg($ p,\gamma $ )26Al proton capture reaction will be performed by using the underground JUNA accelerator.
Direct measurement of the resonance strengths and branching ratios of low-energy (p, γ) reactions on Mg isotopes
- Received Date: 2021-04-17
- Available Online: 2021-08-15
Abstract: Proton capture reactions on Mg isotopes are significant in the Mg-Al cycle in stellar H-burning. In particular, the resonance strengths and branching ratios of low-energy resonances in 25Mg(





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: