-
Recently, both experimental and theoretical fields have witnessed a huge growth in research on spallation reactions, ever since the spallation neutron source proved to be a powerful tool in research and applications [1, 2]. In terms of social and ecological impact, spallation reactions are at the heart of the transmutation of long-lived radiotoxic nuclear waste, whose half-life can be drastically shortened to an acceptable scale of hundreds of years via fast fission induced by neutrons. At the same time, this process generates enough energy to supply the electric grid and sustain the facility itself [3-9]. In space missions, preflight assessments on the damaging effects on astronauts and electronic parts must be undertaken with spallation models [10] in order to ensure the success of a space flight. In astrophysics, spallation cross-section is a key input in the evaluation of the propagation of cosmic rays both in the atmosphere and in inter-stellar media [11-13]. In material science, neutrons produced by spallation neutron sources are used to probe the properties of condensed matter [14, 15]. Other applications include the production of rare isotopes [16-19], cancer therapy [20-22], uses in biology [11], and cosmography [23]. Because of the diversity of the applications, as mentioned above, the broad range of reaction conditions, including variations in beam energy and target size, and the complicated reaction mechanisms that spallation reactions entail, great challenges have been imposed on the experimental measurements of the yields and kinematics of spallation products, on the calculation of related observables, and on the theoretical understanding of the underlying mechanisms through which the spallation products emerge. For a comprehensive review on these subjects, we refer the readers to Refs. [24, 25].
Conventionally, spallation reactions are described by a two-step model, as was first envisaged by Seber [26]. In view of this picture, in the first stage, an incident light nucleus with energies from hundreds of MeV to several GeV induces a cascade of collisions through a series of hadron-hadron collisions within a target much heavier than the incident projectile. This process has a momentary duration of only tens of fm/c, in which the incident energy is partly emitted in the form of high energy ejectiles, pions, nucleons and light-charged-particles with
$ Z \le 4 $ (LCPs), for instance, while the remaining part is deposited during the process thermalizing the target nucleus. The latter are often excited to hundreds of MeV along with a rather low angular momentum, typically 20$\hbar $ on average. The first stage is a fast dynamical process, whereas the second stage is a statistical one and several orders of magnitude longer in duration than the first stage. During the second stage, random fluctuations in the distribution of energy and nuclear density multiply locally or globally, respectively, leading the compound nucleus to undergo light particle evaporation or fission sequentially, until all products are fully deexcited. In light of these considerations, very practical numerical codes based on the ideas of intranuclear cascades plus statistical decay have already been developed [27] and improved [28]. They are capable of reproducing both the yields and kinematics of some reaction products to an appreciable accuracy, in particular for spallation reactions at incident energies no lower than 200 MeV. However, in theoretical terms, as pointed out and discussed in Refs. [29-31], more sophisticated reaction mechanisms beyond a simplistic two-step model are required in order to account for the production of intermediate-mass-fragments (IMFs) characterized by experimentally revealed triple-humped kinematics in the velocity distributions [32]. Therefore, these features were studied by introducing the deexcitation mode of multifragmentation through intranuclear-cascades plus statistical-multifragmentation model (INC+SMM) [31] or more sophisticated models, such as the Boltzmann-Langevin-one-body (BLOB) [33] or the quantum-molecular-dynamics model (QMD) [34]. Constant efforts with the goal of improving the description of spallation reactions have served as a major boost towards the improvement of theoretical models for nuclear reactions.On the application side, particularly in the design of the shielding of spallation facilities and astronautical equipment, the energy spectra of LCPs at all angles in spallation reactions are vital information [10], and when experimental data are not available, theoretical simulations become indispensable. In microscopic transport models of nuclear reactions, one approach for treating the pre-equilibrium emission of LCPs and give a reliable account of the double-differential-cross-sections (DDXs) at all angles is a modification of the transport model through incorporating a coalescence mechanism near the target surface for the entire time evolution. This kinematical treatment was first discussed by Goldberger [35] and Metropolis [36] and later modified by Nagle [37] and Mattiello et al. [38]. Nowadays, this mechanism has been implemented in INCL [39-42], QMD [43, 44], and the coalescence exciton model [45], for the refinement of the description of LCPs production in these models. Apart from the abovementioned, particle production and emission in spallation reactions can also be accounted for via alternative approaches, see Ref. [46].
This paper is organized as follows. Sec. II is a brief description of the models employed in this work. Sec. III presents the results of our calculations. Sec. III.A is devoted to a discussion on the reproduction of total yields of spallation fragments under various conditions, and the results are compared with those of previous studies. In Sec. III.B and Sec. III.C, the DDXs of LCPs and neutrons are presented and discussed, which is followed by a brief summary in Sec. IV.
-
The Lanzhou-quantum-molecular-dynamics (LQMD) model [47-49] is employed in this work, wherein the motion of individual nucleons is parameterized into Gaussian wave packets in both coordinate space and momentum space
$ \begin{aligned}[b] \phi_{i}({{r}}, t) =& \frac{1}{(2\pi \sigma_{r}^{2})^{3/4}} {\rm{exp}} \left[-\frac{({{r}}-{{r}}_{i}(t))^{2}}{4\sigma_{r}^{2}} \right] \\ & \times {\rm{exp}}\left(\frac{{\rm i}{{p}}_{i}(t)\cdot{\bf{r}}}{\hbar}\right), \end{aligned} $

(1) where
$ {{r}}_{i}(t) $ and$ {{p}}_{i}(t) $ are the centers of the wave packets in coordinate space and momentum space, respectively. The width of a packet depends on the parameter$ \sigma_{r} $ . These are the parameters to be solved by subjecting the following total wave function of the reaction system to the variational method [50]$ \Phi\big({{r}},t\big) = \prod\limits_{i}\phi_{i}\big({{r}},{{r}}_{i},{{p}}_{i},t\big). $

(2) Neglecting changes in the packet width parameter
$ \sigma_{r} $ over time and setting them as constants, the equations of motion of the wave packet parameters$ {{r}}_{i}^{,} \ s $ and$ {{p}}_{i}^{,} \ s $ are obtained formally as$ \dot{{{r}}_{i}} = \frac{\partial H}{\partial {{p}}_{i}}, \quad \dot{{{p}}_{i}} = -\frac{\partial H}{\partial {{r}}_{i}}, $

(3) together with the density-functional Hamiltonian, which is evaluated by the skyrme interaction in its operator form between the parameterized wave function,
$ \begin{aligned}[b] H =& <\Phi|\hat{H}|\Phi> \\=& T+U_{\rm Coul}+\int V_{\rm loc}\big[\rho({{r}})\big] {\rm d} {{r}} +U_{\rm MDI}, \end{aligned} $

(4) where
$ U_{\rm Coul} $ is the Coulomb energy of the whole system and$ V_{\rm loc} $ is the nuclear potential energy density which is evaluated through the Wigner transformation [51], and takes the form$ \begin{aligned}[b] V_{\rm loc}(\rho) =& \frac{\alpha}{2}\frac{\rho^{2}}{\rho_{0}} +\frac{\beta}{1+\gamma} \frac{\rho^{1+\gamma}}{\rho_{0}^{\gamma}} + E_{\rm sym}^{\rm loc}\big(\rho\big)\rho\delta^{2} \\ &+ \frac{g_{\rm sur}}{2\rho_{0}}\big(\nabla\rho\big)^{2} + \frac{g_{\rm sur}^{\rm iso}}{2\rho_{0}}\Big[\nabla(\rho_{n}-\rho_{p})\Big]^{2}, \end{aligned} $

(5) where
$ \begin{aligned}[b] \rho({{r}},t) =& \int f({{r}}, {{p}}, t){\rm d}{{p}} \\ =& \sum\limits_{i} \frac{1}{(2\pi \sigma_{r}^{2})^{3/2}} {\rm{exp}} \left[-\frac{({{r}} - {{r}}_{i}(t))^{2}}{2\sigma_{r}^{2}}\right], \end{aligned} $

(6) $ \begin{aligned}[b] f({{r}},{{p}},t) =& \sum\limits_{i} f_{i}({{r}},{{p}},t) \\=& \sum\limits_{i} \frac{1}{(\pi \hbar)^{3}} {\rm{exp}} \left[-\frac{({{r}} - {{r}}_{i}(t))^{2}}{2\sigma_{r}^{2}} - \frac{({{p}} - {{p}}_{i}(t))^{2}\cdot 2\sigma_{r}^{2}}{\hbar^{2}}\right], \end{aligned} $

(7) and
$ U_{\rm MDI} $ appearing in Eq. (4) is the momentum dependent interaction term (MDI) [52] and assumes the form$ \begin{aligned}[b] U_{\rm MDI} =& \frac{1}{2\rho_{0}}\sum\limits_{i,j,j\neq i}\sum\limits_{\tau,\tau'}C_{\tau,\tau'}\delta_{\tau,\tau_{i}}\delta_{\tau',\tau_j}\int\int\int {\rm d}{{p}}{\rm d}{{p}}'{\rm d}{{r}} \\ & \times f_{i}({{r}},{{p}},t)\left[{\texttt{ln}}(\epsilon({{p}}-{{p}}')^{2}+1)\right]^{2}f_{j}({{r}},{{p}}',t). \end{aligned} $

(8) The coefficients of each term are the mean-field parameters constrained by reproducing the basic saturation properties and the incompressibility within a sensible range for symmetric nuclear matter. Two sets of mean-field parameters, labelled PAR1 and PAR2, are used in the calculations, as given in Table 1, along with their incompressibilities. In the MDI term,
$ C_{\tau, \tau^{'}} = C_{\rm mom}(1+x) $ for$ \tau = \tau^{'} $ and$ C_{\tau, \tau^{'}} = C_{\rm mom}(1-x) $ for$ \tau\neq\tau^{'} $ , where the subscripts τ and$ \tau^{'} $ stand for isospins whose values are –1 and 1, respectively, and the parameter$ x = -0.65 $ is the strength of the isospin splitting. In the isospin asymmetric terms,$ \rho_{n} $ ,$ \rho_{p} $ , and$ \rho = \rho_{n}+\rho_{p} $ are the neutron, proton, and total densities, respectively, and$ \delta = (\rho_{n}-\rho_{p})/ $ $ (\rho_{n}+\rho_{p}) $ is the isospin asymmetry. The coefficients in the isospin-dependent and density-gradient-dependent terms$ g_{\rm sur} $ ,$ g_{\rm sur}^{\rm iso} $ , and$ \rho_{0} $ are set to 23 MeV fm2, –2.7 MeV fm2, and 0.16 fm-3, respectively.$ \alpha \ /{\rm{MeV}} $ 

$ \beta \ /{\rm{MeV}} $ 

$ \gamma $ 

$ C_{\rm mom} \ /{\rm{MeV}} $ 

$\epsilon \ /({ {\rm{c} }^{\rm{2} } }{\rm{/Me} }{ {\rm{V} }^{\rm{2} } })$ 

$ m^{*}_{\infty}/m $ 

$ K_{\infty} \ /{\rm{MeV}} $ 

PAR1 -226.5 173.7 1.309 0. 0. 1. 230 PAR2 -215.7 142.4 1.322 1.76 $ 5 \times 10^{-4} $ 

0.75 230 Table 1. Skyrme parameters PAR1 and PAR2 used in the LQMD model.
In addition to motions under the nucleons' mean field, collisions between nucleons are another key ingredient in the time evolution of the reaction system. In the simulation, when the spacial separation of any two nucleons in their center-of-mass frame is smaller than a value
$ r_{NN} = \sqrt{\sigma_{NN}(\sqrt{s})/\pi}, $

(9) a collision between the two nucleons is considered, where
$ \sigma_{NN}(\sqrt{s}) $ is the total nucleon-nucleon (NN) scattering cross-section for the invariant mass$ \sqrt{s} $ . The NN elastic scattering cross-section is parameterized to fit the experimentally available data over a wide energy domain [53]. Finally, taking into account the effects of Pauli-blocking due to the fermionic properties of nucleons, it is deceided to either execute a collision or block it by comparing the blocking probability$ 1-(1-F_{i})(1-F_{j}) $ of the two participant nucleons i and j in the final state with a random number; here, the occupation probability$ F_{i} $ is evaluated as$ F_{i} = \frac{2}{h^{3}}\sum\limits_{k\neq i, \tau_{i} = \tau_{k}} O_{ik}^{(x)}O_{ik}^{(p)}, $

(10) where
$ O_{ik}^{(x)} $ and$ O_{ik}^{(p)} $ refer to the overlaps of two hard spheres centered at the wavepacket centroids of the nucleons i and k in coordinate space and momentum space, respectively. In our model, a common pair of radii of$ R_{x} = 3.367 $ fm in coordinate space and$ R_{p} = 112.5 $ MeV/c in momentum space is assigned to the hard spheres of all nucleons. -
At the end of the dynamical evolution when all violent changes have settled and the nucleons are re-aggregated and condensed in the form of individual clusters, a procedure called minimum spanning tree (MST) is used to identify these hot remnants before the transition to statistical decay. In the LQMD model, a constituent nucleon can incorporate a neighboring nucleon of relative momentum and location
$ \Delta p \leqslant 200 $ MeV/c and$ \Delta r \leqslant 3.5 $ fm into a pre-cluster, provided that this new nucleon is also located close to the surface of the cluster within the constraint of a root-mean-square radii. Also, two neighboring pre-clusters can join to form a bigger cluster, if the size of the newly formed cluster is within a limit, which is incorporated as the liquid-drop-model radius.After the hot remnants are reconstructed, the simulation proceeds to the next stage, cooling down by statistical decay. Statistical decay is realized by the GEMINI code [54]. Generally, in the GEMINI code, a compound nucleus experiences a sequence of binary divisions in the form of light particle evaporation or fission until the compound nucleus is thoroughly deexcited. For asymmetric divisions, as for the emission of light particles with Z up to 4, the Hauser-Feshbach formulism is adopted [55], and the decay width of an emitted light particle
$ (Z_{1},A_{1}) $ of spin$ J_{1} $ from a mother nucleus$ (Z_{0},A_{0}) $ of excitation energy$ E^{*} $ and$ J_{0} $ , leaving behind a residue$ (Z_{2},A_{2}) $ of spin$ J_{2} $ , is given by$ \Gamma_{J_{2}}(Z_{1},A_{1}, Z_{2},A_{2}) = {\frac{2J_{1}+1}{2\pi \rho_{0}}} \sum\limits_{l = |J_{0}-J_{2}|}^{J_{0}+J_{2}} \int_{0}^{E^{*}-B-E_{\rm rot}(J_{2})} T_{l}(\epsilon)\rho_{2}{\rm d}\epsilon, $

(11) where
$ \rho_{0} $ and$ \rho_{2} $ are the level densities of the mother and the residual nucleus, respectively, and$ T_{l}(\epsilon) $ is the transmission coefficient. B is the binding energy between the light particle and the residue, and$ E_{\rm rot}(J_{2}) $ is the rotation plus deformation energy of the latter. For asymmetric fission, Moretto's generalized transition-state formalism [56], which determines the fission probability via the phase space density on a ridge line made up of saddle points, is used. For symmetric fission, which is an available option in the code's input, the Bohr-Wheeler formalism [57] is used. Fission barrier heights are mainly calculated through the rotating-finite-range model [58] and both shell and pairing corrections are also considered. Regarding the QMD-GEMINI study of the deexcitation of highly excited nuclei formed in heavy-ion collisions, see Ref. [59] for recent progress. -
For a better description of pre-equilibrium cluster emission, we incorporated the surface coalescence model into the LQMD model following the specifications given in Ref. [39]. When an outgoing nucleon trespasses a certain radial distance
$ R_{0} + D_{0} $ with respect to the center of the mother nucleus, a recursive construction of LCPs from this leading nucleon is initiated by picking up a first nucleon, a second and a third and so on. Here,$ R_{0} = 1.4A_{\rm targ}^{1/3} $ fm, and for the proton incident energies involved,$ D_{0} $ is set to the proper value of 2 fm. In our work, the emissions of all light charged particles with Z up to 4 and A up to 8 are considered. During the process, a pre-cluster picks up a nucleon for the formation of higher clusters according to the following phase space condition:$ R_{Nj} P_{Nj} \leqslant h_{0}, \quad R_{Nj} \geqslant 1 \;{\rm fm} ,$

(12) where
$ R_{Nj} $ is the spatial distance between the pre-cluster N and nucleon j to be picked up, and$ P_{Nj} $ is the relative momentum between these two objects. Let$ {{R}}_{N} $ and$ {{r}}_{j} $ be the position of the pre-cluster and the nucleon in coordinate space, respectively,$ {{p}}_{N} $ and$ {{p}}_{j} $ the momenta, and$ M_{N} $ and$ m_{j} $ the masses of the two objects. Then, they have the following form:$ \begin{aligned}[b] R_{Nj} =& {\big|{{R}}_{N} - {{r}}_{j}\big|}, \\ P_{Nj} =& {\Big|\frac{m_{j}}{M_{N} + m_{j}}{{p}}_{N} - \frac{M_{N}}{M_{N} + m_{j}}{{p}}_{j}\Big|}. \end{aligned} $

(13) The latter is in fact the momentum of either object in their common center-of-mass frame. Though various refinements are available regarding the choice of phase space parameter
$ h_{0} $ , for simplicity, for$ A_{\rm lcp} \leqslant 4 $ we adopted those used in Ref. [39] and Ref. [40], which we labeled as Set 1 and Set 2, as listed in Table 2, while for$ A > 4 $ , the following ansatz, which was proposed in Ref. [28], is used:Construction $ h_{0} $ / (fm MeV/c)

Set 1 Set 2 $ p + n \rightarrow d $ 

387 336 $ d + n \rightarrow t $ 

387 315 $ d + p \rightarrow ^{3} {\rm{He}}$ 

387 315 $ t + p \rightarrow ^{4} {\rm{He}}$ 

387 300 3He $ + n \rightarrow ^{4} {\rm{He}}$ 

387 300 Table 2. Suface coalescence parameters of Set 1 and Set 2.
$ h_{0} = h_{1}(A_{\rm lcp}/5)^{1/3}, $

(14) where
$ h_{1} = 359 $ fm MeV/c. When all possible combinations of background nucleons and the leading nucleon are listed, an emission test is performed according to a hierarchy based on the particle numbers of the clusters. More specifically, a particle is randomly selected from among all others with$ A_{\rm lcp} = 8 $ , and a test is performed to see if its total energy under the target mean field lead to its penetration through the Coulomb plus Woods-Saxon barriers. If the candidate passes the test, it is emitted along its tangential direction and the time evolution of the reaction system is resumed. Otherwise, a cluster of lower$ A_{\rm lcp} $ is selected in the same way and tested and so on. If all tests fail, the penetration test is performed on the leading nucleon to decide whether it is emitted or reflected. The total energy of all emission candidates is calculated according to the following equation:$ E_{\rm lcp} = \sum\limits_{i = 1}^{A_{\rm lcp}} (E_{i} + V_{i}) + B_{\rm lcp}, $

(15) where
$ E_{i} $ and$ V_{i} $ are the kinetic energy and the potential energy of the constituent nucleon i under the target mean field,$ B_{\rm lcp} $ is the binding energy of the cluster, and$ A_{\rm lcp} $ is the mass number of the cluster. Last but not least, in the procedure stated above, all clusters constructed must be appropriately far away from the center of the target nucleus such that they are clusters formed near the target's surface.$ R_{l} $ measures this distance, which is taken to be$ R_{l} = CA_{\rm targ}^{1/3}. $

(16) If C is too small, a too rich production of clusters results and vice versa. More details are given in a brief discussion in the corresponding section.
-
For any one reaction system in this calculation, the maximum impact parameter
$ b_{\rm max} $ is chosen as$ b_{\rm max}^{'}+0.3 $ fm, where$ b_{\rm max}^{'} $ is the smallest impact parameter at which the target no longer suffers from nucleon-nucleon collisions with incident protons passing by. An additional 0.3 fm is reserved for Coulomb excitation. In addition to the maximum impact parameter, the switching time from the dynamical stage to the statistical stage is a determining factor for the reliable reproduction of realistic physical circumstances. In INC simulation, this quantity is given by an established formula [27]. However, in our case this is not proper for the QMD simulation as our model is capable of describing the evolution after the system has been fully excited. The criterion we adopted for selecting the switching time is such that after that moment of time, all observables in question have to be relatively stable in time after the end of the violent fluctuations of the preceding dynamical evolution. Furthermore, during the pre-equilibrium cascade process, nucleon and clusters emitted in the forward direction were generated in an earlier stage, whereas those in the backward direction emerged in a later stage. Because of this, the pre-equilibrium time span must be long enough to cover emissions at all polar angles. Considering all these complications and to reduce CPU time, we set the switching times of$ p + ^{56} {\rm{Fe}}$ and 58Ni as 65 fm/c, those of 112Cd and 107Ag as 85 fm/c, and those of 181Ta, 184W, and 208Pb as 115 fm/c. -
Before discussing LCPs emission, we first restrict our attention to the total yields of spallation fragments in two reaction systems, namely
$ p + ^{56} {\rm{Fe}}$ and$ p+^{208} {\rm{Pb}}$ , both at 1 GeV, as a preparatory step and compare the results with experiments. This is not trivial, as one must guarantee that the overall picture of the process can be correctly reproduced before actually being able to describe the details of the process. For this purpose, instead of an extensive study on fragment yields, in this subsection, only two representative results are presented.We start with a light and well-studied reaction system,
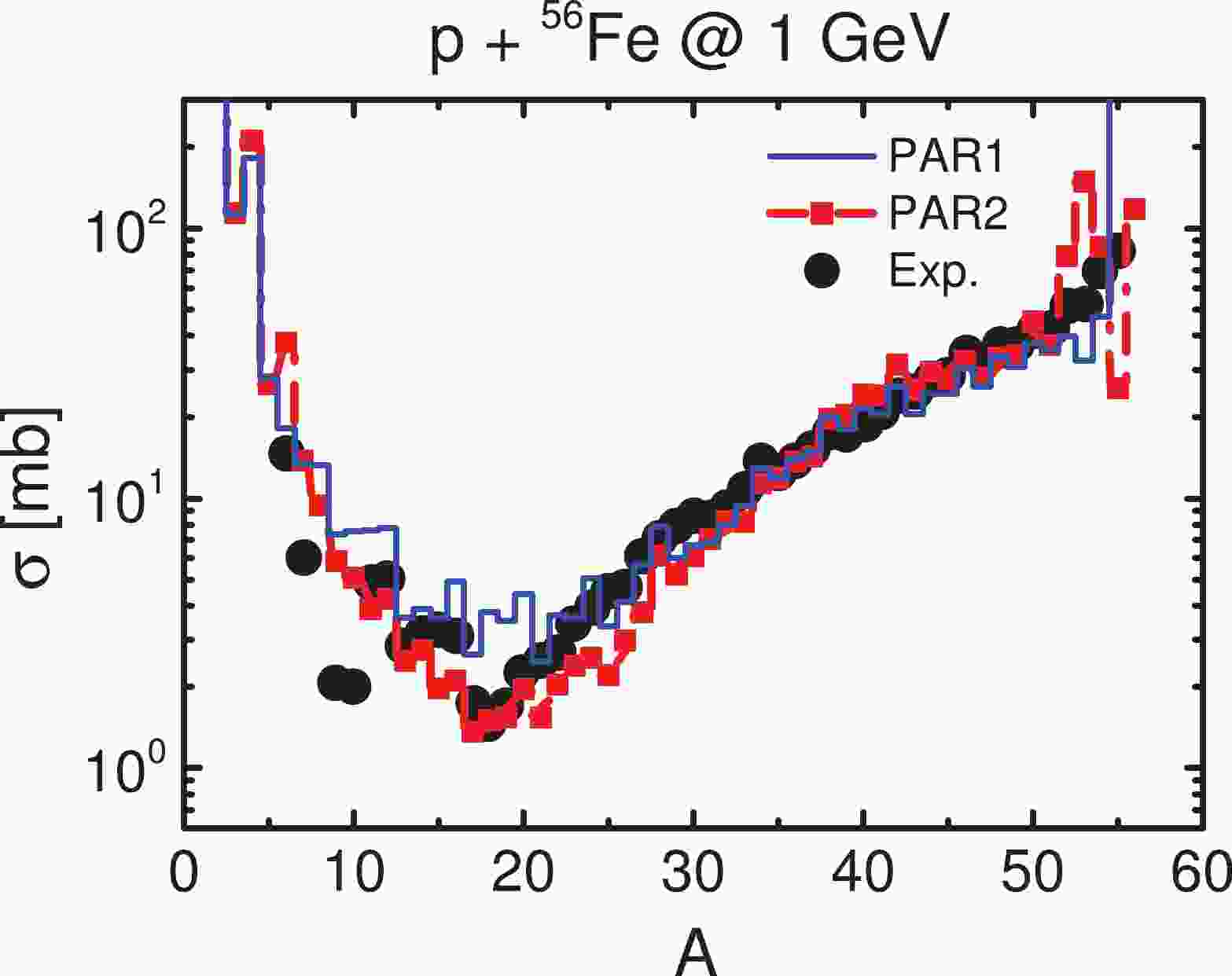
$ p + ^{56} {\rm{Fe}}$ at 1 GeV, and the results of our model are shown in Fig. 1. It can be seen that the experimental results [60] are well reproduced under either momentum dependent or independent mean fields both in terms of trend and values to some extent. Contrary to the conventional conception, however, IMFs yields turn out to be overestimated on an overall scale without MDI, at the cost of an underestimation of the target-like tail. Nevertheless, the local trends are the same for both settings. The differences between the results of the two mean fields may be understood by considering that in the calculation with MDI, the IMFs formed during the reaction are more unstable due to more violent fluctuations, which is caused by the repulsive nature [61] of the MDI at high temperature or high nucleon-nucleon relative momentum, and thus, more nucleons and fewer IMFs are emitted compared with the case without MDI. For a detailed analysis on the experimental data and the results of the INC calculations on IMFs production using the same reaction system, see Ref. [31].
Figure 1. (color online) Calculated total fragment yield as a function of mass number for
$ p+^{56} {\rm{Fe}}$ at an incident energy of 1 GeV. The step line in blue denotes the result obtained with PAR1, the set of parameters without MDI is displayed in Table 1, while the red line denotes the one with PAR2, the set of parameters with MDI. The experimental data are taken from Ref. [60].In the preceding discussion, a light target,
$ ^{56} {\rm{Fe}}$ , was considered. In the next discussion, we focus on another extreme, high-energy proton induced spallation reaction at the same energy but on a very heavy target, 208Pb, for which more pronounced divergences between simulations with and without momentum dependent interactions are expected, as the fission process starts to play a key role. In Fig. 2, the total cross-section plotted as a function of both the atomic number Z and the mass number A is presented. The black dots represent the experimental data which are taken from Ref. [62], the red line represents the calculations with MDI, and the blue line represents the calculations without MDI. It can be seen that above all, calculations with and without MDI both reproduce the main trend and the main features of the experimentally measured spectra. However, it is apparent that the results without MDI give a much better overall fit to the data, whereas the results with MDI peak too early at the target-like end in the plot versus the mass number. This is accompanied by an overestimation in the region between the target-like end and the valley in the middle of the graph. This is due to the spurious emission of nucleons in the presence of MDI, which always tends to induce more fluctuations. As a result, the fission peak is underestimated, as the very target-like residues, which possess lower fission barriers and are thus more likely to experience fission, were less common compared with the results without MDI. To conclude this discussion, let us make one more final comment on the results of the case without MDI. In the statistical decay stage of our simulation, the fission delay used are the parameters as previously prescribed in Ref. [63], instead of the default ones in GEMINI. In Fig. 2, it can be seen that our results are roughly the same as those given in Ref. [63]. The heights of both the fission peak and the target-like tail of the spectra agree very well with the experimental data. Therefore, our results can serve as a further confirmation of the fission delay prescription given in Ref. [63].
Figure 2. (color online) Calculated total fragment yield plotted versus the charge number (left) and the mass number (right) for
$ p+^{208} {\rm{Pb}}$ for an incident kinetic energy of 1 GeV. The step lines in blue denote the results obtained with PAR1, the set of parameters without MDI as displayed in Table 1, while the red lines denote the ones with PAR2, the set of parameters with MDI. The experimental data are taken from Ref. [62]. Herein, the fission delay parameters prescribed in Ref. [63] are adopted instead of the default ones.Now we have succeeded in reproducing the total fragment yields both with light and heavy targets fairly satisfactorily. It seems we are in a position to give the corresponding result for intermediate-mass targets. Great success has been achieved using the relevant models on the market for reproducing the yields and kinematics of spallation reactions on light and heavy targets; however, attempts with medium-mass targets have produced diverging results depending on the models. A satisfactory description of spallation reactions in this sector remains an issue, especially when it comes to yields and kinematics [32, 33] of IMF fragments [34, 64]. This problem has its origin in the so far unquantified competition between asymmetric (fast) fission and multifragmentation, which are comparable in their contribution to IMF production. These two mechanisms are often ill-defined in this excitation energy range (around the threshold of multifragmentation [65]) in their own right. In contrast, experimental data, which are decisive for evaluating different models, are still scarce and suffer from great disagreement among experiments [64]. For these reasons, a successful and consistent description of spallation reactions on medium-mass targets is still a moot point at present and better not explored.
-
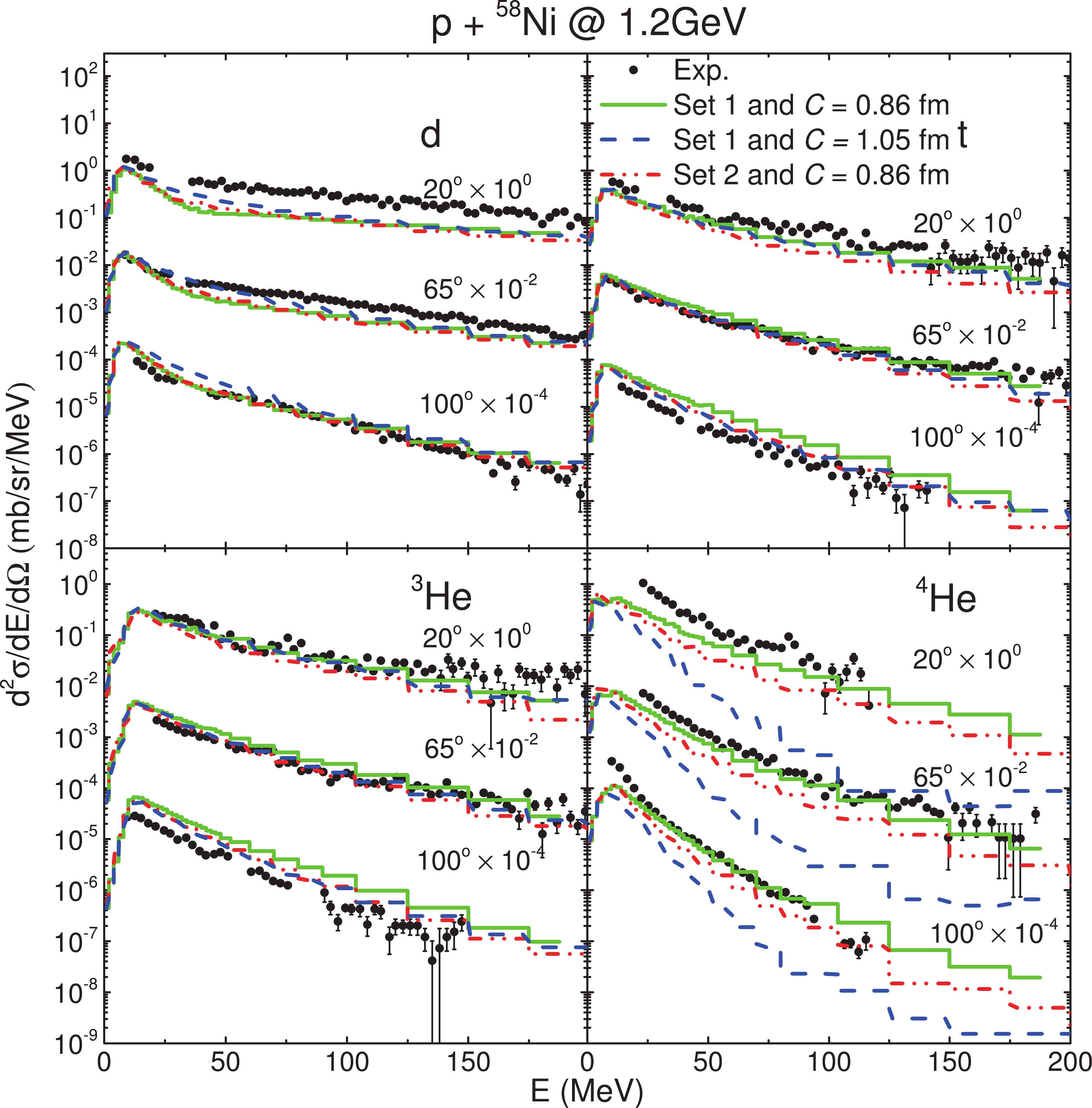
We first consider three reaction systems for the production of high energy LCPs in high-energy proton induced spallation reactions, i.e., p + 58Ni at 1.2 GeV, p + 181Ta at 1.2 GeV, and p + 197Au at 1.2 GeV, for which experimental data are available and the mean field parameters PAR1 are applied. Of course, incorporation of MDI or modification of the mean field parameter in any fashion may suggest related changes in the parameters associated with surface coalescence. However, one can see from Ref. [66] that, though the neutron spectra reproduced at different meanfield parameters differ strikingly in the evaporation-dominated energy domain below 100 MeV, the effect of variations on the mean field parameters upon the emission of preequilibrium neutrons towards the high energy tail is quite minute. Being aware of this, we may expect a similar situation for the results with MDI and for the time being, we keep this in mind for planned studies in the future. As the present work intends to provide an overall description of the spallation reaction and a test of the predictive power of the LQMD model in such a reaction scenario, we did not dig deeper into the vast and arduous task of parameter fitting to the experimental results as was already done in a recent work [67]. Therefore, we just make a few comments on the results we have so far obtained. In Fig. 3 and Fig. 4, the DDXs of light cluster production at three different angles are presented for targets 58Ni and 197Au bombarded on by protons at 1.2 GeV, the values being scaled by a factor of 10-2 for every angle with respect to the previous one. Besides, similar results are presented in Fig. 5 for p + 181Ta at 1.2 GeV.

Figure 4. (color online) Double differential cross-section of d, t, 3He and 4He as a function of kinetic energy and polar angle for p + 197Au at 1.2 GeV calculated with different parameters. The data are taken from Ref. [42].
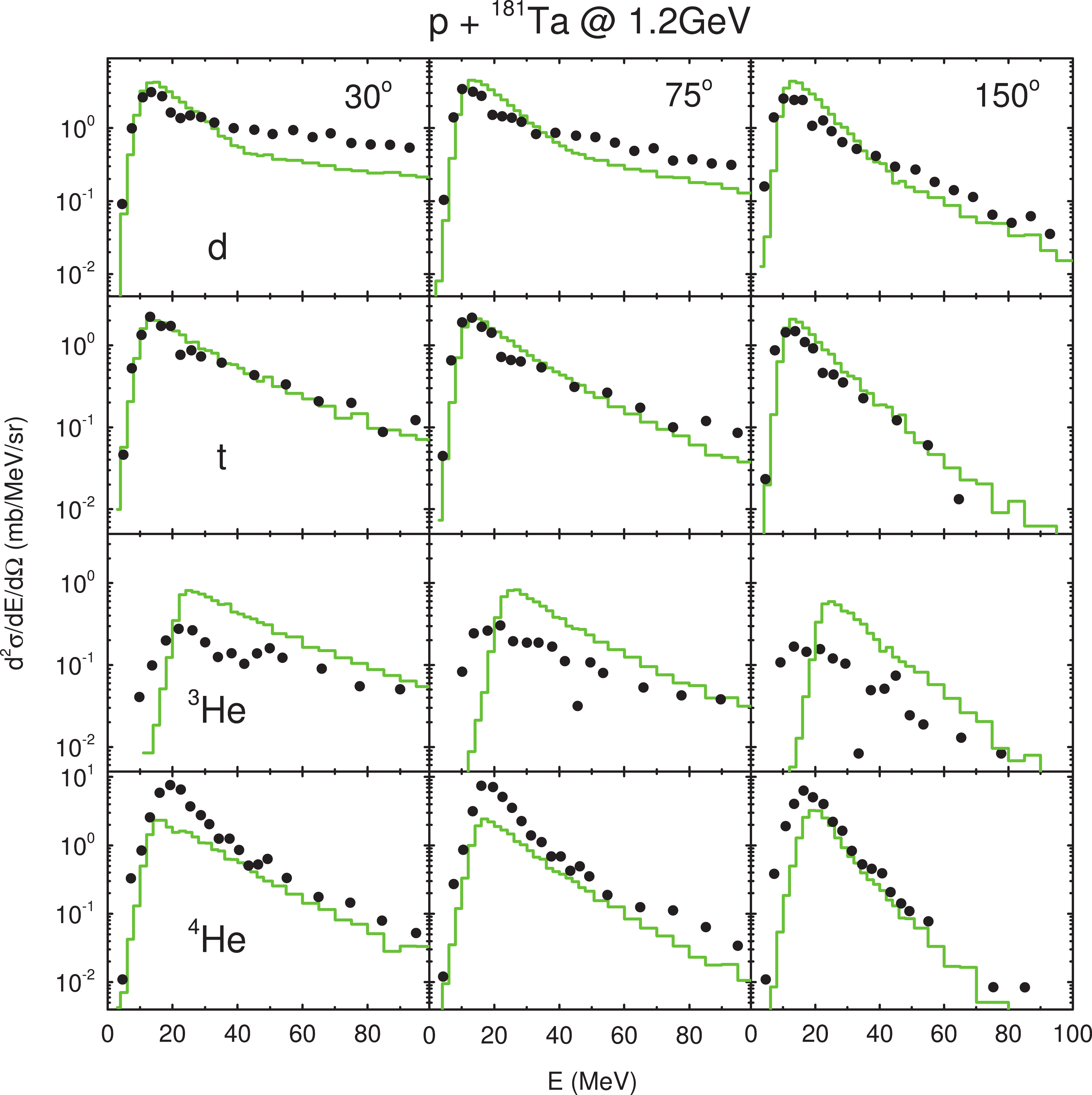
Figure 5. (color online) Double differential cross-section of d, t, 3He a nd 4He as a function of kinetic energy and polar angle for p + 181Ta at 1.2 GeV calculated with
$ C = 0.86 $ fm and phase space parameters Set 1. The data are taken from Ref. [41].We see that in most cases, the high energy tails of the DDXs are reproduced very well except for the very forward angles of d and for large angles of t and 3He. It turns out that with a rather rough set of parameters, a description of a fairly acceptable quality can still be obtained for both light and heavy targets bombarded by high-energy protons. However, the region around the potential barrier is sometimes overestimated and other discrepancies with the experimental data are visible. These can arise from the following sources. Firstly, the production of light clusters in the surface coalescence model is regulated by two types of parameters, the distance coefficient C, which controls the separation of the constructed clusters from the center of the target nucleus, and the phase space parameter
$ h_{0} $ , which controls the size of the clusters in phase space. If the construction of a cluster is not truncated within a proper distance of coefficient C, which we set to$ C = 0.86 $ fm according to empirical knowledge after numerous tests and to a larger value,$ C = 1.05 $ fm, for comparison, an overwhelmingly large number of irrelevant inner crust cluster candidates would lead to an overestimation in the predicted yields of large clusters. In Fig. 3 and Fig. 4, the calculations with three different choices of parameters are plotted using lines in different colours and styles, as indicated by the legends. It can be observed that increasing the threshold separation of the constructed clusters from the target's center by increasing the parameter C results in, to some extent, a similar effect as that of substituting the phase space parameters Set 2 for Set 1, which sets a larger upper bound for the phase space sizes of the constructed clusters. Both settings bring down the high energy tails, except for d. However, for an agreeable reproduction of the high energy tails of the large clusters with respect to the experiments, e.g., the 4He cluster, C must not be too large. Otherwise, the high energy tails of these clusters fall off too early. Secondly, a high quality description of the emergence of the leading nucleons that initiate the construction of the clusters is a prerequisit for a high quality description of cluster production. Moreover, a correct time evolution of the phase space nuclear density distribution of the target nucleus is also important. As seen in the next section, our reproduction of the neutron DDXs is not that desirable quantitatively for backward angles, which may account for the corresponding discrepancies that occur in our cluster DDXs. Thirdly, in our consideration of barrier tunneling, the contribution of the centrifugal potential to the total barrier height is neglected. Some outgoing clusters with energy around the barrier sometimes carry away with them ten to twenty units of angular momentum measured in$\hbar $ , which amounts to the contribution of a 4He cluster with$ l = 10 $ in a 197Au target, and thus, this modifies both the height and the shape of the spectra around the barrier. Apart from the interplay of all these factor, other potential sources may also be responsible for these problems. Nevertheless, considerable effort is required to give a higher quality reproduction of cluster DDXs, but a simple surface coalescence model with these roughly selected parameters implemented in our LQMD model works rather well in describing the key characteristics of light cluster emission in spallation reactions. In Fig. 6, similar results with parameters Set 1 and$ C = 0.86 $ fm are also presented for p + 107Ag at 1.9 GeV.
Figure 6. (color online) Double differential cross-section of d, t, 3He and 4He as a function of kinetic energy and polar angle for p + 107Ag at 1.9 GeV calculated with parameters Set 1 and
$ C = 0.86 $ fm. The data are taken from Ref. [69].Having demonstrated that our model together with the choice of parameter Set 1 and
$ C = 0.86 $ fm are consistent with the experimentally measured LCPs up to 4He, we now proceed one step further and generalize the description up to$ A = 8 $ using these settings. Before doing so, however, we want to clarify two technical points. Firstly, though the old fortran version of GEMINI which we employed in this work actually incorporates the evaporation of LCPs up to 10B, the quality of the description of LCPs emission deteriorates dramatically after 6He. In this situation, we thus have to be content with studying LCP emission in an energy range far below the Coulomb barrier and only where the contribution of statistical evaporation is supposed to be negligible. Interested readers are encouraged to refer to Ref. [69] for the latest simulations of LCPs evaporation beyond$ A = 6 $ with GEMINI++ in parallel with all other currently existing models. Secondly, to achieve a description more consistent with experimental data in terms of LCPs emission of A beyond 4, we find that it is more practical to treat LCPs emission according to the following semi-phenomenological scaling prescriptions. Using the emission of 6Li as an example, first, we treat the emission of 6He in the manner described in Section II, and the energy spectra of 6Li are obtained by scaling those of 6He by an appropriate ratio. Second, the numbers of all 6He and 6Li that have entered the selection procedure are counted. Note that if the procedure was terminated at$ A = 7 $ , no 6He or 6Li would be able to enter the procedure; only those of$ A \ge 7 $ would have entered. Third, the numbers are summed up for all generated events and the ratio of 6Li over 6He is obtained.Thus, the calculated ratios for p + 107Ag at 1.9 GeV are 1.0 for 6He, 1.3 for 6Li, 0.51 for 7Li, 0.22 for 8Li, 0.52 for 7Be, and 0.17 for 8He. The corresponding spectra which follow from this prescription are presented in Fig. 7 and Fig. 8. From these figures one observes that the the yields decrease sequentially from 6Li to 8Li with an increase in the neutron richness, whereas the magnitudes of the spectra are revealed by the experiment [69] to be almost exactly the same for 6Li and 7Li, and exhibit no neutron richness dependence for these two isotopes. All presented results are in agreement with the experiment with the exception of those for 7Li. The results from INCL4.6 are also listed for comparison, and one readily observes that, in the results from INCL4.6, there is no systematic decrease in the spectra from 6Li to 8Li, and the slope of the high-energy tails are all underestimated from 6He to 7Be. We conclude that the prescriptions made in the treatment of LCPs emission beyond
$ A = 6 $ are rather reasonable. As indicated by the experimental data, it is a very salient feature of LCPs emission in spallation reactions that the slopes of the high-energy tails in the spectra of a particular angle are almost the same from isotopes 6Li to 7Be and this may justify our scaling prescription mentioned above. In addition to the above-discussed isotopes, we present herein the result of the rare radioactive isotope 8He, as shown in Fig. 8. We find that the magnitude of the spectra indeed respects the systematics of the neutron richness dependence and thus, is six times lower than that of 6He. However, this is still far higher than the experimental results, in which the 8He production is found to be two orders of magnitude lower than that of 6He. This suggests that transport models coupled with surface coalescence is a rather simplistic picture when it comes to the description of rare radioactive isotope emission, and thus, is not without limitations of its own as it is founded only on a simple classical geometrical argument that does not take into account any structure effects in the dynamical evolution.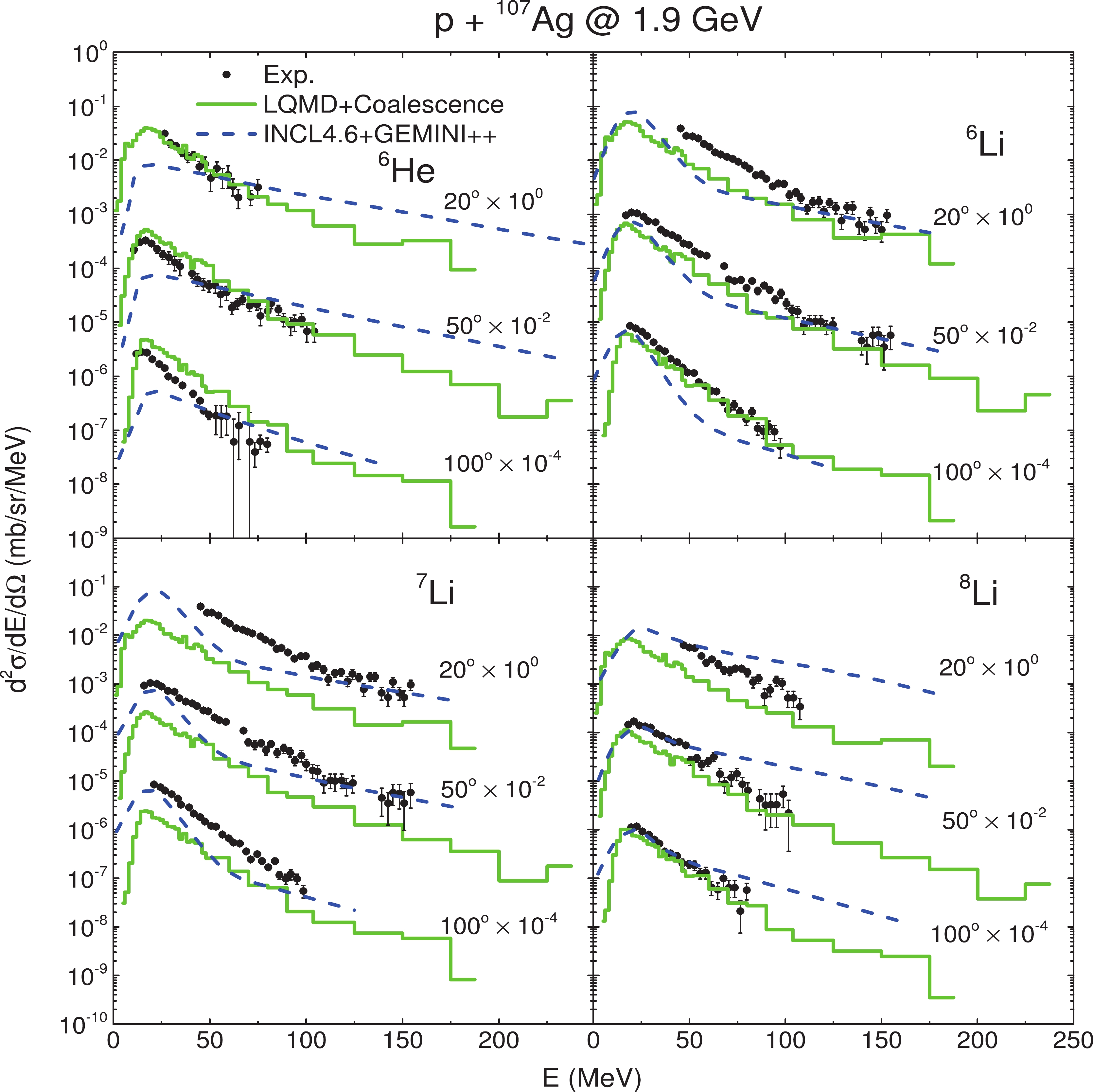
Figure 7. (color online) Double differential cross-section of 6He, 6Li, 7Li and 8Li as a function of kinetic energy and polar angle for p + 107Ag at 1.9 GeV calculated with parameters Set 1. The black dots are experimental data and the blue dashed lines are results from INCL4.6+GEMINI++. Both are taken from Ref. [75].
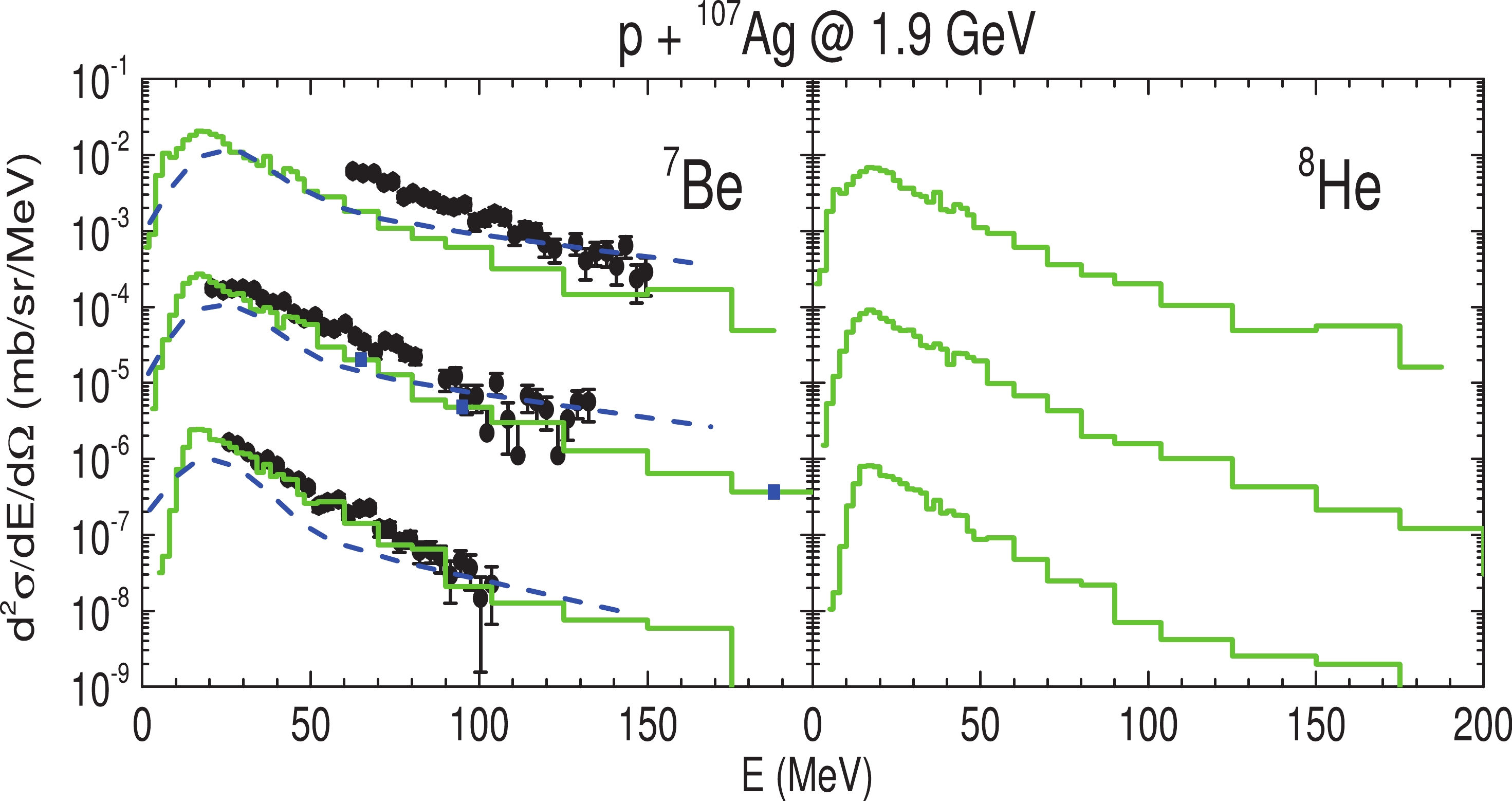
Figure 8. (color online) Same as Fig. 7 but for 7Be and 8He production.
-
In this section, the model is applied to the reproduction of the DDXs of spallation neutrons, which has been intensely investigated experimentally and theoretically on a large number of spallation targets over a vast range of incident energies in the past decades. Accurate neutron DDXs is a vital information for the design and the various utilizations of a spallation neutron source [70]. However, whenever experimental data are not available, theoretical calculation tools, such as the moving source model [71], intranuclear-cascade plus evaporation model (INC+E) [72], or HETC-3STEP [73] play indispensable roles. QMD calculations of the DDXs, which represent the most sophisticated method of these models, were studied by G. Peilert et al. [74] and soon after by K. Niita et al. [75-77]. A comparison of the results with different mean-field parameters has already been studied by Li Ou et al. in Ref. [66].
In this section, the mean field parameters PAR1 are employed to simulate 800 MeV proton-induced spallation reactions on 112Cd, 184W and 208Pb targets. It is obvious from Fig. 9 that the model can reproduce the main trends of the spectra given by experiments. The data are taken from Ref. [78]. However, in the low energy domain around
$ E = 20 $ MeV, the data are somewhat overestimated with an increase in the polar angle, which does not originate from the evaporation stage but simply from the cascade stage in form of extra free neutrons. The high energy tails close to the incident energy at 30° drop too soon, while at larger angles, they are rather nicely reproduced. The ambiguity of the results at energies close to the incident energy is simply due to the quality of the statistics, which is limited by the computational resources available.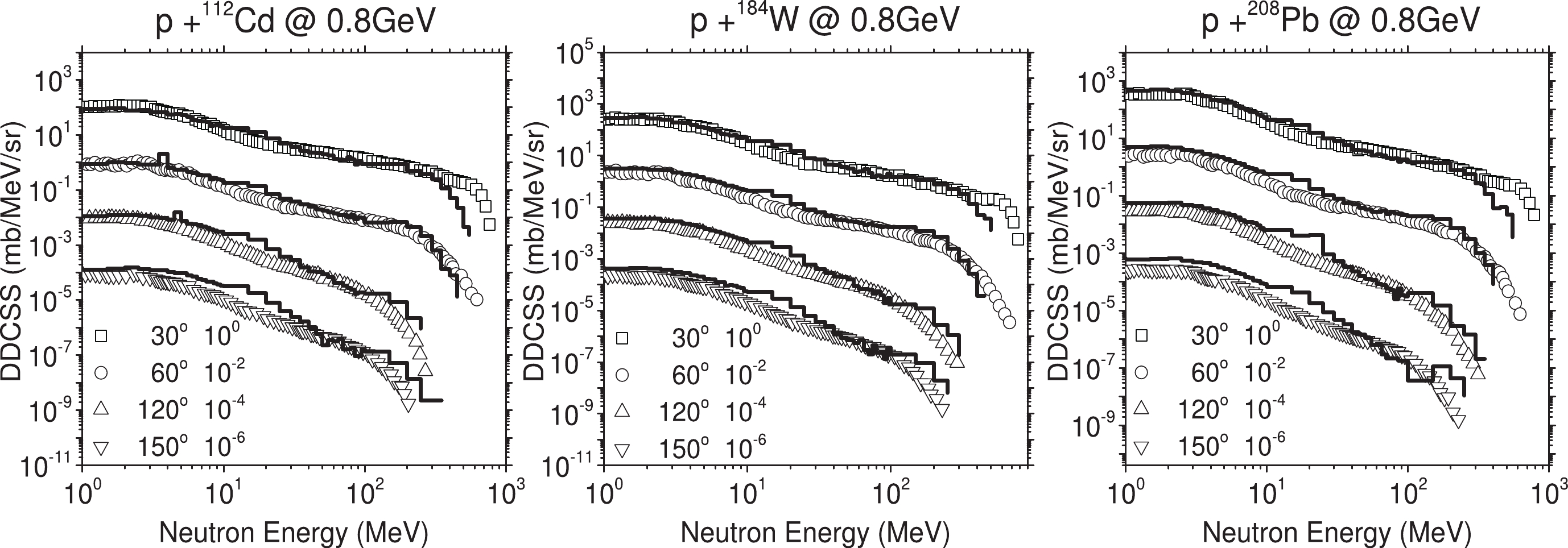
Figure 9. (color online) Calculated neutron DDXs of
$ p+^{112} $ Cd, 184W, 208Pb at 800 MeV. The experimental data are taken from Ref. [78]. -
The nuclear dynamics in spallation reactions of different targets are systematically investigated within the LQMD transport model. An overall description of total fragment yields in the reactions of protons on
$ ^{56} {\rm{Fe}}$ and 208Pb at the incident energy of 1 GeV is given, which provides a sound basis for further inquiry into the detailed aspects of LCPs and neutron emission. The good agreement with the experimental data in terms of total fragment yields using the set of fission delay parameters in the GEMINI code again fortifies the validity of this description. For the description of cluster emissions from statistical decay and the pre-equilibrium stages, the GEMINI code and a simple surface coalescence model are employed. Though the parameters adopted in the surface coalescence model are rough estimates, a rather good overall reproduction of the DDXs of light clusters is achieved with our model. It can be seen that there is a high potential for the model to be refined by polishing the choice of the different parameters and adjusting the potential barrier. For the description of emissions of LCPs beyond$ A = 6 $ , a rather good agreement with experiments is obtained via a semi-phenomenological scaling prescription, except for 7Li, which is an exception to the systematics of neutron richness dependence, and for 8He, which is characterized by its structure effect. For the reproduction of neutron DDXs, three heavy targets 112Cd, 184W and 208Pb at the incident energy of 800 MeV are chosen. The energy spectra are consistent with the available experimental data. The production of rare isotopes in the spallation reactions is feasible via preequilibrium emission.
Light fragment and neutron emission in high-energy proton induced spallation reactions
- Received Date: 2021-03-20
- Available Online: 2021-08-15
Abstract: The dynamics of high-energy proton-induced spallation reactions on target nuclides of 56Fe, 58Ni, 107Ag, 112Cd, 184W, 181Ta, 197Au, and 208Pb are investigated with the quantum molecular dynamics transport model motivated by the China initiative Accelerator Driven System (CiADS) in Huizhou and the China Spallation Neutron Source (CSNS) in Dongguan. The production mechanism of light nuclides and fission fragments is thoroughly analyzed, and the results obtained thereby are compared with available experimental data. The statistical code GEMINI is employed in conjunction with a transport model for describing the decay of primary fragments. For the treatment of cluster emission during the preequilibrium stage, a surface coalescence model is implemented into the model. It is found that the available data in terms of total fragment yields are well reproduced in the combined approach for spallation reactions both on the heavy and light targets. The energetic light nuclides (deuteron, triton, helium isotopes etc) mainly created during the preequilibrium stage are treated within the framework of surface coalescence, whereas their evaporation is described in the conventional manner by the GEMINI code. With this combined approach, a good overall description of light clusters and neutron emission is obtained, and some discrepancies with the experimental data are discussed. Possible production of radioactive isotopes in the spallation reactions is also analyzed, i.e., the 6,8He energy spectra.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: