-
Quantum phase transitions (QPTs) in nuclei have attracted much interest over the past two decades [1-14]. Such QPTs are not of the usual thermodynamic type but are related to changes in the ground state shapes of nuclei, and hence termed "shape phase transitions (SPTs)." In theory, the interacting boson model (IBM) [15] may be the most frequently used framework to study the SPTs in even-even nuclei [2]. Recently, considerable interest has been devoted to the SPTs in odd-A nuclei [16-39]. A theoretical tool to describe odd-A nuclei is the interacting boson-fermion model (IBFM) [40], in which an odd-A nucleus can be approximately considered as an odd-even system with an even-even core (bosons) and unpaired particles (fermions). The SPTs in odd-even systems can be explored as the QPTs between two different dynamical symmetry limits of the boson core, as the ground state shape of the system is assumed to be primarily determined by core deformation. Two approaches of addressing SPTs in the IBFM framework exist: the analysis of the ground state potential surfaces and the direct quantum computation of order parameters [14]. A classical analysis of the ground deformations in the spherical to prolate and spherical to
$ \gamma $ -soft SPTs was recently conducted [34] in the IBFM framework using the coherent state method [40], and the main conclusion was that the single particle (odd particle) can influence different types of SPTs differently [24-26]. However, the ground state deformation cannot be directly observed in experiments. A more practical method of studying SPT is to perform a quantal analysis of the observables that are sensitive to the ground state deformations. Such types of quantities can be accordingly considered to be the effective order parameters to identify the SPTs in experiments [14]. To calculate observables, the IBFM Hamiltonian must be numerically solved in a transitional scenario. The frequently used IBFM code is “ODDA” developed by Scholten [41], with the wave functions expanded in terms of the weak-coupling U(5) basis [40]. Since the IBFM [40] as the standard model for odd-A nuclei can provide a very convenient frame to study SPTs, developing an alternative scheme to solve the model Hamiltonian would be interesting and also expected.This paper has two aspects. First, we introduce the diagonalization scheme of the IBFM Hamiltonian in terms of the weak-coupling SU(3) basis with the SU(3) part constructed using the Draayer-Akiyama algorithm [42, 43]. Second, we study the effects of an odd particle on the SPTs in odd-even systems using the proposed diagonalization scheme. Two types of SPTs are emphasized in this paper, i.e., the spherical to prolate SPT and spherical to
$ \gamma $ -soft SPT. The remainder of the article is arranged as follows. In Sec. II, the IBFM Hamiltonian and diagonalization scheme are introduced, through which the functions of different boson-fermion interactions in the IBFM are examined. Sec. III is devoted to studying the effects of an odd particle on two types of SPTs. Finally, a summary is provided in Sec. IV. -
The IBFM Hamiltonian can be generally expressed as [40]
$ \hat{H} = \hat{H}_\mathrm{B}+\hat{H}_\mathrm{F}+\hat{V}_{\mathrm{BF}} \, , $

(1) where
$ \hat{H}_\mathrm{B} $ represents the IBM Hamiltonian describing the boson core,$ \hat{H}_\mathrm{F} $ is the single particle Hamiltonian describing the unpaired fermions (odd particles), and$ \hat{V}_{\mathrm{BF}} $ represents the boson-fermion interaction. If only the mean-field part is considered, the single particle Hamiltonian can be expressed as$ \hat{H}_\mathrm{F} = \sum\limits_j\varepsilon_j\hat{n}_j\, , $

(2) where
$ \varepsilon_j $ represents the single-particle energies of the spherical orbit j and$ \hat{n}_j = -\sqrt{2j+1}(a_j^\dagger \times\tilde{a}_j)^{(0)}\, $

(3) with
$ \tilde{a}_{j,m_j} = (-1)^{j-m_j}a_{j,-m_j} $ is the fermion number operator. In this paper, only one unpaired fermion confined in a single-j orbit is considered for simplicity. This means that$ \hat{H}_\mathrm{F} $ will only contribute a constant for the excitation energies. For the IBM Hamiltonian, we apply the consistent-Q form [44]$ \hat{H}_\mathrm{B} = \varepsilon_d \hat{n}_{d} +\kappa\hat{Q}_{\mathrm{B}}^{\chi}\cdot \hat{Q}_{\mathrm{B}}^{\chi}\, , $

(4) where the the d-boson number operator is defined as
$ \hat{n}_d = \sqrt{5}(d^\dagger \times\tilde{d})^{(0)}\, $

(5) with
$ \tilde{d}_u = (-1)^ud_{-u} $ , and the quadrupole operator is defined as$ \hat{Q}_\mathrm{B}^{\chi} = (d^{\dagger} s + s^{\dagger} \tilde{d})^{(2)} + \chi (d^{\dagger}\times\tilde{d})^{(2)}\, $

(6) with
$ \chi\in[-\sqrt{7}/2,\; 0] $ . There are three typical dynamical symmetries (DSs) included in the IBM, namely U(5), O(6), and SU(3). We can prove that the Hamiltonian$ H_\mathrm{B} $ is in the U(5) DS when$ \kappa = 0 $ ; it is in the O(6) DS when$ \varepsilon_d = 0 $ and$ \chi = 0 $ ; it is in the SU(3) DS when$ \varepsilon_d = 0 $ and$ \chi = -\sqrt{7}/2 $ . The three DSs in the IBM corresponding to three typical collective modes (or collective shapes) including the spherical vibrator (U(5)), axial rotor (SU(3)), and$ \gamma $ -soft rotor (O(6)). The frequently used boson-fermion interaction can be expressed as [45]$ \hat{V}_{\rm BF} = V_{\mathrm{BF}}^{\mathrm{MON}}+V_{\mathrm{BF}}^{\mathrm{QUAD}}+V_{\mathrm{BF}}^{\mathrm{EXC}}\, , $

(7) which contains the monopole term
$ V_{\mathrm{BF}}^{\mathrm{MON}} = A_j\hat{n}_d\hat{n}_j\, , $

(8) the quadrupole term
$ V_{\mathrm{BF}}^{\mathrm{QUAD}} = \Gamma\hat{Q}_\mathrm{B}^\chi\cdot\hat{q}_\mathrm{F}\, $

(9) with
$ \hat{q}_\mathrm{F} = (\hat{a}_j^\dagger\times\tilde{a}_j)^{(2)}\, $

(10) and the exchange term
$ V_{\mathrm{BF}}^{\mathrm{EXC}} = \Lambda\sqrt{2j+1}:[(d^\dagger\times\tilde{a}_j)^{(j)} \times(\tilde{d}\times a_j^\dagger)^{(j)}]^{(0)}:\, , $

(11) where
$ (:...:) $ denotes normal ordering [40]. The interaction strengthes$ A_j,\; \Gamma $ , and$ \Lambda $ in the boson-fermion interaction can in principle be calculated from the fermion-fermion dynamics [45] and semi-microscopically connected with the Bardeen-Cooper-Schrieffer (BCS) occupation probabilities [46], but here they are applied as the adjustable parameters. -
To obtain the eigenvalues and eigenfunctions, we diagonalize the IBFM Hamiltonian in terms of the weak coupling SU(3) basis:
$\begin{aligned}[b]& |N (\lambda,\mu)\tilde{\chi} (Lj) JM_J\rangle \\=& \sum\limits_{M_L,m_j}\langle LM_L,jm_j|JM_J\rangle|N(\lambda,\mu)\tilde{\chi}LM_L\rangle| jm_j\rangle\, , \end{aligned} $

(12) where N is the total boson number,
$ (\lambda,\mu) $ characterizes the SU(3) irreducible representation, and$ \tilde{\chi} $ denotes the additional quantum number to distinguish the different states with the same$ (\lambda,\mu) $ and L. In Eq. (12),$ L,\; j, \; J $ represent the angular momentum for the boson core, odd particle, and entire system, with the corresponding third components denoted by$ M_L $ ,$ m_j $ , and$ M_J $ , respectively. The SU(3) coupling basis can be characterized by the group chain$ \left |\begin{array}{l} \Big({U(6)}\supset {SU}(3)\supset {SO}(3)\Big)\otimes {SU}_j(2)\supset {SU}_J(2)\supset {SO}_J(2)\\\;\;\;\; N\;\;\;\;\; \; (\lambda,\mu)\; \tilde{\chi}\; \;\;\;\; \; \; L\; \; \; \; \;\;\;\; \; \; \; \; \; \; j\; \;\;\; \; \; \; \; \; \; \; \; \;\;\; \; J\; \; \;\;\;\;\;\; \; \; \; \; \; \; \; M_J\end{array} \right \rangle\, , $

(13) where the additional quantum number
$ \tilde{\chi} $ also labels the multiplicity of L in an SU(3) representation$ (\lambda,\mu) $ . Note that the complete group symmetry for the fermion part with single j should replace${SU}_j(2)$ with$ {U}(2j+1)\supset {SU}(2j+1)\supset {SP}(2j+1)\supset {SU}_j(2)\, $

(14) particularly for the multi-fermion situation because the
$ n^2 $ operators$ (a^\dagger\times\tilde{a})_q^k $ with$ k = 0,\; 1,\cdots,n = 2j $ can generate the maximal group symmetry${U}(2j+1)$ [40]. If only one fermion is considered, as in this scenario, the nontrivial sub-symmetry is only${SU}_j(2)$ .In the diagonalization, the matrix elements of each term involved in the Hamiltonian (1) can be derived using the SU(3) algebraic technique. Here, we use the core-particle coupling term
$ \hat{M}_c = (d^\dagger\times\tilde{d})^2\cdot(a_j^\dagger\times\tilde{a}_j)^2\, , $

(15) which corresponds to part of the quadrupole boson-fermion interaction in Eq. (9), as an example to decsribe the derivation of the Hamiltonian matrix under the SU(3) coupling basis. Using the Wigner-Eckart theorem, the matrix element can be derived as
$ \begin{aligned}[b]& \langle \alpha^\prime (L^\prime j) J^\prime M_J^\prime |\; \hat{M}_c\; |\alpha (Lj) JM_J\rangle \\ =& \delta_{J^\prime J}\delta_{M_J^\prime M_J}(-1)^{L+j+J}\langle \alpha^\prime L^\prime \parallel(d^\dagger\times\tilde{d})^2\parallel \alpha L\rangle\\& \times\left\{\begin{array}{ccc}L^\prime\; j\; J \\ j\; \; L\; 2\end{array} \right\}\langle j\parallel(a_j^\dagger\times\tilde{a}_j)^2\parallel j\rangle \\ =& -5\delta_{J^\prime J}\delta_{M_J^\prime M_J}(-1)^{L^\prime+j+J}\sum\limits_{\alpha^{\prime\prime}L^{\prime\prime}}\left\{\begin{array}{cc}2\; 2\; 2\; \\ LL^\prime L^{\prime\prime}\end{array} \right\} \\ & \times\left\{\begin{array}{cc} L^\prime \; j\; J \\ j\; \; L\; \; 2\end{array} \right\}\langle\alpha^\prime L^\prime\parallel d^\dagger\parallel\alpha^{\prime\prime}L^{\prime\prime}\rangle \langle\alpha^{\prime\prime}L^{\prime\prime}\parallel \tilde{d}\parallel\alpha L\rangle\, , \end{aligned} $

(16) where the abbreviation
$ \alpha\equiv N(\lambda,\mu)\tilde{\chi} $ is used. Clearly, the final results will be determined by the reduced elements of the boson operator under the SU(3) basis. The d-boson operators can be further expressed as the SU(3) irreducible tensors,$ \hat{T}_{\tilde{\chi},LM_L}^{(\lambda,\mu)} $ . In particular, it is expressed as [47]$ d_u^\dagger = A_{1,2u}^{(2,0)},\; \; \tilde{d}_u = B_{1,2u}^{(0,2)}\, . $

(17) Subsequently, the double-barred reduced matrix elements contained in Eq. (16) can be further expanded as
$ \begin{aligned}[b]& \langle \alpha^\prime L^\prime\parallel d^\dagger\parallel \alpha^{\prime\prime} L^{\prime\prime}\rangle\\ =& \sqrt{2L^\prime+1}\; \langle [N](\lambda^\prime,\mu^\prime)\mid\parallel A^{(2,0)} \mid\parallel [N-1](\lambda^{\prime\prime},\mu^{\prime\prime})\rangle\\& \times\langle(\lambda^\prime,\mu^\prime)\tilde{\chi}^\prime, L^\prime;(2,0)1,2 \parallel(\lambda^{\prime\prime},\mu^{\prime\prime})\tilde{\chi}^{\prime\prime},L^{\prime\prime}\rangle\, \end{aligned} $

(18) and
$ \begin{aligned}[b]& \langle \alpha^{\prime\prime} L^{\prime\prime} \parallel\tilde{d}\parallel \alpha L\rangle\\ =&\sqrt{2L^{\prime\prime}+1}\; \langle [N-1](\lambda^{\prime\prime},\mu^{\prime\prime})\mid\parallel B^{(0,2)} \mid\parallel [N](\lambda,\mu)\rangle\\& \times\langle(\lambda^{\prime\prime},\mu^{\prime\prime})\tilde{\chi}^{\prime\prime}, L^{\prime\prime};(0,2)1,2 \parallel(\lambda,\mu)\tilde{\chi},L\rangle\, , \end{aligned} $

(19) for which the triple-barred matrix elements were analytically obtained in [47] and the isoscalar SU(3) wigner coefficients
$ \langle\; ;\parallel\rangle $ can be calculated using the algorithm provided in [42, 43]. Similar derivations can be applied to all the other terms in the IBFM Hamiltonian. Accordingly, the eigenstates of the Hamiltonian can be expanded in terms of the SU(3) coupling basis as$ |N,\xi, JM_J\rangle = \sum\limits_{(\lambda,\mu)\tilde{\chi}L}C_{(\lambda,\mu)\tilde{\chi}L}^{\xi, J M_J}|N (\lambda,\mu)\tilde{\chi} (Lj) JM_J\rangle\, , $

(20) where the expansion coefficients
$ C_{(\lambda,\mu)\tilde{\chi}L}^{\xi,JM_J} $ , with$ \xi $ indicating the$ \xi $ th level for a particular J, can be obtained through diagonalizing the Hamiltonian. -
To analyze the different boson-fermion interactions using the new diagonalization scheme, we compare the lowest-lying levels in between the IBM and IBFM for the three symmetry limits. In the IBM calculations, the parameters (in MeV) involved in the consistent-Q Hamiltonian (4) are applied as
$ (\epsilon_d = 1.0,\; \kappa = 0) $ for the U(5) limit,$ (\epsilon_d = 0, \; \kappa = -1/4,\; \chi = -\sqrt{7}/2) $ for the SU(3) limit and$ (\epsilon_d = 0, \; \kappa = -1/4,\; \chi = 0) $ for the O(6) limit. In the IBFM calculations, the three boson-fermion interactional terms defined in Eqs. (8)-(11) are individually added to the IBM Hamiltonian (4) with the adopted parameters shown in Fig. 1, where the level patterns calculated for$ j = 9/2 $ and$ N = 10 $ are shown for different scenarios. In addition, the parameter$ \chi $ involved in the quadrupole term (9) is set as$ \chi = -\sqrt{7}/2 $ for SU(3) and$ \chi = 0 $ for both O(6) and U(5) to be consistent with the consistent-Q Hamiltonian. As shown in Fig. 1(a1)-(a3), the results indicate that the level degeneracies may exactly occur for the states with$ |j-L|\leqslant J\leqslant j+L $ in the IBFM if only the monopole term is considered and the associated level pattern in each scenario is very similar to the corresponding IBM one. Thus, if no boson-fermion interactions are involved, the exact degeneracies will also occur for the states with$ |j-L|\leqslant J\leqslant j+L $ ; meanwhile, the level energies will be exactly equivalent to the corresponding values in the IBM. This means that the monopole term may only cause a renormalization of the boson level energies in each symmetry limit [40]. In contrast, if only the quadrupole term is involved, as shown in Fig. 1(b1)-(b3), the levels with different J values are not degenerated anymore. Notably, the quadrupole term at a particular strength can cause the level energy splitting in the SU(3) limit to be significantly larger than in the U(5) or O(6) limit. As further shown in Fig. 1(c1)-(c3), the exchange term can also break the level degeneracies, but with the level order in each scenario being different from the one caused by the quadrupole term. Generally, the three types of boson-fermion interactions should all be considered to obtain quantitatively good descriptions of the experimental data [45, 48].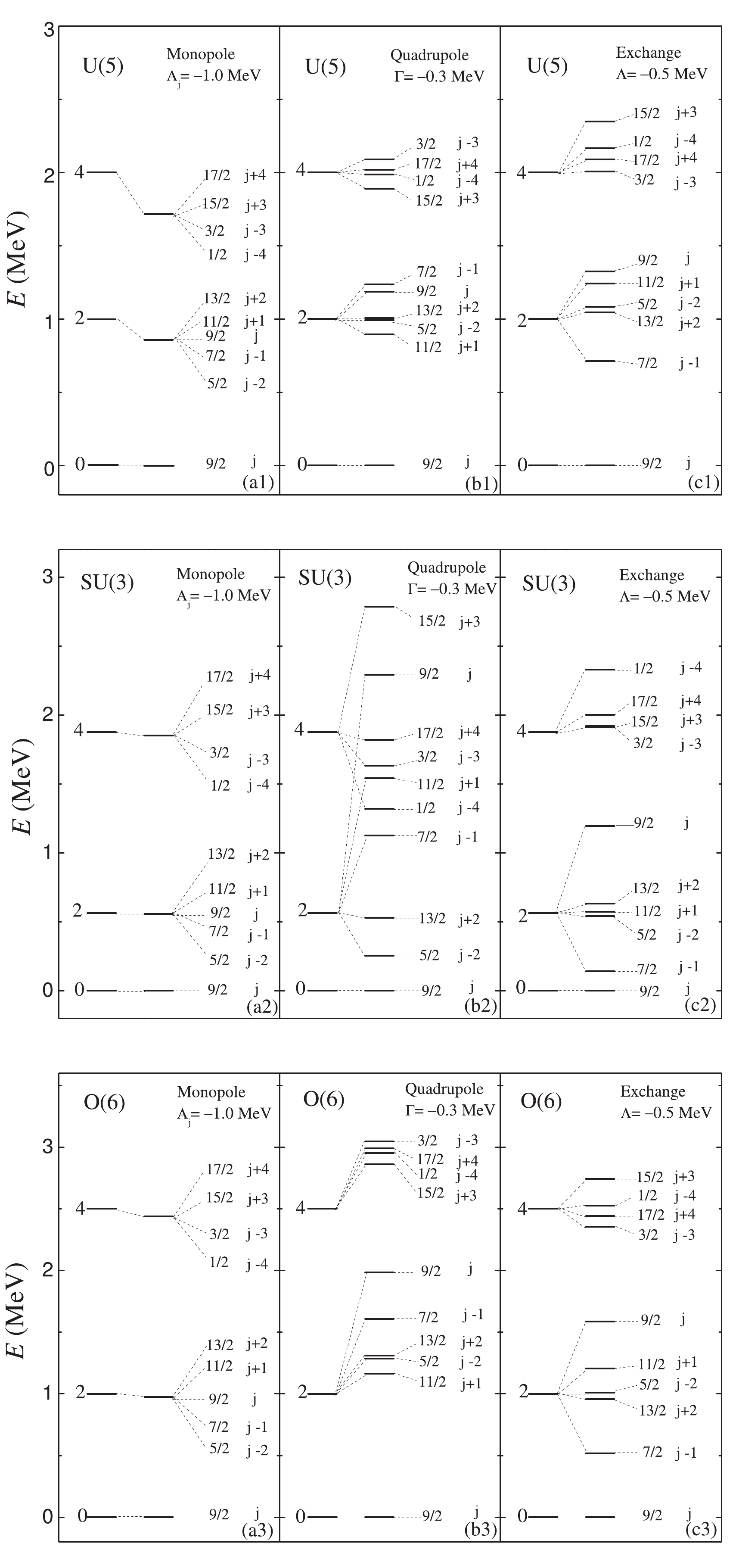
Figure 1. Lowest levels with
$L = 0,\; 2,\; 4$ in the U(5), SU(3), and O(6) limits of the IBM to compare the lowest-lying levels with$J = 1/2-17/2$ in the IBFM, in which the results are solved using the three boson-fermion interactional terms being individually added to each symmetry limit. In the calculations,$j = 9/2$ and$N = 10$ . -
The SPTs in even-even systems can be illustrated as the QPTs in the IBM. The mean-field analysis indicates that the emergence of an additional odd particle in odd-even systems can cause alternative effects on the SPTs [23-25, 34]. To examine the effects of the odd particle, it is convenient to use the consistent-Q IBFM Hamitonian:
$ \hat{H}_{\mathrm{BF}} = \varepsilon \left[ (1-\eta)\hat{n}_{d} - \frac{\eta}{4N}\hat{Q}_{\mathrm{BF}}\cdot \hat{Q}_{\mathrm{BF}} \right] \, , $

(21) where
$ \hat{Q}_{\mathrm{BF}} \equiv \hat{Q}_\mathrm{B}^\chi+\hat{q}_\mathrm{F}\, $

(22) is the quadrupole operator. Compared with Eq. (9), we can derive the strength of the quadrupole boson-fermion interaction in the Hamiltonian (21) as
$ \Gamma = -\frac{\varepsilon\eta}{2N}\, . $

(23) To calculate the
$ B(E2) $ transitional rates and quadrupole moments, we can select the transitional operator as the quadrupole operator defined in (22). For simplicity, we only use the boson part; subsequently, the transitional operator is expressed as$ \hat{T}^{E2} = e\hat{Q}_\mathrm{B}^\chi\, $

(24) where e represents the effective charge. In practice, such an approximation closely agrees with the analysis of some deformed odd-mass nuclei using the microscopic core-quasiparticle coupling model [35]. Accordingly, the
$ B(E2) $ transitional rates and quadrupole moments can be calculated via the formulas$ B(E2;J_i\rightarrow J_f) = \frac{\mid\langle J_f\parallel \hat{T}^{E2}\parallel J_i\rangle\mid^2}{2J_i+1}\, $

(25) and
$ Q(J) = \langle JM_J = J\mid\sqrt{\frac{16\pi}{5}}\hat{T}^{E2}\mid JM_J = J \rangle\, . $

(26) We observed that the consistent-Q Hamiltonian above is as same as that adopted in the classical analysis in [34], which primarily focuses on the quadrupole boson-fermion interaction. This means that some predictions of the classical analysis based on the same Hamiltonian [34] can be checked in this quantal analysis.
First, we focus on the boson core dynamics by removing the fermion term
$ \hat{q}_F $ in the quadrupole operator (22). The IBFM consistent-Q Hamiltonian (21) is then reduced back to the IBM consistent-Q Hamiltonian:$ \hat{H}_{\mathrm{B}} = \varepsilon \left[ (1-\eta)\hat{n}_{d} - \frac{\eta}{4N}\hat{Q}_{\mathrm{B}}\cdot \hat{Q}_{\mathrm{B}} \right] \, , $

(27) which is as same as the one in (4) but with the parameters rewritten as
$ \varepsilon_d = \varepsilon(1-\eta),\; \; \kappa = -\varepsilon\frac{\eta}{4N}\, . $

(28) In discussions, the scale parameter is frequently set to
$ \varepsilon = 1.0 $ . The IBM phase diagram in terms of the parameters in Eq. (27) can be mapped onto the Casten triangle, as shown in Fig. 2. The figure shows that each vertex of the triangle represents a particular DS, i.e., U(5) at$ (\eta,\chi) = (0,0) $ , O(6) at$ (\eta,\chi) = (1,0) $ , and SU(3) at$(\eta,\chi) = $ $ \left(1,-\dfrac{\sqrt{7}}{2}\right)$ . As mentioned earlier, these DSs are alternatively associated with different collective modes or collective shapes (deformations). Accordingly, the transitions between different collective shapes are mapped into the QPTs between different DSs and vice versa. Note that the single group, G, in the IBM phase diagram shown in Fig. 2 should be replaced with the direct product group${G}\otimes {U}(2j+1)$ for the IBFM [40], but we maintain the symbol G to indicate the related scenarios in both IBM and IBFM for convenience.
Figure 2. (color online) Shape phase diagram in the IBM described by the Hamiltonian (27). The dashed line denoting the 1st-order transitional points described by (29) cuts the triangle phase diagram into the spherical and deformed regions.
Based on the mean-field analysis [14], we can prove that the system in the large-N limit experiences a 1st-order QPT at
$ \eta_c = 8/17\simeq0.5 $ on the U(5)-SU(3) leg and a second-order QPT at$ \eta_c = 0.5 $ on the U(5)-O(6) leg. The U(5)-SU(3) QPT may correspond to the spherical to prolate (or the vibrator to axial rotor) SPT in the collective model terminology while the U(5)-O(6) QPT corresponds to the spherical to$ \gamma $ -soft (or the vibrator to$ \gamma $ -soft rotor) SPT. In this paper, the terminology of QPTs of the two models are mutually used without distinction. More generally, the first-order spherical to deformed SPTs (the U(5)-SU(3) QPT-like) may widely occur inside the triangle phase diagram with the critical points, expressed as$ \eta_c = \frac{14}{28+\chi^2}\, . $

(29) In the following, we apply the scenarios with
$ j = 9/2 $ and$ N = 10 $ to discuss the effects of an odd particle on the U(5)-SU(3) and U(5)-O(6) SPTs in the finite systems. In particular, we compare the results solved from the IBFM Hamiltonian (21) to those obtained from the IBM Hamiltonian (27). Note that the effects of different boson-fermion interactions on the spectra in the two types of SPTs have been previously investigated in the IBFM both classically and quantum mechanically [26]. In the following, we focus on revealing the similarities and differences in the critical behaviors of the odd-even and even-even systems. -
First, the lowest-lying levels are computed, and the results evolving as functions of
$ \eta $ in both the U(5)-SU(3) and U(5)-O(6) transitional regions are shown in Fig. 3. As shown in Fig. 3(a), the states with different J values in the odd-even systems are approximately degenerate and are divided into groups with the level energies being close to those with$ L = 0,\; 2,\; 4 $ in the even-even system until$ \eta\sim0.4 $ ; subsequently, the degeneracies are rapidly broken in the range of$ \eta\sim0.4-0.6 $ with the levels reorganized in a spread. This is the finite precursor of the U(5)-SU(3) SPT in odd-even systems. Note that an SPT in a finite system may occur in a parameter region rather than at a point owing to the finite-N effect, which also results in the transitional features not being as sharp as that in the large-N limit [14], where the concept of QPT is rigorously defined. As further shown in Fig. 3(b), the level degeneracies in the odd-even systems clearly break down in the critical region$ \eta\sim0.4-0.6 $ , which confirms that the U(5)-O(6) SPT also occurs in the odd-even systems. In theory, the breaking of level degeneracies can be considered to be a signal for U(5)-O(6) SPT. Meanwhile, the results imply that the transitional features of the second-order QPT (U(5)-O(6) SPT) in a finite-N system may be significantly weaker than those of the first-order QPT (U(5)-SU(3) SPT).
Figure 3. (color online) Low-lying energy levels evolving as functions of the control parameter
$\eta$ in both the U(5)-SU(3) and U(5)-O(6) transitions; the grey color indicates the critical region in a finite-N scenario. In the calculated results, the levels with$L = 0,\; 2,\; 4$ in the IBM (denoted by dashed lines) have been normalized to$E(2_1) = 1.0$ and those with$J = 1/2-17/2$ in the IBFM (denoted by full lines) are normalized to$E(13/2_1) = 1.0$ .To further identify the critical features in a finite-N situation, the energy ratio
$ R_{4/2} $ and the$ B(E2) $ ratio$ B_{4/2} $ are calculated for the two types of SPTs with the corresponding results as a function of$ \eta $ shown in Fig. 4 and Fig. 5, respectively. As shown in Fig. 4(a), a sudden increase in$ R_{4/2} $ can be observed in the critical region of the U(5)-SU(3) SPT, which confirms again that this type of SPT indeed occurs in the odd-even system as in the adjacent even-even system. An interesting observation is that the transitional feature in$ R_{4/2} $ seems to be slightly enhanced in the odd-even system. In contrast, the results shown in Fig. 4(b) indicate that the finite-N precursor of U(5)-O(6) SPT can be also identified from the evolutions of$ R_{4/2} $ but with the transitional amplitude in the odd-even system ($ R_{4/2}\sim2.0-2.3 $ ) being more depressed than in the adjacent even-even system ($ R_{4/2}\sim2.0-2.5 $ ). This means that the U(5)-O(6) SPT may be smoother in the odd-even nuclei owing to the effects of the odd particle, which agrees with the classical analysis provided in [34]. As shown in Fig. 5, the results for the$ B(E2) $ ratio further confirm the finite-N precursors of the SPTs in the odd-even and even-even systems. The figure shows that the U(5)-SU(3) transitional features are strengthened by the effects of the odd particle, and the transitional amplitude of$ B_{4/2} $ in the odd-even system is relatively larger than that in the even-even system. In contrast, the U(5)-O(6) SPT features in the odd-even system become relatively weaker with a smaller amplitude of$ B_{4/2} $ than in the adjacent even-even systems. Reference [49] indicated that ratio$ B_{4/2} $ in the even-even system can be applied as the effective order parameter to distinguish the first-order SPT (U(5)-SU(3)) from the second-order SPT (U(5)-O(6)) by its different evolutional characteristics in the two types of SPTs. We can observe in Fig. 5 that$ B_{4/2} $ in the odd-even system can have the same function as the differences in between the first-order and second-order SPTs become even larger owing to the effects of the odd particle.
Figure 4. (color online) Typical energy ratios evolving as functions of
$\eta$ in the U(5)-SU(3) and U(5)-O(6) SPTs with the definition$R_{4/2}\equiv \frac{E((4+J_g)_1)}{E((2+J_g)_1)}$ , where the ground state spins$J_g = 9/2$ and$J_g = 0$ are used in the calculations for the odd-even and even-even systems, respectively.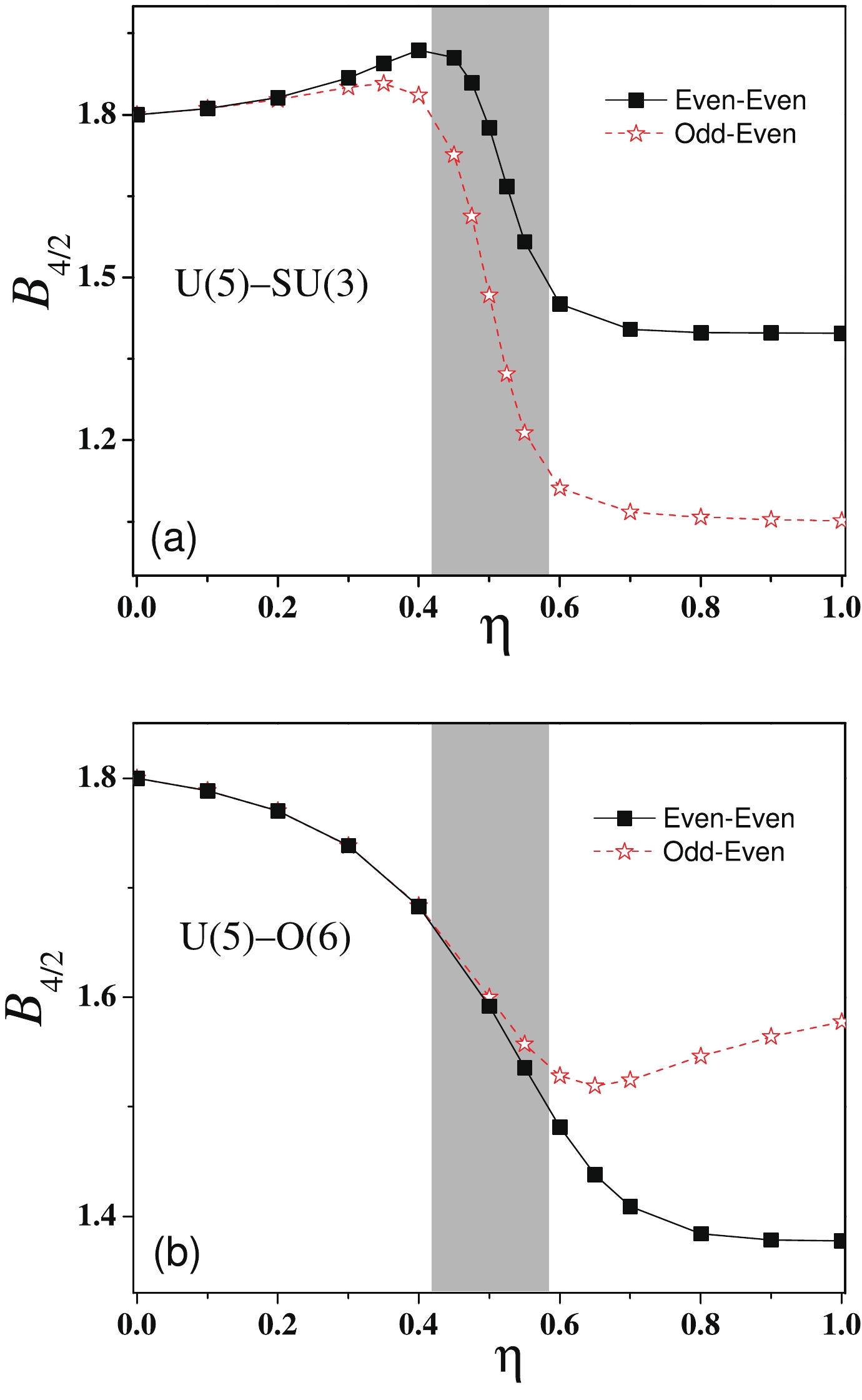
Figure 5. (color online) Same as in Fig. 4 but for the
$B(E2)$ ratios defined as$B_{4/2}\equiv\frac{ B(E2;(4+J_g)_1\rightarrow(2+J_g)_1)}{B(E2;(2+J_g)_1\rightarrow(0+J_g)_1)}$ with$J_g = 9/2$ and$J_g = 0$ used for the odd-even and even-even systems, respectively.To check the deformations of the finite systems in the SPTs, the quadrupole moments of the even-even system,
$ Q(2_1) $ , and those of the odd-even system,$ Q(J_1) $ , have been calculated, and the results as a function of$ \eta $ are shown in Fig. 6. As shown in Fig. 6(a), the quadrupole moments of the selected states in the U(5)-SU(3) transition may all decrease from the nearly zero values to the negative values with the fastest change appearing in$ \eta = 0.4\sim0.6 $ as expected. A noticeable scenario is that$ Q(7/2_1) $ as a function of$ \eta $ may gradually increase until$ \eta\sim0.4 $ before beginning to decrease. A more interesting observation from the sub-panel is that the odd-even differences$ \Delta Q $ for the different states nearly all attain their maxima in the critical region, which indicates that the odd particle can induce a larger fluctuation in the quadrupole deformation in the critical systems. This implies that different deformations (phases) may have more opportunities to coexist in the low-lying structures of the odd-even systems undergoing the U(5)-SU(3) SPT [34]. For the U(5)-O(6) SPT, we can observe from Fig. 6(b) that the quadrupole moments of the even-even system,$ Q(2_1) $ , remains zero in the entire transitional process. It is easy to understand this feature from the selection rule as the transitional operator$ \hat{Q}_\mathrm{B}^{\chi = 0} $ adopted in the calculation for the U(5)-O(6) SPT requires$ \Delta L = \pm2 $ for the yrast states [15]. In contrast, the quadrupole moments of the odd-even system,$ Q(J_1) $ , may all monotonically decrease from zero to the negative values, thus suggesting that the largest odd-even difference of quadrupole deformation in the U(5)-O(6) SPT should appear in the O(6) limit. In addition, the results in Fig. 6(a) are not exactly equivalent to zero for the U(5) limit. This is primarily because of a different transitional operator,$ \hat{Q}_\mathrm{B}^{\chi = -\frac{\sqrt{7}}{2}} $ , being selected for the U(5)-SU(3) SPT to be consistent with the consistent-Q Hamiltonian; however, this observation will not change the conclusions.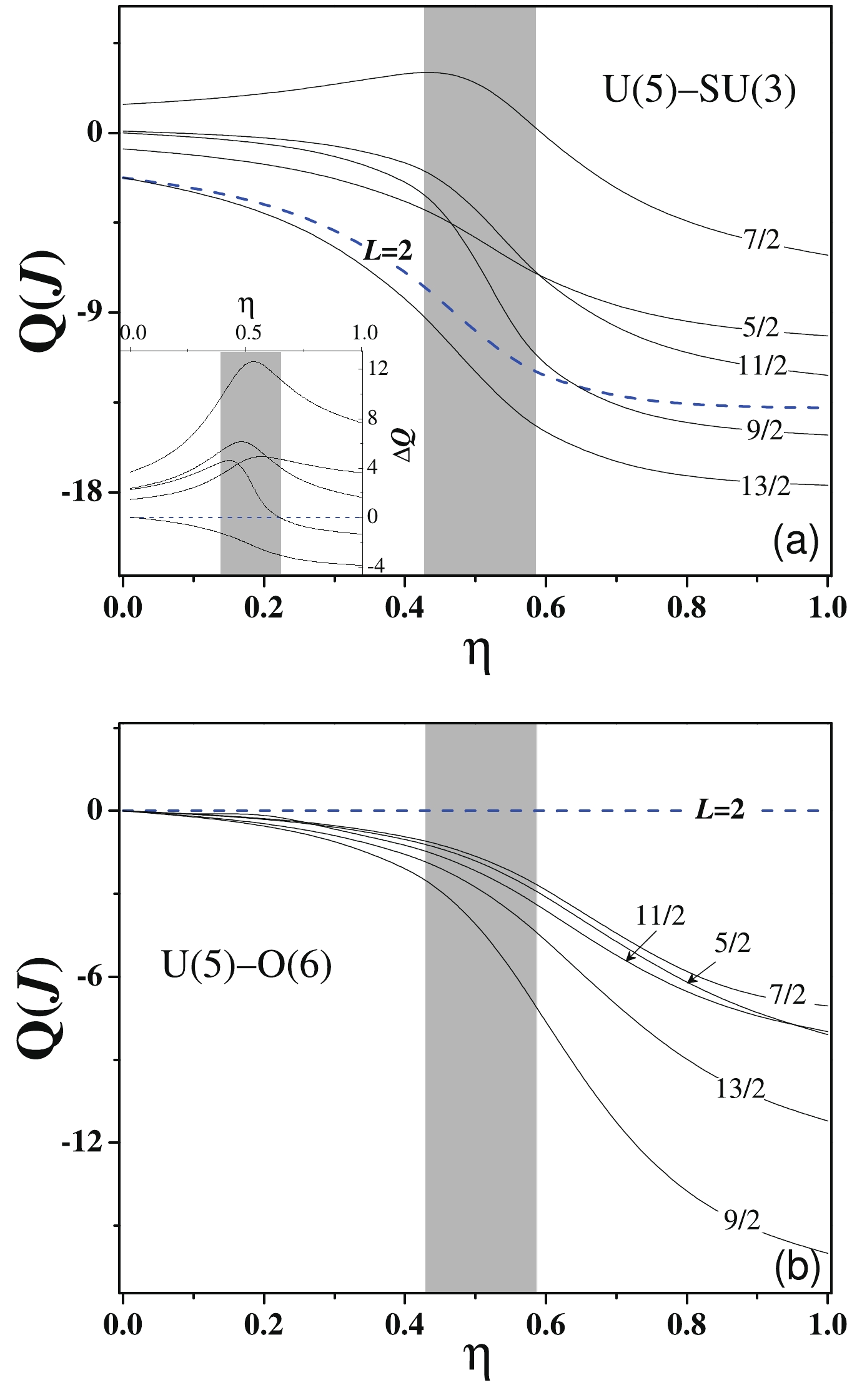
Figure 6. (color online) Quadrupole moments,
$Q(J)$ , evolving as functions of$\eta$ in the two types SPTs. The dashed lines represent the results for the$2_1$ state in the even-even system, and the full lines represent the lowest states with$\mid j-2\mid\leq J\leq j+2$ in the odd-even system. In the calculations, the effective charge in the transitional operator (24) has been set to$e = 1.0$ . The sub-panel shows the odd-even differences of the quadrupole moments defined as$\Delta Q = Q(J_1)-Q(2_1)$ .Finally, we discuss the one-particle-transfer spectroscopic intensities for stripping and pick-up reactions. In leading order, the spectroscopic intensities in the IBFM are described by the square of the one-fermion addition and removal matrix elements [40]. Specifically, we consider the transfer process by adding the even-even system with a
$ j = 9/2 $ fermion to the even-even system or removing a$ j = 9/2 $ fermion from the odd-even system. The corresponding spectroscopic intensities can be calculated using$ I(\mathrm{Even}\rightarrow \mathrm{Odd}) = e_\alpha^2\mid\langle\alpha_fJ_f\parallel a_{9/2}^\dagger\parallel\alpha_iL_i\rangle\mid^2\, $

(30) and
$ I(\mathrm{Odd}\rightarrow \mathrm{Even}) = {e_\alpha^\prime}^2\mid\langle\alpha_f^\prime L_f^\prime\parallel \tilde{a}_{9/2}\parallel\alpha_i^\prime J_i^\prime\rangle\mid^2\,$

(31) where
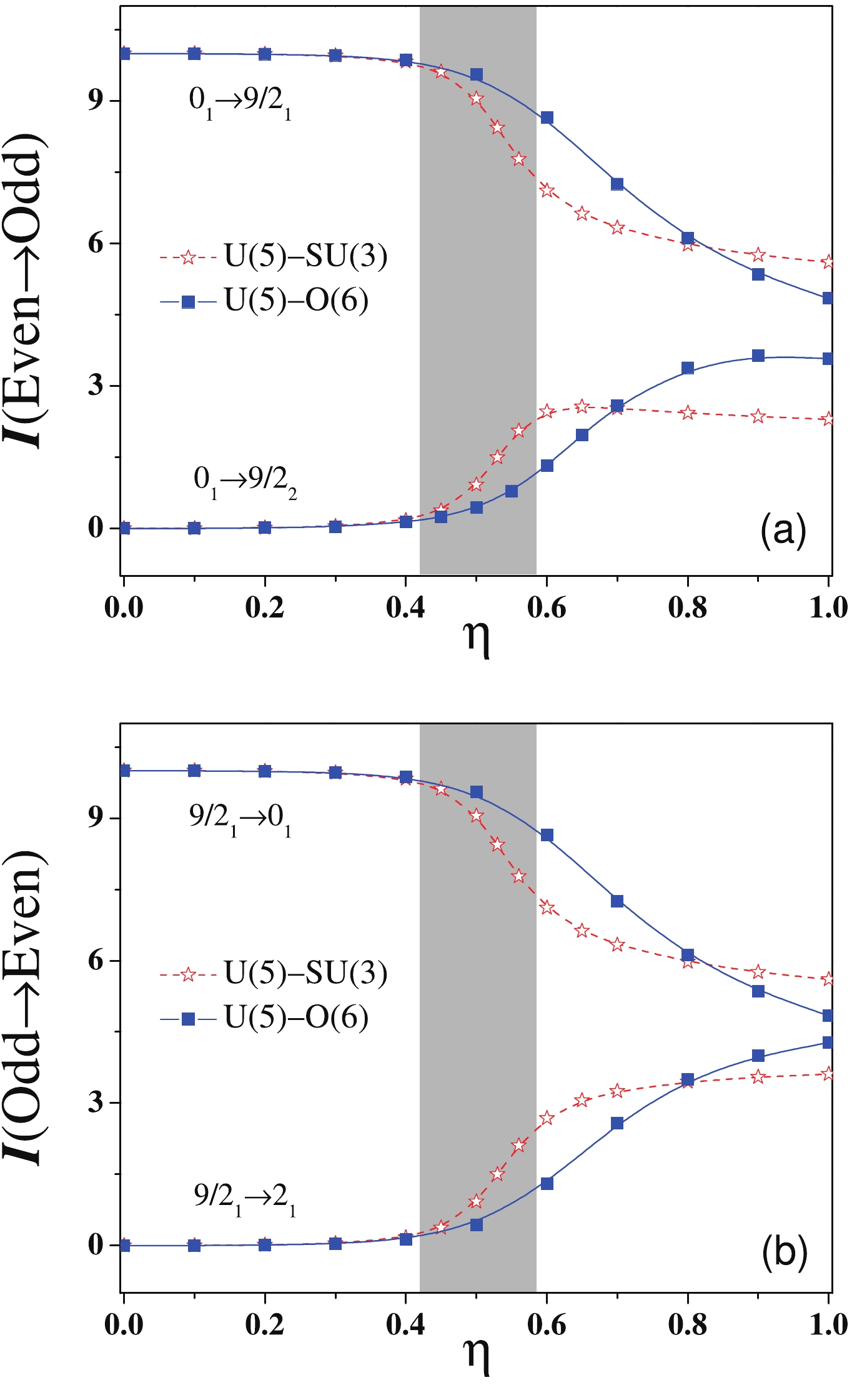
$ e_\alpha (e_\alpha^\prime) $ represents the scale parameter. Clearly, the one-particle-transfer processes can provide a direct connection between the odd-even and even-even systems in a particular SPT.The evolution of one-particle-transfer spectroscopic intensities as a possible signature of the U(5)-O(6) SPT was previously investigated for
$ j = 3/2 $ [19]. Here, we compare the critical features of the spectroscopic intensities in between the U(5)-O(6) and U(5)-SU(3) SPTs. To accomplish this, the calculated results for$ I(0_1\rightarrow9/2_1) $ ,$ I(0_1\rightarrow9/2_2) $ ,$ I(9/2_1\rightarrow0_1) $ and$ I(9/2_1\rightarrow2_1) $ as functions of$ \eta $ are shown in Fig. 7. Fig. 7(a) shows that the intensities for the pick-up reactions,$ I(\mathrm{Even}\rightarrow \mathrm{Odd}) $ , may rapidly either increase or decrease in the critical regions for both the U(5)-SU(3) and U(5)-O(6) SPT but with the transitional signatures in the former being clearly stronger than in the latter. A very similar scenario can be observed in the spectroscopic intensities for stripping reactions,$ I(\mathrm{Odd}\rightarrow \mathrm{Even}) $ , as shown from Fig. 7(b). The results indicate that the evolutions of one-particle-transfer spectroscopic intensities can provide alternative signatures of the SPTs, particularly for the U(5)-SU(3) transition, in addition to those typically used energies and electromagnetic observables. -
A scheme of diagonalizing the IBFM Hamiltonian in terms of the SU(3) coupling basis has been introduced, through which a quantal analysis of the effect of the odd particle on two types of SPTs is performed in the IBFM by comparing the critical behaviors of some select observables. Similar to the even-even systems, we demonstrate that the U(5)-SU(3) and U(5)-O(6) SPTs can also occur in the odd-even system. More importantly, the results indicate that the effects of the odd particle may further strengthen the U(5)-SU(3) transitional features but weaken the U(5)-O(6) ones. This observation closely agrees with the previously classical analysis [24, 25, 34] of the two types of SPTs, thus providing observable proofs of the mean-field predictions. Furthermore, we reveal that the fluctuations of the quadrupole deformations in the odd-even systems become larger when approaching the critical point of the U(5)-SU(3) SPT, which implies the potential for phase coexistence in the critical odd-A nuclei. The paper presents a schematic illustration of the actual scenarios for odd-A nuclei, as the discussions are confined to scenarios with the odd particle being assumed to move in a single j shell. Multi-particle (-hole) in multi-j scenarios may require to be considered for a more general representation, particulalry for searching for the potential phase coexistence in experiments [28]. In addition to the two types of transitions discussed herein, the effects of an odd particle on other types of SPTs (such as the prolate to oblate transition) remain to be studied [16]. Related research is in progress.
Effects of an odd particle on shape phase transitions in odd-even systems
- Received Date: 2021-03-12
- Available Online: 2021-08-15
Abstract: A scheme to solve the Hamiltonian in the interacting boson-fermion model in terms of the SU(3) coupling basis is introduced, through which the effects of an odd particle on shape phase transitions (SPTs) in odd-A nuclei are examined by comparing the critical behaviors of some selected quantities in odd-even and even-even systems. The results indicate that the spherical to prolate (U(5)-SU(3)) SPT and spherical to





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: