-
The four laws of black hole mechanics were initially proposed [1] as mere analogies to the four laws of thermodynamics. The notion of the Bekenstein-Hawking entropy [2-4] provided insights into the microscopic degrees of freedom of black holes. It has an important function in the holographic principle [5, 6] and the AdS/CFT correspondence [7, 8]. From a different perspective, Hawking's approach [9, 10] indicates that black holes emit radiation according to a thermal spectrum, which demonstrates consistency with Bekenstein's results. Wilczek et al. [11, 12] further considered the effect of self-interaction correction to the metric. By employing a semi-classical approximation [12], the related physical process is interpreted as a particle traversing the horizon from inside while moving inward. Mathematically, the interpretation is closely related to the relevant contribution involving only a small interval bounded by the initial and final radii in the immediate vicinity of the horizon [12]. Therefore, the tunneling rate is calculated with respect to the position of the horizon.
The above semi-classical method introduced by Wilczek has incited many subsequent studies (see, e.g., Refs. [13, 14]). Furthermore, it has inspired other approaches [15-18]. Angheben et al. proposed [16] a method of evaluating the imaginary part of the action via the Hamilton-Jacobi equation, which is an extension of the approach by Srinivasan and Padmanabhan [15]. The method can be applied to static metrics, which might be singular at the horizon. Moreover, the proposed procedure is independent of any particular selection of spatial coordinates. However, the formal solution of the Hamilton-Jacobi equation partly relies on the symmetries of a specific metric. Moreover, as the particle's self-gravitation is ignored, the resultant particle emission rate considers only the leading term linear in energy. The method has been examined in the context of a broader class of spacetimes, as well as different types of fields, where consistent results are obtained [17, 19-21].
The particle emission occurring at the horizon of a black hole experiences an effective potential during its course to the spatial infinity. In other words, the resultant spectral flux received by an observer at infinity is further deformed by a frequency-dependent transmission coefficient,
$ \gamma(\omega) $ . To be specific, for an observer located at infinity, the expectation value for the number of a particular particle species of frequency ω is$ \langle n(\omega)\rangle = \frac{\gamma{\omega}}{e^{\beta\omega}\pm 1}\ , $

(1) where β is the inverse of Hawking temperature, and the plus (minus) sign is for fermions (bosons). Here,
$ \gamma(\omega) = \left|\frac{{\cal{T}}}{{\cal{I}}}\right|^2 $

(2) is the greybody factor [22], where
$ {\cal{T}} $ and$ {\cal{I}} $ are the amplitudes of the transmission and incident waves, respectively. However, in literature, the latter is usually defined in the context of an incoming wave from infinity with a known frequency ω, interpreted as the probability of it reaching the horizon of the black hole. Nonetheless, it can be demonstrated [23] that the above probability coincides with that of an outgoing wave in the mode ω to escape to infinity through the effective potential of the black hole. Therefore, Wilczek's perspective of Hawking radiation measures the tunneling probability the barrier penetration governed by the black hole metric. In asymptotically flat spacetimes, it is directly associated with the S-matrix element.At small frequencies, analytical results on the greybody factor can be obtained using the perturbative approach [24]. In contrast, for frequencies with a large imaginary part, the monodromy method [25] has been utilized [23, 26]. Estimations on the bound of the greybody factor have also been conducted [27]. However, generally, as the forms of the effective potentials are rather complicated, the exact solution for a particular metric is not straightforward. As a result, numerical approaches are usually used.
This study involves an attempt to numerically investigate the Hawking radiation and the frequency-dependent transmission coefficient in Reissner-Nordström black hole spacetimes. The remainder of the paper is organized as follows. In Section II, we briefly review the Hawking radiation on the horizon of a black hole. The frequency-dependent transmission coefficient is obtained numerically for various types of fields in Section III. Additional discussions and concluding remarks are provided in the final section.
-
In this section, we briefly review the Hawking radiation at the horizon of a Reissner-Nordström black hole in terms of the Hamilton-Jacobi method [16]. The background n dimensional metric and electromagnetic potential are expressed as
$ \begin{aligned}[b] {\rm d}s^2 =& -f(r){\rm d}t^2+\frac{{\rm d}r^2}{f(r)}+r^2 {\rm d}\Omega_{n-2} \\ {\rm d}A =& A_t(r){\rm d}t, \end{aligned} $

(3) where
$f = 1-\dfrac{8\Gamma((n-1)/2)M}{(n-2)\pi^{(n-3)/2}r^{n-3}}+\dfrac{4\Gamma((n-1)/2)Q^2r^{2(3-n)}}{(n-2)(n-3)\pi^{(n-3)/2}}$

and
$ A_t = \dfrac{Qr^{3-n}}{(3-n)} $ .${\rm d}\Omega_{n-2}$ is a$ n-2 $ dimensional unit sphere. M and Q are the mass and charge of the black hole, respectively. The event horizon$ r_h $ and inner horizon$ r_i = br_h $ satisfy the relationship$ M = \dfrac{(n-2)\pi^{(n-3)/2}(1+b^{n-3})}{8\Gamma((n-1)/2)}r_h^{n-3} $ and
$Q = \dfrac{b^{n-3}(n-2)\pi^{(n-3)/2}}{2\Gamma((n-3)/2)}r_h^{2(n-3)} .$ As a semi-classical approximation, the dynamics of particles with various spin satisfy the Hamilton-Jacobi equation [15, 16, 19-21], namely,
$ g^{\mu\nu}\left(\frac{\partial S}{\partial x^\mu}-qA_\mu\right)\left(\frac{\partial S}{\partial x^\nu}-qA_\nu\right)+m^2 = 0 , $

(4) where m and q are the mass and charge of a particle, respectively. For a static four-dimensional metric, we may seek a solution in the form
$ S = -\omega t+R(r)+Y(\theta,\phi,\cdot\cdot\cdot) . $

(5) By substituting the specific forms of the metric and electromagnetical potential into the above equation, we obtain the following radial equation after separating the variables:
$ -\frac{1}{f}\left(\omega+qA_t\right)^2+fR'^2+m^2 = \frac{\lambda}{r^2} , $

(6) where λ is a constant. Therefore, near the event horizon, we obtain
$ \begin{aligned}[b] R =& \int {\rm d}r \frac{\sqrt{(\omega-\omega_h)^2-f(r)(m^2-\lambda/r^2)}}{f(r)} \\& \to \int \frac{{\rm d}\sigma}{\sigma}\frac{2\sqrt{(\omega-\omega_h)^2-f'(r_h)(r-r_h)(m^2-\lambda/r^2)}}{f'(r_h)} , \end{aligned} $

where
$ \omega_h = -qQ/r_h.\quad \sigma = \int\dfrac{{\rm d}r}{\sqrt{f}} = \dfrac{2\sqrt{r-r_h}}{\sqrt{f'(r_h)}}$

is the leading contribution of the invariant distance. The integral is calculated by deforming the contour to avoid the singularity at the horizon, which picks up half a residue:
$ \Im S = \Im R = \frac{2\pi(\omega-\omega_h)}{f'(r_h)} . $

(7) Note that the result is invariant with respect to time recalibration and spatial diffeomorphism [16]. Subsequently, the quantum tunneling rate from horizon is expressed as
$ \Gamma = \exp\left(-2\Im S\right) = \exp\left(-4\pi\frac{\omega-\omega_h}{f'(r_h)}\right) $

(8) and the Hawking temperature at the horizon is
$ T_h = \frac{f'(r_h)}{4\pi}. $

(9) Here, the Hawking radiation is purely thermal.
In the following, we evaluate the function of the effective potential on the resultant spectral flux, as the emitted particle further penetrates the barrier toward an observer at spatial infinity.
-
For a non-rotating metric, the equation of motion of various fields can be usually simplified using the method of separation of variables, and the radial part of the resultant field equation is
$ \frac{{\rm d}^2\Psi}{{\rm d}r_*^2}+\left((\omega+qA_t)^2-V(r)\right) = 0 . $

(10) The above equation is a Schrodinger-type one, where
$r_* = \int {\rm d}r/f$ is the tortoise coordinate, and V, which is the effective potential, is governed by the specific spacetime and particle state. For asymptotically flat spacetimes,$ V(r\rightarrow r_h) = 0 $ and$ V(r\rightarrow\infty) = V_\infty $ ; therefore, the solutions assume the following asymptotic forms at the horizon and infinity [22]:$ \Psi\sim \begin{array}{c} {\cal{R}}{\rm e}^{-{\rm i}k_Hr_*}+{\cal{I}}{\rm e}^{{\rm i}k_Hr_*} \;\; r\rightarrow r_h ,\\ {\cal{T}}{\rm e}^{{\rm i}k_\infty r_*}+{\cal{A}}{\rm e}^{-{\rm i}k_\infty r_*} \;\; r\rightarrow \infty .\\ \end{array} $

(11) The equation of motion implies that the Wronskians
$ \begin{aligned}[b] W(r\rightarrow r_h) =& -2{\rm i}k_h(\left|{\cal{R}}\right|^2-\left|{\cal{I}}\right|^2), \\ W(r\rightarrow \infty) =& 2 {\rm i} k_\infty(\left|{\cal{T}}\right|^2-\left|{\cal{I}}\right|^2), \end{aligned} $

(12) are conserved; thus, we obtain the following relationship:
$ \left|{\cal{T}}\right|^2-\left|{\cal{A}}\right|^2 = -\frac{k_H}{k_\infty}(\left|{\cal{R}}\right|^2-\left|{\cal{I}}\right|^2). $

(13) For the scenario in this paper, the incident wave propagates outward with amplitude
$ {\cal{I}} $ , and we also require that$ {\cal{A}}\equiv0 . $

(14) For a massless scalar field, the relevant effective potential in the Reissner-Nordström spacetime can be derived from the Klein Gordon equation, which is
$ V = \frac{f}{r^2}\left[l(l+n-1)+\frac{n-2}{2}rf'+\frac{(n-4)(n-2)}{4}f\right] , $

(15) where l is the orbital quantum number of the particle state.
Here, the problem is reduced to that of the one-dimensional barrier penetration. To obtain the transmission coefficient, we resort to solving Eq. (10) numerically with the boundary conditions Eqs. (11) and (14).
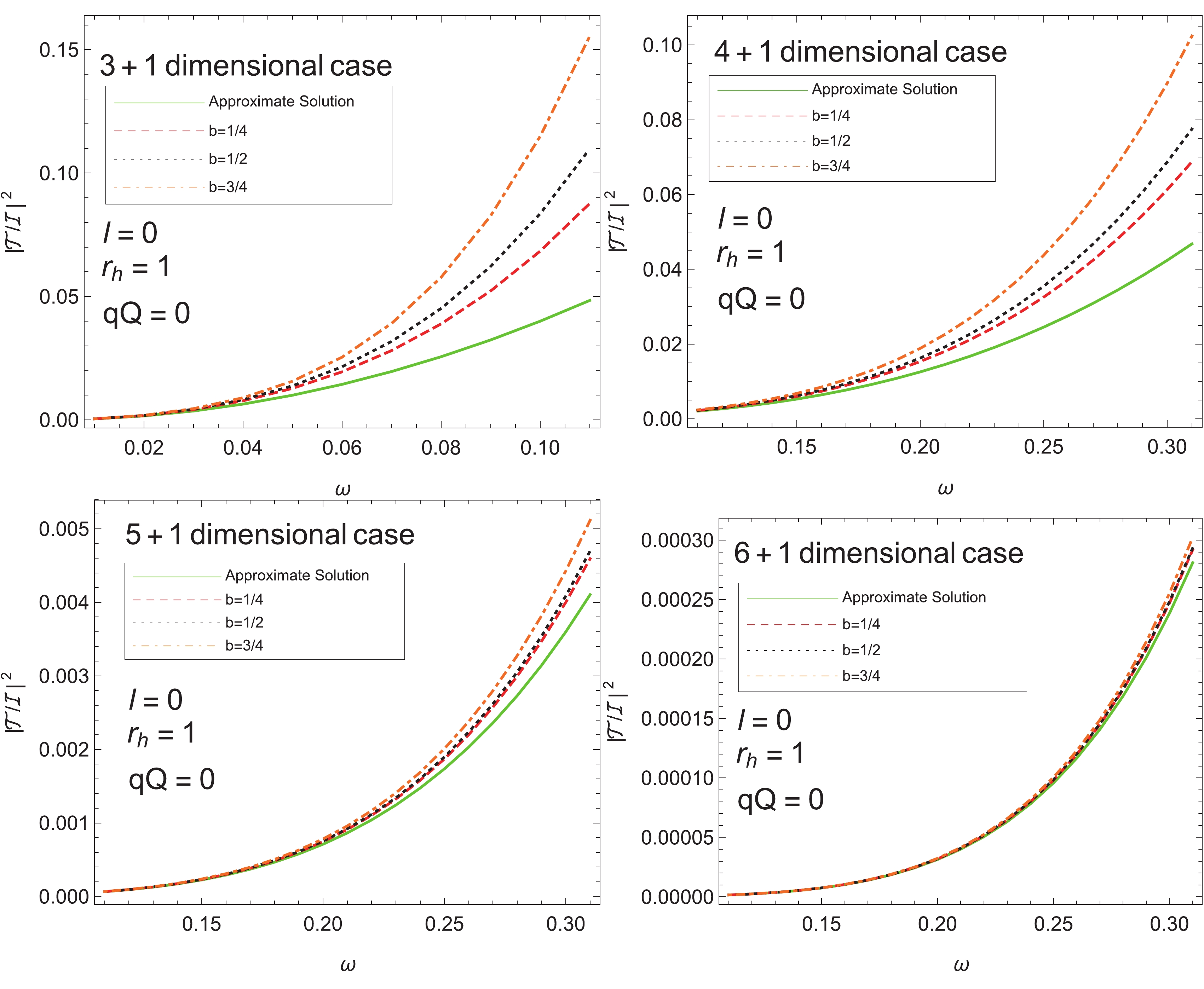
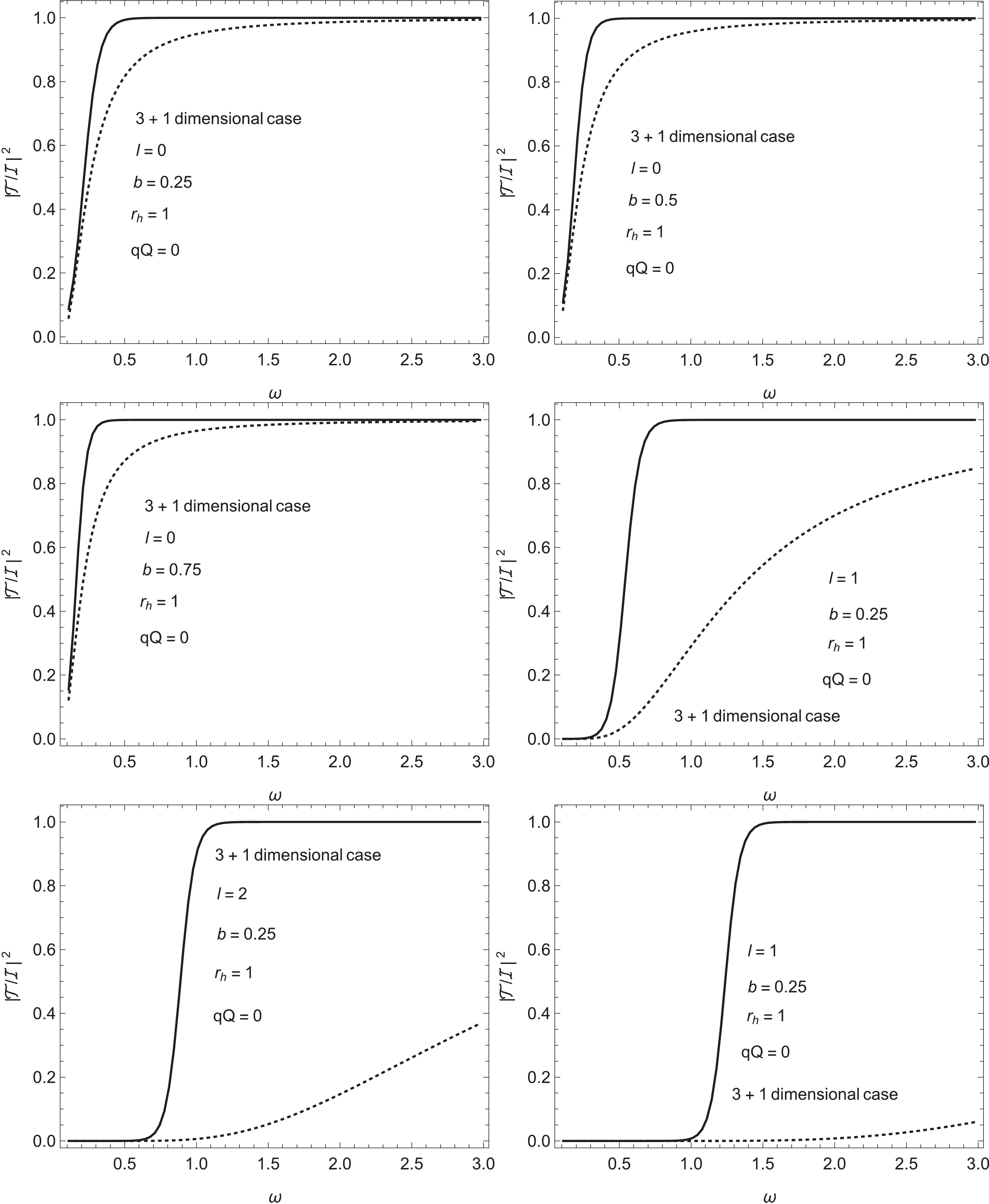
In this study, we use an approach based on numerical integration. We have provided the technical details of the numerical scheme in the appendix, and the results are shown in Figs. 1-6.

Figure 1. (color online) Calculated transmission coefficient
$ \left|\frac{{\cal{T}}}{{\cal{I}}}\right|^2 $ for a massless scalar field as a function of the frequency ω for different values of b. The calculations are performed with$ r_h = 1 $ ,$ qQ = \frac{1}{8} $ , and$ l = 0 $ .
Figure 3. (color online) Same as Fig. 1 for different values of l. The calculations are performed with
$ r_h = 1 $ ,$ qQ = \frac{1}{8} $ , and$ b = \frac{1}{4} $ .
Figure 5. (color online) Calculated transmission coefficient
$ \left|\frac{{\cal{T}}}{{\cal{I}}}\right|^2 $ for a massless scalar field as a function of qQ for different values of b. The calculations are performed with$ r_h = 1 $ ,$ \omega = 1 $ , and$ l = 0 $ .
Figure 6. (color online) Calculated transmission coefficient
$ \left|\frac{{\cal{T}}}{{\cal{I}}}\right|^2 $ for a massless scalar field as a function of qQ for different values of l. The calculations are performed with$ r_h = 1 $ ,$ \omega = 1 $ , and$ b = \frac{1}{4} $ .Figs. 1-4 show the resultant transmission coefficient as a function of the frequcency,
$ \left|\frac{{\cal{T}}}{{\cal{I}}}\right|^2 $ vs. ω, for a massless scalar field. The calculations are performed by varying the parameter of the metric b and the orbital quantum number l. We observe that the transmission coefficient monotonically increases with increasing frequency. As shown in Fig. 2, the values are in agreement with universal analytic results [23, 28] in the low frequency region$ \omega \ll T_h $ and$ \omega r_h \ll 1 $ , as it increases from zero where the frequency vanishes. The physical interpretation is that at very low frequencies, the size of the wavelength is significantly larger than that of a black hole. Therefore an incident wave from infinity is virtually unaffected by the presence of the latter. In contrast, the transmission coefficient eventually saturates to a certain value at the limit of high frequency. In Fig. 4, the obtained results are also compared against the lower bound estimated in Ref. [27]. As shown in Figs. 1 and 3, for four dimensions, we observe that resultant transmission coefficients all converge to the same curve for given$ r_h $ and qQ values and different values of b and l. However, for higher-dimensional scenarios, the convergence becomes more gradual. Moreover, the difference between states with different b and l becomes more significant.In Figs. 5 and 6, we investigate the transmission coefficient as a function of the product of the charge of the particle and the black hole qQ. For all the scenarios, the transmission rate is observed to be a monotonically decreasing function of qQ. The dependence is mostly linear for the given b value and for
$ l = 0 $ . For larger l values, the curves exhibit twisted characteristics, and in the four-dimensional scenario, they are observed to converge eventually. In particular, for$ qQ<0 $ , as the magnitude becomes more significant, the transmission coefficient further increases and eventually exceeds 1. In other words, the resultant spectral flux is amplified by the effective potential. This characterisitc is reminiscent of the superradiance [29], which occurs when the frequency is less than a particular value related to the charge of the black hole. By comparing the results for different spacetime dimensions, we observe that the difference between states with different b and l becomes more pronounced for higher dimensional spacetimes. The slope of the monotonical dependence decreases as l increases, and it becomes more evident as the dimension of spacetime increases. For example, for the$ 5+1 $ and$ 6+1 $ metrics, the transmission coefficient of$ l = 0 $ increases mostly linearly with decreasing qQ, except that the slope for$ 5+1 $ is larger. However, the corresponding slopes for the scenarios with$ l = 1, 2, 3 $ are much less significant compared with the former. -
In summary, we have studied the Hawking radiation in the Reissner-Nordström black hole spacetime for an observer located at infinity. We have evaluated the frequency-dependent transmission coefficient after discussing the thermal radiation emitted in the vicinity of the horizon. We have observed that the transmission coefficients approaches zero as the frequency of the emitted particle vanishes. It is a monotonically increasing function of the frequency and saturates when the frequency is more significant. In four-dimensional spacetime, this feature is demonstrated to be mostly independent of the parameters for particular
$ r_h $ and qQ values. For higher-dimensional spacetimes, the difference between states with different b and l becomes more pronounced. In particular, we observe that the transmission coefficient exceeds 1 when$ qQ<0 $ and the magnitude becomes sufficiently large. This indicates that the spectral flux is further amplified during the course of traversing the curved spacetime. -
This method was initially used to calculate superradiance [22]. For this study, it can be readily adapted for the numerical calculations. The code is implemented in terms of the Mathematica notebook. For the aims of this paper, we introduce the following adaptations. First, we rewrite the radial equation using the coordinate transform
$ x = 1-\dfrac{r_h}{r} $ , such that$ x = 1 $ as$ r\rightarrow\infty $ and$ x = 0 $ as$ r = r_h $ . By expanding the function at$ x = 0 $ and$ x = 1 $ , we can numerically integrate the Schrodinger-type equation from the region near$ x = 0 $ to that near$ x = 1 $ . The code's efficiency lies in its significant accuracy of the numerical implementation for integration in Mathematica.
Hawking radiation received at infinity in higher dimensional Reissner-Nordström black hole spacetimes
- Received Date: 2021-04-30
- Available Online: 2021-08-15
Abstract: In this study, we investigate the Hawking radiation in higher dimensional Reissner-Nordström black holes as received by an observer located at infinity. The frequency-dependent transmission rates, which deform the thermal radiation emitted in the vicinity of the black hole horizon, are evaluated numerically. In addition to those in four-dimensional spacetime, the calculations are extended to higher dimensional Reissner-Nordström metrics, and the results are observed to be sensitive to the spacetime dimension to an extent. Generally, we observe that the transmission coefficient practically vanishes when the frequency of the emitted particle approaches zero. It increases with frequency and eventually saturates to a certain value. For four-dimensional spacetime, the above result is demonstrated to be mostly independent of the metric's parameter and the orbital quantum number of the particle, when the location of the event horizon,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: